Tampering Detection in Absolute Moment Block Truncation Coding (AMBTC) Compressed Code Using Matrix Coding

Abstract

With the increasing use of digital image compression technology, ensuring data integrity and security within the compression domain has become a crucial area of research. Absolute moment block truncation coding (AMBTC), an efficient lossy compression algorithm, is widely used for low-bitrate image storage and transmission. However, existing studies have primarily focused on tamper detection for AMBTC compressed images, often overlooking the integrity of the AMBTC compressed code itself. To address this gap, this paper introduces a novel anti-tampering scheme specifically designed for AMBTC compressed code. The proposed scheme utilizes shuffle pairing to establish a one-to-one relationship between image blocks. The hash value, calculated as verification data from the original data of each block, is then embedded into the bitmap of its corresponding block using the matrix coding algorithm. Additionally, a tampering localization mechanism is incorporated to enhance the security of the compressed code without introducing additional redundancy. The experimental results demonstrate that the proposed scheme effectively detects tampering with high accuracy, providing protection for AMBTC compressed code.

1. Introduction

Digital images are ubiquitous in our daily life. Numerous digital images are transmitted over the Internet and stored on various devices every day. To reduce transmission and storage costs, compression technology is widely used for digital images. Image compression techniques can be categorized into lossless and lossy compressions. Lossless compression allows for the perfect restoration of images, whereas lossy compression does not, though it can still maintain visual quality. One such technique is absolute moment block truncation coding (AMBTC) [1], an effective lossy compression method that has been widely used in recent decades. Due to its low computational complexity, AMBTC is widely applied in various low-bandwidth scenarios. Although many modern microcontrollers are equipped with hardware codecs capable of compressing real-time video streams at low bitrates, such hardware is not always available or suitable, especially in energy-constrained or cost-sensitive environments. In scenarios like battery-powered IoT nodes or systems focusing on still-image storage rather than continuous video transmission, lightweight compression algorithms such as AMBTC remain highly practical. Image compression plays a vital role in efficient storage and transmission, particularly in applications such as social media, video communication, telemedicine, the Internet of Things [2,3], and robotics [4]. Lossy compression is widely adopted as it achieves high compression ratios while preserving visual quality. With the increasing demand for these applications, ensuring data integrity and security has become increasingly important.

Data hiding [5,6,7,8,9], also known as steganography [10,11,12,13,14], is an effective information security technique that embeds information into various carriers, including images, videos, audio, and text [15,16,17,18]. To detect tampering, verification data [19,20,21,22,23,24] or fragile watermarks [25,26,27] are typically embedded in the carrier. Deep learning-based methods [28], particularly techniques such as CNNs [29] and transformers [30], have been applied to tampering detection. However, traditional methods remain more practical in many resource-constrained environments. Despite AMBTC’s many advantages, existing security research has primarily focused on detecting tampering in AMBTC compressed images rather than safeguarding the compressed code itself. Since image integrity depends on the correctness of the compressed code, addressing this level of security is crucial. In 2013, Hu et al. [31] proposed a joint image coding and authentication scheme based on AMBTC, in which authentication data are generated using a pseudo-random sequence and embedded in a bitmap. In 2016, Li et al. [32] introduced a new image authentication scheme that embeds authentication codes into each compressed image block using a reference matrix to protect image integrity. In 2018, Chen et al. [23] addressed the weaknesses of Li et al.’s scheme [32], enhancing the detection rate while maintaining image quality. In the same year, Hong et al. [33] symmetrically perturbed the most significant bits of two quantization levels to generate authentication code candidates. The authentication codes were then embedded in the least significant bits of the two quantization levels to minimize distortion. Hong et al. [34] also proposed generating authentication codes using bitmap and location information. These codes were embedded into the quantization levels via adaptive pixel pair matching, significantly reducing distortion and improving authentication performance. In 2023, Zhou et al. [35] classified blocks as smooth or complex and employed a dual embedding strategy: authentication codes were embedded in the bitmaps of smooth blocks and the quantized values of complex blocks, enhancing image quality.

However, previous schemes have primarily focused on the pixel level, with most simulating cropping attacks or collage attacks for experimental evaluation. This paper proposes a tampering detection scheme at the bit level, which simulates both flipping attacks and block scrambling attacks. Specifically, we use shuffle pairing to establish a one-to-one correspondence between image blocks. A portion of the current block’s bitmap is combined with its quantized values and input into a hash function to generate verification data. The matrix coding [36] algorithm is then used to embed these data into the bitmap of the paired block. During decoding, the verification data generated by the current block’s hash function is compared with the verification data retrieved from the paired block via the matrix coding algorithm to detect tampering and accurately locate the modified area. The key contributions of this paper are as follows:

• Unlike previous tampering detection schemes for AMBTC images, we propose a scheme targeting AMBTC compressed code, focusing on tampering at the bit level.
• The proposed scheme employs matrix coding to embed verification data, maintaining the original file size while preserving visual quality.
• The experimental results show that the proposed scheme achieves an almost 100% detection rate for both flipping and block scrambling attacks, with a 0% false alarm rate and 100% precision, demonstrating superior performance.

The remainder of this paper is structured as follows: Section 2 reviews the AMBTC compression and the matrix coding method. Section 3 details the proposed tampering detection scheme for AMBTC compressed code. Section 4 evaluates the experimental results. Section 5 summarizes the proposed scheme.

2. Related Work

This section reviews two algorithms: absolute moment block truncation coding, which is used for compression, and matrix coding, which is applied in steganography.

2.1. Absolute Moment Block Truncation Coding

In 1984, Lema and Mitchell [1] proposed the absolute moment block truncation coding, which has been widely used in the field of image compression in recent decades. The AMBTC algorithm divides the original image into blocks of size $n\times n$, typically $4\times 4$, calculates the average value of each block, and marks each pixel as 0 if its value is less than the average, or as 1 if it is greater or equal to the average, thus obtaining a bitmap. The average value of the pixels marked as 0 is then calculated and recorded as the low value, while the average value of the pixels marked as 1 is calculated and recorded as the high value. After processing all blocks, the bitmap, low value, and high value of each block constitute the AMBTC compressed code. When reconstructing the image, one simply needs to traverse all blocks. Based on the bitmap, if the value is 0, it is reconstructed with the low value; if it is 1, it is reconstructed with the high value, thus obtaining the AMBTC compressed image.

2.2. Matrix Coding

A matrix coding algorithm [36], initially introduced by Chang et al. in 2008, employs a parity check matrix $H$, as shown in Equation (1). Consider a 7-dimensional cover vector $v=\left[1010100\right]$ and a secret message $m=\left[110\right]$. By applying Equation (2), the syndrome is computed as $Syndrome=m\oplus Hv=\left[110\right]\oplus \left[111\right]=\left[001\right]$. This syndrome is then referenced in

Table 1. Cosets of the matrix coding with the parity check matrix $H$.

$Syndrome$	000	001	010	011	100	101	110	111
$Cosetleader$	0000000	1000000	0100000	0010000	0001000	0000100	0000010	0000001

to identify the corresponding coset leader, which is $\left[1000000\right]$. Using Equation (3), the stego vector $v^{\prime }$ is determined as $v^{\prime }=v\oplus Coset Leader=\left[1010100\right]\oplus \left[1000000\right]=\left[0010100\right]$. In essence, the data embedding process modifies a single bit in the cover vector $v$ based on the coset leader associated with the calculated syndrome. The extraction process is relatively straightforward: by applying Equation (4), the secret message $m^{\prime }$ can be recovered as $m^{\prime }=H{v}^{\prime }=\left[110\right]$.

$$H=\left[\begin{array}{c}0\\ 0\\ 1\end{array} \begin{array}{c}0\\ 1\\ 0\end{array} \begin{array}{c}0\\ 1\\ 1\end{array} \begin{array}{c}1\\ 0\\ 0\end{array} \begin{array}{c}1\\ 0\\ 1\end{array} \begin{array}{c}1\\ 1\\ 0\end{array} \begin{array}{c}1\\ 1\\ 1\end{array}\right].$$

(1)

$$Syndrome=m\oplus Hv.$$

(2)

$$v^{\prime }=v\oplus Coset leader.$$

(3)

$$m^{\prime }=H{v}^{\prime }.$$

(4)

3. Proposed Scheme

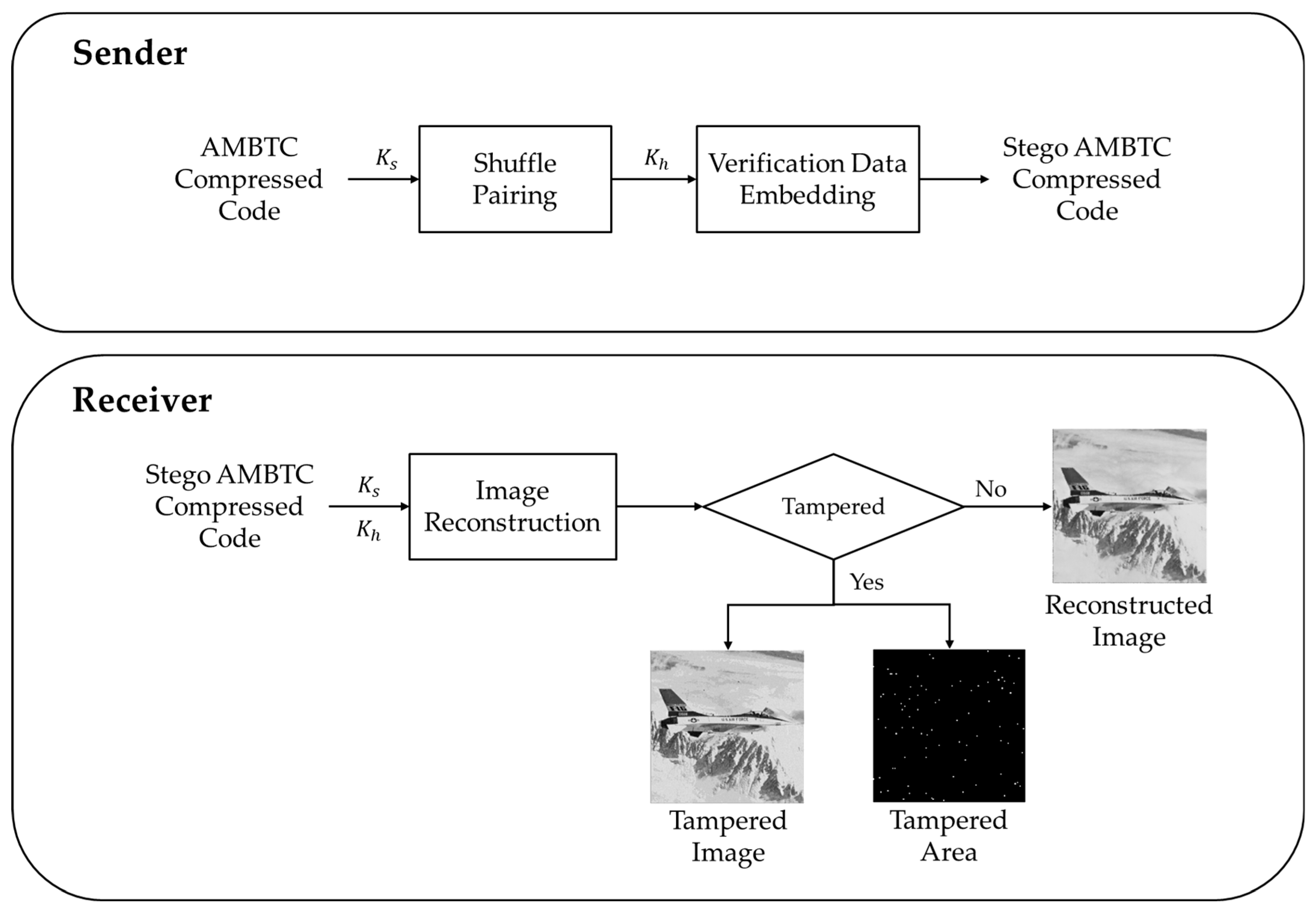
This section elaborates on the proposed matrix coding-based tampering detection scheme in AMBTC compressed code. Figure 1 illustrates the flow of the proposed scheme. For the sender, the image block information is derived from the AMBTC compressed code, and the shuffle key $K_s$ is used to perform a pseudo-random shuffle pairing, ensuring a one-to-one correspondence between the blocks. The original data of the image block is then input into the hash function with the hash key $K_h$ as the seed, generating the verification data. The matrix coding algorithm is then applied to embed the verification data into the bitmap of the paired block. After processing all blocks, the stego AMBTC compressed code is obtained. For the receiver, upon receiving the stego AMBTC compressed code, the block pairing relationship is retrieved using the shuffle key $K_s$. The verification data of the embedded original data are extracted from the bitmap of the paired block using matrix coding. The verification data of the received data are then calculated using the hash key $K_h$. If the two verification datasets match, the reconstructed image is output. If they are inconsistent, it indicates tampering, and the tampered image and tampered area are output.

3.1. Shuffle Pairing

We employ the shuffle pairing strategy to establish a one-to-one correspondence between image blocks while preventing block scrambling attacks. Initially, all image block indices are collected and subjected to a pseudo-random shuffle, with the shuffle key $K_s$ serving as the seed. The shuffled sequence is then evenly divided into two subsequences, where indices at corresponding positions are paired to form a unique mapping. During subsequent operations, each block is linked to another according to this mapping, ensuring that the total number of pairs is half the total number of image blocks. Since embedding a block’s verification data within themselves would make it insensitive to block scrambling attacks, thus failing to detect tampering, the data must instead be stored in their paired block. This way, any modification that alters the pairing index will cause a mismatch in the verification data, enabling the detection of unauthorized modifications.

3.2. Verification Data Embedding

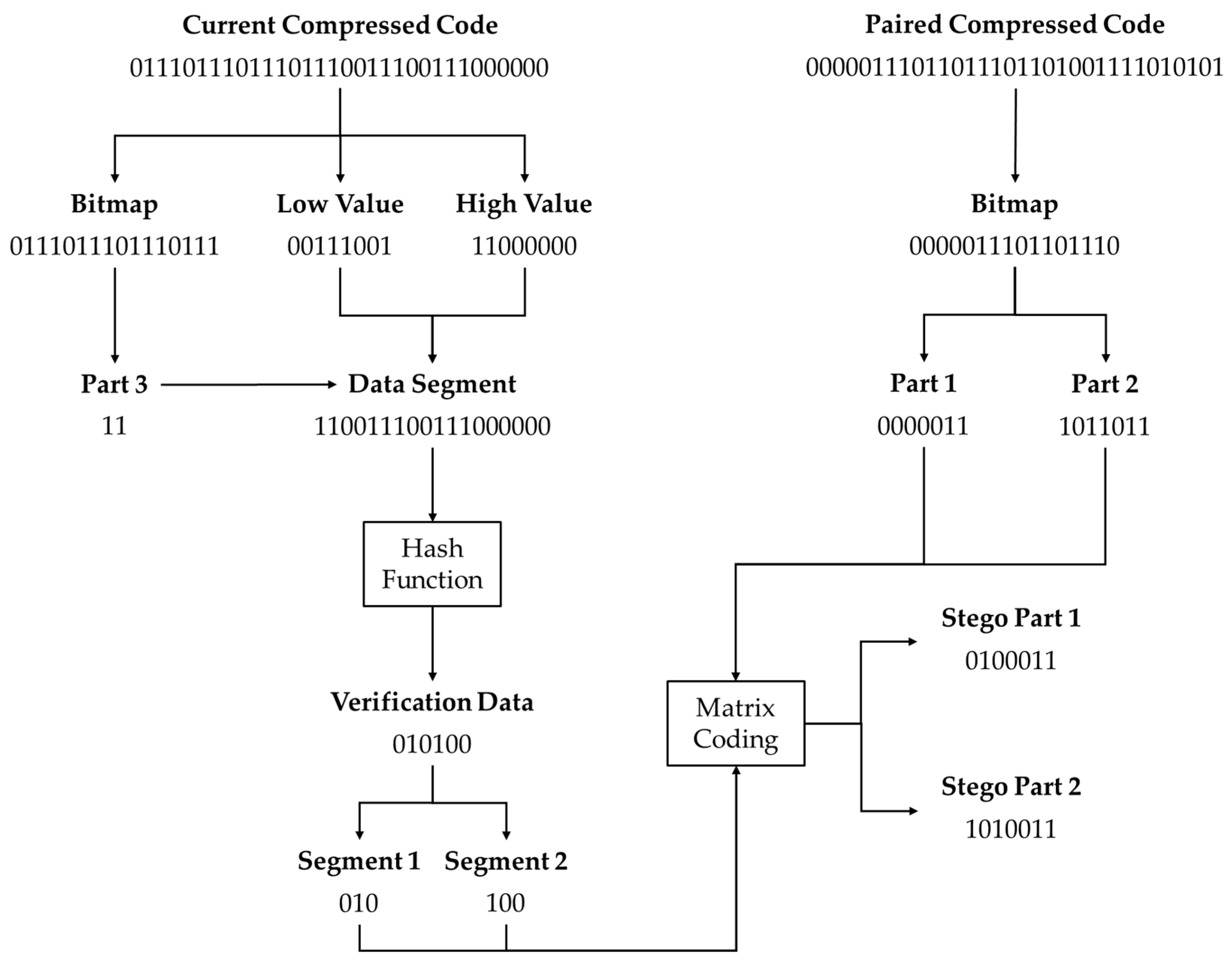
In the proposed scheme, a $4\times 4$ AMBTC compressed code is used as a basic example, where each image block contains a 32-bit compressed code consisting of a 16-bit bitmap, an 8-bit low value, and an 8-bit high value. The bitmap is sequentially divided into three parts of 7 bits, 7 bits, and 2 bits, referred to as Part 1, Part 2, and Part 3, respectively. For each image block, Part 1 and Part 2 of the bitmap are used to embed verification data, while the remaining data are used to generate the verification data. Specifically, Part 3 of the bitmap, together with the low value and the high value, forms an 18-bit data segment. These 18-bit data are then input into a hash function, with the hash key $K_h$ as the seed, to generate 6 bits of verification data. The 6-bit verification data are split into two 3-bit segments and embedded into Part 1 and Part 2 of the bitmap of the paired block using the matrix coding algorithm. Specifically, Part 1 and Part 2 are both 7 bits in length. They serve as the input vectors for the matrix coding algorithm, while the two 3-bit verification segments act as the message for the algorithm, generating two stego vectors. These two stego vectors are then separately overwritten into Part 1 and Part 2 to complete the embedding process.

To further illustrate the details of the verification data embedding, a comprehensive example is provided in Figure 2. The compressed code being processed is referred to as the current compressed code (01110111011101110011100111000000), which is 32 bits long and consists of a 16-bit bitmap (0111011101110111), an 8-bit low value (00111001), and an 8-bit high value (11000000). The bitmap is divided into three parts of 7 bits, 7 bits, and 2 bits, respectively. In the verification data generation stage, only the 2-bit Part 3 (11) is required, which is concatenated with the low value and the high value to form an 18-bit data segment (110011100111000000). This data segment is then fed into the hash function to generate 6-bit verification data (010100), which are further split into two 3-bit segments, namely Segment 1 (010) and Segment 2 (100). Next, according to the pairing relationship established in the shuffle pairing phase, the paired compressed code (000001110110110101001111010101) is identified, and its 16-bit bitmap (0000011101101110) is extracted. This bitmap is also divided into three parts, but only Part 1 (0000011) and Part 2 (1011011) are used in the subsequent embedding process. These parts serve as input vectors for the matrix coding algorithm, while Segment 1 (010) and Segment 2 (100) act as messages. Applying the matrix coding algorithm yields the outputs stego Part 1 (0100011) and stego Part 2 (1010011), which are then overwritten into their corresponding positions within the bitmap to form the paired stego compressed code. It should be noted that the hash function used in this scheme can be flexibly chosen based on specific requirements, as long as it accepts an 18-bit input and produces a 6-bit output. Alternatively, a standard hash function with a larger output size may be used, retaining only the first 6 bits of the result for verification. Common choices include MD5 [37], SHA-256 [38], and BLAKE2 [39]. BLAKE2 natively supports keyed hashing through its built-in key mechanism, while MD5 and SHA-256 require integration with HMAC [40] to achieve the same functionality.

Following the above processing flow, the complete AMBTC stego compressed code is obtained after traversing and processing all image blocks.

3.3. Image Reconstruction and Tampering Detection

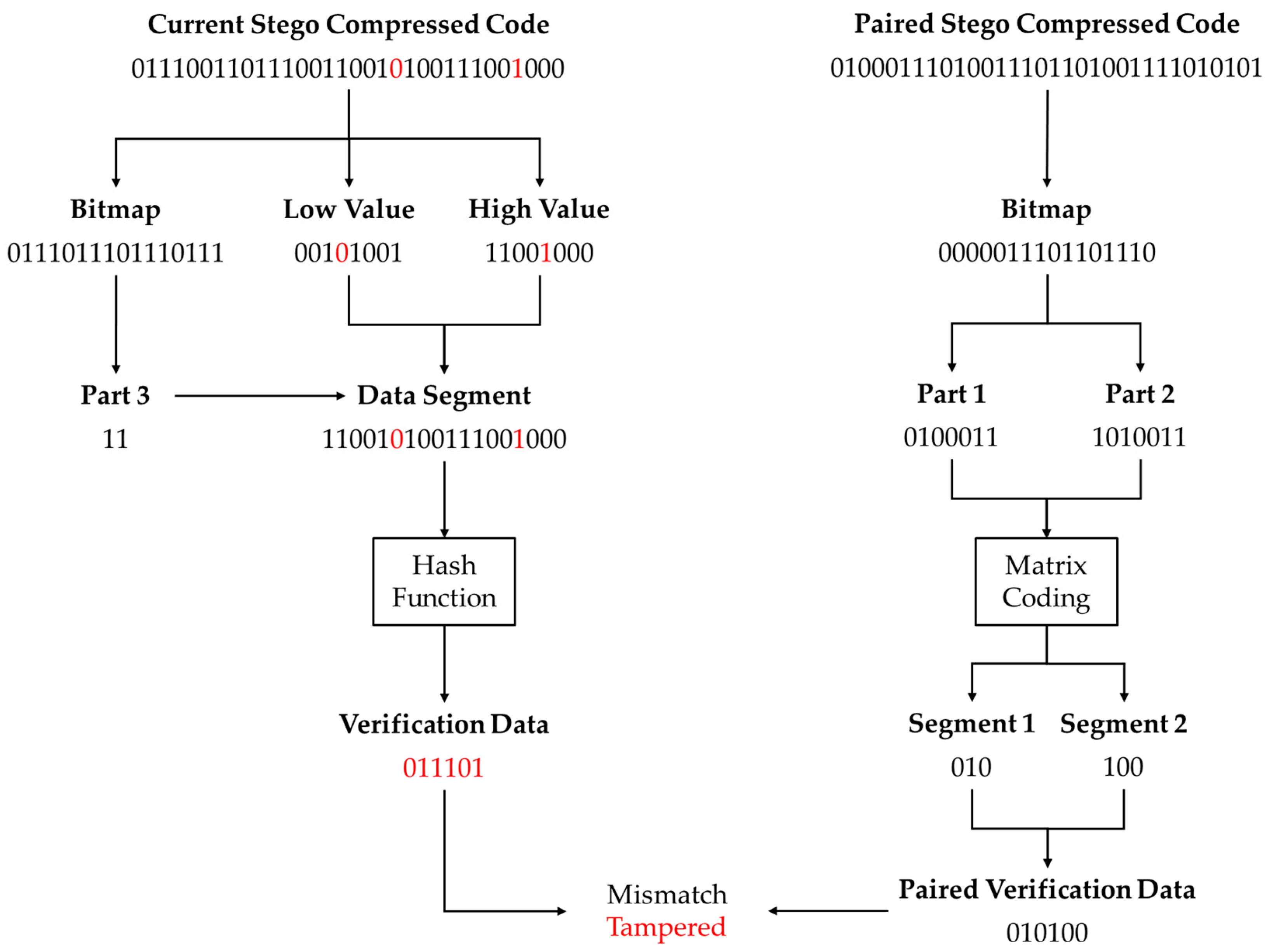
In the proposed scheme, the legitimate receiver holds the shuffle key $K_s$ and the hash key $K_h$. Upon receiving the stego AMBTC compressed code, it first uses the shuffle key $K_s$ as the seed to perform shuffle pairing and determine the block pairing relationship. It then proceeds with the verification process. Specifically, as in the embedding stage, each block’s compressed code consists of 32 bits, with its 16-bit bitmap being split. Part 3 of the bitmap is combined with the 8-bit low value and the 8-bit high value to form an 18-bit data segment, which is then fed into the hash function with $K_h$ as the seed to generate 6-bit verification data. Next, the bitmap is extracted from the paired stego compressed code, and its first and second parts are separately used as input vectors for the decoding algorithm of matrix coding to retrieve Segment 1 and Segment 2, respectively. These segments are then combined to reconstruct the 6-bit paired verification data. By comparing the verification data with the paired verification data, any mismatch indicates that the pair of blocks has been tampered with.

Figure 3 provides a specific example to illustrate this process, where the red mark in the figure indicates the tampered bit. First, the 32-bit current stego compressed code (01110011011100100011100111001000) is read, from which the 16-bit bitmap (0111011101110110) is extracted. The 2-bit Part 3 (10) of the bitmap is then combined with the 8-bit low value (00111001) and the 8-bit high value (11001000) to form an 18-bit data segment (100011100111001000). This data segment is fed into the hash function, generating 6-bit verification data (001100). Next, the paired stego compressed code (01000111010011101101001111010101) is read and split into the bitmap (0000011101101110). This bitmap is further divided, yielding Part 1 (0100011) and Part 2 (1010011). These two parts are then input into the matrix coding algorithm for decoding, extracting Segment 1 (010) and Segment 2 (100), which are combined to reconstruct the 6-bit paired verification data (010100). Finally, by comparing the verification data (001100) with the paired verification data (010100), a mismatch is detected, indicating that the pair of blocks has been tampered with.

The above process is applied to all blocks, where tampered pairs of blocks are assigned a value of 1, while untampered pairs are assigned a value of 0, resulting in a binary image that visually represents the tampered area. Finally, the image can be reconstructed following the AMBTC algorithm.

4. Experimental Results

This section evaluates the performance of the proposed scheme. It should be noted that we focus on attacks on the AMBTC compressed code rather than the decompressed AMBTC image, so all simulated attacks are targeted at the bit level. Figure 4 shows six 512 × 512 grayscale images: Airplane, Baboon, Barbara, Boat, Goldhill, and Peppers, which are used as test images to evaluate the performance of the proposed scheme.

To evaluate visual quality, we use Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), Feature Similarity (FSIM) [41], and Variance Inflation Factor (VIF) [42]. Mean Squared Error (MSE) is used to measure the difference between two images, as shown in Equation (5), where $I$ and $K$ represent the two images, $m$ and $n$ represent the dimensions of the image, and $i$ and $j$ represent the coordinates of the pixel being processed. PSNR is calculated using Equation (6) and is inversely proportional to MSE. Therefore, the lower the MSE, that is, the higher the PSNR, the smaller the difference between the two images, indicating higher visual quality. SSIM is used to measure the similarity of two images, where $x$ and $y$ represent the two images, $\mu$ represents the mean, $\sigma$ represents the standard deviation, and ${\sigma }_{xy}$ represents the covariance between $x$ and $y$, and $C$ is a constant. The range of SSIM is from 0 to 1, and the closer the SSIM is to 1, the more similar the two images are. FSIM evaluates visual quality by measuring the similarity of structural features between two images. The closer the value is to 1, the more similar the two images are. VIF assesses the impact of distortion on the image by considering the variance in pixel values. The closer the value is to 1, the better the image quality.

$$MSE={\displaystyle \frac{1}{m\times n}}{\sum }_{i=1}^m{\sum }_{j=1}^n{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2.$$

(5)

$$PSNR=10\times {log}_{10}{\displaystyle \frac{{255}^2}{MSE}}.$$

(6)

$$SSIM\left(x,y\right)={\displaystyle \frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}}.$$

(7)

The tampering detection performance is evaluated using the true positive rate (TPR), false positive rate (FPR), and precision. True positive (TP) indicates that the actual tampered area that is correctly detected, false positive (FP) indicates that the area is not tampered but is detected as tampered, true negative (TN) indicates that the area that is not tampered and is not detected, and the false negative (FN) indicates that the actual tampered area is not detected. TPR, also known as the detection rate, is calculated using Equation (8) as the ratio of TP to the sum of TP and FN, where a higher value indicates better detection performance. FPR, or the false alarm rate, as shown in Equation (9), is the ratio of FP to the sum of FP and TN, where a lower value is preferred. Precision, as shown in Equation (10), is the ratio of TP to the sum of TP and FP, where a higher value indicates greater reliability in identifying tampered areas. These metrics collectively assess the effectiveness of the proposed scheme in tampering detection.

$$\mathrm{T}\mathrm{P}\mathrm{R}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}.$$

(8)

$$\mathrm{F}\mathrm{P}\mathrm{R}={\displaystyle \frac{\mathrm{F}\mathrm{P}}{\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N}}}.$$

(9)

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}.$$

(10)

Figure 5 presents the AMBTC compressed images and the stego AMBTC compressed images, with the difference being hardly noticeable to the naked eye. For a more objective evaluation,

Table 2. Comparison of visual quality between AMBTC compressed image and stego AMBTC compressed image.

Images	PSNR	SSIM	FSIM	VIF
Airplane	28.6806	0.9208	0.9474	0.8801
Baboon	25.4049	0.8495	0.9151	0.7544
Barbara	27.4961	0.8915	0.9327	0.8251
Boat	28.9548	0.8919	0.9324	0.8530
Goldhill	31.0109	0.8938	0.9338	0.8600
Peppers	29.9246	0.9150	0.9436	0.8946

compares the visual quality by presenting their PSNR and SSIM values. It can be observed that the PSNR is approximately 30 dB, and the SSIM is around 0.9, indicating that the visual quality of the stego AMBTC compressed images is close to that of the AMBTC compressed images.

To ensure the objectivity of the experiment, we used the flipping attack instead of the random noise attack. The key difference is that the flipping attack directly inverts a fixed number of bits, whereas the random noise attack adds noise to a set of bits without guaranteeing any actual change. If the added noise matches the original bit, the bit remains unchanged, resulting in no effective tampering. This randomness introduces uncertainty in the degree of tampering, potentially affecting the consistency and fairness of the evaluation. Therefore, to ensure a precise and consistent number of tampered bits, we chose the flipping attack. Figure 6 shows the visual results of the attack on Baboon, including the tampered images, actual tampered areas, and detected tampered areas at different flipped bit levels. It can be observed that since the attack targets the compressed code level, the image content remains visible even when 10,000 bits are flipped. In terms of detection performance, the actual tampered areas and detected tampered areas are nearly identical.

Table 3. Comparison of visual quality at different flipped bits.

Images	Flipped Bits	PSNR	SSIM	FSIM	VIF
Airplane	No Attack	28.6806	0.9208	0.9474	0.8801
	100	28.5292	0.9172	0.9455	0.8750
	1000	27.1078	0.8895	0.9302	0.8174
	10,000	21.2833	0.6431	0.7815	0.4671
Baboon	No Attack	25.4049	0.8495	0.9151	0.7544
	100	25.3111	0.8474	0.9140	0.7477
	1000	24.5203	0.8284	0.9058	0.6958
	10,000	20.2078	0.6581	0.8198	0.3720
Barbara	No Attack	27.4961	0.8915	0.9327	0.8251
	100	27.3651	0.8885	0.9312	0.8197
	1000	26.2590	0.8639	0.9181	0.7691
	10,000	20.8753	0.6601	0.8019	0.4292
Boat	No Attack	28.9548	0.8919	0.9324	0.8530
	100	28.7583	0.8890	0.9310	0.8448
	1000	27.1360	0.8610	0.9163	0.7779
	10,000	21.0831	0.6368	0.7887	0.4043
Goldhill	No Attack	31.0109	0.8938	0.9338	0.8600
	100	30.7483	0.8909	0.9324	0.8504
	1000	28.2344	0.8620	0.9175	0.7377
	10,000	21.3920	0.6305	0.7880	0.3065
Peppers	No Attack	29.9246	0.9150	0.9436	0.8946
	100	29.6395	0.9118	0.9418	0.8853
	1000	27.7748	0.8807	0.9254	0.8176
	10,000	21.2669	0.6290	0.7795	0.4342

presents a comparison of visual quality at different flipped bit levels, showing that as the number of flipped bits increases, the visual quality degrades. Even when 10,000 bits are flipped, the PSNR remains around 21 dB, suggesting that while the difference is perceptible to the naked eye, the image content is still recognizable, which is consistent with the results shown in Figure 6.

Table 4. Comparison of detection performance at different flipped bits.

Images	Flipped Bits	TPR	FPR	Precision
Airplane	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.26%	0.00%	100.00%
Baboon	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.28%	0.00%	100.00%
Barbara	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.45%	0.00%	100.00%
Boat	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.32%	0.00%	100.00%
Goldhill	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.07%	0.00%	100.00%
Peppers	100	100.00%	0.00%	100.00%
	1000	100.00%	0.00%	100.00%
	10,000	99.15%	0.00%	100.00%

compares the detection performance at different flipped bit levels, demonstrating that across all test images, the FPR remains at 0% and the precision at 100%, indicating that the proposed scheme has no false alarms and ensures completely accurate detections. Furthermore, all test images achieve 100% TPR when flipping 100 and 1000 bits. Even when 10,000 bits are flipped, the TPR remains close to 99%, confirming that the proposed scheme maintains a very high detection rate. It is important to emphasize that the TPR refers to the detection rate rather than the success rate. Therefore, as long as the TPR is nonzero, it can be concluded that the image has been tampered with.

In order to further evaluate the effectiveness of shuffle pairing in the proposed scheme, we conducted an ablation study to examine its impact under the block scrambling attack. Without the shuffle pairing step, the verification data of the proposed scheme are embedded in Part 1 and Part 2 of its own bitmap. In the case of AMBTC compressed code, the block scrambling attack involves segmenting the AMBTC compressed bitstream into 32-bit segments and randomly scrambling several segments to simulate the attack. Figure 7 presents the visual results of the ablation study, in which the Barbara image undergoes block scrambling attacks. The results include tampered images, actual tampered areas, detected tampered areas (with shuffle pairing), and detected tampered areas (without shuffle pairing) for various scrambled block counts. In all cases, the detected tampered areas with shuffle pairing almost or completely correspond to the actual tampered areas, while those without shuffle pairing are entirely black, indicating that no tampering is detected.

Table 5. Comparison of detection performance at different scrambled block counts.

Images	Scrambled Block Counts	with Shuffle Pairing			Without Shuffle Pairing
		TPR	FPR	Precision	TPR	FPR	Precision
Airplane	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.19%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	98.97%	0.00%	100.00%	0.00%	0.00%	N/A
Baboon	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.18%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	98.97%	0.00%	100.00%	0.00%	0.00%	N/A
Barbara	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.39%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	99.29%	0.00%	100.00%	0.00%	0.00%	N/A
Boat	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.19%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	99.08%	0.00%	100.00%	0.00%	0.00%	N/A
Goldhill	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.59%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	99.17%	0.00%	100.00%	0.00%	0.00%	N/A
Peppers	100	100.00%	0.00%	100.00%	0.00%	0.00%	N/A
	500	99.18%	0.00%	100.00%	0.00%	0.00%	N/A
	1000	99.06%	0.00%	100.00%	0.00%	0.00%	N/A

summarizes the detection performance across different scrambled block counts. For 100-block scrambling, with shuffle pairing, the TPR is 100%, FPR is 0%, and precision is 100%. Even for 500-block or 1000-block scrambling, the TPR remains around 99%, demonstrating that shuffle pairing is both essential and effective for detecting block scrambling attacks. In contrast, without shuffle pairing, the TPR is 0%, FPR is 0%, and precision is N/A, as both TP and FP are zero, resulting in an undefined calculation due to a denominator of zero. This indicates that without shuffle pairing, detection fails to identify any tampered regions, as evidenced by the 0% TPR. These findings underscore the necessity and effectiveness of shuffle pairing in detecting block scrambling attacks.

To evaluate the reliability of the proposed scheme under different hashing methods and keys, we conducted a series of experiments. As shown in

Table 6. Comparing the avalanche effects of three different hashing methods.

MD5	SHA-256	BLAKE2
3.05	2.95	3.01

, all three hash functions, MD5 [37], SHA-256 [38], and BLAKE2 [39], exhibit comparable avalanche effects, with average bit differences around three bits after a single-bit flip. This average is based on 100,000 trials. Since the output length is six bits, the average difference approaches 50%, indicating strong avalanche characteristics and a high sensitivity to input changes.

Table 7. Comparison of detection performance with different hash methods at different numbers of flipped bits.

	MD5			SHA-256			BLAKE2
Flipped Bits	TPR	FPR	Precision	TPR	FPR	Precision	TPR	FPR	Precision
100	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%
1000	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%
10,000	99.43%	0.00%	100.00%	99.23%	0.00%	100.00%	99.28%	0.00%	100.00%

presents the detection performance under varying numbers of flipped bits. All three hash methods consistently achieve 100% precision and zero false positive rate across all test cases. Even under a high tampering intensity of ten thousand flipped bits, the true positive rate remains above 99%, confirming the strong detection capability.

Table 8. Comparison of detection performance with different hash keys at 10,000 flipped bits.

	MD5			SHA-256			BLAKE2
	TPR	FPR	Precision	TPR	FPR	Precision	TPR	FPR	Precision
Hash Key 1	99.19%	0.00%	100.00%	99.24%	0.00%	100.00%	99.45%	0.00%	100.00%
Hash Key 2	99.36%	0.00%	100.00%	99.45%	0.00%	100.00%	99.31%	0.00%	100.00%
Hash Key 3	99.17%	0.00%	100.00%	99.35%	0.00%	100.00%	99.19%	0.00%	100.00%
Hash Key 4	99.38%	0.00%	100.00%	99.31%	0.00%	100.00%	99.12%	0.00%	100.00%
Hash Key 5	99.26%	0.00%	100.00%	99.29%	0.00%	100.00%	99.38%	0.00%	100.00%

further evaluates the robustness of the scheme under different hash keys. To ensure a fair comparison across all methods, a symmetric key input of 64 bytes was used consistently. The detection results remain stable across five different keys, with true positive rates consistently above 99% and false positive rates remaining at zero for all methods. These results demonstrate that the proposed scheme is both reliable across various hash functions and resilient to changes in the hash key, ensuring consistent and effective tampering detection performance.

To further evaluate the proposed scheme under different configurations, we tested its performance using a larger block size of 8 × 8. As shown in

Table 9. Comparison of 4 × 4 and 8 × 8 block sizes.

Block Size	Block Number	File Size	Construction Time	Detection Time
4 × 4	16,384	524,288	6.23	3.18
8 × 8	4096	327,680	3.31	0.87

, increasing the block size reduces the number of blocks from 16,384 to 4096 and decreases the file size accordingly. This results in a significant reduction in both construction and detection times, with the detection time remaining at an acceptable level for practical use.

Table 10. Detection performance for 8 × 8 block size at 10,000 flipped bits.

Images	TPR	FPR	Precision
Airplane	99.75%	0.00%	100.00%
Baboon	99.70%	0.00%	100.00%
Barbara	99.71%	0.00%	100.00%
Boat	99.85%	0.00%	100.00%
Goldhill	99.95%	0.00%	100.00%
Peppers	99.75%	0.00%	100.00%

shows the detection performance for the 8 × 8 block size under the condition of 10,000 flipped bits. The proposed scheme achieves excellent results across all tested images, with a TPR above 99.70%, FPR at 0.00%, and precision at 100.00%. These results confirm that the proposed scheme maintains high detection accuracy and robustness even with fewer, larger blocks.

Table 11. Comparison with other AMBTC-based tampering detection schemes.

Schemes	Generation of Authentication Code	Detectable
		Type A Tampering	Type B Tampering
Nguyen et al. [19]	PRNG	NO	NO
Lin et al. [20]	PRNG	Yes	Partially
Zhong et al. [21]	PRNG	NO	Yes
Li et al. [32]	PRNG	NO	NO
Hu et al. [22]	PRNG	NO	Yes
Chen et al. [23]	PRNG	Partially	NO
Hong et al. [33]	Hash function	Yes	Yes
Hong et al. [24]	Hash function	Yes	Yes
Proposed	Hash function	Yes	Yes

compares other AMBTC-based tampering detection schemes, where type A tampering involves flipping two bits in the bitmap, and type B tampering is performed by adding a constant value of 16 to the quantization level. It is important to note that schemes [19,20,21,22,23,32] use a pseudo-random number generator (PRNG) to generate authentication codes, which are unrelated to the content they protect. In contrast, the authentication codes in [24,33] and the proposed scheme are generated by hashing the content to be protected. As a result, these schemes are able to detect both types of tampering.

For the sake of thoroughness, we further evaluated the true positive rate (TPR) at different numbers of flipped bits and block sizes on BOSS [43] and BOWS-2 [44] datasets. As shown in

Table 12. Comparison of TPR at different numbers of flipped bits and block sizes in BOSS and BOW-2 datasets.

Datasets	Metrics	4 × 4			8 × 8
		100	1000	10,000	100	1000	10,000
BOSS	MAX	100.00%	99.75%	99.95%	100.00%	99.56%	100.00%
	MIN	96.94%	98.60%	99.56%	94.62%	97.94%	99.61%
	AVG	99.39%	99.44%	99.83%	98.48%	99.09%	99.95%
BOW-2	MAX	100.00%	99.87%	99.95%	100.00%	99.77%	100.00%
	MIN	96.88%	98.72%	99.61%	96.59%	97.69%	99.61%
	AVG	99.55%	99.43%	99.79%	98.72%	99.06%	99.96%

, the highest TPR for both datasets reaches 100%. Even the minimum values exceed 94%, with average TPRs around 99%, indicating that the proposed scheme remains effective across various images. We observe that both 4 × 4 and 8 × 8 block sizes yield similarly high TPRs, suggesting that the proposed scheme performs robustly regardless of the block size used.

5. Conclusions

This paper proposes a tampering detection scheme for AMBTC compressed codes. Unlike traditional schemes designed for AMBTC compressed images, the proposed scheme operates at the bit level rather than at the pixel level. The proposed scheme first pairs all image blocks one-to-one through shuffle pairing. Then, the original data are processed by a hash function to generate verification data, which are embedded into the bitmap of the paired block using the matrix coding algorithm. After processing all image blocks, the stego AMBTC compressed code is obtained. During decoding, the reverse operation is performed, where the verification data generated by the hash function are compared with the verification data extracted using the matrix coding algorithm. A mismatch indicates tampering in the corresponding pair of blocks, allowing for the detection of altered regions. For image reconstruction, the AMBTC algorithm can be directly applied. Experimental results demonstrate that the proposed scheme effectively detects flipping attacks and block scrambling attacks at various levels. The TPR approaches 100%, the FPR is 0%, and the precision reaches 100%, indicating that the proposed scheme achieves high detection accuracy.