Block-Cipher No-Hit-Zone Sequence-Assisted Spectrum Control Scheme for Distributed Systems

Abstract

In distributed systems, the dense access of wireless devices introduces significant challenges, including severe quasi-synchronous multiple access interference (MAI) and transmission security threats, which limit the effectiveness of traditional orthogonality-based spectrum control schemes. To address these challenges, this paper proposes a new block-cipher no-hit-zone (BC-NHZ) sequence-assisted spectrum control transmission scheme, aimed at enhancing privacy protection and improving overall communication capacity for distributed systems. The BC-NHZ scheme employs block cipher encryption and establishes control sequences to represent the spectrum usage scheme. Moreover, we mathematically prove that the parameters of the BC-NHZ scheme achieve optimal results with respect to the bound of the Hamming correlation. Numerical analysis and simulation results validate the practical feasibility of the BC-NHZ scheme, demonstrating its reliability to relax synchronous requirements while providing enhanced transmission privacy protection performance.

1. Introduction

With the rapid advancement of 5G networks, edge computing, and ultra-reliable low-latency communication (URLLC), the enhanced connectivity and computational capabilities have fundamentally accelerated the adoption of distributed systems (DSs) [1,2,3]. Empowered by these advancements, DSs can seamlessly integrate massive heterogeneous smart devices—ranging from smartphones to IoT sensors—as decentralized processing nodes, achieving superior scalability compared to centralized architectures [4,5,6,7]. According to Statista, the current number of smartphone users worldwide is 7.21 billion, providing a pervasive infrastructure for DS to dynamically allocate tasks across edge devices. This paradigm shift enables applications such as distributed learning in healthcare diagnostics, real-time collaborative robotics, and adaptive traffic prediction systems [8,9]. Unlike traditional centralized approaches, distributed systems exhibit extended operational sustainability through node collaboration and lower maintenance costs by eliminating centralized hardware dependencies [10,11,12,13].

Despite DS offering significant benefits, it also presents several challenging issues that should be further investigated. On the one hand, the coexistence of numerous devices sharing limited spectrum resources results in multi-access interference within DS, reducing communication capacity. The constrained spectrum and complex network structures make strict time synchronization across the entire DS unfeasible, thus offering significant battles to implementing effective communication resource allocation schemes. On the other hand, the open system architecture and broadcast nature of radio propagation expose private information intended for distributed devices to the risk of eavesdropping attacks.

Recent advances in interference and eavesdropping technologies have introduced significant challenges to the security of DS. Interference-based attacks, such as jamming, exploit vulnerabilities in wireless channels, leading to disrupted communications and compromised data integrity [14]. Similarly, eavesdropping, enabled by advancements in hardware and algorithmic techniques, allows attackers to capture sensitive data [15]. The proliferation of wireless networks, while enhancing connectivity, has also increased the attack surface, making it easier for adversaries to exploit wireless system flaws [16]. These challenges are compounded in scenarios involving distributed devices, where swarm communication suffers from heightened risks of interference and unauthorized access. Efforts to counter these threats include integrating interference-canceling techniques and adopting robust encryption strategies, yet these measures face limitations in real-time, high-density environments [17]. Overall, DS necessitates a continuous evolution of countermeasures aligned with modern threats.

Therefore, it is crucial to guarantee reliable data transmission in DS communications while addressing interference and eavesdropping threats. In this paper, we propose a spectrum control transmission scheme based on BC-NHZ sequences for the DS communication network. By employing the proposed scheme, the goal of strengthening the security and improving the network capacity can be achieved. The main contributions of this paper can be summarized as follows:

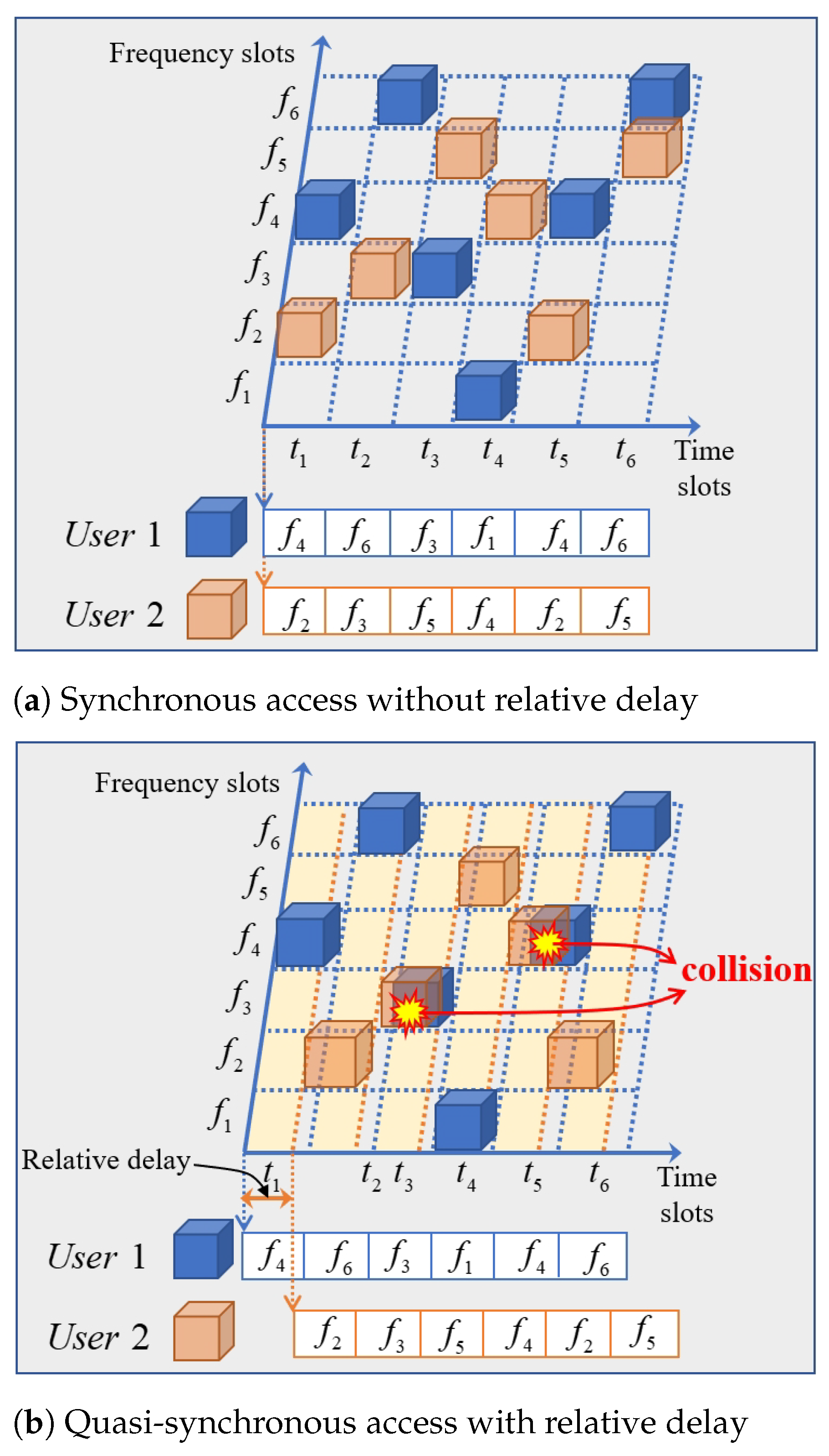
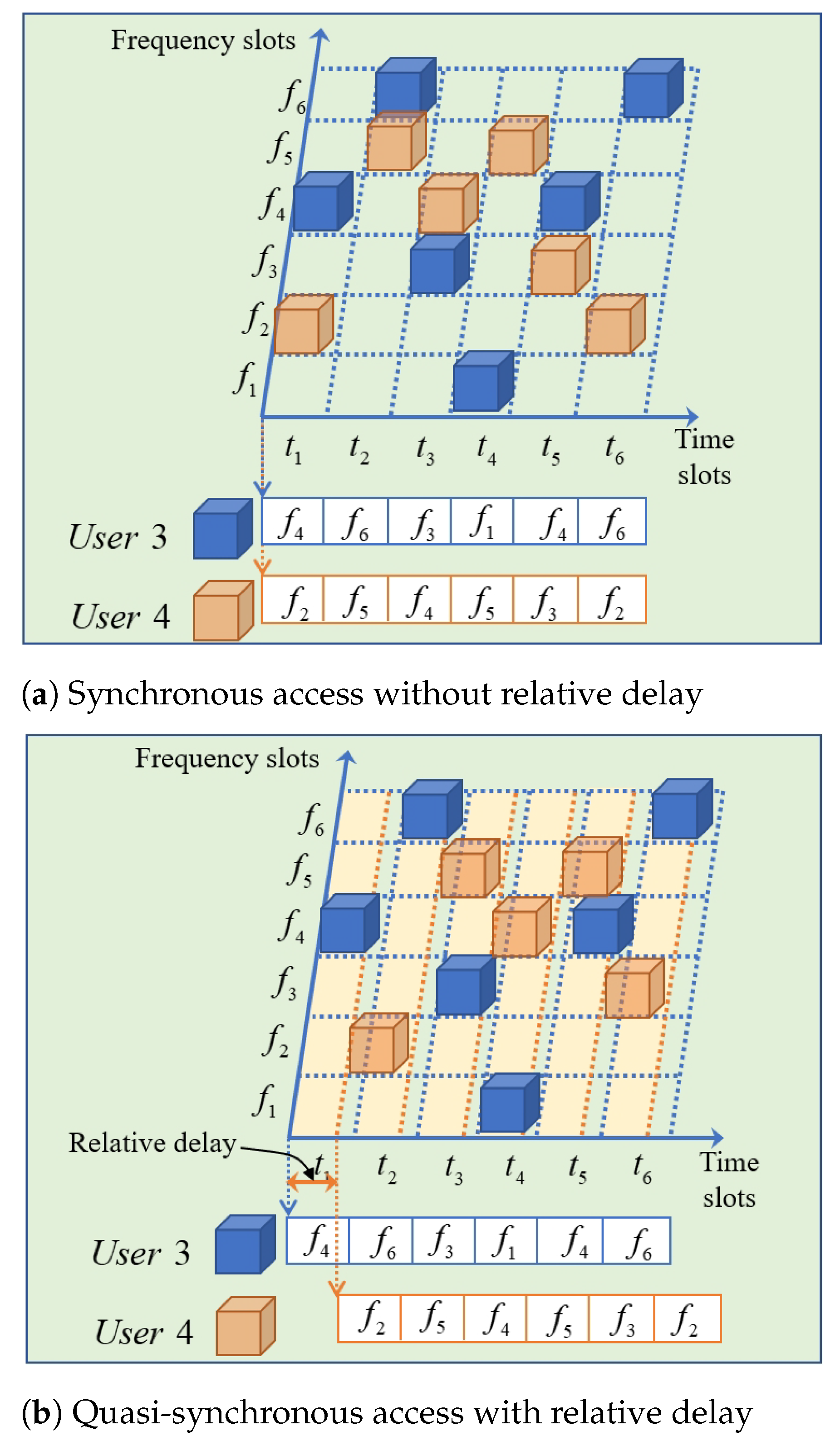
• DS Communication Network Architecture: We propose a DS communication network architecture consisting of multiple devices that dynamically adjust spectrum allocation schemes using control sequences. The network model supports quasi-synchronous access and tolerates signal-relative delay at the receiver. Each device accesses spectrum resources through its own control sequence, ensuring flexible and efficient utilization of the spectrum.
• BC-NHZ sequence-assisted spectrum control scheme: The novel BC-NHZ scheme is introduced, leveraging block cipher encryption to construct a secure NHZ sequence set. This scheme provides robust privacy protection, making the spectrum utilization scheme resistant to deciphering by non-cooperative entities. Additionally, it ensures communication spectrum orthogonality and effectively mitigates MAI among distributed devices, even under conditions of relative delay.
• Performance Analysis and Validation: The performance of the proposed scheme is analyzed through mathematical reasoning and validated via simulation. The results demonstrate that the proposed approach outperforms baseline methods in terms of complexity and network capacity. This makes the BC-NHZ scheme well-suited for DS communication networks, particularly for ensuring high communication quality and privacy protection in decentralized devices with terminal access.

The rest of the paper is organized as follows. The related work is given in Section 2. Section 3 depicts the system model. Then, the proposed scheme and mathematical analysis are elaborated in Section 4. Based on the proposed scheme, Section 5 presents the simulation results and discussion. Finally, the conclusion and future work are shown in Section 6.

2. Related Work

Spectrum control schemes based on sequences are widely employed in wireless communications due to their multiple access capabilities. The spectrum control sequences directly affect the implementation effect of the communication resource allocation schemes [18,19].

The existing research on sequence generation schemes is divided into two categories. One is the traditional pseudo-random sequence, and the construction methods include but are not limited to, the methods based on prime numbers, the methods based on m-sequence, the methods based on GMW sequence, the methods based on ReedSolomon code, and the methods based on Chaos Theory [20,21,22]. These sequences, constructed by these methods, have great randomization performance and are widely used in modern communication. As the demand for reliability and confidentiality of communications is further enhanced, cryptography-based algorithms for generating sequences have emerged [23]. The sequence generation technique based on iterated block cipher is representative of this category [24], which uses the system time of day (TOD) and the system encryption key (KEY) to generate sequences according to the obfuscation and diffusion criterion for cryptographic design proposed by Shannon. Since then, Li et al. have further proved that cryptographic sequences are significantly better than the sequences generated by the traditional chaos theory in terms of long-periodicity, security, randomness, and complexity [25]. Moreover, attribute-based authentication on the cloud ensures secure, privacy-preserving access control for thin clients in distributed systems, enabling verifiable data integrity and decentralized trust management while mitigating identity-linkability risks [26,27]. However, these sequences were not designed with the increasingly crowded spectrum resources, which makes it challenging to adapt to the dense access of decentralized devices.

The other category is spectrum allocation schemes with specific properties, such as sequence sets with orthogonal properties. In the literature [28], based on the frequency hopping multiple access (FHMA) network model for Bluetooth networks, the orthogonal sequences with stochastic mapping and cyclic shift replacement are proposed and analyzed for their throughput and transmission delay. The technique is further applied to cognitive radios, and the orthogonal sequences with a dynamic number of frequency slots have been established in [29].

However, the orthogonal schemes must ensure that the end devices are guaranteed time synchronization, which is difficult to achieve in practical DS scenarios. Figure 1 demonstrates that orthogonal sequences control the frequency usage schemes of $User$ 1 and $User$ 2, eliminating spectrum conflicts under strict synchronization. Terminals send data based on fixed-length frames containing 6 hops during $t_1$∼$t_6$, and each frequency hop is synchronized based on information from TOD. However, in Figure 1b, there are relative time delays, and orthogonal schemes experience severe spectrum conflicts.

In order to break through the limitation of high-precision time synchronization, the concept of a no-hit-zone (NHZ) sequence set has been proposed, which can effectively realize orthogonal multiple access [30,31,32]. As shown in Figure 2, $User$ 3 and $User$ 4 with NHZ sequences eliminate spectrum conflicts, even with relative time delay. Peng et al. analyzed the characteristics and principles of the NHZ and proposed a general construction method for NHZ sequence sets [33,34]. Their methods optimize periodic Hamming sequences of arbitrary lengths by fully aligning column vectors. Liu et al. introduced a new approach for constructing NHZ sequences based on new Hamming correlations, which achieves the theoretical limit [35,36]. Some NHZ sequence sets with new properties have been proposed in recent years. GAO increased the size of the sequence sets under a particular scene, significantly increasing the network capacity [37]. Zeng proposed some constructions of NHZ sequences with wide gap properties for improved FHMA systems under follower jamming [38,39].

Existing NHZ sequences, despite their good orthogonality properties, suffer from small family sizes and simplistic constructions, limiting their suitability for high-throughput, high-security DS networks. There remains a significant research gap in the theory and construction of NHZ sequences to enhance their security and family size. The parameters of sequence sets with NHZ properties from some known constructions and the new ones are listed in

Table 1. Parameters of comparisons among some known NHZ sequence sets and the proposed one.

Length	Family Size	Frequency-Slot Size	NHZ Width	Basic Sequence	Reference
$r(v+1)$	m	$m(v+1)$	v	-	[33]
$r{\displaystyle \prod _{i=1}^I}{v}_i$	${\displaystyle \prod _{i=1}^I}{m}_i$	${\displaystyle \prod _{i=1}^I}{m}_i(v_i+1)$	${\displaystyle \prod _{i=1}^I}(v_i+1)-1$	Optimal NHZ sequence set in [33]	[34]
r	m	$m(v+1)$	v	-	[36]
$lcm(p-1,v)$	$mp$	$pm(v+1)$	v	-	[38]
$r(v+1)$	m	$m(v+1)$	v	Optimal sequence sets in [32]	[39]
r	m	$m(v+1)$	v	Block ciper sequence	This paper

p is a prime; $m,v,r,I,v_1,v_2,\cdots ,v_I$ are positive integers.

. The proposed construction yields optimal NHZ sequence sets with new peculiarities not covered in the literature.

3. Preliminaries

3.1. Definition of No-Hit Zone

This section recalls the mathematical foundations of the Hamming correlation and no-hit zone, constructing an analytical framework that fundamentally governs the interference mitigation capacity and orthogonal efficiency in DS spectrum control architectures.

The Hamming correlation quantifies the positional symbol discrepancy between sequences by counting differing elements at corresponding indices. For orthogonal sequences, this metric vanishes entirely, serving as an ideal interference-free condition. The no-hit zone specifies the maximum permissible timing offset between transmissions that preserves sequence orthogonality in asynchronous channel access scenarios.

Consider a distributed communication network with M devices, and let $\mathbb{G}=\left\{{\mathit{g}}^{\mathbf{1}},{\mathit{g}}^{\mathbf{2}},\cdots ,{\mathit{g}}^{\mathit{M}}\right\}$ be a control sequence set over the alphabet $Q=\{0,1,\cdots ,q-1\}$, where ${\mathit{g}}^{\mathit{u}}=\left(g_0^u,g_1^u,\cdots ,g_{N-1}^u\right)$ for $1\le u\le M$. For presentation convenience, we denote the sequence set $\mathbb{G}$ having alphabet size q, sequence length N, and family size M as $\mathbb{G}(q,N,M)$.

We define

$$h\left(a_0,a_1\right)\triangleq \left\{\begin{array}{cc}1,\hfill & if a_0=a_1;\hfill \\ 0,\hfill & else.\hfill \end{array}\right.$$

(1)

For ${\mathit{g}}^{\mathit{u}},{\mathit{g}}^{\mathit{v}}\in \mathbb{G}$, the Hamming correlation with delay $\tau$ is given by

$$H_{u,v}\left(\tau \right)=\sum _{n=0}^{N-\tau -1}h({g^u}_n,{g^v}_{n+\tau }),\tau =0,1,\cdots ,N-1.$$

(2)

The Hamming correlation indicates the degree of overlap of sequences at different delays. An ideal spectrum control sequence set should have a Hamming correlation of 0 at the delay of interest, thus eliminating MAI.

Then, the width Z of the no-hit zone is under the Hamming correlation defined by

$$\begin{array}{c}{Z}_a=max\left\{C\right|H_{u,u}\left(\tau \right)=0,\forall {\mathit{g}}^{\mathit{u}}\in \mathbb{G},0<\tau \le C\},\hfill \\ Z_c=max\left\{C\right|H_{u,v}\left(\tau \right)=0,\forall {\mathit{g}}^{\mathit{u}},{\mathit{g}}^{\mathit{v}}\in \mathbb{G},u\ne v,0\le \tau \le C\},\hfill \\ Z=min\left\{Z_a,Z_c\right\}.\hfill \end{array}$$

(3)

Liu et al. obtained the following bound under Hamming correlation [36] in 2022. An NHZ sequence set with parameters $(q,N,M)$ is considered optimal if NHZ width Z is the maximum integer solution of the following inequality:

$$Z\le {\displaystyle \frac{q}{M}}-1.$$

(4)

The family size M and alphabet size q have a constraint relationship with Z.

The design of the no-hit zone extends the delay range of sequence orthogonality. In particular, the set of sequences is the traditional set of orthogonal sequences when $Z=0$ (as shown in Table 2). If $Z>0$, we call $\mathbb{G}$ an NHZ sequence set. In order to clearly represent the parameters, we set $\mathbb{G}(q,N,M,Z)$ to denote a sequence set whose NHZ width is Z.

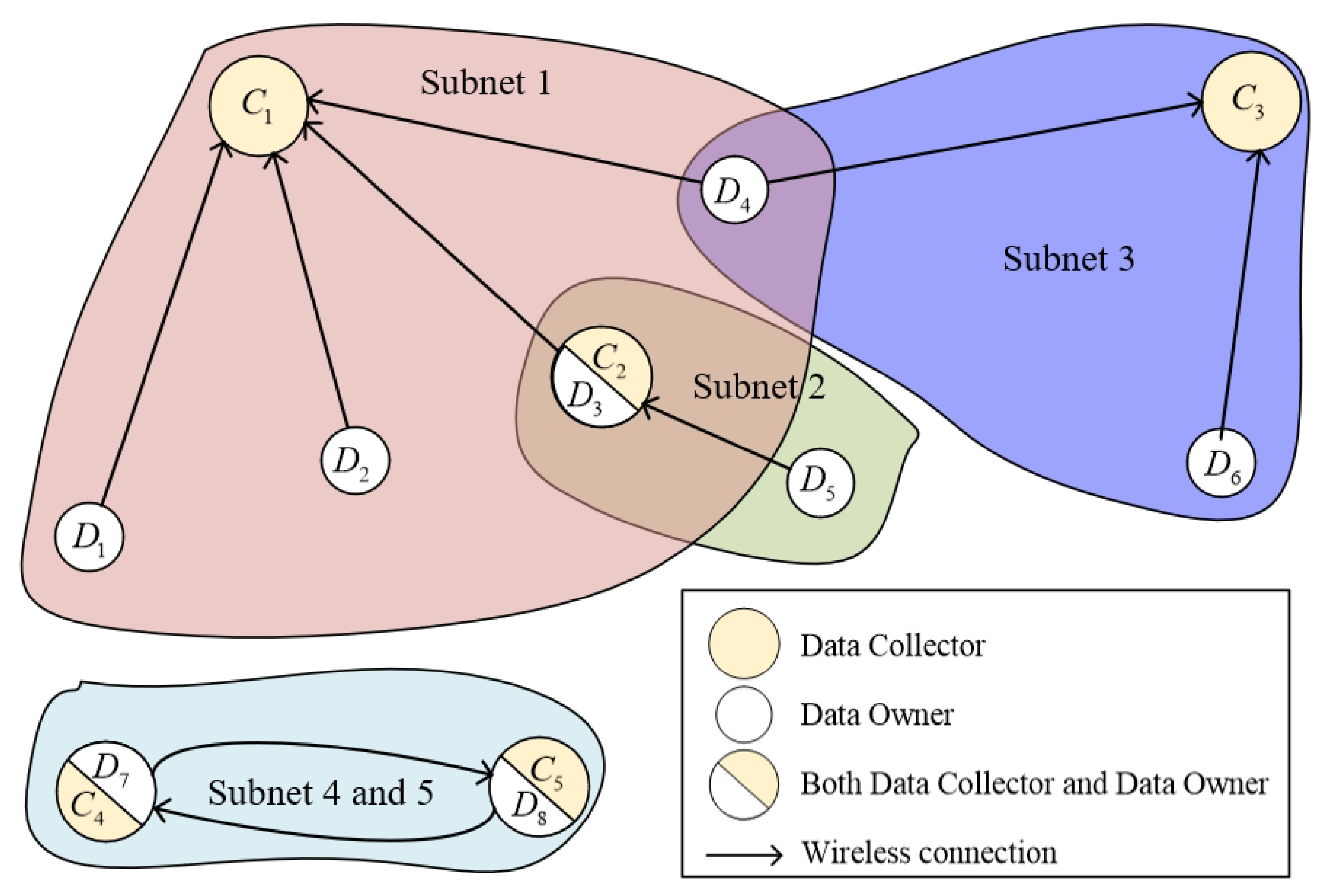
3.2. System Model

Based on real-world application scenarios and the existing DS models, a typical DS communication network scenario is considered in this work, as shown in Figure 3. The DS communication network has multiple sub-network structures, where each sub-network consists of one data collector and multiple data owners, with $C_e(e=1,2,3,...)$ as the data collector and $D_u(u=1,2,3,\dots )$ as the data owner. Specifically, this paper focuses on spectrum control schemes for uplinks of data owners, where packets are transmitted independently by data owners over a shared communication spectrum.

In the DS network, the shared communication spectrum B is divided equally into q frequency slots, and $B=\{b_0,b_1,\cdots ,b_{q-1}\}$. Let T be the hopping interval and $F^u=\{f_0^u,f_1^u,f_2^u,\cdots \}$ denote the spectrum usage scheme of $D_u$, where $f_n^u\in B,(n=0,1,2,\dots )$. Different spectrum resources are allocated to all data owners in different hopping intervals, which realizes the sharing of the whole spectrum for information transmission. Generally, $F^u$ is presented by a sequence ${\mathit{g}}^{\mathit{u}}=\{g_0^u,g_1^u,g_2^u,\cdots \}$ over a set of integers $Q=\{0,1,\cdots ,q-1\}$, where $f_n^u=b_{g_n^u}$.

Based on the transceiver model and the signal analysis presented in [18], the superimposed signals $r\left(t\right)$ with different time delays at the receiver are expressed as:

$$r\left(t\right)=\sum _{u=1}^M{A}_u{y}^u\left(t-{\tau }_u\right).$$

(5)

$A_u$ is the received signal amplitude of the u-th data owner, and ${\tau }_u$ is the relative delay of $D_u$’s signal.

Considering that the signal delay is caused by the superposition of hardware, software, and environmental conditions, we approximate that ${\tau }_u$ obeys a Gaussian distribution with expectation $\mu =0$ and mean square deviation ${\sigma }^2$, and ${\tau }_u$ is independent for different $D_u$.

$y^u\left(t\right)$ is $D_u$’s transmitted waveform and is denoted as

$$y^u\left(t\right)=s^u\left(t\right)p^u\left(t\right),$$

(6)

where

$$p^u\left(t\right)=\sum _{n=0}^{\infty }{e}^{j\left(2\pi f_n^{u}t+{\theta }_u\right)}·w\left(t-nT\right).$$

(7)

$s^u\left(t\right)$ is the baseband modulation signal with transmitted information, $p^u\left(t\right)$ is the carrier controlled by the scheme ${\mathit{g}}^{\mathit{u}}$, and $w\left(t\right)$ is a chip waveform. If $\{g_0^u,g_1^u,g_2^u,\cdots \}$ satisfy $Z>0$ in (3), then the MAI is eliminated when the signal arrival delay does not exceed the width of NHZ.

3.3. Complexity Metric

To validate the privacy protection performance of the spectrum control scheme, we introduce the complexity metric. The scheme $\{g_0^u,g_1^u,g_2^u,\cdots \}$ with a higher complexity means it is more difficult for the hostile to forecast the sequence from the known sequence fragments. In this paper, we choose the FuEn algorithm for evaluating the complexity of a spectrum control policy to reject illegal eavesdroppers. Fuzzy entropy (FuEn) shows better performance than linear complexity and approximate entropy in distinguishing various kinds of sequences and is proven to be less sensitive to the test parameters. The FuEn algorithm is given here.

Let positive integer N be the watch length of the discrete sequence, and fix two non-negative integers m (vector dimension) and r (resolution parameter) with $m<N$. Let $\mathit{l}=\left[l\right(0),l(1),\dots ,l(N-1\left)\right]$ denote the observed part of $\{g_0^u,g_1^u,g_2^u,\cdots \}$. The non-negative integer number space of dimension m is formed by the sequence of vectors

$$\mathit{lv}\left(\mathit{i}\right)=[l\left(i\right),l(i+1),\dots ,l(i+m-1)]-l_0\left(i\right),$$

(8)

where $l_0\left(i\right)=m^{-1}{\displaystyle \sum _{j=0}^{m-1}}l(i+j)$, $0\le i\le N-m$ is window vectors.

According to the nature of sequences $\left\{\mathit{lv}\left(\mathit{i}\right)\right\}$, the distance vector $d_{ij}^{m,N}$ is defined for each $0\le i\le N-m$ as

$$D_{ij}^{m,N}=e^{-\ln 2·{(d_{ij}^{m,N}/r)}^2},j=0,1,\cdots ,N-m,\mathrm{and}j\ne i,$$

(9)

where $d_{ij}^{m,N}=\underset{k=1,2,...,m}{max}\left(\left|l(i+k-1)-l(j+k-1)\right|\right)$.

Thus, the corresponding $C_i^{m,N}\left(r\right)$ applied to evaluating the complexities can be obtained

$$C_i^{m,N}\left(r\right)={(N-m)}^{-1}\sum _{j=1,j\ne i}^{N-m+1}{D}_{ij}^{m,N}.$$

(10)

The complexity metric of $\mathit{l}$ based on FuEn is then defined following the classical one by

$$FuEn(m,r,N)=\ln {\Phi }^{m,N}\left(r\right)-\ln {\Phi }^{m+1,N}\left(r\right),$$

(11)

where ${\Phi }^{m,N}\left(r\right)={(N-m+1)}^{-1}{\displaystyle \sum _{i=1}^{N-m+1}}{C}_i^{m,N}\left(r\right)$.

FuEn has relatively reasonable statistical properties when r is between 0.1 and 0.25 $SD\left(\mathit{l}\right)$ and $SD\left(\mathit{l}\right)$ is the standard deviation of the series $\mathit{l}$ [21].

A more considerable FuEn test value indicates a higher level of complexity and a safer spectrum control scheme. Therefore, it effectively differentiates between most of the existing spectrum control schemes based on sequences.

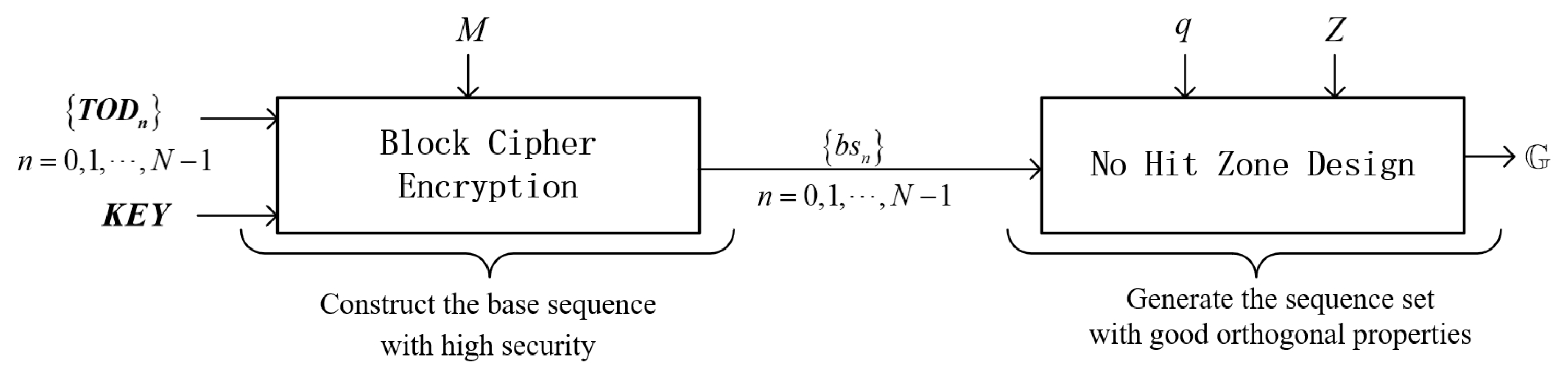
4. The Block-Cipher No-Hit-Zone Sequence Set

In this section, we first proposed a BC-NHZ spectrum control sequence set by block cipher encryption and no-hit zone design. The parameter relationships are discussed and the optimality of the proposed sequence set is proved. Then, we present a numerical example to verify orthogonal performance and parametric relationships.

4.1. The Construction of BC-NHZ Sequence Set

Let Z be a nonnegative integer and $M,N$ be positive integers. The construction of the BC-NHZ sequence set $\mathbb{G}$ [$N,M,M(Z+1),Z$] is as follows. As shown in Figure 4, the BC-NHZ scheme obtains the control sequence set $\mathbb{G}$ by performing the ‘block cipher encryption’ and ‘no hit zone design’ processes. Block cipher encryption is essential for the BC-NHZ spectrum control sequence set as it constructs high-strength cryptographic mechanisms to ensure collision resistance while substantially enhancing decryption resistance complexity, thereby enabling dual guarantees for communication quality and privacy protection in distributed networks.

In the block cipher encryption step, the $\left\{To{d}_n\right\}$ is processed based on the block cipher (BC) algorithm and remapping method to obtain the basic sequence $\left\{b{s}_n\right\}$. With the improved DES algorithm, the code series $\left\{c_n\right\}$ can be generated by utilizing the $Key$ and $\left\{To{d}_n\right\}$. The sequence has good statistical properties, and its detailed construction method and performance analysis in frequency hopping systems can be found in references [25].

$$\begin{array}{c}{c}_n=\{Sbox4\left(P_2^{16}\right)\oplus Sbox5\left(P_4^{16}\right)\oplus Sbox6\left(P_6^{16}\right)\}\\ +\{Sbox4\left(P_1^{16}\right)\oplus Sbox5\left(P_3^{16}\right)\oplus Sbox6\left(P_5^{16}\right)\}\ll 4,\end{array}$$

(12)

where

$$\left\{\begin{array}{c}{P}_{2j}^{i+1}=P_{2j-1}^i\oplus K^i\oplus z_1^i;\hfill \\ P_{2j-1}^{i+1}=Sboxj\left(P_{2j}^i\right)\oplus P_{2j}^i\oplus z_2^i;\hfill \end{array}\begin{array}{c} j\dots 1,2,3.\hfill \end{array}\right.$$

(13)

In (12) and (13), ⊕ is the XOR operation, $i=0,1,2,\dots ,15$ is the number of iterations, $K^n$ is the encryption key obtained from the $Key$, Sbox1–Sbox6 are the substitution boxes that are used for the cipher, and $P_{2j}^{i+1}$, $P_{2j-1}^{i+1}$, $z_1^i$, and $z_2^i$ are medium variables in the iterator with initial values obtained by dividing the $To{d}_n$. $z_1^i$ and $z_2^i$ are equal to $Z_1$ and $Z_2$ separately when $t=8,16$, otherwise they are equal to 0.

By leveraging the remapping method, the basic sequence $\left(b{s}_0,b{s}_1,\cdots ,b{s}_{N-1}\right)$ can be constructed by the following algorithm.

$$b{s}_n=\left(n+c_n\right)modM,forn=0,1,\cdots ,N-1.$$

(14)

Next, to meet the high-performance requirements of the no-hit zone by improving the NHZ algorithm [37], the proposed sequence set $\mathbb{G}=\left\{{\mathit{g}}^{\mathbf{1}},{\mathit{g}}^{\mathbf{2}},\cdots ,{\mathit{g}}^{\mathit{M}}\right\}$ is obtained.

We define $\mathcal{F}(·)$ as a one-to-one function from alphabet $\{0,1,\cdots ,MN-1\}$ to the frequency slot set F. Consequently, $\mathbb{G}=\left\{{\mathit{g}}^{\mathbf{1}},{\mathit{g}}^{\mathbf{2}},\cdots ,{\mathit{g}}^{\mathit{M}}\right\}$ is as follows:

$${\mathit{g}}^{\mathit{u}}=\left(g_0^u,g_1^u,\cdots ,g_{N-1}^u\right),$$

(15)

where

$$g_n^u=\mathcal{F}\left\{{〈b{s}_n+u〉}_M+{〈n〉}_{Z+1}·M\right\},$$

(16)

for $u=1,2,\cdots ,M$, $n=0,1,\cdots ,L-1.$ Here, the function ${〈a〉}_b$ means a modulo b.

The BC-NHZ sequence set $\mathbb{G}$ consists of several integer sequences. Each integer sequence determines the spectrum control scheme of one data owner, and all sequences control all owners to achieve orthogonalized networking with high complexity.

4.2. Parameter Optimality Analysis

Under the requirement of satisfying orthogonal multiple access with relative delay, maximizing the use of the limited spectrum resource to accommodate a more significant number of data owners becomes the core index to measure the spectrum control scheme. By analyzing the Hamming correlation, this subsection demonstrates that the parameter constraint of the proposed BC-NHZ sequence set is optimal with respect to the NHZ bound.

Theorem 1. 

The constructed BC-NHZ scheme $\mathbb{G}$ is an optimal NHZ set concerning the bound (4), and the parameters are concluded as follows: $\mathbb{G}$ has M sequences with the length of N, the width of the NHZ is Z, the size of the frequency-slot set F is $q=M(Z+1)$.

Proof. 

Obviously, $\mathbb{G}$ contains M sequences of length N. For $u\in \{0,1,\cdots ,M-1\}$, $n\in \{0,1,\cdots ,N-1\}$, we have $0\le {〈b{s}_n+u〉}_M\le M-1$ and $0\le M·{〈n〉}_{Z+1}\le MZ$, which immediately leads to $0\le g_n^u\le M(Z+1)-1$. The elements in the constructed sequences take values in the range $\{0,1,\cdots ,M(Z+1)-1\}$, so the size of the frequency-slot sets F is equal to $M(Z+1)$.

For $\forall g^u,g^v\in \mathbb{G}$, the Hamming correlation at time delay $\tau$ is

$$\begin{array}{cc}\hfill H_{u,v}\left(\tau \right)& =\sum _{n=0}^{N-\tau -1}h(g_n^u,g_{n+\tau }^v)\hfill \\ & =\sum _{n=0}^{N-\tau -1}h\left(\begin{array}{c}{〈b{s}_n+u〉}_M+M{〈n〉}_{Z+1},\\ {〈b{s}_{n+\tau }+v〉}_M+M{〈n+\tau 〉}_{Z+1}\end{array}\right)\hfill \\ & =\sum _{n=0}^{N-\tau -1}h\left({〈b{s}_n-b{s}_{n+\tau }+u-v〉}_M,M{〈\tau 〉}_{Z+1}\right).\hfill \end{array}$$

Case 1: $0<\tau \le Z.$ Since ${〈b{s}_n-b{s}_{n+\tau }+u-v〉}_M\le M-1$ and $M{〈\tau 〉}_{Z+1}$, we have $h(g_n^u,g_{n+\tau }^v)=0$, which immediately leads to $H_{u,v}\left(\tau \right)=0$.

Case 2: $\tau =0\mathrm{and}u\ne v,$ then we have $H_{u,v}\left(\tau \right)={\displaystyle \sum _{n=0}^{N-\tau -1}}h\left({〈u-v〉}_M,0\right)=0.$

Hence, $\mathbb{G}$ is a $[q,N,M,Z]$ NHZ sequence set and $q=M(Z+1)$. Therefore, $\mathbb{G}$ is optimal with respect to the bound (4). □

4.3. A Numerical Example of BC-NHZ Sequence Set

The parameters of the BC-NHZ sequence set are preset as $q=20$, $N=22$, $M=5$, and the basic sequence $\left(b{s}_0,b{s}_1,\cdots ,b{s}_{21}\right)$ constructed by the BC algorithm and remapping method is as follows.

$$\begin{array}{c}\left(b{s}_0,b{s}_1,\cdots ,b{s}_{21}\right)\hfill \\ =\left(0103123223012123133210\right).\hfill \end{array}$$

The BC-NHZ sequence set of $\mathbb{G}=\left\{{\mathit{g}}^{\mathit{u}}\right|u=1,2,3,4,5\}$ can be obtained as displayed in the middle of this page according to the proposed algorithm. It is easy to check that the constructed set has five integer sequences with a length of 22; additionally, the size of the alphabet is equal to 20. The constructed $\mathbb{G}$ has a no-hit zone of width $Z=3$, and the parameters make the equation established in (4). Therefore, $\mathbb{G}$ is the optimal NHZ sequence set satisfying the optimal NHZ bound.

$$\underset{\begin{array}{c}\left\{{\mathit{g}}^{\mathit{u}}\right|u = 1, 2, 3, 4, 5\} =\\ \left\{\begin{array}{cccccccccccccccccccccc}(19& 16& 14& 15& 12& 5& 8& 11& 18& 0& 14& 9& 18& 16& 6& 15& 12& 0& 8& 11& 12& 16),\\ (12& 5& 2& 13& 18& 0& 7& 15& 1& 17& 2& 11& 1& 5& 8& 13& 18& 17& 7& 15& 18& 5),\\ (18& 0& 6& 4& 1& 17& 14& 13& 3& 10& 6& 15& 3& 0& 7& 4& 1& 10& 14& 13& 1& 0),\\ (1& 17& 8& 9& 3& 10& 2& 4& 19& 16& 8& 13& 19& 17& 14& 9& 3& 16& 2& 4& 3& 17),\\ (3& 10& 7& 11& 19& 16& 6& 9& 12& 5& 7& 4& 12& 10& 2& 11& 19& 5& 6& 9& 19& 10).\end{array}\right\}\end{array}}{-}$$

The maximum values related to the Hamming correlation at delays $\tau$ are shown in Table 2. For comparison, the pseudorandom sequences [17], the orthogonal sequences [29], and the NHZ sequences [36] are also presented. In Table 2, we mainly focus on the case when the delay $\tau$ is limited within the NHZ width Z (i.e., $\left|\tau \right|\le 3$). For the pseudorandom sequences, the frequency hits always spread over all delays, implying that the DS network suffers from severe MAI. The proposed BC-NHZ and NHZ sequences possess the all-zero Hamming correlations, while the orthogonal sequences attain non-zero Hamming correlation values when $\left|\tau \right|>0$. Thus, the proposed BC-NHZ and NHZ scheme is superior to the orthogonal scheme in MAI suppression.

Table 2. Hamming correlation of comparisons among the proposed BC-nhz and classic sequences.

	$\mathit{\tau }$	…	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4	…
$Proposed$  $BC-NHZ$  $sequences$	$H_{u,u}\left(\tau \right)$	…	2	0	0	0	22	0	0	0	2	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	5	0	0	0	0	0	0	0	5	…
$Pseudorandom$ $sequences$ [17]	$H_{u,u}\left(\tau \right)$	…	1	2	3	4	22	4	3	2	1	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	5	4	3	5	2	5	3	4	5	…
$Trad. Orthogonal$ $sequences$ [29]	$H_{u,u}\left(\tau \right)$	…	1	2	2	2	22	2	2	2	1	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	3	2	2	4	0	4	2	2	3	…
$Optimal$ $NHZ$ $sequences$ [36]	$H_{u,u}\left(\tau \right)$	…	4	0	0	0	22	0	0	0	4	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	6	0	0	0	0	0	0	0	6	…

Table 2. Hamming correlation of comparisons among the proposed BC-nhz and classic sequences.

	$\mathit{\tau }$	…	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4	…
$Proposed$  $BC-NHZ$  $sequences$	$H_{u,u}\left(\tau \right)$	…	2	0	0	0	22	0	0	0	2	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	5	0	0	0	0	0	0	0	5	…
$Pseudorandom$ $sequences$ [17]	$H_{u,u}\left(\tau \right)$	…	1	2	3	4	22	4	3	2	1	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	5	4	3	5	2	5	3	4	5	…
$Trad. Orthogonal$ $sequences$ [29]	$H_{u,u}\left(\tau \right)$	…	1	2	2	2	22	2	2	2	1	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	3	2	2	4	0	4	2	2	3	…
$Optimal$ $NHZ$ $sequences$ [36]	$H_{u,u}\left(\tau \right)$	…	4	0	0	0	22	0	0	0	4	…
	$H_{u,v}\left(\tau \right),u\ne v$	…	6	0	0	0	0	0	0	0	6	…

5. Simulation Results

In this section, the network capacity and complexity metric of the DS network employing the BC-NHZ scheme are simulated to verify communication quality and privacy protection. We recall the following assumptions for system infrastructure and simulation setup:

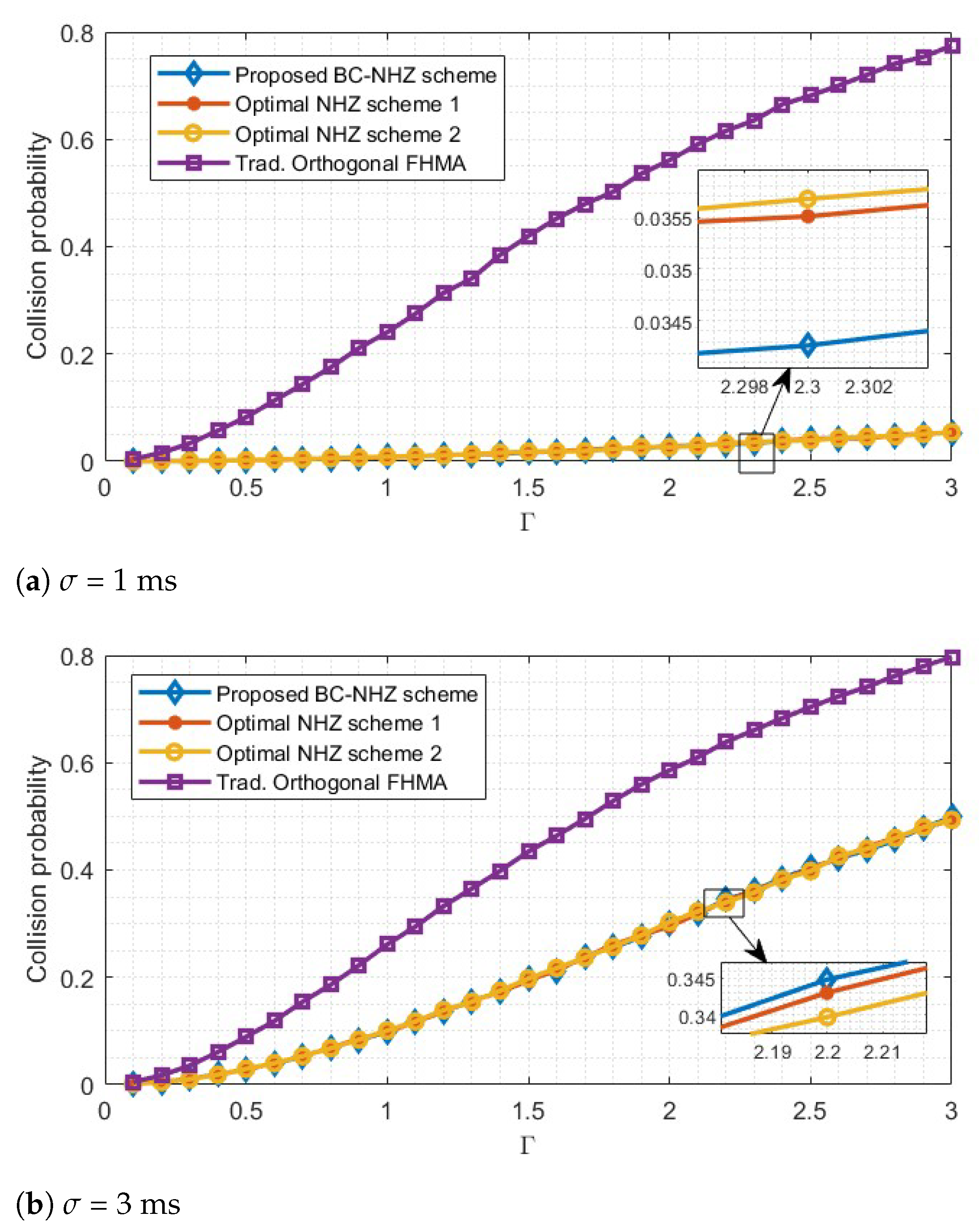
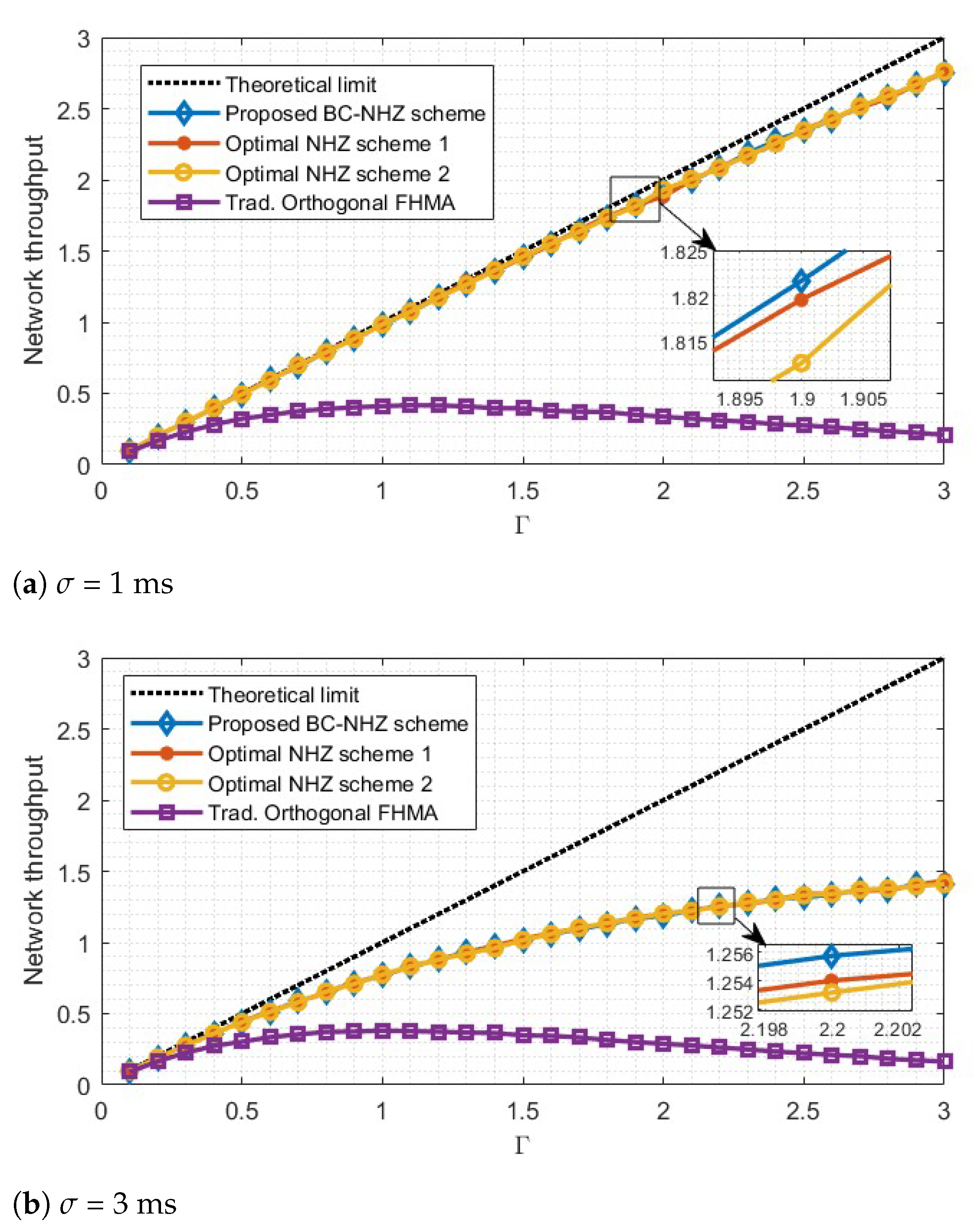
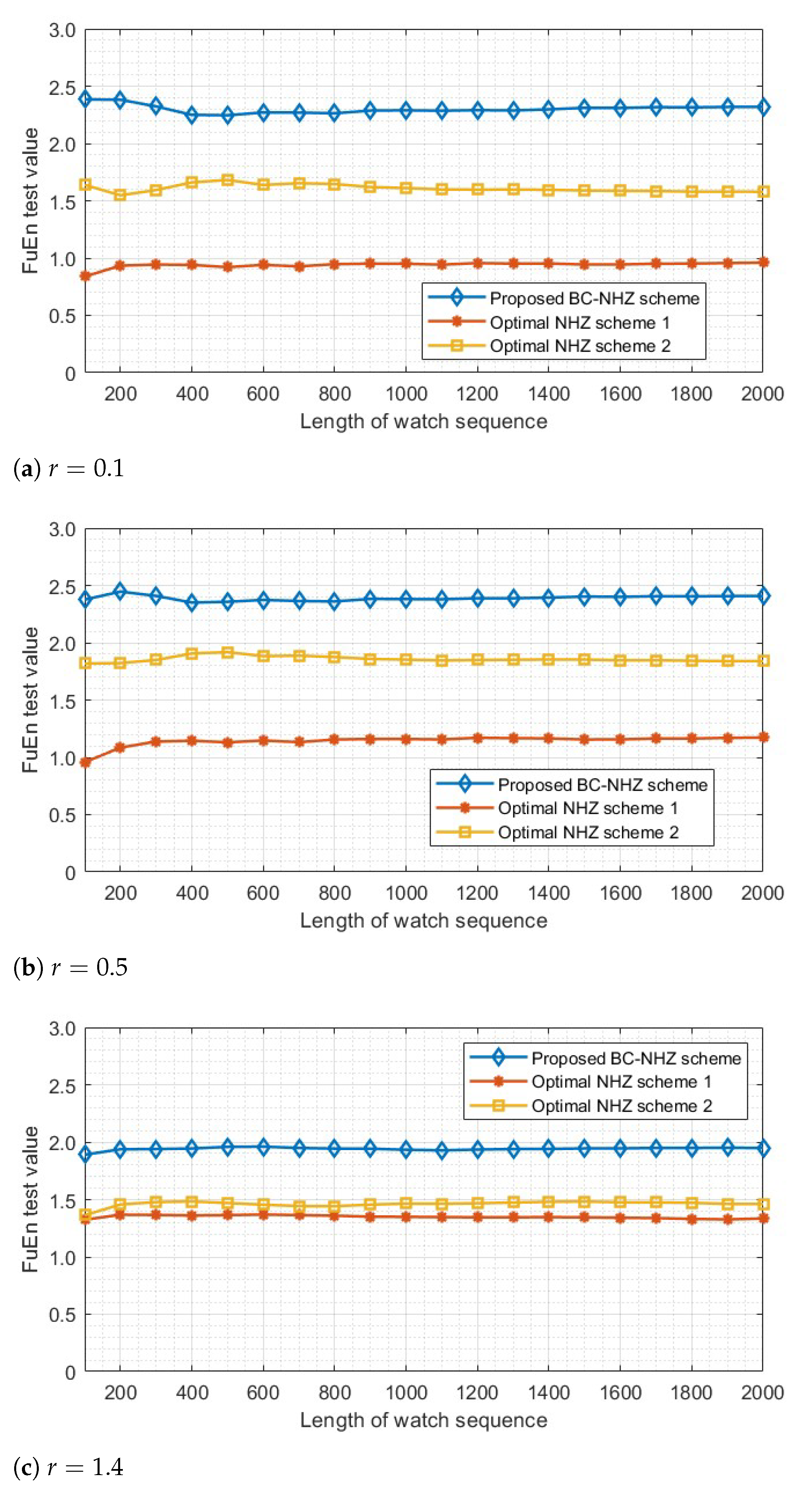
• The quasi-synchronous access mechanism is adopted by practical systems, and $r\left(t\right)$ consists of several $y^u(t-{\tau }_u)$. $D_u$’s relative delay ${\tau }_u$ is independently distributed over ${\tau }_u\sim \mathcal{N}(\mu ,{\sigma }^2)$ for any ${\tau }_u$.
• The shared communication spectrum B is divided equally into 20 frequency slots. The proposed BC-NHZ or the baseline schemes control the communication carrier frequency and continuously vary over frequency slots with a width of 1 MHz, switching the frequency at each time interval T = 1 ms.
• The simulation time length is 260 s, and each hopping interval consists of protection time $T_0$ = 0.2 ms and transmission time $(T-T_0)$ = 0.8 ms.
• The length of the transmitted service packet is $L_{sp}=4$ hopping intervals, and the packet services arrival between data owners are independent and satisfy the Poisson distribution of the DS network’s total arrival rate $\Gamma$.
• For a fair comparison, the adopted spectrum control sequence sets in the following simulations have similar values of parameters, i.e., the frequency-slot size q, the NHZ width Z, the family size M, and so forth.

Under the aforementioned conditions and setup, the BC-NHZ set $\mathbb{G}$ with the parameters of $[q,N,M,Z]$ = $[20,2^{18},5,3]$, as shown in Section 4.1, is constructed by the proposed algorithm. The results are also observed and analyzed against the other optimal NHZ sequence sets concerning the Hamming correlation [36,39], which are denoted as ‘Optimal NHZ Scheme 1’ and ‘Optimal NHZ Scheme 2’.

5.1. Network Capacity

Here, the network capacity is simulated under different arrival rates by two metrics: collision probability and network throughput, as shown in Figure 5 and Figure 6.

The collision probability indicates that two or more data owners use the same frequency slot for transmission at the same hopping interval. The simulation results for the variation of collision probability to the arrival rate $\Gamma$ are shown in Figure 5. The horizontal axis is the packet arrival rate $\Gamma$, and the vertical axis is the corresponding simulated values of collision probability. The proposed scheme is compared here with FHMA transmission strategies using orthogonal sequences in [29] (denoted as ‘Trad. Orthogonal FHMA’).

In Figure 5, it can be seen that the collision probability of all schemes rises with increasing $\Gamma$. This is because when there are more transmission tasks in the network, the signals from several data owners are more likely to transmit simultaneously, leading to more collisions. From Figure 5a,b, the NHZ scheme considerably reduces the collision probability compared to the traditional orthogonal FHMA schemes. For instance, at $\Gamma$ = 3.0 and $\sigma$ = 1 ms, all three NHZ schemes achieve a value of 0.05 compared to 0.77 achieved by traditional orthogonal FHMA. This is because traditional orthogonal FHMA transmission eliminates the MAI when the relative delay is close to 0. In contrast, the NHZ schemes achieve this effect over a wide range of delays. In addition, the root-variance $\sigma$ value of the delay ${\tau }_u$ is assumed to have the value of 1 ms and 3 ms, respectively. The collision probability of optimal NHZ schemes and the proposed scheme increases with the increase in $\sigma$. This is because as the $\sigma$ increases, the discretization of the relative delay of the signals at the receiver increases, resulting in the relative delay between the signals from different data owners exceeding the preset no-hit zone.

The network throughput is the number of packets correctly transmitted by the network per time interval and is a key determinant of the performance of a spectrum control transmission scheme. Figure 6 illustrates the variation in network throughput with arrival rate $\Gamma$. The horizontal axis is the packet arrival rate $\Gamma$, and the vertical axis is the corresponding simulated values of network throughput. The figure takes as a theoretical limit the DS network throughput of all data owners ideally transmitting without mutual interference, and the value of network throughput is equal to $\Gamma$.

In Figure 6, all three NHZ schemes perform better than the competing orthogonal FHMA transmission. The proposed BC-NHZ algorithm’s network throughput increases with the arrival rate $\Gamma$ increasing, while the throughput of traditional orthogonal FHMA increases and then decreases. When $\Gamma >0.5$, the throughput of the NHZ sequence set is significantly higher than that of the conventional orthogonal FHMA. For example, at $\Gamma =3$ and $\sigma =1$, the three NHZ schemes achieve the same value of 2.76 for network throughput compared to 0.21 achieved by FHMA. This is because all three schemes have the same NHZ width. The collision probability is minimal, and even if the network load is large, the interactions of the subnets are not severe, so the throughput becomes more significant with the increase in the network load. In contrast, the traditional orthogonal FHMA scheme uses semi-random multi-access schemes, leading to performance degradation in QS networks. The frequency usage conflict between data users worsens when the network load is significant, leading to a decrease in the network load. In addition, the network throughputs of optimal NHZ schemes and the proposed scheme are more resistant to reaching the theoretical bounds with the increase in $\sigma$. Similarly, this is because as $\sigma$ increases, the discretization of the relative delay of the signals at the receiver increases, resulting in the relative delay between the signals from different data owners exceeding the preset no-hit zone.

In conclusion, the proposed BC-NHZ scheme achieves or is close to the theoretical limit when the relative delay ${\tau }_u$ distribution of the signal is relatively concentrated (e.g., $\sigma$ = 1 ms). Thanks to the excellent properties of the constructed set of BC-NHZ sequences, the proposed scheme is able to achieve the performance of the optimal NHZ scheme and significantly improves the communication capability of QS DS networks.

5.2. Complexity Metric

In this subsection, the complexity metric of the schemes is evaluated using the FuEn test. The sample variances of the three NHZ schemes are measured as 33.38, 33.21, and 33.23, respectively. Thus, with the guidelines established in the literature [20,21], the value of the resolution parameter r is from 0.1 to 1.44 (e.g., $r=0.1,0.5,1.4$), while the vector dimension m is set to 2. Figure 7 illustrates the complexity performance of different sequences under the FuEn test, where the vertical axis represents the FuEn test values and the horizontal axis corresponds to the length of the observation sequence. Based on FuEn applications reported in the existing literature, the observation sequence length in this study is set to $(100,200,.\dots ,2000)$.

From Figure 7, the FuEn metric of the proposed sequence with the cryptographic algorithm remains stable and significantly higher than the other control sequences for different watch lengths because the proposed sequences use cryptographic principles and have excellent resistance to deciphering. In addition, comparing Figure 7a–c, the FuEn values of the three schemes are gradually closer to each other as the resolution parameter r increases. The reason is that a larger r loses part of the statistical information and reduces the sensitivity to random variation.

In conclusion, leveraging a block cipher-based encryption mechanism, our sequence generation algorithm demonstrates superior cryptographic complexity metrics. The FuEn value of the proposed sequence is consistently higher than the other baseline sequences under different conditions, showing higher complexity and stability, proving its excellence in privacy protection.

6. Conclusions and Future Work

In this paper, we addressed the challenges of ensuring communication quality and privacy protection among distributed devices in DS networks. To tackle these issues, we proposed a BC-NHZ sequences-assisted spectrum control scheme that effectively mitigates multiple access interference (MAI) while maintaining network capacity within a specific delay range. Leveraging a block cipher-based encryption mechanism, our sequence generation algorithm demonstrates superior cryptographic complexity metrics. Through rigorous theoretical analysis and simulations, we demonstrated that the BC-NHZ scheme outperforms baseline methods in terms of collision probability and network throughput, highlighting its ability to efficiently utilize limited spectrum resources. Additionally, simulation results confirmed that our BC-NHZ scheme achieves significant improvements in deciphering resistance complexity compared to existing NHZ schemes.

This paper underscores the BC-NHZ scheme’s potential to enhance network capacity and secure transmission in DS communication networks. The proposed design methodology and theoretical insights provide a valuable foundation for future research on secure access schemes in wireless communication systems. However, the block cipher operations introduced in our scheme may exacerbate computational overhead in resource-constrained edge devices, which merits further optimization. Future research should address the trade-off between sequence performance and computational efficiency—a dimension conspicuously absent in existing NHZ sequence set designs, which primarily focus on Hamming correlation metrics.

To address these challenges, our ongoing work aims to: (1) develop lightweight cryptographic primitives that maintain security guarantees while reducing computational complexity and (2) extend the BC-NHZ framework to support hierarchical subnet access control, thereby enabling scalable deployment in large-scale networks. By integrating these enhancements, we seek to create a next-generation secure access scheme that balances theoretical performance, computational efficiency, and practical deployability in emerging wireless ecosystems.