A Modular Prescribed Performance Formation Control Scheme of a High-Order Multi-Agent System with a Finite-Time Extended State Observer
Abstract
1. Introduction
- 1.
- Distributed signal generator for formation: We developed a novel distributed signal generator mechanism to coordinate the formation. This virtual reference generator produces trajectory signals that each agent tracks, enabling the group of high-order agents to achieve the desired formation shape. Unlike traditional leader–follower schemes, the signal generator approach provides a unified reference without requiring a designated leader, and it inherently facilitates synchronization between agents.
- 2.
- Finite-time extended state observer (FTESO): A finite-time extended state observer was designed for each agent to estimate the compounded effect of model uncertainties and external disturbances in real time. The observer was proven to converge in finite time, providing fast and accurate estimates of unmeasured states (such as higher-order derivatives and disturbance forces). These estimates were used to actively compensate for the uncertainties in the control law, which substantially improved the robustness.
- 3.
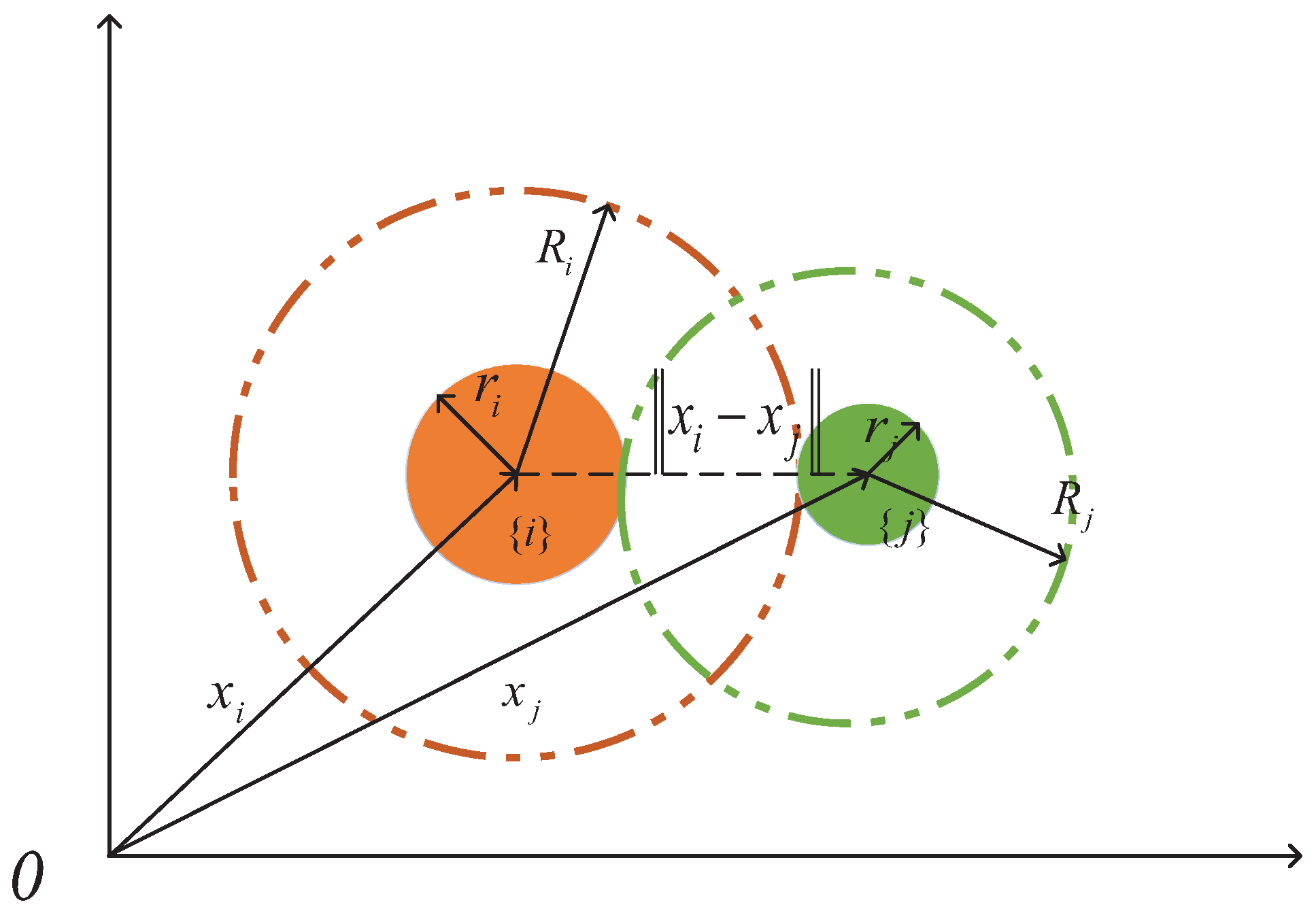
- Prescribed performance control with connectivity guarantees: We formulated a distributed control law that incorporates the prescribed performance bounds into the feedback loop. By embedding the signal generator outputs as reference trajectories and utilizing the FTESO estimates, the proposed controller drives each agent’s tracking error to remain within a predefined performance funnel and reach zero in finite time. This ensures that both transient and steady-state performance specifications are met. Notably, by carefully designing the performance functions (constraints on the tracking errors), the controller guarantees connectivity maintenance and collision avoidance throughout the formation maneuver. Inter-agent distance errors are confined within safe limits so that all agents stay connected and no collisions occur by design.
2. Preliminaries
2.1. Graphs and Rigidity Theory
2.2. Problem Formulation
3. Distributed LESO-Based Prescribed Performance Design
3.1. Distributed Prescribed Performance Signal Generator Design
3.2. FTESO-Based Prescribed Performance Tracking Controller Design
3.2.1. FTESO Design
3.2.2. Prescribed Performance Tracking Controller Design
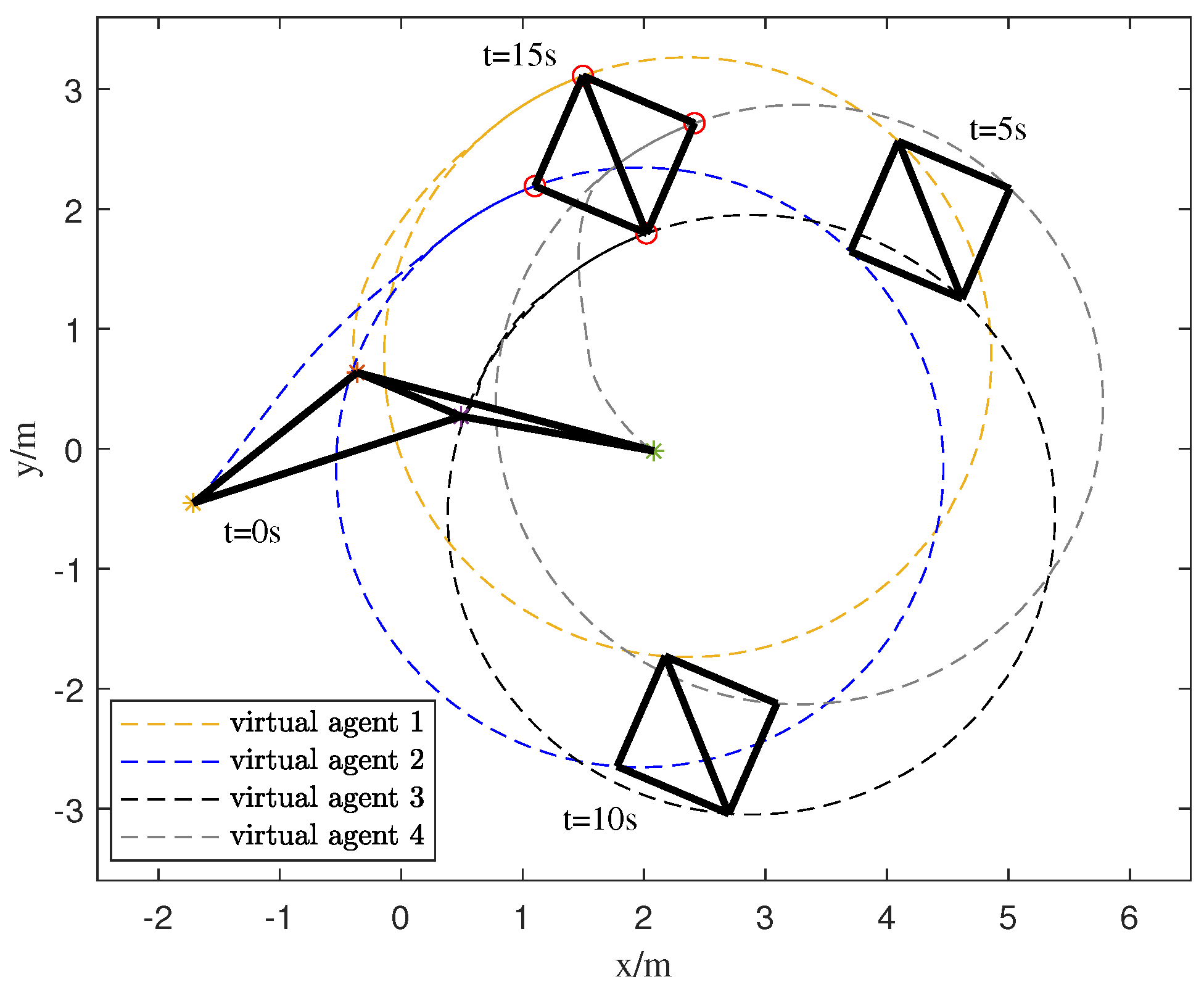
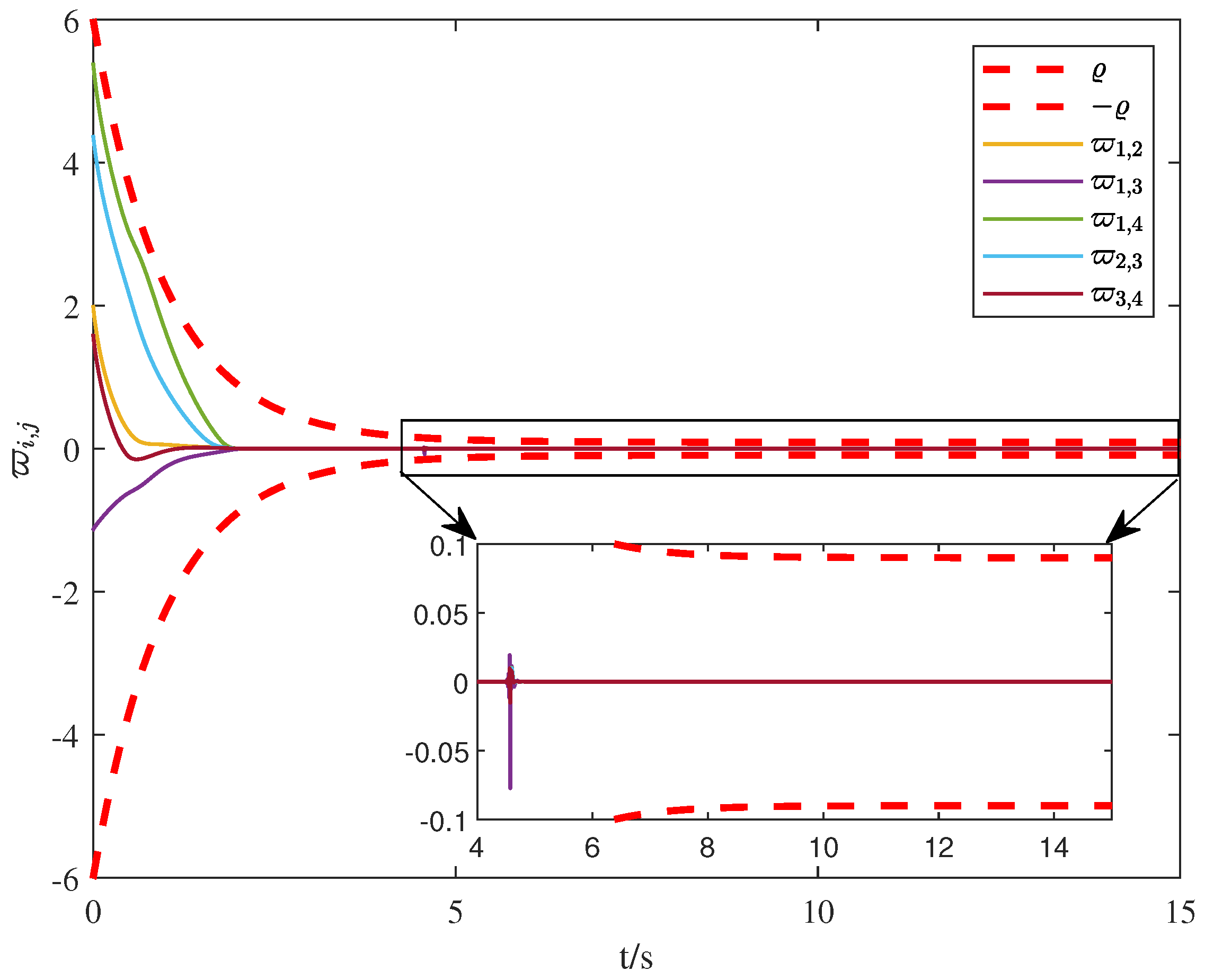
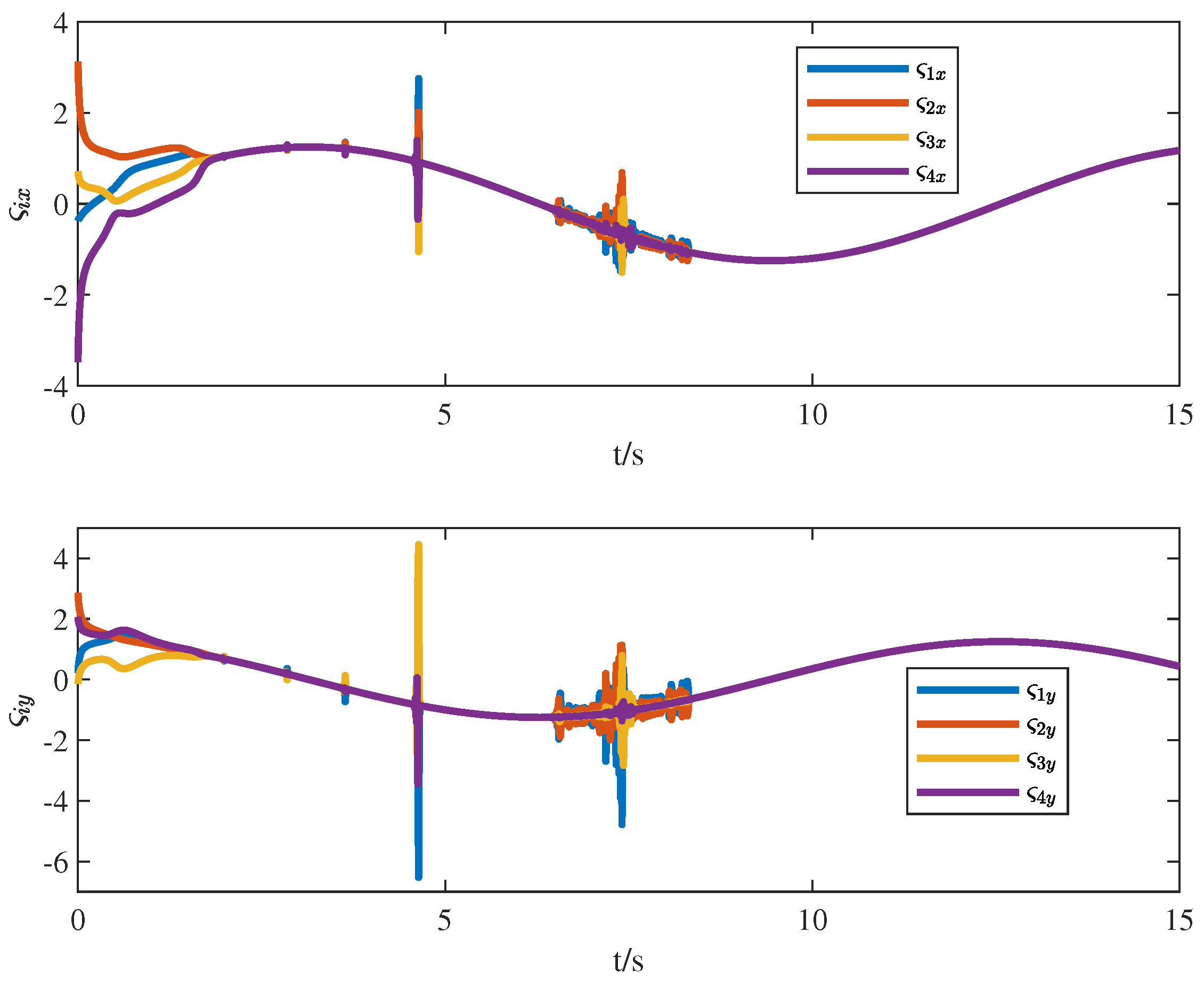
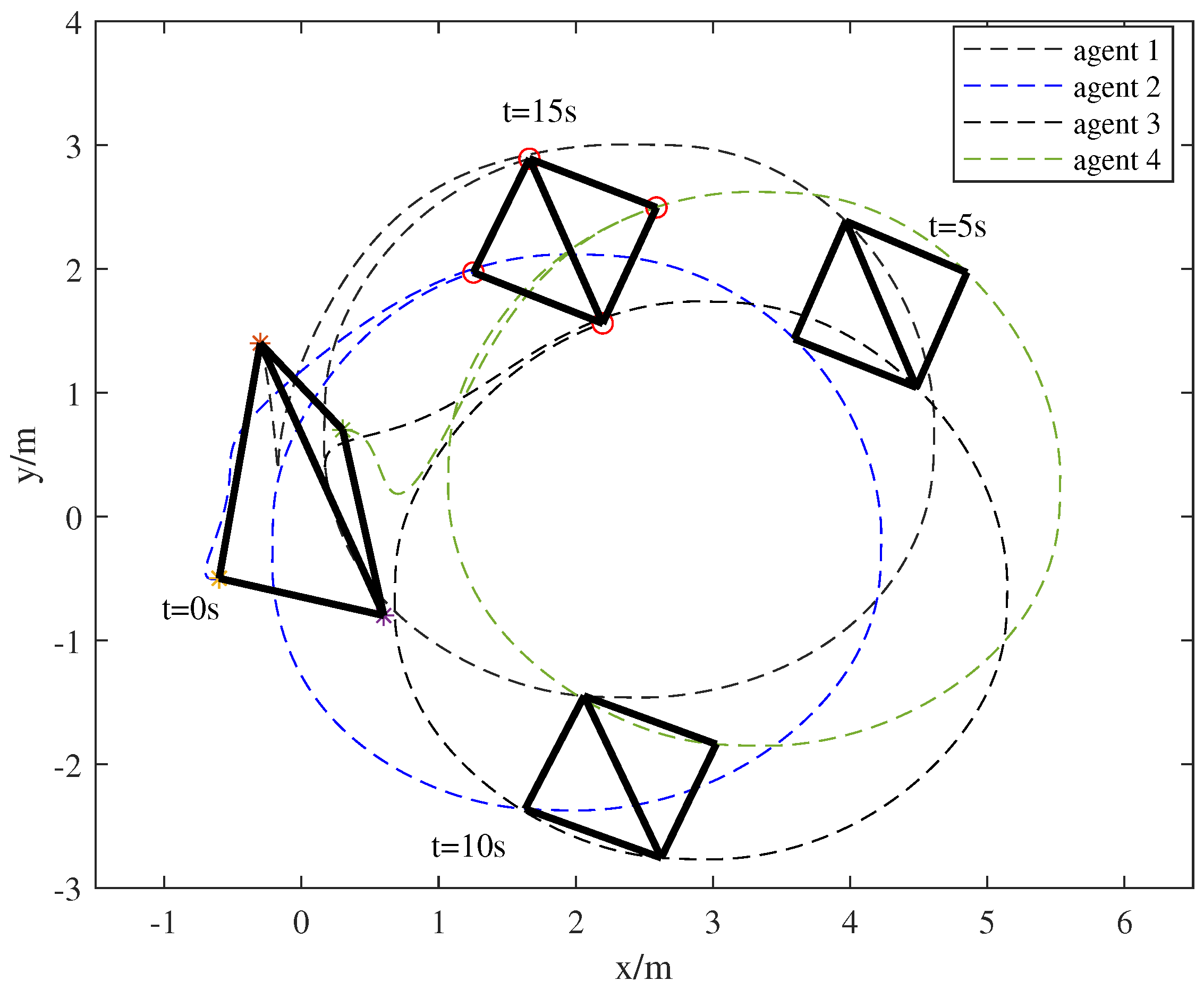
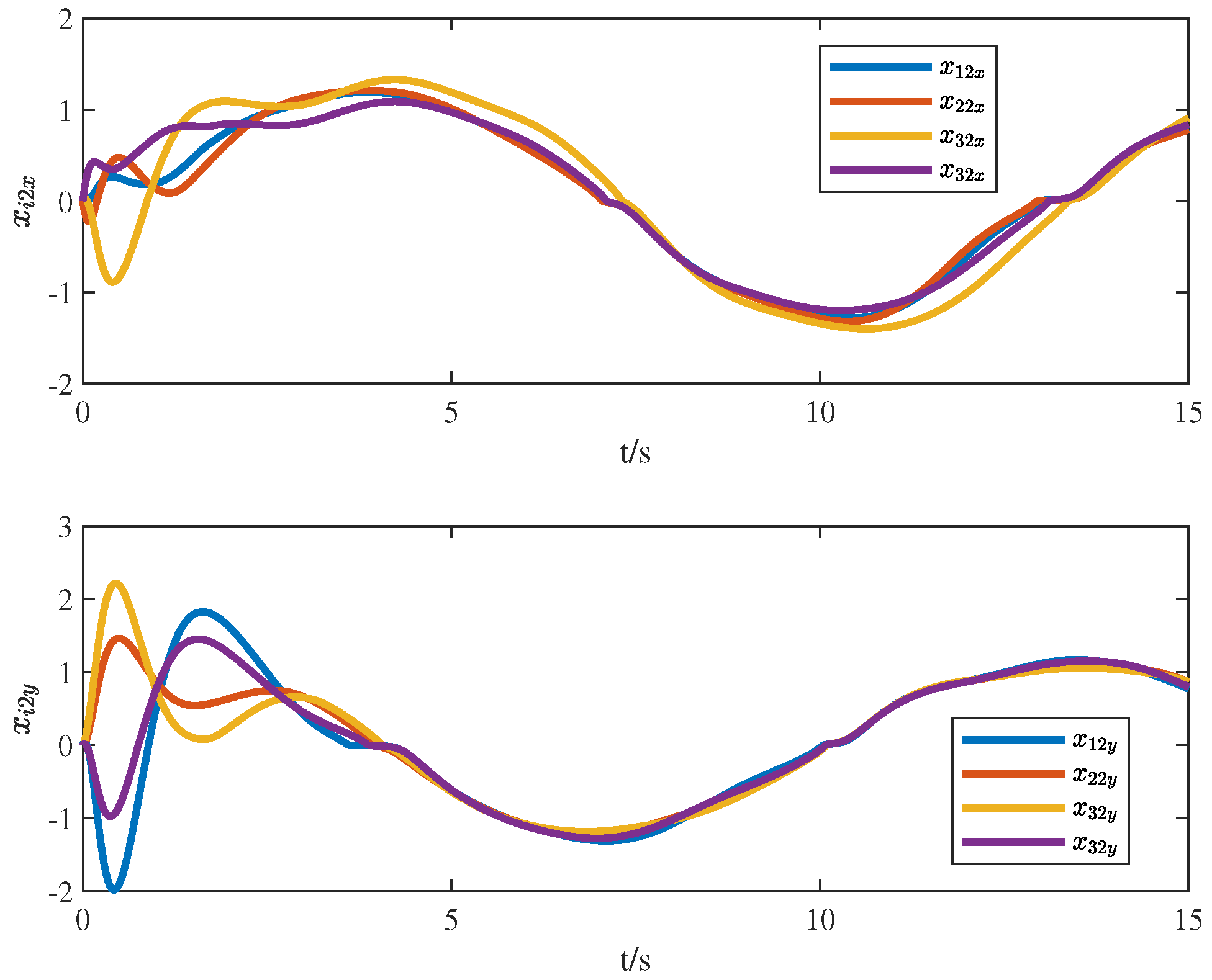
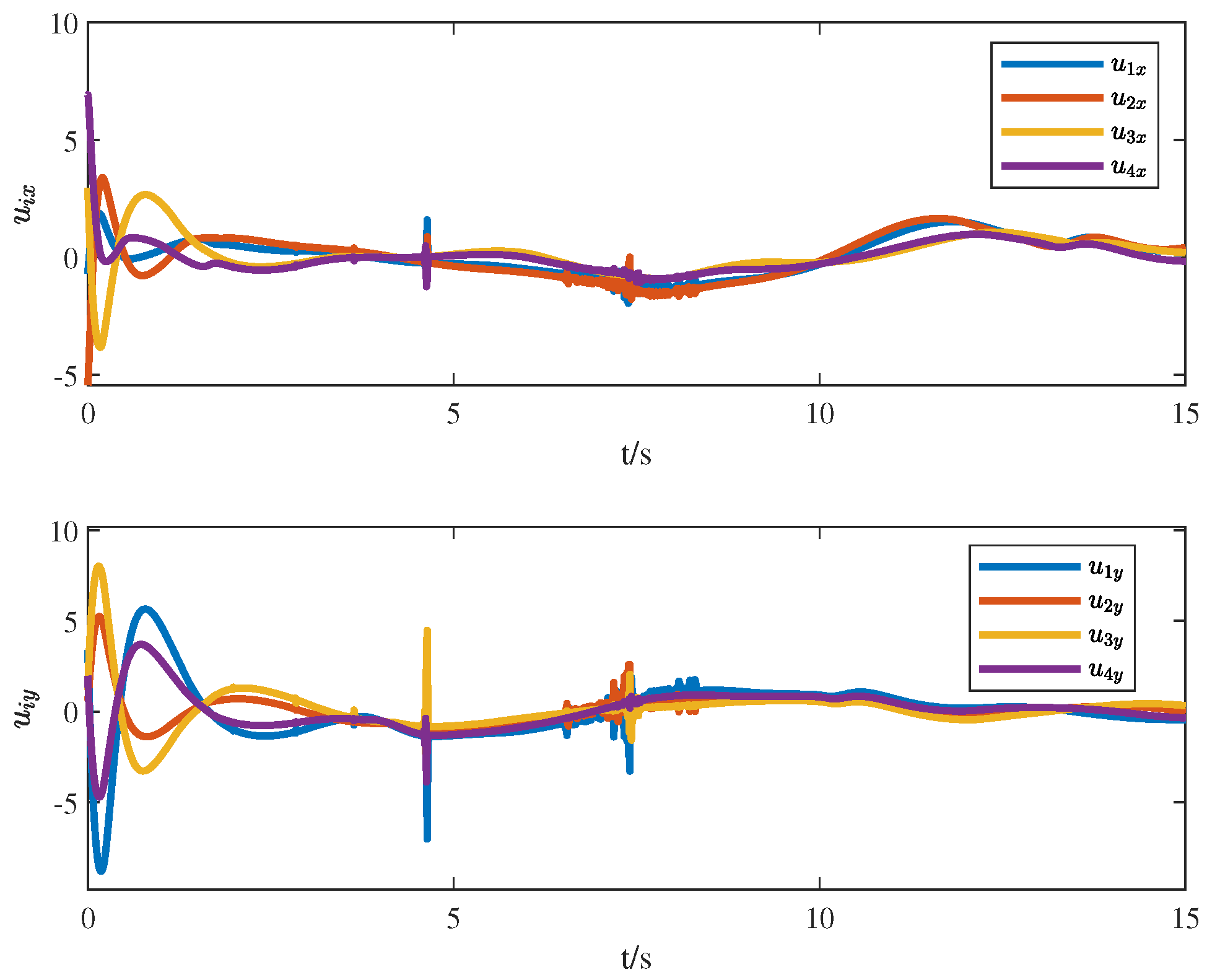
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Cai, K.; Qu, T.; Gao, B.; Chen, H. Consensus-based distributed cooperative perception for connected and automated vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8188–8208. [Google Scholar] [CrossRef]
- Meng, Z.; Ren, W.; Cao, Y.; You, Z. Leaderless and leader-following consensus with communication and input delays under a directed network topology. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2010, 41, 75–88. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Yu, S.; Yan, Y. Fixed-time stability of stochastic nonlinear systems and its application into stochastic multi-agent systems. Iet Control Theory Appl. 2021, 15, 126–135. [Google Scholar] [CrossRef]
- Chen, F.; Ren, W. On the control of multi-agent systems: A survey. Found. Trends Syst. Control 2019, 6, 339–499. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, G.; Wan, Y.; Fu, J. Consensus tracking control for a class of general linear hybrid multi-agent systems: A model-free approach. Automatica 2023, 156, 111198. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, B.; Han, Q.L. Dynamic event-triggered scaled consensus of multi-agent systems in reliable and unreliable networks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 1124–1136. [Google Scholar] [CrossRef]
- Lu, M.; Liu, L. Leader-following attitude consensus of multiple rigid spacecraft systems under switching networks. IEEE Trans. Autom. Control 2019, 65, 839–845. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, X.; Wang, Y.; Huang, L.; Wei, Q. Quantization-based event-triggered H∞ consensus for discrete-time Markov Jump fractional-order multiagent systems with DoS Attacks. Fractal Fract. 2024, 8, 147. [Google Scholar] [CrossRef]
- Wu, K.; Hu, J.; Ding, Z.; Arvin, F. Finite-time fault-tolerant formation control for distributed multi-vehicle networks with bearing measurements. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1346–1357. [Google Scholar] [CrossRef]
- de Marina, H.G. Maneuvering and robustness issues in undirected displacement-consensus-based formation control. IEEE Trans. Autom. Control 2020, 66, 3370–3377. [Google Scholar] [CrossRef]
- Shojaei, K. Output-feedback formation control of wheeled mobile robots with actuators saturation compensation. Nonlinear Dyn. 2017, 89, 2867–2878. [Google Scholar] [CrossRef]
- Choi, Y.H.; Yoo, S.J. Neural-network-based distributed asynchronous event-triggered consensus tracking of a class of uncertain nonlinear multi-agent systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2965–2979. [Google Scholar] [CrossRef]
- Zhao, W.; Yu, W.; Zhang, H. Observer-based formation tracking control for leader–follower multi-agent systems. IET Control Theory Appl. 2019, 13, 239–247. [Google Scholar] [CrossRef]
- Xue, W.; Madonski, R.; Lakomy, K.; Gao, Z.; Huang, Y. Add-on module of active disturbance rejection for set-point tracking of motion control systems. IEEE Trans. Ind. Appl. 2017, 53, 4028–4040. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Saarakkala, S.E.; Awan, H.A.A.; Molsa, E.; Tuovinen, T. Observers for sensorless synchronous motor drives: Framework for design and analysis. IEEE Trans. Ind. Appl. 2018, 54, 6090–6100. [Google Scholar] [CrossRef]
- Zhang, D.; Deng, C.; Feng, G. Resilient cooperative output regulation for nonlinear multiagent systems under DoS attacks. IEEE Trans. Autom. Control 2022, 68, 2521–2528. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, S.; Jiang, H.; Mei, X. Distributed fixed-time optimization for multi-agent systems over a directed network. Nonlinear Dyn. 2021, 103, 775–789. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, K. Optimal consensus for uncertain high-order multi-agent systems by output feedback. Int. J. Robust Nonlinear Control 2022, 32, 2084–2099. [Google Scholar] [CrossRef]
- Qiao, Y.; Huang, X.; Yang, B.; Geng, F.; Wang, B.; Hao, M.; Li, S. Formation tracking control for multi-agent systems with collision avoidance and connectivity maintenance. Drones 2022, 6, 419. [Google Scholar] [CrossRef]
- Chen, L.; Shi, M.; de Marina, H.G.; Cao, M. Stabilizing and maneuvering angle rigid multiagent formations with double-integrator agent dynamics. IEEE Trans. Control Netw. Syst. 2022, 9, 1362–1374. [Google Scholar] [CrossRef]
- Gong, X.; Cui, Y.; Shen, J.; Xiong, J.; Huang, T. Distributed optimization in prescribed-time: Theory and experiment. IEEE Trans. Netw. Sci. Eng. 2021, 9, 564–576. [Google Scholar] [CrossRef]
- Dai, S.L.; Lu, K.; Fu, J. Adaptive finite-time tracking control of nonholonomic multirobot formation systems with limited field-of-view sensors. IEEE Trans. Cybern. 2021, 52, 10695–10708. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Wang, C.; Kao, Y.; Jiang, Y. A fixed-time distributed extended state observer for uncertain second-order nonlinear system. ISA Trans. 2023, 138, 373–383. [Google Scholar] [CrossRef]
- Ge, P.; Li, P.; Chen, B.; Teng, F. Fixed-time convergent distributed observer design of linear systems: A kernel-based approach. IEEE Trans. Autom. Control 2022, 68, 4932–4939. [Google Scholar] [CrossRef]
- Qin, D.; Wu, J.; Liu, A.; Zhang, W.-A.; Yu, L. Cooperation and coordination transportation for nonholonomic mobile manipulators: A distributed model predictive control approach. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 848–860. [Google Scholar] [CrossRef]
- Derakhshannia, M.; Moosapour, S.S. Disturbance observer-based sliding mode control for consensus tracking of chaotic nonlinear multi-agent systems. Math. Comput. Simul. 2022, 194, 610–628. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Wu, Q.; Li, S. A modular optimal formation control scheme of multiagent systems with application to multiple mobile robots. IEEE Trans. Ind. Electron. 2021, 69, 9331–9341. [Google Scholar] [CrossRef]
- Jackson, B.; Jordan, T. Connected rigidity matroids and unique realizations of graphs. J. Comb. Theory Ser. B 2005, 94, 1–29. [Google Scholar] [CrossRef]
- Hendrickson, B. Conditions for unique graph realizations. Siam J. Comput. 1992, 21, 65–84. [Google Scholar] [CrossRef]
- Sun, Z.; Mou, S.; Deghat, M.; Anderson, B. Finite time distributed distance-constrained shape stabilization and flocking control for d-dimensional undirected rigid formations. Int. J. Robust Nonlinear Control 2015, 26, 2824–2844. [Google Scholar] [CrossRef]
- Mehdifar, F.; Bechlioulis, C.P.; Hashemzadeh, F. Baradarannia M. Prescribed performance distance-based formation control of multi-agent systems. Automatica 2020, 119, 109086. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, J. Stabilization and Regulation of Nonlinear Systems; Springer International Publishing: Cham, Switzerland, 2015; pp. 0018–9286. [Google Scholar]
- Li, B.; Hu, Q.; Yang, Y. Continuous finite-time extended state observer based fault tolerant control for attitude stabilization. Aerosp. Sci. Technol. 2019, 84, 204–213. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.; Zuo, Z.; Ge, X.; Zhang, X. Collective behaviors of mobile robots beyond the nearest neighbor rules with switching topology. IEEE Trans. Cybern. 2018, 48, 1577–1590. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Inform. 2013, 9, 427–438. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Han, W.; Zhang, C.; Zhang, G. A Modular Prescribed Performance Formation Control Scheme of a High-Order Multi-Agent System with a Finite-Time Extended State Observer. Electronics 2025, 14, 1783. https://doi.org/10.3390/electronics14091783
Shi Z, Han W, Zhang C, Zhang G. A Modular Prescribed Performance Formation Control Scheme of a High-Order Multi-Agent System with a Finite-Time Extended State Observer. Electronics. 2025; 14(9):1783. https://doi.org/10.3390/electronics14091783
Chicago/Turabian StyleShi, Zhihan, Weisong Han, Chen Zhang, and Guangming Zhang. 2025. "A Modular Prescribed Performance Formation Control Scheme of a High-Order Multi-Agent System with a Finite-Time Extended State Observer" Electronics 14, no. 9: 1783. https://doi.org/10.3390/electronics14091783
APA StyleShi, Z., Han, W., Zhang, C., & Zhang, G. (2025). A Modular Prescribed Performance Formation Control Scheme of a High-Order Multi-Agent System with a Finite-Time Extended State Observer. Electronics, 14(9), 1783. https://doi.org/10.3390/electronics14091783





