Torque Ripple Reduction in Switched Reluctance Machines Considering Phase Torque-Generation Capability
Abstract
1. Introduction
- (1)
- Decoupling the phase turn-on angle from the starting angle of the TSF enables flexible adjustment of the turn-on angle to enhance torque-generation capability, achieving an approximately 10% reduction in torque ripple.
- (2)
- During commutation intervals, torque errors are compensated by the phase with greater torque-tracking ability, as evaluated using TPA characteristics, resulting in a 26% reduction in torque ripple without sacrificing efficiency.
- (3)
- A PWM-integrated DITC method is proposed to address large torque increments caused by limited practical control frequencies, effectively constraining torque within the hysteresis band and achieving a 25% reduction in torque ripple.
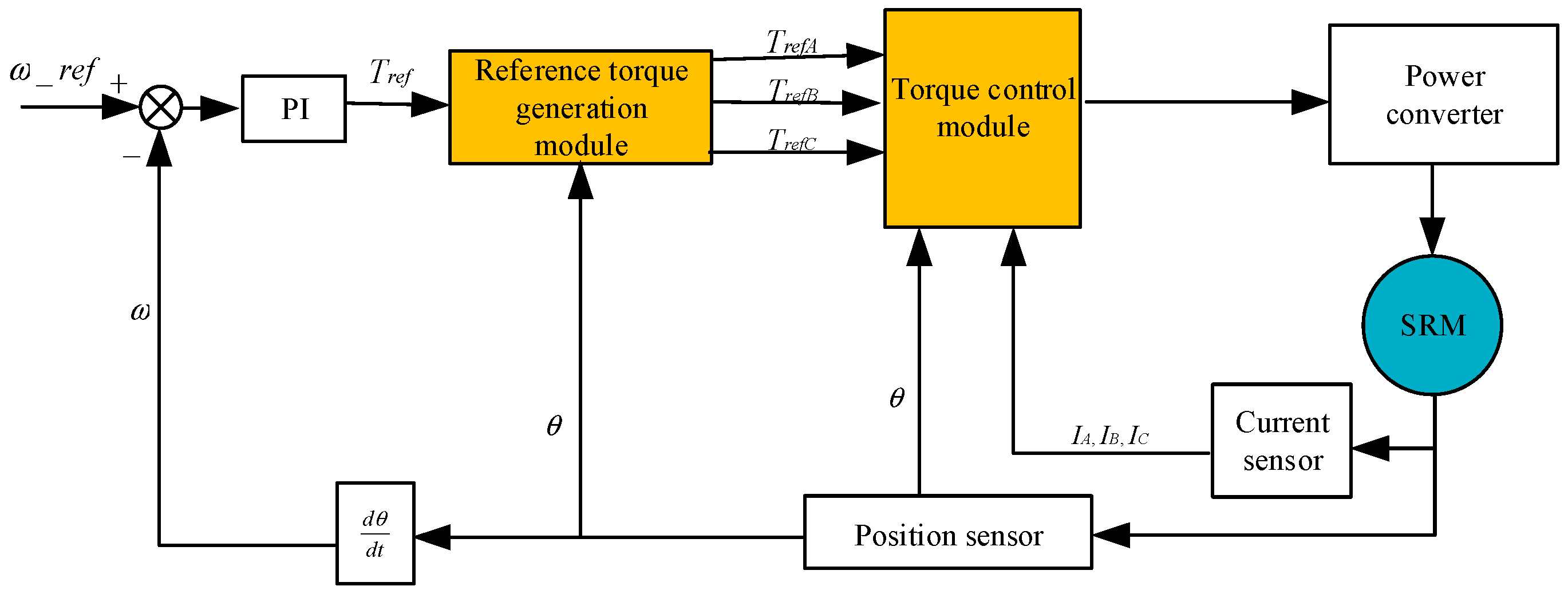
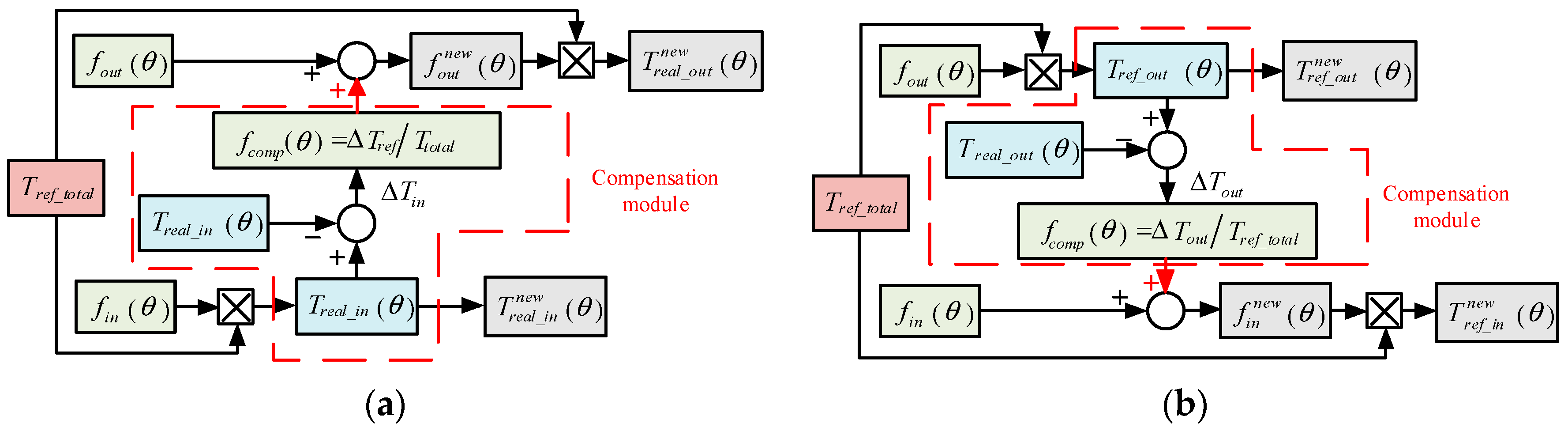
2. Online Compensated Torque-Sharing Function
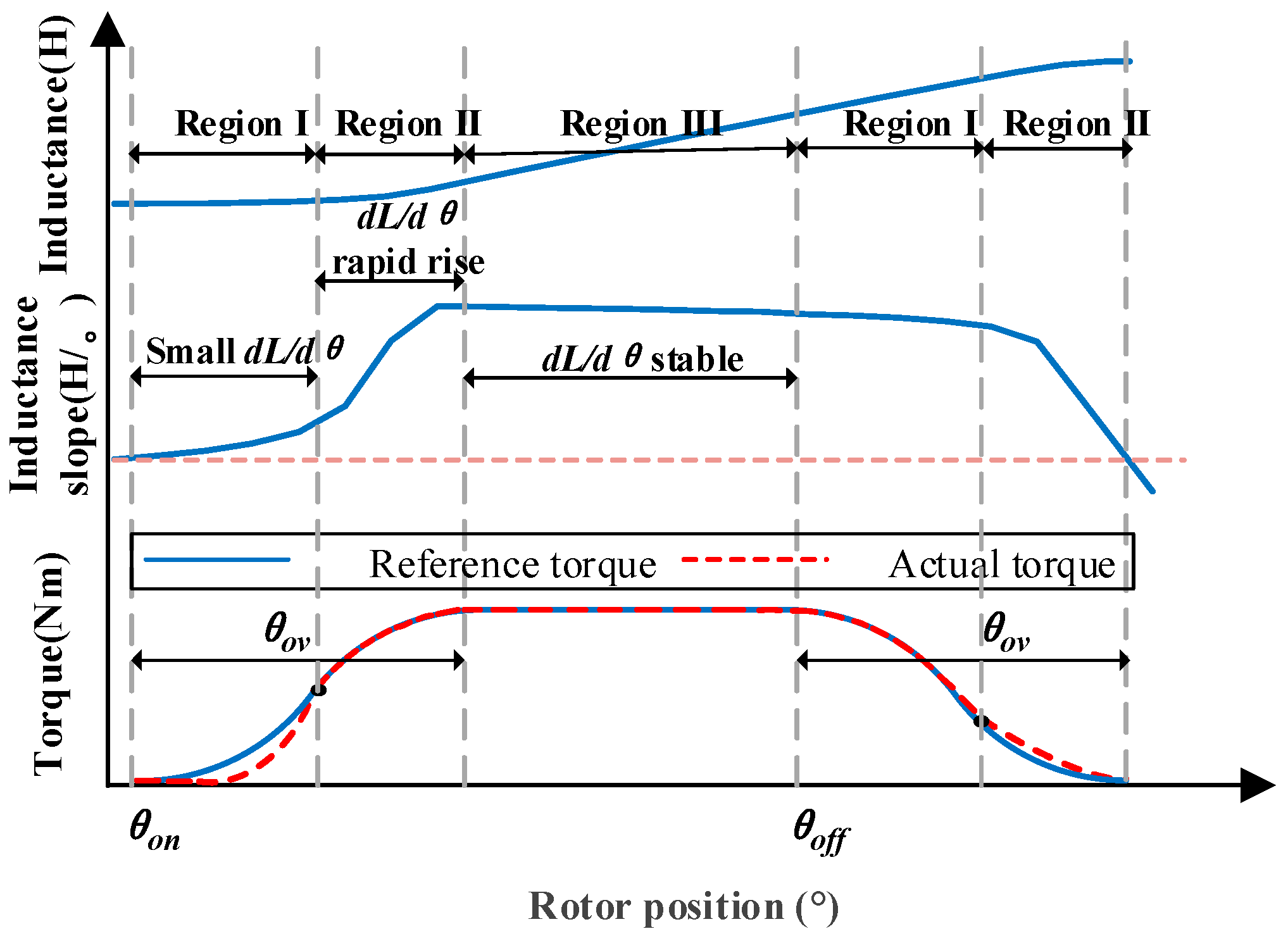
2.1. Origin of Torque Ripple
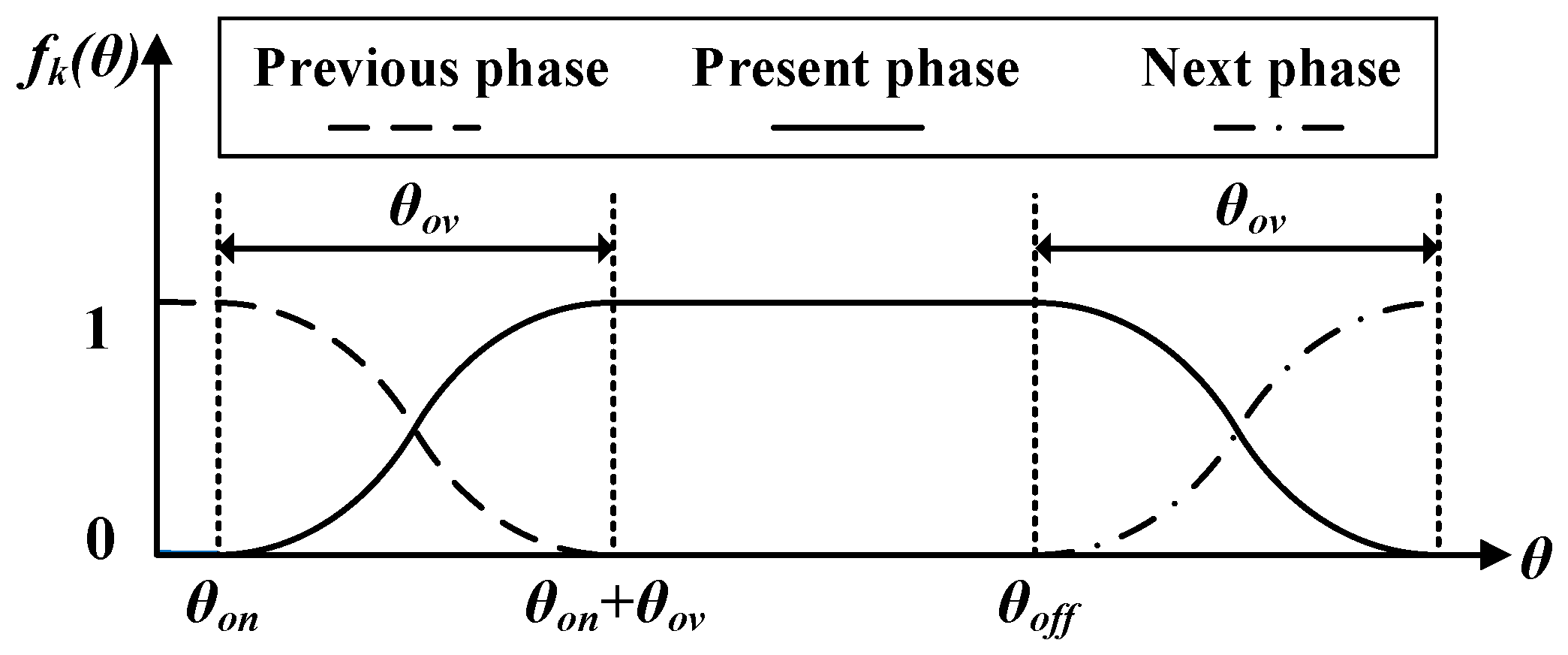
2.2. Conventional TSF
- (1)
- θon < θ < θon + θov: The present phase and the previous phase overlap. Here, the reference torque of the present phase increases, while the reference torque of the previous phase decreases.
- (2)
- θon + θov < θ < θoff: The reference torque of the previous phase has returned to zero. Only the present phase is excited, to provide the total torque.
- (3)
- θoff < θ < θoff + θov: The present phase and the next phase overlap. Here, the reference torque of the present phase decreases, while the reference torque of the next phase increases;
- (4)
- Others: The present phase is turned off, and the reference torque is zero.
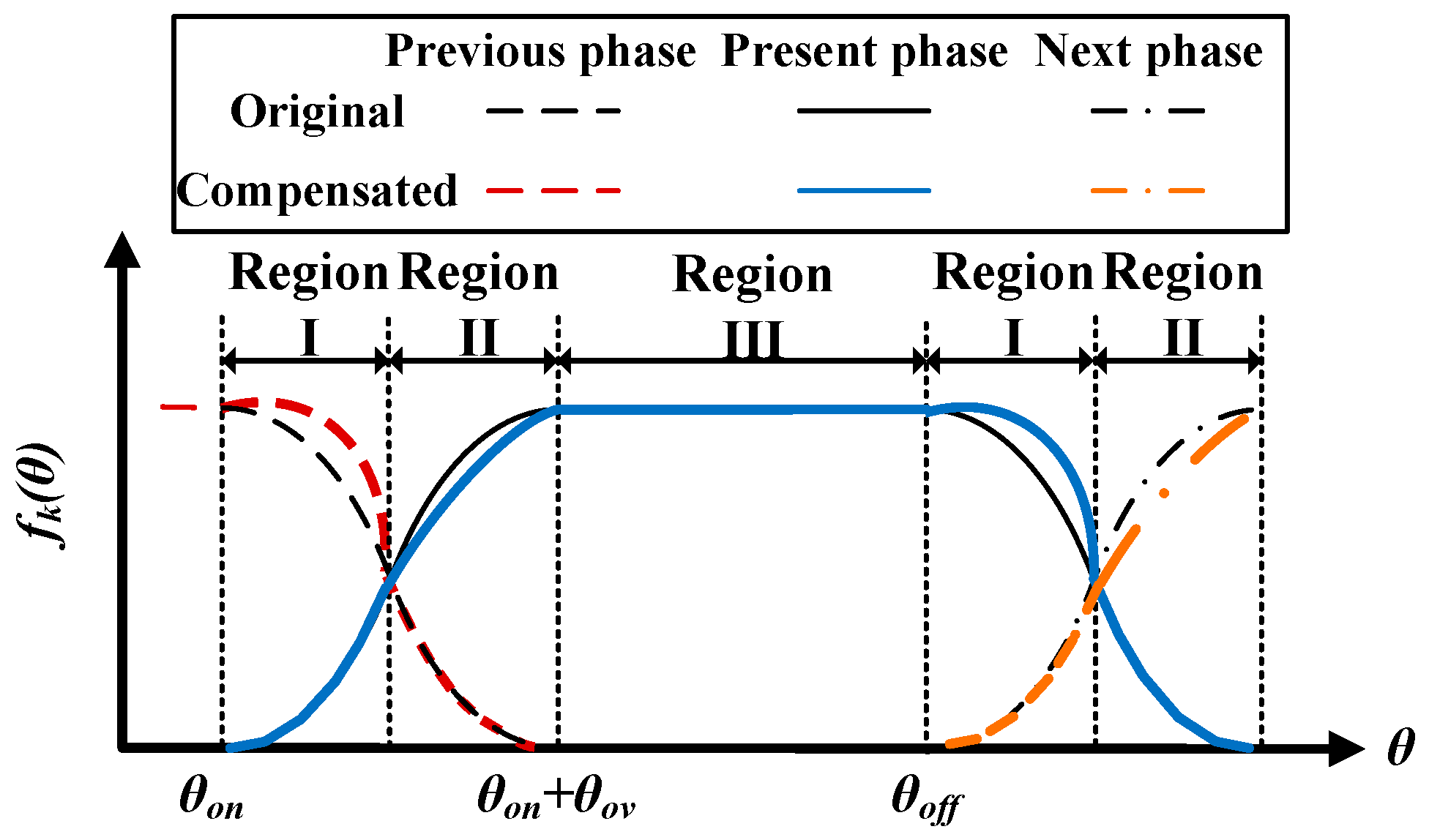
2.3. OCTSF
3. Improved OCTSF Considering the Phase Torque-Generation Capability
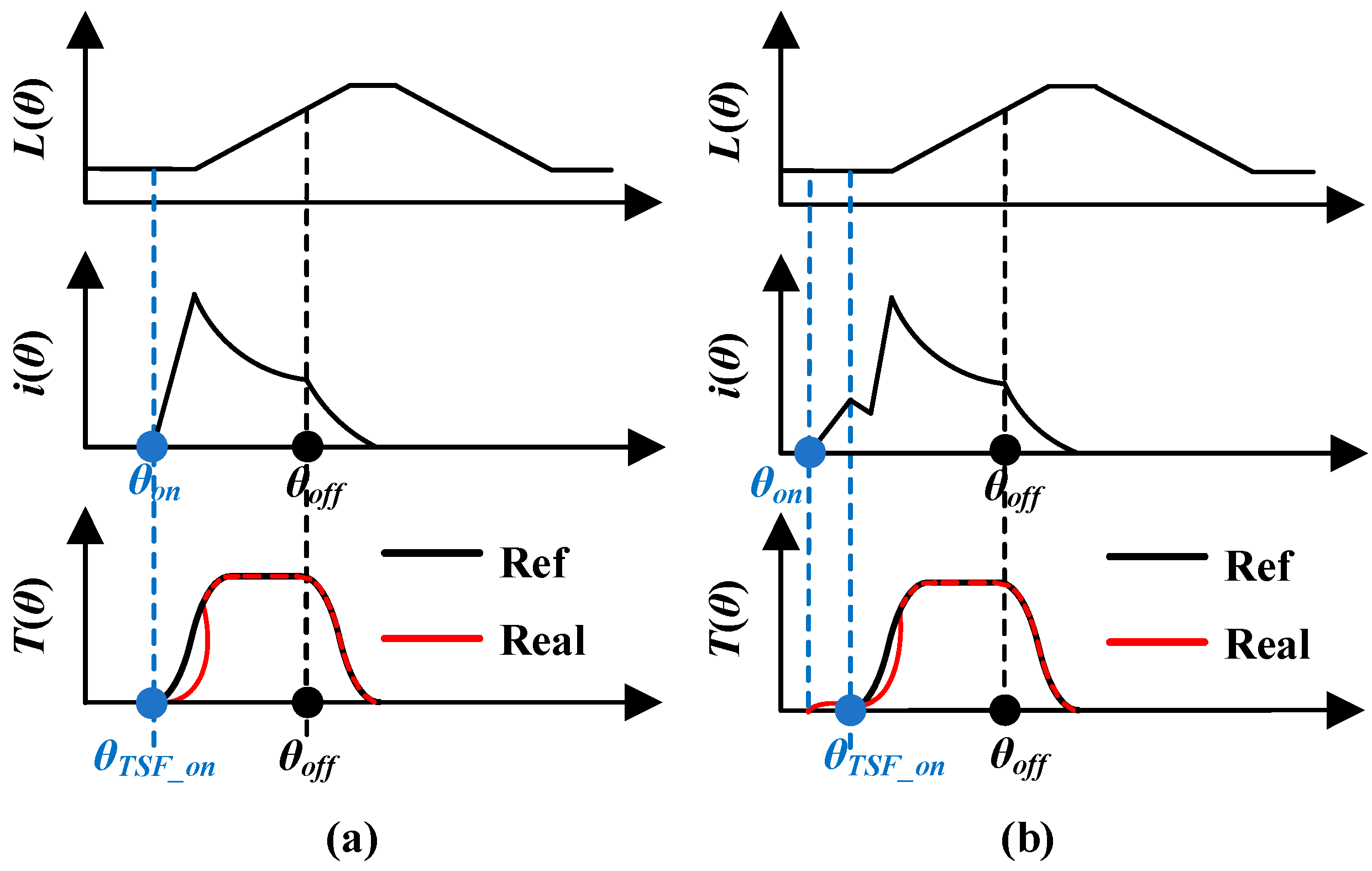
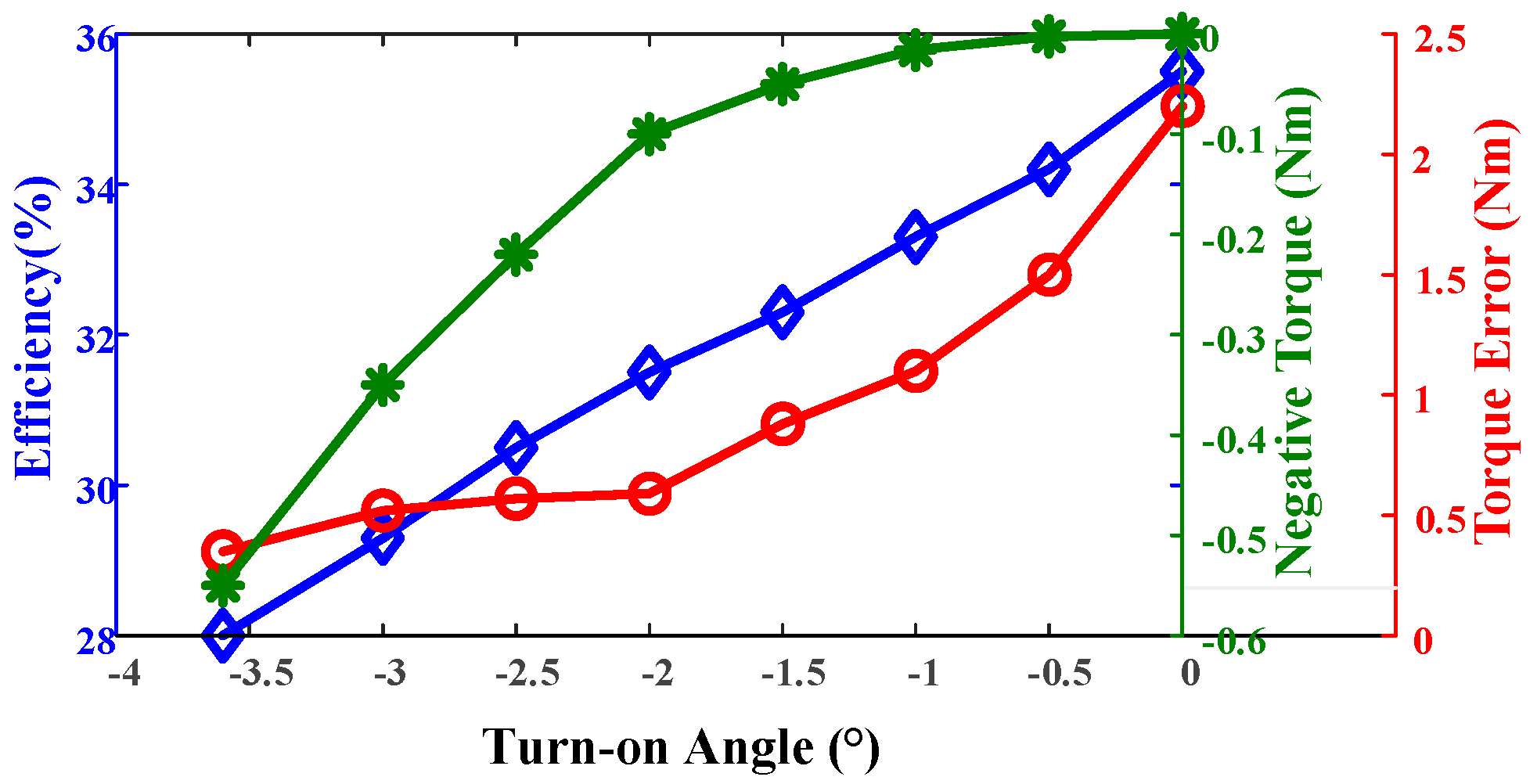
3.1. Turn-On Angle Advancement
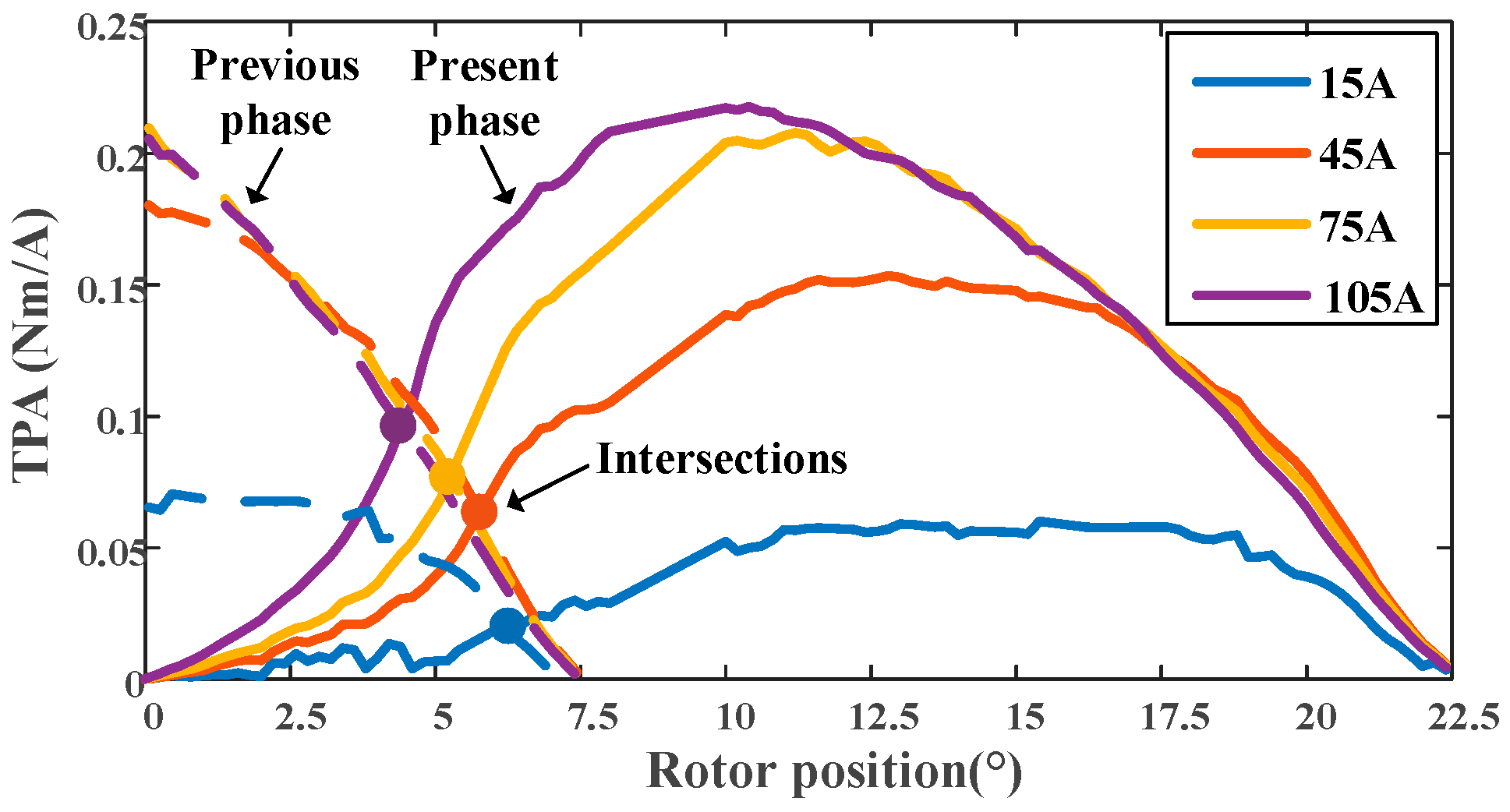
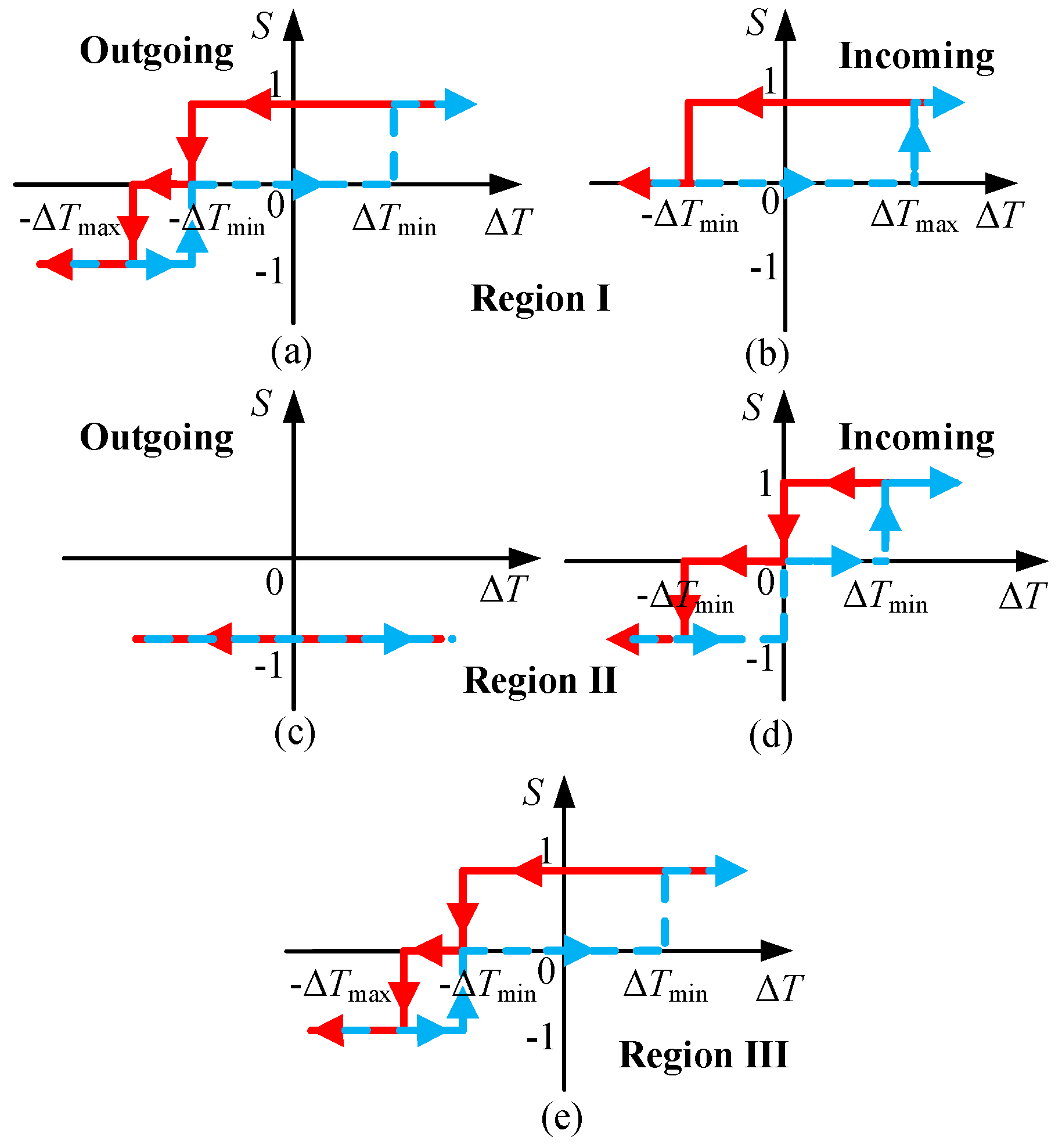
3.2. TPA-Based Commutation Separation
- (1)
- At the same speed, as θon advances, the separation point also advances. However, the variation range is very narrow and within [4.5°, 5.3°].
- (2)
- When θon is fixed, with the increase in speed, the current-decreasing rate of the outgoing phase is faster, and the current-increasing rate of the incoming phase is slower, resulting in a slight increase in the separation point. However, the variation is smaller than 0.4° from 300 rpm to 1500 rpm.
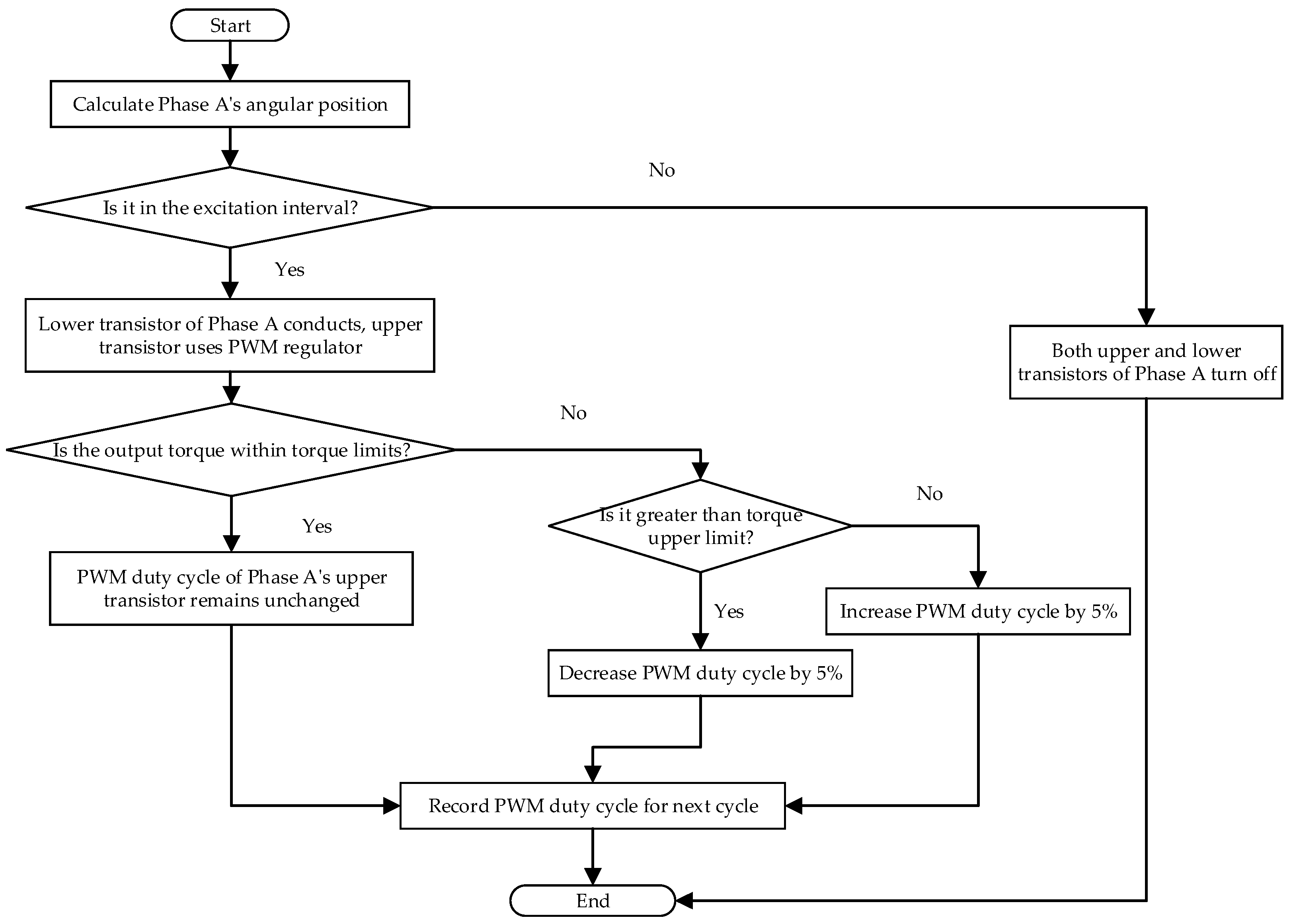
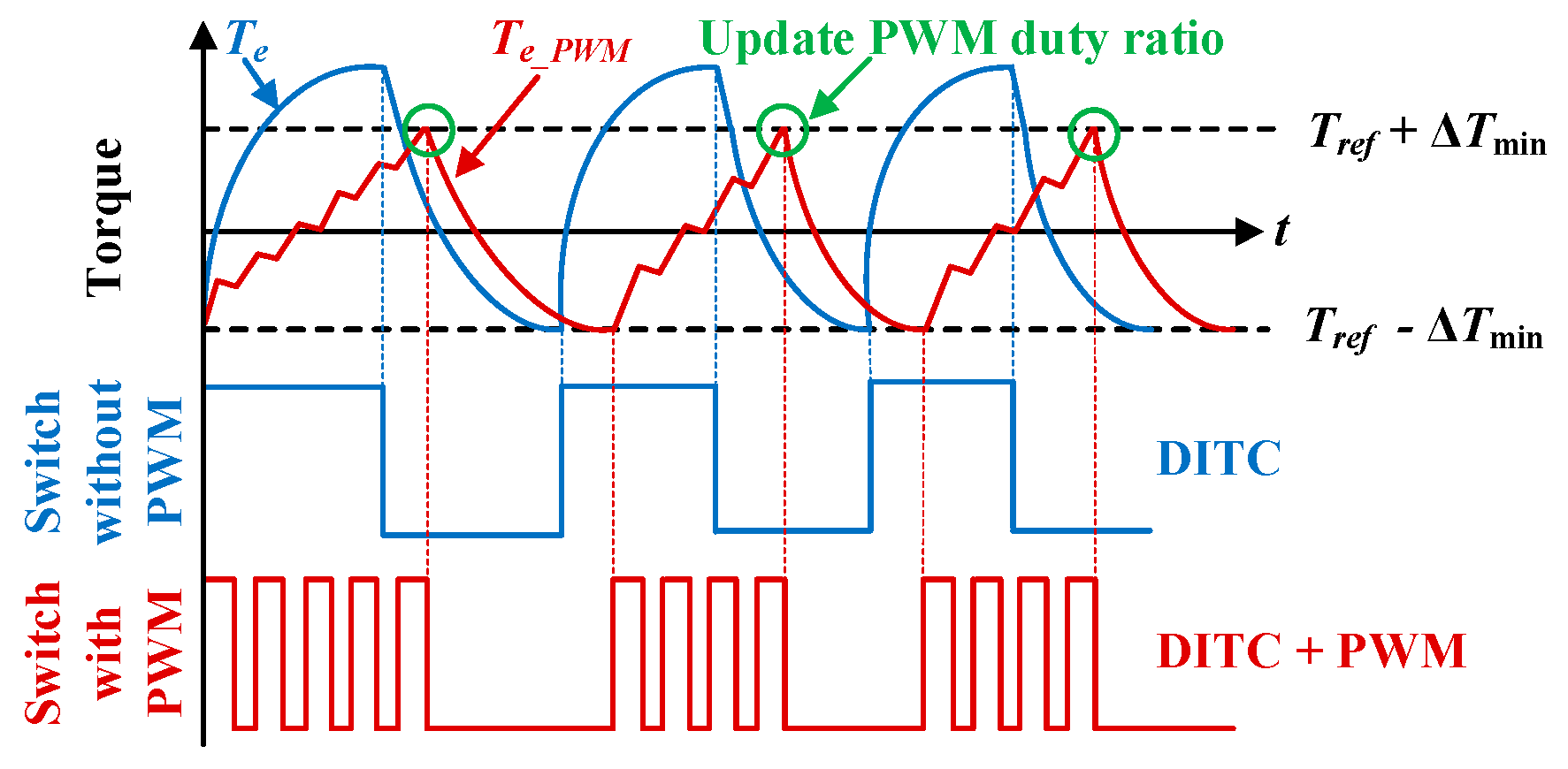
4. DITC Combined with a PWM Regulator
4.1. DITC
4.2. Torque Change Rate Considering the Control Frequency
4.3. PWM Regulator
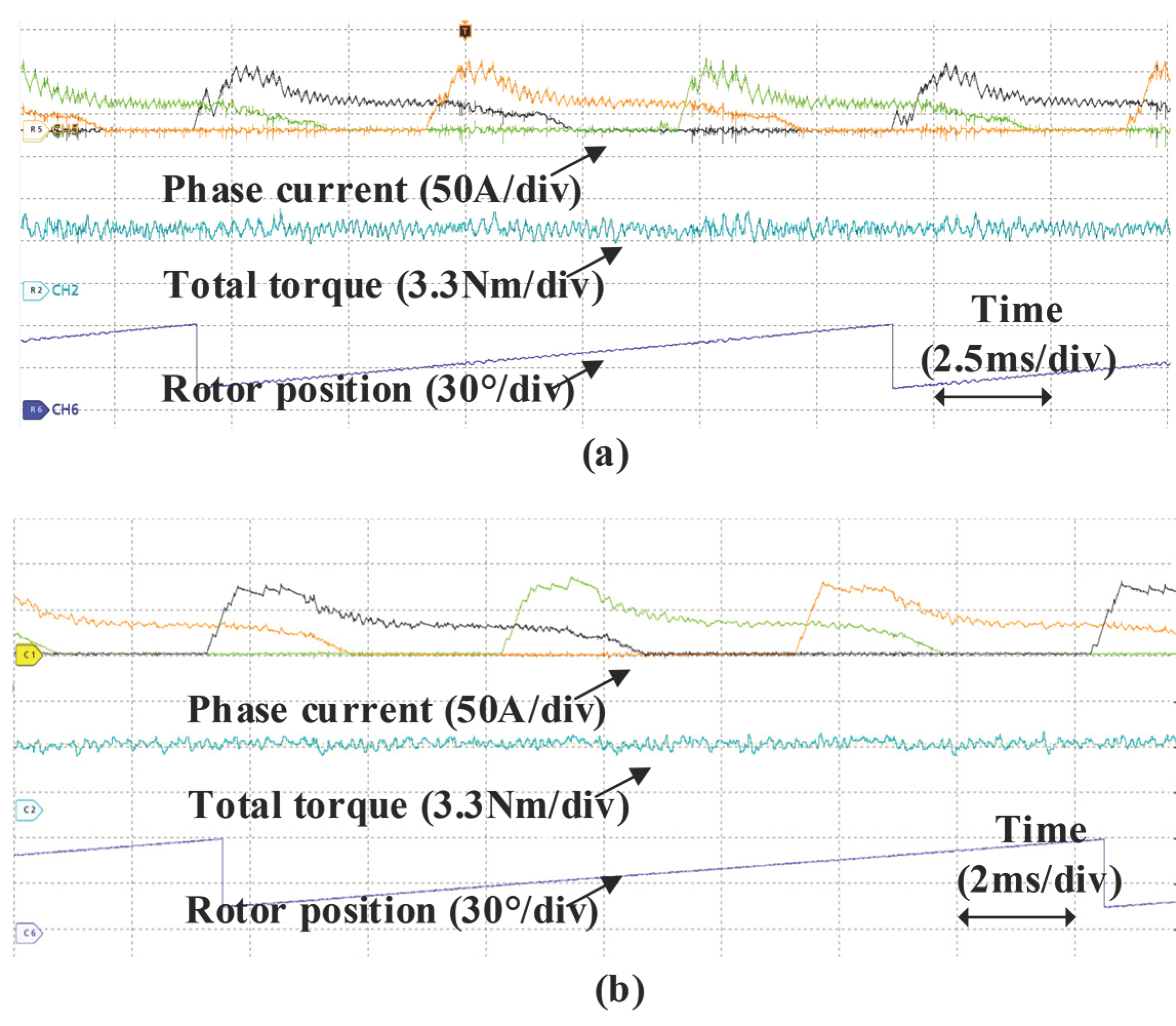
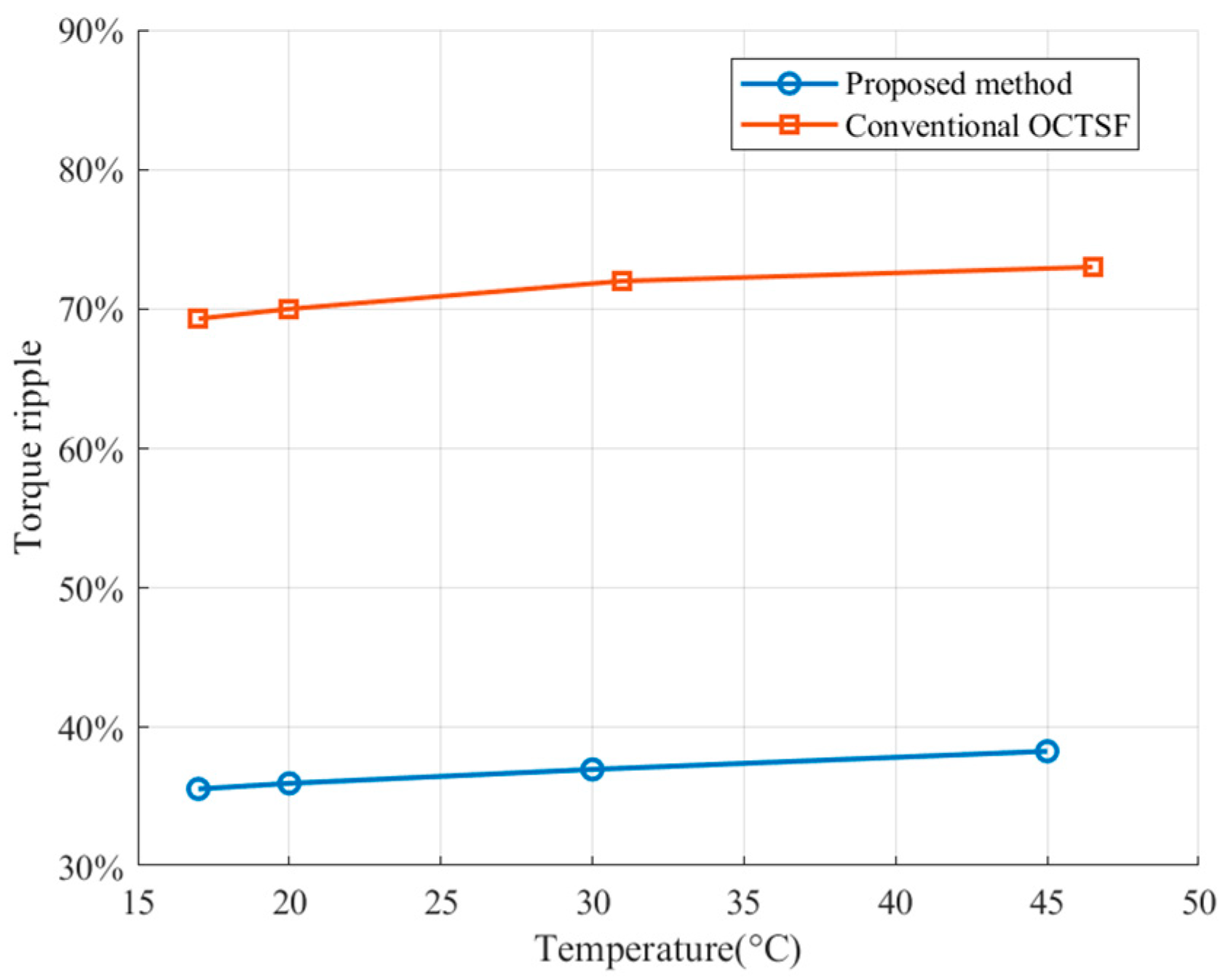
5. Experimental Verification
6. Conclusions
- (1)
- Although the proposed method has only been validated for the 12/8 topology, it is theoretically applicable to machines with two or more phases. Further studies are needed to verify its generalization to other topologies.
- (2)
- The method has demonstrated good performance at speeds below 1500 rpm, and it has shown excellent torque ripple suppression performance across a load range from half the rated torque to three times the rated torque. To expand its applicability, further research is required to assess its effectiveness at higher speeds.
- (3)
- In this paper, the separation point is treated as a constant. To enhance accuracy under varying operating conditions, future work could investigate the use of adaptive or predictive methods to dynamically optimize this value.
- (4)
- This study primarily focused on error compensation for optimizing TSF. Future research could explore the application of techniques such as genetic algorithms or neural networks to achieve more refined TSF optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TSF | Torque-sharing function |
| SRM | switched reluctance machine |
| TPA | torque per ampere |
| DITC | direct instantaneous torque control |
| MPC | model predictive control |
| OCTSF | online compensated TSF |
| ERCFL | effective rate-of-change of flux linkage |
References
- Yan, W.; Chen, H.; Liao, S.; Liu, Y.; Cheng, H. Design of a Low-Ripple Double-Modular-Stator Switched Reluctance Machine for Electric Vehicle Applications. IEEE Trans. Transp. Electrif. 2021, 7, 1349–1358. [Google Scholar] [CrossRef]
- Song, S.; Liu, W.; Dieter, P.; Uwe, S. Detailed Design of a High Speed Switched Reluctance Starter/Generator for More/All Electric Aircraft. Chin. J. Aeronaut. 2010, 23, 216–226. [Google Scholar]
- Fan, J.; Jung, I.; Lee, Y. Position Estimation of a Two-Phase Switched Reluctance Motor at Standstill. Machines 2021, 9, 359. [Google Scholar] [CrossRef]
- Radun, A.V. Design considerations for the switched reluctance motor. IEEE Trans. Ind. Appl. 1995, 31, 1079–1087. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, X.; Deng, Z.Q. Modeling and Analysis of Radial Levitation and Axial Reluctance Force for Four Degree of Freedom Bearingless Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2020, 68, 11895–11906. [Google Scholar] [CrossRef]
- Howey, B.; Bilgin, B.; Emadi, A. Design of an External-Rotor Direct Drive E-Bike Switched Reluctance Motor. IEEE Trans. Veh. Technol. 2020, 69, 2552–2562. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, Y.; Wang, J. Design of Switched Reluctance Motor(SRM) Servo Control for Robot Joints. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET), Chengdu, China, 12–15 May 2023. [Google Scholar]
- Zhang, X.; Yang, Q.; Ma, M.; Lin, Z.; Yang, S. A Switched Reluctance Motor Torque Ripple Reduction Strategy With Deadbeat Current Control and Active Thermal Management. IEEE Trans. Veh. Technol. 2020, 69, 317–327. [Google Scholar] [CrossRef]
- Lee, D.H.; Liang, J.; Lee, Z.G.; Ahn, J.W. A Simple Nonlinear Logical Torque Sharing Function for Low-Torque Ripple SR Drive. IEEE Trans. Ind. Electron. 2009, 56, 3021–3028. [Google Scholar] [CrossRef]
- Yan, W.; Wang, W.; Li, H.; Chen, H.; Yu, F.; Zhang, D.; Yang, H.; Wang, Q. Investigation on Different Stator Structures of the Axial-Radial Flux Switched Reluctance Motors. IEEE Trans. Ind. Electron. 2024, 71, 5474–5484. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.S.; Kwon, B.I.; Kim, B.T. New Rotor Shape Design for Minimum Torque Ripple of SRM Using FEM. IEEE Trans. Magn. 2004, 40, 754–757. [Google Scholar] [CrossRef]
- Kusumi, T.; Hara, T.; Umetani, K.; Hiraki, E. Simultaneous Tuning of Rotor Shape and Phase Current of Switched Reluctance Motors for Eliminating Input Current and Torque Ripples with Reduced Copper Loss. IEEE Trans. Ind. Appl. 2020, 56, 6384–6398. [Google Scholar] [CrossRef]
- Kondelaji, M.A.J.; Mirsalim, M. Segmented-Rotor Modular Switched Reluctance Motor with High Torque and Low Torque Ripple. IEEE Trans. Transp. Electrif. 2020, 6, 62–72. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, K.W.E.; Ho, S.L. Optimization and Evaluation of Torque-Sharing Functions for Torque Ripple Minimization in Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2009, 24, 2076–2090. [Google Scholar] [CrossRef]
- Li, H.; Bilgin, B.; Emadi, A. An Improved Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Machines. IEEE Trans. Power Electron. 2019, 34, 1635–1644. [Google Scholar] [CrossRef]
- Ye, J.; Bilgin, B.; Emadi, A. An Offline Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Motor Drives. IEEE Trans. Energy Convers. 2015, 30, 726–735. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C.; Hu, Y.; Si, J. OCTSF for torque ripple minimisation in SRMs. IET Power Electron. 2016, 9, 2741–2750. [Google Scholar] [CrossRef]
- Sun, J.; Yang, Z.; Sun, X.; Ge, S.; Diao, K.; Feng, L.; Wang, B. An Adaptive Direct Torque Control with Reconstructed Voltage Vectors for Six-Phase Switched Reluctance Motor. IEEE Trans. Transp. Electrif. 2024, 10, 10262–10271. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, R.-Y. Sensorless Direct Torque Control using the Inductance Inflection Point for a Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2018, 65, 9336–9345. [Google Scholar] [CrossRef]
- Xu, A.; Shang, C.; Chen, J.; Zhu, J.; Han, L. A New Control Method Based on DTC and MPC to Reduce Torque Ripple in SRM. IEEE Access 2019, 7, 68584–68593. [Google Scholar] [CrossRef]
- Hao, Z.; Yu, Q.; Cao, X.; Deng, X.; Shen, X. An Improved Direct Torque Control for a Single-Winding Bearingless Switched Reluctance Motor. IEEE Trans. Energy Convers. 2020, 35, 1381–1393. [Google Scholar] [CrossRef]
- Li, W.; Cui, Z.; Ding, S.; Chen, F.; Guo, Y. Model Predictive Direct Torque Control of Switched Reluctance Motors for Low-Speed Operation. IEEE Trans. Energy Convers. 2022, 37, 1406–1415. [Google Scholar] [CrossRef]
- Cai, J.; Dou, X.; Cheok, A.D.; Yan, Y.; Zhang, X. Overview of the Direct Torque Control Strategy in Switched Reluctance Motor Drives. IEEE Trans. Transp. Electrif. 2025, 11, 1617–1628. [Google Scholar] [CrossRef]
- Husain, I.; Ehsani, M. Torque ripple minimization in switched reluctance motor drives by PWM current control. IEEE Trans. Power Electron. 1996, 11, 83–88. [Google Scholar] [CrossRef]
- Ye, J.; Malysz, P.; Emadi, A. A Fixed-Switching-Frequency Integral Sliding Mode Current Controller for Switched Reluctance Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 381–394. [Google Scholar] [CrossRef]
- Ge, L.; Zhong, J.; Cheng, Q.; Fan, Z.; Song, S.; De Doncker, R.W. Model Predictive Control of Switched Reluctance Machines for Suppressing Torque and Source Current Ripples Under Bus Voltage Fluctuation. IEEE Trans. Ind. Electron. 2023, 70, 11013–11021. [Google Scholar] [CrossRef]
- Fang, G.; Ye, J.; Xiao, D.; Xia, Z.; Emadi, A. Computational-Efficient Model Predictive Torque Control for Switched Reluctance Machines with Linear-Model-Based Equivalent Transformations. IEEE Trans. Ind. Electron. 2022, 69, 5465–5477. [Google Scholar] [CrossRef]
- Cai, J.; Dou, X.; Song, S.; Cheok, A.D.; Yan, Y.; Zhang, X. Flux-Linkage Loop-Based Model Predictive Torque Control for Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2025, 72, 2435–2443. [Google Scholar] [CrossRef]
- Fang, G.; Scalcon, F.P.; Xiao, D.; Vieira, R.P.; Gründling, H.A.; Emadi, A. Advanced Control of Switched Reluctance Motors (SRMs): A Review on Current Regulation, Torque Control and Vibration Suppression. IEEE Open J. Ind. Electron. Soc. 2021, 2, 280–301. [Google Scholar] [CrossRef]
- Hu, Y.; Gu, C.; Zhang, Z.; Kang, Z.; Li, Y. Torque Ripple Minimization of Six-Phase Switched Reluctance Motor Based on Enhanced Direct Instantaneous Torque Control. IEEE Trans. Transp. Electrif. 2024, 10, 4371–4382. [Google Scholar] [CrossRef]
- Song, S.; Fang, G.; Hei, R.; Jiang, J.; Ma, R.; Liu, W. Torque Ripple and Efficiency Online Optimization of Switched Reluctance Machine Based on Torque per Ampere Characteristics. IEEE Trans. Power Electron. 2020, 35, 9608–9616. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Z.; Cui, X. Research on Novel Direct Instantaneous Torque Control Strategy for Switched Reluctance Motor. IEEE Access 2020, 8, 66910–66916. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C. Optimized Direct Instantaneous Torque Control for SRMs With Efficiency Improvement. IEEE Trans. Ind. Electron. 2021, 68, 2072–2082. [Google Scholar] [CrossRef]
- Yu, Q.; Cao, X.; Deng, X.; Zhu, T.; Deng, Z.; Liu, C. An Improved Control Strategy to Reduce Torque Spikes and Ripple for Bearingless Switched Reluctance Motors. IEEE Trans. Ind. Inform. 2024, 20, 5147–5159. [Google Scholar] [CrossRef]







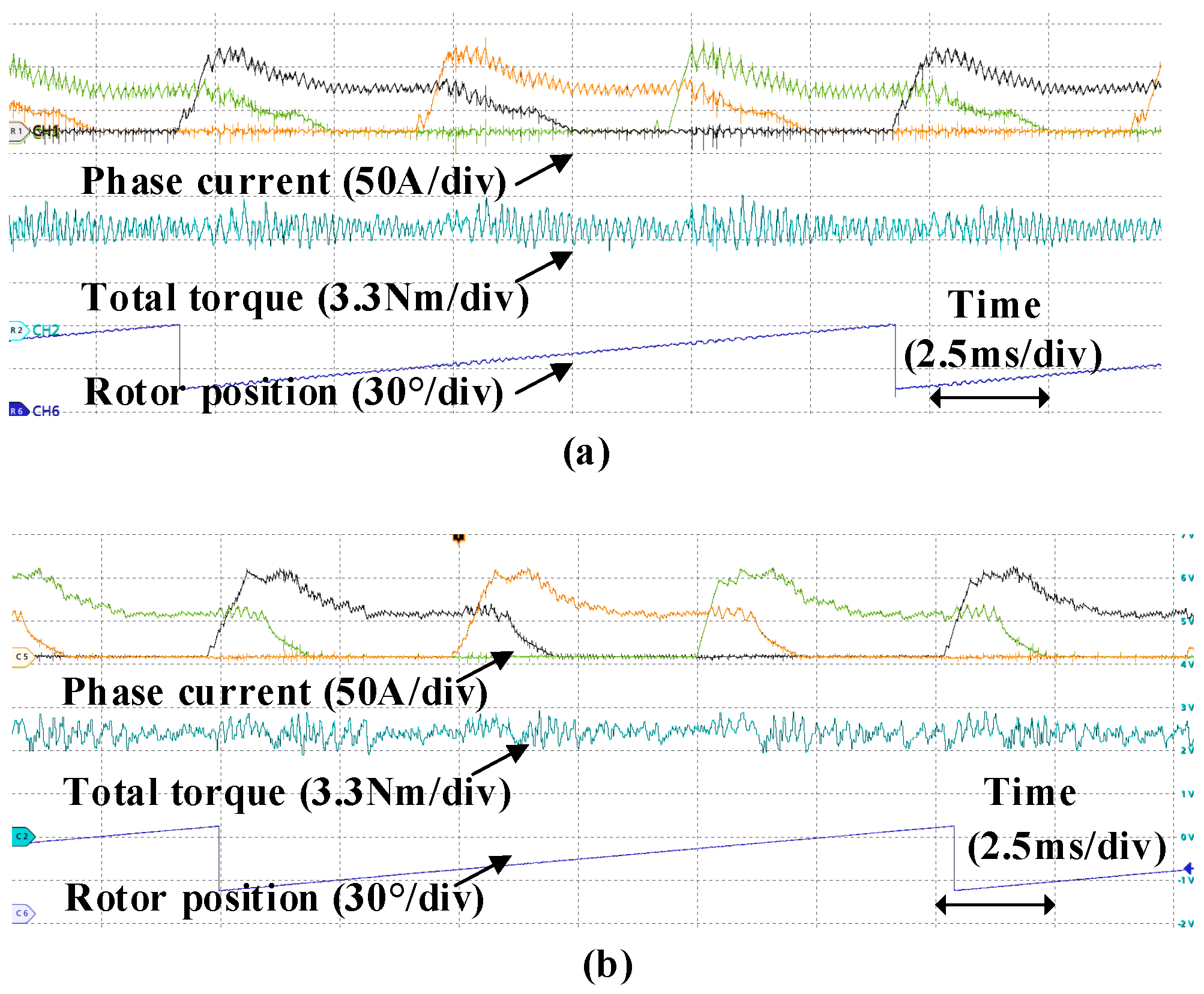

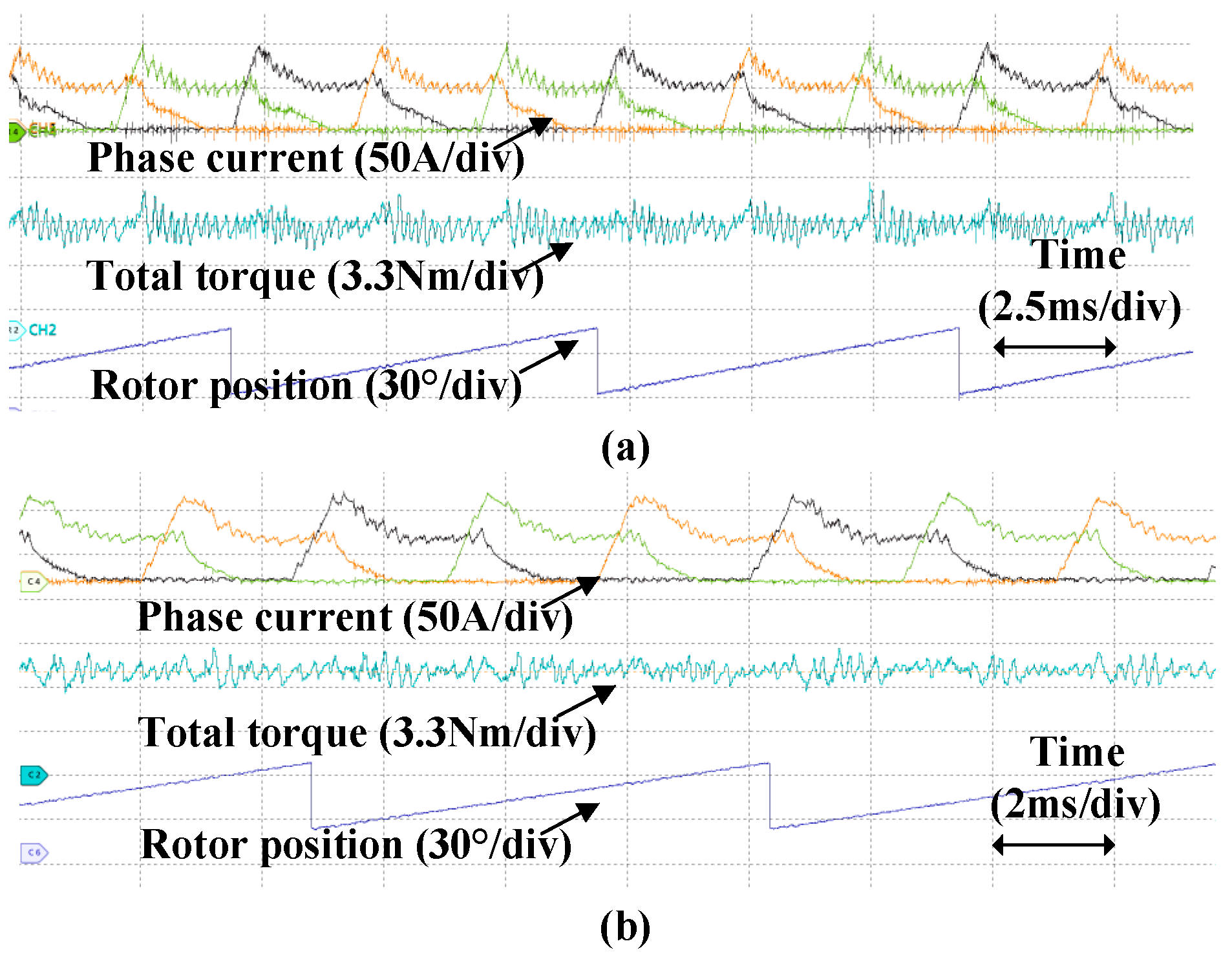
| Item | Value |
|---|---|
| Stator slots and roto poles | 12/8 |
| Stator outer diameter | 138 mm |
| Stator yoke thickness | 9.5 mm |
| Air gap length | 0.3 mm |
| Rotor outer diameter | 81.4 mm |
| Shaft diameter | 20 mm |
| Axial length | 70 mm |
| Lamination material | DW465-50 |
| Turns per pole | 24 |
| Rated voltage | 60 V |
| Rated power | 1.5 kW |
| Rated torque | 4 Nm |
| Rated speed | 3500 r/min |
| Working Condition | Torque Ripple (%) | Fluctuation Suppression Rate (%) | Efficiency (%) | ||
|---|---|---|---|---|---|
| Conv. | Prop. | Conv. | Prop. | ||
| 500 rpm, 4 Nm | 69.3 | 35.6 | 48.6% | 43.9 | 45.0 |
| 500 rpm, 8 Nm | 63.4 | 31.2 | 50.8% | 46.8 | 48.1 |
| 1000 rpm, 4 Nm | 70.3 | 38.7 | 45% | 60.3 | 61.0 |
| 1000 rpm, 8 Nm | 67.8 | 33.6 | 50.4% | 63.3 | 63.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, S.; Guo, X.; Liu, Z.; Zhang, P.; Ding, Y.; Hua, W. Torque Ripple Reduction in Switched Reluctance Machines Considering Phase Torque-Generation Capability. Electronics 2025, 14, 1757. https://doi.org/10.3390/electronics14091757
Chai S, Guo X, Liu Z, Zhang P, Ding Y, Hua W. Torque Ripple Reduction in Switched Reluctance Machines Considering Phase Torque-Generation Capability. Electronics. 2025; 14(9):1757. https://doi.org/10.3390/electronics14091757
Chicago/Turabian StyleChai, Shijie, Xiaoqiang Guo, Zhiyu Liu, Peng Zhang, Yueheng Ding, and Wei Hua. 2025. "Torque Ripple Reduction in Switched Reluctance Machines Considering Phase Torque-Generation Capability" Electronics 14, no. 9: 1757. https://doi.org/10.3390/electronics14091757
APA StyleChai, S., Guo, X., Liu, Z., Zhang, P., Ding, Y., & Hua, W. (2025). Torque Ripple Reduction in Switched Reluctance Machines Considering Phase Torque-Generation Capability. Electronics, 14(9), 1757. https://doi.org/10.3390/electronics14091757







