1. Introduction
With the advancement of 6G technology, multiple-input, multiple-output (MIMO) systems play a crucial role in enhancing data transmission speed and spectral efficiency in wireless communication. In MIMO systems, multiple signal streams are transmitted simultaneously through different antennas, significantly increasing data rates. However, at the receiver end, these overlapping signals interfere with one another, making signal separation a challenging task. Consequently, MIMO detection becomes a fundamental component of the receiver, responsible for accurately recovering transmitted signals while mitigating interference and noise. Efficient MIMO detection techniques are essential in optimizing system performance, reducing error rates, and ensuring reliable communication in next-generation networks [
1].
Traditionally, MIMO detection has been implemented using methods such as sphere decoding (SD), minimum mean square error (MMSE), and zero forcing (ZF) to achieve near-optimal performance while maintaining relatively low computational complexity [
2]. However, since these methods process the received signal using linear operations, their performance often deteriorates in high-interference scenarios. In contrast, maximum likelihood (ML) detection offers optimal performance by exhaustively searching for the most likely transmitted signal. However, its computational complexity increases exponentially with the number of antennas and symbols, rendering it impractical for large-scale MIMO systems.
To address these challenges, nonlinear MIMO detection techniques have been proposed. In [
3], a pipelined architecture for a MIMO sphere detector was introduced to efficiently mitigate interference in subsequent signals. The Belief Propagation (BP) algorithm, proposed in [
4], is an advanced approach designed to effectively handle high-antenna configurations and low inter-channel correlation. Additionally, to reduce system complexity, iterative matrix–vector multiplication techniques, such as the Neumann Series Expansion (NSE) [
5], Gauss–Seidel (GS) [
6], and Conjugate Gradient (CG) [
7,
8] techniques, have been explored. However, these iterative methods may introduce processing delays and degrade performance under fading channel conditions. Consequently, developing a MIMO detection strategy that ensures high reliability while minimizing decoding time remains a critical challenge in modern wireless communication systems [
8].
Recently, with the advancement of deep learning (DL), various fields, including image processing [
9,
10,
11], network security [
12,
13], storage systems [
14,
15], and wireless communication [
16,
17], have leveraged its powerful capabilities. Among these applications, deep learning models have also been increasingly explored for MIMO detection, offering promising improvements in both accuracy and efficiency [
18]. Several studies have utilized model-driven DL to enhance iterative MIMO detection algorithms [
19,
20,
21]. In [
22], convolutional neural networks (CNNs) were introduced as a data-driven solution for MIMO detection, demonstrating improved detection accuracy across various channel conditions. These DL-based MIMO detection methods have exhibited superior performance compared to traditional detection techniques. More recently, graph neural networks (GNNs), which leverage graph-structured data for signal processing, have emerged as a promising DL approach. GNNs have been successfully applied in diverse domains, including image processing, network security, and wireless communication [
23,
24,
25,
26,
27], making them a potential candidate for advanced MIMO detection [
28].
In this study, we propose a novel MIMO detection model that integrates the Viterbi algorithm (VA) with a GNN to enhance detection efficiency. In the proposed approach, the VA is first employed to pre-detect the received signal, generating an initial estimate that serves as the input to the GNN model. Within the GNN framework, the received and initial signals are structured as a Tanner graph, forming the foundation for GNN processing. The initial signal is then iteratively refined through the message-passing operations of the GNN model. Finally, the updated signal values at the graph nodes serve as the output, which is compared with the original transmitted signal to train the GNN.
Simulation results demonstrate that the proposed model significantly improves the symbol error rate (SER) in MIMO detection compared to traditional approaches and existing deep learning-based models. The key contributions of this work are summarized as follows:
- -
Integration of the VA with a GNN to enhance MIMO detection performance;
- -
Utilization of the Tanner graph structure for effective processing of received signals;
- -
Iterative signal refinement through GNN-based message-passing operations to improve detection accuracy;
- -
Demonstration of superior performance in terms of SER through extensive simulations.
The remainder of this paper is organized as follows:
Section 2 provides background information on MIMO detection, the VA, and graph neural networks (GNNs).
Section 3 introduces and analyzes the proposed model in detail.
Section 4 presents the simulation results and evaluates the performance of the proposed approach. Finally,
Section 5 concludes the paper by summarizing the key findings and outlining potential directions for future research.
2. Background
2.1. MIMO Detection
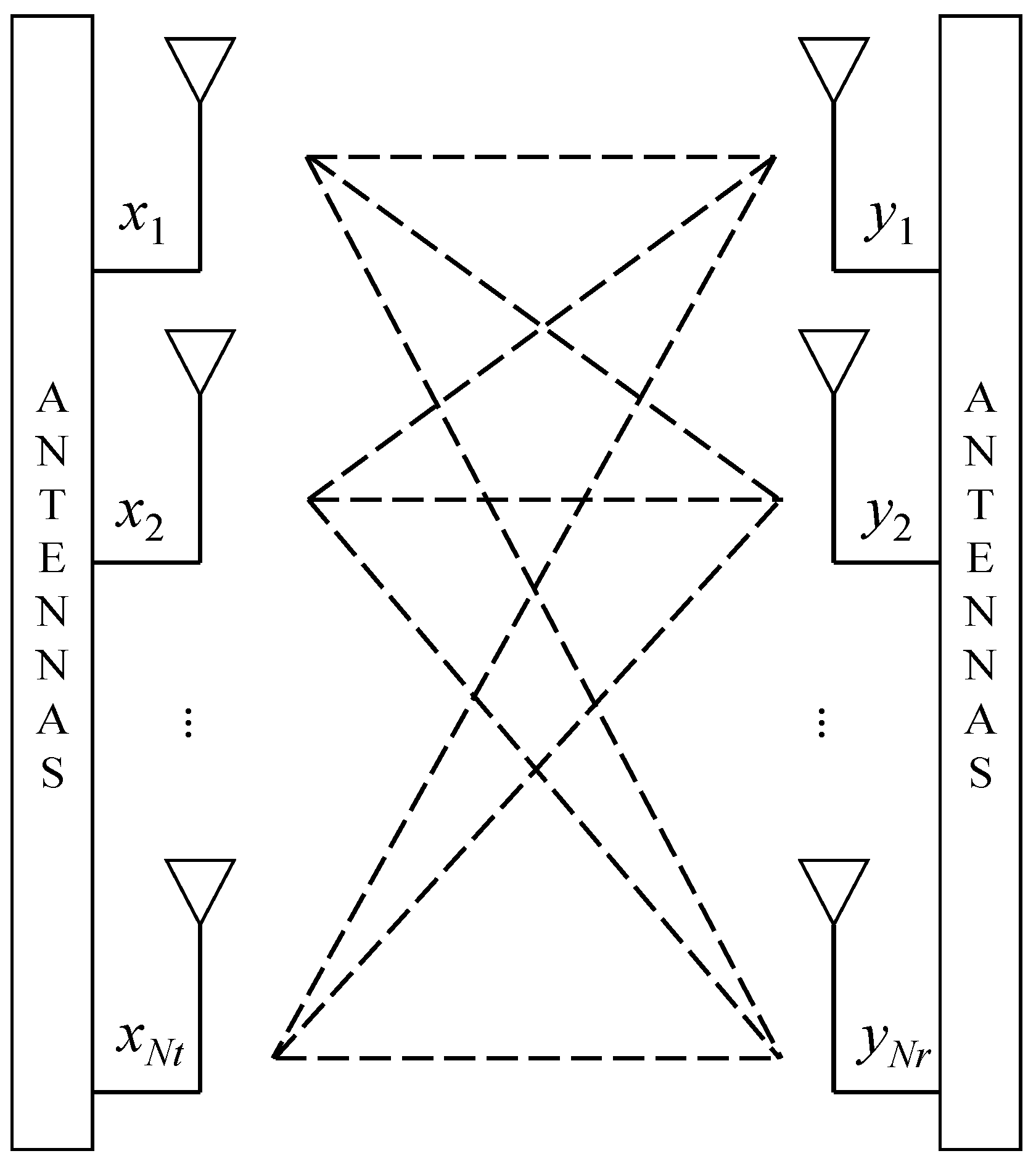
In a MIMO system, the original signal is modulated into
x using quadrature amplitude modulation (QAM), where
= {
s1,
s2, …,
sM} represents the constellation set of an
M-QAM scheme and
sm denotes one of the constellation points. The modulated signal (
x) is then transmitted through multiple antennas. The system comprises
Nt transmitting antennas and
Nr receiving antennas, as illustrated in
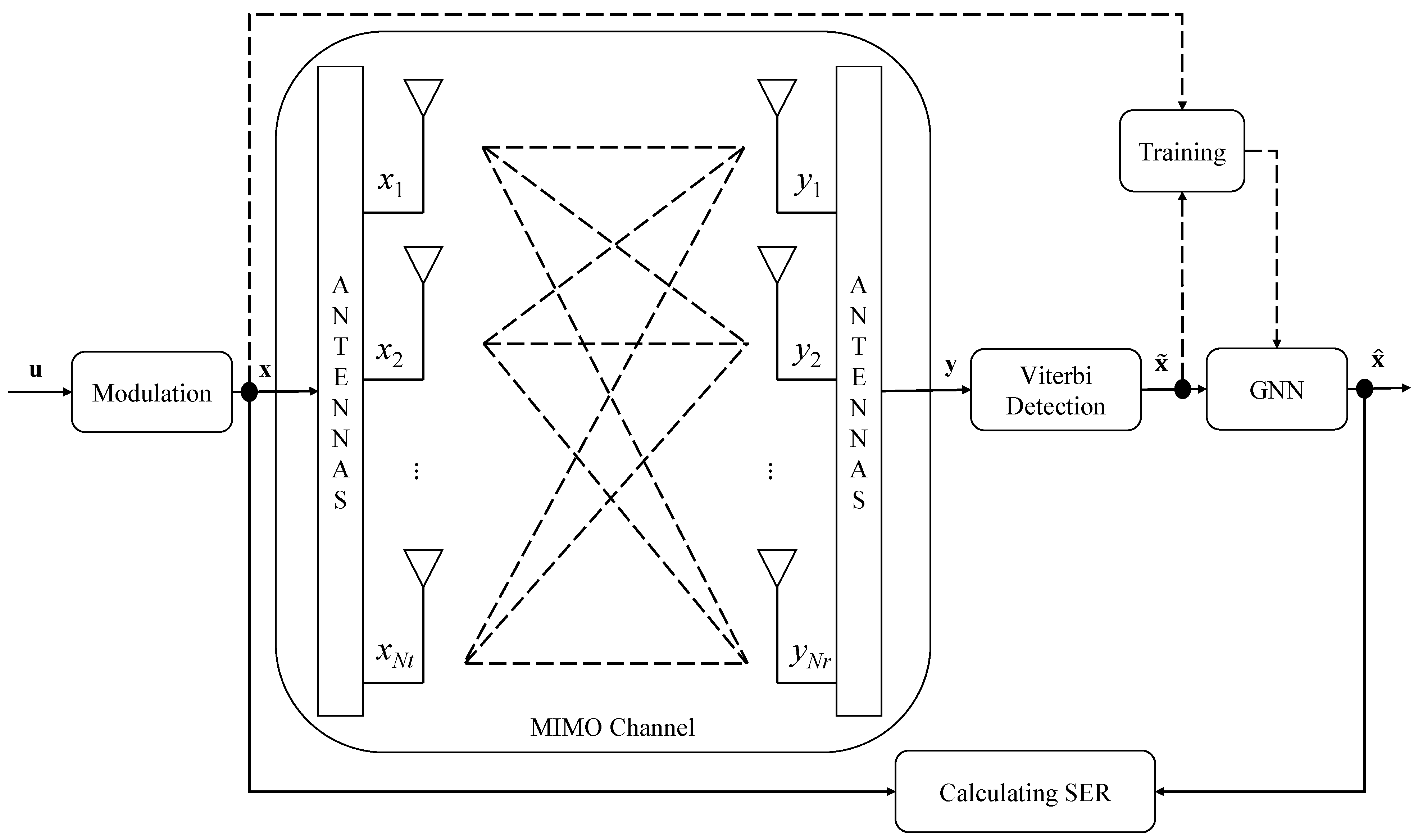
Figure 1.
The received signal vector (
y ) can be written as
In Equation (1),
H represents the channel matrix, which contains the coefficients corresponding to the communication links between the transmitter and receiver. The vector expressed as
x denotes the modulated or transmitted signals. Finally,
w represents the additive white Gaussian noise (AWGN) with zero mean and variance (
). These parameters are modeled using complex numbers to characterize a Rayleigh fading channel. However, for easier implementation in programming and coding, we transform the complex-valued model into an equivalent real-valued representation, as presented below.
With the definitions provided in Equation (2), the MIMO channel can be expressed as follows:
In Equation (3),
wr has a variance of
. Finally, the signal-to-noise ratio (SNR) on a dB scale is defined as follows:
where
Es represents the energy per transmit antenna. The total transmit energy is normalized such that
NtEs = 1. Additionally, the energy of the signal in Equation (3) is half of
Es, denoted as
Er =
Es/2.
In traditional MIMO detection, the received signal (
y) is processed using a filtering approach to mitigate interference and recover the transmitted signal (
x). The filtering coefficients are designed based on the channel matrix (
H) to suppress interference while minimizing the effects of noise. The general linear detection model is expressed as follows:
where
W is the filtering matrix, which varies for zero-forcing (ZF) and minimum mean square error (MMSE) methods. The ZF filter is derived by applying the Moore–Penrose pseudo-inverse of the channel matrix (
H):
The MMSE filter incorporates the noise variance (
) to balance interference suppression and noise minimization:
where
I is the identity matrix and (⋅)
H represents the Hermitian transpose (conjugate transpose). With the above filters, it is evident that ZF and MMSE are simple methods for detecting the original signal. However, these methods cannot match the performance of maximum likelihood (ML) detection, which is an optimal MIMO detection technique that determines the transmitted signal (
x) by exhaustively searching for the candidate that best matches the received signal (
y). While ML detection achieves the minimum SER, it is computationally expensive, particularly for large-scale MIMO systems. The ML detection rule finds the
x that minimizes the Euclidean distance between the received signal and the expected signal (
Hx):
The ML detection method evaluates all possible transmitted symbol combinations and selects the one that minimizes the error. While ML achieves the lowest SER among MIMO detection methods, its computational complexity grows exponentially with the number of transmit antennas (Nt) and the modulation order (M). Specifically, for an Nt-antenna system using M-ary modulation, the complexity is MNt, making ML detection impractical for large-scale MIMO systems.
To overcome this challenge, we propose the use of the VA to reduce complexity while maintaining near-optimal detection performance. Originally designed for the decoding of convolutional codes, the VA is a dynamic programming approach that efficiently finds the most likely transmitted sequence through a trellis-based search, avoiding the need for brute-force enumeration.
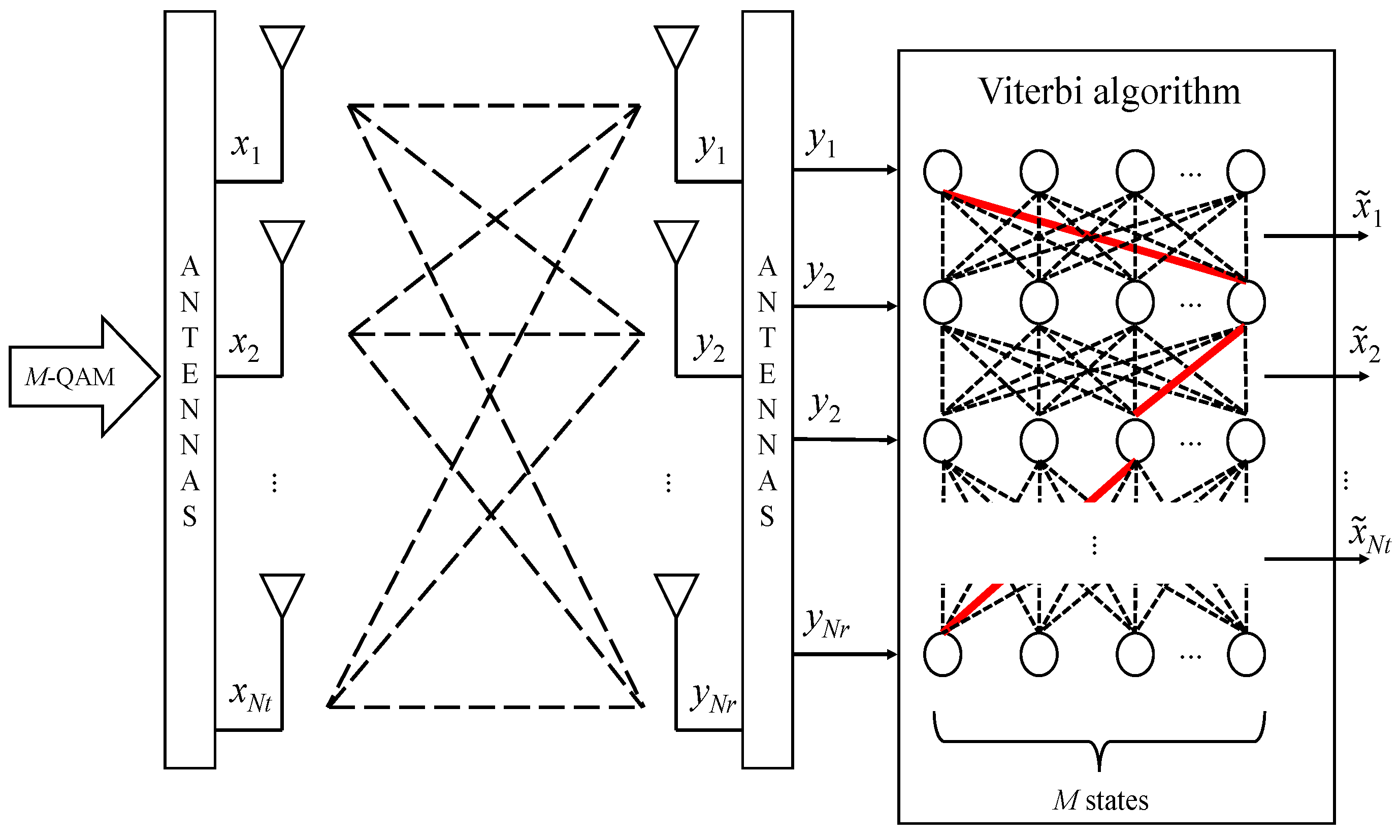
2.2. Viterbi Algorithm
In the VA for MIMO detection, the modulation order (
M) determines the number of states in the trellis, while the number of receiving antennas (
Nr) defines the number of state transitions at each step. This structure allows the algorithm to efficiently explore possible transmitted symbol sequences while reducing computational complexity. The trellis structure of the VA for MIMO detection is illustrated in
Figure 2.
In the VA, the trellis diagram represents all possible sequences of transmitted symbols (dashed lines), while the most likely path is estimated and selected (highlighted in red). Each node in the trellis corresponds to a possible state, i.e., a possible transmitted symbol combination. The branch metric is expressed as follows:
Let t = {1, 2, 3, …, Nt} represent the index of the transmitting antenna, corresponding to the t-th time step in the trellis. The branch metric at the t-th time step is denoted as dt. The matrix (Ht) consists of the first t columns of the channel matrix (H). In the symbol vector (xt) elements x(t − 1) represent the symbols from the historic path of the trellis, while the t-th element corresponds to each state in the trellis (e.g., the first state is s1, the second state is s2, and so on).
In each state, the cumulative path metric is calculated as follows:
The path metric () is initialized to zero at t = 0, i.e., . Finally, at t = Nr, the path with the minimum cumulative path metric is selected to detect the signal (x). This ensures that only the most probable sequence of symbols is retained.
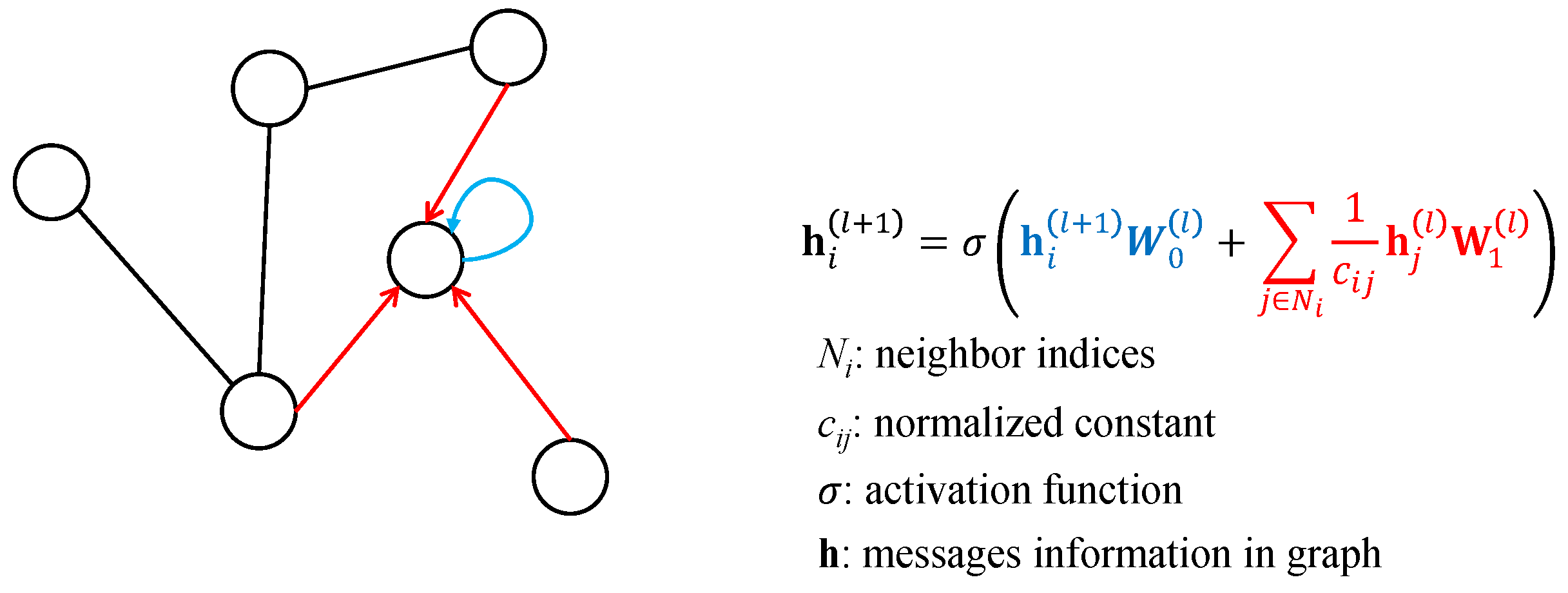
2.3. GNN
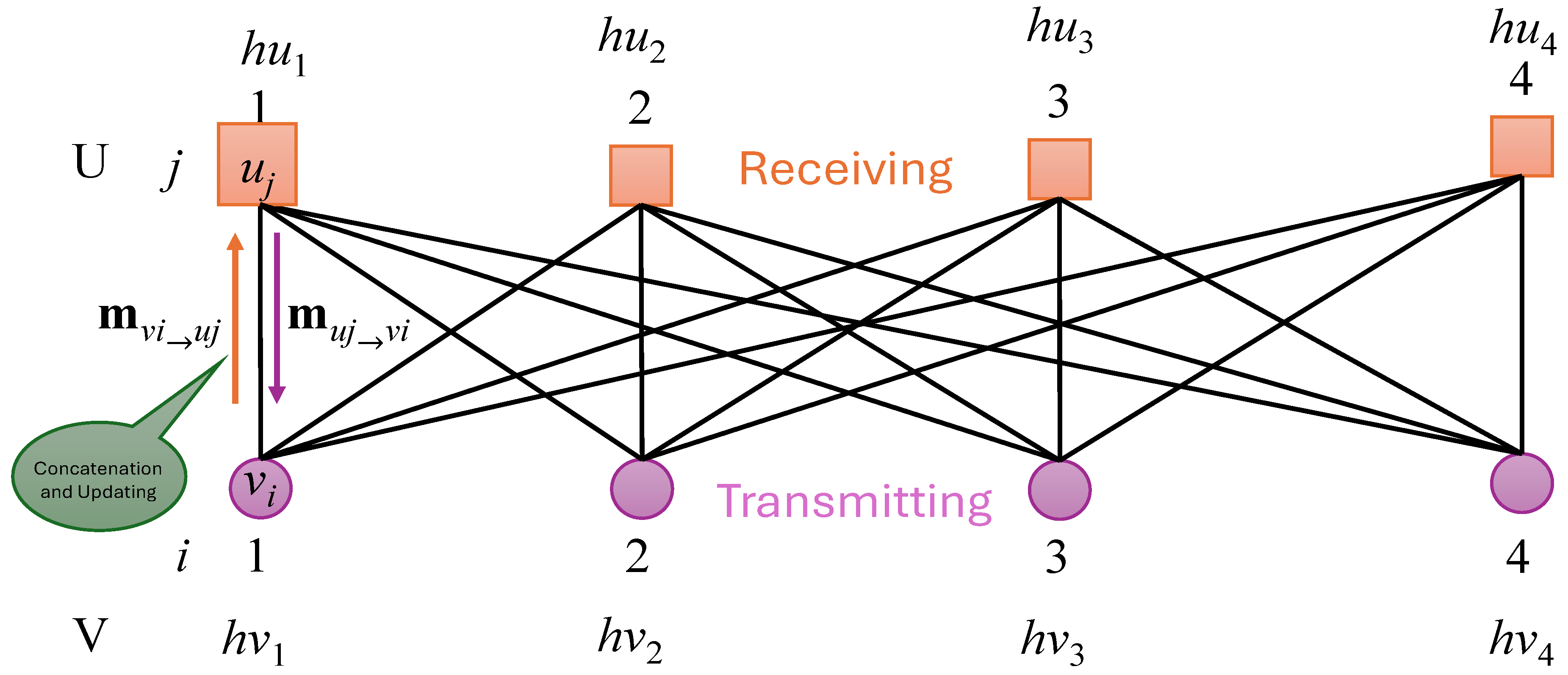
Unlike other models that process data in matrix or vector formats, GNNs use a graph structure to organize the data. This structure enables GNNs to capture the relationships between elements in the dataset, allowing them to extract features more effectively than other models when working with graph-based data, such as social networks, telecommunications networks, and molecular structures. A graph is composed of nodes (representing entities) and edges (representing the connections between nodes). The primary goal of a GNN is to learn an embedding for each node that incorporates information from its neighboring nodes, reflecting the local graph structure. Once these embeddings are learned, they can be used to generate predictions or outputs related to the graph data. The GNN mechanism is illustrated simply in
Figure 3.
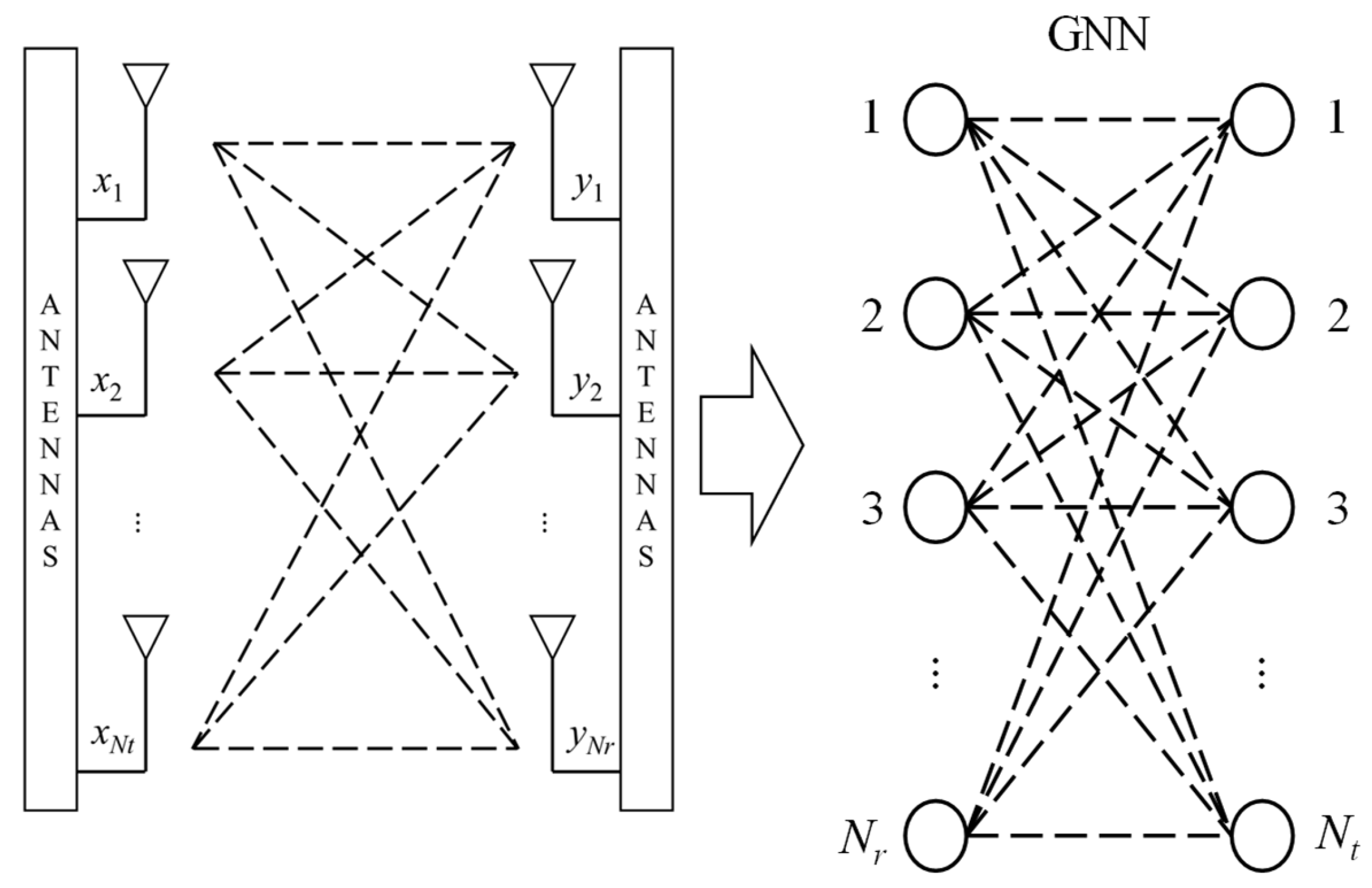
In
Figure 3, different colors are used to correspond to the formulas that compute the messages along the arrows. In this paper, we design a GNN structure based on the MIMO configuration. Each antenna is represented as a node, and the connections between antennas are represented as edges in the GNN structure. The transmitting and receiving antennas are paired to form the Tanner graph, as shown in
Figure 4. We then apply the GNN calculation mechanism to this Tanner graph.
3. Viterbi-GNN for MIMO Detection
In
Figure 5, user data (
u) are first modulated into
x. The output of the MIMO channel (
y) is then processed through Viterbi detection to estimate the initial transmitted signal (
). Next,
is passed through a GNN to update its values and enhance performance. During training, signals
and
y are used for message passing within the GNN model. Finally,
is updated to
and compared with the original
x in the loss function. In the testing phase, signals
and
x are used to evaluate SER performance.
The output of the VA usually takes hard values, which are not suitable as input for the GNN model. Therefore, in our proposed model, we convert the VA output into soft values. Since the VA output approximates the transmitted signal, we use the following expression to estimate the noise present in the received signal:
From (11), we create the soft output as
The
(where 0
1) controls the level of the soft output. As
decreases, the output approaches hard values, while as
increases, the output becomes softer. However, excessively large values of
can introduce noise, leading to a loss of information from the original signal. In this paper, we use
= 1 based on [
29]. By incorporating soft values in the inner detection process, our proposed model preserves the information of the received signal before providing it to the GNN. As a result, the soft output enhances system performance.
Next, we consider the GNN as a bipartite graph, as shown in
Figure 6.
We implement the GNN as follows:
- -
First, the output of Viterbi detection is input to V nodes by a linear input embedding (hvi = w, where i = 1, 2, …, Nt) and w are trainable coefficients that project the scalar () into a D-dimensional space.
- -
The message value from V to U is calculated as
where
is the MLP model with parameters of
. [
hvi‖
huj] denotes the concatenation of vectors
hvi and
huj.- -
Next, the information on node uj is calculated by the following equation:
where
E{.} is the expectation operation.
- -
Similarly, from U to V, we can update the message value according to the following expression:
- -
We calculate the information on node vj as follows:
- -
The information from U to V and from V to U is updated through N loops. After decoding, the final estimate is = qThvi, where q is another trainable vector that converts hvi, which is D-dimensional, into a scalar ().
The structure of the multilayer perceptron (MLP) in the GNN consists of three layers: an input layer with
D = 20 inputs based on [
25] (e.g.,
D-dimensional in GNN structure), a hidden layer with 40 neurons, and an output layer with
D outputs. We use the “tanh” function as the activation function in the MLP.
To train the GNN, we use cross-entropy as the loss function, defined as
where
p(
xi) represents the true probability, which is 1 for an appearing symbol and 0 for a non-appearing symbol. The estimated probability (
(x)) is given by the sigmoid function as follows:
We use standard stochastic gradient descent (SGD)-based training with the Adam optimizer. The overall process of the GNN is illustrated in
Figure 7.
Finally, we compare signal with x to estimate the SER performance.
In our proposed model, the VA is used as a dynamic programming approach to approximate ML detection in MIMO systems. GNNs model the MIMO system as a graph, where nodes represent transmitted symbols and edges capture interference or correlations. GNNs excel in handling high-dimensional, non-linear, and noisy data, and can adapt to varying channel conditions and imperfect channel state information.
A key limitation of GNNs is the lack of initial values for transmitting nodes in the Tanner graph. To address this, we use the VA to generate structured initializations, providing the GNN with a strong starting point. This combination leverages the VA’s sequential consistency and the GNN’s learning ability, resulting in improved detection performance over standalone methods.
4. Results and Discussion
In this section, we configure the simulation to evaluate the model shown in
Figure 5. We generate 10,000 samples for each SNR, with each sample containing
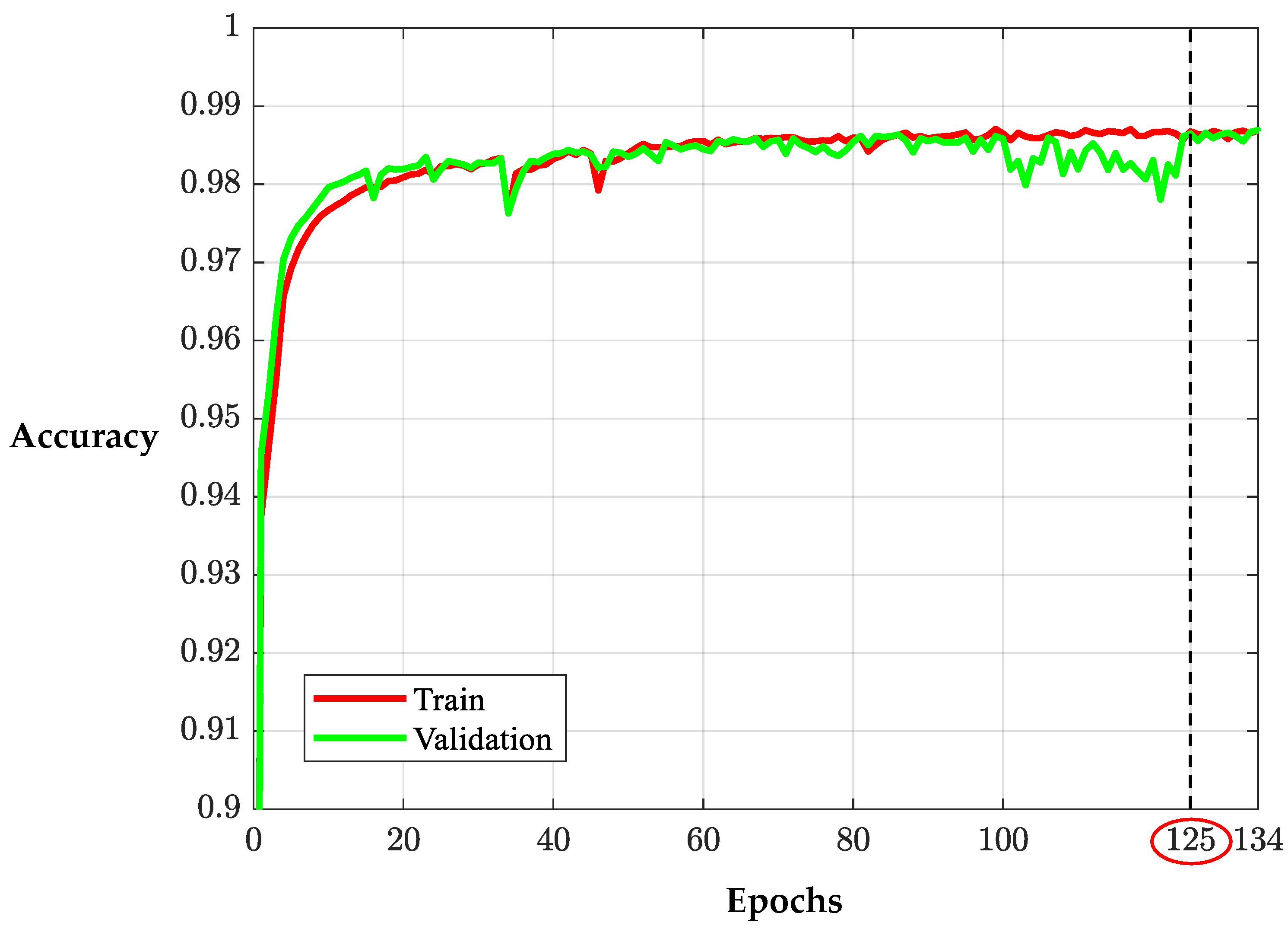
Nt symbols transmitted through the MIMO channel. The simulation is conducted on a computer equipped with an Intel i5-11400 CPU (2.6 GHz), a GTX 1650 GPU, 16 GB of RAM, and MATLAB 2023a. To collect training data, we generate 10,000 samples with randomly selected SNR values ranging from 9 to 15 dB. The training accuracy curve is shown in
Figure 8. In addition, the training parameters are summarized in
Table 1.
From the learning curves in
Figure 8, we observe that after the
epoch, the validation curve stabilizes and closely follows the training curve. This behavior indicates that the learning process has converged and reached an optimal performance point. Based on comparative examination conducted around this epoch, we select the
epoch as the optimal point for training the parameters of the GNN model.
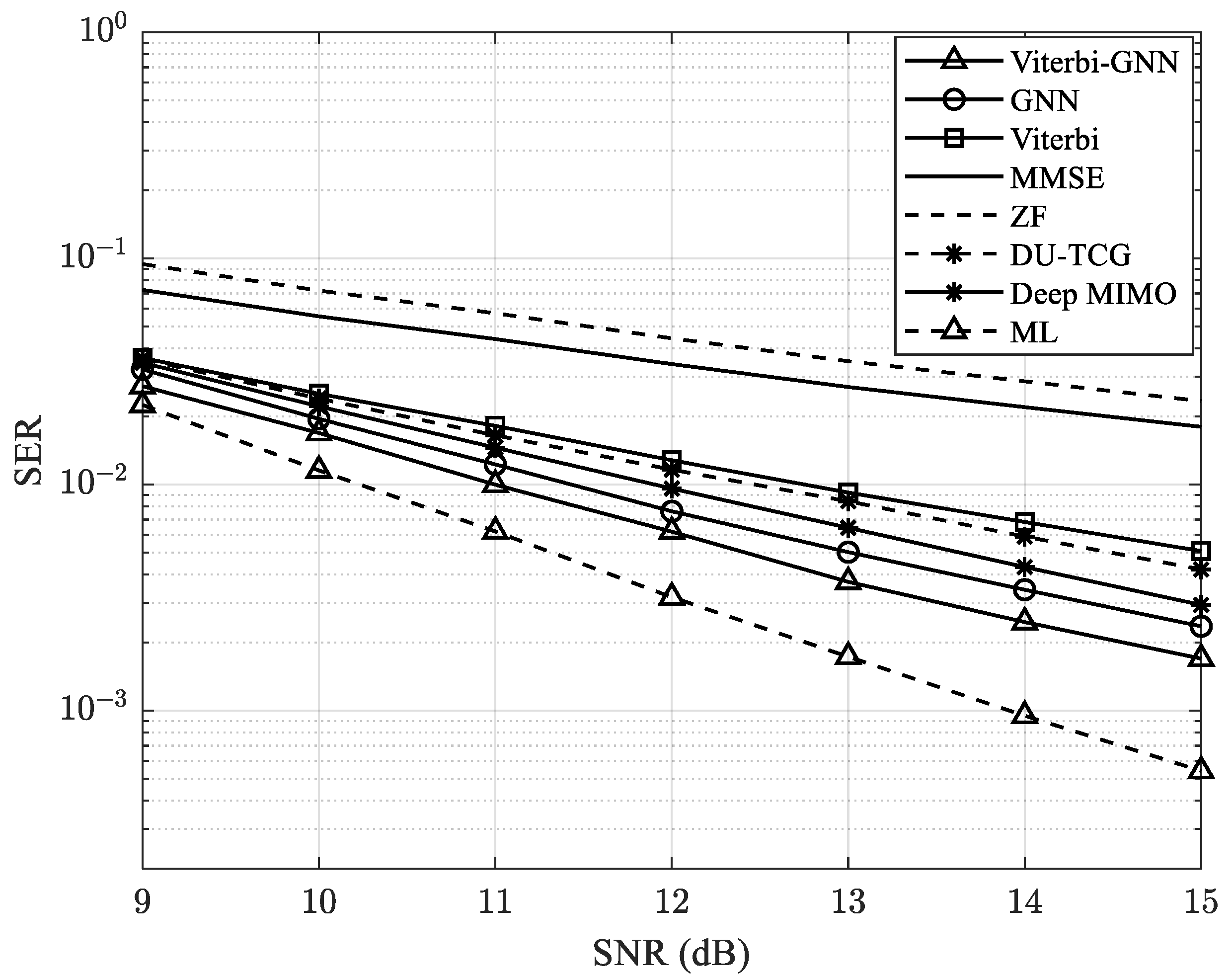
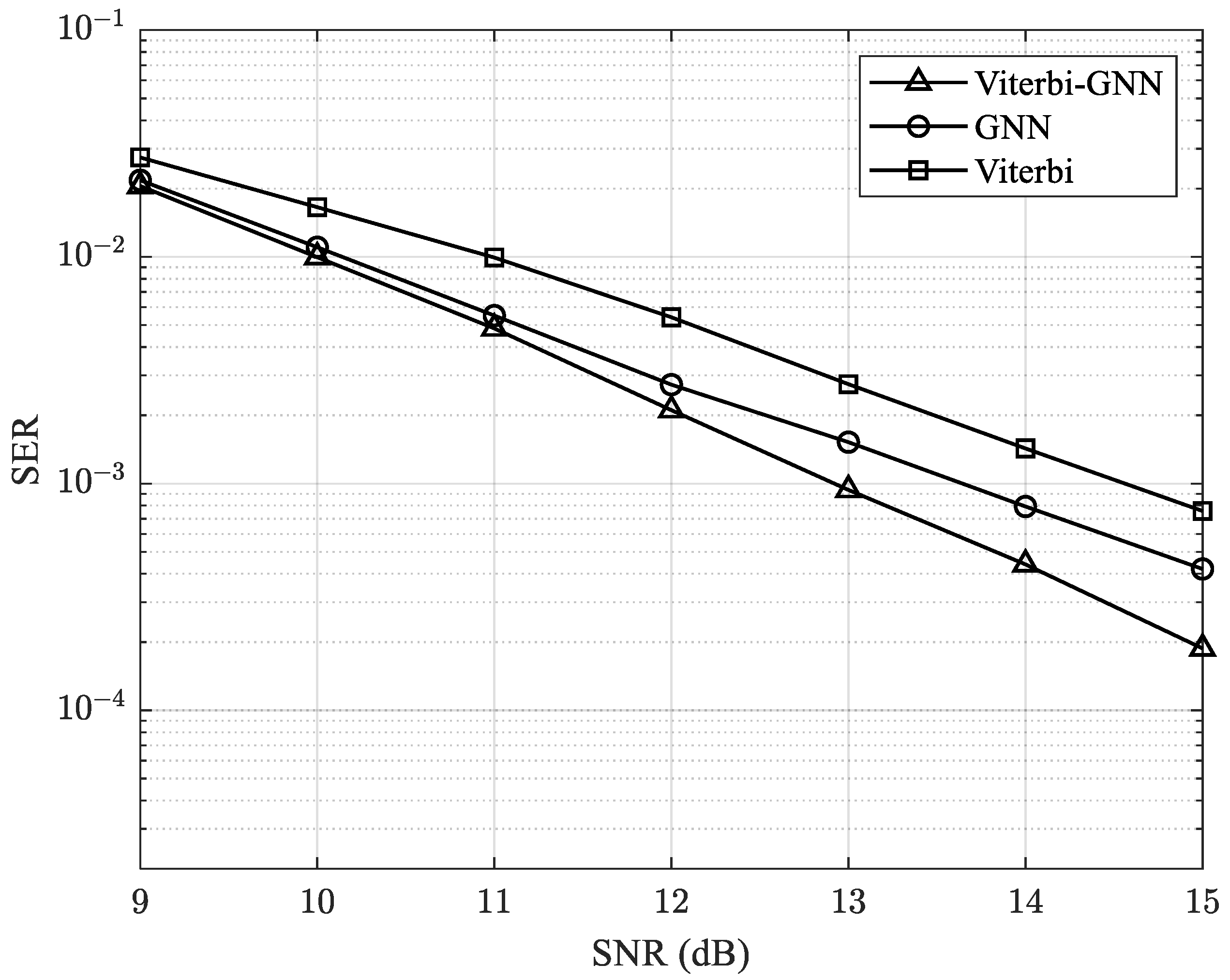
In the first experiment, we simulate the proposed model with
Nr =
Nt = 10 and quaternary phase-shift keying (QPSK) modulation (i.e., 4-QAM for a 10 × 10 MIMO system). The results are shown in
Figure 9.
In
Figure 9, our proposed model, Viterbi-GNN, is compared with several baseline methods. The GNN model employs only a GNN-based approach to detect the received signal and recover the original transmitted signal, while Viterbi refers to the model described in [
30]. Deep MIMO corresponds to the model introduced in [
19], and DU-TCG denotes the deep-unfolded, Tikhonov-regularized conjugate gradient algorithm presented in [
8].
Our results demonstrate that the proposed Viterbi-GNN model achieves improved SER performance compared to both traditional and previously proposed deep learning methods. However, it does not surpass the performance of the ML detector, which remains the optimal method for minimizing SER. The ML approach exhaustively searches for the most likely transmitted signal, offering the highest accuracy at the expense of considerable computational complexity.
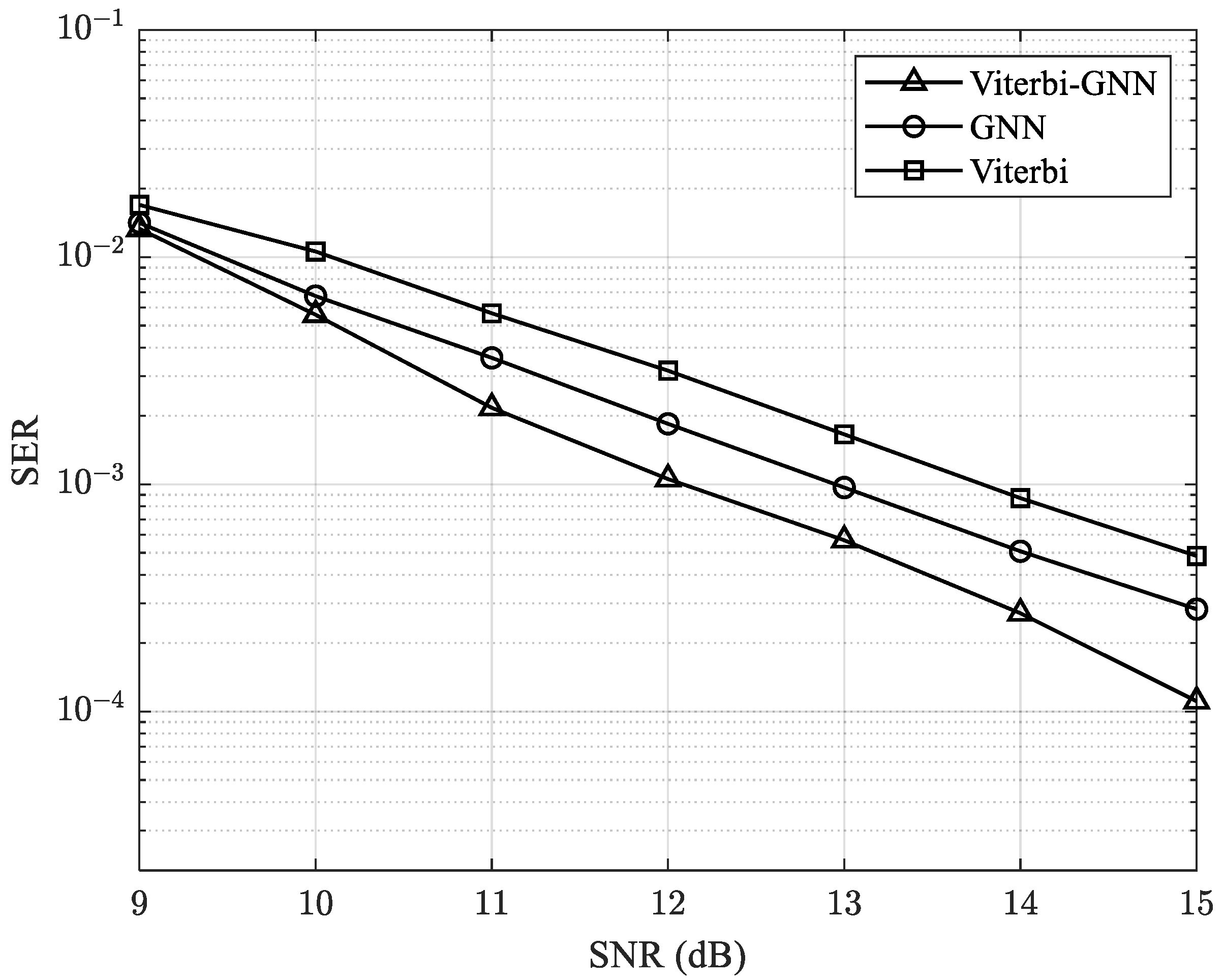
In the next set of experiments, we increase the number of antennas in the MIMO system to 20 × 20 and 25 × 25 to analyze its impact on system performance. The results, as shown in
Figure 10 and
Figure 11, demonstrate a clear improvement in SER as the number of antennas increases. This enhancement can be attributed to the improved spatial diversity and signal processing capabilities provided by a larger antenna array, which helps mitigate interference and enhance overall transmission reliability.
In the next experiment, we configure the MIMO system with a 10 × 10 antenna setup and change the modulation scheme to 16-QAM. The results, presented in
Figure 12, provide insights into the impact of modulation on system performance. This experiment helps illustrate how increasing the modulation order affects factors such as the SER and overall transmission efficiency.
From
Figure 12, it can be observed that as the modulation order (
M) increases, the system experiences higher error rates due to several factors. First, the Euclidean distance between symbols decreases, making them more susceptible to noise and interference. Additionally, higher-order modulations are more sensitive to channel fading and distortion, further impacting performance. While these modulations enhance spectral efficiency, this benefit comes at the cost of a higher SER, unless offset by sufficient power and advanced error correction techniques. Nevertheless, our proposed model still outperforms traditional and previous methods, demonstrating improved performance in mitigating these challenges.
Finally, we consider the complexity by using processing time to detect one symbol with 10 × 10 4-QAM antennas. The results are presented in
Table 2. We can see the trade-off between SER performance and the complexity of the models.
5. Conclusions
In this study, we propose a novel Viterbi-GNN detection model for MIMO systems that combines the VA and GNN to enhance detection performance while reducing computational complexity. The VA is used as a pre-processing step to generate an initial estimate of the transmitted signal, which is subsequently refined through a graph-based iterative learning process in the GNN model. By leveraging the Tanner graph structure, our approach effectively captures both the spatial correlations in MIMO channels and the structured dependencies of received signals. Simulation results demonstrate that the Viterbi-GNN detector achieves a lower SER compared to previous MIMO detection methods. However, compared to some previous models, our approach involves a trade-off between detection performance and processing latency.
In future work, we aim to optimize the model structure and reduce computational complexity through techniques such as model compression, pruning, and stochastic computing. We also plan to evaluate the model using real-world 5G/6G testbed datasets to assess its practical applicability. Additionally, we will explore the integration of modulation coding schemes and joint detection–decoding architectures to further enhance system performance and efficiency.