A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning
Abstract
1. Introduction
Related Works
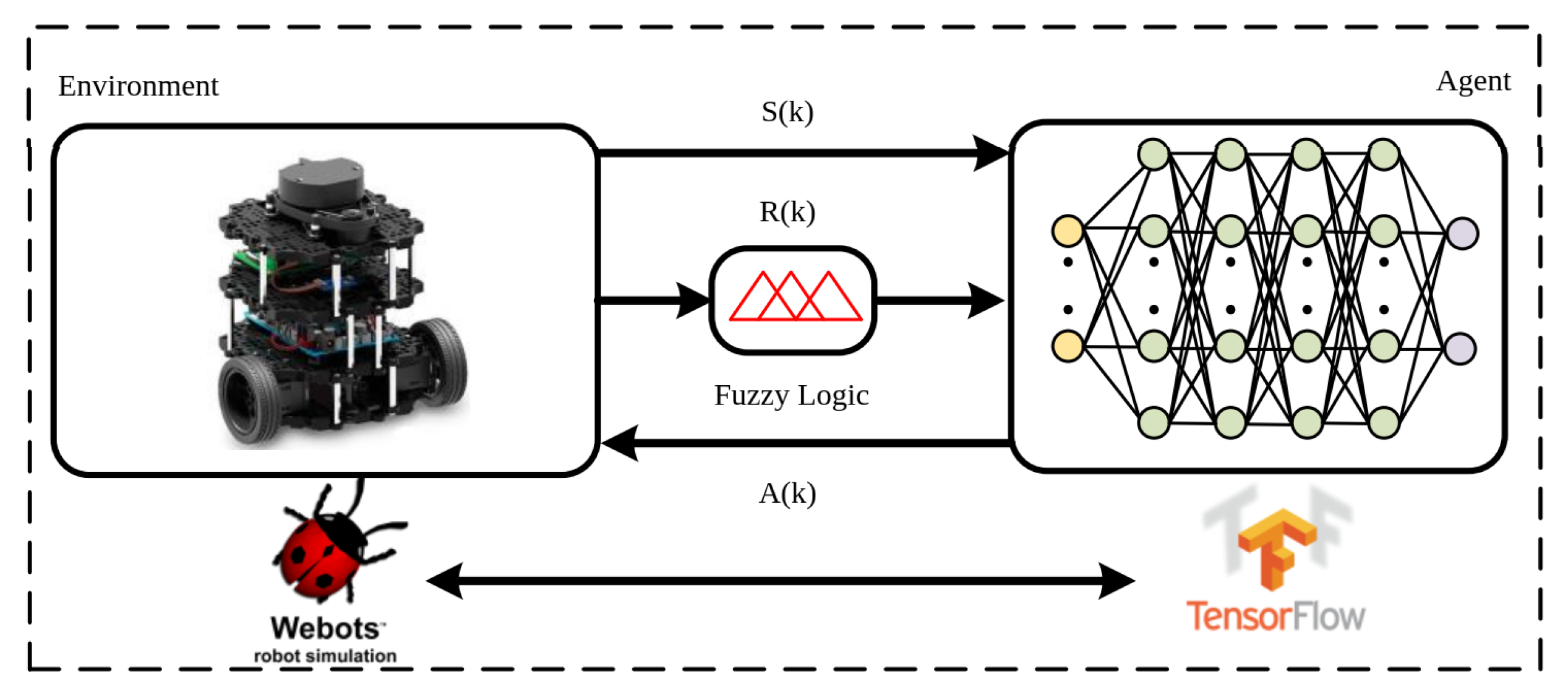
2. Methodology
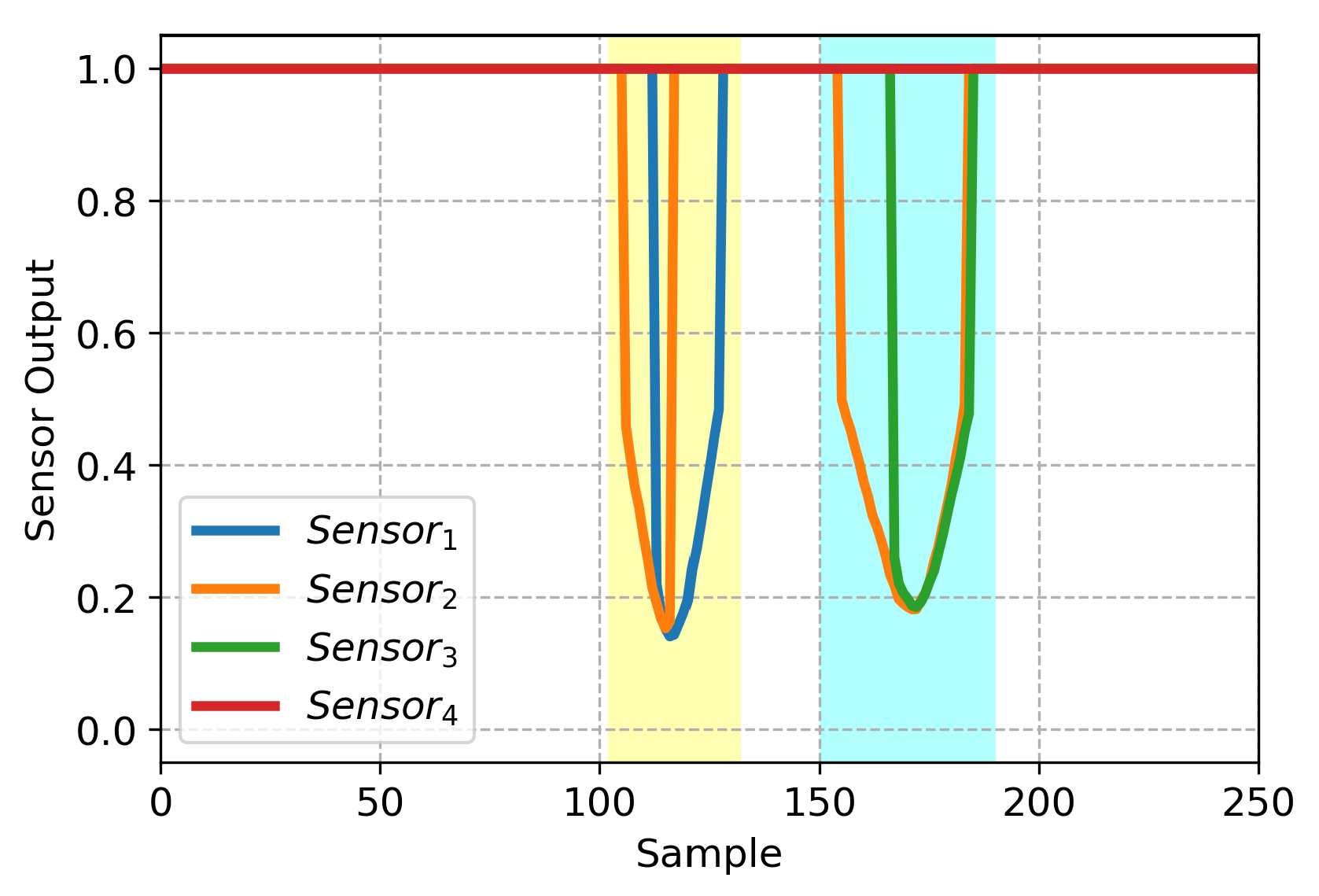
2.1. Environment Structure
2.1.1. Classical Reward Function
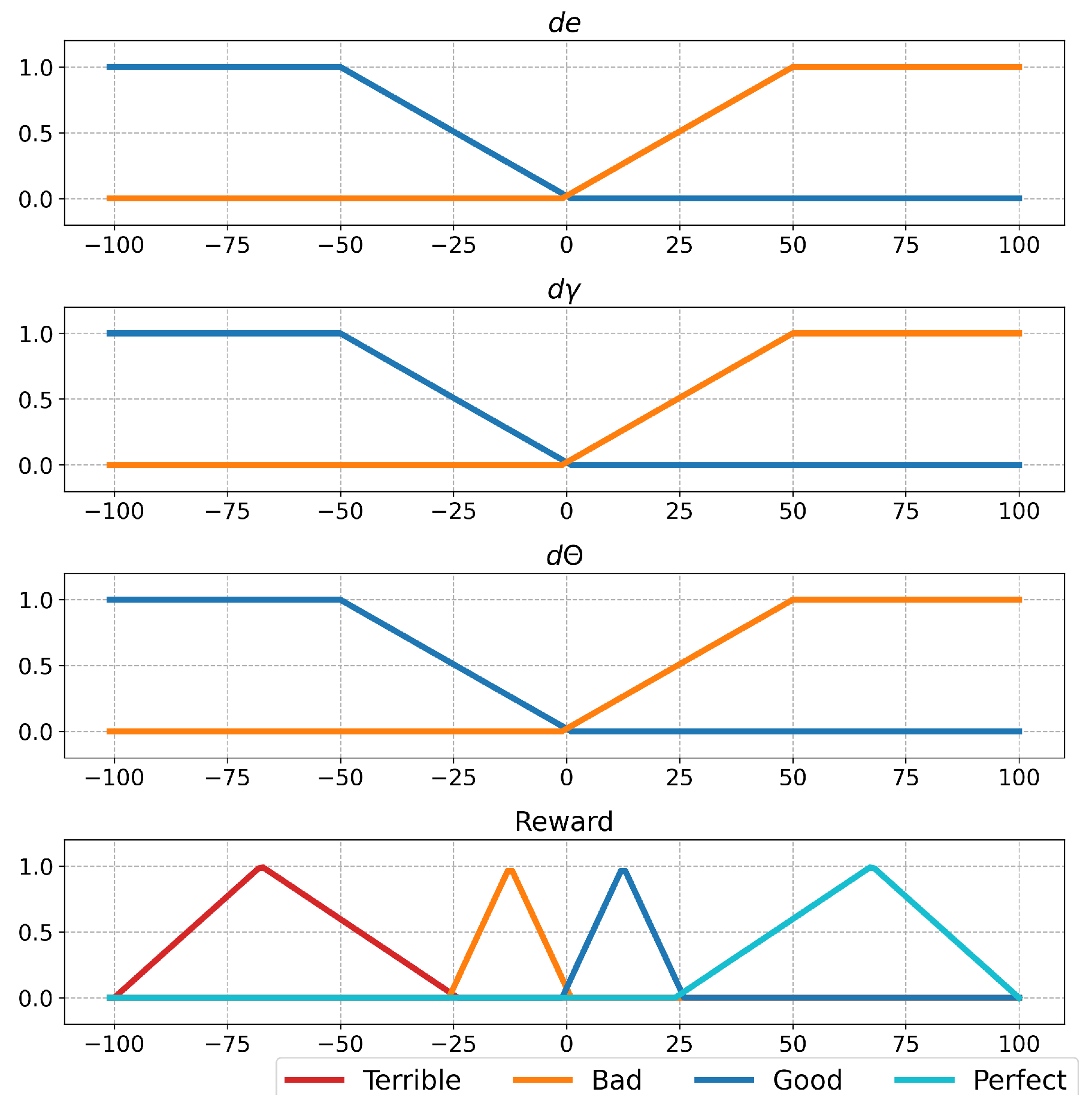
2.1.2. Fuzzy Logic Reward Function
2.2. Agent Structure
Proximal Policy Optimization Algorithm (PPO)
| Algorithm 1 Proximal Policy Optimization Algorithm. |
| for episode: 1 → M do Initialize Reset environment and obtain for iteration: 1 → T do Get according to Compute end for Compute new weight by optimizing surrogate Update networks end for |
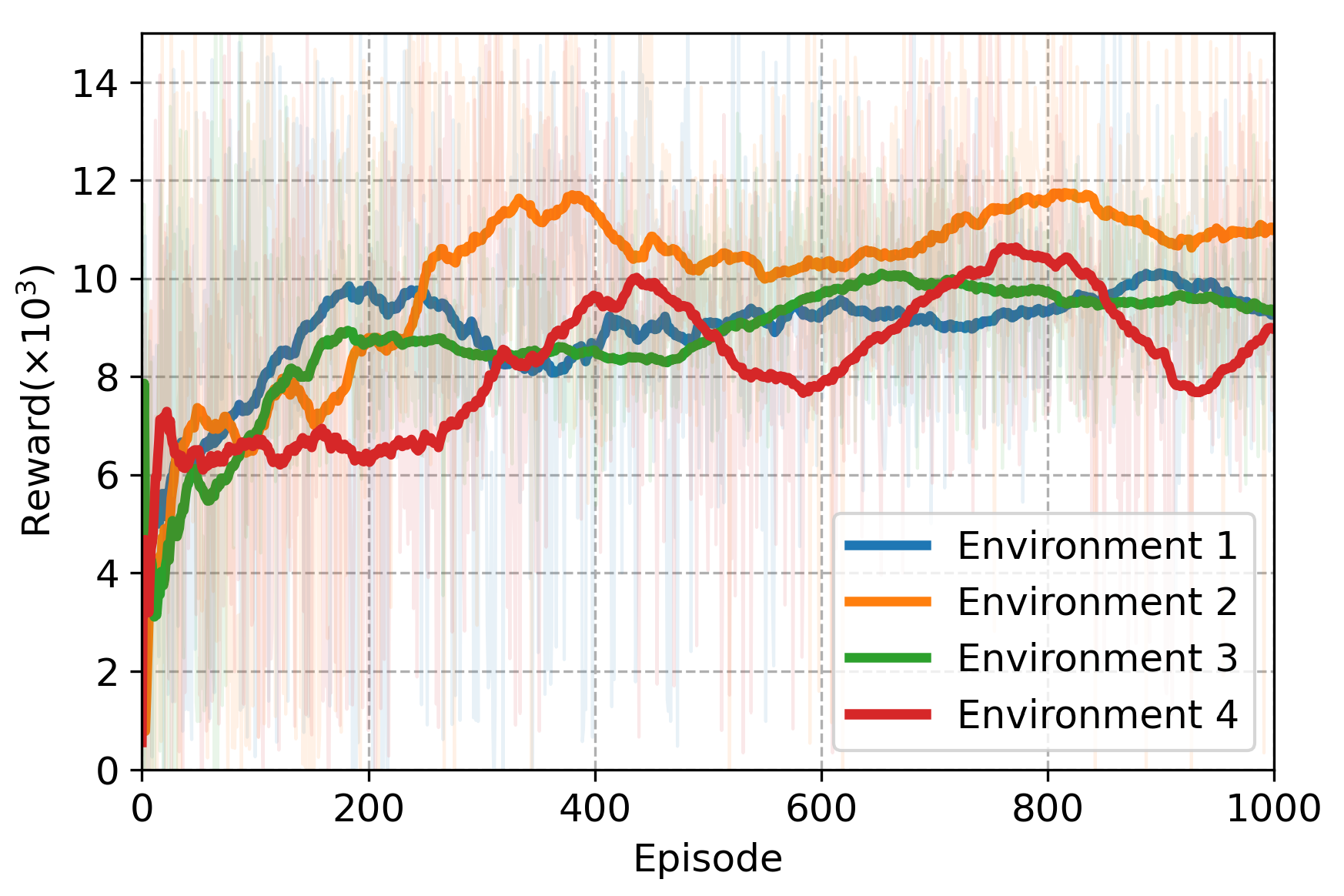
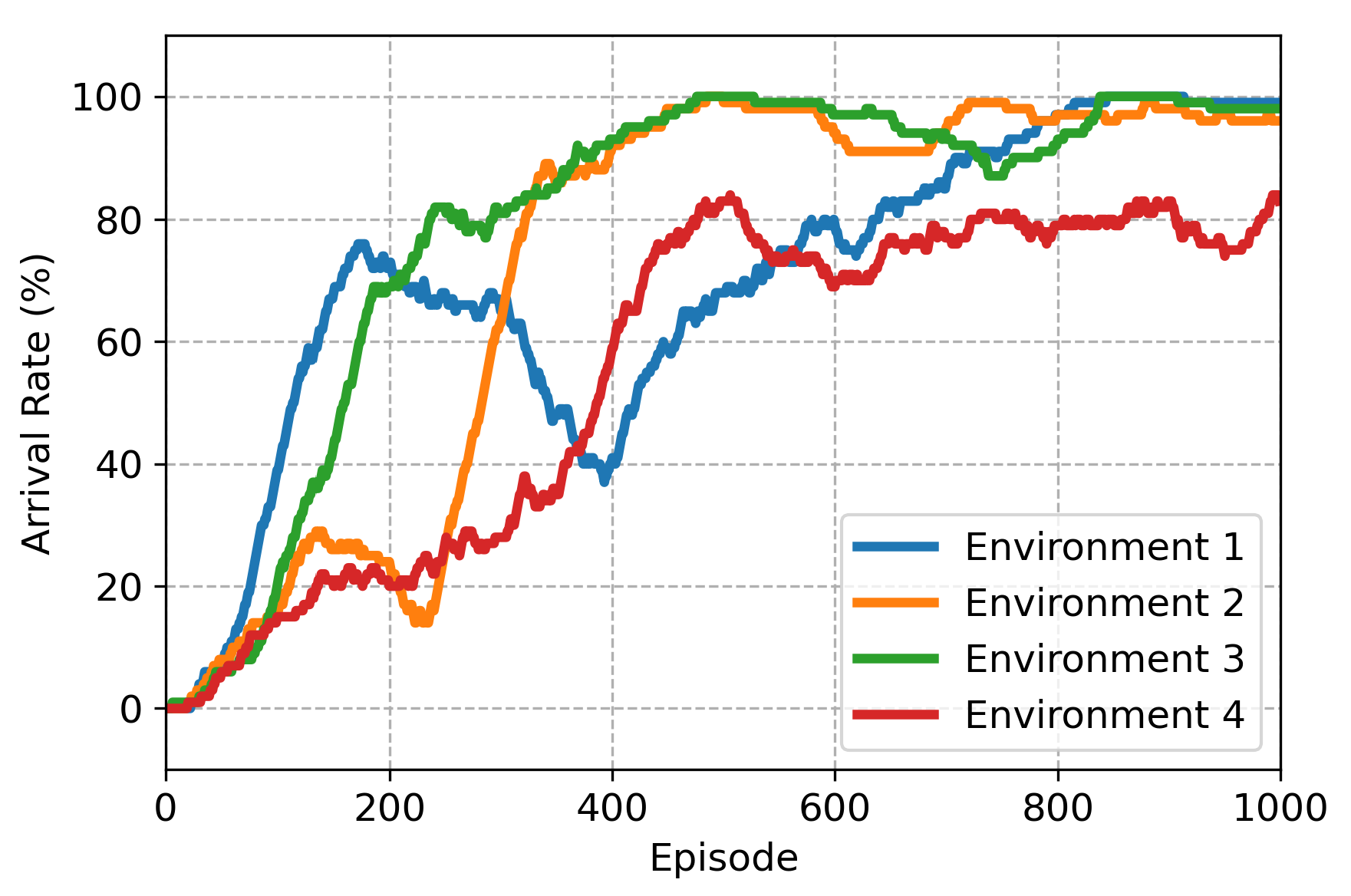
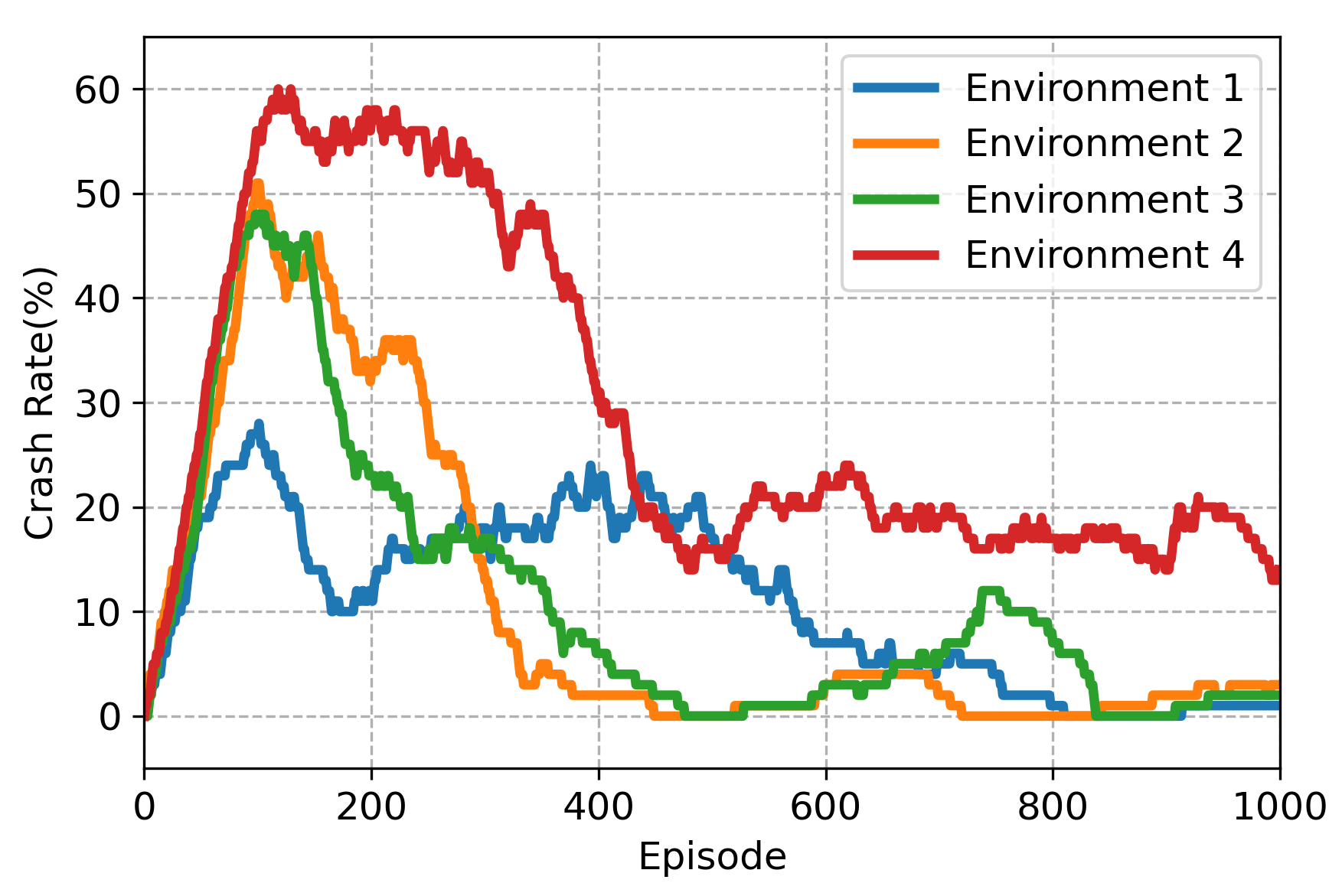
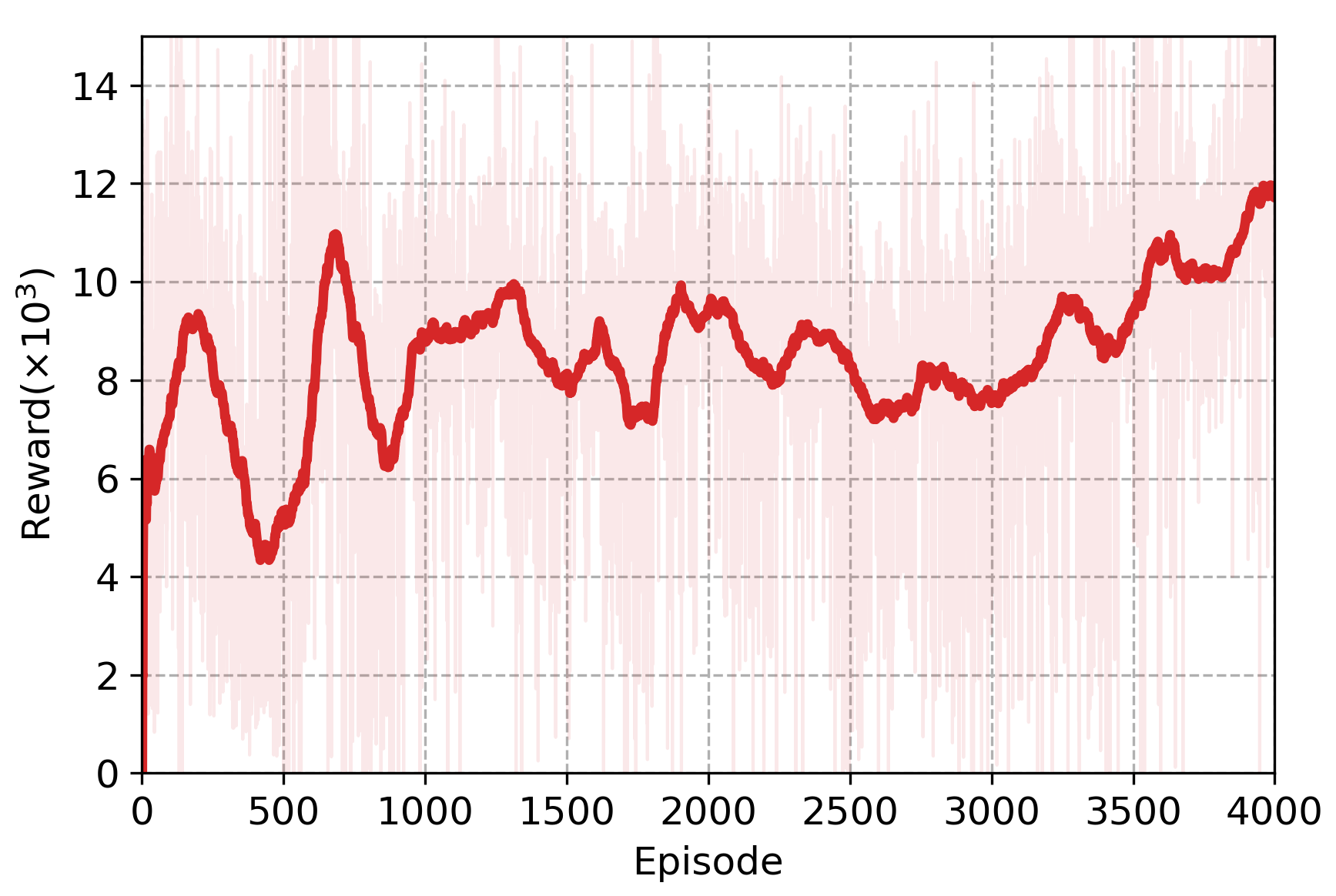
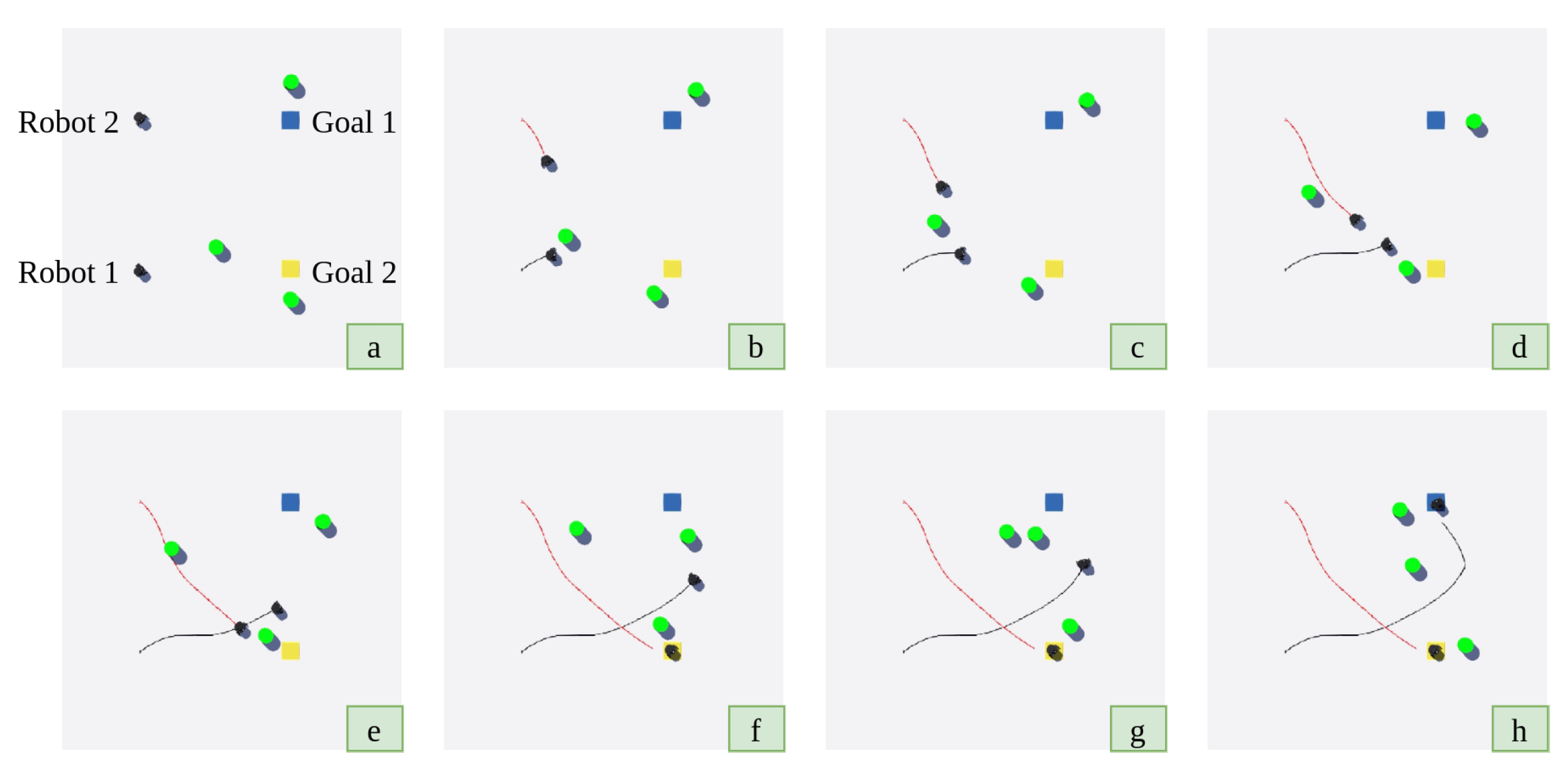
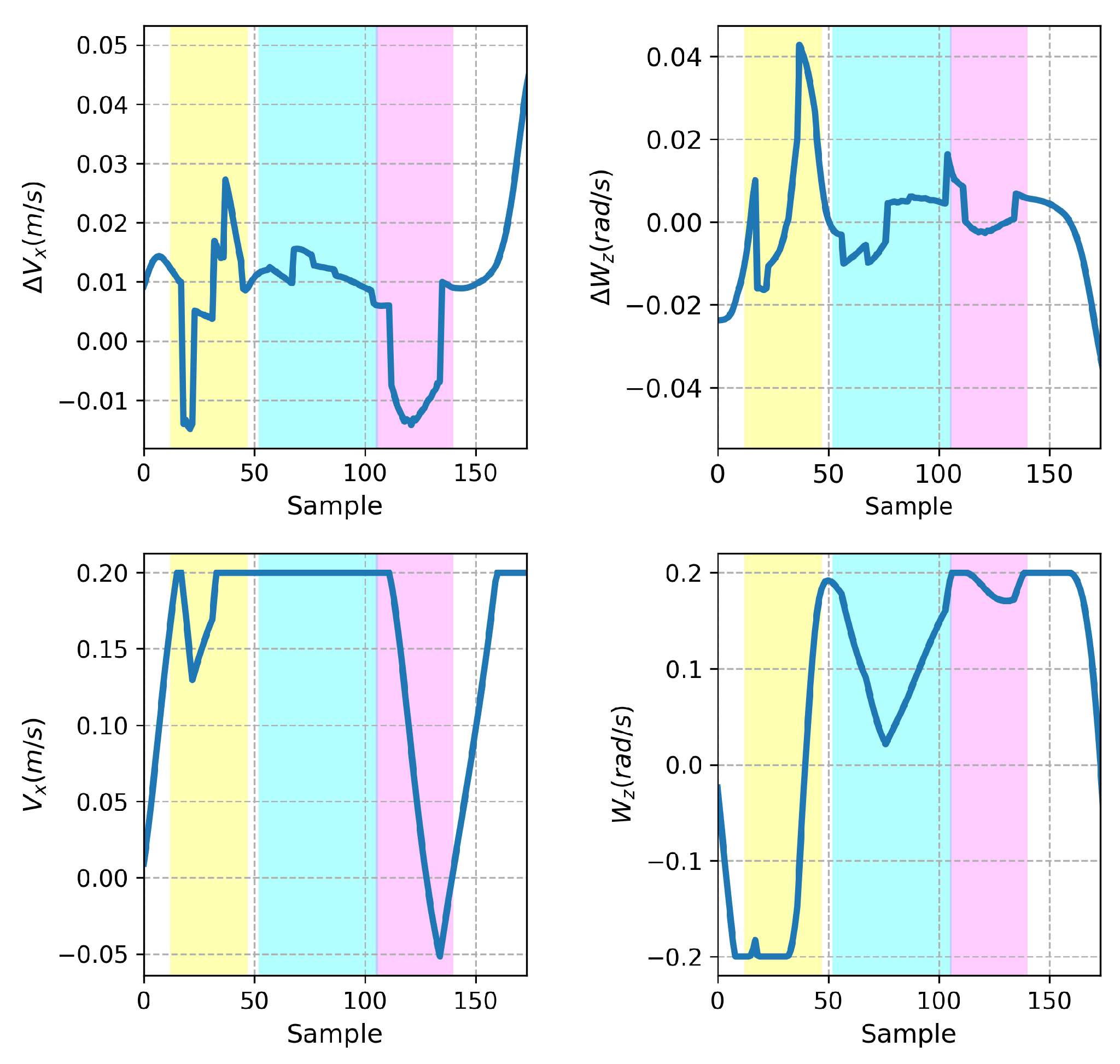
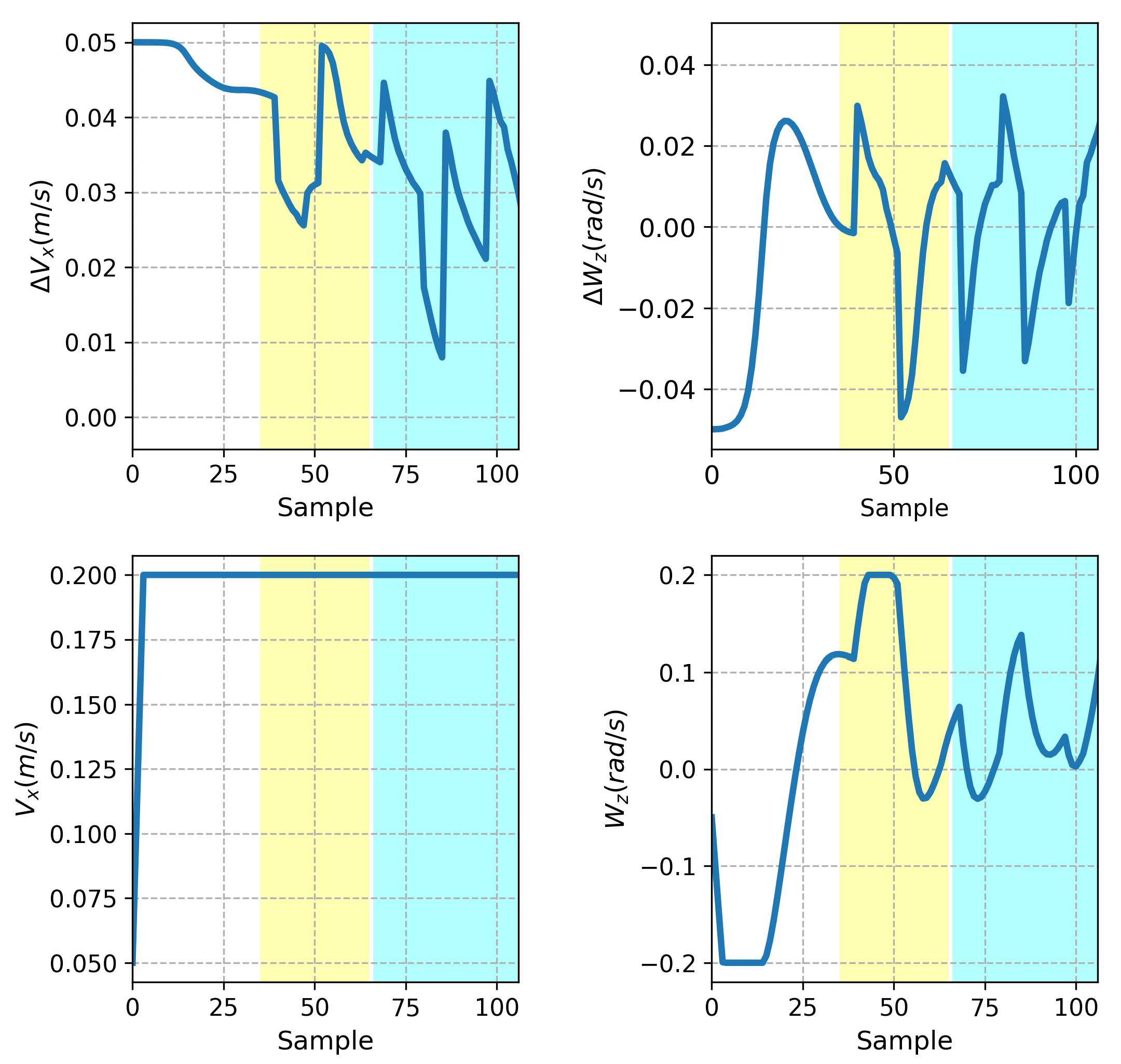
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Wang, H.; Xie, Y.; Guo, M. Path planning for multiple mobile robots under double-warehouse. Inf. Sci. 2014, 278, 357–379. [Google Scholar] [CrossRef]
- Kumar, N.V.; Kumar, C.S. Development of collision free path planning algorithm for warehouse mobile robot. Procedia Comput. Sci. 2018, 133, 456–463. [Google Scholar] [CrossRef]
- Alves, J.G.; Lizarralde, F.; Monteiro, J.C. Control Allocation for Wheeled Mobile Robots Subject to Input Saturation. IFAC—PapersOnLine 2020, 53, 3904–3909. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Song, C.; Cao, J.; Xiao, F.; Zhang, X.; Xu, Z.; Song, S. Self-supervised reinforcement learning-based energy management for a hybrid electric vehicle. J. Power Sources 2021, 514, 230584. [Google Scholar] [CrossRef]
- Jiang, P.; Song, S.; Huang, G. Attention-based meta-reinforcement learning for tracking control of AUV with time-varying dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6388–6401. [Google Scholar] [CrossRef]
- Song, R.; Jang, S.; Wang, Y.; Hanssens, D.M.; Suh, J. Reinforcement learning and risk preference in equity linked notes markets. J. Empir. Financ. 2021, 64, 224–246. [Google Scholar] [CrossRef]
- Wang, H.; Jing, J.; Wang, Q.; He, H.; Qi, X.; Lou, R. ETQ-learning: An improved Q-learning algorithm for path planning. Intell. Serv. Robot. 2024, 17, 1–15. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; Liu, L. Exploring unknown environments: Motivated developmental learning for autonomous navigation of mobile robots. Intell. Serv. Robot. 2024, 17, 197–219. [Google Scholar] [CrossRef]
- Ganjeh-Alamdari, M.; Alikhani, R.; Perfilieva, I. Fuzzy logic approach in salt and pepper noise. Comput. Electr. Eng. 2022, 102, 108264. [Google Scholar] [CrossRef]
- Senthilkumar, G.; Mayavan, T.; Manikandan, H. Prediction of mechanical characteristics of friction welded dissimilar EN 10028P 355 GH steel and AISI 430 steel joint by fuzzy logic analysis. Mater. Today Proc. 2022, 68, 2182–2188. [Google Scholar] [CrossRef]
- Mishra, D.K.; Thomas, A.; Kuruvilla, J.; Kalyanasundaram, P.; Prasad, K.R.; Haldorai, A. Design of mobile robot navigation controller using neuro-fuzzy logic system. Comput. Electr. Eng. 2022, 101, 108044. [Google Scholar] [CrossRef]
- Boztas, G.; Aydogmus, O. Implementation of Pure Pursuit Algorithm for Nonholonomic Mobile Robot using Robot Operating System. Balk. J. Electr. Comput. Eng. 2021, 9, 337–341. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.; Song, B. A New Approach to Smooth Path Planning of Mobile Robot Based on Quartic Bezier Transition Curve and Improved PSO Algorithm. Neurocomputing 2021, 473, 98–106. [Google Scholar] [CrossRef]
- Hou, W.; Xiong, Z.; Wang, C.; Chen, H. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning. Robot. Auton. Syst. 2021, 148, 103949. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Deng, X.; Li, R.; Zhao, L.; Wang, K.; Gui, X. Multi-obstacle path planning and optimization for mobile robot. Expert Syst. Appl. 2021, 183, 115445. [Google Scholar] [CrossRef]
- Tripathy, H.K.; Mishra, S.; Thakkar, H.K.; Rai, D. CARE: A Collision-Aware Mobile Robot Navigation in Grid Environment using Improved Breadth First Search. Comput. Electr. Eng. 2021, 94, 107327. [Google Scholar] [CrossRef]
- Mylvaganam, T.; Sassano, M. Autonomous collision avoidance for wheeled mobile robots using a differential game approach. Eur. J. Control. 2018, 40, 53–61. [Google Scholar] [CrossRef]
- Li, H.; Savkin, A.V. An algorithm for safe navigation of mobile robots by a sensor network in dynamic cluttered industrial environments. Robot. Comput.-Integr. Manuf. 2018, 54, 65–82. [Google Scholar] [CrossRef]
- Maldonado-Ramirez, A.; Rios-Cabrera, R.; Lopez-Juarez, I. A visual path-following learning approach for industrial robots using DRL. Robot. Comput.-Integr. Manuf. 2021, 71, 102130. [Google Scholar] [CrossRef]
- Schmitz, A.; Berthet-Rayne, P. Using Deep-Learning Proximal Policy Optimization to Solve the Inverse Kinematics of Endoscopic Instruments. IEEE Trans. Med. Robot. Bionics 2020, 3, 273–276. [Google Scholar] [CrossRef]
- Wen, S.; Wen, Z.; Zhang, D.; Zhang, H.; Wang, T. A multi-robot path-planning algorithm for autonomous navigation using meta-reinforcement learning based on transfer learning. Appl. Soft Comput. 2021, 110, 107605. [Google Scholar] [CrossRef]
- Tan, X.; Chng, C.B.; Su, Y.; Lim, K.B.; Chui, C.K. Robot-assisted training in laparoscopy using deep reinforcement learning. IEEE Robot. Autom. Lett. 2019, 4, 485–492. [Google Scholar] [CrossRef]
- Tallamraju, R.; Saini, N.; Bonetto, E.; Pabst, M.; Liu, Y.T.; Black, M.J.; Ahmad, A. Aircaprl: Autonomous aerial human motion capture using deep reinforcement learning. IEEE Robot. Autom. Lett. 2020, 5, 6678–6685. [Google Scholar] [CrossRef]
- Gangapurwala, S.; Mitchell, A.; Havoutis, I. Guided constrained policy optimization for dynamic quadrupedal robot locomotion. IEEE Robot. Autom. Lett. 2020, 5, 3642–3649. [Google Scholar] [CrossRef]
- Zhang, D.; Bailey, C.P. Obstacle avoidance and navigation utilizing reinforcement learning with reward shaping. In Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications II; SPIE: Bellingham, WA, USA, 2020; Volume 11413, pp. 500–506. [Google Scholar]
- Zhao, T.; Wang, M.; Zhao, Q.; Zheng, X.; Gao, H. A path-planning method based on improved soft actor-critic algorithm for mobile robots. Biomimetics 2023, 8, 481. [Google Scholar] [CrossRef]
- Wong, M.F.; Tan, C.W. Aligning Crowd-Sourced Human Feedback for Reinforcement Learning on Code Generation by Large Language Models. arXiv 2025, arXiv:2503.15129. [Google Scholar] [CrossRef]
- Zheng, R.; Dou, S.; Gao, S.; Hua, Y.; Shen, W.; Wang, B.; Liu, Y.; Jin, S.; Liu, Q.; Zhou, Y.; et al. Secrets of rlhf in large language models part i: Ppo. arXiv 2023, arXiv:2307.04964. [Google Scholar]
- Azlan, N.; Zainudin, F.; Yusuf, H.; Toha, S.; Yusoff, S.; Osman, N. Fuzzy logic controlled miniature LEGO robot for undergraduate training system. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 2184–2188. [Google Scholar]
- Singh, N.H.; Thongam, K. Mobile robot navigation using fuzzy logic in static environments. Procedia Comput. Sci. 2018, 125, 11–17. [Google Scholar] [CrossRef]
- Pandey, A.; Parhi, D.R. MATLAB simulation for mobile robot navigation with hurdles in cluttered environment using minimum rule based fuzzy logic controller. Procedia Technol. 2014, 14, 28–34. [Google Scholar] [CrossRef][Green Version]
- Xu, J.X.; Guo, Z.Q.; Lee, T.H. Design and implementation of a Takagi–Sugeno-type fuzzy logic controller on a two-wheeled mobile robot. IEEE Trans. Ind. Electron. 2012, 60, 5717–5728. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Vu, C.T. Mobile Robot Motion Control Using a Combination of Fuzzy Logic Method and Kinematic Model. In Intelligent Systems and Networks; Springer: Singapore, 2022; pp. 495–503. [Google Scholar]
- Karaduman, B.; Tezel, B.T.; Challenger, M. Enhancing BDI agents using fuzzy logic for CPS and IoT interoperability using the JaCa platform. Symmetry 2022, 14, 1447. [Google Scholar] [CrossRef]
- Lu, J.; Ma, G.; Zhang, G. Fuzzy Machine Learning: A Comprehensive Framework and Systematic Review. IEEE Trans. Fuzzy Syst. 2024, 32, 3861–3878. [Google Scholar] [CrossRef]
- Xie, Z.; Sun, T.; Kwan, T.; Wu, X. Motion control of a space manipulator using fuzzy sliding mode control with reinforcement learning. Acta Astronaut. 2020, 176, 156–172. [Google Scholar] [CrossRef]
- Khater, A.A.; El-Nagar, A.M.; El-Bardini, M.; El-Rabaie, N.M. Online learning of an interval type-2 TSK fuzzy logic controller for nonlinear systems. J. Frankl. Inst. 2019, 356, 9254–9285. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, W.; Cheng, N.; Gao, J. Trajectory tracking control for rotary steerable systems using interval type-2 fuzzy logic and reinforcement learning. J. Frankl. Inst. 2018, 355, 803–826. [Google Scholar] [CrossRef]
- Vemireddy, S.; Rout, R.R. Fuzzy reinforcement learning for energy efficient task offloading in vehicular fog computing. Comput. Netw. 2021, 199, 108463. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Tang, B.; Cheng, Y. Conditional DQN-based motion planning with fuzzy logic for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2020, 23, 2966–2977. [Google Scholar] [CrossRef]
- Hinojosa, W.M.; Nefti, S.; Kaymak, U. Systems control with generalized probabilistic fuzzy-reinforcement learning. IEEE Trans. Fuzzy Syst. 2010, 19, 51–64. [Google Scholar] [CrossRef]
- Chen, G.; Lu, Y.; Yang, X.; Hu, H. Reinforcement learning control for the swimming motions of a beaver-like, single-legged robot based on biological inspiration. Robot. Auton. Syst. 2022, 154, 104116. [Google Scholar] [CrossRef]
- Liu, J.; Lu, H.; Luo, Y.; Yang, S. Spiking neural network-based multi-task autonomous learning for mobile robots. Eng. Appl. Artif. Intell. 2021, 104, 104362. [Google Scholar] [CrossRef]
- Xiao, H.; Chen, C.; Zhang, G.; Chen, C.P. Reinforcement learning-driven dynamic obstacle avoidance for mobile robot trajectory tracking. Knowl.-Based Syst. 2024, 297, 111974. [Google Scholar] [CrossRef]
- Cui, T.; Yang, X.; Jia, F.; Jin, J.; Ye, Y.; Bai, R. Mobile robot sequential decision making using a deep reinforcement learning hyper-heuristic approach. Expert Syst. Appl. 2024, 257, 124959. [Google Scholar] [CrossRef]
- Yan, C.; Chen, G.; Li, Y.; Sun, F.; Wu, Y. Immune deep reinforcement learning-based path planning for mobile robot in unknown environment. Appl. Soft Comput. 2023, 145, 110601. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, C.; Hu, C.; Zhang, J. Event-triggered reconfigurable reinforcement learning motion-planning approach for mobile robot in unknown dynamic environments. Eng. Appl. Artif. Intell. 2023, 123, 106197. [Google Scholar] [CrossRef]
- Bai, Z.; Pang, H.; He, Z.; Zhao, B.; Wang, T. Path Planning of Autonomous Mobile Robot in Comprehensive Unknown Environment Using Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 22153–22166. [Google Scholar] [CrossRef]
- Choi, J.; Lee, G.; Lee, C. Reinforcement learning-based dynamic obstacle avoidance and integration of path planning. Intell. Serv. Robot. 2021, 14, 663–677. [Google Scholar] [CrossRef]
- Khnissi, K.; Jabeur, C.B.; Seddik, H. A smart mobile robot commands predictor using recursive neural network. Robot. Auton. Syst. 2020, 131, 103593. [Google Scholar] [CrossRef]
- Duguleana, M.; Mogan, G. Neural networks based reinforcement learning for mobile robots obstacle avoidance. Expert Syst. Appl. 2016, 62, 104–115. [Google Scholar] [CrossRef]
- Shantia, A.; Timmers, R.; Chong, Y.; Kuiper, C.; Bidoia, F.; Schomaker, L.; Wiering, M. Two-stage visual navigation by deep neural networks and multi-goal reinforcement learning. Robot. Auton. Syst. 2021, 138, 103731. [Google Scholar] [CrossRef]
- Low, E.S.; Ong, P.; Cheah, K.C. Solving the optimal path planning of a mobile robot using improved Q-learning. Robot. Auton. Syst. 2019, 115, 143–161. [Google Scholar] [CrossRef]
- Lin, G.; Zhu, L.; Li, J.; Zou, X.; Tang, Y. Collision-free path planning for a guava-harvesting robot based on recurrent deep reinforcement learning. Comput. Electron. Agric. 2021, 188, 106350. [Google Scholar] [CrossRef]
- Mabu, S.; Tjahjadi, A.; Hirasawa, K. Adaptability analysis of genetic network programming with reinforcement learning in dynamically changing environments. Expert Syst. Appl. 2012, 39, 12349–12357. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Gao, H.; Chen, C.; Liu, Z.; Deng, Z. Adaptive neural network tracking control-based reinforcement learning for wheeled mobile robots with skidding and slipping. Neurocomputing 2018, 283, 20–30. [Google Scholar] [CrossRef]
- Bingol, M.C. Reinforcement Learning-Based Safe Path Planning for a 3R Planar Robot. Sakarya Univ. J. Sci. 2022, 26, 127–134. [Google Scholar] [CrossRef]
- Bingol, M.C. Development of Neural Network Based on Deep Reinforcement Learning to Compensate for Damaged Actuator of a Planar Robot. In Proceedings of the Global Conference on Engineering Research (Globcer’21), Bandırma, Türkiye, 2–5 June 2021. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]







| Parameter | Value |
|---|---|
| Gravity | 9.81 |
| Time Step | 128 |
| Constraint Force Mixing | 10−5 |
| Error-Reduction Parameter | 0.2 |
| Optimal Thread Count | 1 |
| Physics Disable Time | 1 |
| Physics Disable Linear Threshold | 0.01 |
| Physics Disable Angular Threshold | 0.01 |
| Line Scale | 0.1 |
| Drag Force Scale | 30 |
| Drag Torque Scale | 5 |
| Rules | Reward | |||||
|---|---|---|---|---|---|---|
| 1 | if | Good | Good | Good | then | Perfect |
| 2 | if | Good | Good | Bad | then | Good |
| 3 | if | Good | Bad | Good | then | Good |
| 4 | if | Good | Bad | Bad | then | Bad |
| 5 | if | Bad | Good | Good | then | Good |
| 6 | if | Bad | Good | Bad | then | Bad |
| 7 | if | Bad | Bad | Good | then | Bad |
| 8 | if | Bad | Bad | Bad | then | Terrible |
| C( ± SD) | A( ± SD) | S( ± SD) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Environment 1 | 6 | 20 | 15 | 249 | 24.0 ± 9.54 | 614 | 63.5 ± 17.70 | 365 | 39.4 ± 26.25 | 13 | 73 | 60 | 7 | 93 | 86 |
| 10 | 20 | 15 | 253 | 24.1 ± 18.28 | 672 | 70.3 ± 19.19 | 419 | 46.3 ± 37.35 | 17 | 75 | 58 | 2 | 94 | 92 | |
| 8 | 15 | 15 | 244 | 25.0 ± 15.57 | 591 | 60.3 ± 17.45 | 347 | 35.34 ± 31.08 | 2 | 88 | 86 | 2 | 94 | 92 | |
| 8 | 25 | 15 | 327 | 32.2 ± 17.42 | 406 | 40.6 ± 35.71 | 79 | 8.4 ± 51.87 | 10 | 81 | 71 | 7 | 88 | 81 | |
| 8 | 20 | 12 | 183 | 17.5 ± 6.25 | 682 | 70.4 ± 15.29 | 499 | 52.9 ± 20.33 | 10 | 89 | 79 | 7 | 92 | 85 | |
| 8 | 20 | 18 | 198 | 19.0 ± 16.63 | 717 | 74.3 ± 25.28 | 519 | 55.2 ± 41.60 | 11 | 89 | 78 | 2 | 94 | 92 | |
| 8 | 20 | 15 | 214 | 19.6 ± 11.00 | 658 | 68.7 ± 19.37 | 444 | 49.1 ± 29.55 | 14 | 80 | 66 | 5 | 92 | 87 | |
| 110 | 10.4 ± 7.87 | 748 | 76.0 ± 17.92 | 638 | 65.6 ± 25.57 | 1 | 99 | 98 | 0 | 100 | 100 | ||||
| Environment 2 | 6 | 20 | 15 | 466 | 46.5 ± 10.80 | 378 | 38.9 ± 13.07 | −88 | −7.6 ± 23.37 | 37 | 48 | 11 | 29 | 61 | 32 |
| 10 | 20 | 15 | 440 | 43.7 ± 12.75 | 384 | 39.3 ± 22.75 | −56 | −4.5 ± 34.72 | 33 | 58 | 25 | 18 | 79 | 61 | |
| 8 | 15 | 15 | 462 | 47.8 ± 15.42 | 411 | 40.7 ± 21.49 | −51 | −7.0 ± 35.92 | 16 | 80 | 64 | 16 | 80 | 64 | |
| 8 | 25 | 15 | 500 | 50.4 ± 5.10 | 354 | 36.3 ± 12.80 | −146 | −14.1 ± 14.81 | 44 | 53 | 9 | 44 | 54 | 10 | |
| 8 | 20 | 12 | 395 | 38.1 ± 15.98 | 467 | 48.4 ± 21.92 | 72 | 10.3 ± 37.65 | 30 | 54 | 24 | 20 | 78 | 58 | |
| 8 | 20 | 18 | 478 | 49.3 ± 13.45 | 430 | 43.6 ± 18.30 | −48 | −5.7 ± 30.81 | 30 | 67 | 37 | 24 | 75 | 51 | |
| 8 | 20 | 15 | 278 | 25.4 ± 14.93 | 604 | 64.1 ± 21.92 | 326 | 38.6 ± 36.74 | 30 | 62 | 32 | 10 | 87 | 77 | |
| 109 | 9.27 ± 14.31 | 773 | 79.6 ± 28.57 | 644 | 70.4 ± 42.67 | 3 | 96 | 93 | 0 | 100 | 100 | ||||
| Environment 3 | 6 | 20 | 15 | 243 | 22.7 ± 15.42 | 667 | 69.3 ± 19.50 | 424 | 46.5 ± 34.84 | 13 | 82 | 69 | 4 | 91 | 87 |
| 10 | 20 | 15 | 222 | 20.3 ± 13.30 | 651 | 67.6 ± 19.79 | 429 | 47.3 ± 32.74 | 10 | 83 | 73 | 9 | 89 | 80 | |
| 8 | 15 | 15 | 445 | 45.5 ± 14.25 | 399 | 39.6 ± 18.03 | −46 | −5.9 ± 31.35 | 16 | 77 | 61 | 16 | 78 | 62 | |
| 8 | 25 | 15 | 737 | 76.4 ± 34.43 | 246 | 21.9 ± 3266 | −491 | −54.4 ± 67.08 | 8 | 87 | 79 | 8 | 88 | 80 | |
| 8 | 20 | 12 | 288 | 27.9 ± 9.71 | 584 | 60.6 ± 17.18 | 296 | 32.7 ± 26.30 | 24 | 64 | 40 | 11 | 87 | 76 | |
| 8 | 20 | 18 | 435 | 42.8 ± 7.58 | 488 | 51.0 ± 12.27 | 53 | 8.2 ± 19.63 | 43 | 54 | 11 | 25 | 73 | 48 | |
| 8 | 20 | 15 | 273 | 27.0 ± 13.83 | 581 | 59.2 ± 20.78 | 308 | 32.1 ± 34.43 | 10 | 86 | 76 | 9 | 88 | 79 | |
| 112 | 9.7 ± 11.74 | 849 | 87.6 ± 17.24 | 737 | 77.9 ± 28.93 | 2 | 98 | 96 | 0 | 100 | 100 | ||||
| Environment 4 | 6 | 20 | 15 | 522 | 52.1 ± 15.93 | 386 | 39.6 ± 21.10 | −136 | −12.5 ± 36.50 | 38 | 59 | 21 | 29 | 67 | 38 |
| 10 | 20 | 15 | 494 | 49.6 ± 12.77 | 419 | 42.6 ± 13.58 | −75 | −6.9 ± 26.02 | 42 | 54 | 12 | 31 | 63 | 32 | |
| 8 | 15 | 15 | 576 | 57.8 ± 11.29 | 348 | 35.8 ± 11.92 | −228 | −22.0 ± 22.68 | 49 | 46 | −3 | 36 | 63 | 27 | |
| 8 | 25 | 15 | 444 | 43.7 ± 13.97 | 484 | 49.6 ± 17.50 | 40 | 5.9 ± 30.90 | 38 | 59 | 21 | 22 | 73 | 51 | |
| 8 | 20 | 12 | 481 | 47.4 ± 16.27 | 432 | 44.8 ± 16.67 | −49 | −2.5 ± 32.77 | 42 | 56 | 14 | 25 | 69 | 44 | |
| 8 | 20 | 18 | 514 | 51.4 ± 16.68 | 407 | 40.9 ± 17.35 | −107 | −10.5 ± 33.81 | 33 | 66 | 33 | 21 | 70 | 49 | |
| 8 | 20 | 15 | 470 | 45.8 ± 18.99 | 444 | 47.2 ± 22.77 | −26 | 1.4 ± 41.50 | 51 | 40 | −11 | 15 | 79 | 64 | |
| 299 | 29.7 ± 16.13 | 598 | 60.5 ± 24.06 | 299 | 30.8 ± 40.18 | 14 | 83 | 69 | 15 | 84 | 69 | ||||
| Arrival Time (s) | Distance Traveled (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Env | Crashed | Arrived | Score | Min | Max | Median | Min | Max | Median |
| 1 | 0 | 100 | 100 | 15.872 | 40.32 | 23.808 | 3.122 | 8.02 | 4.705 |
| 2 | 0 | 100 | 100 | 18.944 | 34.176 | 24.064 | 3.716 | 6.774 | 4.747 |
| 3 | 0 | 100 | 100 | 16.00 | 34.04 | 22.144 | 3.133 | 7.748 | 4.362 |
| 4 | 7 | 91 | 84 | 17.152 | 32.00 | 24.064 | 3.203 | 6.252 | 4.637 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bingol, M.C. A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning. Electronics 2025, 14, 1593. https://doi.org/10.3390/electronics14081593
Bingol MC. A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning. Electronics. 2025; 14(8):1593. https://doi.org/10.3390/electronics14081593
Chicago/Turabian StyleBingol, Mustafa Can. 2025. "A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning" Electronics 14, no. 8: 1593. https://doi.org/10.3390/electronics14081593
APA StyleBingol, M. C. (2025). A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning. Electronics, 14(8), 1593. https://doi.org/10.3390/electronics14081593







