A Comprehensive Robustness Analysis of Grid-Forming Virtual Synchronous Machine Systems for the Evaluation of Frequency Performance
Abstract
1. Introduction
| References | Stability Forms |
|---|---|
| [3,5,6,22] and this paper | Small Signal Stability |
| [7,8,23] and this paper | Robust Stability |
| [9,11,12] | Transient Stability |
| [13,15,21] | Frequency and Voltage Stability |
| [10,14] | Fault Ride-Through and System Stability |
| [18,19,20] | Low-Frequency Oscillation Stability |
- The sensitivity and robustness impacts of the system can be quantitatively identified through the proposed robustness model, which provides guidance and direction for controller design to mitigate the effects of disturbances on the controller;
- A judgment criterion for robustness identification is proposed, which can give physical insights into the frequency property of GFMCS subjected to disturbances;
- This study investigates the influence mechanism of damping and inertia coefficients on the robustness of grid-forming converter systems (GFMCS). Optimizing the controller parameters can effectively enhance the dynamic stability and robustness of the system. These contributions provide a theoretical basis and practical guidance for the optimized design of VSG control systems.
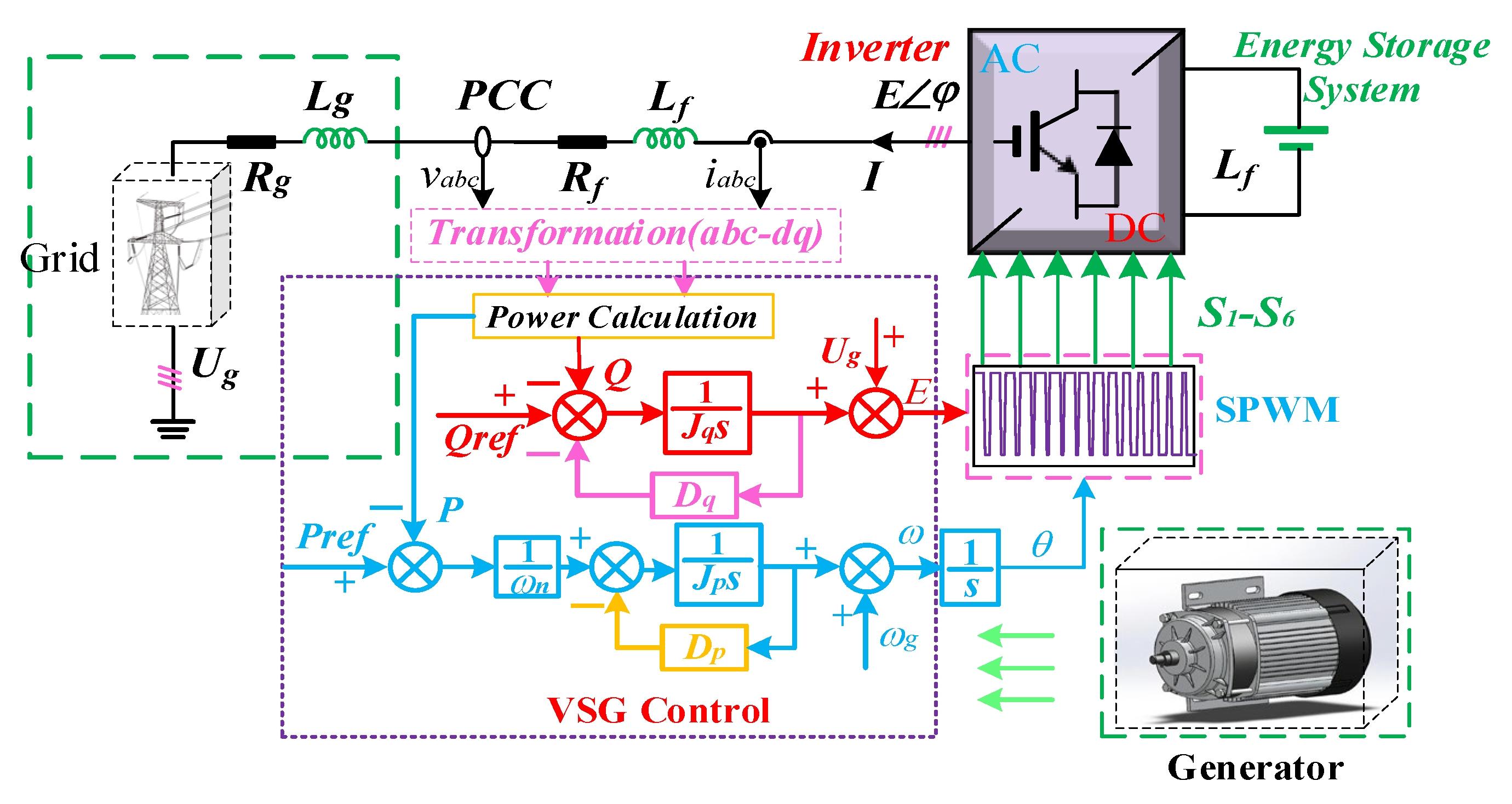
2. Modeling and Sensitivity Analysis of a Grid-Forming VSG System
2.1. A Brief Introduction to VSG
2.2. The Modeling Method for Analysis
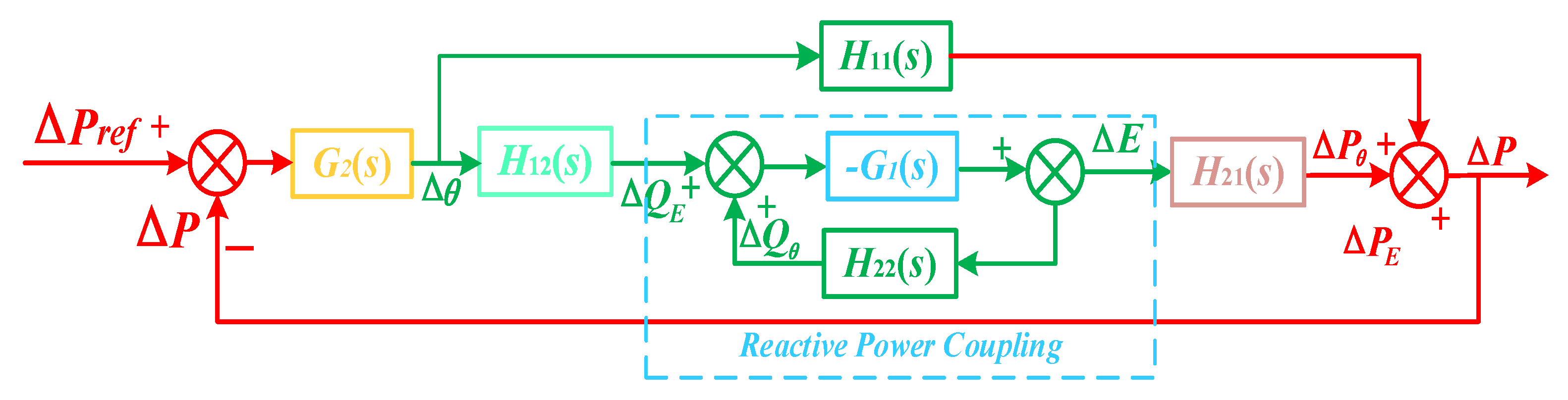
3. Sensitivity Analysis
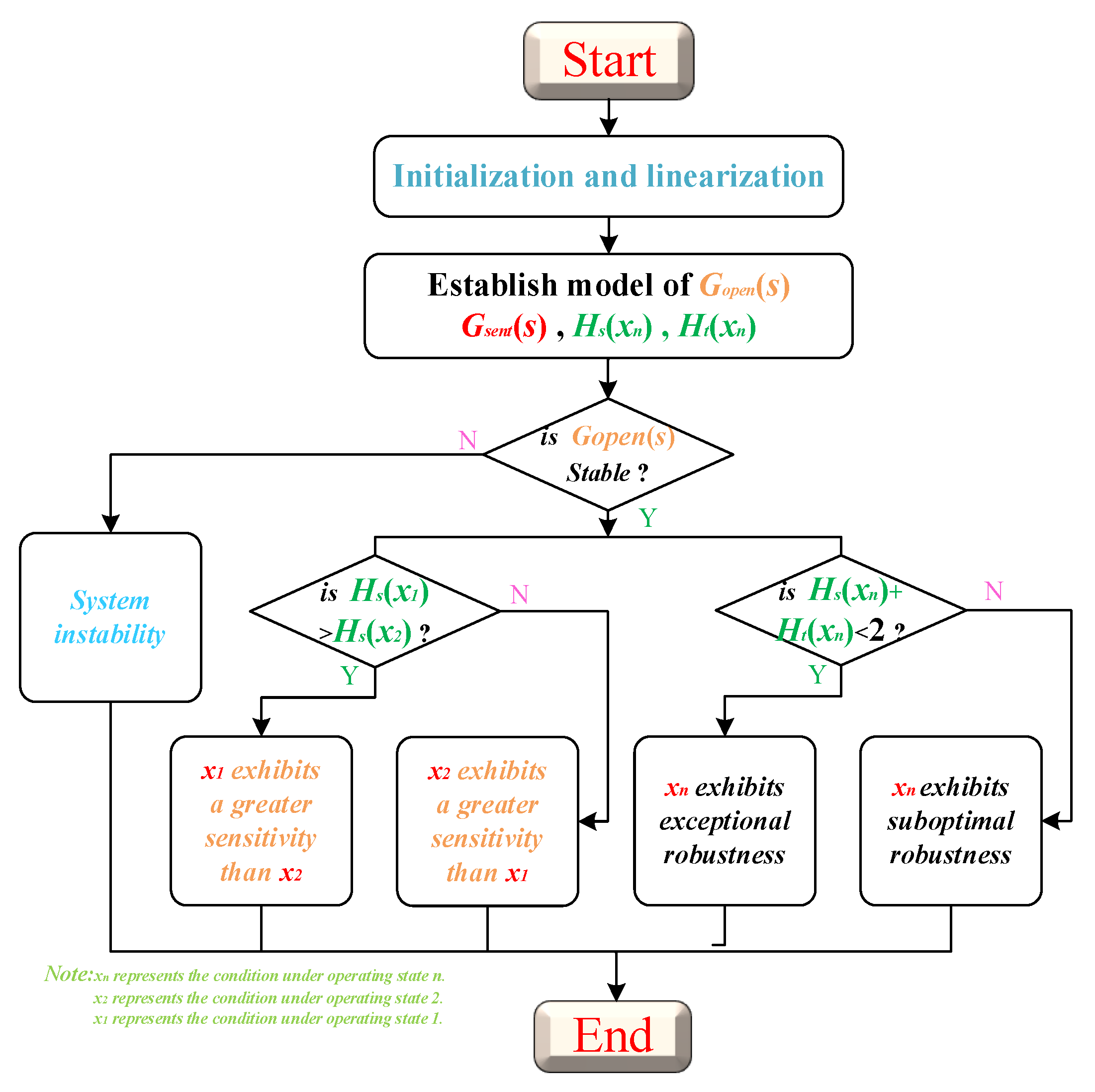
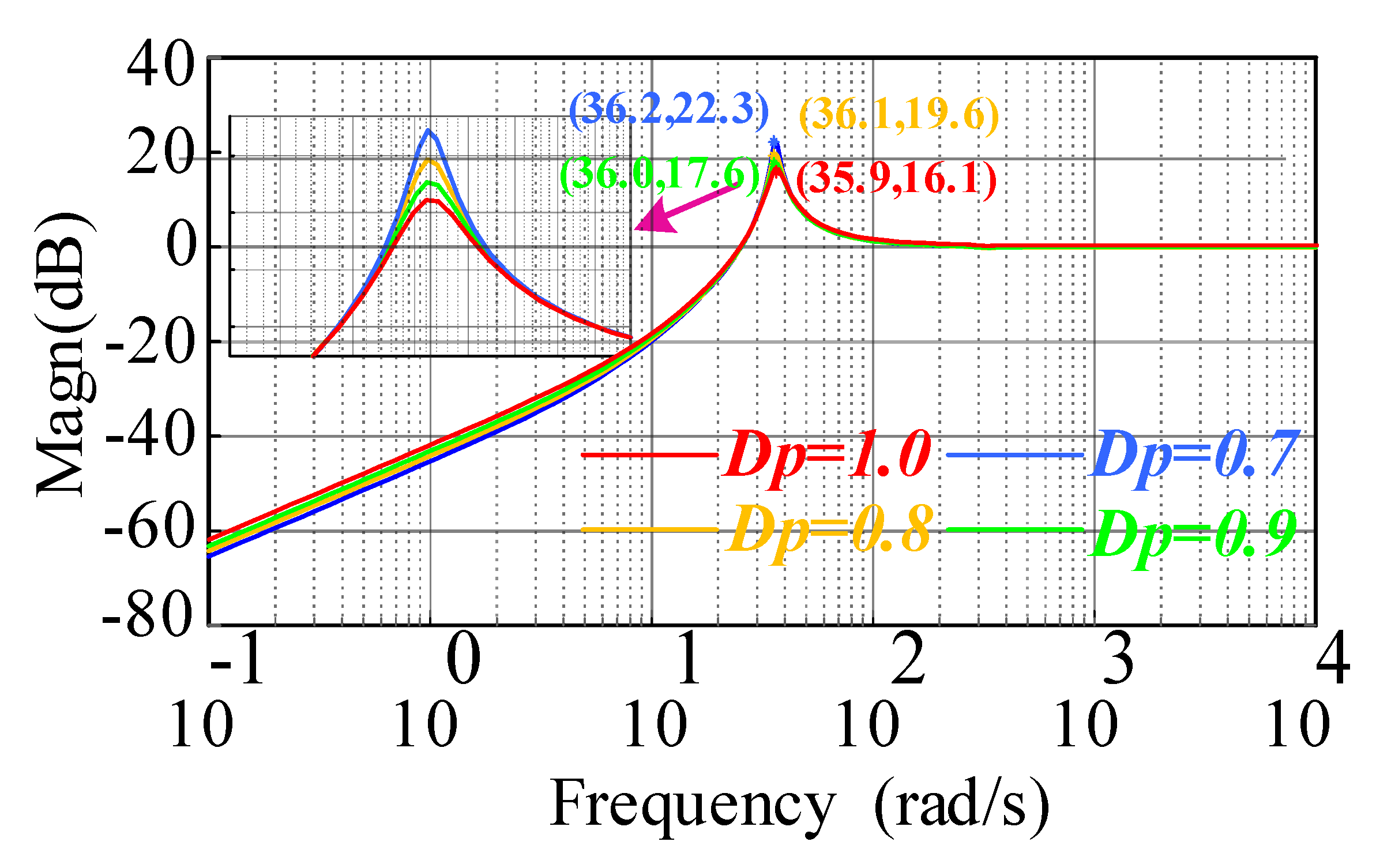
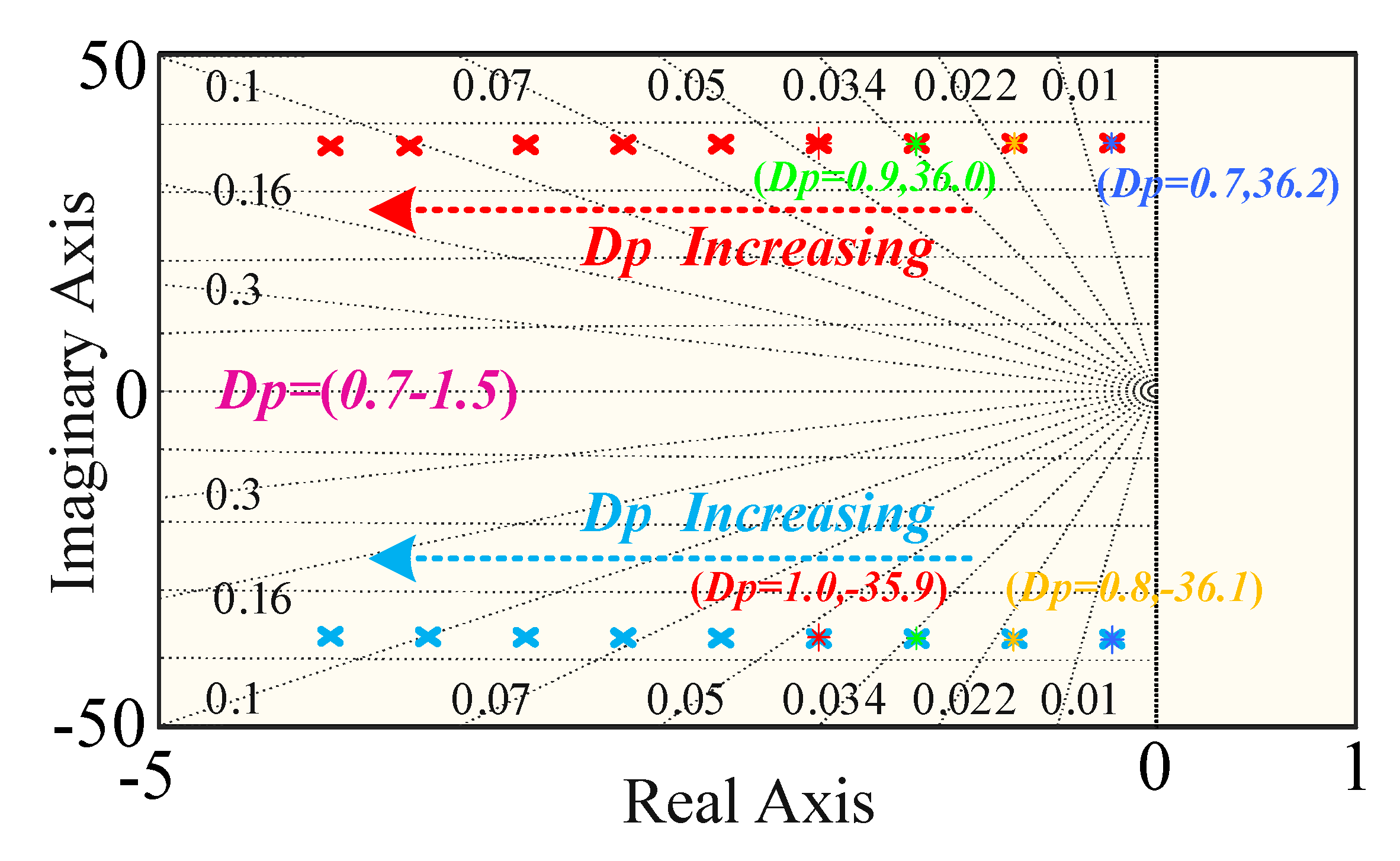
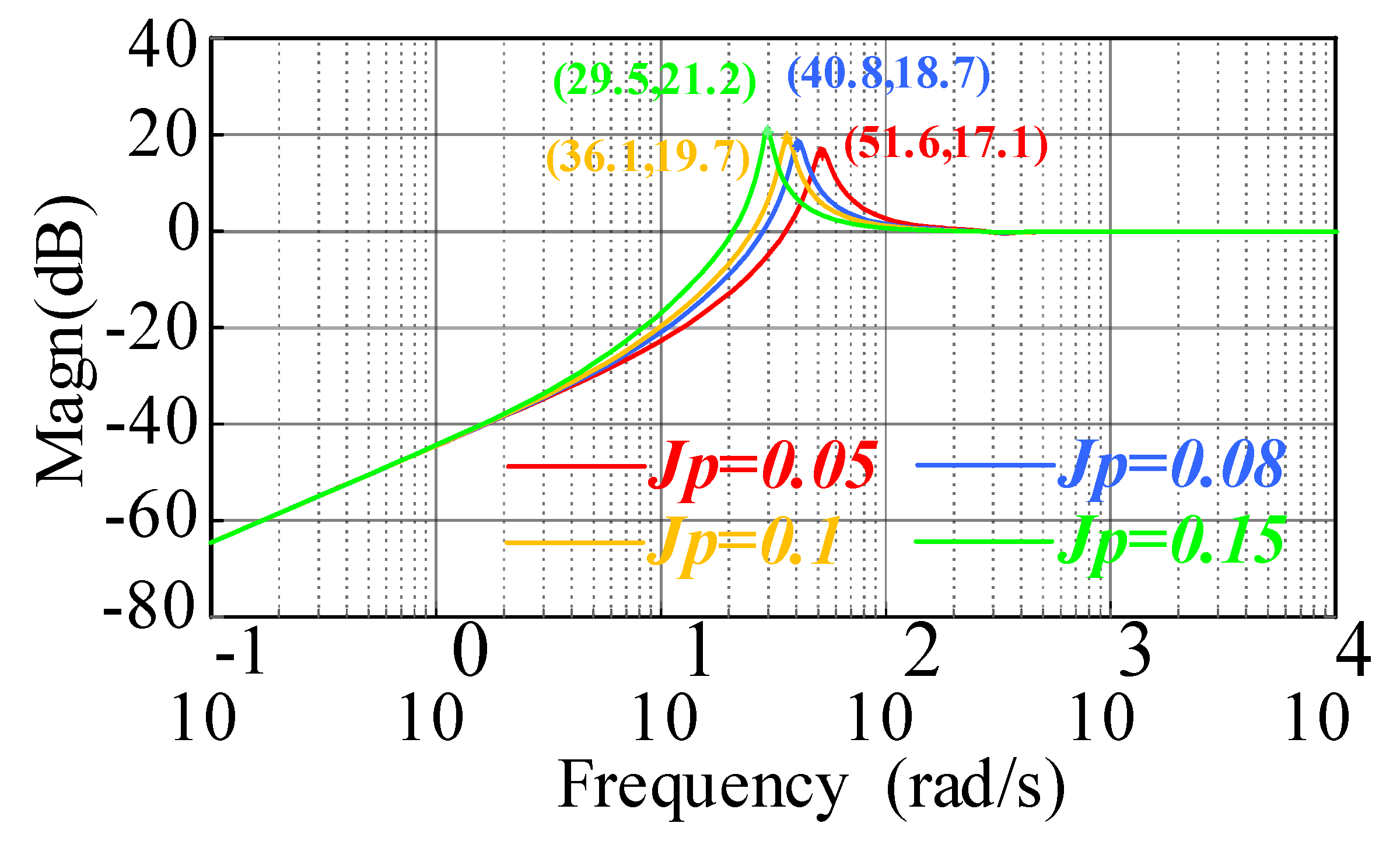
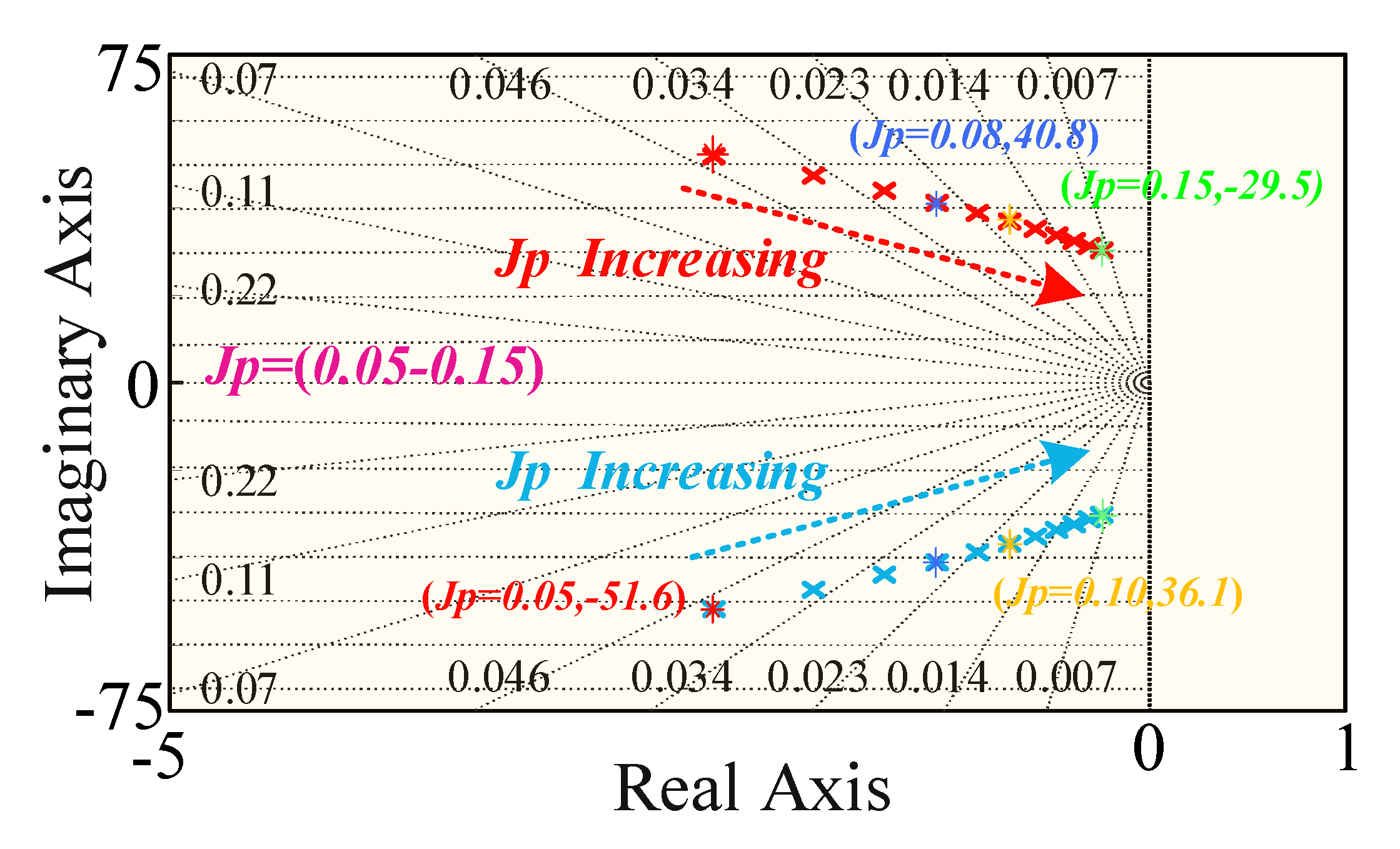
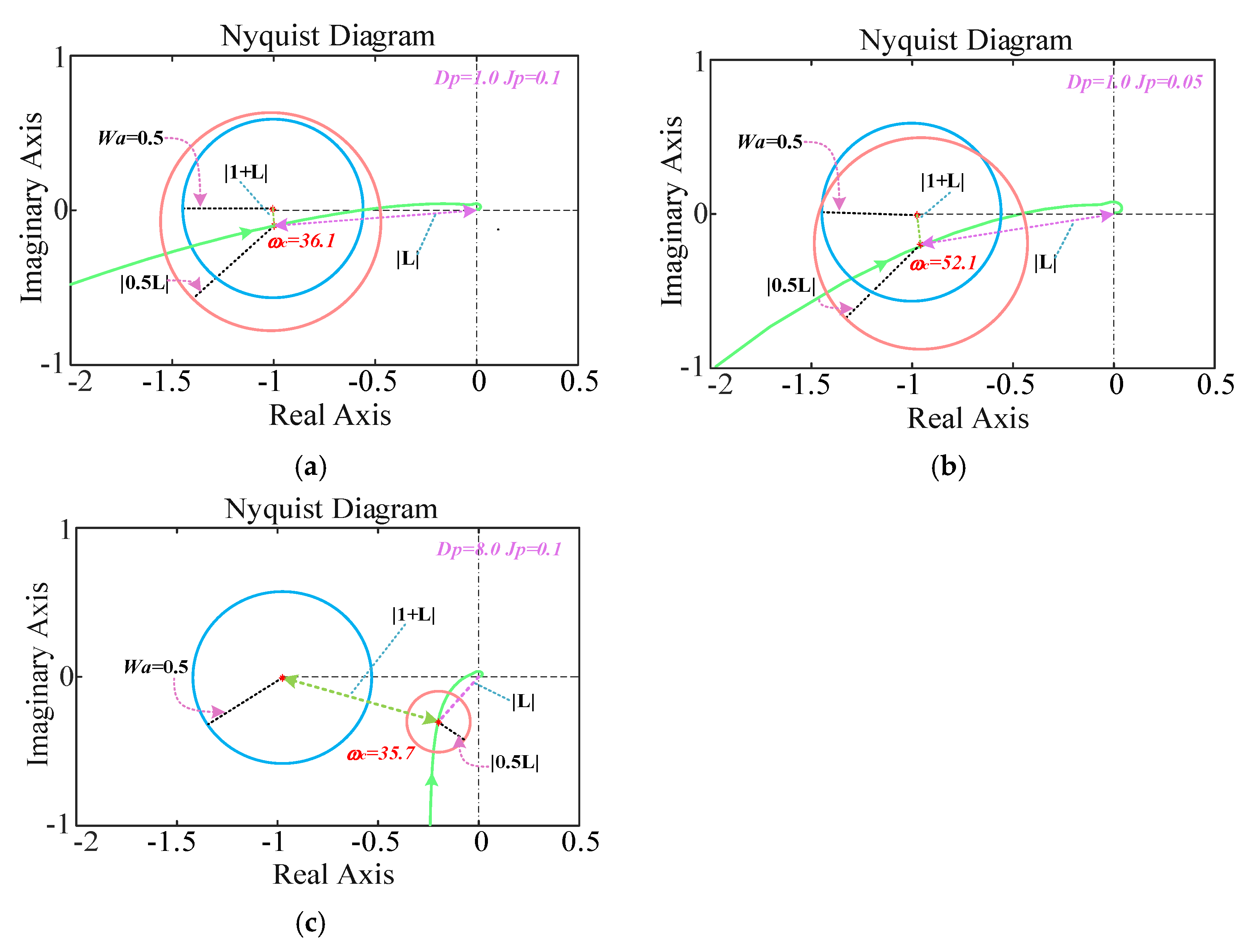
4. Robustness Analysis
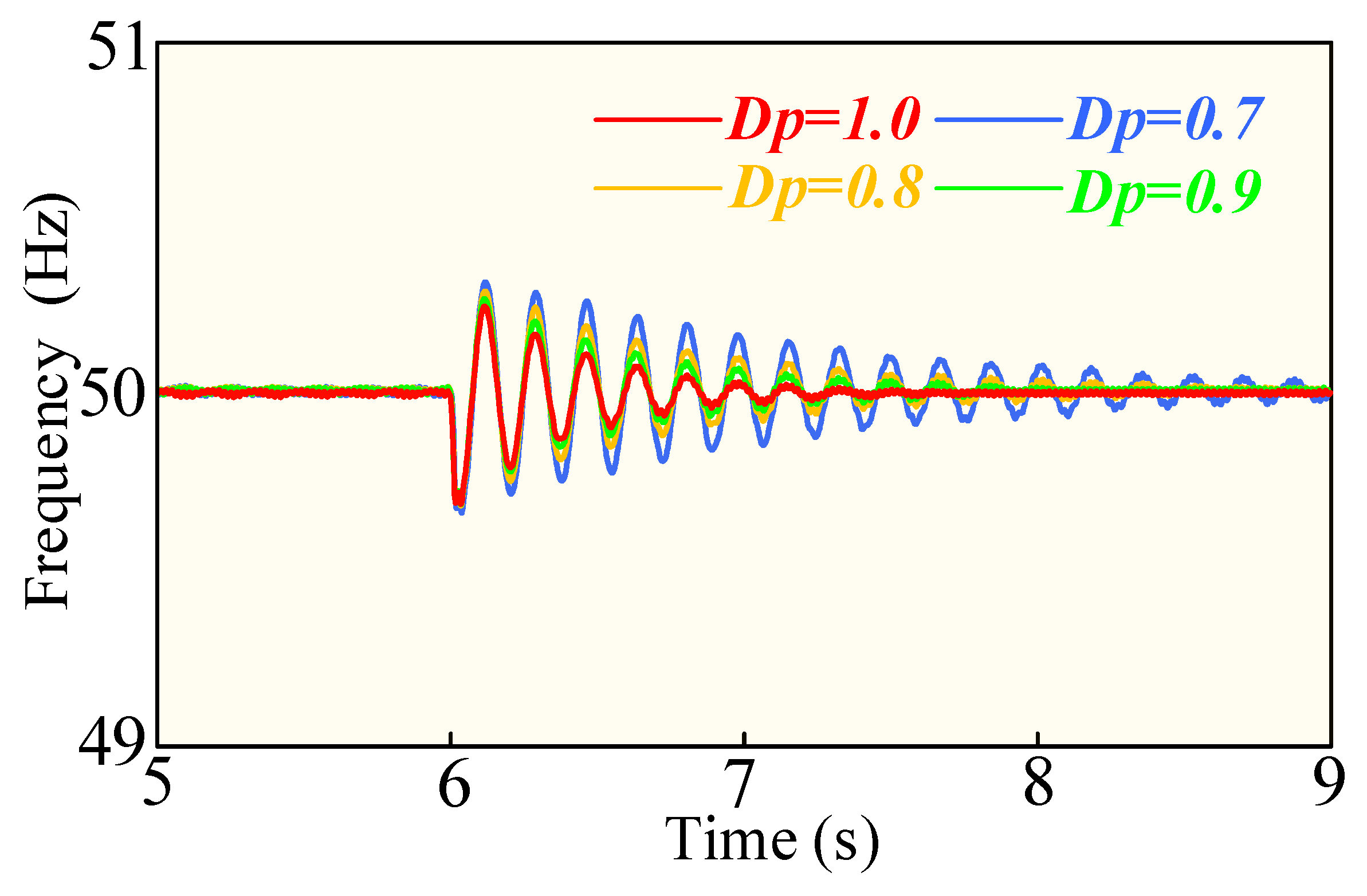
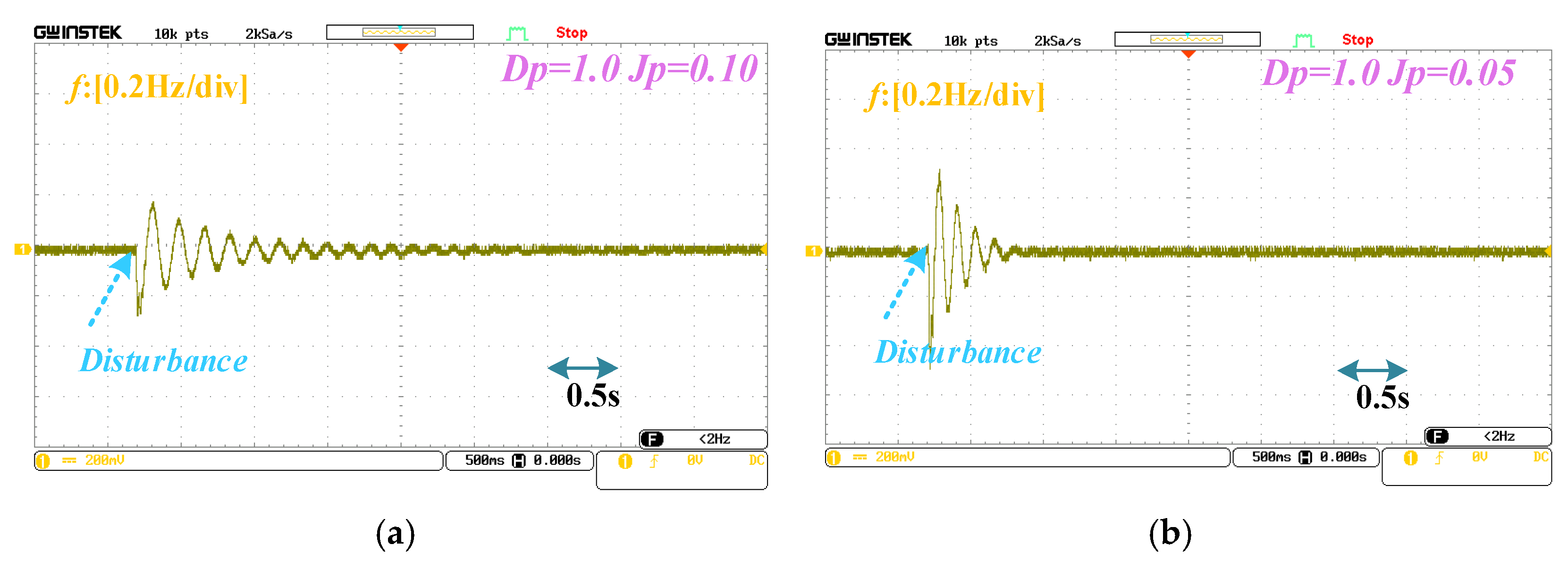
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaabjerg, F.; Yang, Y.; Ma, K. Power electronics—Key technology for renewable energy systems—Status and future. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, Istanbul, Turkey, 2–4 October 2013; pp. 1–6. [Google Scholar]
- Liyanage, C.; Nutkani, I.; Meegahapola, L.; Jalili, M. Sensitivity Analysis of the Cascaded Virtual Synchronous Generator based Grid Forming Inverter. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tayyab, M.; Awadallah, S.K.E. Investigation of virtual synchronous generator control parameters for small signal stability at different levels of renewable resource penetration. In Proceedings of the 2024 4th International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 8–10 January 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Kuang, Y.; Li, Y.; Wang, W.; Cao, Y. An adaptive virtual synchronous generator control strategy for VSC-MTDC systems and sensitivity analysis of the parameters. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2631–2635. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, J.; Zhao, Y.; Yin, H. Parameters Tuning of Flexible Drooped Synchronous Power Controller Based on Small Signal Modeling and Sensitivity Analysis. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 886–891. [Google Scholar] [CrossRef]
- Adu, J.A.; Kyererneh, K.A.; Otchere, I.K. Virtual Synchronous Generator: Parameter Sensitivity Analysis. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Zhang, P.; Sun, Q.; Gui, Y.; Wang, P. System Modeling and Robust Stability Region Analysis for Multi-Inverters Based on VSG. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 6042–6052. [Google Scholar] [CrossRef]
- Khatibi, M.; Ahmed, S. Robust Controller Design for a Virtual Synchronous Generator (VSG) Using Linear Matrix Inequalities. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3253–3258. [Google Scholar] [CrossRef]
- Su, H.; Mao, Z.; Li, P. Robust Parameters Based on VSG & Virtual Inductor Design Considering Power Decoupling. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 1185–1190. [Google Scholar] [CrossRef]
- Mallemaci, V.; Pugliese, S.; Mandrile, F.; Carpaneto, E.; Bojoi, R.; Liserre, M. Robust Stability Analysis of the Simplified Virtual Synchronous Compensator for Grid Services and Grid Support. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 1188–1195. [Google Scholar] [CrossRef]
- Zhu, D.; Ma, Y.; Li, X.; Fan, L.; Tang, B.; Kang, Y. Transient Stability Analysis and Damping Enhanced Control of Grid-Forming Wind Turbines Considering Current Saturation Procedure. IEEE Trans. Energy Convers. 2024. [Google Scholar] [CrossRef]
- Yang, H.; Chu, Y.; Ma, Y.; Zhang, D. Operation Strategy and Optimization Configuration of Hybrid Energy Storage System for Enhancing Cycle Life. J. Energy Storage 2024, 95, 112560. [Google Scholar]
- Li, C.; Yang, Y.; Li, Y.; Liu, Y.; Blaabjerg, F. Modeling for Oscillation Propagation with Frequency-Voltage Coupling Effect in Grid-Connected Virtual Synchronous Generator. IEEE Trans. Power Electron. 2025, 40, 82–86. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Z.; Hu, J.; Zou, X.; Kang, Y.; Guerrero, J.M. Rethinking Fault Ride-Through Control of DFIG-Based Wind Turbines from New Perspective of Rotor-Port Impedance Characteristics. IEEE Trans. Sustain. Energy 2024, 15, 2050–2062. [Google Scholar]
- Li, C.; Yang, Y.; Blaabjerg, F. Mechanism Analysis for Oscillation Transferring in Grid-Forming Virtual Synchronous Generator Connected to Power Network. IEEE Trans. Ind. Electron. 2025. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Q.; Liu, Y.; Ma, Y.; Zhang, D. Demand response strategy of user-side energy storage system and its application to reliability improvement. J. Energy Storage 2024, 92, 112150. [Google Scholar]
- Li, C.; Yang, Y.; Cao, Y.; Aleshina, A.; Xu, J.; Blaabjerg, F. Grid Inertia and Damping Support Enabled by Proposed Virtual Inductance Control for Grid-Forming Virtual Synchronous Generator. IEEE Trans. Power Electron. 2023, 38, 294–303. [Google Scholar] [CrossRef]
- Wang, G.; Fu, L.; Hu, Q.; Ma, F.; Liu, C.; Lin, Y. Low Frequency Oscillation Analysis of VSG Grid-Connected System. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 631–637. [Google Scholar] [CrossRef]
- Zhang, H.; Li, D.; Liu, H.; Sun, D.; Yang, Y.; Shao, Y.; Sun, Y. Comparison of Low Frequency Oscillation Characteristic Differences between VSG and SG. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 668–673. [Google Scholar] [CrossRef]
- Li, X.; Chen, G. Improved Adaptive Inertia Control of VSG for Low Frequency Oscillation Suppression. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Du, Y.; Gao, X.; Yang, Y.; Cao, Y.; Blaabjerg, F. Self-Stability and Induced-Stability Analysis for Frequency and Voltage in Grid-Forming VSG System with Generic Magnitude–Phase Model. IEEE Trans. Ind. Inform. 2024, 20, 12328–12338. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Hu, W.; Shu, S.; Yu, P.; Zhang, Z.; Blaabjerg, F. Unified Modeling and Analysis of Dynamic Power Coupling for Grid-Forming Converters. IEEE Trans. Power Electron. 2022, 37, 2321–2337. [Google Scholar] [CrossRef]
- Deng, H.; Fang, J.; Tang, Y.; Debusschere, V. Coupling Effect of Active and Reactive Power Controls on Synchronous Stability of VSGs. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nascimento, T.F.D.; Salazar, A.O. Power Coupling Influence on Virtual Synchronous Generator Control in Grid-Forming DG Systems. In Proceedings of the 2023 15th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 22–25 October 2023; pp. 1–6. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, X.; Ye, Z.; Lyu, K.; Dong, W.; Xiong, X.; Zhao, C.; Li, C. A Comprehensive Robustness Analysis of Grid-Forming Virtual Synchronous Machine Systems for the Evaluation of Frequency Performance. Electronics 2025, 14, 1516. https://doi.org/10.3390/electronics14081516
Mao X, Ye Z, Lyu K, Dong W, Xiong X, Zhao C, Li C. A Comprehensive Robustness Analysis of Grid-Forming Virtual Synchronous Machine Systems for the Evaluation of Frequency Performance. Electronics. 2025; 14(8):1516. https://doi.org/10.3390/electronics14081516
Chicago/Turabian StyleMao, Xun, Zidan Ye, Kai Lyu, Wangchao Dong, Xinhua Xiong, Chanjuan Zhao, and Chang Li. 2025. "A Comprehensive Robustness Analysis of Grid-Forming Virtual Synchronous Machine Systems for the Evaluation of Frequency Performance" Electronics 14, no. 8: 1516. https://doi.org/10.3390/electronics14081516
APA StyleMao, X., Ye, Z., Lyu, K., Dong, W., Xiong, X., Zhao, C., & Li, C. (2025). A Comprehensive Robustness Analysis of Grid-Forming Virtual Synchronous Machine Systems for the Evaluation of Frequency Performance. Electronics, 14(8), 1516. https://doi.org/10.3390/electronics14081516





