MDFFN: Multi-Scale Dual-Aggregated Feature Fusion Network for Hyperspectral Image Classification
Abstract
1. Introduction
- In hyperspectral image classification tasks, transformer-based methods offer advantages in establishing global dependencies. However, they cannot extract fine-grained local features as effectively as CNN-based methods. Therefore, it is necessary to explore an architecture that can capture critical spatial–spectral features both locally and globally, thereby improving classification performance.
- Existing multi-scale CNN–transformer hybrid methods are capable of capturing more discriminative features. However, their embedding methods tend to distort local spatial–spectral and positional information, resulting in the loss of valuable information during the classification process. This loss makes it challenging to distinguish cases of “same objects with different spectra” and “different objects with the same spectrum”. Thus, exploring new multi-scale feature extraction modules that can highlight discriminative information is crucial for addressing the class imbalance issue in HSI classification.
- Existing multi-scale approaches typically rely on attention mechanisms for feature fusion [18,23]. Nevertheless, the interaction between different features is still insufficient, which limits the effective exploration of spatial and spectral diversity in complex environments. Consequently, we should design a more flexible multi-scale feature fusion method.
- In order to fully extract discriminative features locally and globally, we propose a new multi-scale network for HSI classification called MDFFN. MDFFN combines the respective representational capabilities of CNN and transformer, offering significant advantages in multi-scale feature extraction and feature fusion, showing superior classification performance.
- To address the issue of critical information loss in patch embedding of existing multi-scale methods, the MCIE module is designed to extract multi-scale spatial–spectral features under different receptive fields of HSI. The module employs a multi-scale pooling operation to aggregate local features, smoothing the data and suppressing noise while retaining more spatial and spectral information, thus enabling the network to achieve satisfactory performance even with imbalanced datasets.
- To adequately fuse multi-scale features, we designed the DACA module to realize the interaction of features at different scales to capture the complementary and relevant information between the features, which can alleviate the problem of information loss caused by the feature fusion process.
- We conducted extensive experiments on three benchmark HSI datasets. The results reveal that the MDFFN outperforms the state-of-the-art methods in classification performance, particularly when dealing with imbalanced datasets, leading to substantial improvements in classification accuracy.
2. Related Work
2.1. Deep Learning for HSI Classification
2.2. Multi-Scale CNN
2.3. Multi-Scale Transformer
3. Materials and Methods
3.1. The Structure of the Multi-Scale Dual-Aggregated Feature Fusion Network
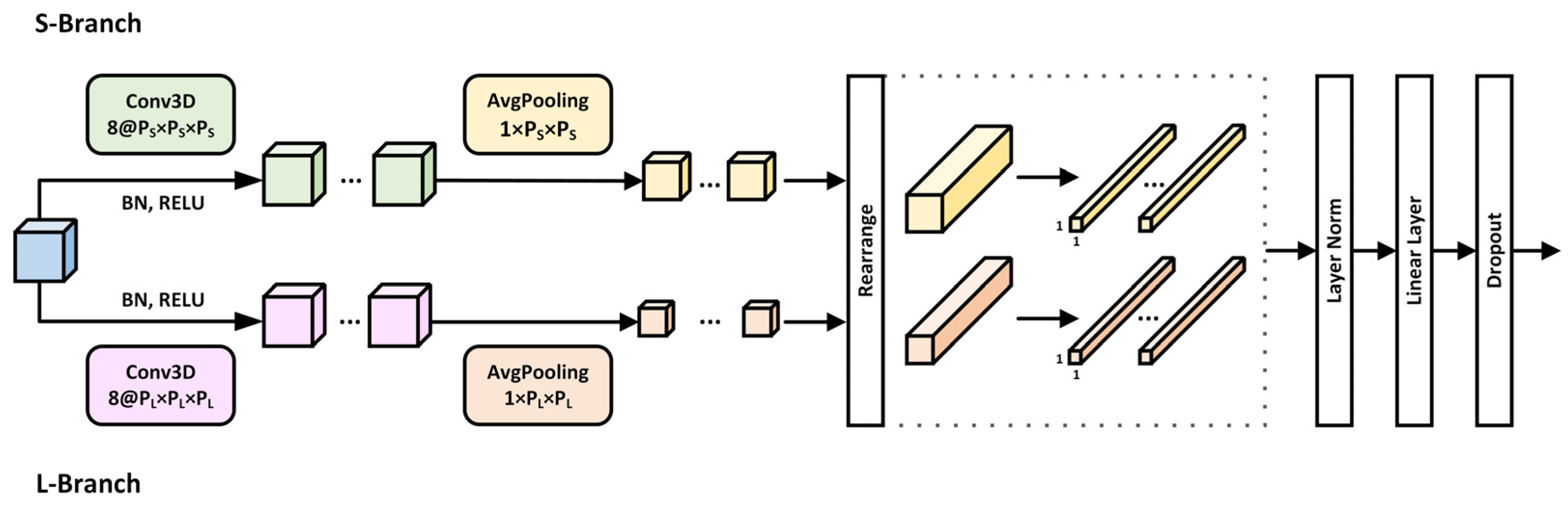
3.2. Multi-Scale Convolutional Information Embedding
- Three-Dimensional Convolutional Blocks
- 2.
- Embedding Operation
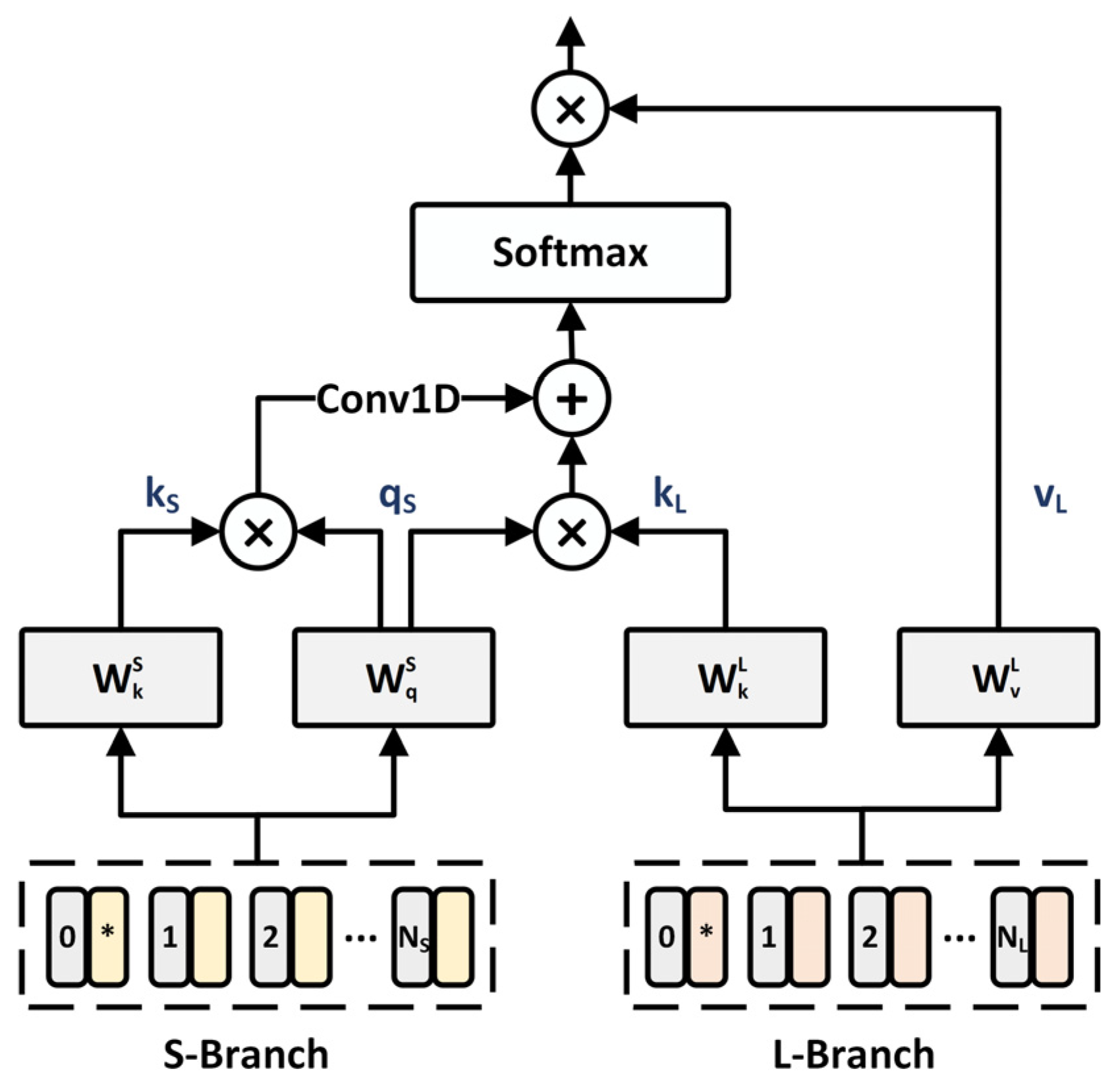
3.3. Dual Aggregated Cross-Attention
4. Experimental Results and Discussion
4.1. Dataset Description
- Indian Pines Dataset
- 2.
- Pavia University Dataset
- 3.
- Houston 2013 Dataset
4.2. Experimental Setup
- Training details: For a fair comparison, all experiments are conducted on an Intel® Xeon® Platinum 8358P CPU @ 2.60GHz processor and an NVIDIA GeForce RTX 3090 GPU (24GB) (NVIDIA Corporation, Santa Clara, CA, USA), utilizing the PyTorch 1.11 framework with Python 3.8. To minimize the errors in the experiments, all results are the average and standard deviation of 10 independent runs. For model training, we utilize the Adam optimizer to learn the weights, set the batch size to 100 and the learning rate to 1 × 10−4. To ensure the model is sufficiently trained and performing at its best, we run the model for 100 epochs.
- Evaluation metrics: We employ three widely used metrics to evaluate the classification performance of different models: overall accuracy (OA), average accuracy (AA), and kappa coefficient (Kappa). Additionally, to facilitate a more intuitive comparison among the models, we visualize the classification results for qualitative analysis.
- Experimental details: In order to more rationally validate the performance of the proposed MDFFN method, we set up five detailed experiments.
- (a)
- Comparison with state-of-the-art methods: we compare the proposed MDFFN model with representative baseline methods and state-of-the-art backbone methods for validating the performance.
- (b)
- Visual evaluation: the experimental results are visualized to provide a clear and intuitive demonstration of the progressiveness of the model.
- (c)
- Efficiency analysis: we quantitatively evaluate the computational efficiency of the proposed method by comparing parameter counts, FLOPs, training time, and testing time with state-of-the-art methods.
- (d)
- Ablation experiments: ablation experiments are conducted to verify the effectiveness of the MCIE and DACA modules in the network.
- (e)
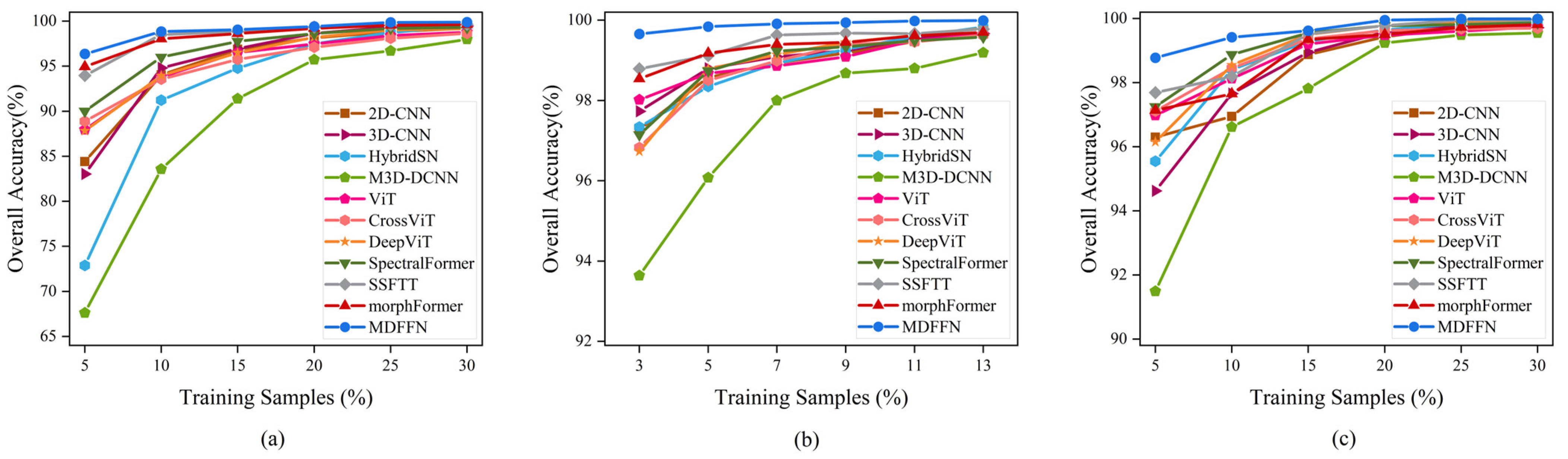
- Parameter sensitivity experiments: parameter sensitivity experiments are set up to evaluate the performance of MDFFN with different combinations of S-branch size and L-branch size, different depths of the multi-scale transformer, and different proportions of training samples on the experimental results.
- Comparison with state-of-the-art backbone networks: To validate the performance of the proposed MDFFN, we selected several representative baseline methods and state-of-the-art backbone methods, including CNN-based methods (i.e., 2D-CNN [46], 3D-CNN [46], HybridSN [33], and M3D-DCNN [36]), transformer-based methods (i.e., ViT [16], CrossViT [18], DeepViT [17], and SpectralFormer [34]), as well as CNN–transformer hybrid-based methods (i.e., SSFTT [19], morphFormer [20], and MSNAT [22]). In order to make a reasonable comparison, the experiments basically maintain consistent parameter settings. Regarding parameters, we set the spatial size of morphFormer and MSNAT to 11 × 11, and the other methods to 15 × 15. For the patch size, ViT and DeepViT are 3, while for the multi-scale methods CrossViT and MDFFN, the small branch is set to 3 and the large branch to 5. The depth of ViT, CrossViT, DeepViT, and MDFFN is set to 3, and the dimension is set to 512. Otherwise, all other parameters not listed are set to their default values. More details can be found in the original papers.
4.3. Results and Analysis
4.3.1. Comparison with State-of-the-Art Methods
- The performance in the overall method
- 2.
- The performance in multi-scale feature extraction and fusion
- 3.
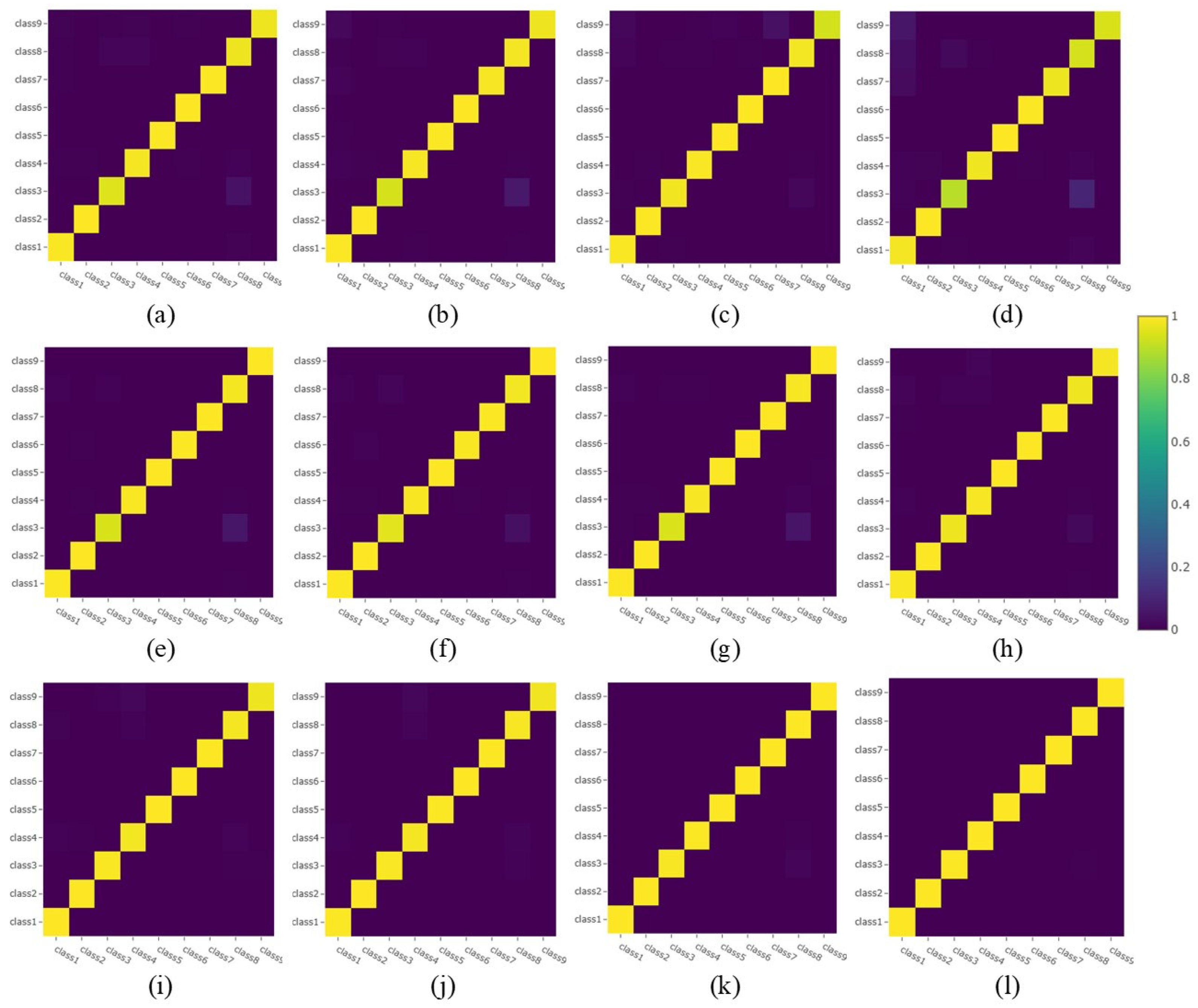
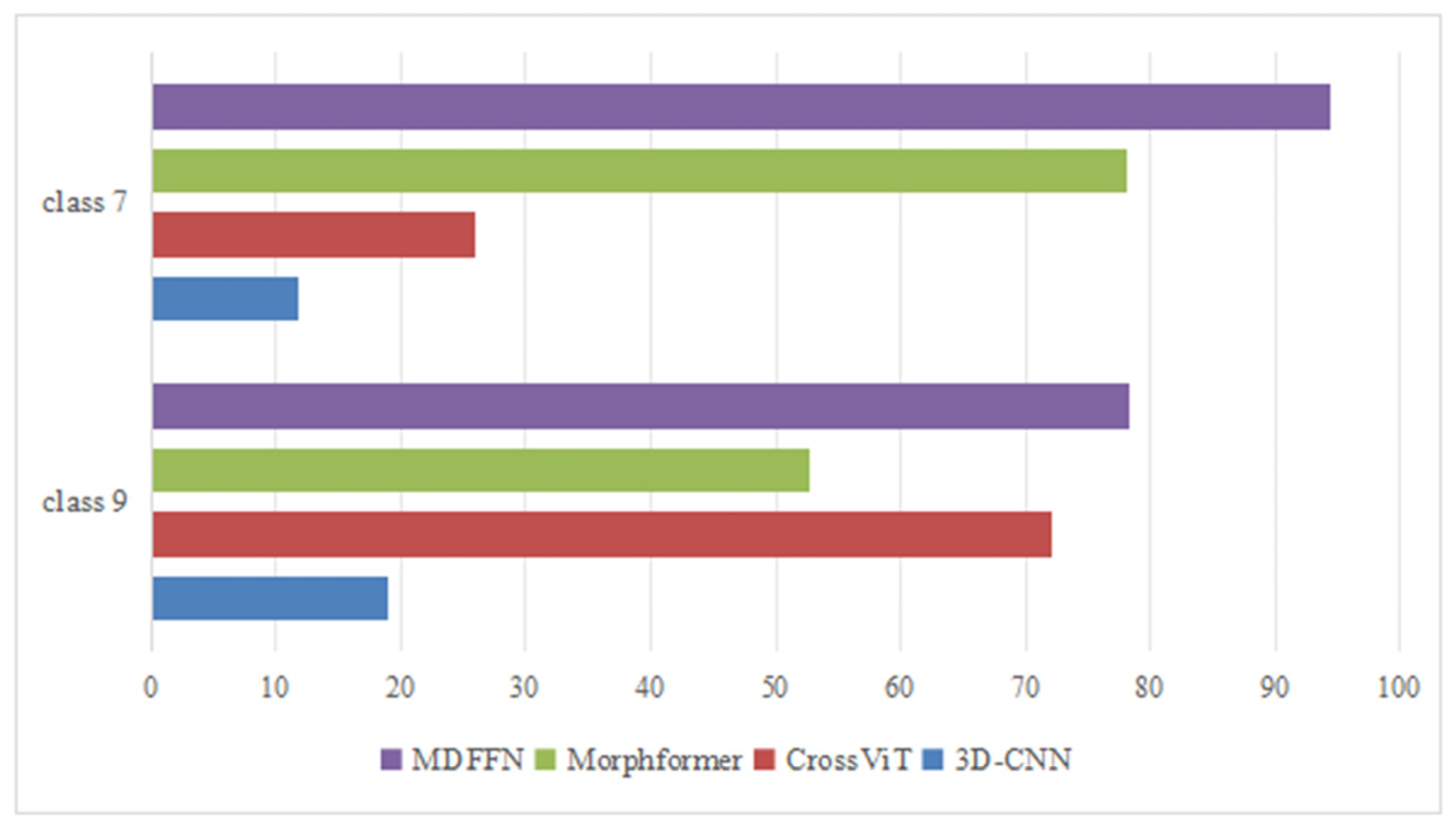
- The performance on imbalanced datasets
- 4.
- The visualization of confusion matrices on imbalanced datasets
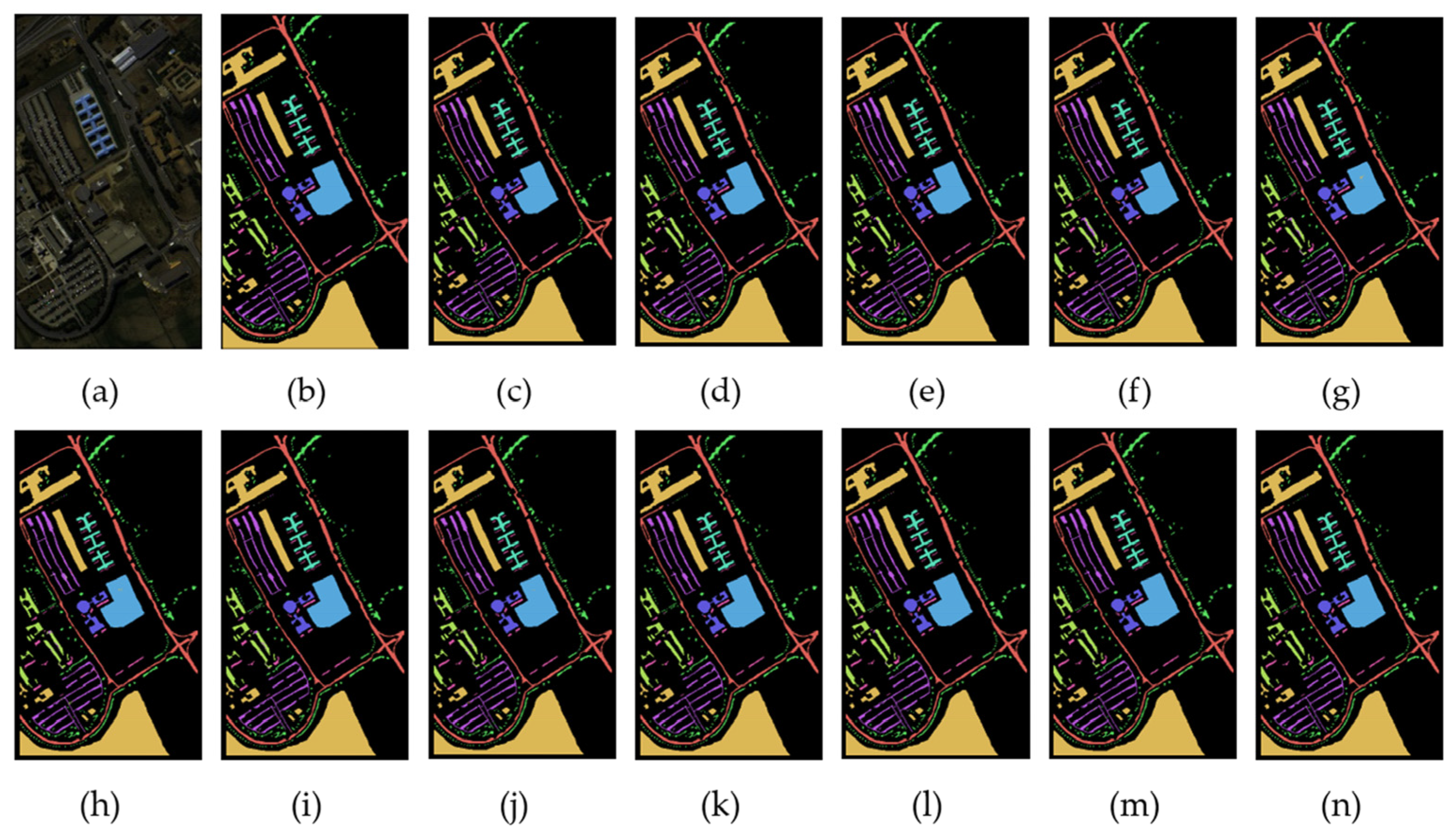
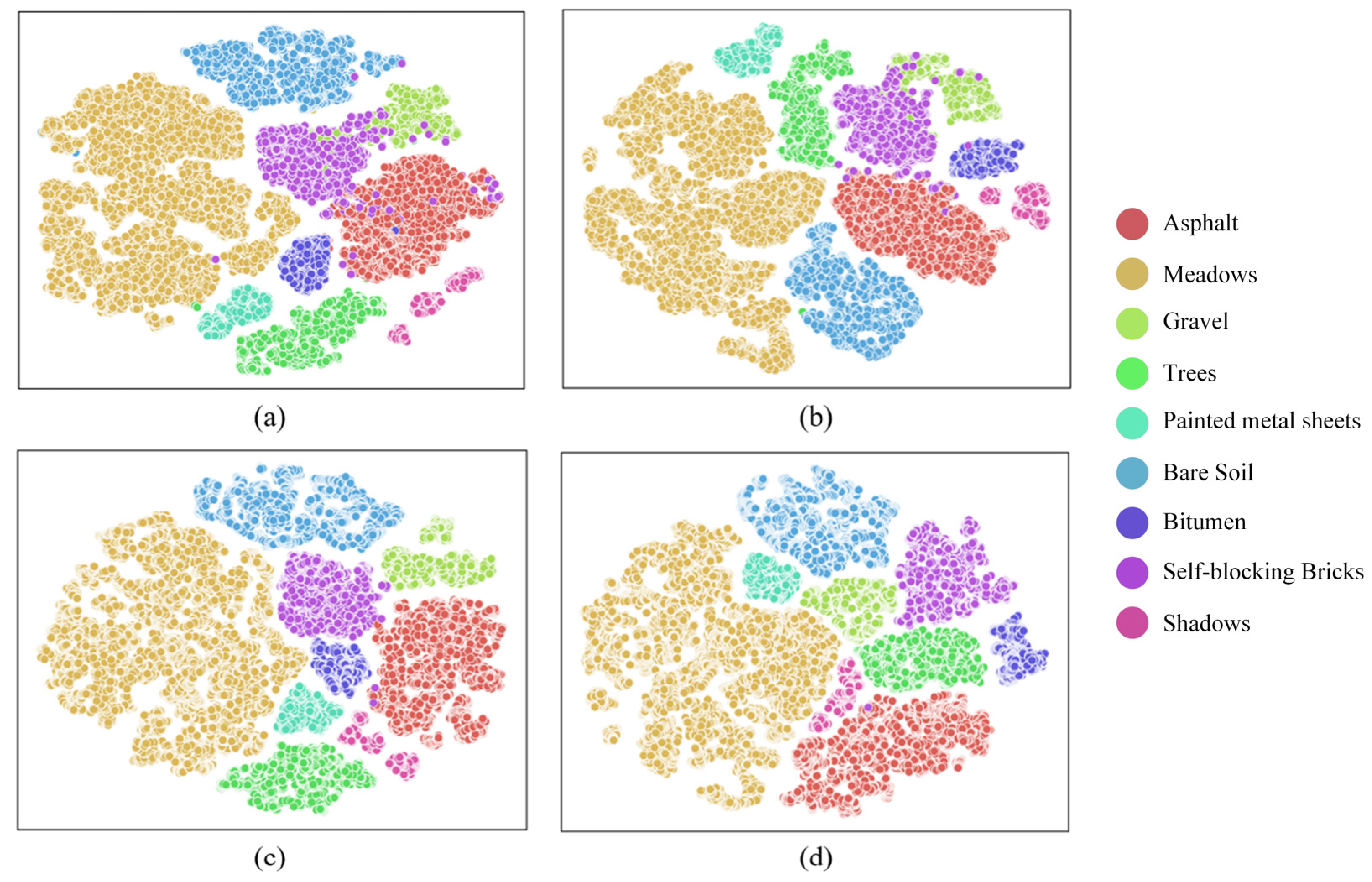
4.3.2. Visual Evaluation
4.3.3. Efficiency Analysis
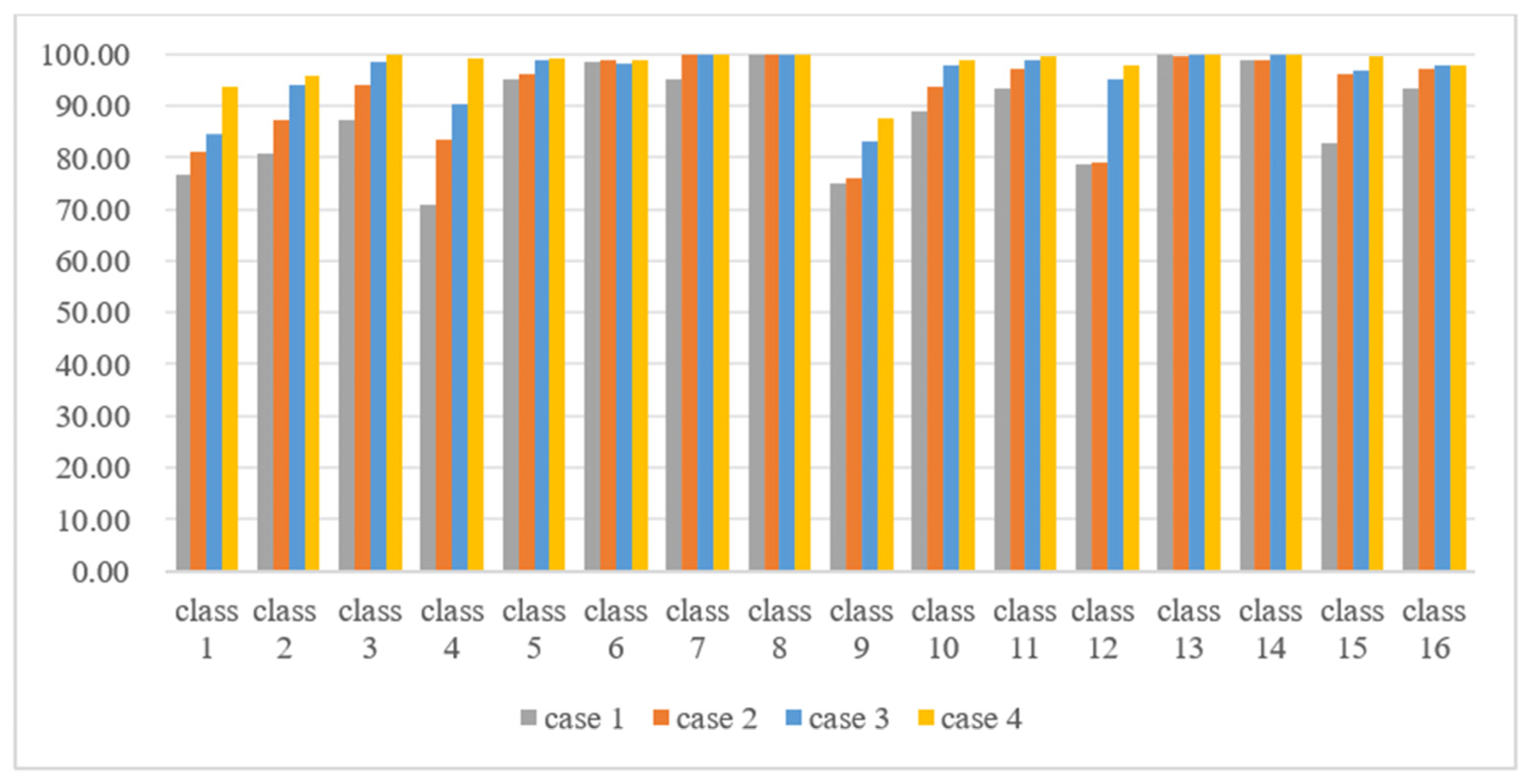
4.3.4. Ablation Experiments
- (a)
- The CrossViT model with multi-scale feature fusion is selected as the basic architecture.
- (b)
- To validate the effectiveness of the multi-scale convolutional information embedding module in MDFFN, the experiment uses the linear projection embedding module based on CrossViT as a comparison.
- (c)
- To validate the effectiveness of the dual aggregation cross-attention module in MDFFN, the experiment adopts the cross-attention module based on CrossViT as a comparison.
- The performance for different combinations of the modules
- 2.
- The visualization of feature maps of each module
4.3.5. Parameter Sensitivity Experiments
- Combinations in multi-scale patch sizes
- 2.
- Number of multi-scale transformer layers
- 3.
- Proportion of training samples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDFFN | Multi-scale dual-aggregated feature fusion network |
| MCIE | Multi-scale convolutional information embedding |
| DACA | Dual aggregated cross-attention |
| HSI | Hyperspectral image |
| DL | Deep learning |
| 2D-CNN | Two-dimensional convolutional neural networks |
| 3D-CNN | Three-dimensional convolutional neural networks |
| HybridSN | Hybrid spectral CNN |
| M3D-DCNN | Multi-scale 3D deep convolutional neural network |
| MHSA | Multi-head self-attention |
| ViT | Vision transformer |
| SSFTT | Spectral–spatial feature tokenization transformer |
| MSNAT | Multi-scale neighborhood attention transformer |
| PCA | Principal component analysis |
| FFN | Feed-forward network |
| MLP | Multilayer perceptron |
| IP | Indian Pines |
| PU | Pavia University |
| T-SNE | T-distributed stochastic neighbor embedding |
References
- Khan, A.; Vibhute, A.D.; Mali, S.; Patil, C.H. A Systematic Review on Hyperspectral Imaging Technology with a Machine and Deep Learning Methodology for Agricultural Applications. Ecol. Inform. 2022, 69, 101678. [Google Scholar] [CrossRef]
- Alboody, A.; Vandenbroucke, N.; Porebski, A.; Sawan, R.; Viudes, F.; Doyen, P.; Amara, R. A New Remote Hyperspectral Imaging System Embedded on an Unmanned Aquatic Drone for the Detection and Identification of Floating Plastic Litter Using Machine Learning. Remote Sens. 2023, 15, 3455. [Google Scholar] [CrossRef]
- Sousa, F.J.; Sousa, D.J. Hyperspectral Reconnaissance: Joint Characterization of the Spectral Mixture Residual Delineates Geologic Unit Boundaries in the White Mountains, CA. Remote Sens. 2022, 14, 4914. [Google Scholar] [CrossRef]
- Zhu, W.; Sun, X.; Zhang, Q. DCG-Net: Enhanced Hyperspectral Image Classification with Dual-Branch Convolutional Neural Network and Graph Convolutional Neural Network Integration. Electronics 2024, 13, 3271. [Google Scholar] [CrossRef]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese Transformer Network for Hyperspectral Image Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526419. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, H.; Yang, R.; Wang, W.; Luo, Q.; Tu, C. Hyperspectral Image Classification Based on Double-Branch Multi-Scale Dual-Attention Network. Remote Sens. 2024, 16, 2051. [Google Scholar] [CrossRef]
- Liu, G.; Wang, L.; Liu, D.; Fei, L.; Yang, J. Hyperspectral Image Classification Based on Non-Parallel Support Vector Machine. Remote Sens. 2022, 14, 2447. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; He, W.; Gu, Q.; Xu, S.; Mao, Z.; Tu, S. MSLM-RF: A Spatial Feature Enhanced Random Forest for On-Board Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5534717. [Google Scholar] [CrossRef]
- Wang, X. Hyperspectral Image Classification Powered by Khatri-Rao Decomposition-Based Multinomial Logistic Regression. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530015. [Google Scholar] [CrossRef]
- Lv, N.; Han, Z.; Chen, C.; Feng, Y.; Su, T.; Goudos, S.; Wan, S. Encoding Spectral-Spatial Features for Hyperspectral Image Classification in the Satellite Internet of Things System. Remote Sens. 2021, 13, 3561. [Google Scholar] [CrossRef]
- Chen, C.; Ma, Y.; Ren, G. Hyperspectral Classification Using Deep Belief Networks Based on Conjugate Gradient Update and Pixel-Centric Spectral Block Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4060–4069. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.-I. Feedback Attention-Based Dense CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501916. [Google Scholar] [CrossRef]
- Mei, S.; Li, X.; Liu, X.; Cai, H.; Du, Q. Hyperspectral Image Classification Using Attention-Based Bidirectional Long Short-Term Memory Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5509612. [Google Scholar] [CrossRef]
- Wang, J.; Guo, S.; Huang, R.; Li, L.; Zhang, X.; Jiao, L. Dual-Channel Capsule Generation Adversarial Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501016. [Google Scholar] [CrossRef]
- Ye, Z.; Li, C.; Liu, Q.; Bai, L.; Fowler, J. Computationally Lightweight Hyperspectral Image Classification Using a Multiscale Depthwise Convolutional Network with Channel Attention. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929v2. [Google Scholar]
- Zhou, D.; Kang, B.; Jin, X.; Yang, L.; Lian, X.; Jiang, Z.; Hou, Q.; Feng, J. DeepViT: Towards Deeper Vision Transformer. arXiv 2021, arXiv:2103.11886. [Google Scholar]
- Chen, C.-F.; Fan, Q.; Panda, R. CrossViT: Cross-Attention Multi-Scale Vision Transformer for Image Classification. 2021. Available online: https://openaccess.thecvf.com/content/ICCV2021/papers/Chen_CrossViT_Cross-Attention_Multi-Scale_Vision_Transformer_for_Image_Classification_ICCV_2021_paper.pdf (accessed on 7 September 2024).
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Haut, J.M.; Du, Q.; Plaza, A. Spectral–Spatial Morphological Attention Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503615. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, Y.; Yu, Z. Dual Attention Transformer Network for Hyperspectral Image Classification. Eng. Appl. Artif. Intell. 2024, 127, 107351. [Google Scholar] [CrossRef]
- Qiao, X.; Roy, S.K.; Huang, W. Multiscale Neighborhood Attention Transformer with Optimized Spatial Pattern for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5523815. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Lu, C.; Li, B. A Novel Transformer Network with a CNN-Enhanced Cross-Attention Mechanism for Hyperspectral Image Classification. Remote Sens. 2024, 16, 1180. [Google Scholar] [CrossRef]
- Wang, W.; Liu, L.; Zhang, T.; Shen, J.; Wang, J.; Li, J. Hyper-ES2T: Efficient Spatial–Spectral Transformer for the Classification of Hyperspectral Remote Sensing Images. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 103005. [Google Scholar] [CrossRef]
- Gong, H.; Li, Q.; Li, C.; Dai, H.; He, Z.; Wang, W.; Li, H.; Han, F.; Tuniyazi, A.; Mu, T. Multiscale Information Fusion for Hyperspectral Image Classification Based on Hybrid 2D-3D CNN. Remote Sens. 2021, 13, 2268. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, K.; Wu, H.; Iwahori, Y.; Chen, H. Multi-Scale Residual Spectral–Spatial Attention Combined with Improved Transformer for Hyperspectral Image Classification. Electronics 2024, 13, 1061. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Hamouda, M.; Ettabaa, K.S.; Bouhlel, M.S. Smart Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IET Image Process. 2020, 14, 1999–2005. [Google Scholar] [CrossRef]
- Fei, X.; Wu, S.; Miao, J.; Wang, G.; Sun, L. Lightweight-VGG: A Fast Deep Learning Architecture Based on Dimensionality Reduction and Nonlinear Enhancement for Hyperspectral Image Classification. Remote Sens. 2024, 16, 259. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hu, T.; Yuan, J.; Wang, X.; Yan, C.; Ju, X. Spectral-Spatial Features Extraction of Hyperspectral Remote Sensing Oil Spill Imagery Based on Convolutional Neural Networks. IEEE Access 2022, 10, 127969–127983. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, Y.; Zhang, X. Hyperspectral Image Classification Based on Optimized Convolutional Neural Networks with 3D Stacked Blocks. Earth Sci. Inf. 2022, 15, 383–395. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral Image Transformer Classification Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5528715. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-Scale 3D Deep Convolutional Neural Network for Hyperspectral Image Classification. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale Octave 3D CNN with Channel and Spatial Attention for Hyperspectral Image Classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Zhang, J.; Shang, X.; Hu, Y.; Zhang, S.; Wang, J. A New Dual-Branch Embedded Multivariate Attention Network for Hyperspectral Remote Sensing Classification. Remote Sens. 2024, 16, 2029. [Google Scholar] [CrossRef]
- Li, W.; Chen, H.; Liu, Q.; Liu, H.; Wang, Y.; Gui, G. Attention Mechanism and Depthwise Separable Convolution Aided 3DCNN for Hyperspectral Remote Sensing Image Classification. Remote Sens. 2022, 14, 2215. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. 2021. Available online: https://openaccess.thecvf.com/content/ICCV2021/papers/Liu_Swin_Transformer_Hierarchical_Vision_Transformer_Using_Shifted_Windows_ICCV_2021_paper.pdf (accessed on 10 September 2024).
- He, W.; Huang, W.; Liao, S.; Xu, Z.; Yan, J. CSiT: A Multi-Scale Vision Transformer for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9266–9277. [Google Scholar] [CrossRef]
- Chen, H.; Zendehdel, N.; Leu, M.C.; Yin, Z. Fine-Grained Activity Classification in Assembly Based on Multi-Visual Modalities. J. Intell. Manuf. 2024, 35, 2215–2233. [Google Scholar] [CrossRef]
- Chen, H.; Miao, F.; Chen, Y.; Xiong, Y.; Chen, T. A Hyperspectral Image Classification Method Using Multifeature Vectors and Optimized KELM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, S.; Du, W.; Cheng, X. An Improved 3D-2D Convolutional Neural Network Based on Feature Optimization for Hyperspectral Image Classification. IEEE Access 2023, 11, 28263–28279. [Google Scholar] [CrossRef]
- Gu, Q.; Luan, H.; Huang, K.; Sun, Y. Hyperspectral Image Classification Using Multi-Scale Lightweight Transformer. Electronics 2024, 13, 949. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral Image Classification with Deep Learning Models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]




| No. | Class | Training | Testing |
|---|---|---|---|
| 1 | Alfalfa | 5 | 41 |
| 2 | Corn—no till | 143 | 1285 |
| 3 | Corn—min till | 83 | 747 |
| 4 | Corn | 24 | 213 |
| 5 | Grass—pasture | 48 | 435 |
| 6 | Grass—trees | 73 | 657 |
| 7 | Grass—pasture–mowed | 3 | 25 |
| 8 | Hay—windrowed | 48 | 430 |
| 9 | Oats | 2 | 18 |
| 10 | Soybean—no till | 97 | 875 |
| 11 | Soybean—min till | 245 | 2210 |
| 12 | Soybean—clean | 59 | 534 |
| 13 | Wheat | 20 | 185 |
| 14 | Woods | 126 | 1139 |
| 15 | Building—grass-trees-drives | 39 | 347 |
| 16 | Stone—steel-towers | 9 | 84 |
| Total | 1024 | 9225 |
| No. | Class | Training | Testing |
|---|---|---|---|
| 1 | Asphalt | 663 | 5968 |
| 2 | Meadows | 1865 | 16,784 |
| 3 | Gravel | 210 | 1889 |
| 4 | Trees | 306 | 2758 |
| 5 | Painted metal sheets | 134 | 1211 |
| 6 | Bare soil | 503 | 4526 |
| 7 | Bitumen | 133 | 1197 |
| 8 | Self-blocking bricks | 368 | 3314 |
| 9 | Shadows | 95 | 852 |
| Total | 4277 | 38,499 |
| No. | Class | Training | Testing |
|---|---|---|---|
| 1 | Healthy grass | 125 | 1126 |
| 2 | Stressed grass | 125 | 1129 |
| 3 | Synthetic grass | 70 | 627 |
| 4 | Tree | 124 | 1120 |
| 5 | Soil | 124 | 1118 |
| 6 | Water | 33 | 292 |
| 7 | Residential | 127 | 1141 |
| 8 | Commercial | 124 | 1120 |
| 9 | Road | 125 | 1127 |
| 10 | Highway | 123 | 1104 |
| 11 | Railway | 123 | 1112 |
| 12 | Parking lot 1 | 123 | 1110 |
| 13 | Parking lot 2 | 47 | 422 |
| 14 | Tennis court | 43 | 385 |
| 15 | Running track | 66 | 594 |
| Total | 1502 | 13,527 |
| Class | CNN-Based Methods | Transformer-Based Methods | CNN-Transformer Hybrid-Based Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D-CNN | 3D-CNN | HybridSN | M3D-DCNN | ViT | CrossViT | DeepViT | SpectralFormer | SSFTT | morphFormer | MSNAT | MDFFN | |
| 1 | 42.68 ± 7.50 | 79.76 ± 8.93 | 24.39 ± 10.12 | 32.68 ± 12.20 | 80.73 ± 9.66 | 70.24 ± 9.80 | 89.02 ± 2.73 | 73.41 ± 4.15 | 94.15 ± 5.89 | 96.59 ± 5.79 | 71.46 ± 12.91 | 93.90 ± 2.50 |
| 2 | 90.05 ± 0.96 | 91.05 ± 1.15 | 90.29 ± 4.47 | 81.73 ± 2.24 | 87.22 ± 0.92 | 85.75 ± 0.83 | 87.99 ± 1.01 | 91.23 ± 0.47 | 95.14 ± 0.39 | 94.44 ± 0.63 | 93.81 ± 2.11 | 95.82 ± 0.21 |
| 3 | 95.03 ± 1.42 | 93.98 ± 1.53 | 92.37 ± 5.99 | 65.92 ± 9.88 | 92.77 ± 1.36 | 93.64 ± 1.29 | 92.78 ± 1.49 | 96.12 ± 0.49 | 99.59 ± 0.40 | 98.18 ± 0.64 | 99.09 ± 0.91 | 99.91 ± 0.19 |
| 4 | 78.64 ± 3.06 | 75.73 ± 8.70 | 63.66 ± 15.22 | 30.19 ± 10.62 | 77.28 ± 5.88 | 89.01 ± 2.79 | 90.05 ± 2.39 | 91.69 ± 2.75 | 100.00 ± 0.00 | 99.20 ± 1.09 | 95.73 ± 3.16 | 99.20 ± 0.37 |
| 5 | 95.29 ± 1.43 | 98.09 ± 1.31 | 94.76 ± 1.35 | 91.08 ± 1.93 | 96.14 ± 0.85 | 96.16 ± 0.73 | 96.90 ± 0.34 | 96.94 ± 0.50 | 99.52 ± 0.30 | 99.15 ± 0.81 | 95.24 ± 1.10 | 99.38 ± 0.40 |
| 6 | 98.40 ± 0.51 | 97.93 ± 0.49 | 97.78 ± 3.40 | 96.41 ± 1.68 | 99.24 ± 0.34 | 98.58 ± 0.38 | 98.25 ± 0.64 | 99.07 ± 0.38 | 99.73 ± 0.40 | 99.36 ± 0.59 | 97.78 ± 1.19 | 99.01 ± 0.27 |
| 7 | 34.40 ± 11.48 | 97.20 ± 5.08 | 40.00 ± 24.98 | 30.40 ± 19.03 | 97.60 ± 2.65 | 92.00 ± 7.16 | 64.40 ± 12.58 | 95.20 ± 5.00 | 78.40 ± 28.41 | 100.00 ± 0.00 | 94.40 ± 6.97 | 100.00 ± 0.00 |
| 8 | 99.93 ± 0.15 | 99.51 ± 0.49 | 99.91 ± 0.15 | 99.74 ± 0.28 | 99.98 ± 0.07 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.88 ± 0.21 | 100.00 ± 0.00 | 99.98 ± 0.07 | 99.93 ± 0.15 | 99.95 ± 0.09 |
| 9 | 13.33 ± 3.69 | 58.89 ± 16.14 | 34.44 ± 10.48 | 28.89 ± 24.70 | 60.00 ± 12.37 | 80.00 ± 11.97 | 39.44 ± 9.44 | 50.00 ± 8.61 | 36.11 ± 14.96 | 70.56 ± 16.11 | 48.89 ± 19.85 | 87.78 ± 4.16 |
| 10 | 93.25 ± 1.22 | 94.39 ± 2.00 | 94.19 ± 2.11 | 81.82 ± 3.28 | 94.69 ± 0.85 | 91.99 ± 1.00 | 92.77 ± 1.33 | 94.59 ± 0.71 | 98.75 ± 0.63 | 98.56 ± 0.84 | 97.25 ± 1.24 | 99.01 ± 0.40 |
| 11 | 98.11 ± 0.34 | 97.38 ± 0.69 | 97.97 ± 0.86 | 93.92 ± 1.12 | 96.58 ± 1.17 | 96.36 ± 0.68 | 97.03 ± 0.42 | 97.69 ± 0.36 | 99.47 ± 0.21 | 99.06 ± 0.40 | 98.05 ± 1.06 | 99.47 ± 0.17 |
| 12 | 79.48 ± 3.38 | 84.61 ± 3.61 | 70.86 ± 18.74 | 59.10 ± 10.20 | 79.74 ± 3.48 | 77.96 ± 2.07 | 83.41 ± 2.86 | 93.65 ± 1.37 | 97.98 ± 0.61 | 95.34 ± 1.24 | 96.67 ± 1.40 | 97.72 ± 0.38 |
| 13 | 98.32 ± 1.04 | 98.38 ± 1.57 | 93.57 ± 10.55 | 94.97 ± 3.71 | 100.00 ± 0.00 | 99.73 ± 0.27 | 97.51 ± 1.80 | 97.73 ± 0.99 | 99.62 ± 0.49 | 98.65 ± 0.97 | 99.24 ± 0.69 | 100.00 ± 0.00 |
| 14 | 99.71 ± 0.17 | 99.41 ± 0.70 | 99.65 ± 0.29 | 97.39 ± 1.14 | 99.27 ± 0.27 | 98.72 ± 0.23 | 98.36 ± 0.36 | 99.30 ± 0.41 | 99.97 ± 0.04 | 99.95 ± 0.07 | 99.51 ± 0.26 | 99.99 ± 0.03 |
| 15 | 95.68 ± 2.99 | 95.53 ± 2.07 | 55.62 ± 22.05 | 97.39 ± 1.14 | 93.20 ± 1.69 | 97.03 ± 0.78 | 93.11 ± 1.52 | 94.24 ± 1.91 | 99.08 ± 1.11 | 98.50 ± 0.82 | 95.79 ± 2.05 | 99.65 ± 0.28 |
| 16 | 75.00 ± 2.77 | 84.40 ± 4.75 | 60.60 ± 33.20 | 53.45 ± 17.40 | 96.07 ± 3.11 | 97.86 ± 1.39 | 82.62 ± 6.63 | 96.43 ± 2.71 | 88.33 ± 3.40 | 96.55 ± 1.95 | 91.67 ± 6.00 | 97.98 ± 0.76 |
| OA (%) | 94.04 ± 0.34 | 94.80 ± 0.78 | 91.23 ± 3.39 | 83.57 ± 1.86 | 93.82 ± 0.41 | 93.57 ± 0.23 | 93.95 ± 0.36 | 96.01 ± 0.14 | 98.52 ± 0.15 | 98.15 ± 0.21 | 97.10 ± 0.81 | 98.85 ± 0.09 |
| AA (%) | 80.46 ± 1.03 | 90.39 ± 1.76 | 75.63 ± 7.21 | 68.10 ± 4.25 | 90.66 ± 1.38 | 91.56 ± 1.02 | 87.73 ± 1.19 | 91.70 ± 0.88 | 92.86 ± 2.33 | 96.50 ± 1.15 | 92.16 ± 2.22 | 98.05 ± 0.32 |
| Kappa (%) | 93.18 ± 0.39 | 94.06 ± 0.90 | 89.95 ± 3.91 | 81.03 ± 2.18 | 92.94 ± 0.46 | 92.65 ± 0.26 | 93.09 ± 0.42 | 95.45 ± 0.16 | 98.32 ± 0.17 | 97.89 ± 0.23 | 96.70 ± 0.92 | 98.69 ± 0.10 |
| Class | CNN-Based Methods | Transformer-Based Methods | CNN-Transformer Hybrid-Based Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D-CNN | 3D-CNN | HybridSN | M3D-DCNN | ViT | CrossViT | DeepViT | SpectralFormer | SSFTT | morphFormer | MSNAT | MDFFN | |
| 1 | 99.52 ± 0.11 | 99.52 ± 0.18 | 99.48 ± 0.68 | 99.14 ± 0.43 | 99.38 ± 0.19 | 99.40 ± 0.19 | 99.79 ± 0.08 | 99.63 ± 0.15 | 99.94 ± 0.05 | 99.91 ± 0.05 | 99.89 ± 0.14 | 99.99 ± 0.02 |
| 2 | 100.00 ± 0.00 | 99.98 ± 0.01 | 100.00 ± 0.01 | 99.95 ± 0.03 | 99.98 ± 0.01 | 99.99 ± 0.00 | 99.98 ± 0.01 | 99.98 ± 0.01 | 99.99 ± 0.01 | 99.99 ± 0.01 | 99.99 ± 0.01 | 100.00 ± 0.00 |
| 3 | 95.80 ± 0.88 | 95.98 ± 0.98 | 97.20 ± 1.00 | 91.20 ± 0.93 | 93.01 ± 1.29 | 95.85 ± 0.52 | 95.64 ± 0.94 | 95.99 ± 0.87 | 99.49 ± 0.16 | 98.54 ± 0.48 | 98.34 ± 1.33 | 99.70 ± 0.27 |
| 4 | 98.86 ± 0.13 | 98.85 ± 0.43 | 98.76 ± 1.12 | 98.13 ± 0.46 | 99.65 ± 0.14 | 98.98 ± 0.18 | 98.42 ± 0.40 | 99.19 ± 0.19 | 98.61 ± 0.24 | 98.60 ± 0.34 | 99.72 ± 0.13 | 99.85 ± 0.06 |
| 5 | 99.90 ± 0.09 | 99.84 ± 0.15 | 99.70 ± 0.63 | 99.93 ± 0.20 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.88 ± 0.12 | 99.98 ± 0.05 | 99.97 ± 0.08 | 99.97 ± 0.07 | 99.99 ± 0.02 | 100.00 ± 0.00 |
| 6 | 100.00 ± 0.00 | 99.98 ± 0.03 | 99.99 ± 0.01 | 99.75 ± 0.26 | 99.59 ± 0.16 | 99.83 ± 0.08 | 99.96 ± 0.04 | 99.85 ± 0.08 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.99 ± 0.04 | 100.00 ± 0.00 |
| 7 | 99.74 ± 0.28 | 99.82 ± 0.26 | 98.65 ± 3.49 | 98.72 ± 0.79 | 99.97 ± 0.05 | 99.94 ± 0.07 | 99.84 ± 0.26 | 99.87 ± 0.23 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.76 ± 0.34 | 100.00 ± 0.00 |
| 8 | 97.36 ± 0.72 | 98.22 ± 0.96 | 96.40 ± 2.63 | 95.00 ± 0.78 | 98.37 ± 0.30 | 97.40 ± 0.43 | 98.96 ± 0.28 | 97.91 ± 0.50 | 98.77 ± 0.45 | 98.82 ± 0.21 | 99.19 ± 0.46 | 99.86 ± 0.10 |
| 9 | 97.52 ± 0.65 | 96.10 ± 1.42 | 94.42 ± 4.89 | 95.31 ± 1.52 | 100.00 ± 0.00 | 99.84 ± 0.16 | 99.31 ± 0.60 | 98.37 ± 0.61 | 97.23 ± 0.32 | 97.56 ± 0.49 | 99.82 ± 0.39 | 100.00 ± 0.00 |
| OA (%) | 99.34 ± 0.09 | 99.39 ± 0.12 | 99.21 ± 0.48 | 98.67 ± 0.17 | 99.34 ± 0.07 | 99.38 ± 0.04 | 99.51 ± 0.06 | 99.44 ± 0.06 | 99.69 ± 0.04 | 99.65 ± 0.06 | 99.80 ± 0.14 | 99.96 ± 0.02 |
| AA (%) | 98.74 ± 0.18 | 98.70 ± 0.27 | 98.29 ± 1.13 | 97.46 ± 0.33 | 98.88 ± 0.13 | 99.02 ± 0.06 | 99.09 ± 0.11 | 98.97 ± 0.13 | 99.33 ± 0.04 | 99.26 ± 0.12 | 99.63 ± 0.29 | 99.93 ± 0.04 |
| Kappa (%) | 99.13 ± 0.12 | 99.19 ± 0.16 | 98.95 ± 0.63 | 98.24 ± 0.22 | 99.12 ± 0.09 | 99.18 ± 0.05 | 99.36 ± 0.07 | 99.26 ± 0.07 | 99.59 ± 0.05 | 99.54 ± 0.07 | 99.73 ± 0.19 | 99.95 ± 0.02 |
| Class | CNN-Based Methods | Transformer-Based Methods | CNN-Transformer Hybrid-Based Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D-CNN | 3D-CNN | HybridSN | M3D-DCNN | ViT | CrossViT | DeepViT | SpectralFormer | SSFTT | morphFormer | MSNAT | MDFFN | |
| 1 | 95.97 ± 2.17 | 98.39 ± 0.68 | 99.25 ± 0.36 | 96.70 ± 1.06 | 97.08 ± 0.76 | 98.05 ± 1.20 | 98.53 ± 0.94 | 99.77 ± 0.24 | 96.58 ± 1.86 | 98.57 ± 0.64 | 97.80 ± 1.02 | 99.25 ± 0.37 |
| 2 | 99.39 ± 0.42 | 99.42 ± 0.62 | 99.77 ± 0.16 | 99.62 ± 0.20 | 99.76 ± 0.06 | 99.86 ± 0.06 | 99.81 ± 0.29 | 99.89 ± 0.07 | 99.19 ± 0.52 | 99.17 ± 0.34 | 99.65 ± 0.16 | 99.89 ± 0.04 |
| 3 | 99.79 ± 0.07 | 99.98 ± 0.05 | 99.98 ± 0.05 | 99.94 ± 0.08 | 100.00 ± 0.00 | 99.92 ± 0.08 | 99.82 ± 0.13 | 100.00 ± 0.00 | 99.62 ± 0.11 | 99.78 ± 0.15 | 99.98 ± 0.05 | 99.87 ± 0.06 |
| 4 | 97.79 ± 0.75 | 96.42 ± 1.51 | 97.59 ± 1.24 | 96.88 ± 1.69 | 99.04 ± 0.44 | 98.88 ± 0.49 | 97.89 ± 0.84 | 98.56 ± 0.50 | 97.27 ± 1.00 | 96.81 ± 1.45 | 99.50 ± 0.86 | 99.29 ± 0.55 |
| 5 | 99.95 ± 0.08 | 99.79 ± 0.33 | 100.00 ± 0.00 | 99.73 ± 0.40 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.91 ± 0.27 | 100.00 ± 0.00 | 99.99 ± 0.03 | 99.99 ± 0.03 | 100.00 ± 0.00 |
| 6 | 90.65 ± 3.35 | 96.61 ± 1.73 | 98.29 ± 2.16 | 93.15 ± 2.56 | 99.97 ± 0.10 | 99.93 ± 0.21 | 99.42 ± 0.49 | 99.76 ± 0.43 | 99.76 ± 0.41 | 99.90 ± 0.31 | 99.01 ± 1.42 | 100.00 ± 0.00 |
| 7 | 93.81 ± 1.92 | 95.07 ± 0.98 | 94.77 ± 1.61 | 93.19 ± 1.96 | 97.43 ± 0.56 | 96.93 ± 0.59 | 96.26 ± 0.57 | 96.61 ± 0.61 | 96.03 ± 1.20 | 95.03 ± 0.84 | 97.03 ± 1.04 | 98.20 ± 0.44 |
| 8 | 90.45 ± 3.96 | 95.01 ± 1.54 | 97.66 ± 0.82 | 94.10 ± 0.99 | 97.45 ± 0.67 | 97.62 ± 0.46 | 98.02 ± 0.40 | 97.75 ± 0.60 | 95.37 ± 1.25 | 96.95 ± 1.17 | 95.49 ± 1.27 | 98.18 ± 0.74 |
| 9 | 92.83 ± 2.37 | 95.97 ± 2.31 | 97.08 ± 1.26 | 93.01 ± 1.96 | 95.47 ± 0.94 | 97.24 ± 0.76 | 97.95 ± 0.99 | 97.83 ± 0.75 | 97.97 ± 1.65 | 97.66 ± 1.44 | 94.08 ± 2.22 | 98.97 ± 0.39 |
| 10 | 99.36 ± 0.62 | 99.48 ± 0.44 | 99.68 ± 0.27 | 98.31 ± 1.74 | 99.57 ± 0.29 | 99.66 ± 0.22 | 99.83 ± 0.14 | 99.66 ± 0.28 | 99.81 ± 0.41 | 99.77 ± 0.24 | 99.81 ± 0.17 | 100.00 ± 0.00 |
| 11 | 96.91 ± 0.77 | 99.10 ± 0.54 | 99.81 ± 0.19 | 98.71 ± 0.87 | 99.90 ± 0.14 | 99.99 ± 0.03 | 99.98 ± 0.04 | 99.54 ± 0.29 | 99.73 ± 0.39 | 99.18 ± 0.53 | 97.37 ± 2.59 | 100.00 ± 0.00 |
| 12 | 97.95 ± 1.51 | 98.77 ± 0.65 | 99.39 ± 0.18 | 98.70 ± 0.30 | 98.75 ± 0.34 | 99.04 ± 0.13 | 98.86 ± 0.23 | 99.19 ± 0.13 | 99.50 ± 0.14 | 99.45 ± 0.44 | 99.15 ± 0.28 | 99.61 ± 0.04 |
| 13 | 85.92 ± 2.74 | 88.15 ± 2.92 | 90.50 ± 4.56 | 79.27 ± 5.44 | 81.59 ± 2.80 | 84.79 ± 3.04 | 89.27 ± 1.89 | 94.41 ± 1.06 | 92.37 ± 0.83 | 93.06 ± 2.91 | 95.05 ± 1.34 | 99.10 ± 0.49 |
| 14 | 99.51 ± 0.34 | 99.22 ± 0.94 | 99.97 ± 0.08 | 99.95 ± 0.16 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.82 ± 0.17 | 100.00 ± 0.00 | 100.00 ± 0.00 | 98.99 ± 1.04 | 100.00 ± 0.00 |
| 15 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.98 ± 0.05 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.83 ± 0.18 | 99.48 ± 0.24 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.95 ± 0.11 | 99.95 ± 0.11 | 100.00 ± 0.00 |
| OA (%) | 96.38 ± 0.54 | 97.66 ± 0.40 | 98.41 ± 0.30 | 96.62 ± 0.55 | 98.13 ± 0.12 | 98.45 ± 0.19 | 98.55 ± 0.20 | 98.88 ± 0.12 | 98.19 ± 0.27 | 98.32 ± 0.35 | 98.12 ± 0.34 | 99.42 ± 0.07 |
| AA (%) | 96.02 ± 0.54 | 97.43 ± 0.37 | 98.25 ± 0.50 | 96.08 ± 0.65 | 97.73 ± 0.19 | 98.12 ± 0.26 | 98.34 ± 0.22 | 98.85 ± 0.11 | 98.21 ± 0.22 | 98.35 ± 0.39 | 98.19 ± 0.29 | 99.49 ± 0.07 |
| Kappa (%) | 96.08 ± 0.59 | 97.47 ± 0.44 | 98.28 ± 0.33 | 96.34 ± 0.60 | 97.98 ± 0.12 | 98.33 ± 0.20 | 98.43 ± 0.22 | 98.79 ± 0.13 | 98.05 ± 0.29 | 98.18 ± 0.38 | 97.97 ± 0.37 | 99.37 ± 0.08 |
| Methods | Params (MB) | FLOPs (GB) | Training Time (s) | Testing Time (s) |
|---|---|---|---|---|
| 2D-CNN | 0.39 | 0.02 | 10.04 | 0.62 |
| 3D-CNN | 0.26 | 0.04 | 17.36 | 0.90 |
| HybridSN | 1.19 | 0.11 | 14.46 | 0.88 |
| M3D-DCNN | 0.21 | 0.03 | 16.17 | 0.78 |
| ViT | 9.60 | 0.50 | 27.59 | 1.19 |
| CrossViT | 69.87 | 2.29 | 93.68 | 4.07 |
| DeepViT | 9.60 | 0.50 | 34.04 | 1.34 |
| SpectralFormer | 0.14 | 0.01 | 114.71 | 16.17 |
| SSFTT | 0.15 | 0.03 | 12.80 | 0.76 |
| morphFormer | 0.06 | 0.01 | 52.57 | 2.63 |
| MSNAT | 0.12 | 0.02 | 35.75 | 0.99 |
| MDFFN | 21.15 | 0.78 | 57.15 | 1.93 |
| Case | Dataset | Module | OA (%) | AA (%) | Kappa (%) | |
|---|---|---|---|---|---|---|
| MCIE | DACA | |||||
| 1 | Indian Pines | × | × | 90.49 ± 0.69 | 88.39 ± 1.06 | 89.12 ± 0.79 |
| 2 | × | √ | 94.07 ± 0.26 | 91.70 ± 0.75 | 93.22 ± 0.29 | |
| 3 | √ | × | 97.52 ± 0.35 | 95.44 ± 0.97 | 97.17 ± 0.40 | |
| 4 | √ | √ | 98.85 ± 0.09 | 98.05 ± 0.32 | 98.69 ± 0.10 | |
| 1 | Pavia University | × | × | 98.57 ± 0.12 | 97.85 ± 0.23 | 98.10 ± 0.16 |
| 2 | × | √ | 99.14 ± 0.09 | 98.72 ± 0.10 | 98.86 ± 0.12 | |
| 3 | √ | × | 99.89 ± 0.03 | 99.82 ± 0.06 | 99.86 ± 0.04 | |
| 4 | √ | √ | 99.96 ± 0.02 | 99.93 ± 0.04 | 99.95 ± 0.02 | |
| 1 | Houston 2013 | × | × | 96.37 ± 0.29 | 95.69 ± 0.39 | 96.07 ± 0.31 |
| 2 | × | √ | 97.96 ± 0.10 | 97.43 ± 0.12 | 97.79 ± 0.11 | |
| 3 | √ | × | 98.90 ± 0.15 | 99.07 ± 0.14 | 98.81 ± 0.16 | |
| 4 | √ | √ | 99.42 ± 0.07 | 99.49 ± 0.07 | 99.37 ± 0.08 | |
| Spatial Size | S-Branch () | L-Branch () | OA (%) | AA (%) | Kappa (%) | FLOPs (G) | Params (M) |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 98.02 ± 0.16 | 95.87 ± 0.74 | 97.74 ± 0.18 | 0.66 | 20.92 |
| 12 | 2 | 6 | 98.51 ± 0.10 | 96.08 ± 0.95 | 98.29 ± 0.12 | 0.90 | 21.03 |
| 15 | 3 | 5 | 98.85 ± 0.09 | 98.05 ± 0.32 | 98.69 ± 0.10 | 0.78 | 21.15 |
| 18 | 3 | 6 | 99.04 ± 0.12 | 98.22 ± 0.73 | 98.90 ± 0.14 | 1.05 | 21.39 |
| 20 | 4 | 5 | 98.96 ± 0.12 | 98.34 ± 0.42 | 98.81 ± 0.13 | 0.96 | 21.51 |
| 24 | 4 | 6 | 98.80 ± 0.04 | 97.71 ± 0.53 | 98.63 ± 0.05 | 1.27 | 21.96 |
| Depth | OA (%) | AA (%) | Kappa (%) | FLOPs (G) | Params (M) |
|---|---|---|---|---|---|
| 1 | 98.28 ± 0.15 | 97.05 ± 0.44 | 98.04 ± 0.17 | 0.28 | 7.23 |
| 3 | 98.85 ± 0.09 | 98.05 ± 0.32 | 98.69 ± 0.10 | 0.78 | 21.15 |
| 5 | 98.91 ± 0.04 | 98.34 ± 0.58 | 98.76 ± 0.05 | 1.28 | 35.07 |
| 7 | 98.85 ± 0.06 | 97.40 ± 0.45 | 98.68 ± 0.07 | 1.78 | 48.98 |
| 9 | 98.84 ± 0.11 | 97.58 ± 0.92 | 98.68 ± 0.13 | 2.28 | 62.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Luo, X.; Deng, Y.; Zhao, F.; Yang, X.; Chen, J.; Chen, J. MDFFN: Multi-Scale Dual-Aggregated Feature Fusion Network for Hyperspectral Image Classification. Electronics 2025, 14, 1477. https://doi.org/10.3390/electronics14071477
Song G, Luo X, Deng Y, Zhao F, Yang X, Chen J, Chen J. MDFFN: Multi-Scale Dual-Aggregated Feature Fusion Network for Hyperspectral Image Classification. Electronics. 2025; 14(7):1477. https://doi.org/10.3390/electronics14071477
Chicago/Turabian StyleSong, Ge, Xiaoqi Luo, Yuqiao Deng, Fei Zhao, Xiaofei Yang, Jiaxin Chen, and Jinjie Chen. 2025. "MDFFN: Multi-Scale Dual-Aggregated Feature Fusion Network for Hyperspectral Image Classification" Electronics 14, no. 7: 1477. https://doi.org/10.3390/electronics14071477
APA StyleSong, G., Luo, X., Deng, Y., Zhao, F., Yang, X., Chen, J., & Chen, J. (2025). MDFFN: Multi-Scale Dual-Aggregated Feature Fusion Network for Hyperspectral Image Classification. Electronics, 14(7), 1477. https://doi.org/10.3390/electronics14071477





