Enhancing Quadruped Robot Walking on Unstructured Terrains: A Combination of Stable Blind Gait and Deep Reinforcement Learning

Abstract

Legged robots, designed for high adaptability, are poised for deployment in hazardous tasks traditionally undertaken by humans, particularly in unstructured terrains where their wheeled counterparts cannot operate. Nevertheless, using them in unstructured settings necessitates advanced control techniques to maneuver without depending entirely on visual signals or pre-programmed instructions. To address these challenges, this research proposes a novel walking algorithm for quadruped robots that blends a stable blind gait without needing any visual cues with deep reinforcement learning to enhance mobility across diverse terrains. The algorithm’s effectiveness was evaluated virtually, emphasizing the ability to regulate the robot’s leg movements and posture when reaching obstacles. Our results demonstrated a success rate of over 90% in the stair-climbing task, suggesting that the algorithm improved the robot’s mobility and stability. Although emphasizing a steady blind gait reduces reliance on visual cues, incorporating the algorithm with further sensory inputs and environmental awareness may improve the robot’s functionality and versatility in practical situations. More dynamic gaits and a wider variety of static and dynamic obstacles will be the focus of future algorithm development. Furthermore, validation in the real world will aid in detecting any shortcomings or potential areas for enhancement in the algorithm, thereby improving its adaptability and resilience in diverse settings and assignments.

1. Introduction

Recent developments in legged robotics have opened avenues for autonomous inspection and maintenance tasks in environments that are too challenging for conventional wheeled robots. Such terrains could include uneven grounds, rubble after disasters, or areas with multiple barriers [1]. Legged robots excel in these scenarios, offering a degree of mobility that mimics biological organisms, thus enabling navigation through hazardous or inaccessible locales [2]. For example, Lee et al. demonstrated the potential of reinforcement learning to develop robust controllers for blind quadrupedal locomotion, enhancing adaptability in diverse and challenging natural environments [3].

Specifically, operating without reliance on visual cues presents distinct advantages, particularly in unstructured and unpredictable environments. Visual sensors, while powerful, can be significantly hampered by environmental conditions such as darkness, fog, smoke, or dust. In disaster scenarios, for example, visibility is often severely reduced due to smoke and debris, and in subterranean or cave environments lacking ambient light, visual-based navigation becomes unreliable or impossible. Furthermore, visual sensors are susceptible to physical damage or malfunction, making vision-dependent robots ineffective. In contrast, a stable blind gait, relying on proprioceptive and tactile feedback from leg sensors, allows the robot to maintain locomotion and stability even when visual information is degraded or completely absent. This inherent robustness makes robots with blind gait algorithms significantly more versatile and dependable in a wider range of unstructured, real-world scenarios where visual systems may fail.

However, optimizing walking algorithms for legged robots to maintain stability poses marked challenges that deter their widespread adoption in crucial operations [4]. These robots often struggle with changes in landscape topography [5], demonstrate insufficient resilience in the face of external disturbances [6], and rely heavily on pre-set locomotion patterns that may not suit all situations or require advanced visual sensors [7,8,9]. In many real-world scenarios, visual data can become unreliable due to darkness, dust, or occlusion, making vision-based perception insufficient. Consequently, our approach focuses on force and joint sensing (i.e., proprioceptive feedback) to ensure stable locomotion even in visually degraded environments. To avoid these limitations, this study proposes pioneering methods that combine classical control models with the flexibility of machine learning to significantly improve robot adaptability and performance in mobile terrain navigation [10].

This paper proposes a novel walking algorithm that integrates a stable blind gait with deep reinforcement learning techniques [11]. The stable blind gait uses leg sensors instead of visual sensors to maintain stability and precisely control leg movements [12]. At the same time, the deep reinforcement learning module facilitates adaptation to varying terrains and operational requirements [13]. This integrated approach aims to provide legged robots with improved mobility, adaptability, and autonomy, extending their operational capabilities [14]. The overall structure of this integrated approach is illustrated in Figure 1. An overview of the motion planning approach is shown in the Supplementary Materials (Video S1).

This research imparts two primary enhancements to the domain of legged robotics. Firstly, it advances a freshly merged mechanism encompassing deep reinforcement learning within the robust architectural confines of a stable blind gait [15]. The fusion emphasizes not just steadiness through the blind gait methodology [16] but also the adaptability enabled by deep reinforcement learning to fine-tune movements in response to specific environmental cues [17]. Secondly, the methodology’s efficacy was verified by physics-based simulations that demonstrate the robot’s skill in ascending stairs—a task illustrative of its forte in maneuvering through structured challenges [1,8]. The algorithm adeptly integrates the tactics of blind gait with a deep learning system, essential to harmoniously controlling robot posture and locomotion, thereby ensuring stable progression through various terrain profiles [18,19]. Iterative adjustments of gait parameters through the deep learning agent empower the robot to overcome stair barriers with improved positioning accuracy [20,21].

In this study, we aim to fill a critical gap in legged robotics by addressing the twin challenges of maneuverability in complex terrains and the need for robust adaptability in dynamic environments without sophisticated sensors. The presented algorithm breaks new ground by integrating a stable blind gait with deep reinforcement learning, paving the way for more autonomous, stable, and flexible locomotion strategies. In the future, this research will contribute significantly to the field, with implications that may extend beyond the current applications. As legged robots increasingly become part of our operational toolkit, the advancements detailed herein will be crucial in optimizing their potential for diverse applications in various domains.

2. Related Works

The exploration of quadruped robotics has led to remarkable advances in gait planning and stability, laying the groundwork for subsequent innovations. Early studies, such as those by McGhee and Frank [16], established the fundamental principles of static stability in quadruped locomotion. Building on these principles, Zhang et al. [1] developed a static gait planning method that adapts to terrain complexity in real-time. This technique aligns with the emphasis of the present work on stable and adaptable locomotion.

Control and simulation techniques have also seen significant progress. Coros et al. [22] crafted a simulation model capable of a broad spectrum of gaits, employing various control strategies. Similarly, Dai and Tedrake [5] focused on generating stable trajectories for walking robots on uneven terrain through convex optimization. These methods resonate with the algorithm presented in this paper, where the fusion of model-based stability with machine learning adaptability is central to the proposed approach.

The challenge of terrain adaptability has been addressed through innovative solutions. Focchi et al. [23] demonstrated a heuristic-based planning approach that enables quadrupeds to traverse complex terrains without visual feedback, while Prayogo and Triwiyatno [24] used a 6 DoF IMU to stabilize on uneven surfaces. Lee et al. have made a notable advance in the control and adaptability of quadruped robots [3]. Their work successfully developed a robust controller via reinforcement learning, specifically designed for blind quadrupedal locomotion in natural environments. This approach resulted in impressive zero-shot generalization from simulation to real-world conditions, including dynamic terrains such as mud, snow, and rubble.

Research on blind quadruped or vision-free legged robots strongly emphasizes their ability to navigate stairs and obstacles through proprioceptive and sensor-based controls. These robots are particularly valuable when vision-based systems are unreliable, such as in dark or cluttered spaces. Current research efforts are dedicated to enhancing the stability and adaptability of these robots, focusing on stable gait design, zero-moment point control, force control strategies, and the effective integration of proprioceptive feedback. For example, ref. [25] introduces an end-to-end learning-based motion controller relying solely on proprioceptive sensing, enabling robust collision detection and response in complex 3D environments and thereby improving the robot’s ability to traverse diverse terrains without visual sensors. In parallel, ref. [26] presents the self-learning latent representation (SLR) method, demonstrating superior performance in navigating steps, climbing stairs, and traversing varied terrains when compared to state-of-the-art algorithms, again without relying on privileged information. Reinforcement learning techniques also play a crucial role, as exemplified by [27], who utilized RL to develop locomotion controllers that are resilient to external forces, which is vital for maintaining stable walking and effective obstacle negotiation. While vision-based parkour systems, such as that explored by [28], highlight the agility achievable with visual input, vision-free approaches prioritize robust, sensor-driven locomotion for reliable navigation in challenging and sensorially limited environments. Instead, proprioceptive integration and force-responsive control are key strategies for achieving stability and effective navigation for blind quadruped robots in these complex conditions.

These advancements reflect the adaptability and robustness the current research aims to enhance by integrating deep reinforcement learning into the stable gait framework.

Machine learning, particularly reinforcement learning, has emerged as a transformative force in controlling quadruped robots. Li et al. [29] and Shao et al. [30] exemplified this trend by integrating learning algorithms to generate versatile and adaptable locomotion strategies. The present work extends these concepts employing the Soft Actor–Critic algorithm (SAC) [31], chosen for its reliable convergence properties and exploration driven by entropy, particularly beneficial in continuous control tasks. Unlike Proximal Policy Optimization (PPO) [32] or Twin Delayed DDPG (TD3) [33], the SAC algorithm allows a more stable balance between exploration and exploitation due to its maximum entropy reinforcement learning framework. This characteristic is pivotal for climbing stairs, where the agent must fine-tune foot placement parameters and explore novel gait configurations. Similar hierarchical or mapless RL methods—such as those of Sun et al. [34] and Xie et al. [35]—address continuous action spaces in modular robots; however, our focus is specifically on stable, vision-free quadruped locomotion in structured obstacles (e.g., stairs). Consequently, we employed the SAC algorithm for its demonstrated sample efficiency and robust policy optimization in tasks that demand precise continuous control.

Bioinspired designs and self-recovery capabilities have also been explored, with Kang et al. [14] generating animal-like motions and Zhang et al. [17] enhancing self-recovery control. These contributions inspire current research, emphasizing natural, adaptable movements and the capacity to recover from perturbations, which is crucial for real-world applications.

In contrast to the aforementioned works, the primary novelty of this research lies in the specific integration of a stable blind gait framework with deep reinforcement learning. Although prior studies, such as Lee et al. [3], have demonstrated the effectiveness of reinforcement learning for achieving robust blind quadrupedal locomotion, our approach is distinguished by its explicit combination of a model-based stable blind gap as a foundational element with a deep reinforcement learning agent for gait optimization and adaptation. Lee et al. [3], for example, focused on learning a robust locomotion controller directly through reinforcement learning from scratch. Our method, conversely, leverages the inherent stability and robustness of a predesigned stable blind gait and strategically employs deep reinforcement learning to enhance and refine this gait, specifically for improved performance in challenging structured environments such as staircases. This *integrated algorithmic architecture*, where deep reinforcement learning is used to optimize a pre-existing stable locomotion framework, represents a novel contribution that differs from purely end-to-end learning paradigms or approaches that do not explicitly incorporate a stable gait foundation. Furthermore, our focus on vision-free stair climbing provides a distinct application context, showcasing the practical utility of our integrated approach for navigating structured obstacles within complex, unstructured settings.

In summary, quadruped robotics has evolved through several methodical and interconnected advancements, each contributing to developing more capable and autonomous systems. The research presented here capitalizes on these contributions, proposing a novel algorithm that marries the reliability of a stable blind gait with the flexibility of deep reinforcement learning. As the field progresses, the fusion of these techniques paves the way for legged robots to tackle an even wider array of complex and dynamic environments, further bridging the gap between robotic capabilities and the multifaceted demands of real-world applications.

3. Materials and Methods

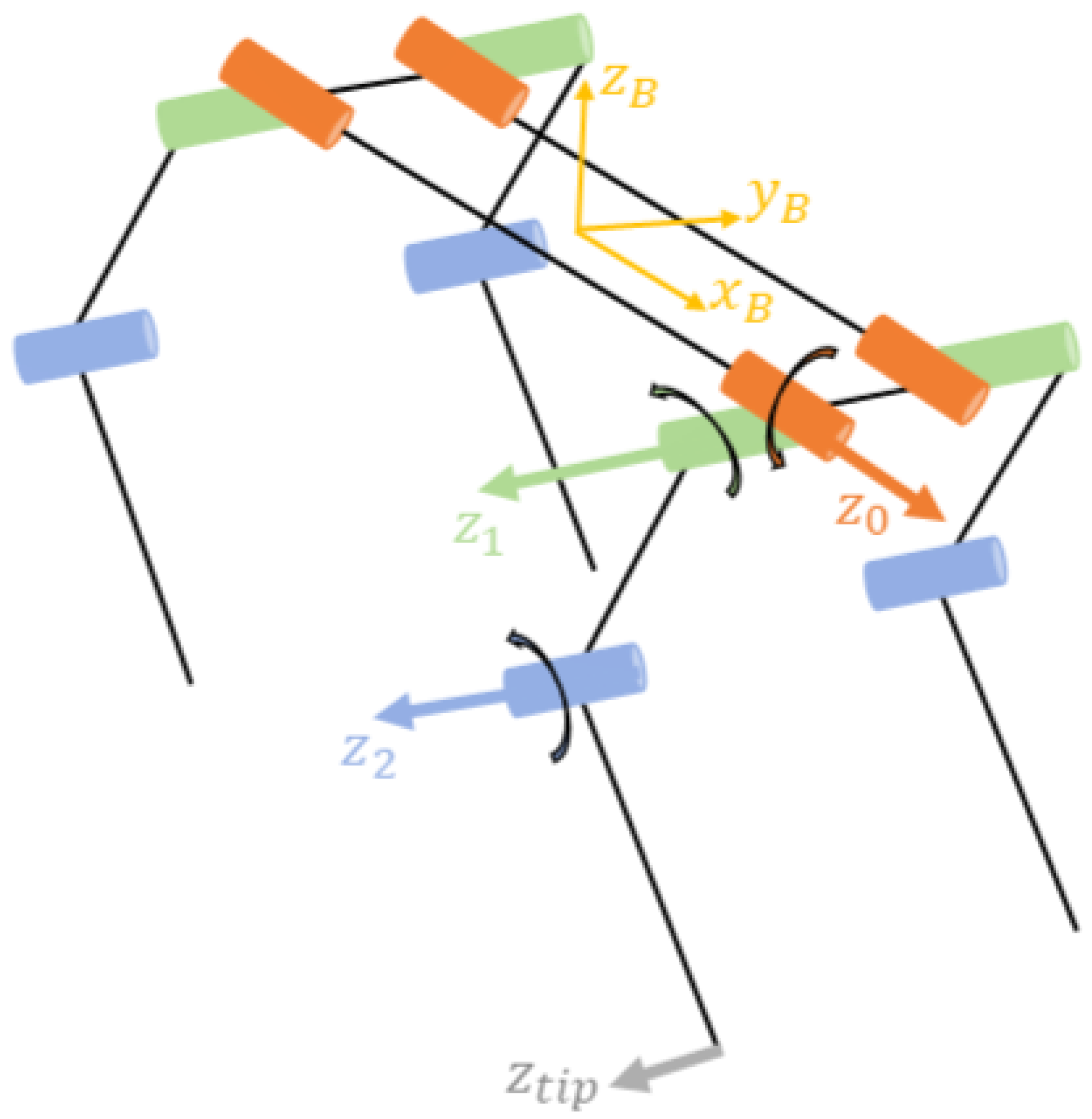
3.1. Kinematic Model

The robot kinematic model is a crucial component in understanding and controlling the movement of the quadruped robot. Figure 2 illustrates the kinematic structure of our quadruped robot.

This model represents the geometric relationships between the robot’s body and its legs, providing a framework for calculating the positions and orientations of each joint and leg endpoint. Understanding this model is essential for developing effective control strategies, particularly in the context of our stable blind gait and reinforcement learning approach.

3.2. Stable Blind Gait

The stable blind gait is a fundamental component of our approach, designed to ensure the robot’s stability without relying on visual input. This section details the theoretical underpinnings and practical implementation of our stable blind gait strategy.

To evaluate the effectiveness of our proposed algorithm in navigating unstructured terrains, we specifically chose stair climbing as a representative and demonstrably challenging task. Staircases are ubiquitous structured obstacles within otherwise unstructured or human-modified environments, making stairs a practically relevant capability for legged robots for real-world deployment. Furthermore, stair climbing inherently demands both stability and adaptability. The robot must maintain balance while transitioning between discrete height levels, requiring precise control of foot placement and center of mass (CoM) management, which directly aligns with the core principles of our stable blind gait algorithm. Critically, stair climbing in a vision-free context effectively highlights the advantages of our sensor-based approach. Without relying on visual perception of the stairs, the robot must depend on proprioceptive and tactile feedback from its leg sensors to perceive and successfully negotiate the steps, thus showcasing the robustness and efficacy of our blind gait strategy. Finally, stair climbing provides a nontrivial yet manageable challenge for an initial study focused on demonstrating the feasibility and proof-of-concept of our integrated algorithm, offering a balance between task complexity and experimental tractability.

3.2.1. Theoretical Underpinnings of Quasi-Static Gait

The quasi-static gait paradigm revolves around ensuring continuous static equilibrium throughout the robot’s locomotion cycle. This approach is based on the foundational principle that at any given point during the walking process, the robot’s posture is such that it could theoretically remain indefinitely stable, even in the event of an unexpected cessation of movement. This concept is based on seminal work in the field, such as Pongas et al. [36], Hao et al. [12], and Li et al. [18], who have extensively explored the dynamics and applications of this strategy.

3.2.2. Advantages in Unstructured Terrains

The application of the quasi-static gait in navigating unstructured terrains is a direct response to the inherent unpredictability and complexity of these environments. By prioritizing static stability, robots employing this gait are better equipped to traverse uneven surfaces and negotiate obstacles that would otherwise pose a significant challenge to more dynamic but less stable locomotion strategies. This approach effectively ameliorates the risk factors associated with locomotion in such environments, primarily the threat of toppling or loss of stability, as highlighted in research by Or and Rimon [37], Ye et al. [21], and Ding et al. [38].

3.2.3. Static Stability Analysis

The assessment of static stability, predominantly through the lens of the support polygon as described by McGhee and Frank [16], is a critical aspect of this gait strategy. The central thesis here is that stability is maintained as long as the projection of the robot’s center of mass (CoM) remains within the confines of this polygon. However, as Inkol and Vallis [39] posit, exclusive reliance on this analysis is insufficient, given its disregard for dynamic factors such as body inertia and leg accelerations.

To address these limitations, researchers have proposed and implemented various methodologies. Focchi et al. [40] discuss the active control of the robot’s CoM, which involves strategic premovement shifts to counteract the destabilizing effects of inertia. Similarly, the work of Kajita et al. [41] on precise leg swing trajectory planning ensures that foot placements are meticulously calculated to maintain the CoM within the desired support polygon. These strategies collectively enhance the stability and reliability of the quasi-static gait, allowing for more robust navigation across diverse terrains.

Figure 3 illustrates the stability condition, showing how the robot maintains equilibrium by carefully aligning its CoM within the confines of the support polygon.

3.2.4. Swing Leg Trajectory

A carefully selected parabolic function determines the swinging leg trajectory, characterized by a set of parameters as presented in

Table 1. Swing leg trajectory parameters.

Parameter	Explanation
$dx$	The displacement in the x-direction in the world frame
$dy$	The displacement in the y-direction in the world frame
h	The height of the leg movement

.

During the robot’s swing phase, its leg motion is optimized through a parabolic trajectory that ensures smooth and controlled movement while minimizing jerk and acceleration, enhancing efficiency. This process involves several calculated steps: Initially, the robot determines its Center of Polygon (CoP), which represents the ideal position for its center of mass (CoM) and is crucial for maintaining balance during the leg swing. Subsequently, the CoM is adjusted to align with the CoP, optimizing stability throughout the swing. The parabolic trajectory is then discretized into distinct points for precise control over the leg’s motion. Inverse kinematics calculations are performed for each point to determine the necessary joint angles for the desired leg position. The robot iteratively progresses through these calculated points, ensuring its accurate and smooth motion. Figure 4 visually represents the leg trajectory, highlighting these steps.

To facilitate optimal movement, the robot requires precise control of its legs, achieved through the seamless integration of a parabolic trajectory, inverse kinematics, and force sensors. The parabolic trajectory guarantees fluid leg swings and inverse kinematics precisely aligns the joints. Crucial for obstacle detection, the force sensor at the leg’s end detects contact with objects or terrain. Upon sensing a force exceeding a threshold, it instructs the robot’s controller to halt the leg swing immediately. This combination of technologies ensures precision and control, boosting the robot’s reactivity to obstacles and aiding in collision avoidance and stable locomotion. The stable step algorithm is summarized in Algorithm 1. The symbols and parameters used in Algorithm 1 are defined in

Table 2. Symbols and parameters for Algorithm 1.

Symbol	Definition
$leg\_id$	Identifier of the leg to be moved (1–4)
$dx$	Desired displacement in the x-direction (world frame)
$dy$	Desired displacement in the y-direction (world frame)
h	Height of the leg movement during the swing phase
$CoP$	Center of Polygon, the ideal CoM position for stability
$CoM$	Center of mass of the robot
$F_z$	Vertical force sensor reading at the leg tip
$ϵ$	Force threshold for ground contact detection
$\theta$	Vector of joint angles calculated by inverse kinematics
$J_i$	Joint angle for joint i (after IK calculation)

.

Algorithm 1 Stable Step Algorithm
Require:
1: $leg\_id$   2: $\Delta x,\Delta y$   3: h   4: $ϵ$	▹ Target leg identifier ▹ Position adjustment ▹ Target foot height ▹ Ground force threshold
Ensure:   5: Stable leg placement while maintaining dynamic balance   6: Compute Center of Pressure (CoP) from support polygon   7: Adjust center of mass (CoM) to align with CoP: $CoM\leftarrow CoP$   8: while $F_z\le ϵ$ do       ▹ Ensure ground force stability   9:     Compute inverse kinematics: $\theta \leftarrow IK(leg\_trajectory)$   10:     Apply joint positions: $J\leftarrow \theta$   11: end while   12: if $F_z>ϵ$  then   13:     Confirm stable ground contact   14:     return Success   15: else   16:     return Failure (Unstable contact detected)   17: end if

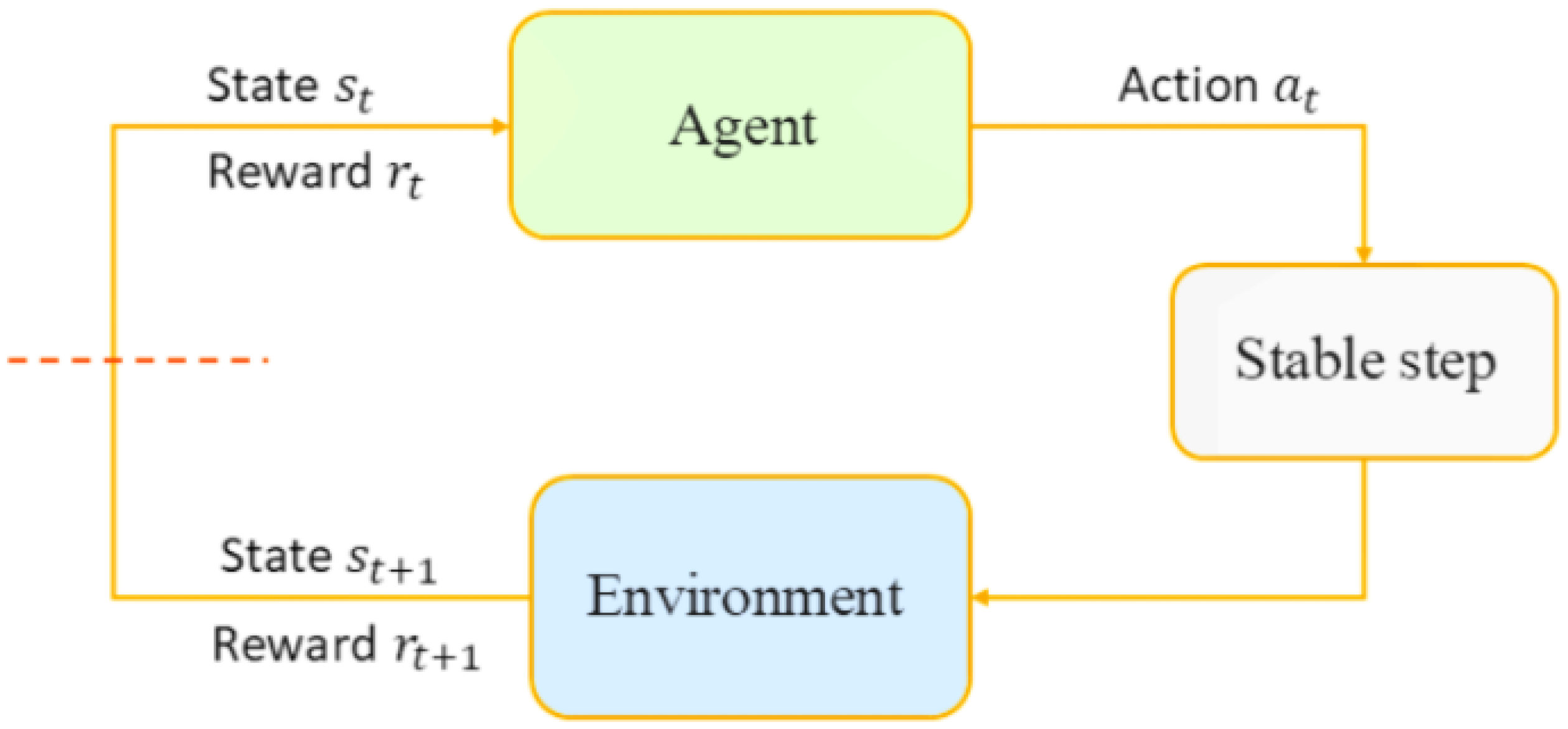
3.3. Reinforcement Learning and Stable Blind Gait Combined Algorithm

In this study, we implemented a novel approach to enable quadruped robots to navigate stairs, a challenge due to the complexity of the terrain and the need to maintain balance. Our methodology integrates advanced deep reinforcement learning (DRL) algorithms, specifically a Soft Actor–Critic (SAC) algorithm [31], with the stable step algorithm to enhance the robot’s navigation skills. We also incorporate a model-based approach that utilizes the robot’s kinematics to further optimize the walking algorithm.

3.3.1. Integration of SAC and Stable Step

The SAC algorithm, known for its sophisticated policy optimization, plays a key role in our approach. The algorithm fine-tunes decision-making policies by balancing reward maximization and strategic exploration. This is crucial for adapting the robot’s behavior to the intricacies of stair navigation. We utilized the SAC algorithm to enable the robot to process environmental feedback and adapt in real time to its movement strategies.

In addition, we incorporated the stable step algorithm, ensuring that the robot maintains stability and balance while traversing stairs. It gives the robot a solid understanding of gait mechanics, which is crucial for traversing stairs and other irregular surfaces. We integrated the stable step to establish the initial movement parameters, which the SAC algorithm subsequently refines.

This combination of advanced algorithms allows the robot to navigate stairs with high speed and stability, even in the presence of obstacles or without visual input. To evaluate the effectiveness of our novel walking algorithm, we performed experiments on a quadruped robot in a simulated environment.

Integrating a stable blind gait with deep reinforcement learning enhances the capabilities of quadruped robots, demonstrating significant improvements in navigating complex terrains without visual input. Visual data can become unreliable in many real-world scenarios due to darkness, dust, or occlusion, making vision-based perception insufficient. Consequently, our approach focuses on force and joint sensing (ie, proprioceptive feedback), aiming to ensure stable locomotion even in visually degraded environments.

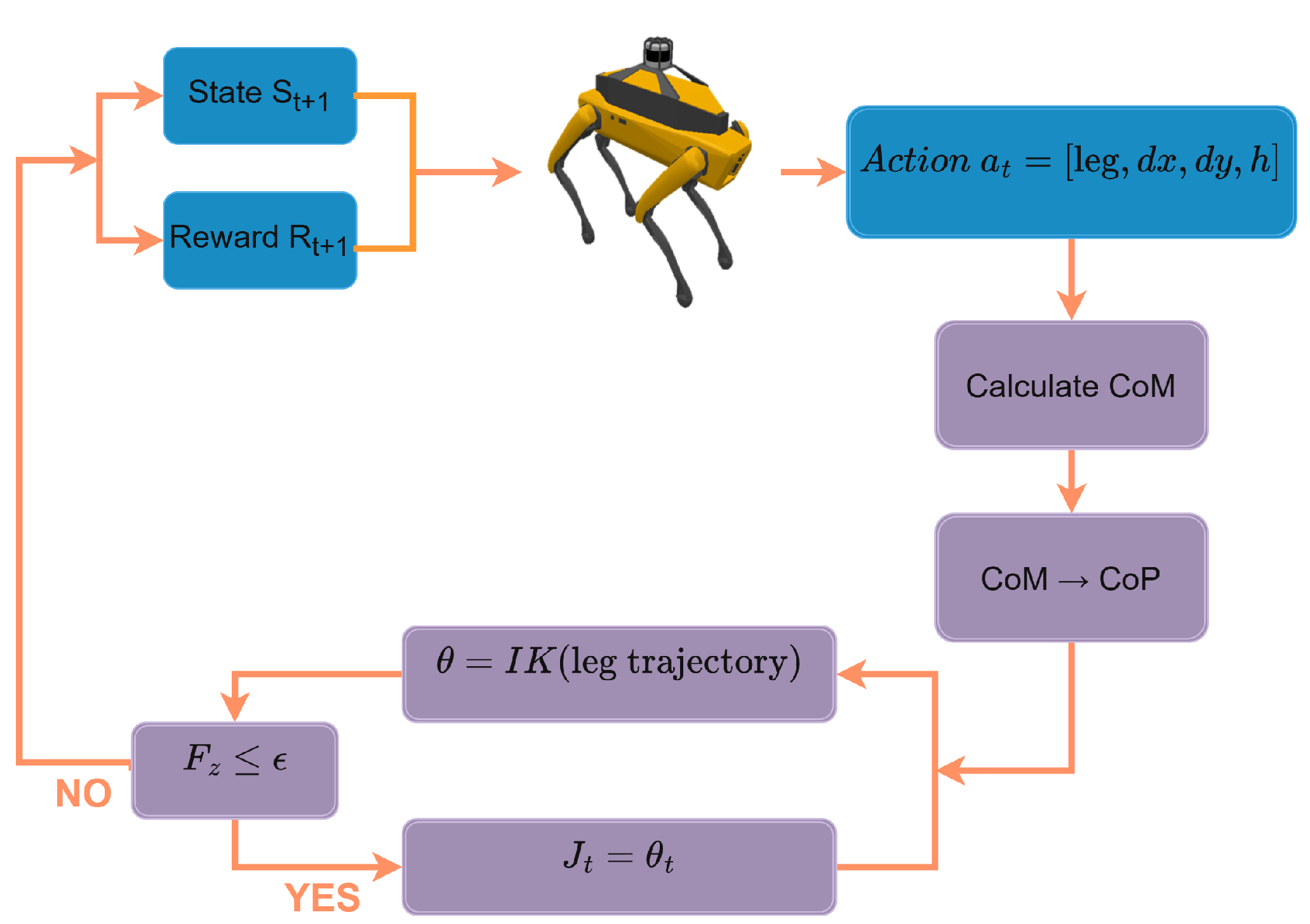
3.3.2. Algorithm Structure

Figure 5 illustrates the detailed structure of the combined algorithm. This diagram shows how the reinforcement learning components (in blue) interact with the stable step methodology (in gray).

3.3.3. Algorithm Pseudocode

The pseudocode for our reinforced learning and stable step combined Algorithm is presented in Algorithm 2. The symbols and parameters used in Algorithm 2 are defined in

Table 3. Symbols and parameters for Algorithm 2.

Symbol	Definition
$episode$	One complete training iteration
s	Current state observed by the agent
a	Action selected by the agent’s policy
$\pi (·|s)$	Policy function, probability of actions given state s
r	Reward received after taking action a
$s^{\prime }$	Next state observed after taking action a
$leg\_id,dx,dy,h$	Components of action a, parameters for stable step (Algorithm 1)

.

Algorithm 2 Reinforcement Learning with Stable Step

1: for each training episode do 2:     Initialize simulation environment 3:     Get initial state s 4:     while robot has not fallen AND target not reached do 5:         Sample $action=[leg\_identifier,\mathrm{\Delta }x,\mathrm{\Delta }y,height]\sim \pi (·|s)$ 6:         Execute stable step sequence: 7:         Compute Center of Polygon (CoP) 8:         Align center of mass: $Co{M}_{new}\leftarrow CoP$ 9:         while ground reaction force $F_z\le ϵ$ do 10:            Calculate joint angles: $\theta =IK(leg\_trajectory)$ 11:            Update joint positions: $J_i={\theta }_i$ 12:         end while 13:         Observe resulting state $s^{\prime }$ 14:         Calculate reward r for transition 15:         Update policy $\pi$ using experience tuple $(s,action,r,s^{\prime })$ 16:         Update current state: $s\leftarrow s^{\prime }$ 17:     end while 18: end for

This algorithm demonstrates how the SAC algorithm and stable step components work together. The SAC algorithm determines the action to take, which includes selecting which leg to move and the parameters for the movement. The stable step algorithm executes this action while ensuring the robot maintains stability throughout the movement.

3.4. Implementation

Simulator Environment and API Connection

This research harnesses the capabilities of CoppeliaSim (Edu version, v4.3.0), integrated with the Bullet 2.83 physics engine, renowned for its precision in simulating dynamic physical interactions. CoppeliaSim’s adoption of the Lua scripting language facilitates efficient and flexible programming within the simulation framework, enhancing the simulation’s adaptability to various experimental requirements.

Central to this study is the integration of CoppeliaSim with the ZeroMQ remote API (using pyzmq v22.3.0), which significantly improves how external applications interact with the simulation environment. This integration enables real-time control and data exchange between the walking algorithm, computed in external applications, and the simulated robot in CoppeliaSim, providing a realistic and dynamic environment for algorithm development and evaluation. The remote API offers two operational modes: stepped interaction for detailed control and a non-stepped mode replicating natural simulator dynamics. This flexibility is important to accommodate various experimental scenarios and research needs. The API also enables remote simulator management, allowing users to load scenes and control simulation states (start, pause, and stop) from a distance, adding convenience and efficiency to the research process.

In this research, the ZeroMQ remote API is utilized adroitly to orchestrate the simulation through an external Python script (using Python v3.9 and libraries including NumPy v1.22.0). This approach is strategically chosen to take advantage of the capabilities of the Stable Baselines3 deep learning library [42] (v1.7.0) in conjunction with a custom designed environment in OpenAI Gym (v0.21.0), a platform at the forefront of reinforcement learning research. The integration of the Python script with CoppeliaSim is a critical component of the study, enabling the seamless fusion of advanced machine learning methodologies with CoppeliaSim’s high-fidelity simulation capabilities. This intricate integration is further elucidated in the connection setup diagram, which provides a clear visual representation of this comprehensive and streamlined system architecture, as shown in Figure 6.

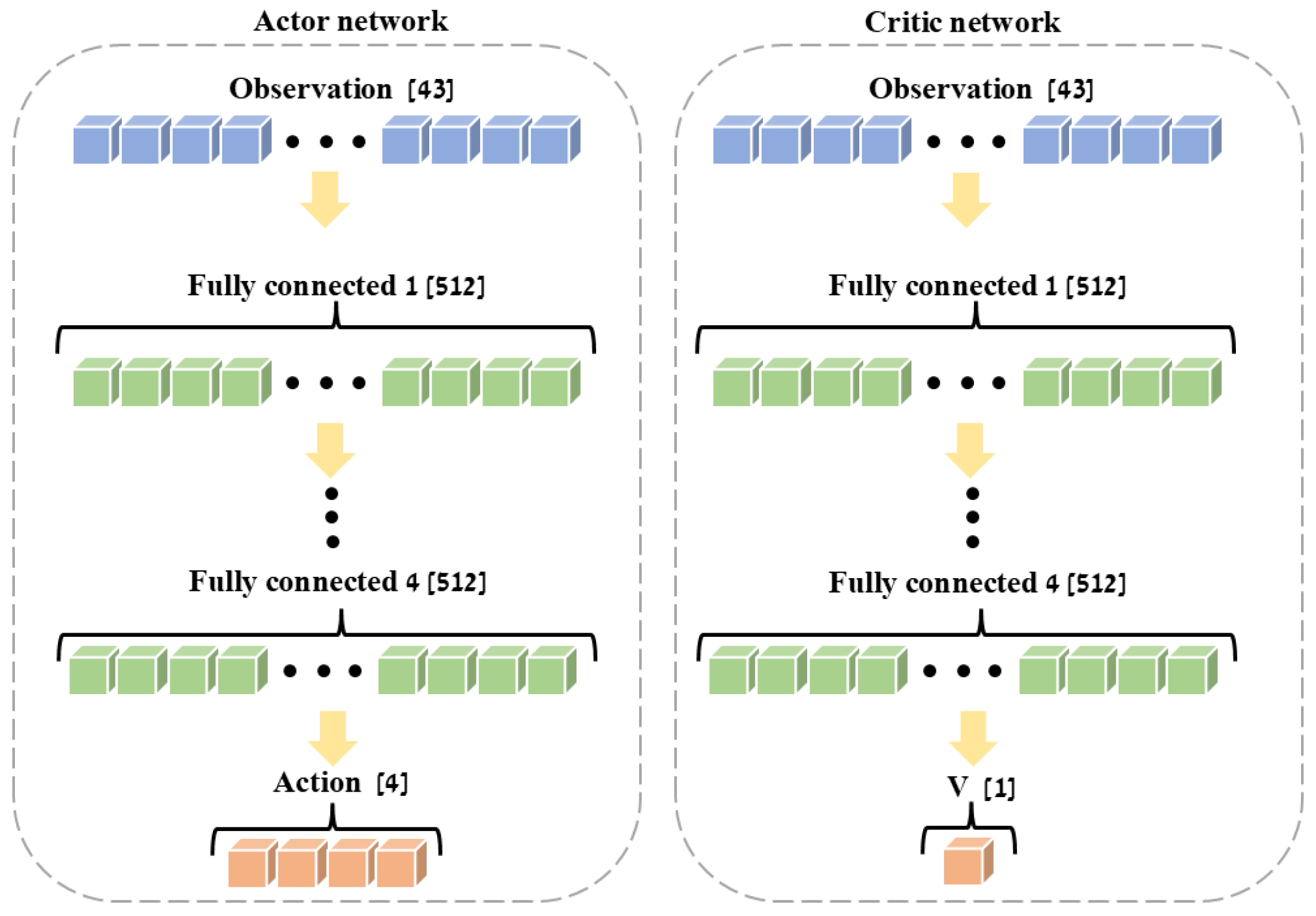
3.5. Network Architecture and Hyperparameters

The proposed walking algorithm for quadruped robots utilizes a policy network and a critic network, consisting of four fully connected hidden layers with 512 neurons each, using the ReLU activation function. The architecture of the policy network, $\pi \left(s_t\right|\theta )$, is structured to produce a four-dimensional vector essential for determining stochastic action. In contrast, the critic network, designed to output a singular scalar value $V\left(s_t\right)$, functions as a value function assessing the expected return from the state $s_t$.

The choice of hyperparameters significantly influences the efficiency of the learning algorithm. The hyperparameters, such as learning rate, discount factor, and batch size, are carefully tuned to ensure optimal performance and convergence of the algorithm. Figure 7 illustrates the policy network architecture.

3.6. Observation and Action Space

The observation space contains the world coordinate system’s goal, CoM, and leg tip positions. It also includes the forces measured by the robot’s sensors at each leg’s tip. The force data were normalized using a maximum normalization method, rescaling the data so that the highest absolute value becomes 1 while maintaining the relative proportions of other values.

The action space contains a leg ID, which determines which leg the agent will move and the parameters of the stable step leg trajectory:

$$a_t=[\mathrm{leg}\_\mathrm{id},dx,dy,h]$$

(1)

where $dx\in [0.05,0.2]$ m, $dy\in [-0.05,0.05]$ m, and $h\in [0.05,0.2]$ m. The leg ID is an integer between 1 and 4.

3.7. Reward Shaping

In the context of reaching a target position, particularly an after-obstacle position, the reward shaping includes positive rewards for progressing towards the target and penalties for undesirable behaviors like falling or deviating from the target path.

The robot receives a negative reward for falling:

$$r_{\mathrm{fall}}=-0.3$$

(2)

A negative reward is given if the difference in the y-position of the robot and the target is greater than 0.25 m:

$$\mathrm{If}|y_{\mathrm{pos}}-y_{\mathrm{target}}|>0.25\mathrm{m},\mathrm{then}{r}_y=-0.3$$

(3)

An exponentially growing reward encourages the robot to move forward:

$$r_x=10·e^{5\left({\displaystyle \frac{x}{1.5}}-1\right)}$$

(4)

To prevent the robot from standing still, a negative reward is assigned if the robot does not move forward by at least 1.5 cm:

$$r_{\mathrm{nm}}=-0.1$$

(5)

A stair-climbing reward is given when all four legs have passed the stair:

$$r_{\mathrm{stair}}={\displaystyle \frac{200}{\mathrm{steps}}}$$

(6)

This encourages the robot to climb the stair using a minimal number of steps.

3.8. Simulation Setup and Parameters

To rigorously evaluate the performance of our proposed algorithm, we conducted extensive virtual experiments using the CoppeliaSim simulation environment. CoppeliaSim, coupled with the Bullet 2.83 physics engine, provides a high-fidelity platform to simulate robot dynamics and environmental interactions. We utilized CoppeliaSim’s ZeroMQ remote API to interface our Python-based reinforcement learning algorithm with the simulated quadruped robot.

The reinforcement learning agent was specifically trained to climb stairs on a staircase obstacle with a consistent height of 10 cm. For the generalization evaluation, we tested the trained model’s performance on three distinct stair configurations, each with a different step height: 7 cm, 10 cm (identical to the training stair), and 13 cm. For each height of the stairs, we conducted 100 evaluation episodes to assess the success rate of stair climbing.

During the simulations, we measured and recorded the following key performance parameters to quantitatively validate the algorithm’s effectiveness:

• Stair Climbing Success Rate: The percentage of simulation episodes in which the robot successfully ascended the stair obstacle and reached the target position without falling. Reported as a percentage (%) for each stair height (7 cm, 10 cm, 13 cm) in

  Table 4. Stair climbing success rates for different stair heights.

  Stair Height [cm]	Success Rate [%]
  10	93
  7	98
  13	65

  .
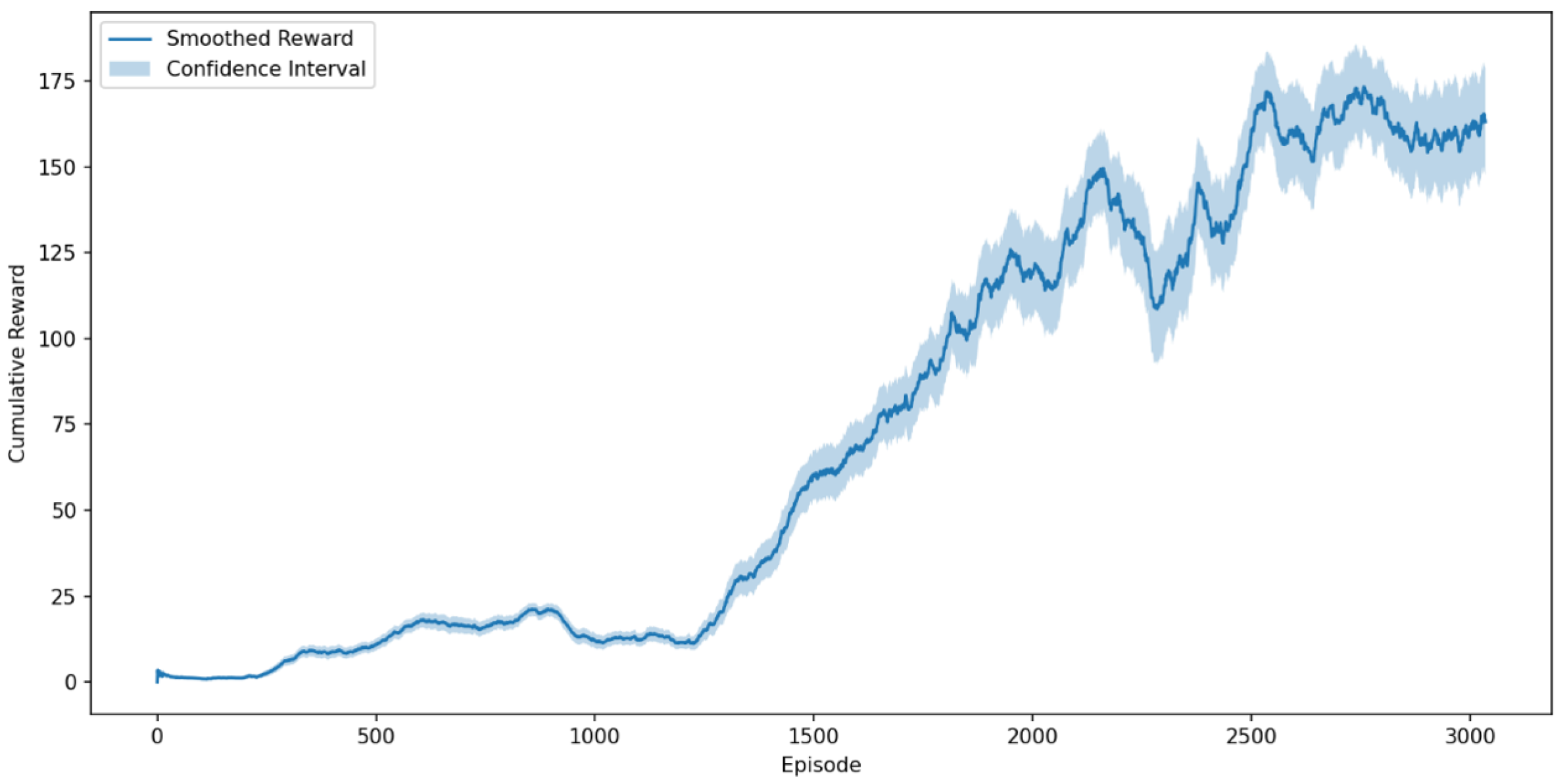
• Cumulative Reward per Episode: The total reward accumulated by the reinforcement learning agent during a single simulation episode. The rolling average of this parameter over training episodes, along with the 95% confidence interval, is presented in Figure 9.
• Steps to Climb (Successful Episodes): The average number of stable steps taken by the robot to successfully ascend the stair obstacle in episodes where the stair climb was completed without falling. This metric, while not explicitly presented as a separate figure or table, is implicitly reflected in the stair-climbing reward function (Equation (6)).

These parameters were systematically measured and analyzed to evaluate the performance, generalization capabilities, and progression of the learning of our proposed algorithm.

4. Results

A 10 cm high staircase was selected as the training obstacle in this study. The agent’s objective was to reach a designated target atop a stair. For comparison, the robot’s behavior using a stable gait with fixed parameters is shown in the Supplementary Materials (Video S2). As elaborated in the section on reward shaping, the agent’s goal was to navigate all four legs over the stair obstacle.

A binary system was employed to chronicle the learning trajectory. At the end of each episode, a value of 0 or 1 was recorded. A value of 1 signified the successful completion of the stair climbing task, while a 0 indicated the failure to complete the task. This binary tracking enabled a comprehensive illustration of the learning process.

4.1. Learning Progression

The progression of the agent’s learning in numerous episodes is depicted in Figure 8. The graph shows the rolling average of the agent’s stair-passing accomplishments, with a window size of 50 episodes. Through this visual representation, one can readily observe the evolution of the agent’s proficiency in surmounting the stair obstacle over time.

Analyzing the graph, it becomes evident that as the episodes progress, the agent demonstrates an increasing frequency of successfully climbing the stairs, indicating a positive trend in its learning process. Initially, the agent struggles with the task, as reflected by the lower success rates in the early episodes. However, over time, the agent learns effective strategies to overcome the stair obstacle, resulting in a significant performance improvement.

4.2. Cumulative Reward Analysis

The cumulative reward smoothed graph, and its confidence interval are shown in Figure 9. This graph presents the rolling average of the cumulative reward per episode, with a window size of 100 episodes, along with a 95% confidence interval.

The confidence interval is computed using:

$$c=1.96·{\displaystyle \frac{\sigma }{\sqrt{n}}}$$

(7)

where $\sigma$ is the standard deviation, n is the window size, and 1.96 corresponds to a 95% confidence level.

The graph demonstrates a positive trend in the cumulative reward as the episodes progress, signifying that the agent consistently achieves higher cumulative rewards with each episode. This indicates that the agent is not only improving in task completion but also optimizing its actions to maximize the rewards based on the defined reward shaping.

4.3. Model Generalization

To examine the generalization of the model, we performed 100 prediction tests on three different obstacles: the original stairs (height = 10 cm), a shorter stair (height = 7 cm), and a higher stair (height = 13 cm). The results are presented in Table 4.

It can be seen that the robot successfully climbed the original stair 93% of the time (Video S3, Supplementary Materials). The success rate increased to 98% for the lower stair (Video S8, Supplementary Materials) but decreased to 65% for the higher stair (Video S9, Supplementary Materials). These results demonstrate the model’s ability to successfully climb obstacles similar to the training environment, with some generalization to slightly different conditions. The reduced success rate on the higher staircase indicates that while the model has learned effective strategies within a certain range, its performance diminishes when it encounters conditions significantly different from the training data. Additional simulation trials illustrating various scenarios are provided in the Supplementary Materials (Videos S7–S14).

The observed decrease in the success rate from 93% on the 10 cm stair to 65% on the 13 cm stair highlights the model’s sensitivity to variations in stair height and the limitations of its generalization capabilities in the current training regime. This performance drop on higher stairs is probably attributable to the fact that the reinforcement learning agent was primarily trained on 10 cm stairs. The training data were thus concentrated around this specific stair height, and the model’s learned policy became optimized for this particular scenario. Consequently, when presented with significantly higher stairs (13 cm), representing conditions outside the primary training distribution, the model’s performance understandably diminished due to insufficient experience with such challenging step dimensions. The increase in the success rate to 98% on the lower 7 cm stair further supports this interpretation. The improved performance on the shorter stair suggests that the model does generalize effectively to *easier* instances of the stair-climbing task, where the step height is reduced but still within reasonable proximity to the training height. This indicates that the learned policy is somewhat adaptable within a limited range around the training parameter space but exhibits performance degradation when extrapolated to conditions significantly outside of that range.

4.4. Discussion

It is important to emphasize that the primary novelty of this research lies in the proposed algorithmic framework: the synergistic integration of a stable blind gait with deep reinforcement learning. Although stable gait control and reinforcement learning have been individually explored in legged robotics, our work introduces and validates a novel integrated architecture that combines these techniques to achieve robust, vision-free locomotion in unstructured environments. The inherent stability provided by the blind gait foundation is complemented by the adaptive and optimization capabilities of the SAC-based deep reinforcement learning agent, resulting in a system that is stable and capable of learning effective strategies to navigate challenging terrains such as stairs. This integrated approach, rather than individual components in isolation, represents the core contribution of this study.

Although a direct quantitative comparison with a wide range of stair climbing methods is beyond the scope of this initial study, we can qualitatively assess the potential advantages and disadvantages of our integrated approach with more traditional legged robot control techniques. Compared to purely model-based control methods, our DRL component offers enhanced adaptability to uncertainties and complexities inherent in unstructured terrains, as the robot learns directly from interaction rather than relying solely on pre-defined models. This adaptability is particularly beneficial in vision-degraded environments where accurate environmental models may be difficult to obtain. Furthermore, the stable gait foundation provides inherent robustness and balance, potentially surpassing the stability margins of purely learning-based approaches that require extensive training to achieve comparable levels of robustness. However, relying on reinforcement learning, our method likely incurs a higher computational cost during training than simpler, purely analytical methods. Training time and data requirements are also inherent considerations for DRL-based approaches. Future quantitative benchmarking will be crucial to evaluate these qualitative assessments rigorously and precisely characterize the trade-offs between our integrated approach and other stair-climbing techniques.

A key aspect of our approach is the integration of deep reinforcement learning (DRL) with the stable blind gait algorithm. While generalization remains challenging in DRL models, we argue that DRL provides essential benefits within our framework, even when environmental conditions deviate from the training data. One of the primary advantages of DRL is its ability to dynamically optimize and fine-tune the gait parameters for stair climbing. The stable blind gait ensures baseline stability but operates based on pre-defined leg movement parameters. In contrast, the DRL agent learns through interaction to adjust these parameters—specifically, the displacement parameters ($\mathrm{\Delta }x$ and $\mathrm{\Delta }y$) and leg lift height (h) in the stable step algorithm—to maximize stability and efficiency on stairs. This learned optimization surpasses the capabilities of a fixed-parameter gait, enabling a more adaptive and task-specific control policy. In addition, based on sensor feedback, DRL improves the robot’s real-time ability to adapt its gait. An example of the robot recovering from a momentarily stuck leg is shown in the Supplementary Materials (Video S4). The agent refines its movements by continuously adjusting its actions in response to force sensor readings, accounting for subtle variations in terrain and robot dynamics. This sensor-driven adaptability significantly improves stair-climbing performance compared to a purely analytical stable blind gait approach, demonstrating the value of integrating DRL for dynamic-legged locomotion.

Integrating a stable blind gait with deep reinforcement learning enhances the capabilities of quadruped robots, demonstrating significant improvements in navigating complex terrains without visual inputs. Our results show a high success rate of 93% in negotiating stair obstacles, underscoring the effectiveness of our approach in enhancing stability and adaptability.

Consistent with the findings of Lee et al. [3], who highlighted the robustness of reinforcement learning in diverse environments, our work further exemplifies the benefits of combining model-based stability with the adaptive capabilities of deep learning. This synergy not only facilitates navigation over challenging terrain but also ensures static stability through the use of a stable blind gait.

Despite these achievements, the model’s reliance on training with specific obstacles presents a limitation, potentially hindering its ability to generalize to unfamiliar terrains. Addressing this challenge will be crucial for future studies to improve adaptability and transferability. Furthermore, the current stable blind gait, while ensuring stability, sacrifices the speed and fluidity seen in natural animal locomotion. Future work should explore the incorporation of dynamic gaits with reinforcement learning to achieve more efficient and natural movement patterns.

Our findings support the initial hypothesis that integrating a stable blind gait with reinforcement learning would improve the robot’s mobility and adaptability in unstructured environments. This has profound implications for deploying robots in scenarios where visual sensors are non-viable, such as in hazardous or inaccessible areas.

In a broader context, our approach expands the potential applications of legged robots, making them more suitable for tasks like search and rescue, environmental monitoring, and exploration in challenging conditions. This research contributes to developing autonomous robotic systems capable of overcoming unforeseen challenges in dynamic and varied environments.

4.4.1. Limitations

A primary limitation of the current study is the model’s specialization to the specific training environment. Having been trained solely on stair climbing with a consistent 10 cm step height, the deep reinforcement learning policy is likely optimized for scenarios resembling this condition. Consequently, we anticipate that the robot’s performance may be optimal for stairs with heights near 10 cm but could degrade when encountering stairs of significantly different dimensions or entirely novel terrain types. The current model lacks extensive generalization capabilities due to the focused nature of the training data.

4.4.2. Future Work

Future research should focus on improving the generalizability of the algorithm for effective locomotion across various terrains. One promising direction is the implementation of incremental learning methods. By sequentially training the robot on a broader range of stair heights and, subsequently, on other types of unstructured terrain, we can aim to develop a more versatile and adaptable control policy. Incremental learning techniques can also mitigate catastrophic forgetting, ensuring that the robot retains previously learned skills as it learns new ones. Furthermore, incorporating additional sensory modalities, such as tactile sensors on the robot’s feet, could provide richer and more direct feedback about the terrain surface and contact conditions. Tactile information could enable the robot to better perceive and adapt to roughness, compliance, and slope variations, improving stability and maneuverability in truly unstructured environments.

Future research should focus on several key strategies to mitigate the observed performance degradation on higher stairs and enhance the algorithm’s robustness to varying stair dimensions. Firstly, expanding the training dataset to include a wider range of stair heights is crucial. Training the reinforcement learning agent on stairs with heights varying significantly around the current 10 cm training height, for example, from 5 cm to 15 cm or even 20 cm, would expose the model to a more diverse set of step dimensions and likely lead to a more generalized and robust policy. Secondly, exploring different training curricula could be beneficial. Instead of starting training directly on 10 cm stairs, future work could investigate a curriculum that begins training on more challenging, higher stairs (e.g., 15 cm or 20 cm). Training in more difficult scenarios from the outset can force the agent to learn more fundamental and adaptable locomotion strategies that are inherently applicable to simpler scenarios (lower stairs). This “hard-first” training approach could lead to more robust and generalizable policies than starting with easier tasks. A stair height estimation mechanism could significantly improve the robot’s adaptability. By equipping the robot with sensors, such as tactile sensors on its legs or depth sensors, to estimate the height of the upcoming stair before initiating the climbing motion, the robot could dynamically adjust its gait parameters and control policy based on the perceived step height. This proactive adaptation would likely enhance performance across a wider range of stairs and improve the algorithm’s overall versatility in unstructured environments.

Future work should also include more rigorous quantitative evaluations to validate our integrated approach’s advantages further. Ablation studies, for example, could assess the individual contributions of the stable gait and the SAC algorithm by comparing the performance of the fully integrated system to configurations using only the stable gait control or employing simpler reinforcement learning algorithms in conjunction with the stable gait. Furthermore, comparative benchmarking against state-of-the-art legged robot locomotion methods, including model-based and learning-based approaches, would provide valuable insights into our proposed algorithm’s performance characteristics and potential advantages relative to existing techniques.

Expanding this methodology by incorporating training and experimentation with a broader range of obstacles is recommended for future work. This iterative process will help develop a repository of specialized expert agents, each tailored to navigate specific terrains. By strategically combining these agents based on the unique characteristics of the terrain, a comprehensive and successful rescue mission can be executed.

Future research could explore applying this combined approach with a dynamic gait instead of a stable one, aiming to achieve faster and more natural locomotion. Integrating reinforcement learning with gait generation algorithms can optimize agility, balance control, and energy efficiency, enhancing overall movement capabilities. Additionally, expanding the training scope to encompass diverse terrains will improve the model’s generalization, enabling adaptation to various environments. The integration of dynamic gaits with reinforcement learning has the potential to enhance both speed and adaptability, leading to more fluid and efficient robotic motion. Further improvements in environmental awareness through additional sensory inputs will strengthen the robot’s ability to interact with complex surroundings, paving the way for more sophisticated and versatile robotic applications.

Furthermore, future research will investigate the generalizability of our proposed method to a broader spectrum of tasks and unstructured terrains beyond stairs. While this study focused on stair ascent as a demonstrative challenge, the underlying principles of the integrated stable blind gait and deep reinforcement learning approach suggest the potential for broader applicability. Future work will explore extending the algorithm’s performance to navigate more diverse environments, such as steep inclines, uneven terrain with discrete obstacles, and more complex, continuously varying landscapes like rocky or mountainous terrains. The inherent robustness of the stable blind gait and the adaptive capacity of the deep reinforcement learning agent provide a foundation for generalization. The stable blind gait offers a base level of stability and terrain adaptability that is not specific to stair geometries, and the DRL agent’s ability to learn optimized gait parameters based on sensor feedback and environmental interaction could be leveraged to adapt to different terrain characteristics through further training in more diverse simulated environments. Future research may incorporate additional sensory inputs, such as inclinometers to provide slope information or more sophisticated tactile sensor arrays to capture richer terrain surface properties to enhance generalization. These enhancements could improve the robot’s ability to perceive and adapt to the complexities of truly diverse and challenging environments, including steep mountain slopes and similar demanding terrains. Although this study emphasizes a blind gait approach, direct comparisons with hybrid or purely vision-based methods would be valuable to fully understand the trade-offs in performance and robustness. For instance, combining limited visual input (when available) with force/joint sensing may further enhance obstacle negotiation. We leave this as an avenue for future investigation.

Furthermore, future research should focus on broadening the training scope to include diverse terrains and enhancing the generalization capabilities of the model. Integrating dynamic gaits with reinforcement learning could lead to faster and more natural robot movements. Incorporating additional sensory input and improving environmental awareness will further enhance the robot’s ability to interact with its surroundings, paving the way for more sophisticated and versatile robotic applications. Although this study emphasizes a blind gait approach, direct comparisons with hybrid or purely vision-based methods would be valuable to fully understand the trade-offs in performance and robustness. For example, combining limited visual input (when available) with force/joint sensing may further enhance obstacle negotiation. We leave this as an avenue for future investigation.

5. Conclusions

This paper presents a novel motion planning algorithm that combines analytical and learning approaches. The first component involves implementing a stable blind gait, which includes various aspects such as kinematics, inverse kinematics, CoM control, support polygon analyses, and swing leg movement. The second component focuses on constructing and training a reinforcement learning agent specifically designed for stair climbing, utilizing the stable blind gait algorithm. The combined algorithm achieved a remarkable success rate of 93% in overcoming the stair obstacle. This research demonstrates the promising potential of integrating model-based and learning-based algorithms to create a robust and adaptive walking algorithm.