Abstract
This paper presents a controller for a direct current (DC) grid-connected single-stage solar photovoltaic (PV) converter. The proposed controller provides both static and dynamic voltage support to the grid voltage. Unlike the common practice, it allows a small and controlled offset in the PV voltage in proportion to the power flowing through the converter, which enhances the system’s stability margins. A novel feedback branch from the grid voltage is introduced to enable grid voltage support. Additionally, the controller includes a current-limiting feature to protect the converter switches from overcurrent transients. The proposed approach combines and designs the voltage and current controllers using an optimal full-state feedback approach. This results in a systematic design with optimal and robust properties. Detailed simulations, comparisons, and experimental results are presented in this paper to verify the effectiveness of the proposed approach. Particularly, the experimental findings demonstrate improved stability during local load disturbances and grid fluctuations, with lower voltage drops, reduced grid current variations, lower stress on the grid, and reduced losses in the grid network compared to conventional controllers.
1. Introduction
Recently, due to the increasing adoption of distributed energy resources (DERs) including battery energy storage (BES) systems, renewable energy sources (RESs) especially the solar photovoltaic (PV) systems, and DC loads (e.g., light-emitting diode (LED) lighting, computation devices, electric vehicles, and DC motor drive systems), DC microgrids (DC-MGs) are gaining increasing attention [1]. DC-MGs have advantages such as higher transmission efficiency, lower costs, no need for reactive power control, and for frequency or phase synchronization [2,3].
DC/DC (or DC) converters are used as interface devices in DC grids [4,5]. For a DC grid with many converter-based DERs, it is crucial for each converter to provide “support” to its terminal voltage, enabling the DC grid to operate in a robust and stable manner, similar to the existing alternating current (AC) power grid. In the AC power grid, the high penetration of power-electronic-based DER and RES units has raised critical concerns about the reduced kinetic inertia of the grid [6]. In synchronous generators (SGs), the kinetic energy of the rotor naturally responds to the disturbances. Additionally, the governor system implements a droop function that adjusts power based on frequency deviations. These two support components are referred to as “dynamic” (or inertia) and “static” (or droop) supports.
To address this issue in AC systems and improve power system stability with a large number of inverter-based resources (IBRs), an effective method is to adopt virtual inertia strategies. The virtual synchronous machine (VSM) concept has been proposed in various forms to emulate the behaviors of SGs [7,8,9]. A similar concept was proposed in [10,11] for DC and hybrid DC/AC systems. In [12], a virtual inertia approach is introduced that adjusts the droop gain based on the state-of-charge (SOC) of the BES. In [13,14,15], a capacitor emulation approach is presented, which provides dynamic support during system disturbances. A controller with a virtual capacitor and a virtual inductor is introduced in [16] to provide virtual inertia and improve the dynamic characteristics of DC-MGs. The control systems in [12,13,14,15,16] use nested proportional-integral (PI) voltage and current controllers, whose performance can degrade due to interactions between the loops, especially in weak grid conditions [17].
To generate an inertia response for BES systems, a capacitor emulation method is introduced in [18], where the integrating function is removed from the outer voltage control (VC) loop. This method is more flexible and systematic than the previous research studies because it merges the VC and current control (CC) loops, with all controller gains designed together using optimal control. In [19], a droop control is used to adjust the output current reference of a BES and provide an inertia response to the grid voltage. A distributed virtual inertia control is introduced in [20], which uses the derivative of the square of the DC-bus voltage to calculate the inertia power. Dividing this power by the bus voltage yields a current reference. In [21], an adaptive droop term of the grid voltage is added to the current reference to provide dynamic support. However, the control schemes presented in [16,19,20,21] are all applied only to BES, and do not address PV voltage control. Additionally, they all use conventional PI controllers in their CC loops.
In [22], the rate of change in voltage (ROCOV) is calculated using a high-pass filter to add an inertia term to the reference of PV power. This reference is then divided by the PV voltage to find the reference for PV current. However, the effect of the size of the DC-link capacitor is not discussed. For this method to work properly, the capacitor would need to be small, which may not be feasible given other control objectives. In [23], a two-stage PV inverter is proposed, where the first-stage DC/DC converter provides static grid support. Dynamic support is provided by the DC-link capacitor, which adjusts the slope of the PV power curve in the droop function of grid frequency. In [24], a single-stage PV inverter with grid support is introduced, using grid frequency droop to adjust power in a virtual synchronous machine (VSM) mechanism. Both static and dynamic grid support are provided by the combination of the PV system and the capacitor. However, the methods in [23,24] are not directly applicable to DC grid applications.
This literature review reveals that there is still a lack of adequate control systems for PV converters that provide DC grid support. With the increasing penetration of PV sources and the proliferation of DC grids, it is essential to establish a balance between maximum power point tracking (MPPT) and grid support and stability aspects for DC grid applications. Accordingly, in this paper, an enhanced control approach is proposed to provide both static and dynamic support for DC grid-connected single-stage PV converters. First, the proposed controller leverages the approaches of [17,18] to allow a small and controlled voltage offset in the PV-side capacitor. This will immediately introduce more robustness to the control system, as shown in [17]. Next, the proposed controller uses an additional feedback branch from the grid voltage in its VC loop. This term causes the PV voltage to instantaneously mimic a fraction of the grid voltage fluctuations. It is shown in this paper that this added feedback gives the converter the ability to provide both static and dynamic grid voltage support. The combination of these elements enables the system to maintain grid stability under varying conditions.
Key contributions of this paper include the following:
- Static and Dynamic Grid Support: The controller offers both static and dynamic voltage support, improving overall grid stability in grid-connected PV systems.
- Controlled Voltage Offset: A small, controlled voltage offset in the PV-side capacitor enhances system robustness and improves stability margins, as shown in [17].
- Grid Voltage Feedback: A novel feedback loop from the grid voltage is introduced in the VC loop, allowing the PV converter to adapt instantaneously to grid voltage fluctuations and provide dynamic grid support.
- Optimal Control Design: The controller is designed using the linear quadratic tracker (LQT) method, ensuring optimal and robust control gains.
- Current-Limiting Protection: The controller integrates a current-limiting strategy to protect the converter from overcurrent transients and safeguard system components.
- Adaptability for PV Systems: While inspired by [17,18], the controller is specifically adapted for PV applications, offering direct grid support tailored to the dynamics of PV converters.
Detailed analytical, simulation, and laboratory experimental results are provided to demonstrate the effectiveness of the proposed controller.
2. Study System and Problem Statement
Figure 1 shows the power circuit (plant) of the study system. The numerical values are given in Table 1. A set of PV panels is connected to a DC grid through a power electronic converter (PEC). The PEC is a standard full-bridge voltage-source converter (VSC) with the source-side (or PV-side) capacitor (C), and the output-side (or grid-side) filter (). The grid is modeled by a voltage source () behind an impedance ( and ), which is a common way of modeling a practical grid based on Thevinin’s theorem of circuit theory. The larger values of these impedances indicate weaker grid terminals. The grid side terminal voltage, i.e., at the point of common coupling (PCC), is denoted by . The small resistor models the on-state resistance of the converter switches and the parasitic resistance of the output inductor (). The capacitor voltage and its reference value are denoted by and , respectively.
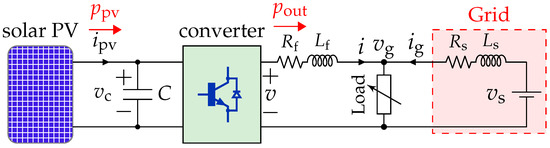
Figure 1.
Power circuit of the study system.

Table 1.
Nominal values of study system parameters.
Problem Statement: (1) Control the PV-side voltage. (2) Limit the converter output current against short-circuit transients. (3) Provide static and dynamic support to the grid voltage.
Mathematical Model: This system is modeled by power balance and voltage equations
where is the power injected to the grid assuming that the converter losses and interfacing filter instantaneous power are neglected, and is the derivative of the capacitor energy. Using the Taylor series, the relationship between the capacitor energy and its voltage can be approximated as , where capital letters indicate the rated values and lowercase variables represent the instantaneous values. These lead to the block diagram model shown in Figure 2. In this model, is the converter modulation signal. In this diagram, the PV panels are modeled as a power source , where I is the solar irradiance and T is the temperature. The function f is the power-voltage characteristics of the PV panels, which is a nonlinear function. Explicitly engaging this function in modeling and analysis complicates the process. Therefore, in this study, the PV power is treated as a disturbance to the control system. A robustly designed control system will be able to tolerate its variations, as shown in this paper.
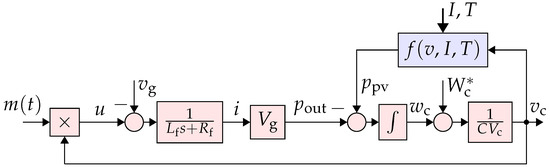
Figure 2.
Block diagram representation (model) of the study system plant (excluding the controller).
3. Proposed Controller: Structure and Design
3.1. Structure
The basic structure of proposed controller is shown in Figure 3. Its components and their differences with the conventional controller, shown in Figure 4, are described below. (1) The voltage controller is a simple gain . The constant value is equal to the rated current. The conventional approach uses a PI compensator in the VC loop. (2) The current controller comprises an additional feedback from the capacitor voltage that makes the controller a full-state feedback, allowing optimal control designs with enhanced flexibility and performance robustness. (3) The feed-forward terms and are utilized for the soft start, and also improves the current-limiting feature. (4) The linearity of the loop is increased using the input linearization term that divides u to . (5) The current-limiting is performed by a saturation block and a freeze/release mechanism [17], unlike the conventional controller, which requires an anti-windup technique. (6) The grid voltage support properties are added and explained in Section 3.2.
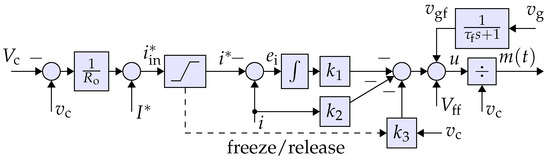
Figure 3.
Block diagram representation of the proposed controller.
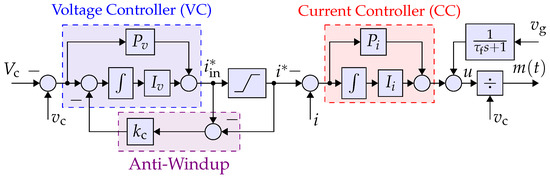
Figure 4.
Block diagram representation of the conventional controller.
3.2. Grid Voltage Support Property
As shown in Figure 5, a new branch is added for coupling the grid voltage and the capacitor reference voltage through a droop gain. This will enable the grid voltage support feature for this controller, as explained in the following.
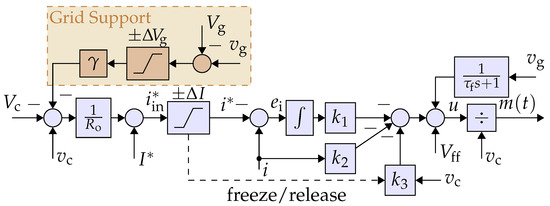
Figure 5.
Proposed modified controller with grid voltage support capability.
The proposed controller of Figure 5 establishes
assuming , which is a valid assumption because the current control loop is much faster than the voltage control loop. This indicates that the capacitor voltage changes linearly with the grid voltage. The constant determines the ratio of the grid voltage changes to the capacitor voltage changes. For example, the grid support branch with a , and a 20 V change in grid voltage, mirrors a 40 V change on the PV voltage.
Static Support: Equation (2) indicates that . This means that a unit increase (or decrease) of grid voltage causes volts of increase (or decrease) in the PV voltage. Since the characteristics are almost linear on the right side of the PV curve (as shown in Figure 6), this translates to a linear decrease (or increase) of the power, similar to the droop control approach to provide steady-state (or static) support for the grid voltage based on its offsets from the rated value.
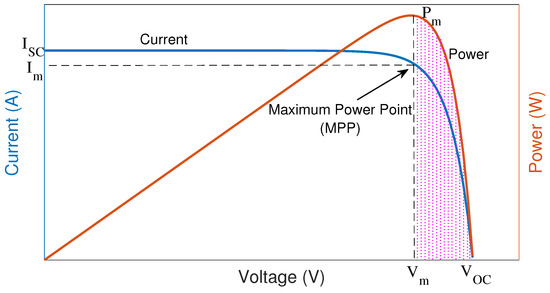
Figure 6.
Solar PV characteristics, showing the I-V and P-V curves of a typical PV panel.
Dynamic Support (or Inertia): Equation (2) also indicates that when a fast disturbance of the grid voltage occurs, . This indicates stabilizing inertia because a rapid change in grid voltage causes a similar change in the capacitor voltage, making the capacitor absorb or release energy. This dynamic response is also partially augmented by the PV power: a rise or fall in PV voltage leads to a reduction or increase in its power. Both factors act as stabilizing inertia, but the capacitor effect is the dominant one.
3.3. Capacitor Design
The capacitor size is designed based on the desired level of inertia power ,
For example, if the desired inertia power is per of grid voltage rate of change, with , and V, then is calculated for the study system in this paper.
3.4. Design of VC Loop
The parameter acts like a virtual resistance that establishes the relationship
because the CC is fast, i.e., . This serves as a guide for the design of : for the entire range of current, e.g., , and for the rated grid voltage, the voltage fluctuates between and . For % change in the capacitor voltage, i.e., ,
is obtained. For example, if we allow only 5% change in the capacitor voltage, is obtained.
Further Discussion on Selections of , γ, and : Equation (2) indicates that variations of around the set-point of are given by . Assume that (1) the converter current can change within the wide range of , and (2) the grid voltage can change within . Then, will change between where
In order to provide successful grid voltage support, should remain on the right side of the maximum power point of the PV characteristics for the entire range of system operation. This means and .
3.5. Design of CC Loop
The CC must be fast enough to quickly limit the converter current during fault incidents. In addition, its time constant cannot be shorter than a few times the switching cycle. For a switching frequency, the controller time constant is chosen within to , corresponding to CC poles within to .
The steady-state equations are derived by considering both the system plant (shown in Figure 2) and the controller (shown in Figure 3). In Figure 3, assume , , , and is the control signal. Thus, the state space equations are derived as
To regulate the converter current to its reference value, a robust linear quadratic tracker (R-LQT) presented in [25] is used. This can be converted to a linear quadratic regulator (LQR) problem by applying to both sides of (6) to obtain
where and . Note that , , , and are constant values and their derivatives become zero. We can summarize (7) in a general state-space form as
The LQR approach optimally designs the controller gains K to regulate and minimize the cost function , where is a positive semi-definite matrix. The cost function is
The parameters are systematically adjusted as follows to achieve a desired transient response. The LQR solution is achieved in MATLAB using the “lqr” command [26].
Step I: Increase gradually (while ) until the dominant poles achieve an acceptable speed.
Step II: Freeze and increase to achieve an acceptable damping of complex dominant poles.
Step III: Fine-tune the pole locations (if needed) by freezing and and gradually increasing .
Figure 7 shows the closed-loop poles for varying from to , varying from to , and varying from to . Changing and results in the desired speed and damping, and is not needed; however, it is shown for clarity. This yields the value of designed controller gains as with poles located at and . (Notice that the slow pole corresponds to capacitor voltage and is disabled during the current limiting mode.)
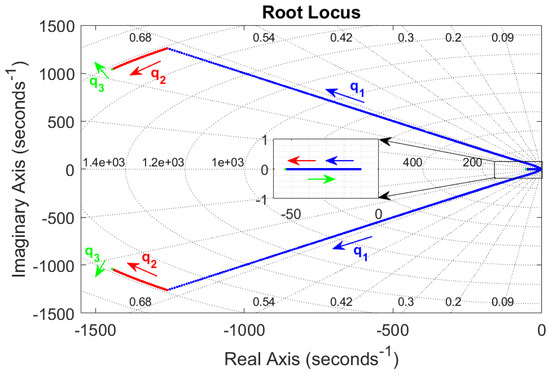
Figure 7.
Trajectory of closed-loop poles for the controller design when (blue), (red), (green) change from to , to , and to , respectively.
4. Design Rationale: Controlled Voltage Offset vs. MPPT
The proposed controller in this paper intentionally avoids the traditional MPPT approach, which strives to operate the PV system at its maximum power point (MPP) under varying conditions. Instead, it allows a small and controlled voltage offset in the PV voltage to provide both static and dynamic grid voltage support. This feature enhances system stability rather than prioritizing maximum power extraction. Specifically, the voltage offset is designed to interact with the grid voltage, enabling the system to support the grid without the tight regulation of the MPP.
In an MPPT-based system, the PV voltage is adjusted to track the MPP, ensuring that the power output is maximized at all times. The power generation under MPPT can be described as a function of the voltage at the maximum power point, i.e., . However, in the proposed control approach, the PV voltage is allowed to deviate from the MPP in a controlled manner to provide grid voltage support. The power curtailment due to this offset can be quantified as follows:
This represents the reduction in power generation to enable grid support. Despite the curtailment, the system still contributes energy to the grid, providing dynamic and static support to maintain grid stability. The curtailment, while reducing energy production, ensures that the system is more resilient to grid disturbances and improves stability margins. The level of power production and that of achieved grid support are in trade-off and must be selected according to the needs in a given system.
5. Simulation Results
The power system parameters are given in Table 1 and those of the control system in Table 2. The conventional controller is designed based on [17] to result in the same speed and damping as the proposed controller. The unipolar PWM switching method of [27] is used. The used PV characteristics at
25 °C and is shown in Figure 8, which indicates a maximum power of 5075 W at 535 V with an open-circuit voltage of 650 V. When biased at V, it generates 4 kW. It should be noted that determines the level of PV power curtailment in order to allow adequate grid support. In practice, this can be determined by a secondary controller, which may also take into consideration the irradiance level and temperature conditions. For this study system and the selected values of parameters, i.e., , V (10% of 400 V), and A, we notice that V and V, which are within the acceptable range of V.

Table 2.
Control system parameters for the study system.
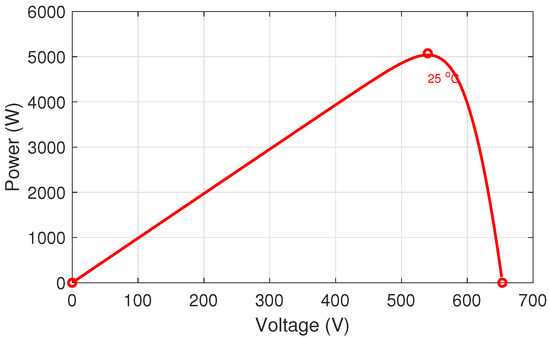
Figure 8.
P-V characteristics of the selected PV panel for the study system.
5.1. PV Power Disturbances (Scenario A)
In this study, the solar irradiance of the PV array changes to half at s, returns to rated at s, doubles at s, and returns to rated at s. Two cases of strong and weak grid connections are simulated.
(1) Strong Grid Connection (Scenario A-1): Figure 9 shows the results. The grid voltage is firm and unchanged. When the power changes, the proposed controller adaptively adjusts the PV voltage according to (4). The following conclusions are made:
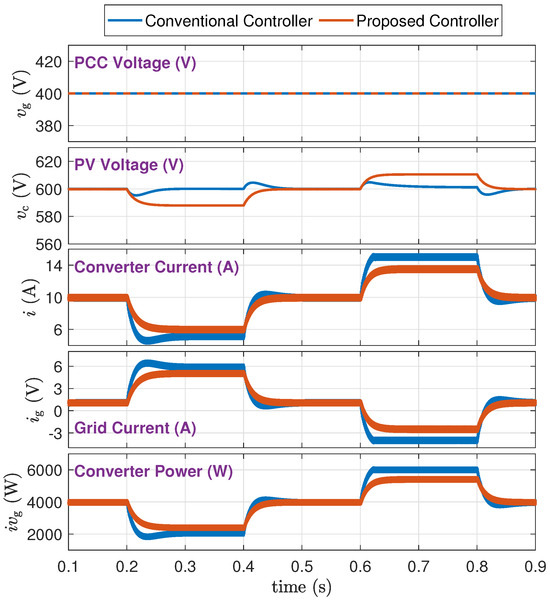
Figure 9.
PV power disturbances at strong grid situation (Scenario A-1).
- 1.
- From a trace of : the proposed method adaptively adjusts the PV voltage and power.
- 2.
- From a trace of : the proposed method reduces stress on both the converter and the grid. Specifically, lower fluctuations and steady values of indicate reduced power loss in the grid network.
(2) Weak Grid Connection (Scenario A-2): Figure 10 shows the simulation results. Here, the grid voltage also experiences fluctuation. As a result, the proposed controller also responds to those fluctuations with dynamic and static supports according to (2) and (3). The following specific conclusions are made:
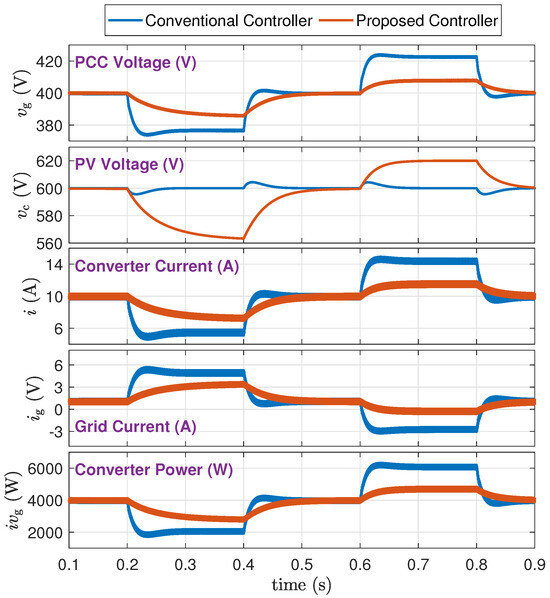
Figure 10.
PV power disturbances at weak grid situation (Scenario A-2).
- 1.
- From a trace of : The proposed method supports the grid voltage and maintains it within tighter limits. Specifically, when the PV power drops during 0.2 s to 0.4 s, the grid voltage drop is reduced from about 22 V to about 12 V. When the PV power increases from 0.6 s to 0.8 s, the grid voltage rise is reduced from about 22 V to about 7 V.
- 2.
- From a trace of : The proposed method adaptively adjusts the PV voltage and power.
- 3.
- From a trace of : The proposed method alleviates stress on both the converter and the grid. Specifically, lower fluctuations and steady values of indicate a reduction in power loss within the grid network.
5.2. Grid Voltage Disturbances (Scenario B)
Here, the proposed controller is tested under two major grid disturbances: (1) small (fast and slow) voltage changes modeled by a trapezoid function, and (2) deep voltage drop. Both strong and weak grid connections are studied.
(1) Small Disturbance, Strong Grid (Scenario B-1): Figure 11 illustrates the results when a trapezoidal disturbance of (i.e., ) is introduced to the grid voltage () behind a zero impedance, i.e., a “strong” grid condition. The proposed controller provides grid support according to (2) and (3). The following specific conclusions are made:
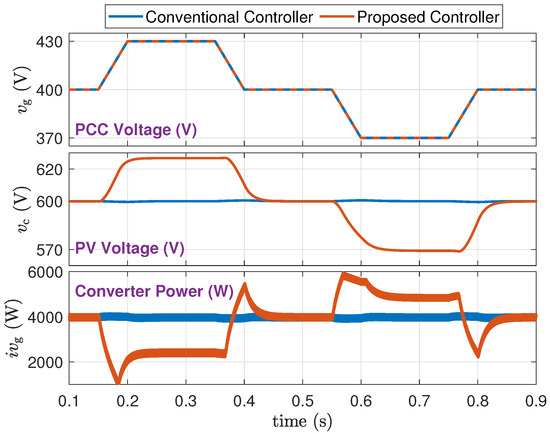
Figure 11.
Small grid disturbance, strong connection (Scenario B-1).
- 1.
- From a trace of : The proposed method adaptively adjusts the PV voltage and power.
- 2.
- From a trace of : The proposed method adaptively adjusts the power to support the grid.
- 3.
- Right before s, the converter current-limiting limits the converter current at 15 A.
(2) Small Disturbance, Weak Grid (Scenario B-2): Figure 12 is for the grid impedance and , i.e., a “weak” grid condition. The following conclusions are made:
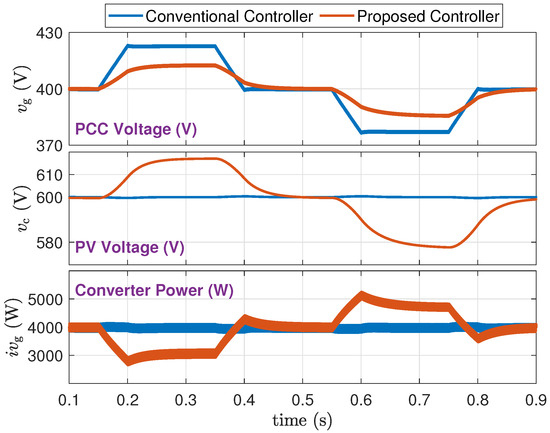
Figure 12.
Small grid disturbance, weak connection (Scenario B-2).
- 1.
- From a trace of : The proposed method supports the grid voltage and maintains it within tighter limits. Specifically, the grid voltage fluctuations have been reduced by almost 50%.
- 2.
- From a trace of : The proposed method adaptively adjusts the PV voltage and power.
- 3.
- From a trace of : The proposed method adaptively adjusts the power to support the grid.
In both Figure 11 and Figure 12, from the trace of converter power , the inertial and stabilizing behavior of the proposed controller in response to the grid voltage is clearly observed. It is also specifically observed that the converter power goes above the maximum PV power (which is 5.075 kW) around s. This transient power is released from the PV capacitor much the same way that kinetic inertia is produced in a synchronous generator. The amount of inertia power that is produced complies with the capacitor design of Section 3.3, i.e., 100 W per every 20 V/s change in the grid voltage.
(3) Large Disturbance (Scenario B-3): Figure 13 shows the current-limiting feature of the converter when a deep grid voltage drop (from 400 V to 200 V) occurs during s. Both (conventional and proposed) controllers succeed in limiting the current at the pre-specified limit of A.
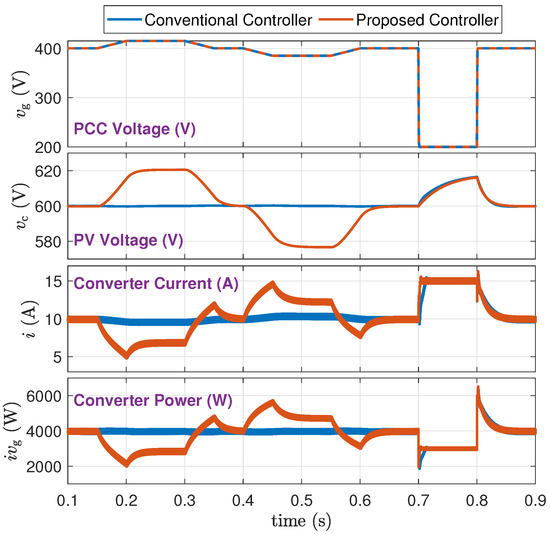
Figure 13.
Deep grid voltage drop (Scenario B-3).
5.3. Impact of (Scenario C)
The parameter in the proposed controller provides a degree of freedom to flexibly adjust the level of grid support without a need to change the PV capacitor size. This section inspects and illustrates this property. Figure 14, Figure 15 and Figure 16 (Scenarios C-1, C-2, C-3), respectively, show three cases of , 2, and 3 while other parameters remain unchanged. The following conclusions are made from this study:
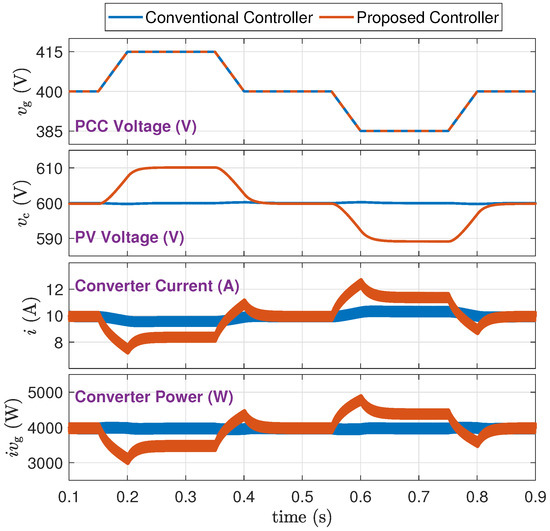
Figure 14.
Simulation results for and strong grid (Scenario C-1).
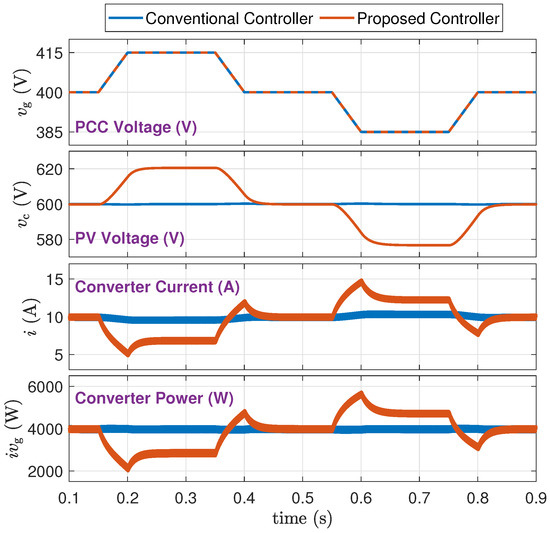
Figure 15.
Simulation results for and strong grid (Scenario C-2).
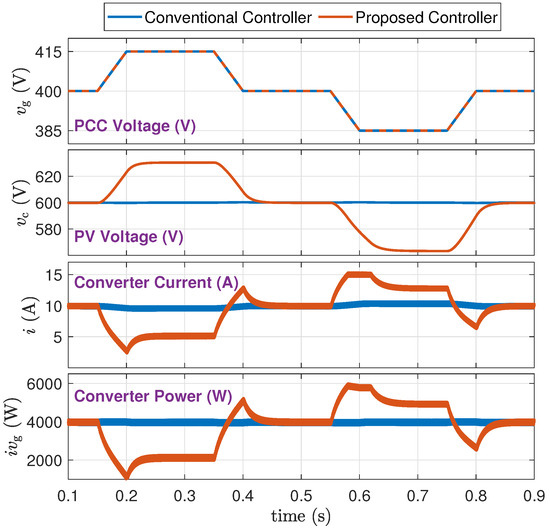
Figure 16.
Simulation results for and strong grid (Scenario C-3).
- 1.
- From a trace of : increasing proportionally increases the level of static and dynamic support that is provided by the proposed controller.
- 2.
- From a trace of : increasing widens the range of PV voltage to allow a higher level of grid support.
- 3.
- From a trace of : The converter current is successfully limited at 15 A whenever needed.
Therefore, as long as there is no other system constraint that may impose the PV capacitor size, the parameter can properly be used to minimize the size of the capacitor while ensuring an adequate level of grid support is obtained.
Figure 17 (Scenario C-4), repeats that of Scenario C-2 but here the grid is weakened by adding and . The proposed method succeeds in providing grid support and confining the oscillations of the grid voltage within a much smaller range compared with the conventional controller.
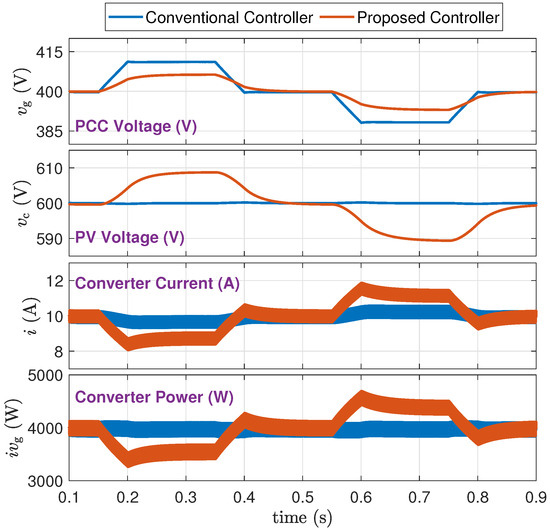
Figure 17.
Simulation results for and weak grid (Scenario C-4).
6. Experimental Results
6.1. Experimental Setup
Figure 18 shows the photograph of the laboratory setup based on the circuit diagram of Figure 19. The system includes two modules of Agilent E4360A PV emulators (Agilent Technologies, Santa Clara, CA, USA) which one of them is used as the converter resource, and the other one is directly connected to the PCC through a resistor. The characteristics of the first PV emulator are as follows: Maximum voltage () is 65 V, open-circuit voltage () is V, maximum current () is A, and the short-circuit current () is A. The second PV emulator operates at its maximum power point and is utilized to generate disturbances on the PCC voltage. The grid is modeled by a voltage source in series with an impedance, where V, , and mH, to mimic a weak grid situation. A Chroma programmable electronic load 63802 is used as the local load initially adjusted at . The desired PCC voltage is 35 V.

Figure 18.
Photograph of the experimental setup.
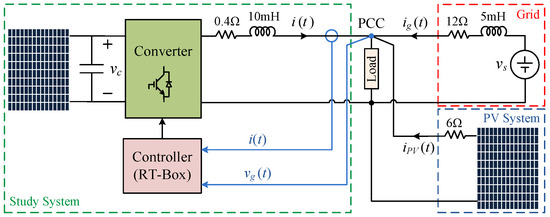
Figure 19.
Schematic circuit diagram of the experimental setup.
The PV converter is a full-bridge VSC with unipolar PWM at the switching frequency of 5 kHz. The output filter inductance is 10 mH, and its parasitic resistance is . The capacitor across the PV is mF. The proposed controller (shown in Figure 5) is designed based on the method of Section 3.5 with , , and . Its gains are 15,849, , and , and the closed-loop poles are at and . Other settings are , A, , V, and A. The controller is implemented in RT-Box from Plexim [28]. The conventional controller (shown in Figure 4) is designed as , , , and to have similar speed and damping. Its anti-windup gain () is 100.
6.2. Experimental Results
Case I [Local Load Disturbances]: Figure 20 and Figure 21 show the responses of the controllers to a local load sudden increase. In the proposed controller, the PV voltage is flexible. As a result, it provides inertia support, which prevents the load voltage from a sudden drop. Moreover, the level of the steady-state drop in the voltage is lower (down to V in the proposed controller compared to V in the conventional controller). This grid-supportive behavior lowers the burden on the grid: the grid current in the proposed controller changes from A to A, while in the conventional controller, it changes from A to A. This indicates lower stress on the grid and lower losses in the grid network. Figure 22 and Figure 23 show the responses to a load decrease. Similar conclusions are drawn.
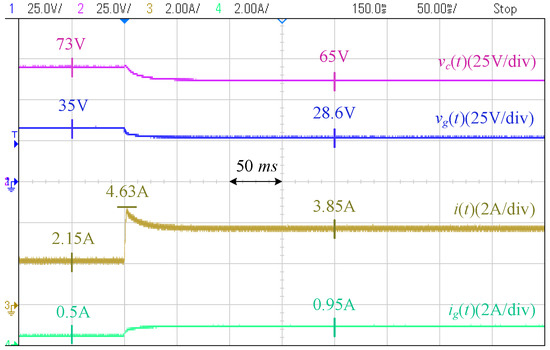
Figure 20.
Response of proposed controller to load increase (Case I).
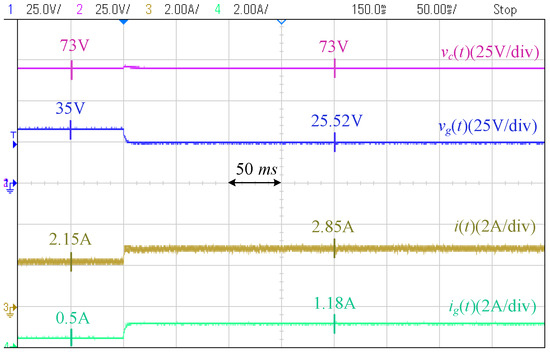
Figure 21.
Response of conventional controller to load increase (Case I).
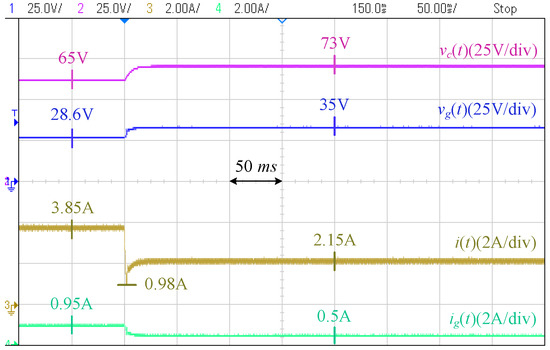
Figure 22.
Response of proposed controller to load decrease (Case I).
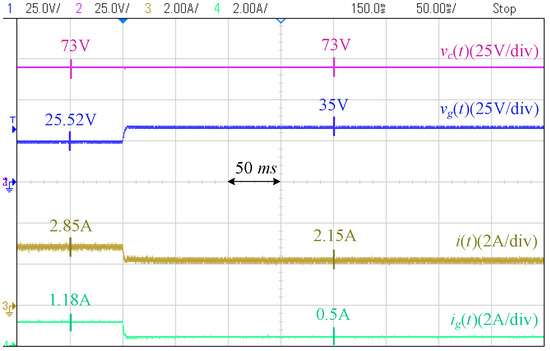
Figure 23.
Response of conventional controller to load decrease (Case I).
Case II [Grid Disturbance]: Figure 24 and Figure 25 show the results when the current injected by the second PV decreases from A to A. The PCC voltage in the proposed controller decreases from 35 V to 31 V, while it decreases to V in the conventional controller. The grid current in the proposed controller has a A increase, but it increases twice in the conventional controller. Figure 26 and Figure 27 show the responses when the current of the second PV increases from A to A. Similar conclusions are drawn.
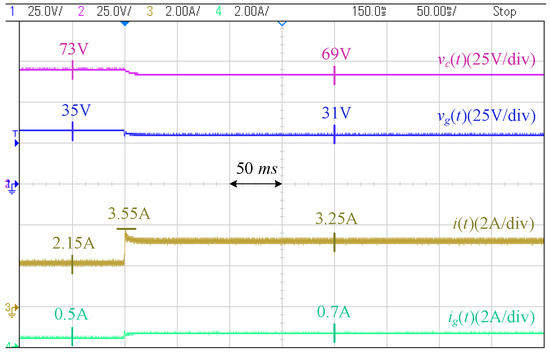
Figure 24.
Response of proposed controller to grid disturbance 1 (Case II).
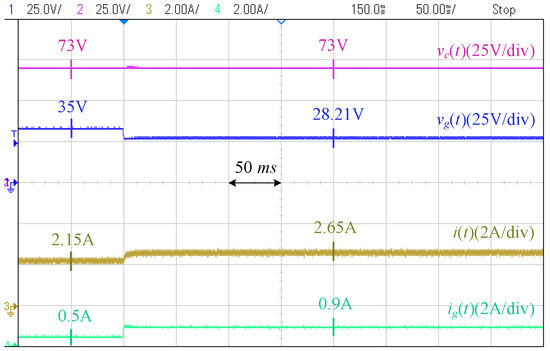
Figure 25.
Response of conventional controller to grid disturbance 1 (Case II).
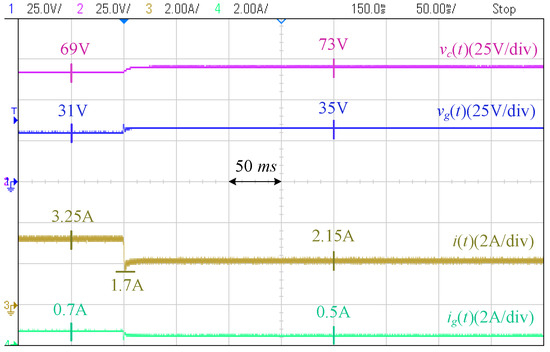
Figure 26.
Response of proposed controller to grid disturbance 2 (Case II).
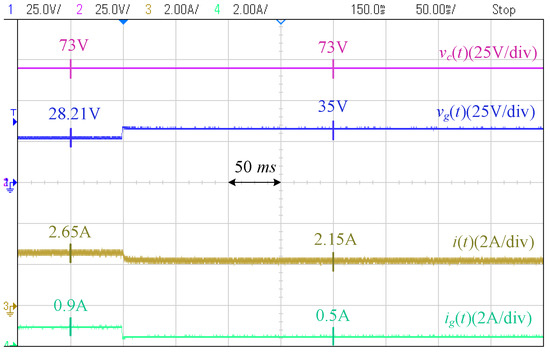
Figure 27.
Response of conventional controller to grid disturbance 2 (Case II).
Case III [Current Limiting]: In this case, the PCC voltage abruptly drops from 35 V to zero. The severe drop in the PCC voltage demands high current from the converter, and as can be seen in Figure 28 and Figure 29, both controllers quickly respond and inject the current and limit it at the pre-specified value of 5 A. The fault is cleared after 180 ms, and both controllers return to their normal operation. However, the PCC voltage in the conventional controller has a larger overshoot (up to 55 V) compared to the 47 V in the proposed controller.
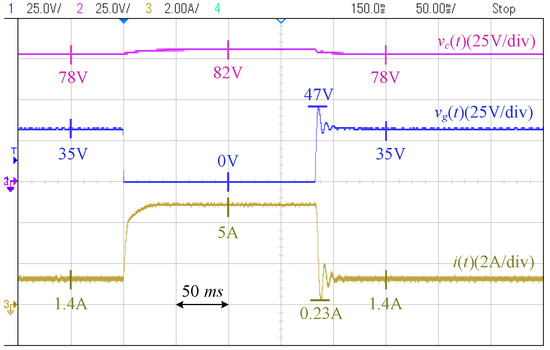
Figure 28.
Current limiting by the proposed controller.
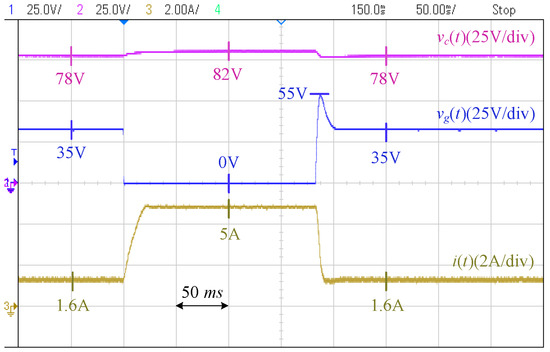
Figure 29.
Current limiting by the conventional controller.
7. Conclusions
This paper proposes a novel controller for DC grid-connected single-stage PV converters. Unlike conventional approaches, which typically aim to maintain a constant PV voltage, the proposed controller allows for a small and controlled offset in the PV voltage in proportion to the power flowing through the converter. This relaxed approach to DC-bus regulation results in a significantly wider stability margin for the system. A key feature of the proposed controller is the inclusion of a feedback loop from the grid voltage into the voltage control loop, which enables the converter to actively provide grid voltage support. This addition enhances the converter’s interaction with the grid while maintaining a simpler structure compared to traditional controllers. The proposed design combines the voltage and current controllers using an optimal full-state feedback approach, resulting in a systematic design that offers both optimal performance and robust stability. Additionally, the controller includes a current-limiting function to protect the converter from transient overcurrents, further improving system reliability. Detailed simulations, comparisons, and experimental results validated the effectiveness of the proposed controller under different practical scenarios, confirming its potential to improve the performance, stability, and robustness of DC grid-connected PV systems.
While the proposed controller effectively improves stability and grid support, it does not simultaneously maximize power extraction from the PV system. Future research could focus on two directions: (1) adding an alternative energy storage device, such as a properly sized battery, in parallel to the PV capacitor such that the grid support can be achieved from the combination of PV and battery without losing the MPPT, and (2) researching the optimal selection of power curtailment level (characterized by the selection of in the proposed controller) and the levels of dynamic and static supports (characterized by the capacitor size and the controller parameter ). Additionally, the scalability of the controller for larger PV systems should be explored to ensure its applicability in high-capacity installations. Thus, the integration of energy storage systems could further improve system reliability and grid interaction, while adaptive tuning of control parameters, including and , based on real-time grid conditions, may optimize performance in dynamic environments. Overall, the proposed controller offers significant potential for enhancing grid-connected PV systems, and future work should address these areas to improve both power maximization and grid support in real-world deployments.
Author Contributions
Conceptualization, A.Z. and M.K.-G.; Methodology, A.Z. and M.K.-G.; Validation, A.Z. and M.K.-G.; Formal analysis, A.Z. and M.K.-G.; Investigation, A.Z. and M.K.-G.; Writing—original draft, A.Z.; Writing—review & editing, A.Z. and M.K.-G.; Supervision, M.K.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yousefizadeh, S.; Bendtsen, J.D.; Khooban, M.H.; Blaabjerg, F.; Dragičević, T. Tracking Control for a DC Microgrid Feeding Uncertain Loads in More Electric Aircraft: Adaptive Backstepping Approach. IEEE Trans. Ind. Electron. 2019, 66, 5644–5652. [Google Scholar] [CrossRef]
- Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M.; Skrlec, D. Advanced LVDC Electrical Power Architectures and Microgrids: A step toward a new generation of power distribution networks. IEEE Electrif. Mag. 2014, 2, 54–65. [Google Scholar] [CrossRef]
- Planas, E.; Andreu, J.; Gárate, J.I.; Martínez de Alegría, I.; Ibarra, E. AC and DC technology in microgrids: A review. Renew. Sustain. Energy Rev. 2015, 43, 726–749. [Google Scholar] [CrossRef]
- Wu, T.-F.; Chang, C.-H.; Lin, L.-C.; Yu, G.-R.; Chang, Y.-R. DC-Bus Voltage Control with a Three-Phase Bidirectional Inverter for DC Distribution Systems. IEEE Trans. Power Electron. 2013, 28, 1890–1899. [Google Scholar] [CrossRef]
- Ganesan, S.I.; Pattabiraman, D.; Govindarajan, R.K.; Rajan, M.; Nagamani, C. Control Scheme for a Bidirectional Converter in a Self-Sustaining Low-Voltage DC Nanogrid. IEEE Trans. Ind. Electron. 2015, 62, 6317–6326. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator with Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Beck, H.-P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1–6. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An Improved Virtual Inertia Control for Three-Phase Voltage Source Converters Connected to a Weak Grid. IEEE Trans. Power Electron. 2019, 34, 8660–8670. [Google Scholar] [CrossRef]
- Shucheng, T.; Ge, D.; Hui, Z.; Na, Z.; Xi, X. Virtual DC machine control strategy of energy storage converter in DC microgrid. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016; pp. 1–5. [Google Scholar]
- Unamuno, E.; Paniagua, J.; Barrena, J.A. Unified Virtual Inertia for ac and dc Microgrids: And the Role of Interlinking Converters. IEEE Electrif. Mag. 2019, 7, 56–68. [Google Scholar] [CrossRef]
- Zhi, N.; Ding, K.; Du, L.; Zhang, H. An SOC-Based Virtual DC Machine Control for Distributed Storage Systems in DC Microgrids. IEEE Trans. Energy Convers. 2020, 35, 1411–1420. [Google Scholar] [CrossRef]
- Unamuno, E.; Barrena, J.A. Design and small-signal stability analysis of a virtual-capacitor control for DC microgrids. In Proceedings of the 19th European Conference on Power Electronics and Applications (EPE ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–10. [Google Scholar]
- Zhu, X.; Meng, F.; Xie, Z.; Yue, Y. An Inertia and Damping Control Method of DC–DC Converter in DC Microgrids. IEEE Trans. Energy Convers. 2020, 35, 799–807. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Xu, J.; Blaabjerg, F.; Dragičević, T. Virtual Inertia Control Strategy for Improving Damping Performance of DC Microgrid with Negative Feedback Effect. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1241–1257. [Google Scholar]
- Jami, M.; Shafiee, Q.; Bevrani, H. Dynamic Improvement of DC Microgrids Using a Dual Approach Based on Virtual Inertia. J. Mod. Power Syst. Clean Energy 2022, 10, 667–677. [Google Scholar]
- Zakerian, A.; Sharma, R.; Karimi-Ghartemani, M.; Karimi, H. Improving Stability and Power Sharing of Bidirectional Power Converters by Relaxing DC Capacitor Voltage. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6973–6984. [Google Scholar] [CrossRef]
- Sharma, R.; Zakerian, A.; Karimi-Ghartemani, M. Local Controller for an Autonomous Grid-Supportive Battery Energy Storage System. IEEE Trans. Power Electron. 2022, 37, 2191–2202. [Google Scholar] [CrossRef]
- Swaminathan, G.V.; Periasamy, S.; Lu, D.D.-C. Capacitor Current Control Based Virtual Inertia Control of Autonomous DC Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 6908–6918. [Google Scholar]
- Zhu, X.; Xie, Z.; Jing, S.; Ren, H. Distributed virtual inertia control and stability analysis of dc microgrid. IET Gener. Transm. Distrib. 2018, 12, 3477–3486. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Xu, L.; Meng, J.; Hei, Y. Adjustable Inertial Response from the Converter with Adaptive Droop Control in DC Grids. IEEE Trans. Smart Grid 2019, 10, 3198–3209. [Google Scholar]
- Hosseinipour, A.; Hojabri, H. Virtual inertia control of PV systems for dynamic performance and damping enhancement of DC microgrids with constant power loads. IET Renew. Power Gener. 2018, 12, 430–438. [Google Scholar]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Grid-supporting inverters with improved dynamics. IEEE Trans. Ind. Electron. 2018, 66, 3655–3667. [Google Scholar]
- Ebrahimi, M.; Khajehoddin, S.A.; Karimi-Ghartemani, M. A Single Stage Virtual Synchronous Machine. IEEE Int. Conf. Ind. Technol. (ICIT) 2019, 1643–1648. [Google Scholar]
- Karimi-Ghartemani, M.; Khajehoddin, S.A.; Jain, P.; Bakhshai, A. Linear quadratic output tracking and disturbance rejection. Int. J. Control. 2011, 84, 1442–1449. [Google Scholar]
- MATLAB. Available online: https://www.mathworks.com (accessed on 11 December 2023).
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- RT BOX. Available online: https://www.plexim.com/products/rt_box (accessed on 20 January 2021).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).