Fast-Fading Modeling in Wireless Industrial Communications
Abstract
1. Introduction
- Rice Factor Analysis via Ray Tracing (RT) Simulations: Fast-fading samples were collected for different combinations of MD, MS, SP, and frequency compared with the literature.
- Machine Learning-Based Prediction: An ML model was trained to predict K based on the industrial setting’s characteristics, capturing complex dependencies.
- Empirical Formula for K Estimation: A simple analytical model is proposed to estimate K from MD, MS, and frequency, providing a computationally efficient alternative.
2. Related Work
3. Assessment Framework
3.1. Industrial Environment Representation
3.2. Ray Tracing Simulation
3.3. Small-Scale Fading
3.4. Rice Factor Computation
- Fast-fading collection: In each scenario, the received signal amplitude is computed in every Rx location with respect to each Tx position. The corresponding small-area average is then achieved through spatial averaging over the corresponding 3 × 3 grid. Finally, the fast-fading contribution is computed according to Euquation (2). In this way, Approximately 13,000 samples of are collected for each scenario.
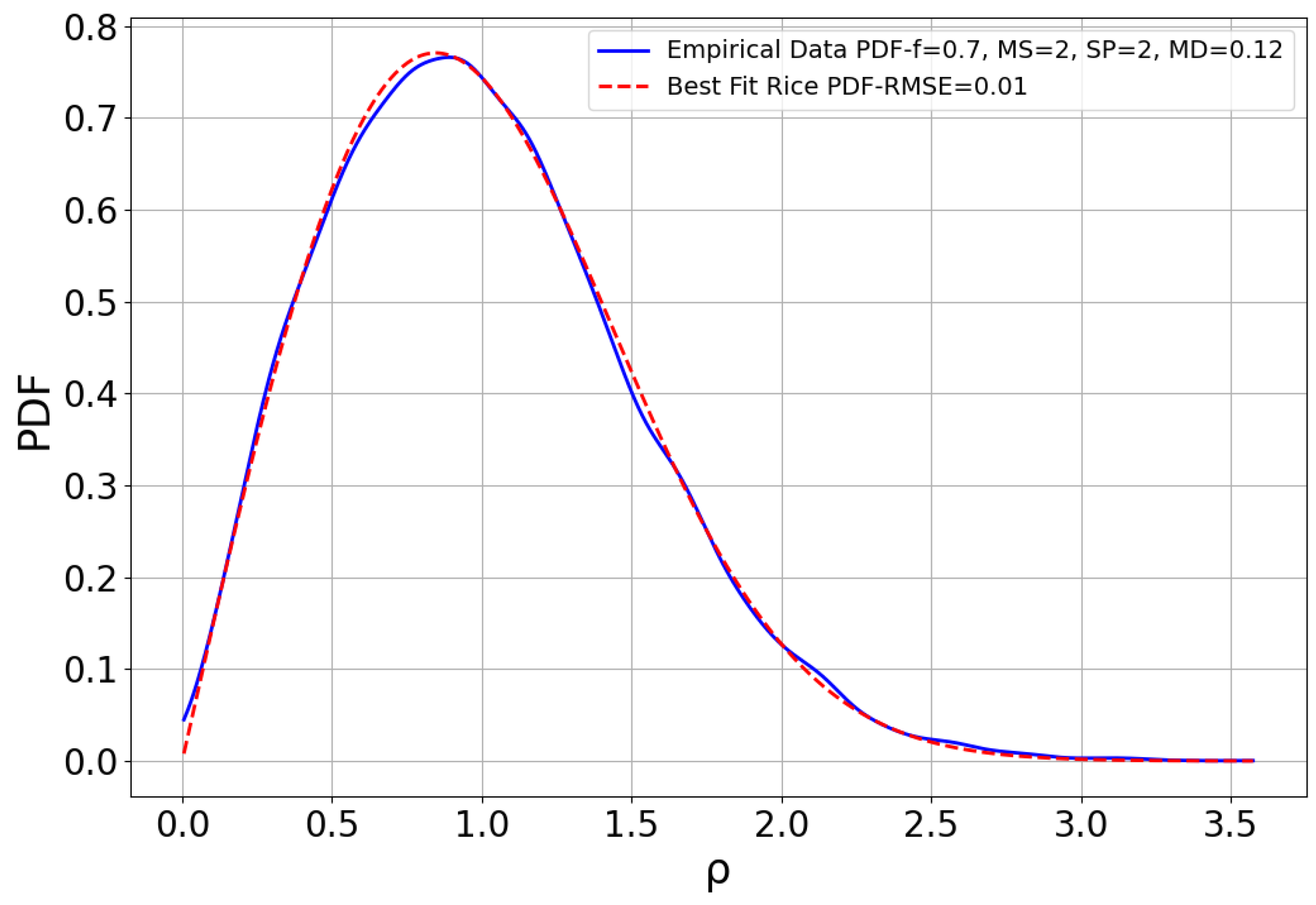
- Empirical PDF Construction: The PDF of the samples is extracted from the empirical data.
- Rice Distribution Fitting: The Rice distribution is fitted to the empirical PDF, and the corresponding K value is recorded to fill the database necessary to train and test the ML model.
- Dataset Compilation: The final dataset is compiled, containing columns for the features of each scenario (MS, SP, MD, and f) and the corresponding output K.
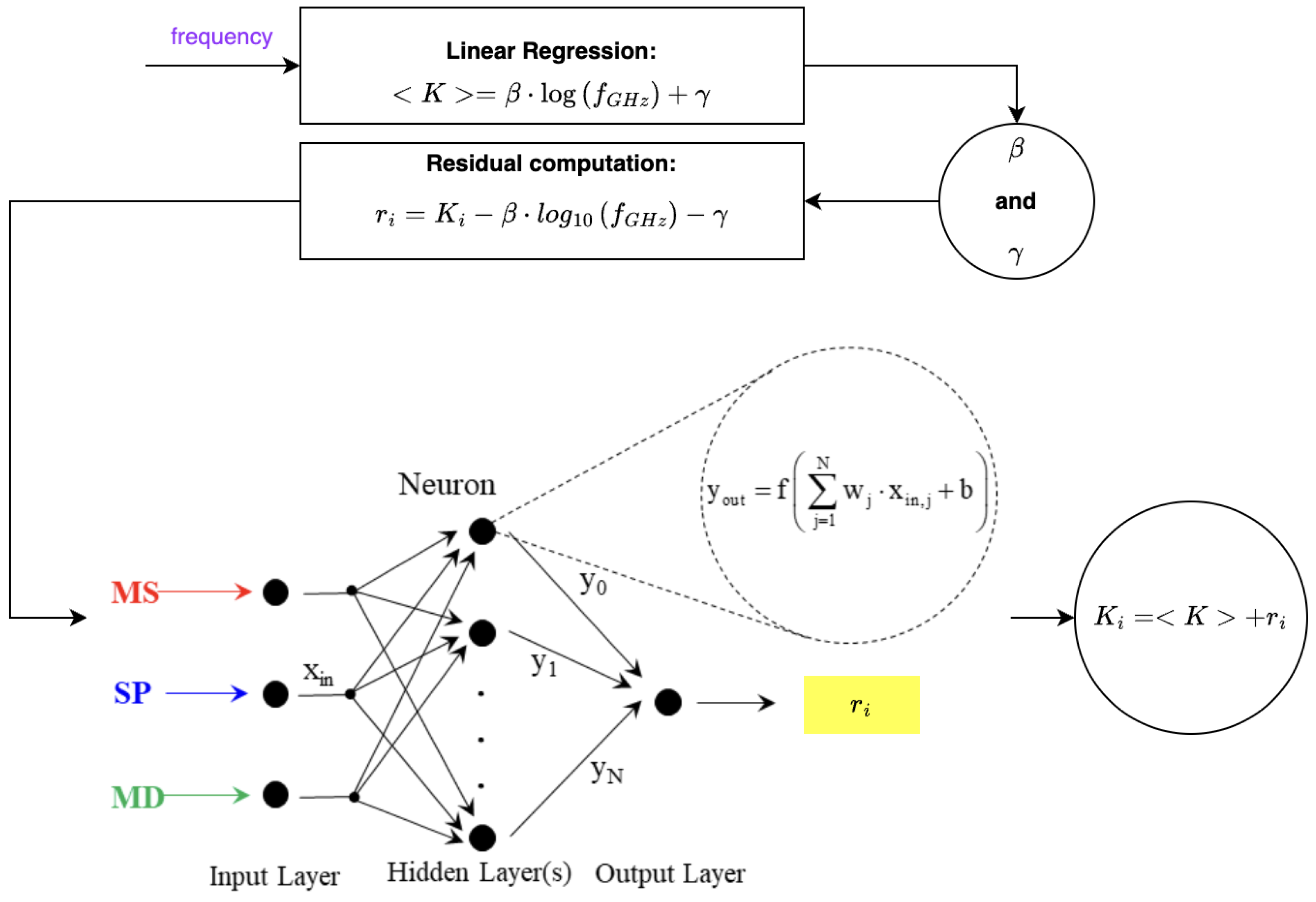
3.5. Machine Learning
- A single linear regression is performed to estimate the frequency dependence of the Rice factor K. The regression model is defined as follows:where and are the regression coefficients. This step provides an initial estimate of K, capturing its average trend as a function of the logarithm of frequency. The coefficients are determined using the least squares method, minimizing the difference between the measured K values and the predicted trend.
- While the linear regression captures the overall frequency dependence, the actual values of deviate from the estimated trend due to environmental factors. The residuals quantify these deviations:
- A Multi-Layer Perceptron (MLP) is employed to model the residuals as a function of the environmental parameters MS, SP, and MD. The MLP consists of an input layer, hidden layers, and an output layer, with the following operations: The input layer receives the three geometrical features MS, SP, and MD. Hidden layers apply non-linear transformations using neurons, each performing the following:where are the trainable weights, b is the bias term, and is an activation function (e.g., ReLU). In the training process, the MLP is trained using backpropagation and gradient descent to minimize the error between the predicted residuals and the actual residuals . In the output layer, the final estimate of the residual is produced. Finally, the corrected Rice factor is estimated by adding the predicted residual to the regression model:
4. Results and Discussion
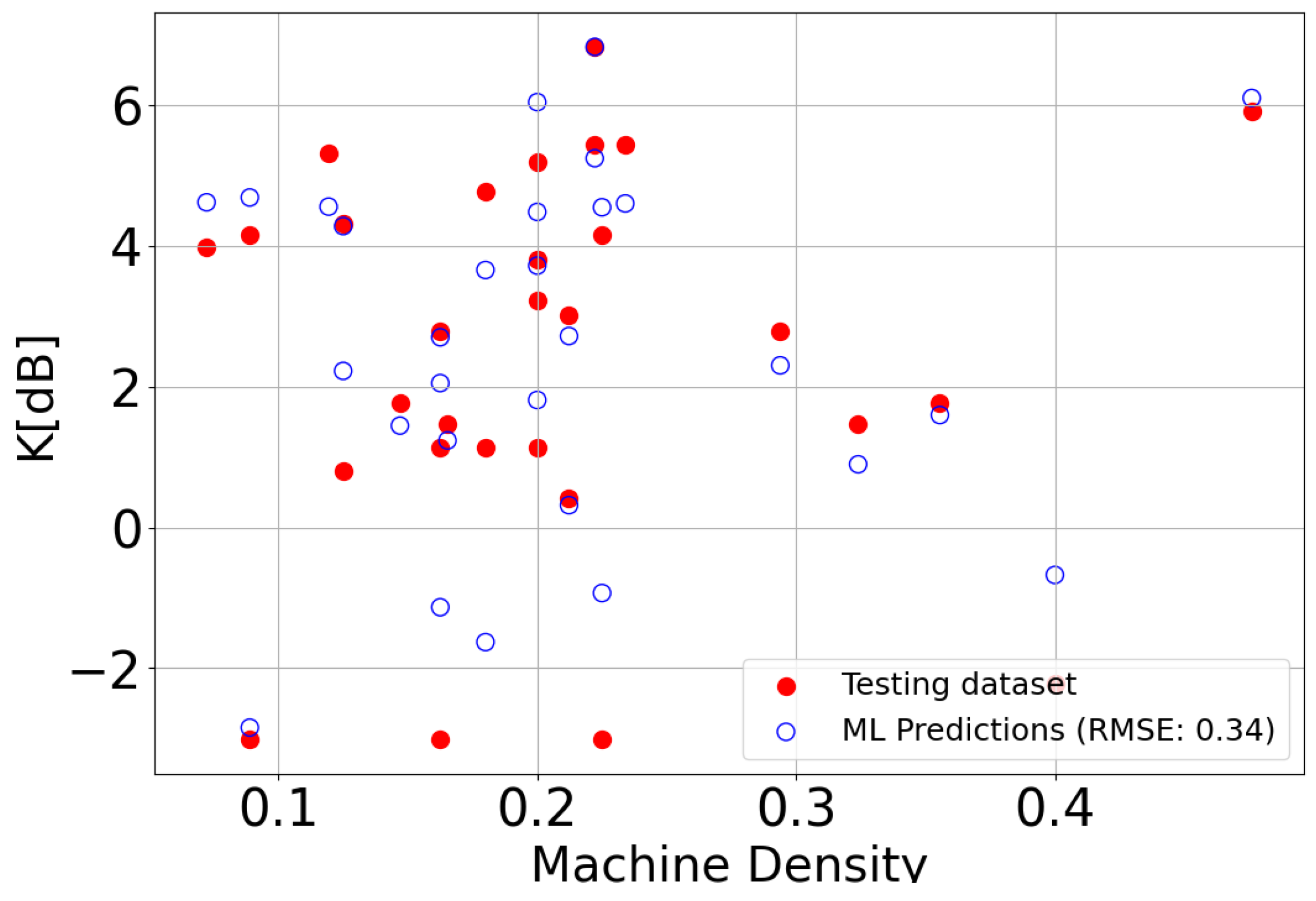
4.1. ML Model Evaluation
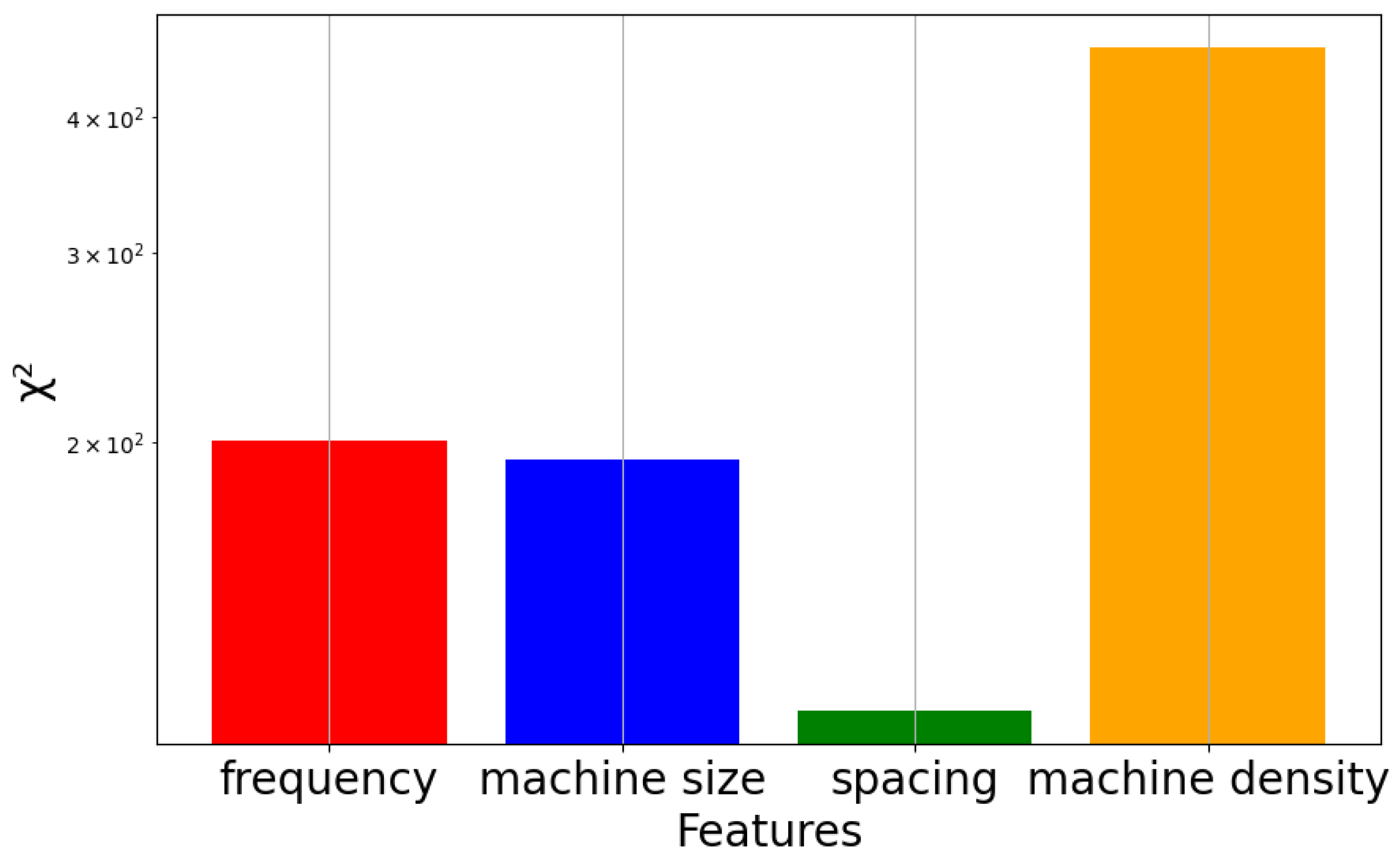
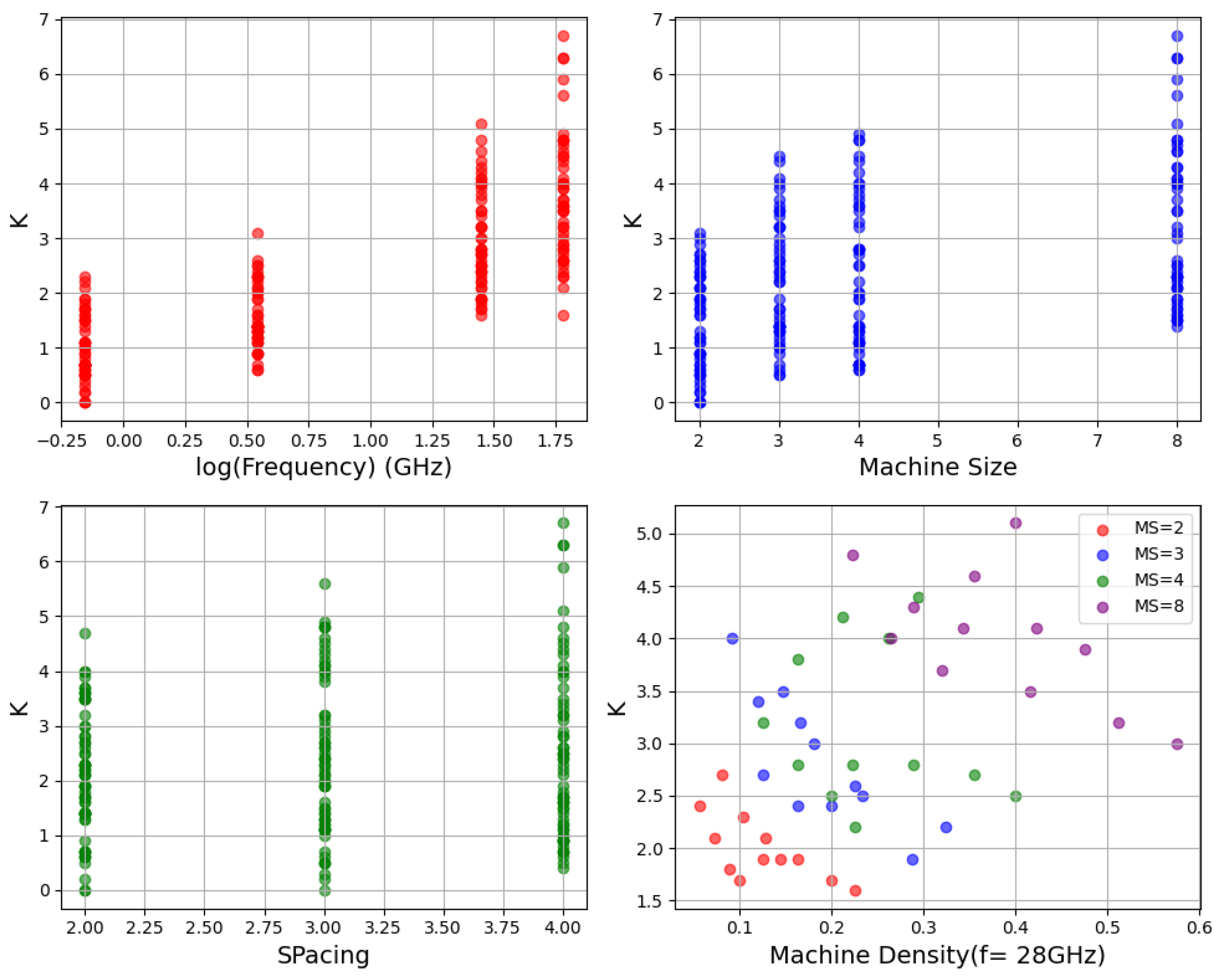
4.2. Feature Importance and Analysis
4.3. Empirical Formula
5. Comparison with the Literature
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MD | Machine density |
| MS | Machine size |
| SP | Spacing between machines |
| f | frequency |
| RT | Ray Tracing |
| ML | Machine learning |
| LoS | Line of sight |
| PG | Path Gain |
| Probability Density Function | |
| MLP | Multi-Layer Perceptron |
| RMSE | Root Mean Squared Error |
References
- Vitturi, S.; Tramarin, F.; Seno, L. Industrial Wireless Networks: The Significance of Timeliness in Communication Systems. IEEE Ind. Electron. Mag. 2013, 7, 40–51. [Google Scholar] [CrossRef]
- Candell, R.; Kashef, M.; Perez-Ramirez, J.; Conchas, J. An IEEE Standard for Industrial Wireless Performance Evaluation. IEEE Internet Things Mag. 2023, 6, 82–88. [Google Scholar]
- Zurawski, R. Industrial Communication Systems; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Cheffena, M. Industrial Wireless Communications over the Millimeter Wave Spectrum: Opportunities and Challenges. IEEE Commun. Mag. 2016, 54, 66–72. [Google Scholar] [CrossRef]
- Bertoni, H.L. Radio Propagation for Modern Wireless Systems; Prentice Hall Professional Technical Reference: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Saunders, S.R.; Zavala, A.A. Antennas and Propagation for Wireless Communication Systems; Prentice Hall Professional Technical Reference: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Zadeh, M.H.; Barbiroli, M.; Fuschini, F. A Machine Learning Approach to Wireless Propagation Modeling in Industrial Environment. IEEE Open J. Antennas Propag. 2024, 5, 727–738. [Google Scholar] [CrossRef]
- Yegani, P.; McGillem, C. Industrial Wireless Systems: Radio Propagation Measurements. IEEE Trans. Comm. 1991, 39, 10. [Google Scholar]
- Ferreira, M.; Ambroziak, S.; Cardoso, F.; Sadowski, J.; Correia, L. Fading Modeling in Maritime Container Terminal Environments. IEEE Trans. Veh. Tech. 2018, 67, 10. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.; Hong, J.Y.; Lim, J.S.; Chong, Y.J. Propagation Characteristics of an Industrial Environment Channel at 4.1 GHz. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 20–22 October 2021. [Google Scholar]
- Tanghe, E.; Joseph, W.; Verloock, L.; Martens, L.; Capoen, H.; Herwegen, K.V.; Vantomme, W. The industrial indoor channel: Large-scale and temporal fading at 900, 2400, and 5200 MHz. IEEE Trans. Wirel. Comm. 2008, 7, 7. [Google Scholar]
- Candell, R.; Remley, C.; Quimby, J.; Novotny, D.; Curtin, A.; Papazian, P.; Koepke, J.D.G.; Hany, M. A Statistical Model for the Factory Radio Channel; Technical Report, NIST Technical Note; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. [Google Scholar]
- Croonenbroeck, R.; Underberg, L.; Wulf, A.; Kays, R. Measurements for the development of an enhanced model for wireless channels in industrial environments. In Proceedings of the 2017 IEEE 13th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Rome, Italy, 9–11 October 2017. [Google Scholar]
- Al-Saman, A.; Mohamed, M.; Cheffena, M.; Moldsvor, A. Wideband Channel Characterization for 6G Networks in Industrial Environments. Sensors 2021, 21, 2015. [Google Scholar] [CrossRef] [PubMed]
- ETSI TR 138 901; Study on Channel Model for Frequencies from 0.5 to 100 GHz. Technical Report; ETSI: Sophia Antipolis, France, 2020.
- Fuschini, F.; Vitucci, E.; Barbiroli, M.; Falciasecca, G.; Degli-Esposti, V. Ray tracing propagation modeling for future small-cell and indoor applications: A review of current techniques. Radio Sci. 2015, 50, 469–485. [Google Scholar] [CrossRef]

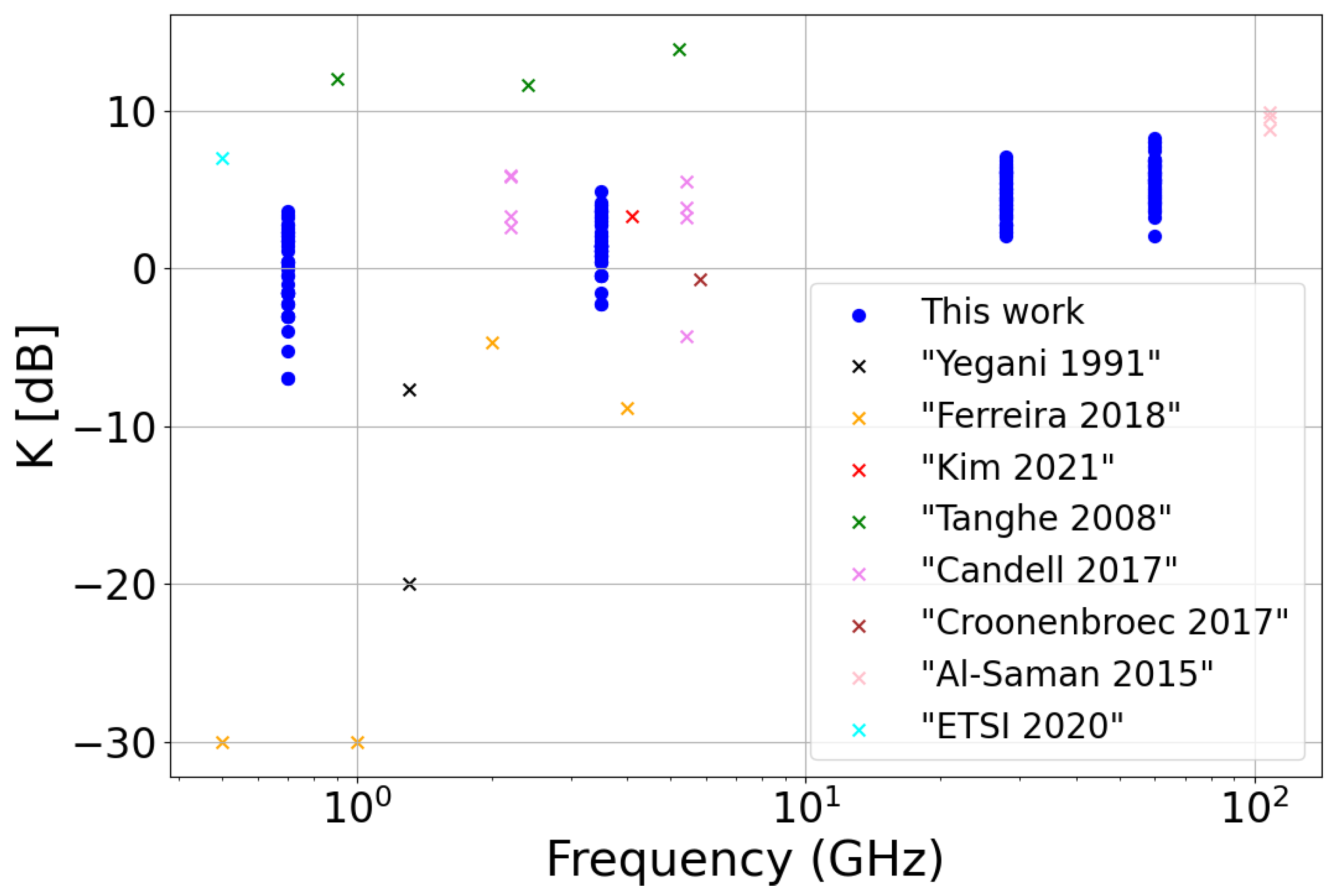
| Ref. | Freq. (GHz) | Type | LoS/NLoS | K | Notes |
|---|---|---|---|---|---|
| [8] | 1.3 | Measurements | Mixed | ∼, 0.17 | Heavy clutter |
| [9] | 0.5 1 2 4 | Measurements | Mixed | ∼ ∼ 0.34 0.13 | Outdoor industrial area (maritime container terminals) |
| [10] | 4.1 | Measurements | LoS | 2.16 | |
| [11] | 0.9 2.4 5.2 | Measurements | Mixed | 15.8 14.4 24.5 | Fast fading triggered by movement of workers and/or machinery and/or fork-lift throughout the industrial layout |
| [12] | 2.2 5.4 | Measurements | Mixed | 1.82, 2.14, 3.8, 3.9, 154.9 0.37, 2.09, 2.45, 3.55, 16.6 | |
| [13] | 5.8 | Measurements | LoS/NLoS | 0.86 (LoS) 0.27 (NLoS) | |
| [14] | 108 | Measurements | LoS | 7.6, 9.1, 9.8 | Directional horn antennas (G 21 dB) |
| [15] | 0.5–100 | Unclear | LoS | 5 | Standard deviation of K = 6.3 |
| MS [m] | 2, 3, 4, 8 |
| SP [m] | 2, 3, 4 |
| T | 0.1, 0.2, 0.35, 0.5 |
| f [GHz] | 0.7, 3.5, 28, 60 |
| Parameter | Value |
|---|---|
| Hidden Layer Sizes | (8, 4) |
| Maximum Iterations | 3000 |
| Early Stopping | True |
| Learning Rate | 0.001 |
| Activation Function | ReLU |
| Solver | Adam |
| Model | RMSE | Min K | Max K |
|---|---|---|---|
| ML Model | 0.34 | 0 | 6.7 |
| Empirical Formula | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossein Zadeh, M.; Barbiroli, M.; Fuschini, F. Fast-Fading Modeling in Wireless Industrial Communications. Electronics 2025, 14, 1378. https://doi.org/10.3390/electronics14071378
Hossein Zadeh M, Barbiroli M, Fuschini F. Fast-Fading Modeling in Wireless Industrial Communications. Electronics. 2025; 14(7):1378. https://doi.org/10.3390/electronics14071378
Chicago/Turabian StyleHossein Zadeh, Mohammad, Marina Barbiroli, and Franco Fuschini. 2025. "Fast-Fading Modeling in Wireless Industrial Communications" Electronics 14, no. 7: 1378. https://doi.org/10.3390/electronics14071378
APA StyleHossein Zadeh, M., Barbiroli, M., & Fuschini, F. (2025). Fast-Fading Modeling in Wireless Industrial Communications. Electronics, 14(7), 1378. https://doi.org/10.3390/electronics14071378







