Frequency-Domain Steganography with Hexagonal Tessellation for Vision–Linguistic Knowledge Encapsulation

Abstract

With the rapid development of technologies such as vision–language modeling, sharing images with corresponding descriptions has become a common means of information transfer. Studying data-hiding techniques for JPEG images can protect sensitive descriptions, such as personal information associated with them while sharing images. Therefore, research on data-hiding techniques for JPEG images is of significant importance. However, existing methods that modify discrete cosine transform (DCT) coefficients still have room for improvement in increasing their embedding capacity while minimizing file size expansion. To address this issue, this paper proposes a knowledge encapsulation method for JPEG images using a special hexagonal tessellation matrix. First, a special hexagonal tessellation matrix is constructed based on the characteristics of non-zero AC coefficients. Then, non-zero AC coefficients in JPEG images are paired to form coordinate pairs, and the data are embedded by modifying the non-zero AC coefficient pairs into the coordinates corresponding to the secret data. Experimental results demonstrate that, compared to the previously proposed JPEG image data-hiding schemes, the proposed approach achieves a higher embedding capacity, a minimal file size increase (FSI), and an acceptable peak signal-to-noise ratio (PSNR).

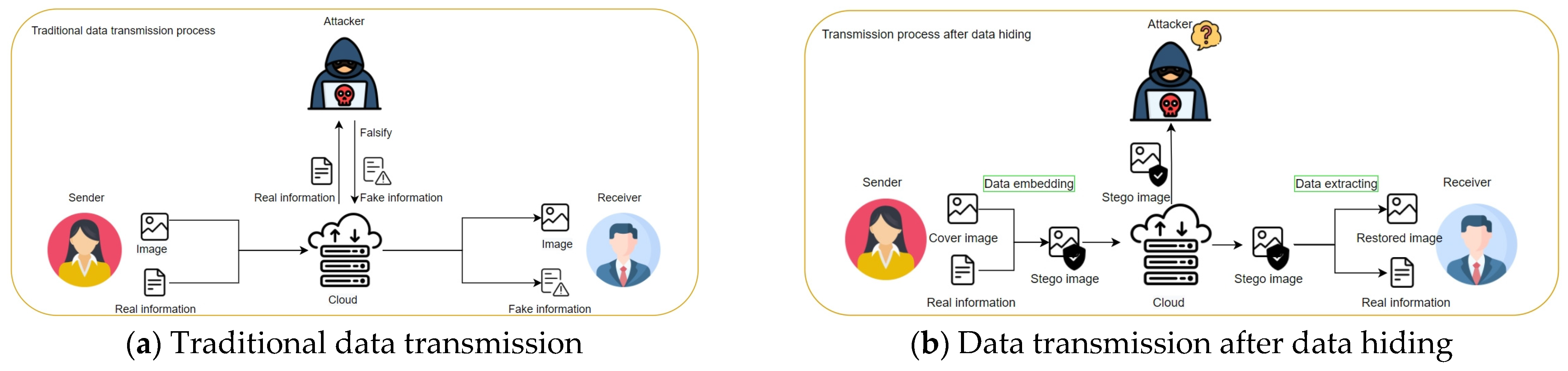
1. Introduction

In the digital era, the combination of images and textual descriptions has become a primary means of information transmission. This integration of visual and textual content is ubiquitous across both everyday and professional domains: social media posts pair personal photographs with emotional narratives, news reports combine field photography with detailed descriptions, medical systems link diagnostic information with medical images, and geographic information systems associate satellite imagery with precise location data and environmental parameters. This multimodal approach to information transmission not only enriches content delivery but also presents significant research opportunities in artificial intelligence.

Recent advances in multimodal artificial intelligence technologies, particularly vision–language models (VLMs), have been remarkable. These models demonstrate sophisticated capabilities in image comprehension, intelligent text–image correlation, and description generation from visual inputs. While this technological progress has enhanced the automated processing of multimodal content, it has also introduced new security challenges. As illustrated in Figure 1a, when descriptive text contains sensitive information (such as medical records, personal identification data, or trade secrets), direct transmission alongside images risks unauthorized access or malicious manipulation. To address these security concerns, data hiding [1,2,3,4,5,6,7,8] offers an effective solution, as shown in Figure 1b, enabling secure transmission by embedding textual information within images. However, traditional data-hiding methods, primarily designed for uncompressed images, face significant challenges in practical scenarios where JPEG compression is prevalent.

Figure 1. This is a diagram comparing the security of data transmission with and without steganography protection. (a) Without protecting the data with steganography, the attacker can discover and tamper with the data. (b) Data are protected using steganography, and it is difficult for the attacker to discover the secret data.

JPEG compression is a fundamental image compression technology that employs a lossy algorithm to significantly reduce file sizes, lowering both storage and transmission costs. The algorithm leverages human visual system characteristics to compress high-frequency components that are imperceptible to human observers, thus preserving images’ visual quality. Additionally, JPEG allows users to adjust the compression quality factor (QF), enabling a customizable balance between image quality and file size. As an international standard, JPEG is supported by nearly all operating systems, devices, and applications, ensuring compatibility and cross-platform usability. In the context of rapid internet development, images have become a dominant content format. For resource-constrained devices like smartphones, JPEG’s efficient compression and decoding mechanisms make it the preferred format for sharing images on social media. Despite the emergence of advanced compression technologies, JPEG maintains its prominence in digital imaging due to its technical maturity, ubiquitous support, and operational flexibility. However, an inherent conflict exists between data-hiding techniques, which rely on redundancy, and compression algorithms, which aim to eliminate it. Consequently, balancing hiding capacity, image fidelity, and file size in JPEG images remains a critical research challenge.

This paper proposes a novel JPEG image knowledge encapsulation method based on hexagonal tessellation. Our approach begins by constructing a specialized matrix plane without zero coordinates, filled with hexagonal patterns. During JPEG compression, non-zero AC coefficients are paired to form coordinates. Secret data embedding is achieved by modifying these AC coefficient pairs according to coordinates corresponding to the secret data in the hexagon-filled matrix. Experimental results demonstrate that the generated stego images maintain PSNR values close to the original, allowing recipients to interpret image content without original image restoration. Recipients can extract the hidden data by pairing non-zero AC coefficients from the received stego JPEG image and matching them against the hexagon-filled matrix. Compared to existing JPEG data-hiding methods, our approach achieves a superior embedding capacity while maintaining a visual quality similar to the original image and minimizing any file size increments.

2. Related Works

This section briefly reviews three types of methods for data hiding in JPEG images and introduces a method for data hiding in JPEG images using histogram shifting [9].

2.1. Schemes Based on Modified Quantization Tables

There are three types of data-hiding schemes for JPEG images. The first type is data-hiding schemes based on modified quantization tables [10,11]. This type of method divides certain elements in the quantization table by an integer equal to 2 [10] or greater than 2 [11], simultaneously multiplying the corresponding discrete cosine transform (DCT) coefficients by this integer, and then using some data-hiding technique in these modified coefficients, such as the least significant bit (LSB)-replacing technique. This type of method can generate stego images with a high visual quality, but it significantly increases the file size.

2.2. Schemes Based on Modified Huffman Coding

The second category achieves data embedding by modifying the Huffman coding [12]. This technique maps the variable length code (VLC) in the Huffman table to one or more unused VLCs. This kind of method offers a relatively low embedding capacity. In these schemes, compared with other schemes, the embedding capacity of the method would be low.

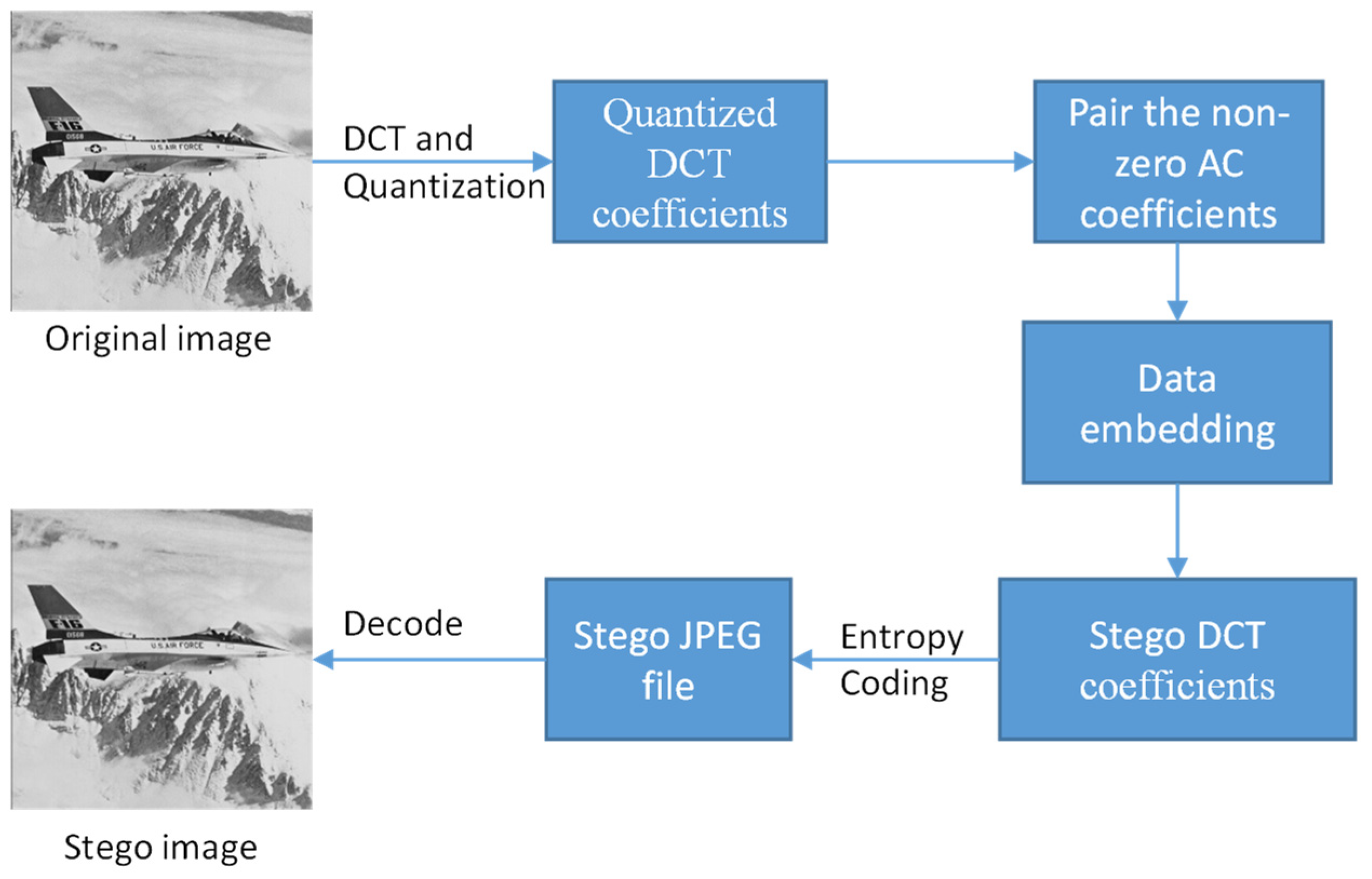
2.3. Schemes Based on Modified Frequency Coefficent

The third kind is the methods based on modified discrete cosine transform (DCT) coefficients [9,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. To embed data without significantly increasing the file size, there are some researchers who modify the DCT coefficients. In early research, the method proposed in [13] suggested compressing the LSB planes of certain quantized DCT coefficients for data embedding. Chang et al. [14] proposed leveraging the coefficients with two consecutive zero values in the middle-frequency part to hide secret data. Xuan et al. [15] proposed selecting multiple binary pairs in the histogram of quantized DCT coefficients and utilizing histogram shift to accommodate the payload. As an improved version of Xuan et al.’s method, Sakai et al. [16] proposed measuring the smoothness of an 8 × 8 DCT block by evaluating the fluctuations of the Direct Current (DC) coefficients in its adjacent blocks and choosing smooth blocks for data embedding. Huang et al. [17] proposed preferentially selecting DCT blocks containing more zero-valued coefficients for data embedding and embedding data into the Alternating Current (AC) coefficients with values of 1 and −1 in the block, while shifting other non-zero AC coefficients. As an improved version of Huang et al.’s method, Wedaj et al. [18] proposed estimating the embedding efficiency of all 63 frequency bands and preferentially choosing the bands with a higher efficiency for data embedding. Hou et al. [19] proposed evaluating the distortion of each frequency band and preferentially choosing the bands with a smaller distortion during the data embedding process. He et al. [20] proposed estimating the negative-impact model of frequency bands and preferentially utilizing frequencies with smaller negative exponents for data embedding. He et al. [21] proposed a JPEG data-hiding method based on improved block sorting and frequency selection. Li and Huang [9] introduced a JPEG image data-hiding method grounded in a two-dimensional histogram. In their methodology, every two consecutive non-zero Alternating Current (AC) coefficients are grouped into a non-zero AC coefficient pair (NACP). These NACPs are then modified in accordance with a two-dimensional mapping, namely pairwise non-zero AC coefficient expansion, for data-embedding purposes. Li et al. [22] progressively improved the two-dimensional histogram shifting mechanism by ignoring the coefficients along the diagonal. Furthermore, they developed a progressive mapping mechanism [23] to preserve the majority of coefficients. Xiao et al. [24] presented a JPEG data-hiding method that integrates multi-histogram modification with rate distortion optimization. A rate distortion model was formulated to adaptively identify the expansion bins for diverse histograms. A computationally efficient greedy algorithm, characterized by low complexity, was employed to solve the rate distortion model, thereby attaining a near-optimal embedding solution. Subsequently, Xiao et al. [25] proposed another JPEG image RDH method based on the modification of multiple two-dimensional histograms. In this approach, every two non-zero AC coefficients from adjacent DCT blocks within each frequency band are paired up, and a coefficient-pairing strategy is utilized to modify these pairs. Yang et al. [26] developed a JPEG data-hiding method centered around a coefficient priority selection strategy. This method computes the distortion value for each AC coefficient and preferentially selects those with lower distortion values for data hiding. Weng et al. [27] proposed a versatile data-hiding framework for JPEG images. This framework encompasses multiple two-dimensional histograms and can accommodate two distinct scenarios: one involves incorporating non-zero AC coefficients into data embedding, while the other excludes them. Through the use of adaptive thresholds and the selection of two-dimensional histogram mappings, their method enhances the embedding performance under a given payload, preserving both visual quality and file size. Xiong et al. [28] created six mapping types with different embedding efficiencies and proposed an improved two-dimensional histogram mapping method. Li et al. [29] analyzed the local histogram characteristics across varying texture images and developed a dynamic iterative histogram modification framework. Their approach incorporates adaptive parameters that regulate the two-dimensional histogram iteration frequency based on the required payload, thereby generating optimal histogram modification mappings.

2.4. Observations and Insights

While the existing methods achieve a satisfactory image quality and reduce file size increases, histogram shifting techniques require a sufficient displacement space, resulting in numerous non-zero AC coefficients being modified solely to create an embedding space. These modifications not only fail to embed data but also degrade visual quality and increase file sizes. However, JPEG compression is inherently lossy, causing distortion to the original image. The human eye is less sensitive to high-frequency noise, and the human visual system has a masking effect that does not significantly affect the perceived quality of the entire image if the noise is evenly distributed or localized. Consequently, images remain visually acceptable even at PSNR values around 30 dB, while PSNR values exceeding 40 dB indicate a virtually imperceptible distortion, signifying high-quality images. Therefore, if we can maintain PSNR values above 40 dB between stego-compressed images and normal compressed images, the presence of embedded data becomes difficult to detect.

This observation suggests that the perfect reversibility of cover images may not be essential. Instead, we can sacrifice cover image reversibility while maintaining the PSNR within acceptable ranges to achieve a higher embedding capacity and smaller file size increments. To achieve these objectives, we propose a novel JPEG image data-hiding method based on hexagonal tessellation. This method begins by constructing a specialized matrix plane without zero coordinates, subsequently filled with hexagonal patterns. During JPEG compression, non-zero AC coefficients are paired to form coordinates. Secret data embedding is accomplished by modifying these AC coefficient pairs according to coordinates corresponding to the secret data in the hexagonal-filled matrix. Recipients can extract hidden data by pairing non-zero AC coefficients from the received stego JPEG image and matching them against the hexagon-filled matrix. Our approach demonstrates a superior performance in embedding capacity and visual quality preservation and minimal file size increments.

2.5. Method Based on Histogram Shifting

In the method proposed by Li and Huang [9], the JPEG bitstream is decoded to obtain the quantized discrete cosine transform (DCT) coefficients. The coefficients are divided into non-overlapping $8\times 8$ blocks, denoted as $\{B₁, B₂, \dots , Bₙ\}$, where $n$ represents the total number of blocks. Each block is scanned in a zigzag order to generate a coefficient sequence, with the first coefficient being the DC coefficient and the remaining 63 being AC coefficients. The frequency of zero AC coefficients within each block is used to estimate the smoothness of the coefficient sequence.

Subsequently, all blocks are sorted in descending order of smoothness, with embedding beginning in the smoothest blocks. Each pair of consecutive non-zero AC coefficients is combined to form a non-zero AC pair (NACP). Once all the NACPs are generated, data embedding is performed based on the constructed two-dimensional histogram. Figure 2 provides an example of such a histogram, where only the three categories in the first quadrant are described, as the other three quadrants follow a similar process. In Figure 2, the directional arrows represent the modifications of Non-zero AC Pair (NACP) coefficients following data embedding or shifting operations. During data embedding, all NACPs are classified into three categories, each with different embedding efficiencies:

Figure 2. This is an example of a 2D histogram.

• Red class: If an NACP falls into this category, it is modified in four directions, allowing for the embedding of 2 bits of secret data;
• Green class: If an NACP belongs to this category, it is modified in two directions, enabling the embedding of 1 bit of secret data;
• Blue class: If an NACP falls into this category, it is modified in only one direction, resulting in displacement without data embedding.

All NACPs are adjusted accordingly to embed the required payload, yielding the stego image.

In Li and Huang’s method [9], a significant number of NACPs belong to the blue class, which requires modification but does not contribute to the data embedding. This limitation reduces the embedding capacity of the JPEG images and leads to an unnecessary file size expansion. To better utilize NACPs and minimize redundant modifications, we propose a data-embedding approach using a special hexagonal tessellation matrix for JPEG images.

3. Proposed Scheme

In this section, we will introduce a method using a special hexagonal tessellation matrix to embed secret data into the non-zero AC pairs. This section first introduces the special hexagonal tessellation matrix construction method, followed by the data-embedding process, and concludes with the extraction of secret data. Figure 3 presents the framework of the proposed method, which will be explained in detail in the subsequent sections.

Figure 3. The framework of the proposed method.

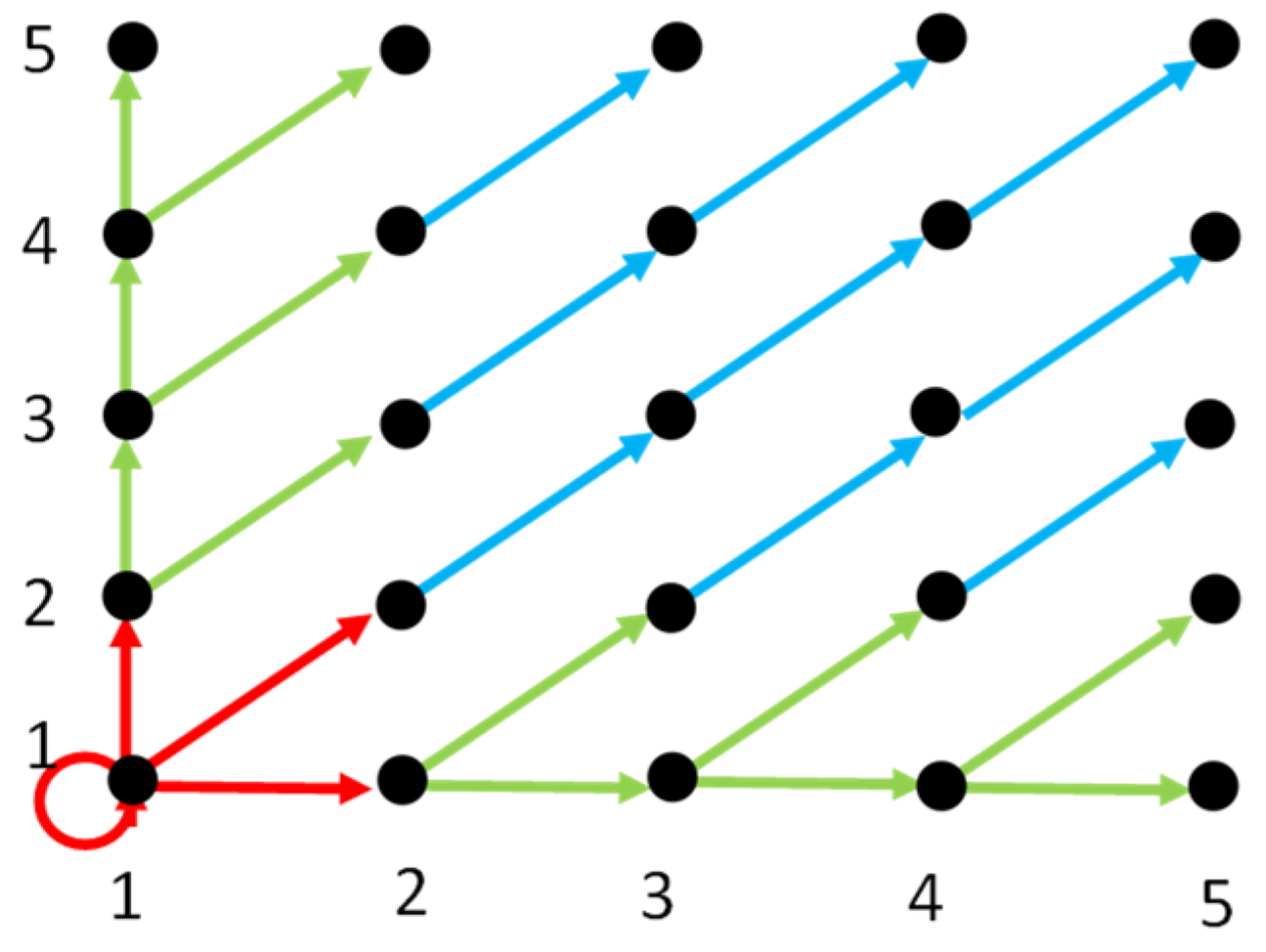
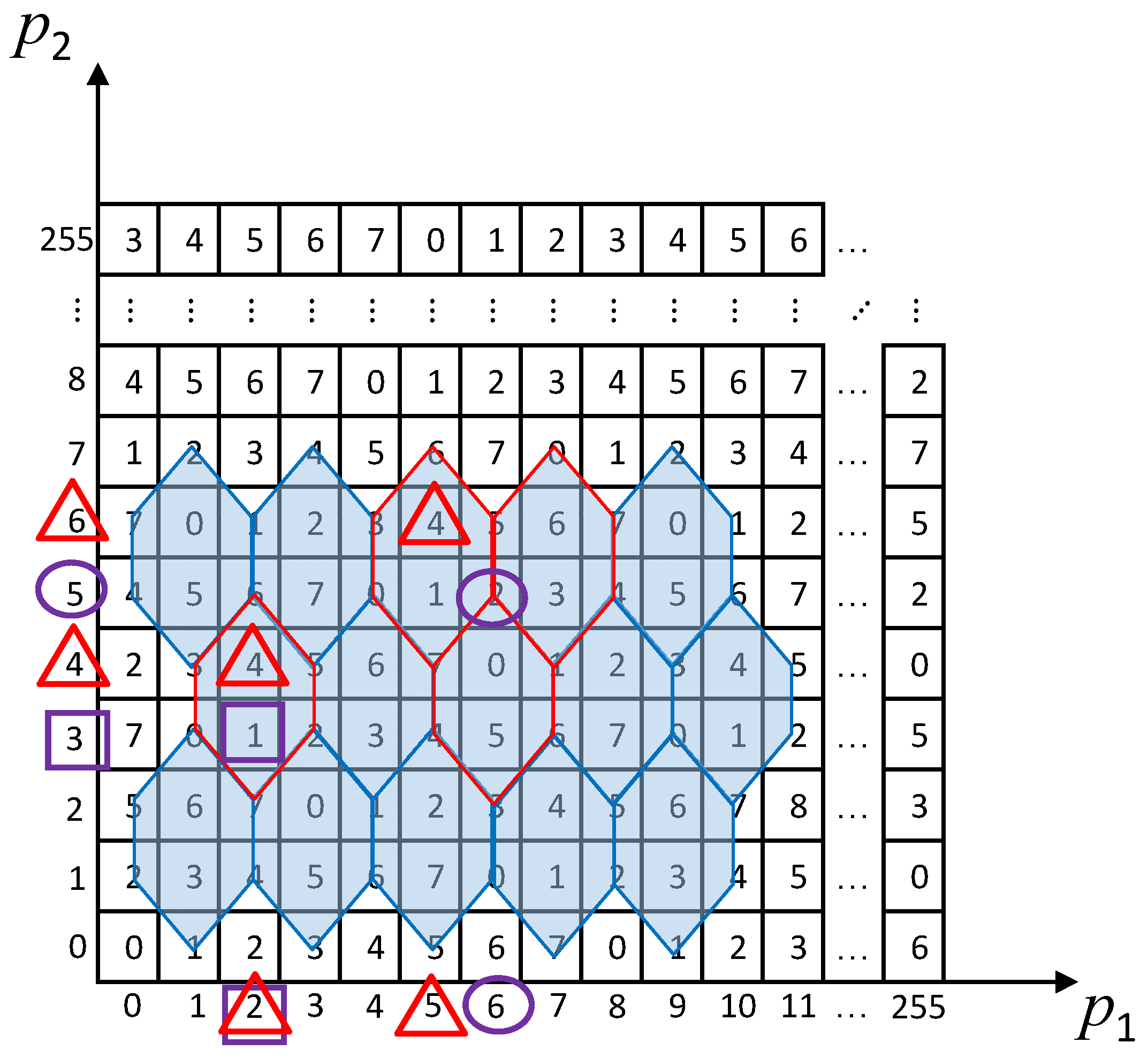
3.1. Special Hexagonal Tessellation Matrix Construction

The method of hiding data by filling hexagons in the matrix plane was first proposed by Chang et al. [2,3,4,5,6], who named this matrix the turtle shell matrix. This method requires the data hider to construct a $256\times 256$ reference matrix overlaid with turtle shells. Within this matrix, adjacent elements differ by 1 along the X-axis, while along the Y-axis, the differences alternate between 2 and 3. The construction function is defined in Equation (1), where (x, y) represent the coordinates of the matrix, and the range of x and y is [0, 255]. Multiple non-overlapping turtle shells are placed within the reference matrix (such as the blue hexagons in Figure 4), each containing eight numbers ranging from 0 to 7. These numbers consist of six elements along the shell’s edge and two elements on its back. By using pixel pairs from the cover image as matrix coordinates, a decimal number can be identified within a turtle shell. During the embedding process, secret data are first converted into decimal form. If the coordinate value of a pixel pair matches the embedded data, no modification is required. Otherwise, adjustments are made based on the position of the embedded value: If the coordinate lies on the turtle’s back, it is replaced with the coordinate of the embedded data found within the same turtle shell. If the coordinate is on the turtle shell’s edge, adjacent shells are examined to find the closest coordinate corresponding to the embedded data, which is then used for replacement. If the coordinate is outside the turtle shell, located at the matrix boundary, the nearest $3\times 3$ block is searched to find and replace the coordinate with the embedded data. Figure 4 illustrates the embedding and extraction process of Chang et al.’s scheme.

$$matrix\left(x,y\right)=\left((x mod 8)+⌊{\displaystyle \frac{y}{2}}⌋\times 5+\left(y-2\times ⌊{\displaystyle \frac{y}{2}}⌋\right)\times 2\right)mod 8.$$

(1)

Figure 4. This is an example of a turtle shell matrix.

Let us assume an example where pixel pairs (2, 3) and (6, 5) from the cover image need to embed the binary secret information $(100 100)₂$, which corresponds to the decimal values 4 and 4. In the figure, pixel pair coordinates are marked with purple, while the secret information is highlighted in red. To embed the first secret number 4 into pixel pair (2, 3), we need to locate pixel pair (2, 3) in the reference matrix. Since (2, 3) is positioned on the turtle’s back and its corresponding element does not match the embedded data, we replace it with the coordinate (2, 4), marked with a red triangle, where the embedded data are located. Next, to embed the second secret number 4 into pixel pair (6, 5), we observe that (6, 5) is on the turtle shell’s edge. We then examine adjacent turtle shells to find the nearest coordinate corresponding to the secret number 4. The closest matching coordinate is (5, 6), marked with a red triangle, which replaces the original pixel pair (6, 5).

During the extraction process, the receiver simply maps the stego pixel pairs (2, 4) and (5, 6) back onto the reference matrix to retrieve the decimal secret data 4 and 4. Converting these values to binary restores the original secret information $(100 100)₂$. Similar to the method of Chang et al. [2], our proposed hexagonal tessellation embedding method first requires constructing a special matrix. We consider the coordinate (1, 1) as the origin and assign it a value of 0. Then, for the values along the X-axis, the difference between every two adjacent values is 1. For the values along the Y axis, the difference between every two adjacent values is 2 and 3, alternately. Eventually, a special hexagonal tessellation matrix is constructed, where the X-axis coordinate range is $[-1024,-1]\cup [1,1023]$, and the Y-axis coordinate range is $[-1024,-1]\cup [1,1023]$. It is noteworthy that the special hexagonal tessellation matrix we constructed deliberately excludes a zero axis. This design decision stems from our scheme’s fundamental approach of embedding data exclusively within non-zero AC coefficients. The inclusion of a zero axis in the hexagonal tessellation matrix would potentially result in the modification of corresponding AC coefficients to zero during the embedding process, consequently affecting both the encoding of the compressed file and the visual quality of the resulting stego image. The specific matrix construction formula is as follows:

$$matrix\left(x,y\right)=\left\{\begin{array}{c}\left\{\left(x-1\right)mod 8+⌊{\displaystyle \frac{y-1}{2}}⌋\times 5+\left[\left(y-1\right)-⌊{\displaystyle \frac{y-1}{2}}⌋\times 2\right]\times 2\right\}mod 8, 1023\ge x\ge \mathrm{1,1023}\ge y\ge 1\\ \left\{\left(x-1\right)mod 8+⌊{\displaystyle \frac{y}{2}}⌋\times 5-\left[y-⌊{\displaystyle \frac{y}{2}}⌋\times 2\right]\times 3\right\}mod 8, 1023\ge x\ge 1,-1024\le y\le -1\\ \left\{x mod 8+⌊{\displaystyle \frac{y-1}{2}}⌋\times 5+\left[\left(y-1\right)-⌊{\displaystyle \frac{y-1}{2}}⌋\times 2\right]\times 2\right\}mod 8,-1024\le x\le -\mathrm{1,1023}\ge y\ge 1\\ \left\{x mod 8+⌊{\displaystyle \frac{y}{2}}⌋\times 5-\left[y-⌊{\displaystyle \frac{y}{2}}⌋\times 2\right]\times 3\right\}mod 8, -1024\le x\le -1,-1024\le y\le -1\end{array}\right.,$$

(2)

where $matrix\left(x,y\right)$ means the matrix value of the coordinate ($x,y$). In the special hexagonal tessellation matrix, each hexagon is distributed with values from 0 to 7. Multiple non-overlapping hexagons are placed within the matrix (such as the blue hexagons in Figure 5). We can see an example of an hexagonal tessellation matrix in Figure 5.

Figure 5. This is an example of a hexagonal tessellation matrix.

3.2. Data Hiding Process

After partitioning the image I into non-overlapping 8 × 8 pixel blocks, the spatial-domain data are transformed into the frequency domain using Equations (3) and (4). The computed DCT coefficients are then quantized by dividing them with the JPEG quantization table corresponding to the desired compression quality factor (QF). The quantized DCT coefficients are subsequently read in a zigzag scanning order, converting the two-dimensional representation of the quantized DCT coefficients within each block into a one-dimensional sequence. In each 8 × 8 block, the first coefficient is the DC coefficient, while the remaining 63 are AC coefficients. All non-zero AC coefficients from the blocks are paired into coordinate groups, and each group corresponds to a point P in a special hexagonal tessellation matrix. For every 3 bits of secret data read, they are converted into a decimal value $N$ ($N\in \left[\mathrm{0,7}\right]$).

$$DCT\left(u,v\right)=C(u)C(v)\times {\sum }_{i=0}^7{\sum }_{j=0}^{7}f(i,j)\cos ({\displaystyle \frac{2i+1}{16}}u\pi )\cos ({\displaystyle \frac{2j+1}{16}}v\pi ),$$

(3)

$$C\left(w\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\sqrt{8}}} w=0\\ 0.5 w\ne 0\end{array}\right.,$$

(4)

where $u$ and $v$ are the rows and columns of the block.

The embedding process first determines whether the point P corresponding to the non-zero AC coefficient pair is located inside a hexagon or on its edge within the matrix. If point P is inside a hexagon, the data hider finds the position of value $N$ within the same hexagon and modifies the non-zero AC coefficient pair to match the coordinates of value $N$, thereby completing the data embedding. For example, as shown in Figure 6, the non-zero AC coefficient pair (−5, −3) enclosed in a purple box corresponds to point 3 inside a blue hexagon. To embed the secret data ${\left(101\right)}_2={\left(5\right)}_{10}$, the data hider finds the position of 5 within the same hexagon corresponding to (−5, −3) and modifies the non-zero AC coefficient pair to (−6, −2), embedding the secret data 101.

Figure 6. This is an example of data embedding.

If point P lies on the edge of the hexagon, there are three adjacent shells associated with it. The data hider identifies the position of value N closest to point P within these three hexagons and modifies the non-zero AC coefficient pair. For example, in Figure 6, the non-zero AC coefficient pair (3, 2) enclosed in a purple circle corresponds to point 4, which is located on the edge of a blue hexagon. To embed the secret data ${\left(011\right)}_2={\left(3\right)}_{10}$, the data hider identifies the closest point with a value of 3 in the adjacent hexagon, and the non-zero AC coefficient pair (3, 2) is modified to (2, 2), embedding the secret data 011. If the point P is outside the hexagon, located at the matrix boundary, the nearest 3 × 3 block is searched to find the secret value N and replace the non-zero AC coefficient pair with the coordinate. As observed in Figure 6, when the hexagonal tessellation fully covers the non-zero AC coefficient coordinate space, only a few non-zero AC coefficient pairs at the boundaries lack corresponding hexagonal regions. However, the occurrence of such boundary coefficient pairs is extremely rare. Therefore, when employing a hexagonal tessellation matrix for data embedding, nearly all non-zero AC coefficient pairs can be utilized for embedding. Additionally, each hexagonal matrix contains elements ranging from 0 to 7, allowing for the embedding of 3 bits of data per instance. In summary, using a hexagonal tessellation matrix for data embedding in JPEG images significantly enhances their embedding capacity.

This process is repeated until all secret data have been embedded. If the amount of secret data is small, a termination symbol can be appended at the end of the secret data, while the remaining unused non-zero AC coefficients remain unchanged.

3.3. Data Extraction Process

The data extraction process is simple. Upon receiving the stego JPEG file, the recipient decodes the file according to the standard JPEG coding tables to obtain the DC and AC coefficients of each block. All non-zero AC coefficients are paired into coordinate groups, each of which corresponds to a value N in the special hexagonal tessellation matrix. Each N is then converted into a 3-bit binary number. By concatenating these binary data, the secret data are reconstructed. If a termination symbol is extracted during extraction, it indicates that all the secret data have been extracted, and there are no secret data hidden in the remaining non-zero AC coefficients.

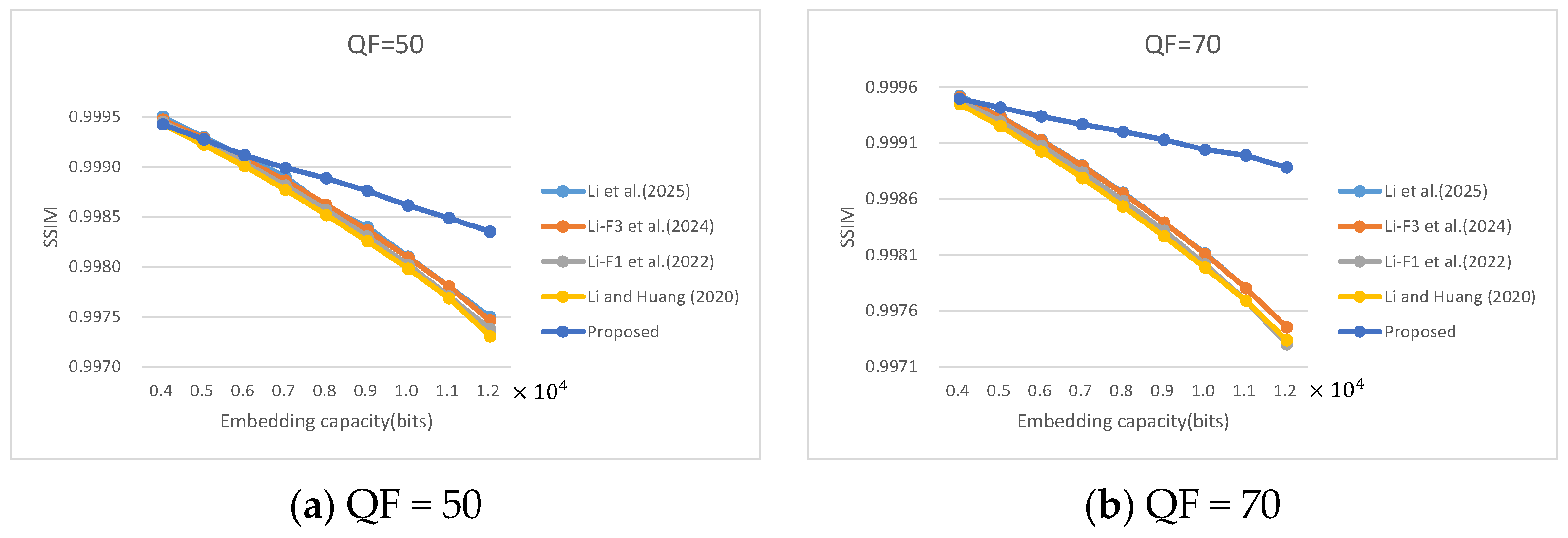
4. Discussion

In this section, a performance analysis of the method proposed in this paper is conducted, and comparisons are made with other existing methods. In the subsequent experiments, this method is tested using the six grayscale test images shown in Figure 7. These grayscale test images are from the commonly used image dataset USC-SIPI. To evaluate the performance of the proposed scheme, this invention analyzes the embedding capacity (EC) (unit: bits), file size increment (FSI) (unit: bits), entropy, file growth rate, peak signal-to-noise ratio (PSNR) (unit: dB), and Structural Similarity Index Measure (SSIM) of the proposed scheme.

$$MSE={\displaystyle \frac{1}{h\times w}}\sum _{i=1}^h\sum _{j=1}^w(O_{ij}-M_{ij}{)}^2,$$

(5)

$$\mathrm{PSNR}=10{\log }_{10}{\displaystyle \frac{{\left(\max \right)}^2}{\mathit{MSE}}}\left(\mathrm{dB}\right),$$

(6)

$$\phi \left(o_{\alpha }, d_{\alpha }\right)={\displaystyle \frac{\left(2{\mu }_o^{\alpha }{\mu }_d^{\alpha }+c_1\right)\left(2{\sigma }_{od}^{\alpha }+c_2\right)}{\left[{\left({\mu }_o^{\alpha }\right)}^2+{\left({\mu }_d^{\alpha }\right)}^2+c_1\right]\left[{\left({\sigma }_o^{\alpha }\right)}^2+{\left({\sigma }_d^{\alpha }\right)}^2+c_2\right]}},$$

(7)

$$\mathrm{SSIM}={\displaystyle \frac{1}{b}}\sum _{\alpha =1}^b\phi (o^{\alpha }, d^{\alpha })$$

(8)

Figure 7. Test images. (a) Airplane; (b) Baboon; (c) Boat; (d) Lake; (e) Peppers; (f) Splash.

Equations (5) and (6) define the computation of the PSNR, while Equations (7) and (8) outline the methodology for calculating the SSIM. In Equation (5), $h\times w$ denotes the image resolution, with $O_{ij}$ and $M_{ij}$ representing the pixel in the cover and stego images, respectively. In Equation (6), the term max refers to the maximum pixel, set at 255. The PSNR is measured in decibels (dB). In Equation (7), $\mu$ and $\sigma$ signify the mean and standard deviation, while constants $c_1$ and $c_2$ are assigned near-zero values to maintain stability in the SSIM computation. Equation (8) introduces $b$, the total number of blocks, and $\alpha$, the block index.

Typically, a PSNR exceeding 30 dB implies that the distortions introduced by data embedding remain undetectable to the human eye, with higher PSNR values indicating reduced visual degradation. Similarly, SSIM values closer to 1 suggest minimal perceptual differences between the stego and cover images.

Table 1, Table 2 and Table 3 present various performance metrics of the proposed method at a maximum embedding capacity across different test images and quality factors (QFs). Since the proposed method utilizes a special hexagonal tessellation matrix embedding approach, all non-zero AC coefficient pairs can be used for secret data embedding, with each pair embedding three bits. Consequently, the proposed method achieves a higher maximum embedding capacity than other approaches. The maximum embedding capacity refers to the highest amount of information that can be embedded in the test image using the proposed scheme. Image entropy measures the level of randomness, with values closer to eight indicating greater randomness. Here, $e_{original}$ represents the entropy of the original JPEG image, while $e_{stego}$ denotes the entropy of the stego JPEG image. As shown in the tables, embedding the maximum amount of data slightly increases the entropy of the stego JPEG image. However, this increase is minimal, demonstrating that even at full embedding capacity, the proposed scheme has a negligible effect on the image’s overall randomness. Even when all non-zero AC coefficient pairs are used for embedding, the file size increase remains minimal, reaching a maximum of only 5.34%, regardless of compression quality. Specifically, when the QF = 90, the file size increase does not exceed 5% for any test image, which is considered acceptable.

Table 1. Performance of proposed scheme on test images when QF = 90.

Image	FSI	Rate	PSNR	SSIM	${\mathit{e}}_{\mathit{o}\mathit{r}\mathit{i}\mathit{g}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}$	${\mathit{e}}_{\mathit{s}\mathit{t}\mathit{e}\mathit{g}\mathit{o}}$	Max EC
Airplane	16,596	3.34%	44.00	0.9853	6.7145	6.7190	107,343
Baboon	37,840	3.08%	39.51	0.9857	7.3651	7.3657	223,236
Boat	25,704	4.26%	41.74	0.9782	7.2137	7.2155	140,427
Lake	26,642	4.16%	40.65	0.9769	7.4612	7.4646	151,038
Peppers	24,931	4.80%	41.67	0.9716	7.5955	7.5971	121,728
Splash	16,573	4.43%	44.77	0.9794	7.2609	7.2673	92,886

Table 2. Performance of proposed scheme on test images when QF = 80.

Image	FSI	Rate	PSNR	SSIM	${\mathit{e}}_{\mathit{o}\mathit{r}\mathit{i}\mathit{g}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}$	${\mathit{e}}_{\mathit{s}\mathit{t}\mathit{e}\mathit{g}\mathit{o}}$	Max EC
Airplane	12,393	4.06%	43.71	0.9853	6.7240	6.7268	72,333
Baboon	24,578	3.94%	38.31	0.9853	7.3711	7.3716	160,677
Boat	16,934	4.40%	41.79	0.9802	7.2090	7.2102	92,280
Lake	16,715	4.16%	41.35	0.9818	7.4479	7.4508	98,193
Peppers	15,083	4.87%	42.99	0.9793	7.5943	7.5952	73,956
Splash	12,179	5.06%	44.72	0.9803	7.2668	7.2711	57,543

Table 3. Performance of proposed scheme on test images when QF = 70.

Image	FSI	Rate	PSNR	SSIM	${\mathit{e}}_{\mathit{o}\mathit{r}\mathit{i}\mathit{g}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}$	${\mathit{e}}_{\mathit{s}\mathit{t}\mathit{e}\mathit{g}\mathit{o}}$	Max EC
Airplane	9442	3.91%	43.49	0.9860	6.7287	6.7325	57,012
Baboon	21,407	4.33%	37.93	0.9851	7.3735	7.3741	129,621
Boat	13,288	4.51%	41.96	0.9828	7.2039	7.2050	72,150
Lake	13,423	4.28%	41.68	0.9834	7.4492	7.4512	77,412
Peppers	11,963	5.03%	43.34	0.9817	7.5951	7.5955	55,797
Splash	9912	5.34%	44.90	0.9813	7.2706	7.2743	42,132

In terms of visual quality, only the texture-rich Baboon image exhibits slightly lower PSNR and SSIM values. However, even for Baboon, the PSNR remains at 37.93 dB. But the maximum embedding ability of Baboon is also higher than that of other test images. Other test images maintain PSNR values above 40 dB under full embedding conditions, ensuring imperceptible visual differences to the human eye. This indicates that an observer attempting to detect hidden data based on visual quality alone would find it difficult, as the visual quality of the proposed method remains highly similar to that of the original JPEG image.

We utilized ChatGPT-4o(GPT-4-turbo) to generate corresponding descriptions for the six test images shown in Figure 7. As demonstrated in Table 4, contemporary AI technology effectively performs image analyses and generates appropriate textual descriptions. The bit requirements for encoding these textual descriptions are relatively modest; in the examples presented in Table 4, a maximum of 6000 bits sufficiently describes the test images, well within the maximum embedding capacity of our proposed method. These results confirm the feasibility of encapsulating textual descriptions within images using the proposed knowledge encapsulation method.

Table 4. Generated descriptions for images using ChatGPT-4o.

Image	Description Generated by ChatGPT-4o	Bits
Airplane	The black-and-white photograph captures a U.S. Air Force jet, possibly a General Dynamics F-16 prototype, soaring above a rugged, snow-covered mountain range. The aircraft’s sleek, aerodynamic form, featuring a pointed nose and delta wings, is prominently displayed. Markings on the fuselage include ‘U.S. AIR FORCE,’ while the tail section bears the identification number ‘01568’ and the General Dynamics logo. The jet appears to be in mid-flight, maintaining a high altitude just above the jagged mountain peaks. The background consists of towering, snow-covered mountains, with a partially cloudy sky adding depth to the scene. The monochrome tones highlight the contrast between the aircraft and the dramatic natural landscape.	4800
Baboon	The image is a grayscale close-up photograph of a mandrill, a primate species known for its distinctive facial features. The focus is on the front of the mandrill’s face, showcasing its symmetrical structure. The mandrill has deep-set, round eyes with a piercing gaze, surrounded by dark fur. Its nose is long and prominently structured, with vertical ridges extending down both sides. These ridges are lighter in tone compared to the surrounding facial fur. The nostrils are positioned near the lower part of the nose, just above its closed mouth, which appears neutral. The thick fur around the face creates a sense of depth and texture. Individual hair strands are visible, particularly around the cheeks and chin. The fur consists of varying shades of gray, providing contrast between different regions of the face. The background is out of focus, ensuring that the mandrill’s facial details remain the central visual element. The high contrast and sharpness of the image emphasize the intricate patterns on the mandrill’s face.	4912
Boat	The image depicts a coastal scene with several fishing boats docked on a shore. The boats are positioned in a row, with the one closest to the viewer prominently displaying the name “LA CORNUAILLE” on its hull. The hulls of the boats are weathered, showing signs of wear from their time at sea. The boats are equipped with tall masts and rigging, with fishing equipment such as ropes, nets, and lifebuoys hanging from various parts of the structures. In the background, a lighthouse is visible, adding to the maritime setting. The sky is partly cloudy, with soft clouds scattered throughout. The ground appears to be a mixture of wet sand and small rocks, suggesting that the boats are resting onshore during low tide. To the right of the image, a person wearing a jacket and boots stands near the boats, possibly a fisherman or a worker inspecting the vessels.	6000
Lake	The image depicts a tranquil lake scene with a sailboat gliding across the calm waters. The photograph is framed by tall pine trees in the foreground, which provide a natural border to the serene landscape. The lake reflects the surrounding trees and the sky, adding to the peaceful atmosphere. The sailboat, with its white sail, stands out as the focal point, contrasting against the darker tones of the water and trees. In the background, a dense forest stretches across the horizon, with scattered clouds above adding depth to the scene. The overall composition emphasizes the harmony between nature and human activity, creating a picturesque and timeless landscape.	5424
Peppers	The image is a grayscale close-up photograph of a variety of peppers, arranged in an overlapping manner. The assortment includes large bell peppers with smooth, shiny surfaces, as well as elongated chili peppers with slightly wrinkled textures. The peppers are positioned at various angles, creating a natural composition. Light reflections on the surfaces of the peppers add depth and emphasize their three-dimensional shapes. Some peppers have stems attached, which curve slightly, adding an organic feel to the arrangement. The background consists of more peppers, some of which are partially obscured, blending into the scene. The high contrast in the grayscale image helps differentiate the individual peppers, highlighting their contours and subtle surface imperfections.	5200
Splash	The image is a high-speed grayscale photograph capturing a liquid splash that resembles a crown-like formation. The splash occurs in a shallow dish, where a drop of liquid, likely milk or another white fluid, has impacted the surface, creating a symmetrical ring with elongated tendrils extending outward. The liquid forms a near-perfect circular structure, with droplets suspended at the edges, giving it a delicate and dynamic appearance. The dish holding the liquid is smooth and reflective, adding depth to the image. The background is slightly blurred, ensuring that the splash remains the central focus. The lighting is soft and evenly distributed, highlighting the intricate details of the splash without creating harsh shadows or overexposure. The high contrast between the liquid and the background enhances the visual clarity of the motion captured.	5600

In addition, we also tested it on two color images, Baboon and Peppers. Figure 8 presents a comparison of various methods under a quality factor (QF) of 80 with a 10,000-bit embedding capacity. The results demonstrate that, using the proposed scheme, both the highly textured image Baboon and the smoother image Peppers maintain a high visual imperceptibility, making it difficult to distinguish whether data have been embedded.

Figure 8. The visual comparison between the original JPEG images and stego JPEG images for the two testing images with a QF = 80 and embedding capacity of 10,000 bits.

Additionally, our scheme is evaluated against several existing approaches. We compare four different methods at QF values of 50, 70, and 90, with the corresponding results summarized in Table 5. The table indicates that, in most cases, our method outperforms the alternatives. Specifically, while the proposed scheme does not achieve the highest PSNR for the two color test images under QF = 50 with a 1000-bit embedding and QF = 70 with a 3000-bit embedding, it is evident that as the embedding capacity increases, the PSNR of the other methods declines more rapidly, whereas our scheme exhibits a slower degradation. Consequently, Table 5 shows that with increasing data storage, the PSNR of the proposed method gradually surpasses that of the other schemes. This superior performance is attributed to our use of a hexagonal tessellation matrix embedding approach, where each pair of non-zero AC coefficients encodes three bits. As a result, fewer non-zero AC coefficients are required, and no coefficient pairs undergo shifting, thereby reducing unnecessary distortion. In contrast, other methods employ two-dimensional histogram modification, which, at higher embedding capacities, necessitates modifying a greater number of shiftable coefficient pairs to ensure correct extraction and image reversibility. This results in a substantial number of ineffective mappings, ultimately degrading the visual quality.

Table 5. Comparison of visual quality (PSNR) and file size increment (FSI) for four SOTA schemes. Three quality factors (QFs) and three different capacities are tested over two RGB images.

Image	Scheme	PSNR									FSI
		QF = 50			QF = 70			QF = 90			QF = 50			QF = 70			QF = 90
		1000	4000	6000	3000	6000	9000	9000	12,000	15,000	1000	4000	6000	3000	6000	9000	9000	12,000	15,000
Baboon	Li-N [9]	51.32	44.1	41.66	48.78	44.93	42.14	47.17	45.19	43.54	784	3768	5752	3072	6344	10,072	12,016	16,344	19,216
	Li-F1 [22]	52.02	44.28	41.72	49.28	45.06	42.29	47.14	45.16	43.58	712	3208	5816	2864	6192	9832	11,736	15,880	19,152
	Li-F3 [23]	52.26	44.55	41.92	49.37	45.29	42.45	47.25	45.25	43.65	744	3096	5512	2976	5784	9136	10,720	14,496	18,432
	Li [29]	52.3	44.58	42.02	49.44	45.34	42.48	47.28	45.28	43.69	400	3024	5136	2488	5760	9032	11,384	14,464	18,328
	Proposed	51.26	45.32	43.23	49.07	45.96	43.68	47.44	46.22	45.24	184	231	203	335	307	371	392	533	498
Peppers	Li-N [9]	52.04	45.11	42.44	50.86	47.3	44.81	51.82	50.16	48.77	1232	4664	7160	3696	7128	10,240	10,296	13,992	18,896
	Li-F1 [22]	53.79	45.39	42.51	52.05	47.97	45.18	52.08	50.35	48.89	1264	4328	7152	3448	6960	9736	10,288	14,008	17,496
	Li-F3 [23]	53.9	45.84	43.22	52.16	48.21	45.54	52.27	50.55	49.14	1352	4248	6528	3392	6520	9480	9592	13,472	17,440
	Li [29]	53.98	45.94	43.28	52.2	48.3	45.63	52.32	50.59	49.18	1216	4216	6488	3376	6480	9208	9368	13,440	17,848
	Proposed	52.16	48.33	45.91	51.88	49.71	48.69	52.52	51.22	50.32	84	114	123	147	134	177	170	333	360

Regarding file size increments, our approach demonstrates a significant advantage over existing methods. Since each pair of non-zero AC coefficients embeds three bits, under the same payload, fewer non-zero AC coefficients need to be modified, with changes limited to ±1 per modification. Table 5 further reveals that while the FSI generally increases with embedding capacity, exceptions occur—such as at QF = 70, where embedding 6000 bits results in a lower FSI than embedding 3000 bits. This discrepancy arises because the two-dimensional histogram embedding method in other schemes typically expands non-zero AC coefficients, pushing positive values further toward positive infinity and negative values toward negative infinity, leading to a substantial increase in compressed file size. The hexagonal tessellation matrix embedding method facilitates bidirectional coefficient modification, wherein positive values are adjusted toward negative infinity and negative values toward positive infinity, contingent upon the embedded secret data. This approach reduces the bit requirement during the encoding process, thereby effectively mitigating file size expansion.

Figure 9 display the FSI across three test images with different QF values and embedding payloads. Regardless of the test image, the amount of embedded data, or the compression quality, the proposed method consistently results in significantly smaller file size increments compared to the seven other methods. In some cases, the increase is as low as 39 bits, corresponding to only a 0.02% growth rate. The reason for achieving this low FSI is that the special hexagonal tessellation matrix embedding method ensures that each non-zero AC coefficient pair embeds three bits without unnecessary shifting modifications. When embedding a smaller amount of data, fewer non-zero AC coefficients are altered, preserving a larger proportion of unmodified coefficients. A smaller file size increment makes it more difficult for adversaries to infer the presence of hidden data based on a file size analysis.

Figure 9. File size increment (bits) comparison for our scheme and seven advanced JPEG RDH schemes [9,17,19,22,23,26,28].

By analyzing Table 1, Table 2 and Table 3, and Figure 9, we observe that for the test images Airplane and Splash, the FSI of the proposed method at the maximum embedding capacity is still lower than that of other methods that only embed a small amount of information. This suggests that, for similar file size increments, the proposed method enables a significantly higher embedding capacity.

We also conducted SSIM comparison experiments on the BOSSbase v1.01 dataset, with the results presented in Figure 10. The experiments were performed under two quality factor settings, QF = 50 and QF = 70, to evaluate the SSIM of stego images at varying embedding capacities. A higher SSIM value, closer to one, indicates greater similarity between the stego and original images. As shown in Figure 10, the proposed method exhibits the smallest SSIM decline as the payload increases. Although the average SSIM of the proposed method is not the highest at an embedding capacity of 4000 bits, it maintains a higher image similarity than other methods when embedding larger amounts of data. In contrast, other approaches show a significant drop in SSIM, leading to stego JPEG images that deviate more noticeably from their original counterparts.

Figure 10. SSIM comparison for two quality factors (QF = 50, 70) and different embedding capacities. Four SOTA JPEG DH schemes [9,22,23,29] and proposed scheme are tested on BOSSbase v1.01 image set.

5. Conclusions

This paper proposes a knowledge encapsulation method for JPEG images using a special hexagonal tessellation matrix. The proposed approach constructs a special hexagonal tessellation matrix that enables the utilization of all non-zero AC coefficient pairs for secret data embedding. The experimental results demonstrate that the method effectively balances a higher embedding capacity, good visual quality, and smaller file size expansion while preserving the JPEG format. We observed that the proposed scheme occasionally exhibits suboptimal PSNR values when embedding small data volumes. This limitation stems from our sequential embedding approach that does not selectively target specific DCT blocks. Consequently, our future research will focus on developing a smoothness algorithm for DCT blocks, prioritizing embedding in smoother blocks to minimize image distortion at lower embedding capacities.