Optimized Kuhn–Munkres with Dynamic Strategy Selection for Virtual Network Function Hot Backup Migration

Abstract

In Follow-Me Mobile Edge Cloud (FMEC) environments, Virtual Network Function (VNF) instances dynamically move in tandem with user mobility. For latency-sensitive applications, hot backups aim to reduce service downtimes during primary VNF instance failures. However, as the distance between VNF instances and their hot backups shifts due to user mobility, recovery latency can sometimes exceed user expectations, leading to certain backups being perceived as unavailable. To maintain VNF reliability, it becomes essential to either deploy additional hot backups closer to the VNF instances or migrate the deemed unavailable backups to proximity, reinstating their usability. How to effectively leverage both the VNF and its failed hot backups to ensure VNF reliability, meet users’ recovery latency demands, and minimize the overall cost of hot backup migration and redeployment is a challenging problem. To address this challenge, we propose a hybrid approach combining an optimized Kuhn–Munkres algorithm and dynamic strategy selection for cost-efficient hot backup migration. The problem is first formulated as an integer linear programming model and proven Non-deterministic Polynomial-time hard (NP-hard). To address computational complexity, we propose an optimized Kuhn–Munkres algorithm with dynamic strategy selection. The Kuhn–Munkres algorithm accelerates backup migration through network preprocessing and multi-constraint candidate filtering, while adaptively choosing between migration and redeployment via real-time cost analysis. Through extensive experiments, our hybrid migration algorithm achieves equivalent user demand satisfaction as traditional methods while reducing backup VNF (BVNF) migration costs by 15%. The proposed approach combines an optimized Kuhn–Munkres algorithm for efficient candidate selection with dynamic cost-aware strategy switching, ensuring reliable latency-sensitive service in mobile edge environments.

1. Introduction

Mobile edge computing (MEC) is a technology that provides cloud computing resources and services close to end-users and devices at the edge of the network [1]. The technology processes and stores data locally, enabling low-latency and high-bandwidth applications, rather than transmitting it to a central cloud server. MEC is overcoming traditional cloud computing’s bottlenecks, including high network congestion and long communication delays. MEC facilitates new applications and services that require real-time, low-latency data processing, including smart cities, self-driving cars, and augmented reality. Currently, MEC adoption is rapidly accelerating in various industries, such as entertainment, transportation, and healthcare, and is playing a critical role in 5G network and Internet of Things (IoT) advancement [2].

The Follow-Me mobile edge computing technique offers user mobility support [3]. As a user moves to different locations, the VNF migrates to the nearest edge node. Due to Follow-Me mobile edge computing moving computing and storage resources closer to users, it further reduces the distance and volume of data transmission, resulting in lower network costs. In this environment, where VNF instances dynamically migrate to maintain proximity to mobile users, hot backups play a critical role in minimizing service downtime for latency-sensitive applications during primary VNF failures. This approach ensures seamless service continuity through active synchronization and orchestration mechanisms.

The reliability of VNFs is crucial in the context of MEC, as it directly influences the continuity of services provided by MEC. In MEC scenarios, numerous critical applications and services depend on the normal operation of VNFs. The occurrence of VNF failures or unreliability can give rise to the following three issues: Firstly, it can result in service interruptions or performance degradation, manifesting as increased service response times, which can lead to user dissatisfaction. Secondly, it can cause service disruptions or erroneous data processing, thereby increasing the wastage of network resources. Thirdly, security functionalities such as firewalls and intrusion detection systems rely on reliable VNFs to provide protection. If VNFs have vulnerabilities or exhibit unreliability, it can elevate the risks of network attacks or data breaches.

To address these concerns, hot backups are often deployed in MEC environments to ensure high availability and minimize the impact of VNF failures. Hot backups maintain pre-instantiated VNF instances in standby mode, synchronized with the primary instance’s state, enabling sub-second failover capabilities [4]. This failover capability is critical in MEC applications such as augmented reality or autonomous vehicle coordination, where even milliseconds of latency can have severe consequences. By leveraging hot backups, MEC systems can significantly improve service reliability, reduce latency, and ensure seamless operation of essential services.

Deploying multiple replicas of VNF is a common way to improve the reliability of VNF [5]. In the event of VNF failure, service requests automatically switch to an available VNF replica to maintain service continuity. As the user moves, VNF replicas are redeployed to the edge nodes close to the user, reducing bandwidth cost and minimizing service interruption time during potential VNF failures [6].

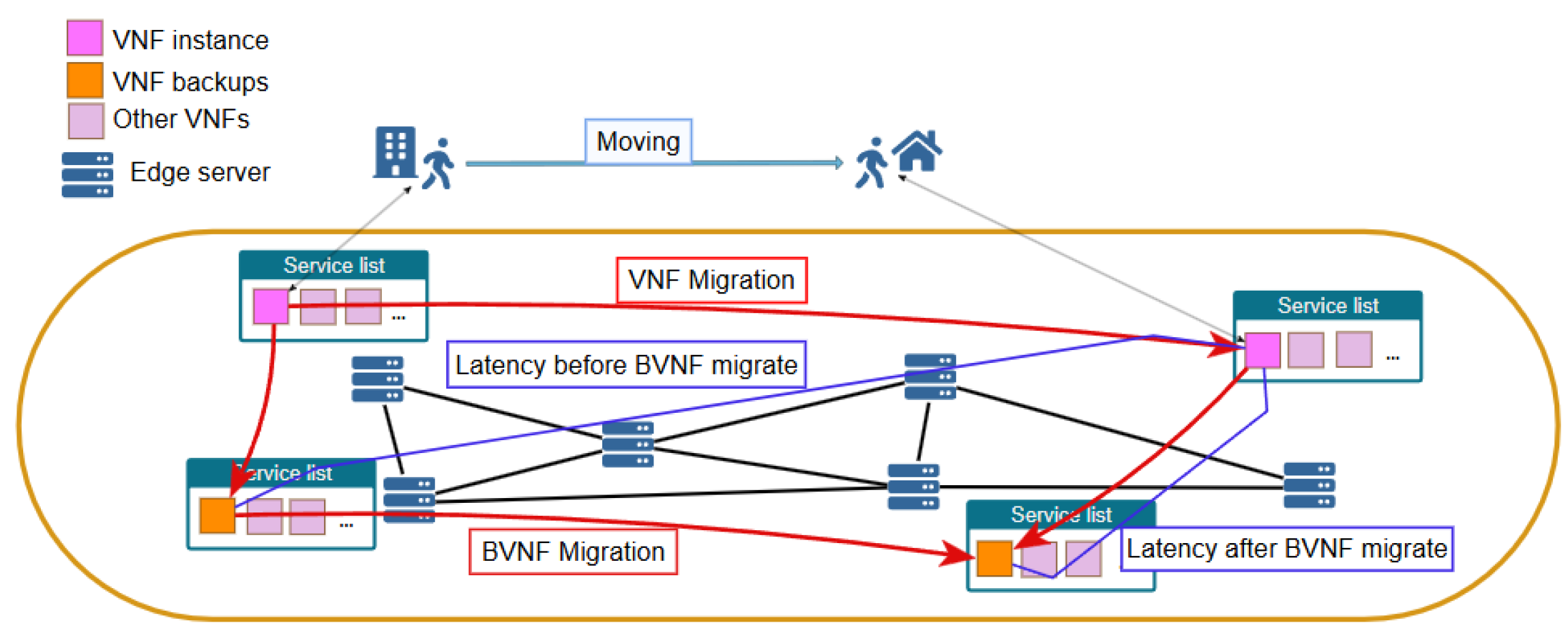
In the FMEC environment, user mobility introduces new complexities related to the deployment and migration of BVNFs. The unpredictable nature of user movement leads to dynamic changes in the latency between VNFs and their corresponding backups. When this latency exceeds a predefined threshold, it can make the backup function inaccessible or unreliable. As a result, when users move to a new region, both the VNFs providing the requested services and their corresponding BVNFs must be either redeployed or migrated to locations that are closer to the user’s new location, as depicted in Figure 1. However, frequent migration of BVNFs increases bandwidth consumption, thereby leading to substantial costs.

In this paper, we demonstrate its NP-hardness by simplifying it into a multidimensional knapsack problem. Additionally, considering the perspectives of mobile users and edge servers, we jointly examine the impact of constraints such as latency, resource limitations, and VNF reliability on edge BVNF migration, thus enhancing the accuracy of the backup migration cost model. The scale of the problem exponentially increases with the number of BVNFs that need to be migrated and the number of potential edge server locations for migration.

To resolve the above challenges, we propose a multi-stage approach. First, the state space is formed by considering the backup and potential migration locations for VNFs. Subsequently, various factors are taken into account to determine the most appropriate algorithm for reducing the state space, aiming to minimize the overall algorithm’s runtime. Next, a thorough evaluation of each state’s priority is conducted. During this process, factors such as resource requirements, reliability, the migration’s bandwidth cost, and latency before and after migration are considered in determining the priority of each state. Finally, based on the prioritization analysis, suitable states are selected for BVNF migration.

The main contributions of this paper are as follows:

• To the best of our knowledge, we are the first to consider the secondary utilization of failed hot backups while deploying BVNFs. In doing so, we aim to minimize deployment and migration costs while taking into account factors such as latency and reliability. We model this problem as an integer linear programming problem and prove that it is NP-hard.
• To alleviate the solution complexity, we introduce a multi-stage algorithm. This algorithm can address the multi-source VNF hot backup migration problem with latency, capacity, and reliability constraints in polynomial time.
• Through extensive experiments, we validate that our proposed hybrid migration algorithm achieves the same level of user demand satisfaction as traditional migration algorithms while reducing BVNF migration costs by approximately 15%.

2. Related Works

The migration and backups of VNF are two critical aspects of Network Function Virtualization (NFV), playing an essential role in ensuring the seamless operation, high availability, and reliability of network services. Over the years, researchers and practitioners have devoted significant efforts to explore and improve VNF migration and backup mechanisms. In this section, we provide a comprehensive review of the existing literature, organizing the discussion into three main areas: VNF reliability, VNF migration approaches, and BVNF strategies.

2.1. VNF Reliability

The issue of VNF reliability in the context of user mobility and recovery latency is a significant concern in telecommunications. As users move, the distance between VNF instances and their hot backups can increase, which may lead to recovery latencies that exceed user expectations. This situation can result in backups being perceived as unavailable, impacting the overall quality of service [7,8,9,10].

• User Mobility: The dynamic nature of user mobility necessitates that VNFs maintain low latency for recovery operations. When the distance between VNFs and their backups increases, the time taken to recover from failures can become unacceptable, leading to service disruptions.
• Recovery Latency: Recovery latency is critical in telecom services where outages must be minimized to milliseconds. If recovery times extend beyond this threshold, users may experience significant service degradation [11,12].
• Backup Availability: Hot backups must be readily accessible to ensure that if a primary VNF fails, service can be quickly restored without noticeable delays. However, as the distance increases, the effectiveness of these backups diminishes, making them seem unavailable when needed [13].

To address these challenges and maintain VNF reliability, several strategies can be employed:

• Deploy Additional Hot Backups: Placing more hot backup instances closer to active VNF instances can significantly reduce recovery times. This approach ensures that backups are within a minimal distance, facilitating quicker failover processes [14].
• Migration of Backups: Another effective strategy is to migrate the backups deemed unavailable closer to their corresponding VNF instances. This proactive measure helps reinstate usability and minimizes latency during recovery operations [11,13].
• Dynamic Resource Management: Implementing dynamic resource management techniques allows for real-time adjustments based on user mobility patterns and network conditions. This includes optimizing the placement of both active and standby VNF instances to ensure they are strategically located for quick recovery [14].

2.2. VNF Migration Approaches

VNF migration is the process of transferring a running VNF instance from one edge server to another without disrupting the service. Several migration approaches have been proposed to optimize VNF performance and resource utilization.

VNF migration can be categorized into offline migration and live migration. In offline migration, services are temporarily terminated during the migration process, while live migration [15,16,17] allows services to continue running without interruption for most of the migration process. Sun et al. [15] introduced improved serial migration strategies, a mixed migration strategy, and developed queuing models to quantify performance metrics. Rong et al. [16] classified states into three types and used three different techniques (warm-up, synchronization, and replay) for migration. Shi et al. [17] achieved live migration by continuously monitoring and dynamically selecting different models based on various memory/disk operations. Some articles utilized machine learning models to predict the probability of VNF failures and proactively initiate migration [17,18].

Cho et al. [19] proposed a novel VNF migration algorithm called VNF Real-time Migration (VNF-RM) aimed at reducing network latency during dynamic resource availability changes. They address the challenges of maintaining performance while migrating VNFs in real-time environments. Afrasiabi et al. [20] focused on optimizing cluster VNF migration while considering inter-VNF latency requirements. They provided insights into efficient migration strategies within service function chains. Wang et al. [21] proposed a method for coordinating updates to both the network function state and the software-defined networking (SDN) forwarding state during VNF migrations, ensuring consistency and reliability in service delivery. Tang et al. [22] presented a real-time VNF migration algorithm utilizing deep belief networks to predict future resource needs, enhancing the efficiency of migration processes in dynamic environments. Carpio et al. [23] discussed the flexibility and programmability offered by NFV, focusing on balancing the migration of VNFs while considering replication strategies to optimize resource usage and performance.

2.3. BVNF Strategies

BVNF mechanisms play a crucial role in protecting critical data and configurations, enabling efficient recovery in the event of VNF failures or disasters [6,24,25].

Wang et al. [25] utilized online learning techniques and the UCB (Upper Confidence Bound) algorithm to estimate the popularity and failure rate of Service Function Chaining (SFC). Subsequently, the RTSD (Real-Time Selection and Deployment) algorithm was employed to implement backup deployment. Shang et al. [6] extended the conventional static backup deployment by additionally considering dynamic backups. According to requirements, an online algorithm is utilized to dynamically adjust the quantity of dynamic backups. Iftikhar et al. [26] proposed a blockchain-based edge network authentication technology (BCAuthEN), which addresses security vulnerabilities in smart city networks through decentralized authentication while ensuring continuous user verification and service availability in real-time edge networks. Ly et al. [27] provided a systematic literature review on the reliability of VNF chains, exploring the application of various algorithms and methods in ensuring reliability. The study covers a range of novel reliability algorithms and analyzes their applicability and effectiveness in modern networks. Yang et al. [28] studied the fault-tolerant placement problem of stateful VNFs, with the optimization goal of accommodating as many requests as possible while ensuring the continuity and stability of service chains.

Recognizing the importance of both VNF migration and backup, some studies have proposed integrated solutions that combine migration and backup mechanisms to achieve enhanced VNF resilience. Aidi et al. [29] leveraged VNF migration to relocate the VNFs in order to minimize the number of shared BVNFs. Gong et al. [30] explored distributed edge computing (DEC) to minimize the delay in executing computation tasks offloaded from end devices, focusing on the optimal computation allocation and communication scheduling policies. Their work offers valuable insights into computation–communication co-design, with efficient algorithms for selecting devices and scheduling communications. Yang et al. [31] proposed a proactive method to avoid routing hotspots in peer-to-peer (P2P) streaming applications by defining an incentive-compatible pricing vector and ensuring that all nodes follow this policy. Their adaptive algorithm for distributed computation of the pricing vector effectively prevents congestion and routing hotspots, as shown by simulation results. Tu et al. [32] studied efficient resource utilization in wireless networks to maximize concurrent multimedia flows under channel saturation, focusing on flow scheduling and channel aggregation policies. They proposed the efficient multi-flow multicast transmission algorithm to implement these policies in practical multicast applications, with simulations demonstrating its effectiveness in increasing multimedia flow admission.

Some studies also employ deep learning techniques to ensure the recovery of failed VNFs. Ishigaki et al. [33] addressed the progressive recovery problem in virtualized networks with limited resources, where interdependencies between VNFs and infrastructure elements complicate the recovery process. They propose DeepPR, a deep reinforcement learning-based technique, which achieves near-optimal solutions and outperforms baseline heuristics in terms of robustness to adversarial failures. Qu et al. [34] proposed a priority-awareness deep reinforcement learning (PA-DRL) algorithm to enhance the reliability and optimization of service function chains (SFC) by dynamically determining backup server placement. Mao et al. [35] proposed a deep reinforcement learning-based online SFC placement method that integrates active and standby VNF instances to enhance fault tolerance and service reliability. Ros et al. [36] proposed a graph neural network-based deep reinforcement learning (GRL-SFT) model to enhance the fault tolerance of service function chains (SFC) in NFV environments. Wang et al. [37] proposed a deep reinforcement learning-based joint VNF partition and hybrid backup algorithm for VNF orchestration, enhancing the reliability and delay performance of network slices at minimal cost. Zhang et al. [38] studied the DT migration problem in MEC networks, aiming to minimize the synchronization and service costs for mobile suppliers and consumers. They proposed a deep reinforcement learning (DRL) algorithm and validated its effectiveness through experimental simulations.

However, the aforementioned articles do not consider utilizing previously deployed BVNFs when discussing BVNFs. Specifically, after each VNF migration, various BVNF methods are employed to redeploy backups around the migrated VNF to reduce backup recovery latency. However, the migration cost of existing BVNFs may be lower than the cost of redeploying BVNFs. In contrast, in our approach, during the VNF migration process, we utilize existing BVNFs. To minimize costs, we only perform the live migration of appropriate BVNFs if the backup recovery time exceeds user requirements, rather than redeploying all BVNFs. The Digital Twin Migrations proposed by Zhang et al. 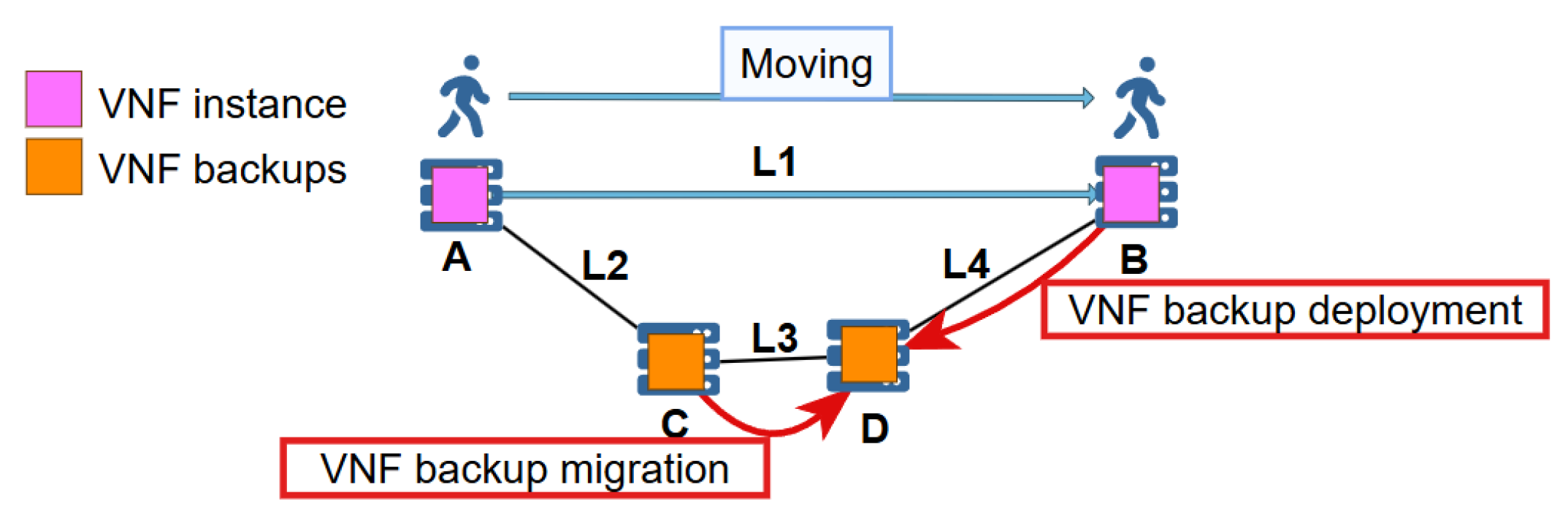[38] in their paper are similar to the VNF hot backup migration in this paper. However, the former considers a one-to-one scenario, while this paper considers a one-to-many scenario. As shown in Figure 2, suppose the VNF instance requested by the user has a backup. When the VNF instance migrates from A to B along with the user’s movement, the BVNFs on edge server C need to be migrated or redeployed to an edge server closer to B due to the high recovery delay between B and C. In this case, the BVNFs need to be redeployed on D. If the migration cost from L3 is less than L4, the BVNF migration algorithm can be used to migrate the backup from C to D. Otherwise, the backup should be redeployed from B to D.

3. System Model and Problem Formulation

3.1. Network Model

In this paper, we examine the Follow-Me MEC system with limited resources and represent it as an undirected weighted graph $G=(V,E)$. The set V represents edge servers in the mobile edge network, and the set $E=e_{u,v}(u,v\in V)$ signifies links between two servers u and v in G.

3.2. User Requests

We use $r_m=(F_m,T_m^{err},C_m)$ to denote a single user request and $R=r_m$ to denote the set of requests. For simplicity, we assume that each user requests a VNF instance and this can be extended to multiple VNF instances. $F_m=\{f_{m,0},f_{m,1},\cdots ,f_{m,n}\}$ denotes the VNF instance and its backups requested by the user request $r_m$. Here, $f_{m,0}$ represents the user’s requested VNF instance, and $f_{m,i}(1\le i\le |F_m\left|\right)$ represents backup instances of the user’s requested VNF instance. The edge server’s location of the BVNF instance $f_{m,i}$ is denoted by $V_{f_{m,i}}$. The parameter $T_m^{err}$ defines the maximum average fault recovery delay that the user’s request $r_m$ can tolerate. In this study, we consider real-time backups and assume that the VNFs and their backups in request $r_m$ utilize the same computing resources, denoted by $C_m$.

3.3. Delay Constraint

Our study uses a binary variable, denoted by $P_{f_{m,i},v_n}$, to identify the placement of BVNFs.

$$P_{f_{m,i},v_n}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{VNF}{f}_{m,i}\mathrm{is}\mathrm{deployed}\mathrm{on}{v}_n\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\forall f_{m,i}\in F_m,\forall v_n\in V,\forall r_m\in R$$

(1)

The value of $P_{f_{m,i},v_n}$ equals 1 if VNF $f_{m,i}$ of request $r_m$ is hosted on edge server $v_n$, and it equals 0 otherwise.

Storing BVNFs on two separate servers can mitigate single-point failures, thereby improving system availability. In the event of a server failure, the backup system can continue to function without interruption and rapidly resume control of the primary instance, thereby ensuring the VNF system remains fully operational.

$$P_{f_{m,i},v_n}+P_{f_{m,j},v_n}=1,\forall f_{m,i},f_{m,j}\in F_m,i\ne j,\forall v_n\in V,\forall r_m\in R$$

(2)

$$\sum _{\forall v_n\in V,\forall r_m\in R}{P}_{f_{m,i},v_n}=1,\forall f_{m,i}\in F_m$$

(3)

Assuming that the delay of the link $(u,v)$ between edge servers u and v is relatively stable, we employ the Dijkstra algorithm to determine the shortest delay between any two edge servers in an undirected weighted graph [25]. We denote the shortest delay between edge servers $(u,v)$ as $l(u,v)$, and represent the set of link delays as $L=l(u,v)\left|\right(u,v)\in V$. It is worth noting that we use $l(V_{f_{m,0}},V_{f_{m,i}})$ to calculate the necessary delay required for recovery from each backup of VNF $f_{m,i}$ in the event of a failure.

Hence, the formula for determining the average delay in recovering from a fault when the VNF instance $f_{0,m}$ fails is obtainable and given as follows:

$$T_{r_m}^{all}={\displaystyle \frac{{\sum }_{i=1}^{|F_m|}l(V_{f_{m,0}},V_{f_{m,i}})}{|F_m|}}$$

(4)

Therefore, the delay constraint that we need to satisfy is:

$$T_{r_m}^{all}\le T_m^{err}$$

(5)

3.4. Resource Constraint

The resource constraints of the edge server must be taken into consideration for successful deployment of the VNF and its backups. To elaborate, the total resource requirements of VNF instances and their backups should not surpass the available resources $ca{p}_n$ on the edge server n.

$$\begin{array}{c}\hfill \sum _{r_m\in R}\sum _{f_{m,i}\in F}{P}_{f_{m,i},v_n}\times C_m\le {cap}_n,\forall v_n\in V\end{array}$$

(6)

3.5. Migration Cost Model

When migrating the backup of a VNF from server u to server v, a transmission cost is incurred, which depends on the link latency $l(u,v)$ between servers u and v. This cost is defined as a generally non-decreasing function $c\left(x\right)$, where $x=l(u,v)$. Since link latency is typically a function of the distance between two nodes, it increases with distance.

We define the transmission cost function $c\left(x\right)$ in a constant-plus-exponential form. This form of cost function can approximate many real-world scenarios by changing the parameters:

$$c\left(x\right)={\alpha }_a+{\alpha }_b{\alpha }_c^{\left(x\right)},x\ge 0$$

(7)

The constants ${\alpha }_a$, ${\alpha }_b$, and ${\alpha }_c$ are fixed values in the model that can be modified based on specific scenarios.

3.6. Reliability Reward Model

To quantify the contribution of BVNFs to VNF reliability, we first calculate the reliability of a VNF instance using the following formula:

$$y=\prod _{f_{m,i}\in F}\prod _{v_n\in V}(1-p_{f_{m,i}})(1-p_{v_n})P_{f_{m,i},v_n,r_m}$$

(8)

where $p_{f_{m,i}}$ denotes the failure probability of VNF $f_{m,i}$, and $p_{v_n}$ denotes the failure probability of edge server $v_n$. The failure probability p is calculated as follows:

$$p={\displaystyle \frac{MTTR}{MTTN+MTTR}}$$

(9)

Mean Time to Normal ($MTTN$) and Mean Time to Repair ($MTTR$) refer to the average time to reach normal operation and the average time to repair, respectively.

When a VNF deploys a backup to an edge server node, it can provide reliability assurance, increasing the VNF’s revenue. This revenue is related to the reliability of the backup and can be defined as a non-decreasing function $d\left(y\right)$. It is essential that the backup is readily available to be used when necessary, as downtimes can severely impact the revenue and user satisfaction.

We define the reliability reward functions $d\left(y\right)$ in a constant-plus-exponential form.

$$d\left(y\right)={\beta }_a+{\beta }_b{\beta }_c^{\left(y\right)}$$

(10)

The constants ${\beta }_a$, ${\beta }_b$, and ${\beta }_c$ are fixed values in the model that can be modified based on specific scenarios.

3.7. Problem Definition

Therefore, we define the migration cost for BVNF $f_{m,i}$ when it migrates from edge server u to edge server v as:

$$C_{f_{m,i}}^{mig}(u,v)={\gamma }_{f_{m,i}}\times c\left(l(u,v)\right)-{\delta }_{f_{m,i}}\times \left(d\right(v)-d(u\left)\right)$$

(11)

${\gamma }_{f_{m,i}}$ and ${\delta }_{f_{m,i}}$ are real-valued parameters. They can be modified according to the user’s emphasis on VNF reliability and transmission cost in order to adapt to different situations.

According to the above description, our problem is to migrate suitable BVNFs to suitable edge servers while considering the constraints of average failure latency and edge server resource, and achieve the minimization of the total migration cost with the consideration of reliability gains. We can obtain the BVNF migration problem formulated as follows:

• Objective:

$$min\sum _{r_m\in R}\sum _{i\in F}{C}_{f_{m,i}}^{mig}(u,v)$$

(12)

3.8. NP-Hardness of BVNF Migration Problems

Theorem 1. 

The BVNF migration problem defined in (12) is an NP-hard problem.

Proof. 

We demonstrate the NP-hardness of BVNF migration by reducing it to the multidimensional knapsack problem, which is a well-established and notorious NP-hard problem with the following definition. The goal of this problem is to select n items from a set of items, Item $=(i_1,i_2,\cdots ,i_m)$, where each item has a unique weight $weigh{t}_i$ and value $valu{e}_i$. Choose n items and place them into a backpack with limited capacity $cap$, so as to maximize the total value of the items while following the constraint that the total weight cannot surpass the backpack’s capacity $cap$.

We can consider the current position $u_i$ and the possible edge server $v_i$ that each backup i can migrate to as an item, with a total of ${\sum }_{i\in n}{u}_i\times v_i$ items. The time delay $T_v$ from the primary VNF to the edge server after backup migration and the total number of backups n that need to be migrated must satisfy the constraint that the total latency from the primary VNF to all n backups cannot exceed $T_{all}$. The reliability value $d\left(v\right)$ of each backup i minus the migration cost from $u_i$ to $v_i$ can be considered as the value of the item. It is NP-hard to maximize the total value of the selected n items while satisfying the above constraints. In this article, we also need to consider the resource constraints of the edge servers for the BVNF migration problem, and each BVNF can only and must be selected once, which imposes additional constraints on the selection of items. Therefore, the problem of BVNF migration is an NP-hard problem [39].    □

4. Optimized Algorithm for the BVNF Migration Problem

In this section, to tackle the issue of BVNF migration, we first conduct a more in-depth analysis in Section 4.1. Subsequently, in Section 4.2 we present corresponding algorithms to address the existing challenges.

4.1. Problem Analysis

We denote the possible edge server $v_i$ that backup i can migrate to and its current position $u_i$ as $s_i=(u_i,v_i)$. However, this further increases the state space $s_i$, and we need to simplify the state space to avoid an excessively long solving time for this problem. When migrating, we prioritize avoiding migration to edge servers with existing BVNFs and locations farther away from the main VNF instance than the current location. The BVNF selection and migration problem can be decomposed into the following steps:

• Preprocessing is performed on the graph within the network model, and the preprocessed network graph can be utilized multiple times before any changes occur in the network nodes. This efficiently decreases the execution time of the algorithm.
• Anticipating whether VNF migration caused by user movement will result in exceeding latency limits, preparations are made for BVNF migration if the latency constraints are exceeded.
• When BVNF migration is required, preliminary filtering of potential migration locations is conducted based on specified constraints. This process reduces the algorithm’s runtime by narrowing down the state space.
• The optimized Kuhn–Munkres algorithm is employed to solve the combinatorial optimization problem. The process involves sequentially computing whether the constraints are satisfied after BVNF migration based on priority.

Throughout this process, we encounter the following challenges: the reliability benefits of dynamic BVNFs, the fault latency of dynamic BVNFs, and the finite resources of edge servers.

To address the challenges mentioned above, we will provide a detailed discussion of our approach and the general process of BVNF migration in Section 4.2 This aims to identify a suitable set of BVNFs for edge migration.

4.2. BVNF Migration Algorithm

To address the issue mentioned above, we propose a BVNF migration algorithm by jointly considering reliability, limited capacity, and latency. As VNFs migrate with users, the fault recovery latency of BVNFs varies. This algorithm reduces the fault recovery latency by migrating suitable BVNFs. Hence, it avoids the costs associated with frequent redeployment of all BVNFs.

We propose an algorithm named the BVNF migration algorithm based on the above ideas.

In Algorithm 1, we first preprocess the network graph G by employing the Dijkstra algorithm to determine the shortest distances between all nodes in G (Line 1). For each mobile user’s request r, we calculate the average fault recovery latency of the VNF after the user migration $af{l}_{mig}$ (Line 3). If $af{l}_{mig}$ is greater than the average fault recovery latency that the user can tolerate, we optimize by migrating BVNFs (Lines 4–17). Based on the edge weights in our network model G, we first filter the nodes eligible for BVNF migration to prevent an excessive number of nodes from negatively affecting the algorithm’s performance (Lines 5–9). Next, we generate a weight matrix based on the current positions of the BVNFs and their potential migration locations (Line 11). We apply the improved Kuhn–Munkres algorithm to solve the minimum weight matching problem, thereby obtaining the feasible BVNF migration options $S_{opt}^{mig}$ (Line 12). For each $S_{opt}^{mig}$, we calculate its priority and subsequently sort the values (Line 13). We calculate the average fault latency after the migration of request $T_{r_m}^{all}$ and compare it with the maximum acceptable average fault latency for users $T_m^{err}$. When $T_{r_m}^{all}$ exceeds the threshold $T_m^{err}$ that users can accept, we select the highest-priority option from the $S_{opt}^{mig}$ for migration. We then recalculate $T_{r_m}^{all}$ after the migration, continuing this process until it meets user requirements (Lines 14–16).

As described above, we designed a BVNF migration algorithm inspired by the Kuhn–Munkres algorithm. This algorithm aims to meet user latency requirements while minimizing the costs associated with BVNF migration. According to Theorem 1, BVNF migration is NP-hard, making it difficult to find an optimal solution within polynomial time.

Therefore, in Algorithm 1, we employ the improved Kuhn–Munkres algorithm to solve the basic minimum weight matching problem. This serves as a local solution for the network graph G, which has been preprocessed using the Dijkstra algorithm. The time complexity of this approach is $O\left(k^3\right)$, where k represents the number of BVNFs.

4.3. Optimized BVNF Migration Algorithm

In Algorithm 2, we introduce an optimized BVNF migration algorithm that integrates Algorithm 1 with the traditional VNF redeployment method to enhance adaptability across different network conditions. The motivation for this approach arises from the observation that Algorithm 1, while effective in many scenarios, does not always outperform traditional VNF redeployment. By dynamically selecting the optimal strategy, Algorithm 2 ensures lower migration costs and better overall performance.

We begin by preprocessing the network graph G using Dijkstra’s algorithm to determine the shortest distances between all nodes in G (Line 1). For each mobile user request r, we calculate the BVNF migration cost $C^{mig}$ based on Algorithm 1 (Line 3). Simultaneously, we compute the cost of redeploying the VNF using a traditional redeployment algorithm $C^{redeploy}$ (Line 4). The objective is to determine which approach incurs the lowest cost while maintaining acceptable latency constraints.

Algorithm 1: BVNF migration algorithm

Algorithm 2: Optimized BVNF migration algorithm

If the migration cost using Algorithm 1 is lower ($C^{mig}\le C^{redeploy}$), we select Algorithm 1 for BVNF migration (Lines 5–7). This process follows the Kuhn–Munkres-based optimization framework outlined in Algorithm 1, where a bipartite graph matching strategy is employed to find the optimal BVNF placement while minimizing migration cost.

Conversely, if the traditional VNF redeployment cost is lower ($C^{redeploy}<C^{mig}$), we utilize the traditional method for backup redeployment (Lines 9–11). This typically involves deploying a new instance of the VNF at a location that minimizes operational cost while satisfying user latency constraints.

The proposed hybrid algorithm dynamically adapts to different network conditions by selecting the optimal migration strategy based on cost minimization. Compared to a static backup migration approach, Algorithm 2 offers greater flexibility and broader applicability across diverse network environments.

Algorithm 2, by combining Algorithm 1 with traditional redeployment techniques, not only ensures that the user’s recovery latency requirements are met but also further reduces the total cost of BVNFs by dynamically selecting the migration strategy.

5. Experiment

5.1. Experimental Setup

This study evaluates the performance of the proposed BVNF migration algorithm through extensive simulation experiments. All simulations were conducted on a laptop running the Windows 11 operating system, equipped with an AMD Ryzen 7 5800H CPU @ 3.20 GHz and 16 GB RAM. Python 3.11 and the NetworkX library were used to construct and simulate the edge network environment.

To comprehensively assess the algorithm’s performance across different environments, we defined a set of adjustable variables. Among them, the following are critical:

• Number of Edge Server Nodes: This variable simulates edge cloud environments of various sizes, ranging from 20 to 200 nodes. When the number of edge server nodes is large, the algorithm optimizes by filtering out nodes that are too far from the VNF instances.
• Number of BVNFs: This variable can be adjusted according to application scenario requirements to improve the reliability of VNFs by increasing the number of backups.
• Graph Sparsity: The sparsity of the network is controlled by adjusting the probability of link existence between edge nodes (link probability ranging from 0.1 to 0.5).
• Link Latency: The latency of the link between two directly connected servers is a random integer between 1 and 20 milliseconds (ms), simulating the uneven transmission delays typically encountered in real networks.
• Total Request Mitigation Cost: The Total Request Mitigation Cost is the sum of all BVNF migration costs in a series of requests, which is calculated using Equation (12).

We simulate mobile user entities by randomly generating user requests. In addition, other relevant variables were set to simulate different environments and requirements to further test the algorithm’s performance. These adjustable variables increase the flexibility of the experiments and allow for verification of the algorithm’s adaptability across a broader range of application scenarios. The generated edge network is modeled as an undirected connected graph to ensure that there is a reachable path between all server nodes. To reduce the randomness introduced by the random generation of network structures, each experimental setup was run multiple times, and the average results were taken.

5.2. Evaluation of the Superiority of Our Algorithm

To validate the superiority of the proposed BVNF migration algorithm, we designed a series of comparative experiments. As discussed earlier, our algorithm primarily addresses several key challenges related to BVNFs in edge environments: the reliability of VNFs, the cost of BVNF deployment or migration, and the recovery delay of BVNFs. In this section, we designed three baseline algorithms for comparison to further assess the performance of our algorithm. The specific comparison algorithms are as follows:

5.2.1. Baseline Algorithms

To evaluate the performance of our algorithm, we designed three baseline algorithms:

• Baseline algorithm 1: This algorithm uses the BVNF migration strategy but does not optimize migration costs. The focus is on meeting user latency constraints, but it may result in high migration overhead.
• Baseline algorithm 2 (Traditional algorithm): This is the conventional VNF migration method. After migrating the VNF instance, a hot backup is redeployed on a nearby node to ensure service reliability [25].
• Baseline algorithm 3: This algorithm employs the BVNF migration strategy while optimizing migration costs to reduce the overhead associated with backup deployment. However, in some scenarios with high user latency constraints, it may not meet the latency requirements of user requests.

5.2.2. Comparison with the Proposed Algorithm

Building upon Baseline algorithm 3, we further combine the advantages of Baseline algorithms 2 and 3. The aim is to meet user latency demands while further reducing the overall cost of BVNF migration. To evaluate its performance, we compare it against the aforementioned three baseline algorithms.

5.2.3. Experimental Methodology and Evaluation Metrics

All algorithms are evaluated under the same experimental conditions, and the main evaluation metrics include:

• Migration Cost: This metric assesses the overall resource consumption required to meet the user’s reliability and backup recovery delay requirements after VNF instance migration. Different environmental parameters may affect this cost.
• User Latency Satisfaction Rate: This measures the proportion of successful service recovery within the user’s requested latency when a VNF instance fails.
• Backup Migration Duration: This metric measures the time taken for BVNF migration to complete after the primary VNF instance migration.

5.3. Experimental Results and Analysis

To comprehensively evaluate the performance of the proposed hybrid migration algorithm, we conducted in-depth experimental analyses across four control variables: the number of BVNFs, the number of user requests, the number of edge network nodes, and the connectivity of the network graph. In the experiments, we compared the three baseline algorithms (Baseline algorithm 1, Baseline algorithm 2, and Baseline algorithm 3) with our optimized BVNF migration algorithm, considering multiple evaluation metrics such as recovery delay, migration cost, and user latency satisfaction rate, to investigate the algorithm’s applicability in different environments. The data presented in the following analysis were derived from 1000 randomly generated user requests.

5.3.1. Impact of Number of BVNFs

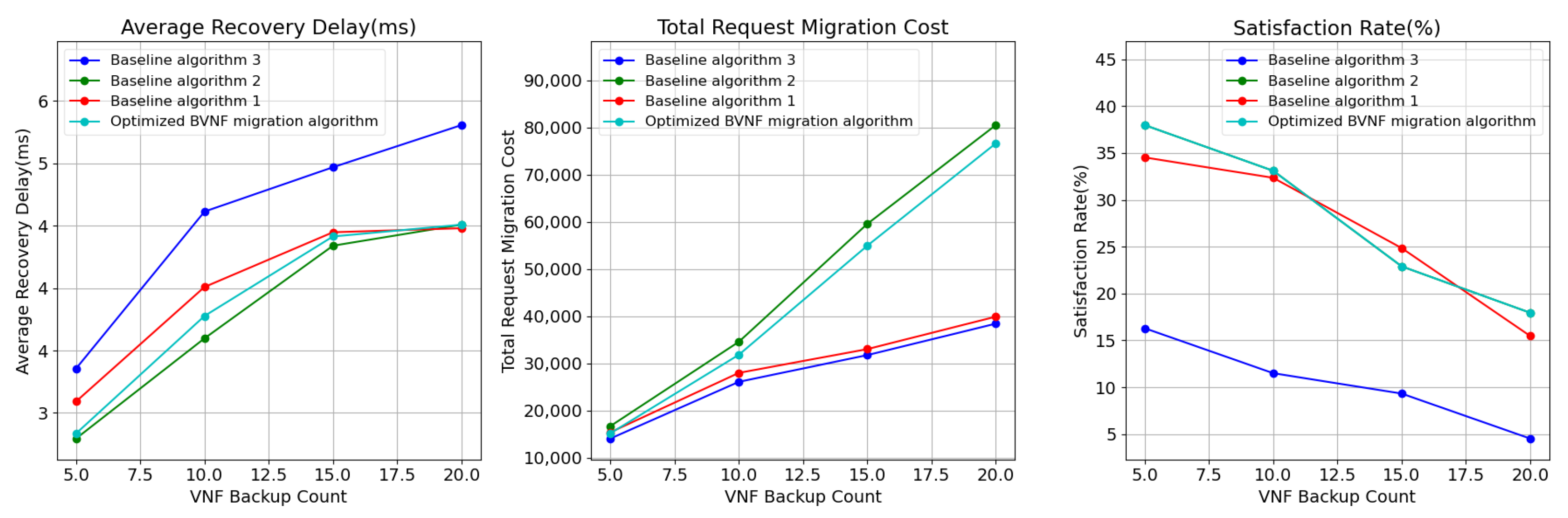
We first evaluated the impact of varying the number of BVNFs on the performance of the different algorithms. The number of backups was gradually increased from 5 to 20, with an interval of 5.

As shown in Figure 3, the satisfaction ratio refers to the proportion of user requests that can be satisfied using the corresponding algorithm, given a latency threshold. For different numbers of BVNFs, Baseline algorithm 3, despite having the lowest BVNF migration cost, only applies to a small portion of user requests. In contrast, our proposed hybrid backup migration algorithm achieves a satisfaction ratio comparable to that of Baseline algorithm 2.

5.3.2. Impact of Number of Edge Network Nodes

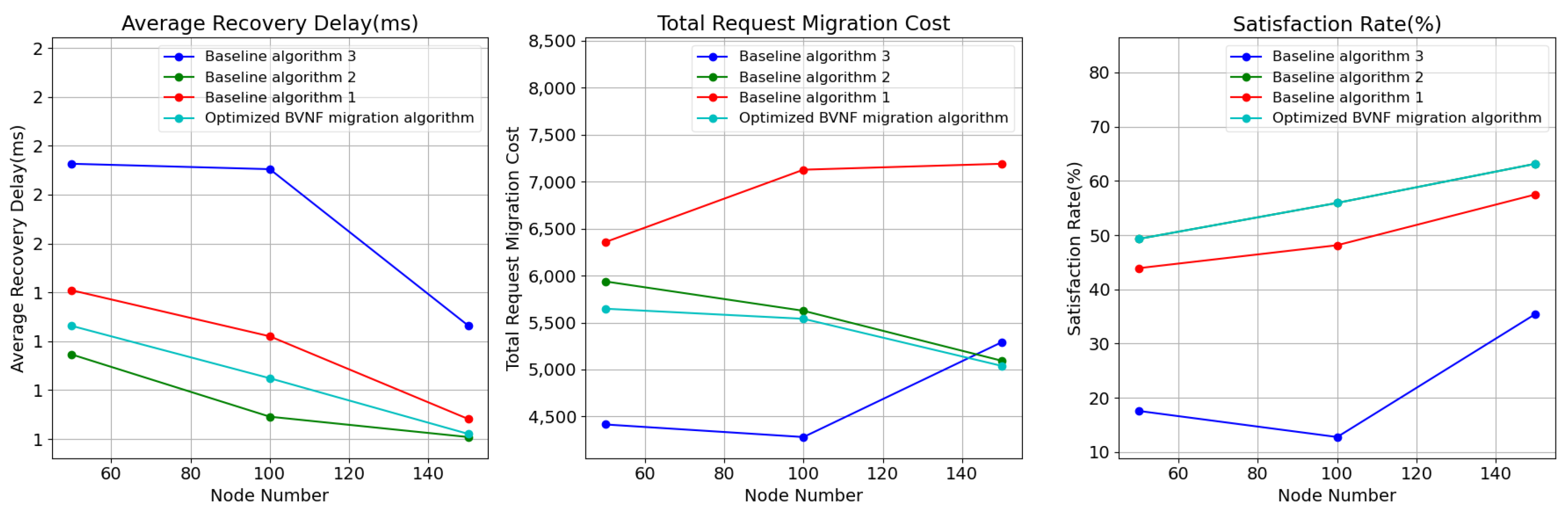
To assess the impact of the scale of the edge network on the algorithm’s performance, we adjusted the number of network nodes, increasing from 50 to 200 with an interval of 50.

As shown in Figure 4, although the overall satisfaction ratio for all algorithms increases significantly with the number of edge network nodes, the satisfaction ratio of Baseline algorithm 3 remains lower than that of the other algorithms. The optimized BVNF migration algorithm achieves the same applicability rate as Baseline algorithm 2, outperforming the other baseline algorithm.

5.3.3. Impact of Network Graph Connectivity

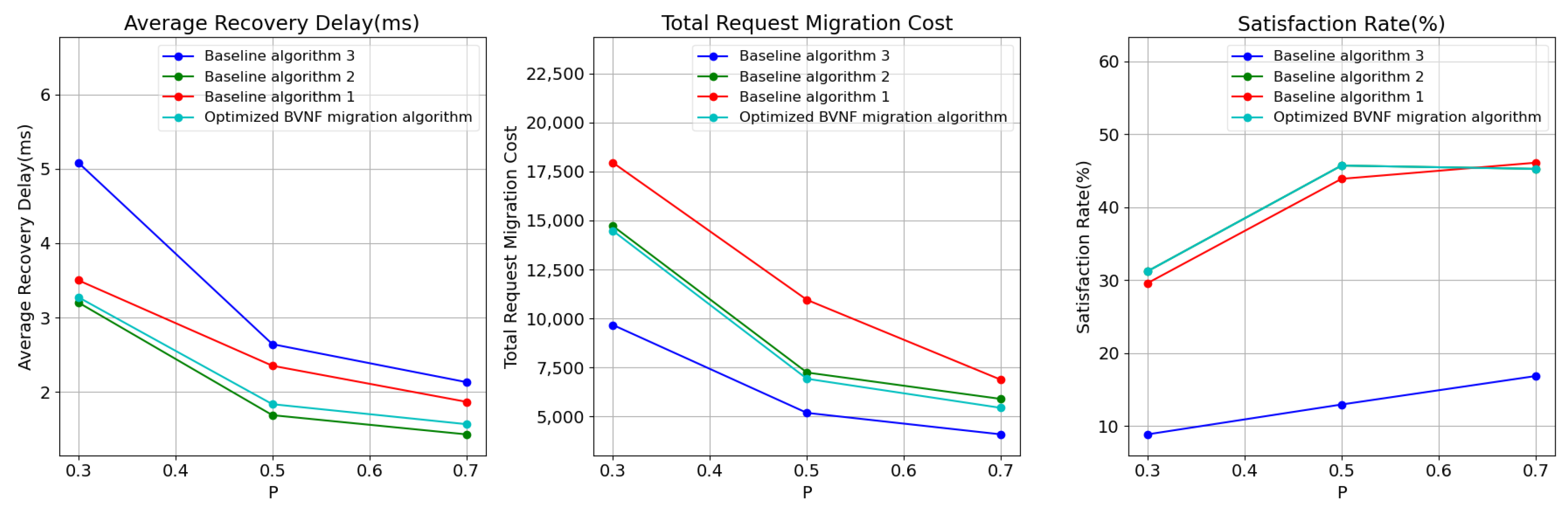
Finally, we analyzed the impact of network graph connectivity on algorithm performance. The connectivity was varied from 0.1 (sparse graph) to 0.7 (high connectivity graph), with an interval of 0.2.

As shown in Figure 5, with the increase in the connectivity of the network model graph, both the average recovery delay and the total recovery delay decrease. The optimized BVNF migration algorithm consistently maintains an average delay that is either lower than or equal to that of the other benchmark algorithms, while its satisfaction rate is higher than or equal to that of the other benchmark algorithms.

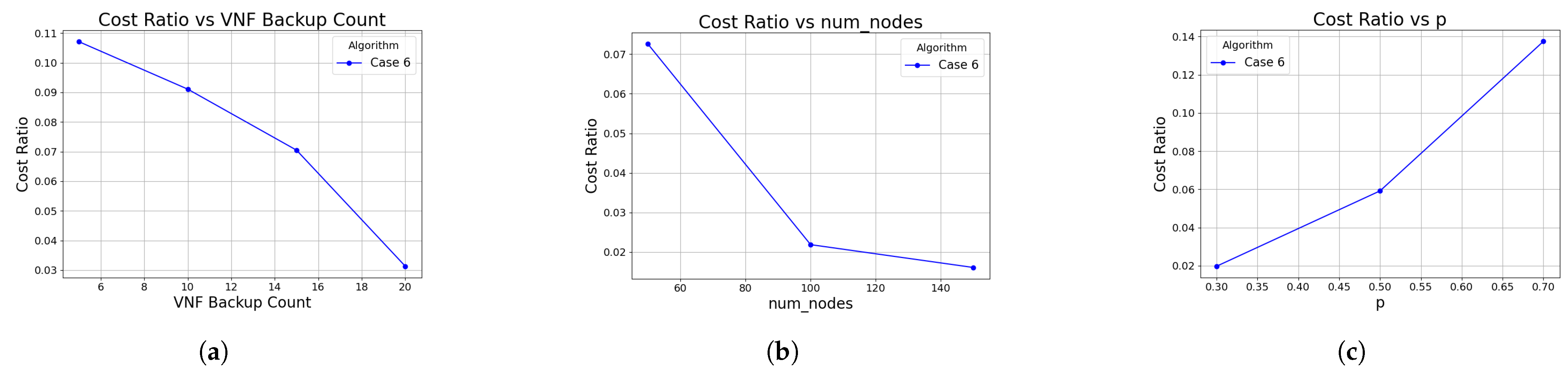
5.4. Summary of Superiority

The experimental results demonstrate that the proposed optimized BVNF migration algorithm achieves the same level of user latency satisfaction as Baseline algorithm 2, while offering lower backup migration costs. The optimization ratio of backup migration costs varies with the number of backups, network graph connectivity, and the number of edge nodes. Additionally, we evaluated the optimization ratio of backup migration costs for the optimized BVNF migration algorithm, as illustrated in Figure 6. The optimization ratio is higher in small-scale, high-connectivity edge networks, or when there are fewer BVNFs, reaching up to approximately 15%.

6. Conclusions

In this paper, we investigated the problem of hot backup migration for latency-sensitive VNFs in FMEC environments. We formulated the problem as an integer linear programming model and proved its NP-hardness. To address the complexity of the problem, we proposed an optimized BVNF migration algorithm that jointly considers latency constraints, resource limitations, and reliability requirements. Our algorithm dynamically selects between backup migration and redeployment strategies to minimize overall migration costs while ensuring service continuity. Theoretical analysis and simulation results demonstrate that our approach significantly reduces the cost of backup migration while maintaining user latency satisfaction at a level comparable to traditional backup deployment methods. However, in our method, the main instance of the VNF experiences a certain delay as the user migrates, which may affect the efficiency of this algorithm, especially when the user moves too fast.

7. Future Work

While our hybrid algorithm demonstrates promising results in balancing migration costs and latency constraints, several challenges remain open for future work:

• Predictive Migration with Spatiotemporal Context Awareness: Integrating spatiotemporal machine learning models could enable proactive backup pre-migration. Predicting user trajectories and VNF handover events may mitigate transitional latency during high-speed movement.
• Multi-Tenant Resource Contention Resolution: Extending our algorithm with game-theoretic mechanisms could resolve resource conflicts in shared edge infrastructure while preserving isolation guarantees.
• Energy–Latency Tradeoff: Renewable energy-aware backup scheduling could dynamically activate/deactivate backups based on edge nodes’ energy profiles, addressing sustainability concerns.
• Cross-Layer Fault Tolerance: Combining hot backups at the Virtual Network Function level with redundancy in physical or virtual links could achieve end-to-end reliability through joint optimization of Network Function Virtualization and Software-Defined Networking.
• Adaptive Backup Granularity: Differential state synchronization based on VNF workload dynamics may reduce migration costs, requiring machine learning-driven granularity prediction models.

These extensions would advance VNF reliability management toward intelligent and sustainable solutions for next-generation edge networks.