End-to-End Lane Detection: A Two-Branch Instance Segmentation Approach
Abstract
1. Introduction and Related Work
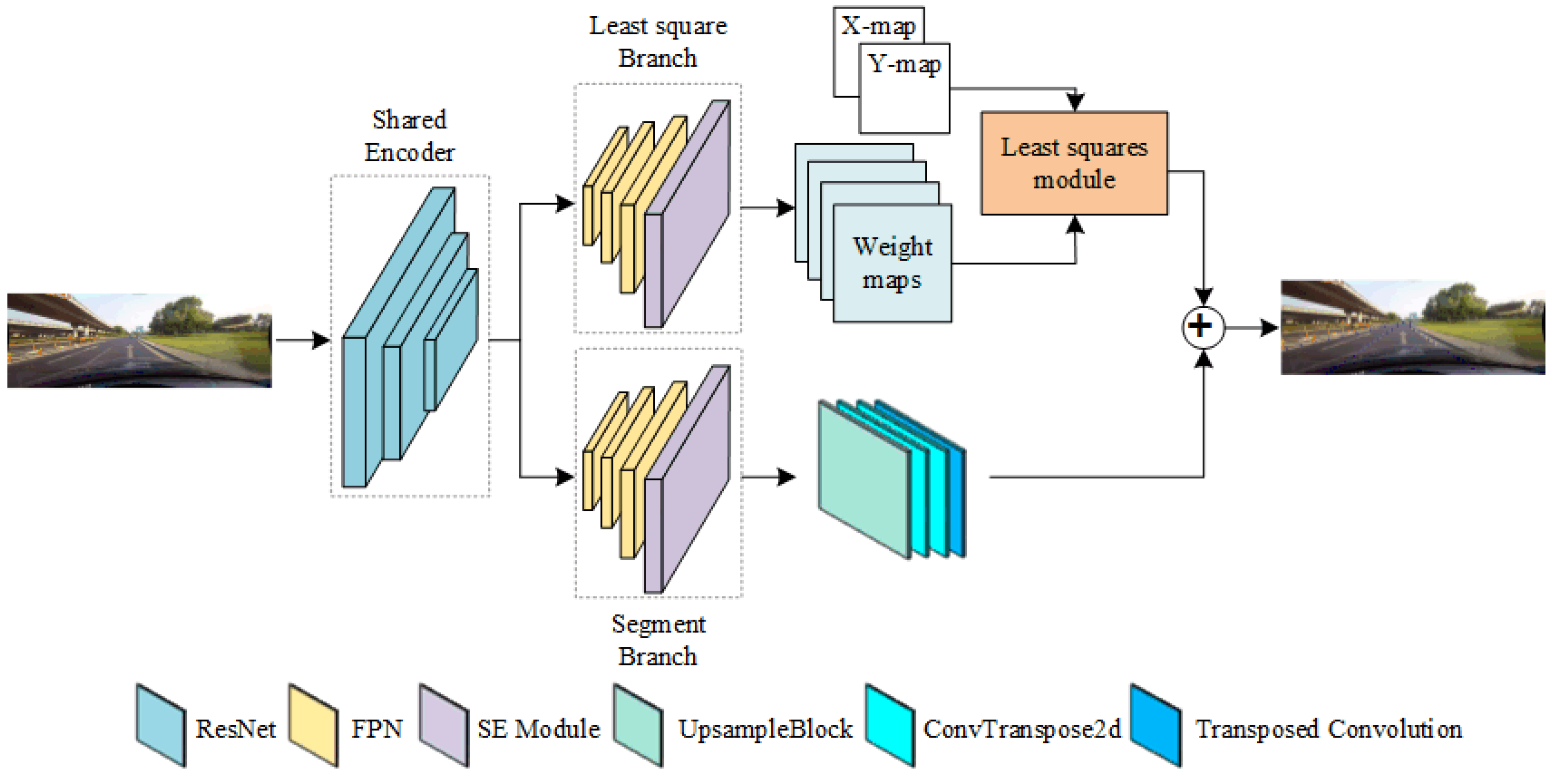
2. Two-Branch Instance Partitioning Network Model
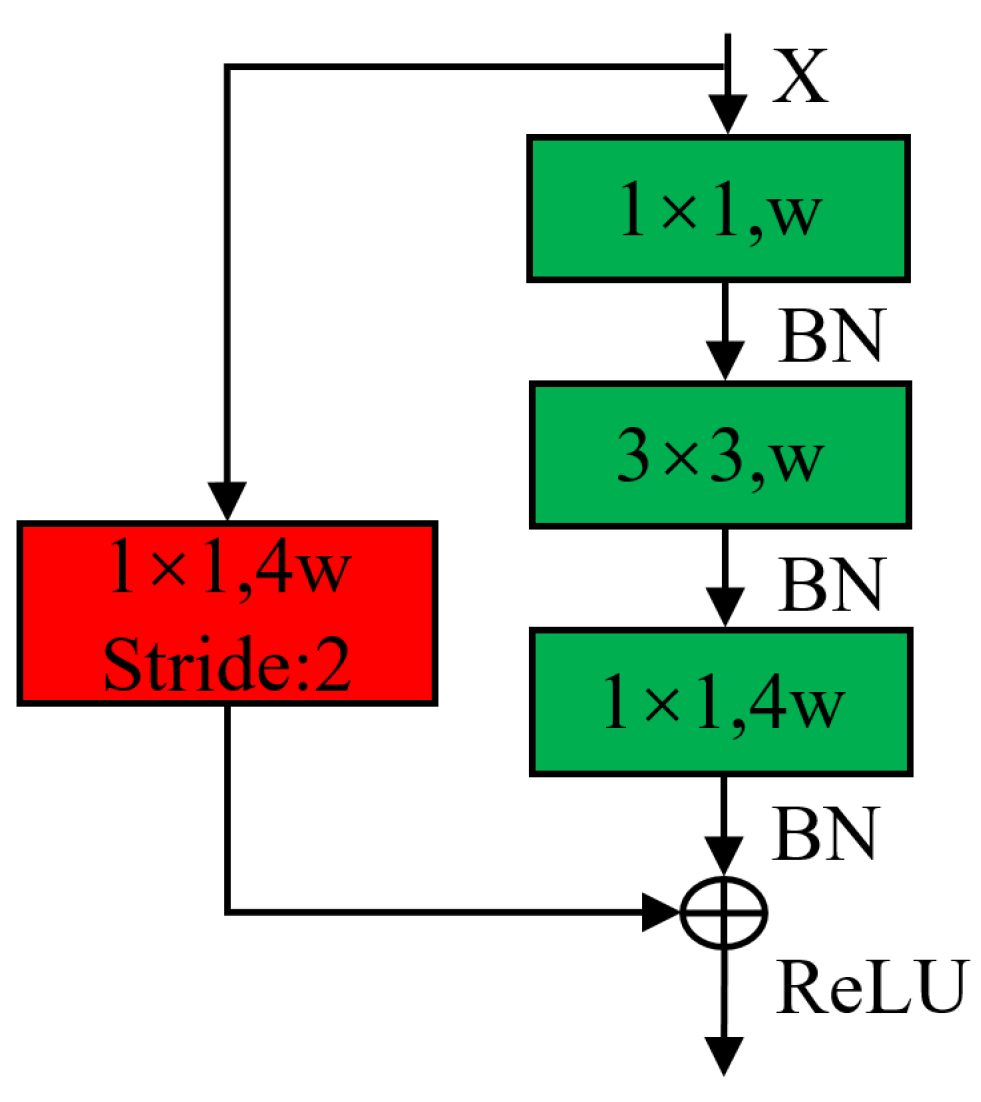
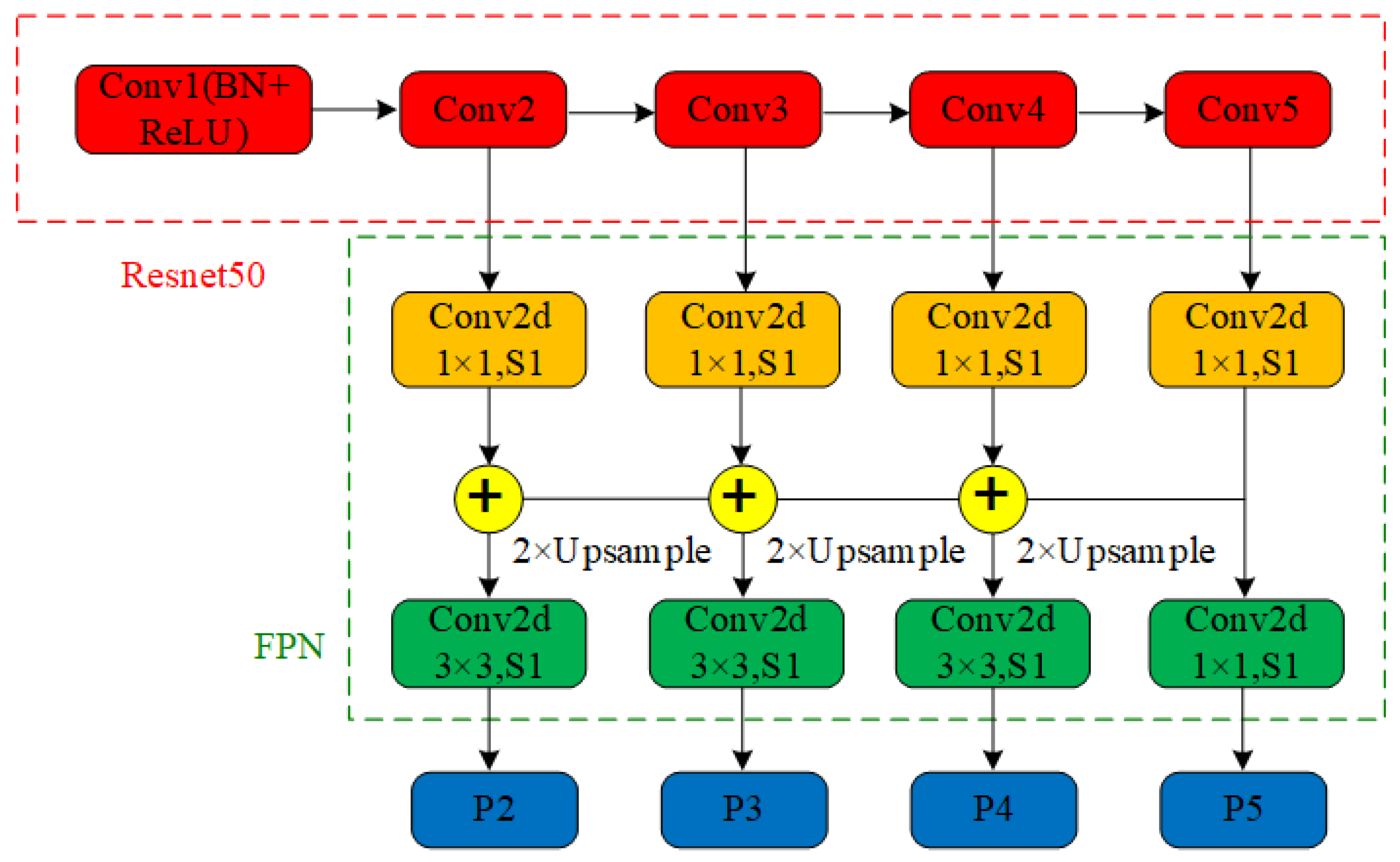
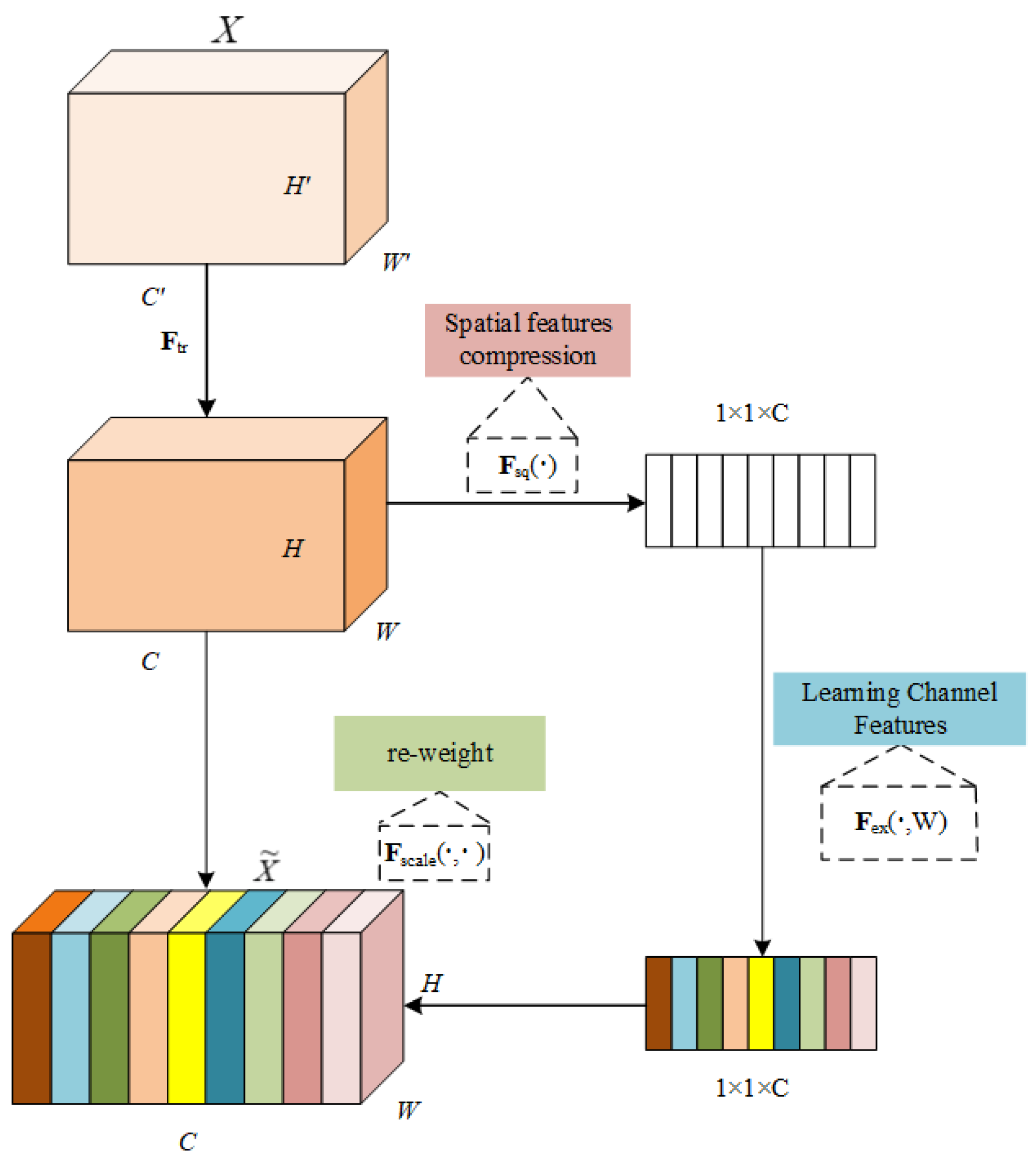
2.1. Segment Branch
2.2. Least Square Branch
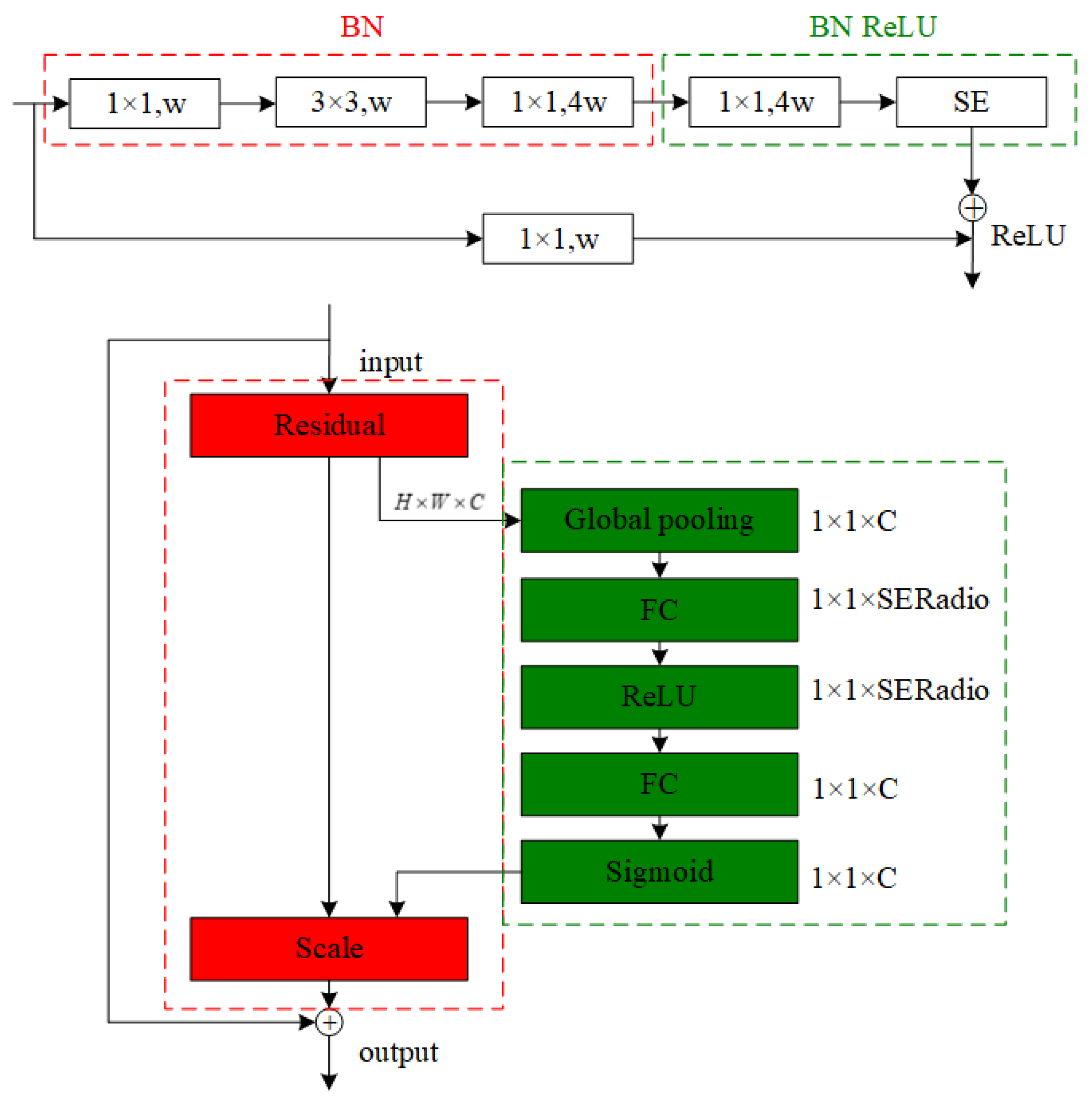
2.3. Feature Recovery Decoding
2.4. Loss Function
3. Evaluation and Experiments
3.1. Datasets
3.2. Evaluation Metrics
3.3. Experimental Results and Analysis
4. Conclusions
- In this paper, the Feature Pyramid Network (FPN) in the encoding-decoding network architecture combined with the residual network (ResNet50) is used to achieve effective recognition and segmentation of each lane line instance in multiple road environments. FPN ensures that multi-scale information from global to local by integrating feature maps from different levels is fully utilized. This not only improves the limitations of traditional methods in dealing with complex scenes such as illumination changes, occlusion, and road damage, but also ensures that advanced semantic features and fine edge details are adequately extracted, thus improving the overall performance of the model.
- To enhance the capability of the decoding network, this paper introduces the expansion convolution, residual join, and weighted least squares fitting modules. The expansion convolution expands the sensory field to capture richer contextual information, which helps to deal with long-distance lane lines; the residual connection promotes the information flow of the deep network, avoids the gradient vanishing problem, and improves the training efficiency; and the weighted least squares fitting module optimizes the estimation of lane line parameters, which strengthens the model’s adaptive ability to different numbers and configurations of lane lines. This design improves the accuracy of the model’s lane line parameter estimation, enabling the model to accurately discriminate between instances of different lane lines and predict their geometries.
- The method proposed in this paper was experimentally tested on two publicly available datasets: CULane and TuSimple. The results demonstrate that the F1 score on the CULane dataset reached 76%, while on the TuSimple dataset it increased to 96.9%. This indicates that the method is both efficient and effective in handling complex road scenarios, particularly under challenging conditions such as highlight, crowd, and night in multi-lane environments, achieving F1 scores of 69.3%, 74.4%, and 71.0%, respectively. Furthermore, this method exhibits excellent environmental adaptability and real-time processing capabilities, providing a reliable lane detection solution for autonomous vehicles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maini, R.; Aggarwal, H. Study and comparison of various image edge detection techniques. Int. J. Image Process. (IJIP) 2009, 3, 1–11. [Google Scholar]
- Liang, D.; Guo, Y.C.; Zhang, S.K.; Mu, T.J.; Huang, X. Lane detection: A survey with new results. J. Comput. Sci. Technol. 2020, 35, 493–505. [Google Scholar]
- Zhang, J.Q.; Duan, H.B.; Chen, J.L.; Shamir, A.; Wang, M. HoughLaneNet: Lane detection with deep Hough transform and dynamic convolution. Comput. Graph. 2023, 116, 82–92. [Google Scholar]
- Zakaria, N.J.; Shapiai, M.I.; Abd Ghani, R.; Yassin, M.N.M.; Ibrahim, M.Z.; Wahid, N. Lane detection in autonomous vehicles: A systematic review. IEEE Access 2023, 11, 3729–3765. [Google Scholar]
- Yu, F.; Wu, Y.; Suo, Y.; Su, Y. Shallow detail and semantic segmentation combined bilateral network model for lane detection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8617–8627. [Google Scholar] [CrossRef]
- Bojarski, M.; Del Testa, D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. arXiv 2016, arXiv:1604.07316. [Google Scholar]
- Yang, Z.; Shen, C.; Shao, W.; Xing, T.; Hu, R.; Xu, P.; Chai, H.; Xue, R. LDTR: Transformer-based lane detection with anchor-chain representation. Comput. Vis. Media 2024, 10, 753–769. [Google Scholar]
- Liu, B.; Ling, Q. Hyper-Anchor Based Lane Detection. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13240–13252. [Google Scholar]
- Tabelini, L.; Berriel, R.; Paixao, T.M.; Badue, C.; De Souza, A.F.; Oliveira-Santos, T. Polylanenet: Lane estimation via deep polynomial regression. In Proceedings of the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 6150–6156. [Google Scholar]
- Van Gansbeke, W.; De Brabandere, B.; Neven, D.; Proesmans, M.; Van Gool, L. End-to-end lane detection through differentiable least-squares fitting. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Pan, X.; Shi, J.; Luo, P.; Wang, X.; Tang, X. Spatial as deep: Spatial CNN for traffic scene understanding. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 32–38. [Google Scholar]
- Neven, D.; De Brabandere, B.; Georgoulis, S.; Proesmans, M.; Van Gool, L. Towards end-to-end lane detection: An instance segmentation approach. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 286–291. [Google Scholar]
- Xu, H.; Wang, S.; Cai, X.; Zhang, W.; Liang, X.; Li, Z. Curvelane-NAS: Unifying lane-sensitive architecture search and adaptive point blending. In Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 689–704. [Google Scholar]
- Che, Q.H.; Nguyen, D.P.; Pham, M.Q.; Lam, D.K. TwinLiteNet: An efficient and lightweight model for driveable area and lane segmentation in self-driving cars. In Proceedings of the International Conference on Multimedia Analysis and Pattern Recognition (MAPR), Quy Nhon, Vietnam, 5–6 October 2023; pp. 1–6. [Google Scholar]
- Wang, J.; Wu, Q.M.J.; Zhang, N. You only look at once for real-time and generic multi-task. IEEE Trans. Veh. Technol. 2024, 73, 12625–12637. [Google Scholar]
- Tabelini, L.; Berriel, R.; Paixao, T.M.; Badue, C.; De Souza, A.F.; Oliveira-Santos, T. Keep your eyes on the lane: Real-time attention-guided lane detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 294–302. [Google Scholar]
- Su, J.; Chen, C.; Zhang, K.; Luo, J.; Wei, X.; Wei, X. Structure guided lane detection. arXiv 2021, arXiv:2105.05403. [Google Scholar]
- Zheng, T.; Huang, Y.; Liu, Y.; Tang, W.; Yang, Z.; Cai, D.; He, X. CLRNet: Cross layer refinement network for lane detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 898–907. [Google Scholar]
- Bäcklund, H.; Hedblom, A.; Neijman, N. A density-based spatial clustering of applications with noise. Data Min. TNM033 2011, 33, 11–30. [Google Scholar]
- Liang, J.; Zhou, T.; Liu, D.; Wang, W. ClustSeg: Clustering for universal segmentation. arXiv 2023, arXiv:2305.02187. [Google Scholar]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; pp. 850–855. [Google Scholar]
- Shepley, A.J.; Falzon, G.; Kwan, P.; Brankovic, L. Confluence: A robust non-IoU alternative to non-maxima suppression in object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11561–11574. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.H.; Zhou, W.; Wang, F.J.; Xiao, B.J.; Dai, S.F. Lane detection based on improved Canny detector and least square fitting. Adv. Mater. Res. 2013, 765, 2383–2387. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Kao, Y.; Che, S.; Zhou, S.; Guo, S.; Zhang, X.; Wang, W. LHFFNet: A hybrid feature fusion method for lane detection. Sci. Rep. 2024, 14, 16353. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]

| Method | Normal | Crowd | Night | No-Line | Shadow | Arrow | Highlight | Curve | Cross | Total | FPS/f |
|---|---|---|---|---|---|---|---|---|---|---|---|
| E2Enet | 91.0% | 73.1% | 67.9% | 46.6% | 74.1% | 85.8% | 64.5% | 71.9% | 2022 | 74.0% | - |
| SCNN | 90.6% | 69.7% | 66.1% | 43.4% | 66.9% | 84.1% | 58.5% | 64.4% | 1990 | 71.6% | 7.5 |
| LaneATT | 91.1% | 73.0% | 69.0% | 48.4% | 70.9% | 85.5% | 65.7% | 63.4% | 1170 | 75.0% | 250 |
| UFLD | 90.7% | 70.2% | 66.7% | 44.4% | 69.3% | 85.7% | 59.5% | 69.5% | 2037 | 72.3% | 322.5 |
| Ours | 92.8% | 74.4% | 71.0% | 47.9% | 75.7% | 88.5% | 88.5% | 70.6% | 1653 | 76.0% | 51.8 |
| Method | F1 | Acc | FP | FN |
|---|---|---|---|---|
| ResNet-18 | 87.8% | 95.8% | 19.0% | 3.9% |
| ResNet-34 | 88.0% | 95.8% | 18.9% | 3.7% |
| LaneNet | 94.8% | 96.4% | 7.8% | 2.4% |
| PolyLaneNet | 90.6% | 93.3% | 9.4% | 9.3% |
| Res34-SAD | 95.9% | 96.6% | 6.0% | 2.0% |
| SCNN | 96.0% | 96.5% | 6.2% | 1.8% |
| Ours | 96.9% | 96.8% | 7.8% | 2.3% |
| Method | A | B | C | F1 |
|---|---|---|---|---|
| Baseline | × | × | × | 66.7% |
| Baseline+A+B | ✓ | ✓ | × | 75.16% |
| Baseline+B+C | × | ✓ | ✓ | 73.59% |
| Baseline+A+C | ✓ | × | ✓ | 74.83% |
| Baseline+A+B+C | ✓ | ✓ | ✓ | 76.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Luo, Z.; Zha, Y.; Zhang, Y.; Tang, Y. End-to-End Lane Detection: A Two-Branch Instance Segmentation Approach. Electronics 2025, 14, 1283. https://doi.org/10.3390/electronics14071283
Wang P, Luo Z, Zha Y, Zhang Y, Tang Y. End-to-End Lane Detection: A Two-Branch Instance Segmentation Approach. Electronics. 2025; 14(7):1283. https://doi.org/10.3390/electronics14071283
Chicago/Turabian StyleWang, Ping, Zhe Luo, Yunfei Zha, Yi Zhang, and Youming Tang. 2025. "End-to-End Lane Detection: A Two-Branch Instance Segmentation Approach" Electronics 14, no. 7: 1283. https://doi.org/10.3390/electronics14071283
APA StyleWang, P., Luo, Z., Zha, Y., Zhang, Y., & Tang, Y. (2025). End-to-End Lane Detection: A Two-Branch Instance Segmentation Approach. Electronics, 14(7), 1283. https://doi.org/10.3390/electronics14071283






