Image Classification in Memristor-Based Neural Networks: A Comparative Study of Software and Hardware Models Using RRAM Crossbars
Abstract
:1. Introduction
- The conductance modulation capability of actual RRAM cells is evaluated at the test chip level through electrical characterization.
- At the software level, an ANN model is defined and trained for image classification, and its model parameters (weights and biases) are generated.
- At the hardware level, the ANN model parameters are mapped to a physical RRAM crossbar array, taking into account the RRAM cell characteristics extracted from silicon measurements.
- The RRAM crossbar array is simulated to demonstrate its ability to perform vector-matrix–multiplication (VMM) directly in the analog domain.
2. Background
2.1. Specifications of the Manufactured RRAM Cells
2.2. OxRAM Conductance Modulation for Synapse Emulation
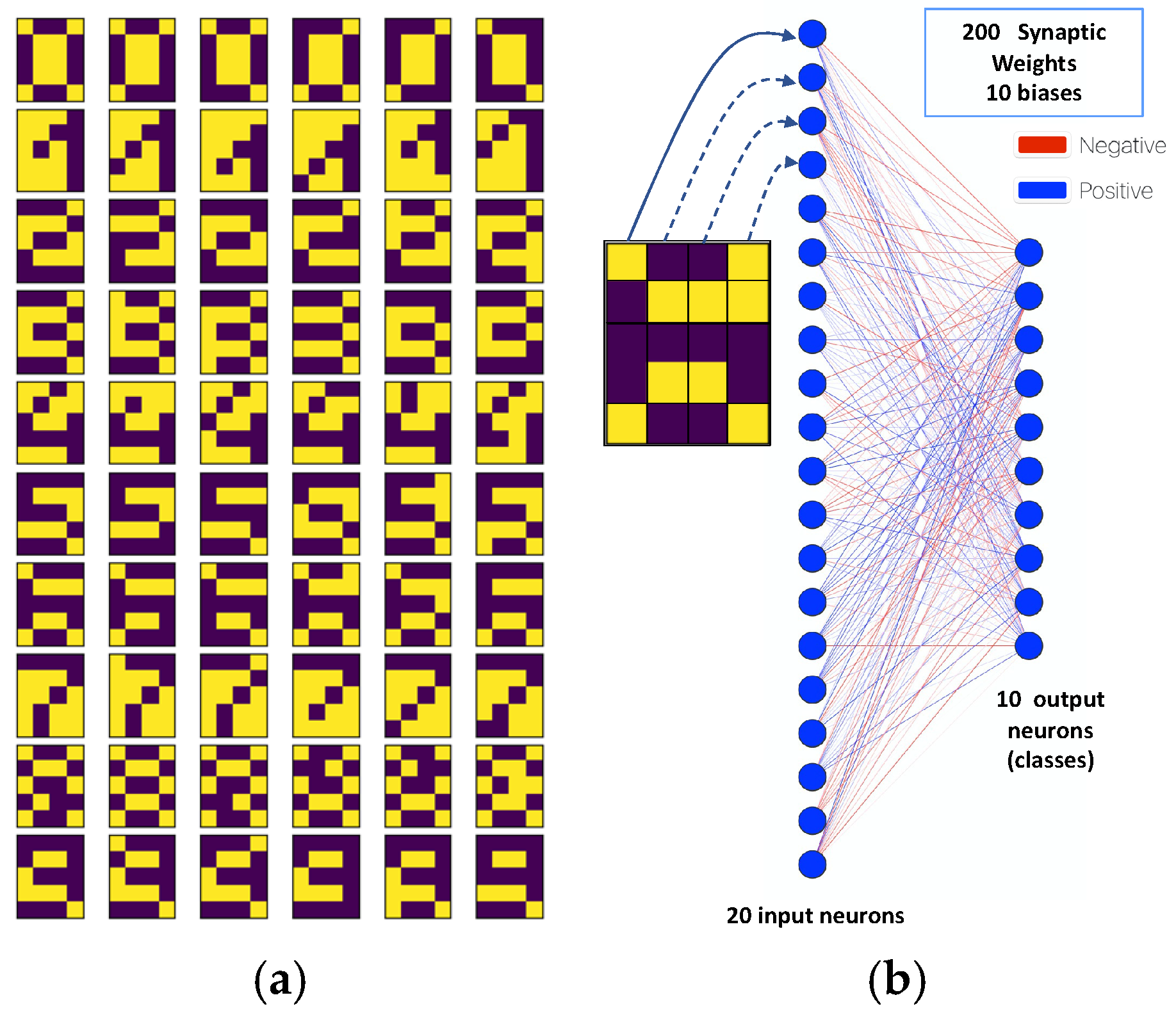
3. Artificial Neural Network Weight Mapping Methodology
3.1. ANN Architecture Definition and Training
3.2. Hardware Mapping of the ANN Model Parameters
3.3. Vector–Matrix Multiplication in a 1T1R Array
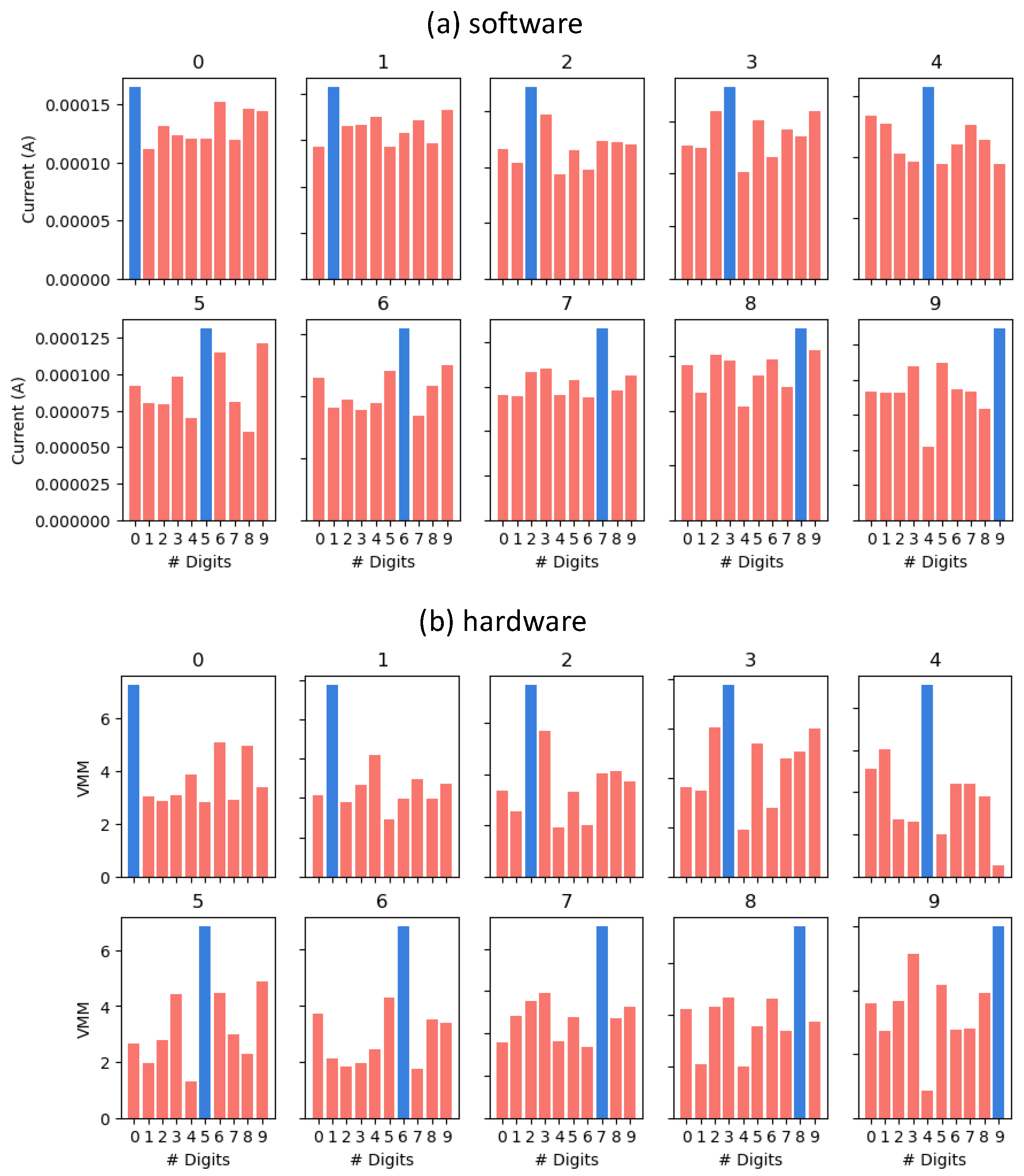
4. Circuit-Level Simulation Results for the Inference Stage
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Linn, E.; Rosezin, R.; Tappertzhofen, S.; Böttger, U.; Waser, R. logic operations in passive crossbar arrays alongside memory operations. Nanotechnology 2012, 23, 305205. [Google Scholar] [CrossRef]
- Aitken, R.; Chandra, V.; Myers, J.; Sandhu, B.; Shifren, L.; Yeric, G. Device and technology implications of the Internet of Things. In Symposium on VLSI Technology (VLSI-Technology): Digest of Technical Papers; IEEE: Honolulu, HI, USA, 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Aziza, H. Embedded Memories. In Silicon Systems for Wireless Lan; World Scientific: Singapore, 2020; Chapter 7; Volume 22, p. 199. ISBN 978-981-121-071-6. [Google Scholar] [CrossRef]
- Indiveri, G.; Linares-Barranco, B.; Legenstein, R.; Deligeorgis, G.; Prodromakis, T.; Tetzlaff, R.; Serrano-Gotarredona, T.; Chicca, E.; Oster, M.; Bartolozzi, C.; et al. Neuromorphic silicon neuron circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef]
- Bi, G.-Q.; Poo, M.-M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef]
- Vatajelu, E.I.; Aziza, H.; Zambelli, C. Nonvolatile memories: Present and future challenges. In Proceedings of the Design & Test Symposium (IDT), 2014 9th International, Algeries, Algeria, 16–18 December 2014; IEEE: Piscateville, NJ, USA, 2014; pp. 61–66. [Google Scholar] [CrossRef]
- Bazzi, H.; Harb, A.; Aziza, H.; Moreau, M.; Kassem, A. RRAM-based non-volatile SRAM cell architectures for ultra-low-power applications. Analog. Integr. Circuits Signal Process. 2021, 106, 351–361. [Google Scholar] [CrossRef]
- Aziza, H.; Moreau, M.; Pérez, A.; Virazel, A.; Girard, P. A capacitor-less CMOS neuron circuit for neuromemristive networks. In Proceedings of the 2019 17th IEEE International New Circuits and Systems Conference (NEWCAS), Munich, Germany, 23–26 June 2019; IEEE: Piscateville, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Vaz, P.I.; Girard, P.; Virazel, A.; Aziza, H. Improving TID Radiation Robustness of a CMOS OxRAM-Based Neuron Circuit by Using Enclosed Layout Transistors. In IEEE Transactions on Very Large Scale Integration (VLSI) Systems; IEEE: Piscateville, NJ, USA, 2021; Volume 29, pp. 1122–1131. [Google Scholar] [CrossRef]
- Aziza, H.; Bazzi, H.; Postel-Pellerin, J.; Canet, P.; Moreau, M.; Harb, A. An Augmented OxRAM Synapse for Spiking Neural Network (SNN) Circuits. In Proceedings of the 2019 14th International Conference on Design & Technology of Integrated Systems In Nanoscale Era (DTIS), Mykonos, Greece, 16–18 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Aziza, H.; Zambelli, C.; Hamdioui, S.; Diware, S.; Bishnoi, R.; Gebregiorgis, A. On the Reliability of RRAM-Based Neural Networks. In Proceedings of the IFIP/IEEE 31st International Conference on Very Large Scale Integration (VLSI-SoC), Dubai, United Arab Emirates, 16–18 October 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Aziza, H.; Perez, A.; Portal, J.M. Resistive RAMs as analog trimming elements. Solid-State Electron. 2018, 142, 52–55. [Google Scholar] [CrossRef]
- Ielmini, D. Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Barlas, M.; Grossi, A.; Grenouillet, L.; Vianello, E.; Nolot, E.; Vaxelaire, N.; Blaise, P.; Traoré, B.; Coignus, J.; Perrin, F.; et al. Improvement of HfO2 based RRAM array performances by local Si implantation. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 14.6.1–14.6.4. [Google Scholar] [CrossRef]
- Aziza, H.; Postel-Pellerin, J.; Bazzi, H.; Canet, P.; Moreau, M.; Della Marca, V.; Harb, A. True random number generator integration in a resistive RAM memory array using input current limitation. IEEE Trans. Nanotechnol. 2020, 19, 214–222. [Google Scholar] [CrossRef]
- Aziza, H.; Canet, P.; Postel-Pellerin, J.; Moreau, M.; Portal, J.M.; Bocquet, M. ReRAM ON/OFF resistance ratio degradation due to line resistance combined with device variability in 28nm FDSOI technology. In Proceedings of the Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS), Athens, Greece, 3–5 April 2017; IEEE: Piscateville, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Aziza, H. Oxide-based Resistive RAM Analog Synaptic Behavior Assessment for Neuromemristive systems. In Memristors—The Fourth Fundamental Circuit Element—Theory, Device, and Applications; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Aziza, H.; Hamdioui, S.; Fieback, M.; Taouil, M.; Moreau, M. Density Enhancement of RRAMs using a RESET Write Termination for MLC Operation. In Proceedings of the Design, Automation 459 & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1877–1880. [Google Scholar] [CrossRef]
- Kim, W.; Menzel, S.; Wouters, D.J.; Waser, R.; Rana, V. 3-Bit multilevel switching by deep reset phenomenon in Pt/W/TaOx /Pt-ReRAM devices. IEEE Electron. Device Lett. 2016, 37, 564–567. [Google Scholar] [CrossRef]
- Aziza, H.; Postel-Pellerin, J.; Moreau, M. STATE: A Test Structure for Rapid and Reliable Prediction of Resistive RAM Endurance. IEEE Trans. Device Mater. Reliab. 2022, 22, 500–505. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, H.Y.; Wu, S.C.; Jiang, Z.; Yu, S.; Hou, T.H.; Philip Wong, H.-S.; Nishi, Y. Improved multi-level control of RRAM using pulse-train programming. In Proceedings of the IEEE International Symposium on VLSI Technology, Systems and Application (VLSI-TSA), Hsinchu, Taiwan, 28–30 April 2014. [Google Scholar] [CrossRef]
- Papandroulidakis, G. Experimental Demonstration of RRAM-Based Computational Cells for Reconfigurable Mixed-Signal Neuro-Inspired Circuits and Systems. Ph.D. Dissertation, University of Southampton, Southampton, UK, 2021. [Google Scholar]
- Lee, Y.-L.; Tsung, P.-K.; Wu, M. Technology trend of edge AI. In Proceedings of the Symposium on VLSI Design, Automation and Test (VLSI-DAT), Hsinchu, Taiwan, 16–19 April 2018; pp. 1–2. [CrossRef]
- Aziza, H.; Postel-Pellerin, J.; Fieback, M.; Hamdioui, S.; Xun, H.; Taouil, M.; Coulié, K.; Rahajandraibe, W. Analysis of Conductance Variability in RRAM for Accurate Neuromorphic Computing. In Proceedings of the 2024 IEEE 25th Latin American Test Symposium (LATS), Maceio, Brazil, 9–12 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Portal, J.M.; Bocquet, M.; Onkaraiah, S.; Moreau, M.; Aziza, H.; Deleruyelle, D.; Kholdoun, T.; Vianello, E.; Levisse, A.; Bastien, G.; et al. Design and simulation of a 128 kb embedded nonvolatile memory based on a hybrid RRAM (HfO2)/28 nm FDSOI CMOS technology. IEEE Trans. Nanotechnol. 2017, 16, 677–686. [Google Scholar] [CrossRef]
- Aguirre, F.; Sebastian, A.; Le Gallo, M.; Song, W.; Wang, T.; Yang, J.J.; Lu, W.; Chang, M.-F.; Ielmini, D.; Yang, Y.; et al. Hardware implementation of memristor-based artificial neural networks. Nat. Commun. 2024, 15, 1974. [Google Scholar] [CrossRef]
- Zidan, M.A.; Fahmy, H.A.H.; Hussain, M.M.; Salama, K.N. Memristor-based memory: The sneak paths problem and solutions. Microelectron. J. 2013, 44, 176–183. [Google Scholar] [CrossRef]
- Hu, M.; Strachan, J.P.; Li, Z.; Grafals, E.M.; Davila, N.; Graves, C.; Lam, S.; Ge, N.; Yang, J.J.; Stanley Williams, R. Dot-product engine for neuromorphic computing. In Proceedings of the DAC’16: Proceedings of the 53rd Annual Design Automation Conference, Austin, TX, USA, 5–9 June 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Hajri, B.; Mansour, M.M.; Chehab, A.; Aziza, H. Oxide-based RRAM models for circuit designers: A comparative analysis. In Proceedings of the International Conference on Design & Technology of Integrated Systems In Nanoscale Era (DTIS), Palma de Mallorca, Spain, 4–6 April 2017. [Google Scholar] [CrossRef]
- Aziza, H.; Fieback, M.; Hamdioui, S.; Xun, H.; Taouil, M. Conductance variability in RRAM and its implications at the neural network level. Microelectron. Reliab. 2025, 166, 115594. [Google Scholar] [CrossRef]
- Yuan, G.; Ma, X.; Ding, C.; Lin, S.; Zhang, T.; Jalali, Z.S.; Zhao, Y.; Li, J.; Soundarajan, S.; Wang, Y. An Ultra-Efficient Memristor-Based DNN Framework with Structured Weight Pruning and Quantization Using ADMM. arXiv 2019, arXiv:1908.11691. [Google Scholar] [CrossRef]
- Aziza, H.; Moreau, M.; Fieback, M.; Taouil, M.; Hamdioui, S. An Energy-Efficient Current-Controlled Write and Read Scheme for Resistive RAMs (RRAMs). IEEE Access 2020, 8, 137263–137274. [Google Scholar] [CrossRef]
- Xiao, T.P.; Bennett, C.H.; Feinberg, B.; Agarwal, S.; Marinella, M.J. Analog architectures for neural network acceleration based on non-volatile memory. Appl. Phys. Rev. 2020, 7, 031301. [Google Scholar] [CrossRef]
- Cho, S.M.; Yoon, R.; Yoon, I.; Moon, J.; Oh, S.; Min, K.S. Optimization of Memristor Crossbar’s Mapping Using Lagrange Multiplier Method and Genetic Algorithm for Reducing Crossbar’s Area and Delay Time. Information 2024, 15, 409. [Google Scholar] [CrossRef]
- Postel-Pellerin, J.; Bazzi, H.; Aziza, H.; Canet, P.; Moreau, M.; Della Marca, V.; Harb, A. True random number generation exploiting SET voltage variability in resistive RAM memory arrays. In Proceedings of the 2019 19th Non-Volatile Memory Technology Symposium (NVMTS), Durham, NC, USA, 28–30 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Lanza, M.; Waser, R.; Ielmini, D.; Yang, J.J.; Goux, L.; Suñe, J.; Kenyon, A.J.; Mehonic, A.; Spiga, S.; Rana, V.; et al. Standards for the Characterization of Endurance in Resistive Switching Devices. ACS Nano 2021, 15, 17214–17231. [Google Scholar] [CrossRef]
- Rana, A.M.; Akbar, T.; Ismail, M.; Ahmad, E.; Hussain, F.; Talib, I.; Imran, M.; Mehmood, K.; Khalid, I.; Nadeem, M.Y. Endurance and Cycle-to-Cycle Uniformity Improvement in Tri-Layered CeO2/Ti/CeO2 Resistive Switching Devices by Changing Top Electrode Material. Sci. Rep. 2017, 7, 39539. [Google Scholar] [CrossRef] [PubMed]
- Fieback, M.; Medeiros, G.C.; Wu, L.; Aziza, H.; Bishnoi, R.; Taouil, M.; Hamdioui, S. Defects, fault modeling, and test development framework for RRAMs. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2022, 18, 1–26. [Google Scholar] [CrossRef]
- Fieback, M.; Wu, L.; Medeiros, G.C.; Aziza, H.; Rao, S.; Marinissen, E.J.; Taouil, M.; Hamdioui, S. Device-Aware Test: A New Test Approach Towards DPPB Level. In Proceedings of the IEEE International Test Conference (ITC), Washington, DC, USA, 9–15 November 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Fieback, M.; Medeiros, G.C.; Gebregiorgis, A.; Aziza, H.; Taouil, M.; Hamdioui, S. Intermittent undefined state fault in RRAMs. In Proceedings of the 2021 IEEE European Test Symposium (ETS), Bruges, Belgium, 24–28 May 2021; IEEE: Piscateville, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Castellani-Coulie, K.; Toure, G.; Portal, J.M.; Ginez, O.; Aziza, H.; Lesea, A. Circuit effect on collection mechanisms involved in single event phenomena: Application to the response of a NMOS transistor in a 90 nm SRAM cell. IEEE Trans. Nucl. Sci. 2011, 58, 870–876. [Google Scholar] [CrossRef]
- Castellani-Coulié, K.; Aziza, H.; Rahajandraibe, W.; Micolau, G.; Portal, J.M. Development of a CMOS Oscillator Concept for Particle Detection and Tracking. IEEE Trans. Nucl. Sci. 2013, 60, 2450–2455. [Google Scholar] [CrossRef]
- Coulié, K.; Aziza, H.; Rahajandraibe, W. Investigation of Single Event Effects in a Resistive RAM Memory Array by Coupling TCAD and SPICE Simulations. J. Electron. Test 2023, 39, 275–288. [Google Scholar] [CrossRef]
- Castellani-Coulié, K.; Bocquet, M.; Aziza, H.; Portal, J.M.; Rahajandraibe, W.; Muller, C. SPICE level analysis of Single Event Effects in an OxRRAM cell. In Proceedings of the 2013 14th Latin American Test Workshop-LATW, Cordoba, Argentina, 3–5 April 2013; pp. 1–5. [Google Scholar] [CrossRef]
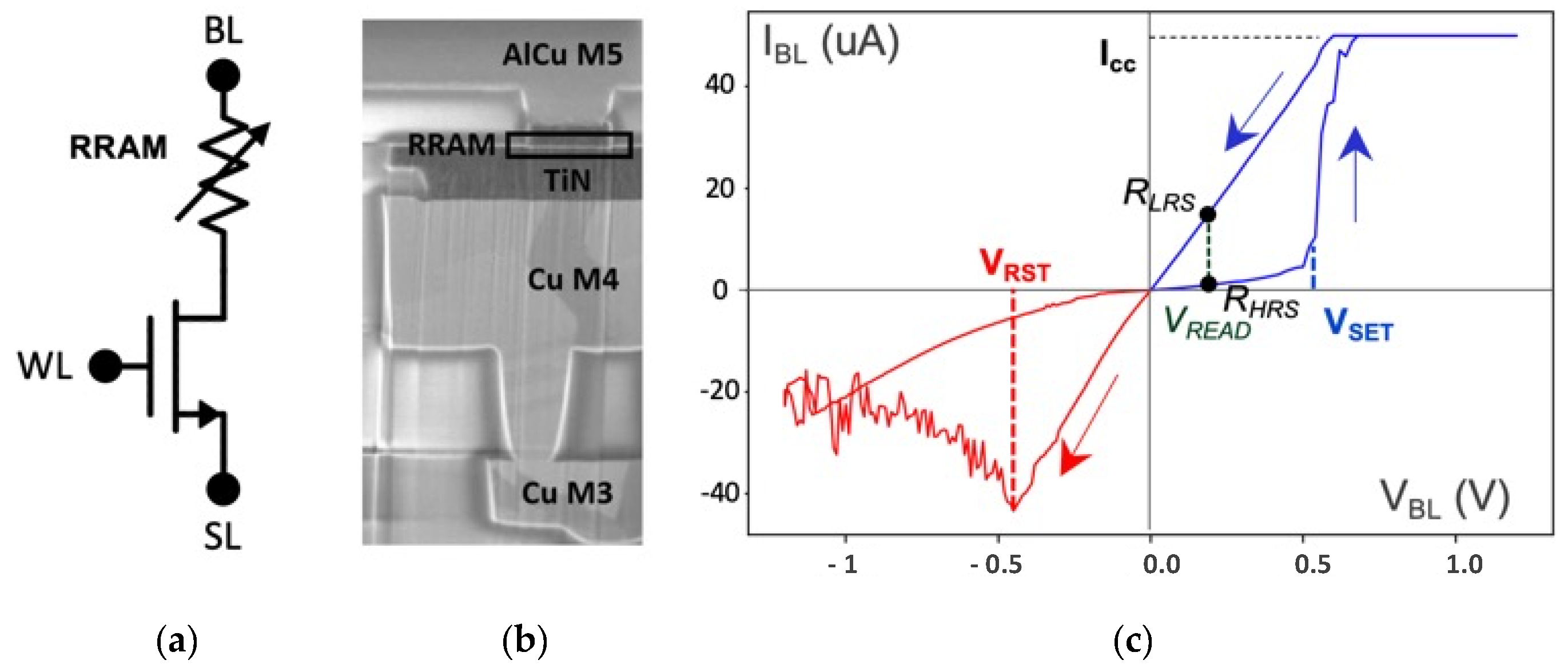



| FMG | RST | SET | READ | |
|---|---|---|---|---|
| WL | 2 V | 2.5 V | 2 V | 2.5 V |
| BL | 3.3 V | 0 V | 1.2 V | 0.1 V |
| SL | 0 V | 1.2 V | 0 V | 0 V |
| Resistance | 10 kΩ | 240 kΩ | 15 kΩ | - |
| Conductance | 100 μS | 4.17 μS | 66.6 μS | - |
| Parameter | Min | Max |
|---|---|---|
| VWL | 1 V | 1.8 V |
| Resistance | 11.5 kΩ | 40.4 kΩ |
| Conductance | 87 μS | 24.7 μS |
| Inference Parameters | Value |
|---|---|
| Crossbar current | 12,686 μA |
| Crossbar power | 37.8 mW |
| Total inference energy | 38 pJ |
| Energy/MAC | 190 fJ/MAC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziza, H. Image Classification in Memristor-Based Neural Networks: A Comparative Study of Software and Hardware Models Using RRAM Crossbars. Electronics 2025, 14, 1125. https://doi.org/10.3390/electronics14061125
Aziza H. Image Classification in Memristor-Based Neural Networks: A Comparative Study of Software and Hardware Models Using RRAM Crossbars. Electronics. 2025; 14(6):1125. https://doi.org/10.3390/electronics14061125
Chicago/Turabian StyleAziza, Hassen. 2025. "Image Classification in Memristor-Based Neural Networks: A Comparative Study of Software and Hardware Models Using RRAM Crossbars" Electronics 14, no. 6: 1125. https://doi.org/10.3390/electronics14061125
APA StyleAziza, H. (2025). Image Classification in Memristor-Based Neural Networks: A Comparative Study of Software and Hardware Models Using RRAM Crossbars. Electronics, 14(6), 1125. https://doi.org/10.3390/electronics14061125





