Theoretical Design and Simulation of a Dual-Band Sheet Beam Extended Interaction Oscillator
Abstract
1. Introduction
2. Physical Model Analysis
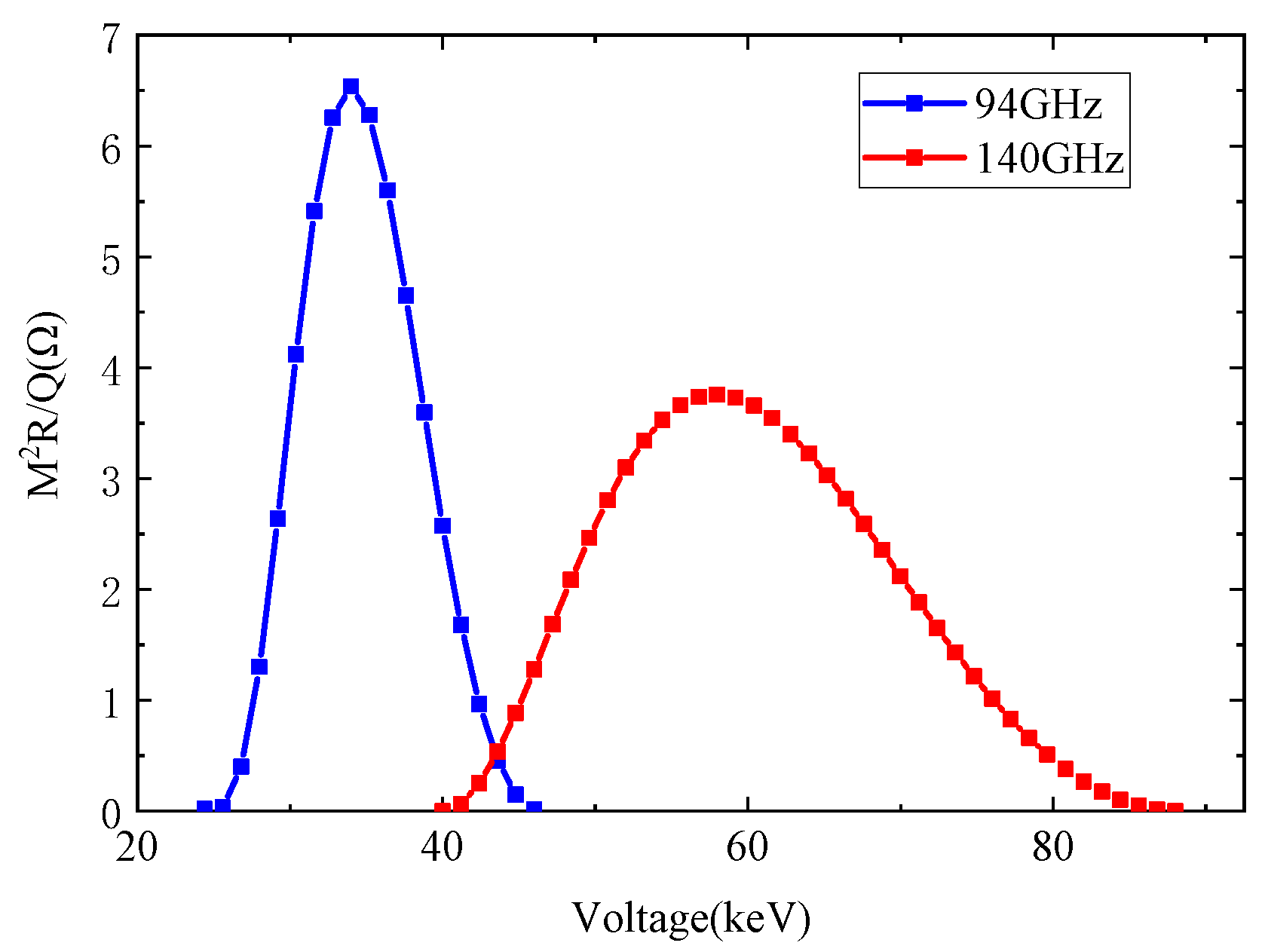
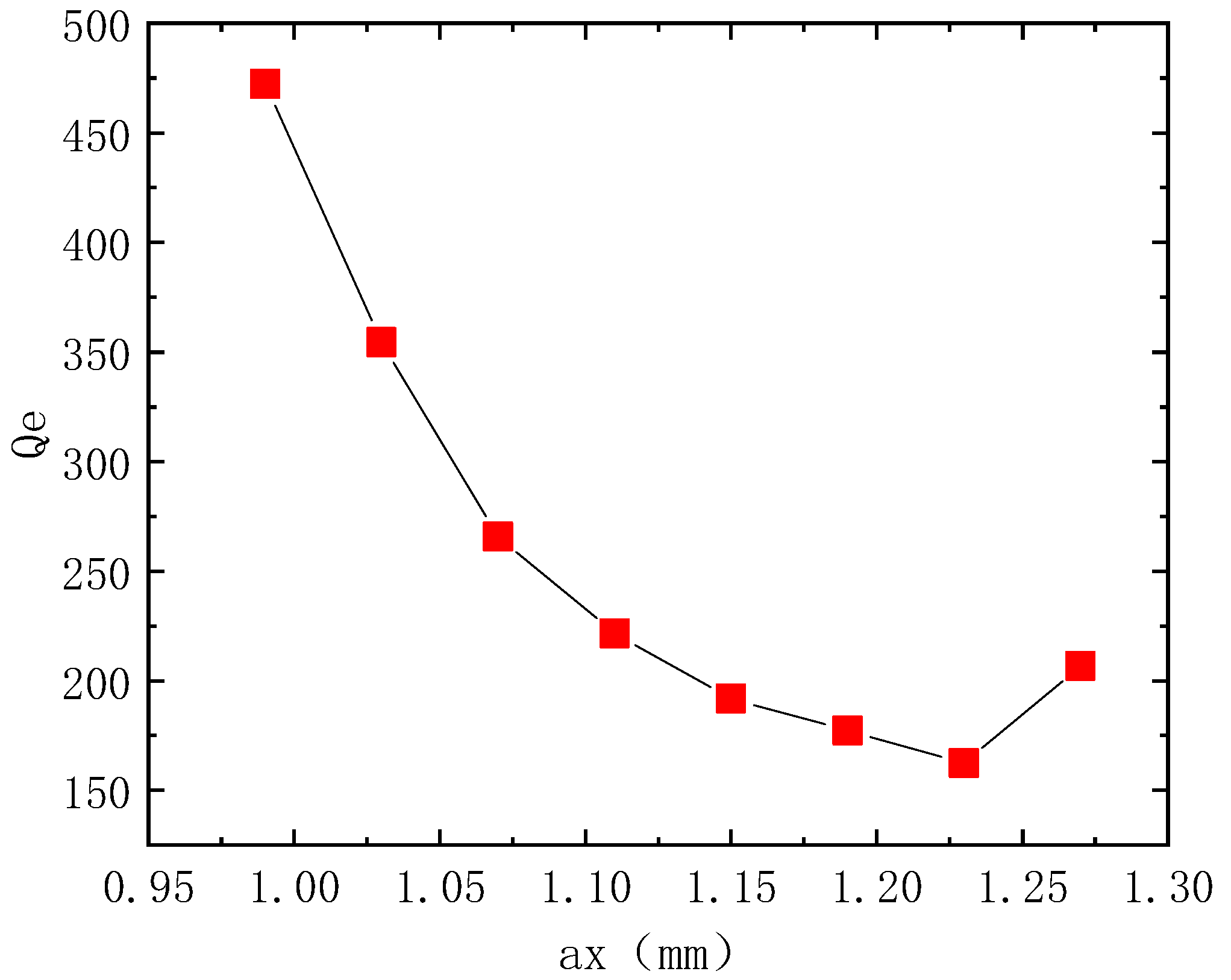
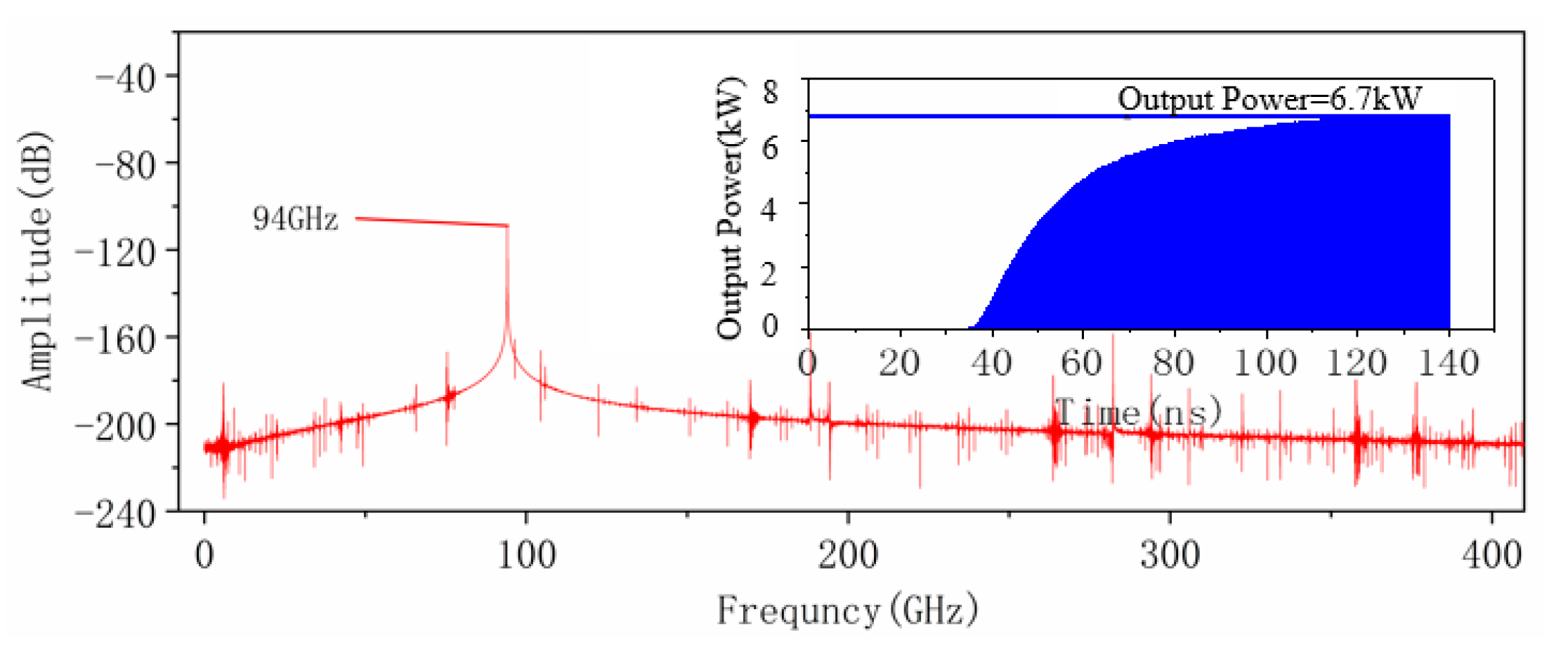
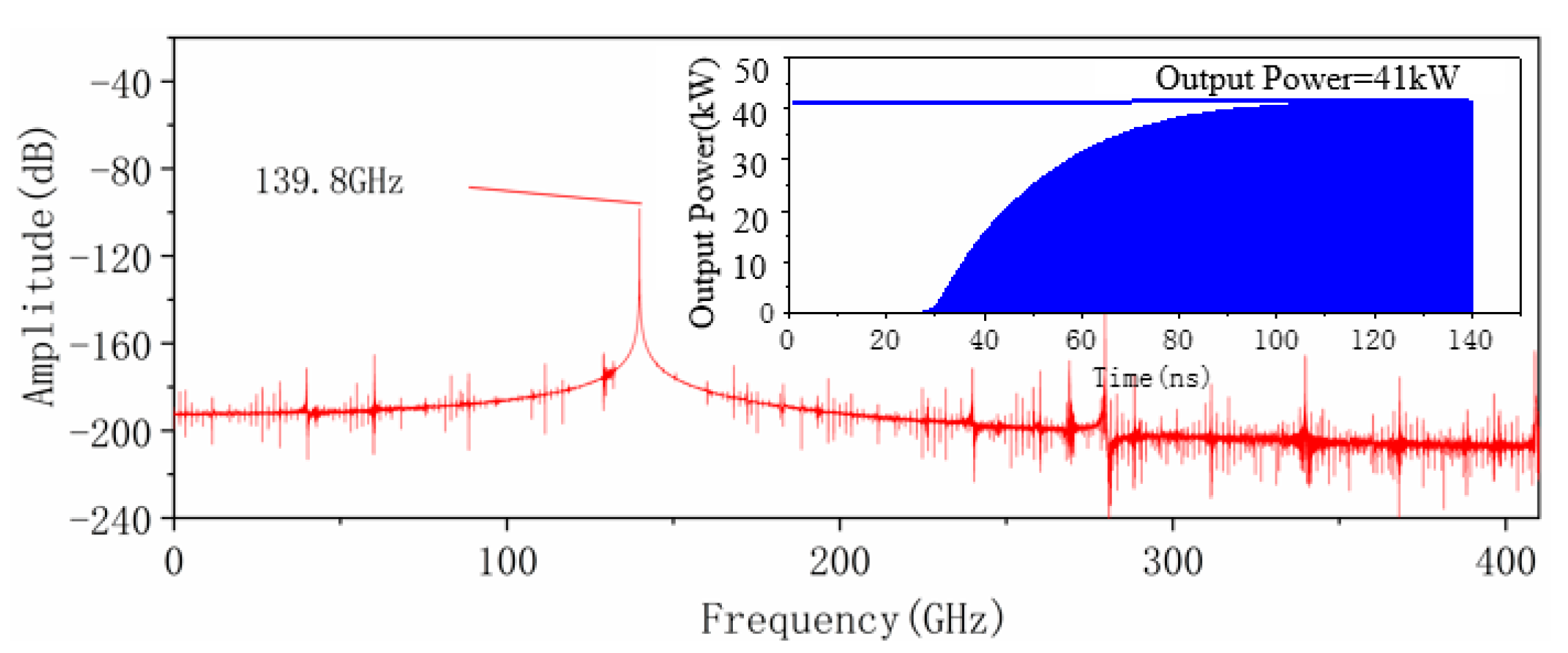
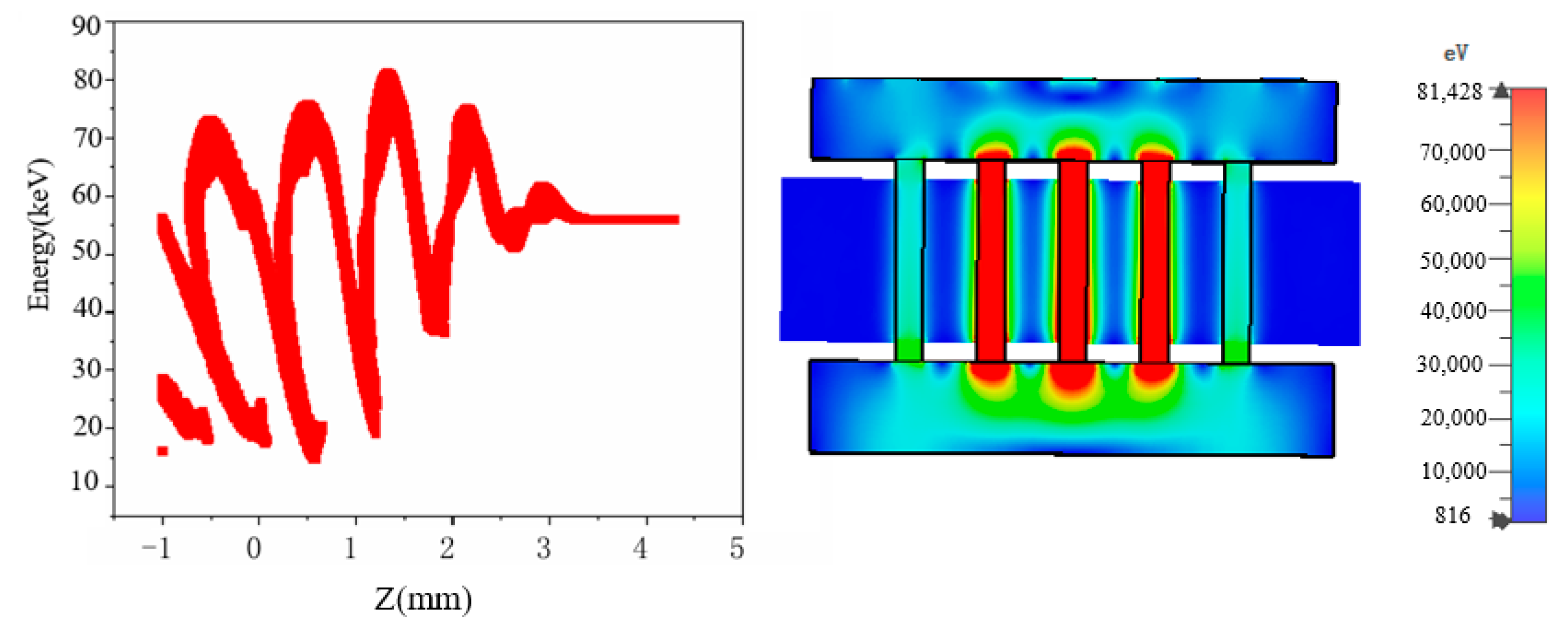
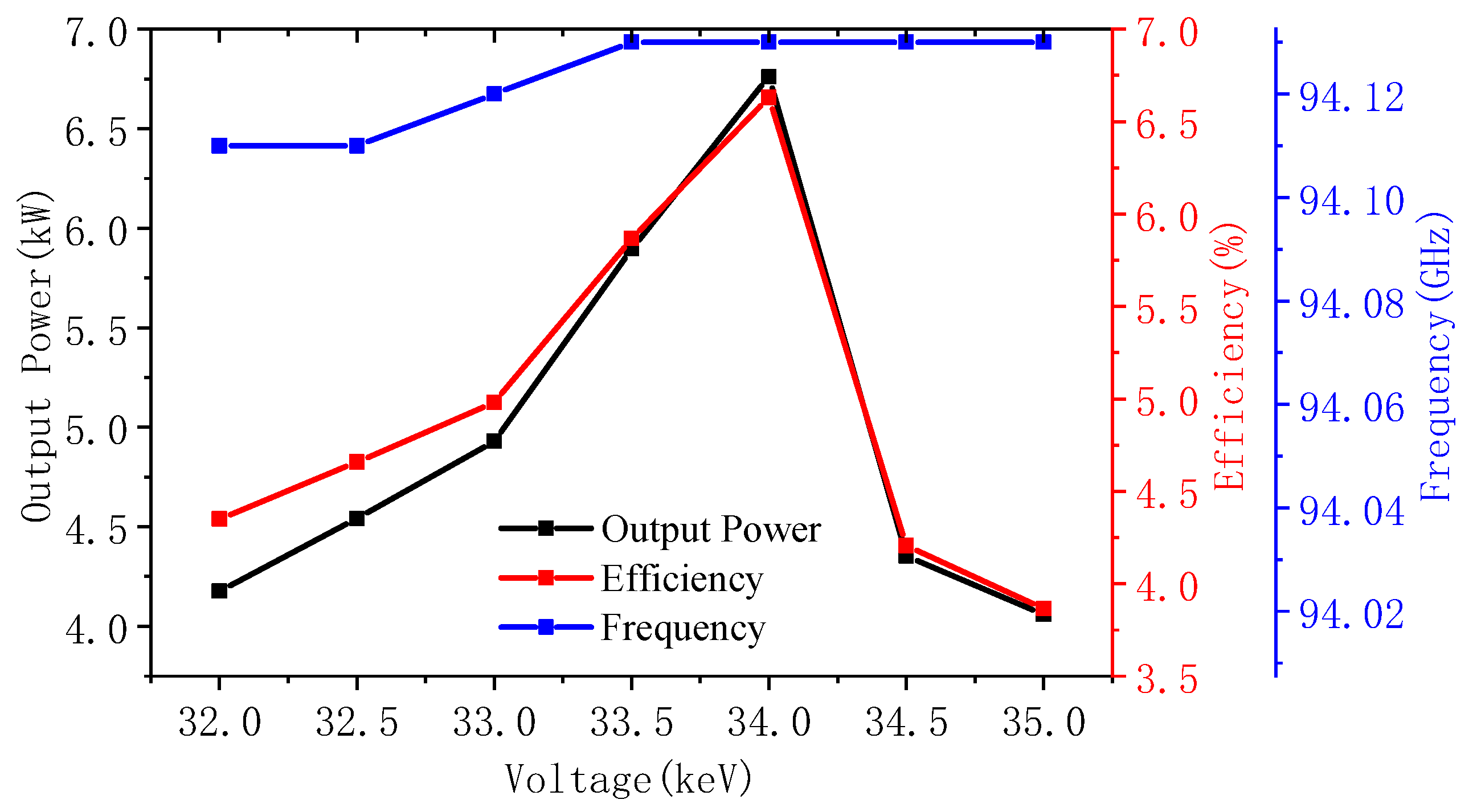
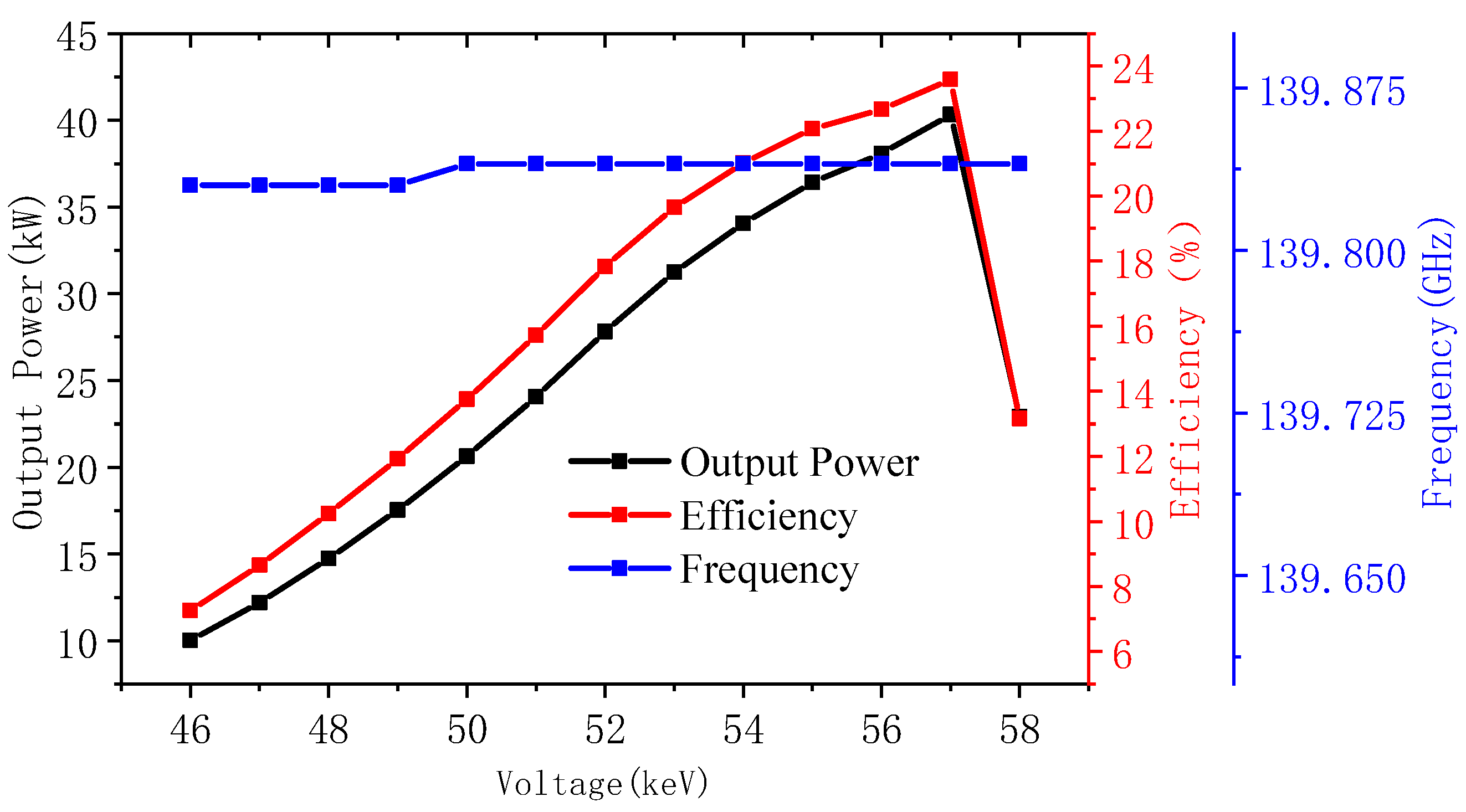
3. PIC Simulation and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tucek, J.C.; Basten, M.A.; Gallagher, D.A.; Kreischer, K.E. Operation of a compact 1.03 THz power amplifier. In Proceedings of the IEEE International Vacuum Electronics Conference, Monterey, CA, USA, 24–26 April 2018; pp. 1–2. [Google Scholar]
- Wang, Z.; Qu, Z.; Li, L.; Shang, X.; Cao, L.; Tang, B.; Xiao, L. Investigation on a broadband 220 GHz extended interaction klystron. In Proceedings of the IEEE International Vacuum Electronics Conference, Busan, Republic of Korea, 28 April–1 May 2019; pp. 1–2. [Google Scholar]
- Bi, L.; Meng, L.; Yin, Y.; Xu, C.; Zhu, S.; Peng, R.; Zeng, F.; Chang, Z.; Wang, B.; Li, H.; et al. Design and Analysis of a High-Order Mode Ladder-Type RF Circuit for Stable Operation in a W-Band Extended Interaction Oscillator. IEEE Trans. Electron Devices 2019, 66, 729–735. [Google Scholar] [CrossRef]
- Berry, D.; Deng, H.; Dobbs, R.; Horoyski, P.; Hyttinen, M.; Kingsmill, A.; MacHattie, R.; Roitman, A.; Sokol, E.; Steer, B. Practical aspects of EIK technology. IEEE Trans. Electron Devices 2014, 61, 1830–1835. [Google Scholar] [CrossRef]
- Shu, G.X.; Wang, J.; Qian, Z. Study of Performance Improvement for a Q-Band Sheet-Beam Traveling-Wave Tube. IEEE Trans. Electron Devices 2018, 65, 3970–3975. [Google Scholar] [CrossRef]
- Steer, B.; Roitman, A.; Horoyski, P.; Hyttinen, M.; Dobbs, R.; Berry, D. Advantages of extended interaction klystron technology at millimeter and sub-millimeter frequencies. In Proceedings of the 2007 16th IEEE International Pulsed Power Conference, Albuquerque, NM, USA, 17–22 June 2007; Volume 2, pp. 1049–1053. [Google Scholar]
- Poseur, J.; Wright, E.; Nguyen, K.T.; Balkcum, A.; Wood, F.N.; Myers, R.E.; Levush, B. Demonstration of a multikilowatt, solenoidally focused sheet beam amplifier at 94 GHz. IEEE Trans. Electron Devices 2014, 61, 1630–1636. [Google Scholar] [CrossRef]
- Pasour, J.; Nguyen, K.T.; Wright, E.; Pershing, D.; Abe, D.; Balkcum, A.; Wood, F.; Myers, R.; Cook, A.; Hanna, J.; et al. High-power mm W sheet beam amplifiers. In Proceedings of the 16th IEEE International Vacuum Electronics Conference, Beijing, China, 27–29 April 2015; pp. 1–2. [Google Scholar]
- Booske, J.H.; Dobbs, R.J.; Joye, C.D.; Kory, C.L.; Neil, G.R.; Park, G.S.; Park, J.; Temkin, R.J. Vacuum electronic high power terahertz sources. IEEE Trans. THz Sci. Technol. 2011, 1, 54–75. [Google Scholar] [CrossRef]
- Chang, Z.W.; Meng, L.; Yin, Y.; Wang, B.; Li, H.; Bi, L.; Peng, R.; Xu, C. Study of a dual-mode W-band extended interaction oscillator. IEEE Trans. Electron Devices 2018, 65, 2620–2625. [Google Scholar] [CrossRef]
- Shu, G.X.; Yin, Y.; Zhang, L.; Zhao, J.P.; Liu, G.; Phelps, A.D.R.; Cross, A.W.; He, W. Demonstration of a planar W-Band, kW-level extended interaction oscillator based on a pseudospark-sourced sheet electron beam. IEEE Electron Device Lett. 2018, 39, 432–435. [Google Scholar] [CrossRef]
- Chen, S.Y.; Liu, J.Q.; Shui, Y.T.; Gao, L.; Jiang, Z.; Bai, J.; Liu, H.; Liu, X.; Zhang, X.; Xu, F.; et al. Design and particle-in-cell simulation of sub-THz sheet beam EIK. In Proceedings of the 41st International Conference Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; pp. 1–2. [Google Scholar]
- Pasour, J.; Nguyen, K.; Wright, E.; Balkcum, A.; Atkinson, J.; Cusick, M.; Levush, B. Demonstration of a 100-kW Solenoidally Focused Sheet Electron Beam for Millimeter-Wave Amplifiers. IEEE Trans. Electron Devices 2011, 58, 1792–1797. [Google Scholar] [CrossRef]
- Soltani, H.B.; Abiri, H. Developing a load-line concept to study the extended interaction oscillators. IEEE Trans. Electron Devices 2017, 64, 3429–3436. [Google Scholar] [CrossRef]
- Wang, J.X.; Barnett, L.R.; Luhmann, N.C.; Shin, Y.M.; Humphries, S. Electron beam transport analysis of W-band sheet beam klystron. Phys. Plasma 2010, 17, 043111. [Google Scholar] [CrossRef]
- Xu, X.T.; Yuan, X.S.; Li, H.L.; Chen, Q.; Zu, Y.; Cole, M.; Xie, J.; Yin, Y.; Yan, Y. Design of a G-Band Extended Interaction Klystron Based on a Three-Coupling-Hole Structure. IEEE Trans. Electron Devices 2022, 69, 1368–1373. [Google Scholar] [CrossRef]
- Ren, X.X.; Wang, J.X.; Dong, K.; Liu, G.; Shu, G.; Fu, H.; Balfour, E.A. Study of a High-Efficiency 34-GHz Sheet Beam Extended Interaction Oscillator with Low Filling Factor. IEEE Trans. Electron Devices 2016, 63, 4074–4080. [Google Scholar]
- Zhang, F.Y.; Liu, W.X.; Jin, Z.H.; Zhang, Z.; Zhang, Z.; Zhao, K.; Xu, J.; Wei, Y.; Lan, F.; Yang, Z. Design and Simulation for 100-Watt-Class 340-GHz Extended Interaction Klystron. IEEE Trans. Electron Devices 2022, 69, 6329–6335. [Google Scholar] [CrossRef]
- Li, R.; Ruan, C.; Zhang, H.; ul Haq, T.; He, Y.; Shan, S. Theoretical Design and Numerical Simulation of Beam-Wave Interaction for G-Band Unequal-Length Slots EIK with Rectangular Electron Beam. IEEE Trans. Electron Devices 2018, 65, 3500–3506. [Google Scholar] [CrossRef]
- Chodorow, M.; Wessel-Berg, T. A high-efficiency klystron with distributed interaction. IRE Trans. Electron Devices 1961, 8, 44–55. [Google Scholar] [CrossRef]
- Jabotinski, V.; Chernin, C.; Nguyen, K.T.; Antonsen, T.M.; Levush, B. Nonperiodic Perturbations in Periodic RF Structures. IEEE Trans. Microw. Theory Tech. 2012, 60, 915–929. [Google Scholar] [CrossRef]
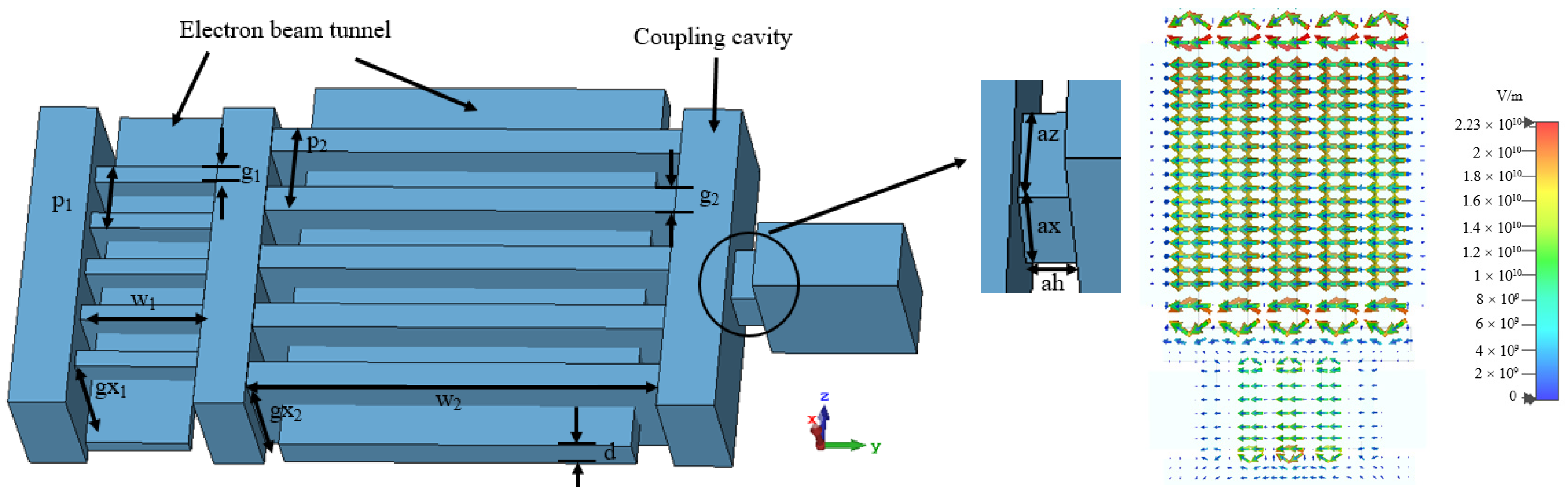



| Symbol | Value (mm) |
|---|---|
| 0.73 | |
| 0.92 | |
| 0.25 | |
| 0.35 | |
| 1.85 | |
| 5.8 | |
| 1.12 | |
| 1.76 | |
| 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, J.; Li, X.; Zhao, Q.; Lu, R.; Liu, X.; Shi, S. Theoretical Design and Simulation of a Dual-Band Sheet Beam Extended Interaction Oscillator. Electronics 2025, 14, 966. https://doi.org/10.3390/electronics14050966
Ling J, Li X, Zhao Q, Lu R, Liu X, Shi S. Theoretical Design and Simulation of a Dual-Band Sheet Beam Extended Interaction Oscillator. Electronics. 2025; 14(5):966. https://doi.org/10.3390/electronics14050966
Chicago/Turabian StyleLing, Jialang, Xiaofeng Li, Qixiang Zhao, Ruiqi Lu, Xingpeng Liu, and Shaoliang Shi. 2025. "Theoretical Design and Simulation of a Dual-Band Sheet Beam Extended Interaction Oscillator" Electronics 14, no. 5: 966. https://doi.org/10.3390/electronics14050966
APA StyleLing, J., Li, X., Zhao, Q., Lu, R., Liu, X., & Shi, S. (2025). Theoretical Design and Simulation of a Dual-Band Sheet Beam Extended Interaction Oscillator. Electronics, 14(5), 966. https://doi.org/10.3390/electronics14050966






