Abstract
Multiclass classification in machine learning often faces significant challenges due to unbalanced datasets. This situation leads to biased predictions and reduced model performance. This research addresses this issue by proposing a novel approach that combines convolutional neural networks (CNNs) with class weights and early-stopping techniques. The motivation behind this study stems from the need to improve model performance, especially for minority classes, which are often neglected in existing methodologies. Although various strategies such as resampling, ensemble methods, and data augmentation have been explored, they frequently have limitations based on the characteristics of the data and the specific model type. Our approach focuses on optimizing the loss function via class weights to give greater importance to minority classes. Therefore, it reduces bias and improves overall accuracy. Furthermore, we implement early stopping to avoid overfitting and improve generalization by continuously monitoring the validation performance during training. This study contributes to the body of knowledge by demonstrating the effectiveness of this combined technique in improving multiclass classification in unbalanced scenarios. The proposed model is tested for oil palm leaves analysis to identify deficiencies in nitrogen (N), boron (B), magnesium (Mg), and potassium (K). The CNN model with three layers and a SoftMax activation function was trained for 200 epochs each. The analysis compared three scenarios: training with the imbalanced dataset, training with class weights, and training with class weights and early stopping. The results showed that applying class weights significantly improved the classification accuracy, with a trade-off in other class predictions. This indicates that, while class weight has a positive overall impact, further strategies are necessary to improve model performance across all categories in this study.
1. Introduction
A fundamental machine learning task is multiclass classification, which involves grouping data into more than two classes [1]. This task is crucial in many fields, such as medical diagnosis, fraud detection, and picture recognition. Significant advantages come from efficient multiclass categorization, including increased security, enhanced decision making, increased efficiency, and the ability to use sophisticated applications [2,3]. In medical diagnostics, for instance, precise multiclass classification can assist in distinguishing between various skin lesions, resulting in more effective treatment strategies and better patient outcomes. In this application, the ability to classify multiple categories accurately is vital. The demand for accurate multiclass classification continues to grow across industries, prompting researchers to explore various methodologies to enhance classification accuracy. However, several obstacles limit multiclass classifiers. A class imbalance can skew the learning process when certain classes have extremely high amounts of data [4]. Extracting valuable features from data is essential yet frequently challenging, especially in high-dimensional areas [5]. Training and implementing sophisticated multiclass classifiers like deep learning models might also be computationally expensive.
The demand for multiclass classification is crucial due to its widespread applications across various fields. Traditional binary classification methods fall short in scenarios where multiple categories must be distinguished. This leads to a need for robust techniques that can effectively handle the complexities inherent in multiclass problems. Class imbalance can also significantly skew model predictions, resulting in poor performance, particularly for the minority class. Imbalanced datasets significantly complicate multiclass classification problems. This imbalance can lead to biased predictions, where the model performs well in the majority class but poorly in the minority [6]. This issue is particularly problematic in critical applications like fraud detection or disease identification. The complexity of the feature space can further complicate the learning process. Various strategies have been proposed to address these challenges, like resampling, ensemble methods, generative models, transfer learning, deep learning, and data augmentation [7,8]. Traditional classification algorithms often favor the majority class, resulting in poor performance for the minority class [9]. Common strategies like oversampling and undersampling can lead to information loss or introduce new biases [10]. Despite these challenges, advancements in ensemble methods and hybrid resampling techniques show promise in providing practical solutions [10,11,12]. Given these complexities and the importance of accurate classification across various domains, multiclass classification remains a dynamic area of research and application in machine learning [13]. Researchers are actively exploring innovative algorithms and strategies to improve classification accuracy, enhance model interpretability, and address the unique challenges of different datasets and application contexts.
Addressing these challenges not only enhances model accuracy and reliability but also contributes to the advancement of machine learning methodologies. It is imperative to explore innovative approaches, such as integrating class weights and early stopping in convolutional neural networks (CNNs). CNNs are a sophisticated class of deep learning algorithms especially designed for image processing [14]. Unlike traditional machine learning models which require manual feature extraction, CNNs automatically learn hierarchical representations of visual features from image data [15]. This property enables CNNs to excel in recognizing patterns and features in visual data, which are essential for image identification tasks. CNNs offer several significant advantages, such as eliminating the need for cumbersome human feature engineering and demonstrating superior performance in various image recognition tasks, including segmentation, object detection, and classification [16]. Additionally, CNNs are robust to changes in object location, exhibiting some invariance to translations and rotations of objects in images.
Despite their strengths, CNNs also have drawbacks. Training deep CNNs can be computationally expensive, requiring substantial time and data [17]. They typically require large amounts of labeled data to perform well. Understanding CNNs’ internal workings can also be challenging. This makes it difficult to interpret their decisions and identify potential biases. In multiclass classification, CNNs provide several benefits by successfully extracting discriminative features from images due to their ability to learn hierarchical representation automatically. However, addressing class imbalances in the training data is crucial for achieving optimal performance. Techniques such as class weights can help improve the effects of class imbalance and the overall classification accuracy by encouraging the model to focus on underrepresented classes during training.
When trained on an imbalanced dataset, CNNs can exhibit bias toward the majority class. To tackle the challenge of improving prediction accuracy in imbalanced datasets, our study explicitly introduces an innovative CNN tailored for this purpose. Previous research has highlighted the challenges posed by class imbalance. However, many existing models still struggle to represent underrepresented classes adequately. This ongoing issue underscores the need for improved methodologies that effectively address these disparities in predictive performance. Our approach focuses on optimizing the loss function via class weights, which are of greater importance to minority classes. This strategy not only reduces bias but also enhances overall accuracy. Additionally, we implement early stopping to avoid overfitting and improve generalization by continuously monitoring validation performance during training. This dual strategy (class weighting and early stopping) strengthens the robustness and generalizability of CNNs and sets a new benchmark for future studies in data analysis. By demonstrating the effectiveness of this combined technique in improving multiclass classification in imbalanced scenarios, our research significantly contributes to the body of knowledge, providing a more reliable framework for leveraging machine learning techniques across various applications.
This article provides a few subsections, including research background, related work, and a newly developed CNN with class weights and early stopping. A numerical experiment is presented alongside its results, findings, discussion, and conclusions.
2. Related Work
In machine learning, multiclass classification is a supervised learning task designed to categorize input data into three or more classes. This task introduces complexities in model training and evaluation, particularly in imbalanced datasets, where traditional metrics like accuracy can be misleading [18]. Unlike binary classification, which deals with two classes, multiclass classification involves multiple categories. This complicates the learning process and the evaluation metrics. The structure of the output layer and the loss function are the main distinctions between these two classification schemes. In binary classification, the output layer typically consists of a single neuron with a sigmoid activation function, producing a probability value between 0 and 1. A threshold of 0.5 is used for [19,20]. In contrast, multiclass classification requires separate neurons for each class in the output layer, applying an activation function to generate probability distribution across all classes.
Imbalanced datasets pose significant challenges in multiclass classification. Various strategies have been proposed to address this problem. Oversampling strategies offer a method to increase the representation of minority classes by creating synthetic samples replicating existing minority samples. One of the most notable oversampling methods is the synthetic oversampling technique (SMOTE), which generates synthetic samples by interpolating existing minority class instances [21]. This enhances the dataset’s balance and improves model performance on imbalanced datasets. Another method, the undersampling technique, reduces the influence of the majority class by selecting samples near the decision boundary or randomly removing majority class samples [22]. Other strategies include cost-sensitive learning and class weights. Cost-sensitive learning modifies the cost function to penalize misclassifications of minority class samples more heavily [23]. Class weights [24] assign higher weights to minority class samples during training, encouraging the algorithm to focus on these underrepresented categories [25].
Table 1 highlights four major approaches to handling dataset imbalance: resampling, ensemble methods, cost-sensitive learning, and class weight. Each approach has its strengths and contributes to improving the performance of classification models on imbalanced datasets. This study selects class weighting as a method to handle dataset imbalance due to its effectiveness in directly addressing the misclassification of minority classes without altering the original dataset. By assigning higher weights to underrepresented classes in the loss function, the model is encouraged to pay more attention to these classes during training. This approach allows for a more balanced consideration of all classes, thereby improving the model’s ability to learn from minor class examples.

Table 1.
Methods for handling class imbalance.
The choice of the activation function and loss mechanism in neural networks significantly impacts model performance. Standard techniques for transforming output values include sigmoid activation, SoftMax, sparse-max, Gumber-SoftMax, and focal loss [32]. SoftMax is widely used to generate probability distributions in multiclass classification tasks [33]. In multiclass classification, categorical cross-entropy is used to evaluate how well the model’s projected probabilities match the actual labels. In binary classification, the binary cross-entropy loss function is utilized [29]. Functions like SoftMax and categorical cross-entropy are foundational for multiclass problems. Meanwhile, techniques such as focal loss provide solutions for class imbalance. Understanding these mechanisms allows practitioners to make decisions when designing neural network architectures. These will result in the enhancement of model performance and applicability across diverse domains.
Convolutional neural networks (CNNs) have proven effective in various classification tasks due to their capability to extract hierarchical features automatically. However, CNNs perform adversely and are affected by class imbalance. Recent studies have shown that applying class weights during training can help this issue by giving more importance to the minority class [30], thereby enhancing model sensitivity and overall performance. Class weights are a widely used technique addressing class imbalance. They assign higher weights to minority classes in the loss function. Models can be trained to focus on correctly classifying these classes. Incorporating class weights in CNN training significantly improves the classification performance of minority classes on imbalanced datasets. Integrating class weights with various neural networks provides a straightforward yet effective solution for imbalance issues.
Early stopping is another optimization technique that monitors model performance on a validation set and stops training when performance is achieved [34]. This method can prevent overfitting, especially when the training data are imbalanced. Combining class weights and early stopping presents a robust approach for optimizing multiclass classification in imbalanced datasets. Integrating these techniques enhances model performance and ensures that minority classes receive attention [27]. Future research should focus on refining these methods and exploring their applicability across various domains, including agriculture, healthcare, finance, and security [35]. Addressing the challenges of class imbalance will contribute significantly to advancements in these critical areas.
3. A CNN with Early Stopping and Class Weighting
In this work, we provide a convolutional neural network (CNN) architecture that effectively addresses the difficulties of imbalanced datasets while improving generalization capabilities. Figure 1 illustrates the new proposed model.
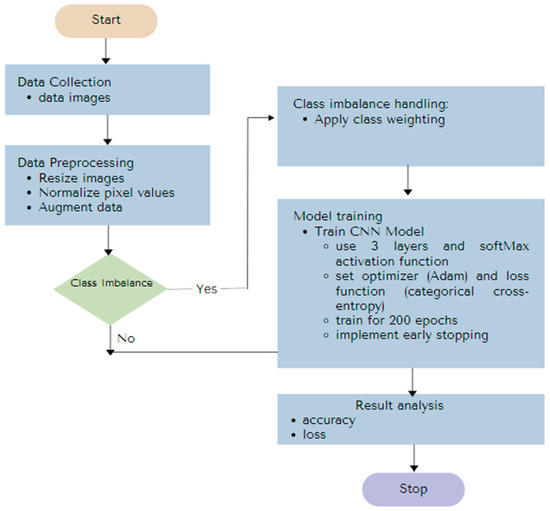
Figure 1.
CNN with class weighting and early stopping.
- Step 1: Data Collection
- These steps include identifying, gathering, and interpreting relevant data from source(s).
- Step 2: Data Preparation
- Data preparation is required to enhance model generalization and input data quality. Several methods can be used to prepare the data, such as image rescaling, data augmentation, target size, and class weight.
- The general formula of class weight is the following:
- : Weight for class
- : Total number of samples in the dataset.
- Number of samples in class
- Total number of classes
This formula ensures that classes with fewer samples have higher weights, encouraging the model to focus more on underrepresented classes during training.
Tuning class weights in unbalanced data is therefore achieved by giving higher weights to minority classes, leading the model to prioritize learning from smaller classes. This effectively overcomes imbalance by placing more emphasis on correctly classifying samples from minority classes than those from the majority class. This is usually achieved by calculating weights in an inversely proportional manner to the class frequency in the dataset. Class weights are typically calculated by taking the inverse proportion of classes in the dataset, giving higher weights to minority classes. In our study, we implemented a Python library. Most machine learning libraries, such as scikit-learn, provide built-in functions to automatically calculate class weights based on the class distribution using the class_weight = ‘balanced’ parameter.
In terms of how the weights should be alternated, it depends on the situation; if a class has far fewer samples, it should have a higher weight to ensure that the model does not ignore it, and if a class has more samples, it should have a lower weight to prevent it from dominating the prediction. The alternation is made before training (to compute the initial class weight based on the class frequency and set the loss function) and during training (for adjustments based on the model performance metric for each class).
If alternations are not performed correctly, this may cause overcompensation, under-compensation, or training instability. Overcompensation occurs if the minority class is given too high a weight. The model may become biased toward the minority class, leading to lower accuracy for the majority class. On the other hand, in under-compensation, if the weights are not adjusted enough, the model will remain biased toward the majority class. This makes the model fail to recognize examples from the minority class. Training instability occurs when sudden weight changes or extreme values can cause training instability and lead to poor convergence.
- Step 3: CNN Modeling
This step develops a CNN architecture with class weight and an early-stopping method to address class imbalance and generalization. The process is as follows:
- -
- Architecture Selection: A CNN architecture (such as ResNet, VGG, or a custom CNN) is selected. The selected architecture should be able to learn unique features from a dataset and effectively extract features from the dataset. Properly selecting architectures, output layer structures, and loss functions is critical for multiclass classification. This configuration facilitates the model’s ability to detect differences between classes efficiently.
- -
- Training Procedure: Using the given dataset, the model is trained while performance metrics (accuracy and loss function) are continuously monitored. The minority class performance receives particular attention since some classes may be overrepresented in the dataset. This situation leads to class imbalance. By performing this step, the model is kept from becoming skewed toward the majority classes.
- -
- Class Weighting: Class weights (Equation (1)) are applied to the loss function to highlight the importance of minority classes during training. Our approach ensures that the model can manage imbalanced datasets by prioritizing accurately and categorizing underrepresented classes. This change lessens the likelihood that minority classes may be overlooked during training.
- -
- Model Generalization: The CNN uses early stopping to monitor the validity loss during training. The model stops training to prevent excess specialization in the majority classes when validation loss either worsens or stays the same. To avoid overfitting or underfitting, this stopping condition ensures that the model learns features for both majority and minority classes more efficiently, improving the model’s generalization capabilities.
- -
- Model Optimization: Adam (adaptive moment estimation) is a popular optimization algorithm for CNNs that combines the benefits of the Momentum and RMSprop algorithms. Momentum keeps track of past gradients to accelerate convergences toward the steepest descent. At the same time, RMSprop adjusts each parameter’s learning rate based on the recent gradient’s magnitude to ensure stability and fast convergence. Model optimization aims to minimize the loss function by modifying the model’s parameters during training, which may improve the model’s performance on the training dataset.
The Adam optimization algorithm [36] is a standard optimization algorithm used to optimize convolutional neural networks [37] used in computer vision. It combines the advantages of two other algorithms, the Momentum and RMSprop optimization algorithms. Consider a CNN trained on images of palm oil leaves to classify nutrient deficiencies. The model starts with random initial weights. The Adam algorithm updates the weights iteratively using gradients of the loss function concerning the weights. Then, it applies momentum to speed up updates in consistent gradient directions and adjust the learning rate for each parameter to avoid overshooting (overshooting occurs when the optimizer takes steps that are too large, causing the model to skip over the optimal point in the loss function) if the learning rate is too high or becoming stuck on plateaus (plateaus are regions in the loss function where gradients are minimal, leading to minimal parameter updates) if the learning rate is too low. Thus, the loss function decreases over epochs, making the model’s predictions more accurate.
The Adam algorithm [38] formulas can be broken down as follows:
- -
- Initialize the model parameters (), learning rate (), and hyper-parameters (, , and ε).
- -
- Compute the gradients () of the loss function () for the model parameters as follows:
- -
- Update the first-moment estimate (m), as follows:
- -
- Update the second-moment estimate (v) as follows:where is a Hadamard product.
- -
- Correct the bias in the first () and second () moment estimates for the current iteration (), as follows:
- -
- Compute the adaptive learning rates () as follows:
- -
- Update the model parameters using the following adaptive learning rates:
- Step 4: Evaluation
The performance indicators used are accuracy and loss. Accuracy measures the proportion of correctly classified instances out of the total cases. A high value of correct predictions indicates a high accuracy. The accuracy is given in Equation (8).
where
- TP = True positive (correctly classified as positive)
- TN = True negative (correctly classified as negative)
- FP = False positive (incorrectly classified as positive)
- FN = False negative (incorrectly classified as negative)
In neural networks, categorical cross-entropy loss is often used for multiclass classification tasks like this. It measures the difference between the predicted probability distribution and the actual label distribution. A lower loss value indicates that the predicted class probabilities are closer to the actual labels. The loss function is given in Equation (9).
where
- N is the total number of samples;
- C is the number of classes (in this case, four—nitrogen, potassium, boron, and magnesium);
- is a binary indicator (0 or 1) if class label is the correct classification for observation ;
- is the predicted probability for class for observation .
This proposed approach shows how the model solves class imbalance and improves classification results for each class using early stopping. The aim is to create a reliable CNN that can generate precise predictions for every class, even in datasets with skewed class distributions. Class weight strategies, early stopping, strict performance monitoring, and a strategic architectural design can help achieve this goal.
The proposed methodology is adaptable to other data modalities, such as tabular data and time series. The structure of different data types, like image data (characterized by pixel grids and RGB channels) and tabular data (organized in rows and columns with numerical and categorical values), requires distinct preprocessing approaches. For instance, image data often benefit from techniques like augmentation, while tabular data necessitate handling missing values and considering data types. Thus, the methodology can be tailored to effectively address the unique challenges presented by each data modality.
4. Numerical Experiment
This section outlines the implementation of the proposed model to assess the nutritional status of palm oil leaves. Given palm oil’s significant economic and environmental role, this section explores the application of the proposed model to examine palm oil leaves. Analyzing leaf nutrient content can identify potential deficiencies and optimize fertilizer application. This contributes to sustainable palm oil production.
- (i)
- Data Collection
The image data for palm oil leaves were extracted from the online repository Kaggle (https://www.kaggle.com/datasets/kvitbio06kvitbio/oil-palm-leaves/data) accessed on 12 August 2024. The file type was PNG, and the size varied from 57 to 60 KB. The images were a collection of close-up photographs of palm oil leaves. The leaves exhibited variations in color, texture, and possible signs of nutrient deficiencies or other abnormalities.
- (ii)
- Data Preparation
Several procedures were taken during data preparation to enhance the input data for model training and improve the overall generalization. The data were prepared using the following guidelines.
- Image Rescaling: The ImageDataGenerator tool rescaled images to a range of [0, 1] to normalize the pixel values. This was significant since raw pixel values usually fall within the [0, 255] range. Normalizing the data helped us speed up the model’s convergence.
- Data Augmentation: The training images were augmented using augmentation techniques, including zoom, shear transformations, and horizontal flipping. This increased the dataset’s size and artificially added diversity. This avoided overfitting and made the model more resilient to changes in the image data.
- Target Size: Every image was resized to 224 × 224 pixels, the standard size. This phase enabled the CNN to handle all inputs consistently, ensuring consistency throughout the dataset.
- Class Weights: class_weight ensured that the model would not disproportionately favor the classes with more samples since the training dataset may have contained imbalanced classes. Class weights provided more balanced predictions by penalizing the model more when it incorrectly classified a minority class.
The dataset was organized into four nutrient classes: boron (B), nitrogen (N), magnesium (Mg), and potassium (K). The nutritional levels in the palm oil leaves were represented by the three condition categories for each nutrient class: excess, normal, and deficiency. As seen in Table 2, the dataset was separated into taring and testing sets.

Table 2.
Dataset composition.
- (iii)
- Modeling
The proposed deep learning technique trained the palm oil leaf image data.
- Model Architecture: The palm oil leaf images were trained using a three-layer CNN. This architecture enabled the model to learn and extract complex features for each class of nutrient (deficiency, normal, and excess) in the leaves.
- Output Layer and Activation: The model used a SoftMax activation function in the output layer to produce a probability distribution across multiple classes, making it suitable for multiclass classification.
- Epochs: The CNN was trained for 200 epochs.
- Early Stopping: ModelCheckPoint saved the best model based on validation performance. Early stopping ensured that the model would retain only the best weights and prevented unnecessary computation.
- Adam Optimizer: The Adam optimizer was used to compile the model. This optimizer’s adaptive learning rate modification features allowed the model to quickly converge on large datasets.
- Loss Function: The divergence between the actual labels and the predicted probability distribution was computed using categorical cross-entropy loss. This loss function is perfect for multiclass classification tasks as it penalizes erroneous predictors across multiple classes.
- (iv)
- Evaluation
Our research used two performance metrics for evaluation: accuracy and loss. Evaluation was essential to understand how well the model generalized to new or unseen data and made accurate predictions. Though accuracy measured the proportion of correct predictions made by the model, it could be misleading in the imbalanced dataset. Hence, the loss was used to quantify the error between the model’s predicted and actual values. Combining these two evaluation metrics was helpful for gaining confidence in the model’s predictions. A well-evaluated model with high accuracy and low loss provides more reliable predictions.
5. Result and Discussion
These sections present the outcomes of the experiments, demonstrating how various strategies for handling imbalanced datasets and avoiding overfitting impacted the model’s ability to detect nutrient deficiencies in palm oil leaves.
Table 3 presents the result from three scenarios: imbalanced, balanced using class weight, and balanced with both class weighting and early stopping. In the first scenario, the data were trained on the original imbalance dataset. The accuracy for various nutrients demonstrated a moderate performance overall. Boron (B) achieved the highest accuracy at 0.7059, while potassium (K) recorded the lowest at 0.6119. The loss values were notably high, particularly for potassium, at 2.8003. This indicates that the model faced challenges in making accurate predictions without addressing class imbalance. This implies that the model was not correctly tuned, resulting in increased loss and less effective prediction, especially for potassium. This situation showed that the model’s accuracy and reliability were compromised as significant prediction errors were made due to imbalanced datasets.

Table 3.
Results.
The second scenario in Table 3 is the model trained on a balanced dataset using class weighting. Modifying the model to address class imbalances using class weights led to an overall increase in accuracy. This was especially true for potassium (K), which rose sharply from 0.6119 to 0.7015. Boron (B) also improved, attaining an accuracy of 0.7500, making it the top-performing class in this scenario. Conversely, the model faced magnesium (Mg) challenges, as its accuracy fell from 0.6923 to 0.4615. This decline may suggest that the magnesium (Mg) samples were inherently more difficult to classify or that the class weights were disproportionately adjusted for imbalances in this category. Indeed, while the model’s performance improved for most classes, it significantly struggled with magnesium. The challenges in classifying magnesium (Mg) may stem from several factors contributing to the lower accuracy in its prediction compared to other nutrients. Magnesium may have complex patterns that are less distinguishable compared to other nutrients. In addition, if the dataset contained a limited number of samples for magnesium, the model may have not learnt enough about the underlying patterns mentioned above. Insufficient data can therefore lead to a lack of generalization.
The third scenario illustrates the implementation of the proposed method, which utilizes class weight and early stopping in a CNN. As shown in Table 3, this approach lowered loss values across all nutrient classes with notable reductions. For instance, nitrogen loss decreased from 1.8329 to 0.6256, and potassium loss dropped from 1.8479 to 0.7659. This decline suggests that the model achieves better convergence, effectively removes overfitting, and enhances generalization. However, the result also indicates a trade-off in precision, particularly for boron (B), whose accuracy fell from 0.7500 to 0.6029. This reduction may have been due to the early-stopping mechanism, which might have limited the model’s ability to learn thoroughly from the boron samples. Additionally, the model’s magnesium (Mg) performance remained low at 0.4615. This opened up the possibility of improving the model via data augmentation, class rebalancing, and feature engineering. Data augmentation can help the model learn better by increasing the diversity in the training datasets by applying transformations such as rotating or scaling. Techniques such as resampling or SMOTE can create more balanced data. On the other hand, feature engineering can be used to investigate and develop additional features that may enhance the model’s ability to distinguish magnesium from different classes.
The study results illustrate the significant impact of managing unbalanced datasets on the model’s ability to classify nutrient deficiencies in palm oil leaves. The model exhibited moderate accuracy across various nutrients without adjusting for class imbalance and struggled to make accurate predictions. This was reflected in the high loss values. In contrast, addressing data imbalance through class weights led to notable improvements in accuracy. Furthermore, the proposed method effectively reduced the loss values for each nutrient class. This indicated better convergence and reduced overfitting. However, this improvement came with a trade-off in precision. The early-stopping mechanism might have limited the model’s ability to learn comprehensively. While the proposed model tackled class imbalance and enhanced performance across most classes, challenges remain. Future research could explore additional techniques to boost classification accuracy for these nutrients.
6. Conclusions
This study investigated the effectiveness of addressing imbalanced datasets through class weights and early-stopping techniques. While this approach significantly reduced loss, the resulting improvements in accuracy varied across different nutrient classes. Consequently, although these methods enhanced model performance to some degree, further efforts are needed, particularly in improving the classification of magnesium, which remains a challenging area for both accuracy and loss. Future research should explore advanced techniques such as data augmentation to better address dataset complexities. Data augmentation techniques can enhance the diversity and quantity of training data, improving the model’s ability to generalize, especially for underrepresented classes. Additionally, enhancing data collection methods for underrepresented classes should be a priority.
Author Contributions
Conceptualization, M.N.R. and N.A.; methodology, N.A. and P.-C.L.; software, M.N.R.; validation, M.N.R. and P.-C.L.; formal analysis, M.N.R. and S.I.; investigation, N.A.; resources, M.N.R. and S.I.; data curation, S.I.; writing—original draft preparation, N.A.; writing—review and editing, P.-C.L.; supervision, N.A.; and funding acquisition, P.-C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Universiti Tun Hussein Onn Malaysia (UTHM) through Tier 1 (Vot Q507) and the National Science and Technology Council (NSTC), Taiwan, under grant number 113-2221-E-035-072.
Data Availability Statement
The image data for palm oil leaves were extracted from the online repository Kaggle (https://www.kaggle.com/datasets/kvitbio06kvitbio/oil-palm-leaves/data) accessed on 12 August 2024. The file type was PNG, and the size varied from 57 to 60 KB. The images were a collection of close-up photographs of palm oil leaves. In these images, the leaves exhibit variations in color, texture, and possible signs of nutrient deficiencies or other abnormalities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jha, A.; Dave, M.; Madan, S. Comparison of binary class and Multiclassclassifier using different data mining classification techniques. In Proceedings of the International Conference on Advancements in Computing & Management (ICACM), Jaipur, India, 13–14 April 2019. [Google Scholar]
- Sevastyanov, L.A.; Shchetinin, E.Y. On methods for improving the accuracy of Multiclass classification on imbalanced data. ITTMM 2020, 20, 70–82. [Google Scholar]
- Fahmi, A.; Muqtadiroh, F.A.; Purwitasari, D.; Sumpeno, S.; Purnomo, M.H. A Multiclass classification of Dengue Infection Cases with Feature Selection in Imbalanced Clinical Diagnosis Data. Int. J. Intell. Eng. Syst. 2022, 15, 176–192. [Google Scholar]
- Das, S.; Datta, S.; Chaudhuri, B.B. Handling data irregularities in classification: Foundations, trends, and future challenges. Pattern Recognit. 2018, 81, 674–693. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dey, L. Introduction to Classification. In Multi-Objective, Multi-Class and Multi-Label Data Classification with Class Imbalance: Theory and Practices; Springer Nature: Singapore, 2024; pp. 1–21. [Google Scholar]
- Cavus, M.; Biecek, P. An Experimental Study on the Rashomon Effect of Balancing Methods in Imbalanced Classification. arXiv 2024, arXiv:2405.01557. [Google Scholar]
- Fayaz, S.; Ahmad Shah, S.Z.; ud din, N.M.; Gul, N.; Assad, A. Advancements in Data Augmentation and Transfer Learning: A Comprehensive Survey to Address Data Scarcity Challenges. Recent Adv. Comput. Sci. Commun. (Former. Recent Pat. Comput. Sci.) 2024, 17, 14–35. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2023, 244, 122778. [Google Scholar] [CrossRef]
- Hort, M.; Chen, Z.; Zhang, J.M.; Harman, M.; Sarro, F. Bias mitigation for machine learning classifiers: A comprehensive survey. ACM J. Responsible Comput. 2024, 1, 1–52. [Google Scholar] [CrossRef]
- Wang, Y.; Rosli, M.M.; Musa, N.; Li, F. Multiclass Imbalanced Data Classification: A Systematic Mapping Study. Eng. Technol. Appl. Sci. Res. 2024, 14, 14183–14190. [Google Scholar] [CrossRef]
- Tanha, J.; Abdi, Y.; Samadi, N.; Razzaghi, N.; Asadpour, M. Boosting methods for Multiclass imbalanced data classification: An experimental review. J. Big Data 2020, 7, 1–47. [Google Scholar] [CrossRef]
- Yang, Y.; Khorshidi, H.A.; Aickelin, U. A review on over-sampling techniques in classification of Multiclass imbalanced datasets: Insights for medical problems. Front. Digit. Health 2024, 6, 1430245. [Google Scholar] [CrossRef]
- Kumar, G.R.; Thippanna, G.; Kumar, K.P. Unveiling the Effectiveness of Multi-Classification Algorithms: A Comprehensive Investigation. J. Comput. Sci. Syst. Softw. 2024, 1, 13–17. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of image classification algorithms based on convolutional neural networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Naranjo-Torres, J.; Mora, M.; Hernández-García, R.; Barrientos, R.J.; Fredes, C.; Valenzuela, A. A review of convolutional neural network applied to fruit image processing. Appl. Sci. 2020, 10, 3443. [Google Scholar] [CrossRef]
- Srivastava, S.; Divekar, A.V.; Anilkumar, C.; Naik, I.; Kulkarni, V.; Pattabiraman, V. Comparative analysis of deep learning image detection algorithms. J. Big Data 2021, 8, 66. [Google Scholar] [CrossRef]
- Alkhawaldeh, I.M.; Albalkhi, I.; Naswhan, A.J. Challenges and limitations of synthetic minority oversampling techniques in machine learning. World J. Methodol. 2023, 13, 373. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Towards Data Sci. 2017, 6, 310–316. [Google Scholar] [CrossRef]
- Yin, B.; Corradi, F.; Bohté, S.M. Accurate and efficient time-domain classification with adaptive spiking recurrent neural networks. Nat. Mach. Intell. 2021, 3, 905–913. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Bansal, A.; Verma, A.; Singh, S.; Jain, Y. Combination of oversampling and undersampling techniques on imbalanced datasets. In International Conference on Innovative Computing and Communications: Proceedings of ICICC 2022; Springer Nature: Singapore, 2022; Volume 3, pp. 647–656. [Google Scholar]
- Mienye, I.D.; Sun, Y. Performance analysis of cost-sensitive learning methods with application to imbalanced medical data. Inform. Med. Unlocked 2021, 25, 100690. [Google Scholar] [CrossRef]
- Fernando, K.R.M.; Tsokos, C.P. Dynamically weighted balanced loss: Class imbalanced learning and confidence calibration of deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2940–2951. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, K.; Bellinger, C.; Corizzo, R.; Branco, P.; Krawczyk, B.; Japkowicz, N. The class imbalance problem in deep learning. Mach. Learn. 2024, 113, 4845–4901. [Google Scholar] [CrossRef]
- Deng, M.; Guo, Y.; Wang, C.; Wu, F. An oversampling method for multi-class imbalanced data based on composite weights. PLoS ONE 2021, 16, e0259227. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
- Ruby, U.; Yendapalli, V. Binary cross entropy with deep learning technique for image classification. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 5393–5397. [Google Scholar]
- Rusiecki, A. Trimmed categorical cross-entropy for deep learning with label noise. Electronics Letters 2019, 55, 319–320. [Google Scholar] [CrossRef]
- Bakirarar, B.; Elhan, A.H. Class Weighting Technique to Deal with Imbalanced Class Problem in Machine Learning: Methodological Research. Türkiye Klin. Biyoistatistik 2023, 15, 19–29. [Google Scholar] [CrossRef]
- Tian, Y.; Su, D.; Lauria, S.; Liu, X. Recent advances on loss functions in deep learning for computer vision. Neurocomputing 2022, 497, 129–158. [Google Scholar] [CrossRef]
- Szandała, T. Review and comparison of commonly used activation functions for deep neural networks. In Bio-Inspired Neurocomputing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 203–224. [Google Scholar]
- Zhu, Q.; He, Z.; Zhang, T.; Cui, W. Improving classification performance of softmax loss function based on scalable batch-normalization. Appl. Sci. 2020, 10, 2950. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, J.; Zhang, Y. A systematic review of early stopping in deep learning. Appl. Sci. 2019, 9, 2348. [Google Scholar]
- Murat, F.; Yildirim, O.; Talo, M.; Baloglu, U.B.; Demir, Y.; Acharya, U.R. Application of deep learning techniques for heartbeats detection using ECG signals-analysis and review. Comput. Biol. Med. 2020, 120, 103726. [Google Scholar] [CrossRef] [PubMed]
- Kingman, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Guo, M.-H.; Xu, T.-X.; Liu, J.-J.; Liu, Z.-N.; Jiang, P.-T.; Mu, T.-J.; Zhang, S.-H.; Martin, R.R.; Cheng, M.-M. Attention mechanisms in computer vision: A survey. Comp. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Jamhuri, M. Understanding the Adam Optimization Algorithm: A Deep Dive into the Formulas. Medium. Available online: https://jamhuri.medium.com/understanding-the-adam-optimization-algorithm-a-deep-dive-into-the-formulas-3ac5fc5b7cd3 (accessed on 29 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).