Abstract
Accurate and robust information on land cover changes in urban and coastal areas is essential for effective urban land management, ecosystem monitoring, and urban planning. This paper details the methodology and results of a pixel-level classification and change detection analysis, leveraging 1945 Royal Air Force (RAF) aerial imagery and 2011 Very High-Resolution (VHR) multispectral WorldView-2 satellite imagery from the broader area of Patras, Greece. Our attention is mainly focused on the changes in the coastline from the city of Patras to the northeast direction and the two major rivers, Charadros and Selemnos. The methodology involves preprocessing steps such as registration, denoising, and resolution adjustments to ensure computational feasibility for both coastal and riverbed change detection procedures while maintaining critical spatial features. For change detection at coastal areas over time, the Normalized Difference Water Index (NDWI) was applied to the new imagery to mask out the sea from the coastline and manually archive imagery from 1945. To determine the differences in the coastline between 1945 and 2011, we perform image differencing by subtracting the 1945 image from the 2011 image. This highlights the areas where changes have occurred over time. To conduct riverbed change detection, feature extraction using the Gray-Level Co-occurrence Matrix (GLCM) was applied to capture spatial characteristics. A Support Vector Machine (SVM) classification model was trained to distinguish river pixels from non-river pixels, enabling the identification of changes in riverbeds and achieving 92.6% and 92.5% accuracy for new and old imagery, respectively. Post-classification processing included classification maps to enhance the visualization of the detected changes. This approach highlights the potential of combining historical and modern imagery with supervised machine learning methods to effectively assess coastal erosion and riverbed alterations.
1. Introduction
Remote sensing technologies have profoundly changed our ability to collect information about the Earth’s surface, allowing for the monitoring and classification of land cover and land use in a variety of scenarios. A combination of techniques, along with advanced classification and analytical tools, have proven to be indispensable in monitoring these dynamic environments. Coastal and riverine systems are constantly influenced by anthropogenic and naturogenic activities, necessitating robust methodologies to detect and analyze their changes over time. Therefore, multitemporal high-resolution datasets have considerably increased the possibility for urban land cover classification, ecological land mapping, and overall sea and land monitoring. This introduction provides a detailed summary of recent research initiatives that investigate the changes in coastlines and riverbeds with different approaches to improve the precision and resilience of change detection.
Zoran and Anderson [1] studied the Romanian Black Sea’s coastal zone to assess transformations caused by nutrient and pollutant loads from rivers, industrial wastewater, and open-water dumping. They utilized multi-sensor satellite data spanning 1975 to 2003 and applied spectral mixture analysis and classification techniques to model land-use changes and sedimentation dynamics, offering critical insights for sustainable land-use planning. Similarly, Kuleli [2] analyzed shoreline changes in the Cukurova Delta on Turkey’s Mediterranean coast from 1972 to 2002. Techniques such as edge detection, band ratioing, and the Digital Shoreline Analysis System (DSAS) were applied to multi-temporal Landsat images to measure accretion and erosion rates. These methods quantify withdrawal rates exceeding 24.5 m/year, driven by sediment transport and river discharge. In the deltaic zones of Istiaia, Greece, Vassilakis, and Papadopoulou-Vrynioti [3] used high-resolution aerial photographs and real-time GPS surveys to quantify coastal erosion and accretion. By incorporating geo-statistical analysis in GIS, they accurately delineated retreat and extension rates, demonstrating the utility of combining high-resolution data with geo-statistical modeling for coastal management. Focusing on the uncertainties of shoreline detection, Dewi et al. [4] employed fuzzy c-means classification (FCM) to monitor shoreline changes in Java, Indonesia, from 1994 to 2015. Their innovative method combined crisp and fuzzy approaches to address positional and methodological uncertainties, achieving high classification accuracy, more specifically a 0.93 kappa value on average for classified images from 1994 to 2015, and reliable change detection.
Xu [5] adopted a multi-temporal analysis approach using Landsat data from 1986 to 2015 to monitor coastline dynamics in Texas, USA. Through annual land-water mapping and linear regression modeling, the study quantified a retreat rate of 0.154 km2/year, linking these changes to sea-level rise and hurricane activity. In India, Misra and Ramakrishnan [6] used Support Vector Regression (SVR) to generate Satellite-Derived Bathymetry (SDB) data for assessing geomorphological changes in Puducherry. This machine learning technique, combined with GIS-based validation methods, effectively mapped accretion and erosion patterns, further enhancing coastal monitoring capabilities. Michałowska and Głowienka [7] analyzed the Baltic Sea coastline’s long-term dynamics using aerial orthophotos spanning 65 years. Their use of historic and modern datasets with GIS analysis revealed periodic erosion and accretion trends influenced by storm events, emphasizing the importance of long-term monitoring. Zoysa et al. [8] investigated shoreline changes along Sri Lanka’s Oluvil coastline from 1991 to 2021. By integrating Landsat imagery with GIS and the DSAS tool, the study quantified accretion and erosion rates near the harbor. Their analysis demonstrated the impacts of harbor construction and highlighted the value of transect-based analysis for detecting spatial variability in coastal changes.
In Greece, Nikolakopoulos et al. [9] examined the Alfios River’s morphological changes from 1977 to 2000. Using multi-temporal Landsat and ASTER imagery, they implemented Principal Component Analysis (PCA) to offset the data from fourteen bands into three with the major volume of information and GIS techniques to map drainage network transformations, identifying significant erosion, reduced meandering, and channel straightening caused by dam construction and gravel extraction. This methodological framework highlights the effectiveness of integrating PCA with GIS for river network monitoring. Li and Damen [10] employed multi-temporal Landsat and SPOT imagery alongside topographic data to detect coastline changes in China’s Pearl River Estuary. Their methodology combined sedimentation and land reclamation mapping with GIS tools, revealing narrowing river channels and heightened flood risks due to rapid urbanization and industrialization. The application of deep learning in remote sensing was demonstrated by Feng et al. [11], who developed a multi-branch convolutional neural network (MBCNN) for coastal land cover classification in the Yellow River Delta, China. Their approach, achieving 93.78% accuracy, leveraging multi-temporal and multi-sensor Sentinel data, improved performance by 6.85% and 3.24%, respectively. The fusion module further enhanced accuracy by about 2% over feature stacking. This approach underscores the potential of deep learning for complex coastal environments. Chen et al. [12] introduced the EMID method to extract river networks using multi-temporal imagery and path-tracking optimization. This two-stage approach employed Random Forest models for water surface mapping and hydrological connectivity analysis, significantly improving river network accuracy. Patel et al. [13] employed the Digital Shoreline Analysis System (DSAS) and Landsat imagery from 1978 to 2018 to monitor alarming shoreline migration near the Mahi River estuary, India. Their methodology integrated NDWI-based shoreline delineation and transect-based displacement analysis to predict future shoreline changes.
More recently, El-Masry et al. [14] investigated multi-decadal coastal change detection along the Mediterranean coast of Egypt, revealing a 47.33 km2 (4.13%) expansion in agricultural land and a 73.13 km2 (6.24%) reduction in bare soil area over three decades. They also reported an increase in built-up areas by 20.51 km2 (1.77%) between 2010 and 2020, highlighting the shift toward tourism and urban development in the region. Similarly, Gomes et al. [15] assessed the use of satellite-derived shorelines and bathymetry for coastal change monitoring in Spain, achieving high horizontal accuracy (RMSE < pixel size) with errors of 5.0 m for Sentinel-2 and 18.8 m for Landsat 5 imagery. Their study demonstrated the capability of satellite data to detect coastal changes across different spatial and temporal scales, though bathymetric assessments remain limited without supplementary in situ data.
Further studies have focused on high-risk coastal regions affected by erosion and accretion dynamics. Kundu and Mandal [16] analyzed shoreline changes in the Sundarban Delta using multi-temporal Landsat imagery, finding that over 80% of transects in the southern parts of the studied islands experienced gradual erosion. The maximum shoreline displacement was recorded at 2715 m between 1975 and 2020, with erosion rates reaching up to 168.2 m/year. Additionally, Bar et al. [17] examined coastal dynamics along India’s eastern coast using optical and SAR imagery, reporting annual erosion rates ranging from 0.62 m to 2.60 m, while accretion rates varied from 0.02 m to 5.99 m. They projected significant shoreline changes, with certain areas expected to retreat by up to 67.49 m over the next 15 years.
In the subsequent sections, we present an analytical overview of our study. Section 2 outlines the study area, and the materials utilized, while Section 3 elaborates on the steps applied to aerial and satellite data for image registration. Section 4 details the methodology and results in coastline change detection. Section 5 examines changes in the two main rivers, Charadros and Selemnos. Finally, in Section 6, we discuss the overall results of the study, address possible imperfections and their underlying causes, and propose improvements for future research.
Building on a range of advanced methodologies, this study focuses on detecting coastline and riverine changes in the broader area of Patras, Greece. By leveraging multi-temporal, high-resolution satellite imagery and analytical techniques, we aim to quantify the shoreline retreat, river morphological changes, and potential environmental drivers influencing these transformations. Specifically, our analysis compares historical aerial and satellite imagery from 1945 and 2011 to assess long-term coastal erosion, riverbed modifications, and land-use changes. The findings provide insights into the geomorphological evolution of the region, offering valuable data for coastal management, urban planning, and environmental monitoring. This work contributes to improving change detection accuracy through methodological enhancements, such as refined image processing and classification techniques. The following section outlines the study area and the datasets used in this analysis.
2. Study Area and Materials
The broader area of the city of Patras was selected as the study area, located within the polygon defined by coordinates 38°20′17″ N to 38°14′39″ N latitude and 21°42′59″ E to 21°50′30″ E longitude. This region encompasses various land cover types; however, our analysis focuses on the binary classification of two categories: sea or not sea and river or not river. The location of the study area is depicted in Figure 1. We utilized Very High-Resolution (VHR) data from the WorldView-2 satellite, which operates in a Sun-synchronous orbit at an altitude of 770 km. The specific dataset used was the WV2_OPER_WV-110_2A_20110708T094541_N38-311_E021-758_4061 product, acquired on 8 July 2011, at 9:45:41 AM. For this analysis, we selected coastal and NIR2 with a 1.6 m spatial resolution, and the Panchromatic band, offering a spatial resolution of 0.4 m. WorldView-2 imagery was freely downloaded after completing access authorization through the ESA TPM Map Catalogue—WorldView-2 European Cities collection data search (https://tpm-ds.eo.esa.int/smcat/WorldView-2/3/Greece/Patra/0/, accessed on 1 October 2024). Additionally, an archive aerial photograph from the Royal Air Force (RAF), captured in 1945, was utilized for comparison. This image of the same area was scanned at high resolution to ensure accuracy in the analysis.
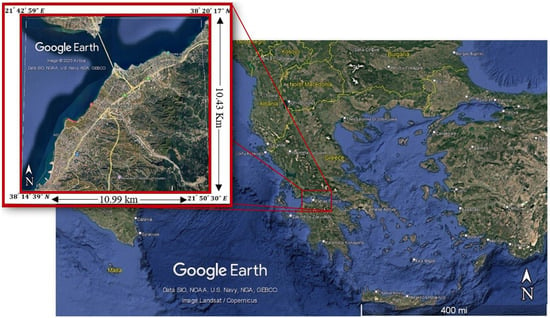
Figure 1.
Study area: The broader area of the city of Patras. Map data ©2024: Google, SIO, NOAA, U.S Navy, NGA, GEBCO, TerraMetrics, Airbus.
The region where the coastline deterioration was examined is around the city of Patras (population of 200,000 citizens) in western Greece and a significant port to Italy. In Figure 1, the position of the region in the eastern Mediterranean is shown, and the magnification shows the exact map of the region. The photo of the region in the red square in Figure 2 was captured in 1945 by the Royal Air Force (RAF). This photo is used in the following for detecting changes in the region 66 years later (2011).
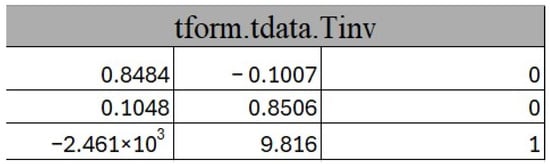
Figure 2.
Tinv matrix is given from cp2tform MATLAB built-in function. This matrix contains the transformation coefficients and .
3. Registration
As mentioned earlier, the panchromatic band of the WorldView-2 satellite with a resolution of 0.4 m, coastal and NIR2 bands with a resolution 1.6 m and an archive aerial photograph from the Royal Air Force (RAF) were used (Figure 3). Since these two data sources do not share the same resolution, a transformation was necessary to correct potential translation, rotation, and scaling distortions. This step ensures that the characteristics from the satellite bands can be accurately assigned to the corresponding pixels in the aerial photograph.

Figure 3.
Registration with affine transformation between the panchromatic image from 2011 and the archive image from 1945 depicting the control points used for determining the affine transformation (a) Fixed VHR panchromatic image; (b) moving archive aerial image; (c) registered archive aerial image.
The registration process was performed using the mutual information method. Specifically, an affine transformation was applied to both datasets after correlating regions of overlap between the images. The registration procedure utilized MATLAB 2022b’s “cpselect” toolbox [18]. Using “cpselect,” regions of mutual information were manually identified and used as inputs for the algorithm in the form of six control points, which remained permanent over time. These control points are illustrated in Figure 3a,b.
To better understand the process of registration, consider two images of the same planar object captured from different viewpoints. Let and be corresponding points in the two images. The coordinates of can be described in terms of the coordinates of using an affine transformation as follows:
Here, A is a non-singular matrix, and t is a two-dimensional vector. A planar affine transformation is defined by six parameters, which account for translation, rotation, scaling, and shearing [19]. Representing this transformation in terms of the image coordinates of the points, (1) can be written as
According to the MATLAB help center, for affine transformation, the following is obtained:
where ; are the transformed coordinates;
are the transformation coefficients for scaling (), rotation (), and shearing (); and are transformation coefficients for translation (, ).
After finding the control points that are more suitable, we used the cp2tform function in order to calculate matrix as shown in Figure 2.
Table 1 illustrates the different affine transformations matrices, i.e., translation, scale, shear, and rotation [20].

Table 1.
Affine transformations matrices.
To present what transformations have been applied in our case, we first have to calculate the coefficients.
Looking at Formula (5), we see that the coefficients are
If we consider that the shearing transformation matrix is , we have
Knowing the coefficients of , we are able to solve the system defined from Equations (6)–(11). This procedure gives us the ability to understand what transformations have taken place and by extension what is really happening behind the MATLAB functions to make the registration happen. The results of the solved system are given in Table 2:

Table 2.
Angle, scaling, shearing, and translation coefficients.
In our case, Table 2 gives us very important information regarding the transformations that were applied. We understand that for the moving image, we have 2461 pixels left offset at the x-axis and 9.81 pixels down at the y-axis. We have almost a uniform scale reduction of the recovered image at about 0.85 and at a clock-wise rotation of about 6.73 degrees with almost no shearing at the x-axis.
The transformation factors were calculated using the VHR panchromatic image and subsequently applied to all layers of the aerial RGB image. This process resulted in the final registered archive aerial image of Patras, as shown in Figure 3c.
4. Coastal Erosion
In this section, the primary objective is to detect coastline changes over time. To achieve this, we performed a series of preprocessing steps combined with the calculation of the Normalized Difference Water Index (NDWI) for WorldView-2 data, ultimately generating two binary maps representing sea and non-sea areas from the two datasets. The changes were then identified by subtracting one binary map from the other. Finally, the results were visualized using a colormap to enhance interpretation and provide a clearer understanding of the detected changes.
4.1. Methodology
As the registration step has been presented in the previous chapter, now there are some steps to prepare the data for feature extraction. First, we applied adaptive histogram equalization to adjust the contrast in order to be able to detect more details and also to make it easier to separate land from the sea (Figure 4).

Figure 4.
The two images after adaptive histogram equalization to enhance the contrast. (a) 1945 archive RAF image; (b) VHR WorldView-2 2011 image.
Additionally, we applied a mild thresholding to zero for pixels with intensity at the middle of the range (0 to 255) to reduce noise without losing important information. As we see in Figure 5, the borders between the sea and the land become clearer.

Figure 5.
The two imageries after thresholding seem to have been “cleared” from noisy pixels near the coastline. (a) 1945 archive RAF image; (b) VHR WorldView-2 2011 image.
Normalized Difference Water Index (NDWI) Calculation
Traditionally, the normalization of a blue band against a Near-Infrared (NIR) band is commonly employed due to the pronounced difference in their spectral responses, which makes water detection more apparent. In this approach, however, the coastal band is utilized instead of the blue band, and it is normalized against the NIR2 band. This choice leverages the greater spectral contrast between these two unique bands, enhancing the sensitivity and precision of the NDWI [21].
Consequently, this method provides a more distinct and refined threshold for accurately identifying areas of standing water, making it particularly effective to find with great precision the coastal borders for Worldview-2 imagery of 2011 (Figure 6b). After calculating this index, we adjust the mask using the same control points as Figure 3a,b with the aim of matching the one masked image with 1.6 m resolution to the panchromatic with 0.4 m for better accuracy.

Figure 6.
Black- and white-masked (a) archive (1945) and (b) recent (2011) imagery, which is used for coastal change detection. The black and white mask emphasizes the land–water interface and accelerates the identification of shoreline shifts and morphological changes over time.
4.2. Coast Comparison Results
To assess the changes at the coastline depicted in Figure 7, we focused on some regions where significant modifications have occurred over time. First, we examined land changes that have emerged since 1945, including coastal expansions influenced by natural processes and human interventions such as the construction of the breakwaters at the ports of Patras and the Rio-Antirio Bridge. The total area of these newly formed regions was quantified by specifying the number of pixels in the image, which represents the recent areas (red color) and the resolution of the spatial resolution of the image. Then, we calculated the area in square meters and kilometers.
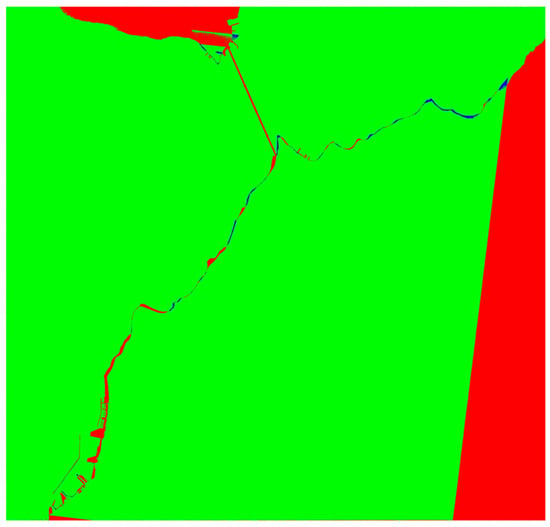
Figure 7.
RGB map of the differences from 1945 to 2011. In red, we have the recently developed sections of the coastline. Blue represents the coastline areas that existed in 1945 but not now, and green represents the areas with mutual information.
Recently formed areas overall
- Number of Pixels: 3,271,929;
- Resolution: 0.4 m × 0.4 m = 0.16 m2 per pixel.
Calculated Area:
- In square meters: 523,508.64 m2;
- In square kilometers: 0.5235 km2.
Another region we chose for further investigation is an attraction pole for residents, especially during the summer months, called Plaz, Patras; we conducted this investigation by performing an accurate comparison of our methodology with Google Earth Pro for this urban coastal region (Figure 8).

Figure 8.
Precision comparison of the area Plaz, Patras, with our methodology (a) and using Google Earth Pro (b). Map data ©2025: Google, Maxar Technologies. In red, we have the recently developed sections of the coastline. Blue represents the coastline areas that existed in 1945 but not now, and green represents the areas with mutual information.
- Number of Pixels (red area): 162,473;
- Resolution: 0.4 m × 0.4 m = 0.16 m2 per pixel.
Calculated Area:
- In square meters: 25,995.68 m2;
- In square kilometers: 0.0260 km2;
- Google Earth calculation: 25,895 m.
Consequently, we examined a region that is directly connected with river changes but drastically affects our shoreline. This region is where Charadros has discharged a huge load of sand, rocks, and other debris, resulting in the creation of a small beach toward the sea (Figure 9).

Figure 9.
Charadros river discharge calculation over the years with our methodology (a,b) using Google Earth Pro. Map data ©2025: Google, Maxar Technologies. In red, we have the recently developed sections of the coastline. Blue represents the coastline areas that existed in 1945 but not now, and green represents the areas with mutual information.
Charadros discharge
- Number of Pixels (red area): 117,184;
- Resolution: 0.4 m × 0.4 m = 0.16 m2 per pixel.
Calculated Area:
- In square meters: 18,749.44 m2;
- In square kilometers: 0.0187 km2;
- Google earth calculation: 17,300 m2.
Finally, there are a lot of areas that existed in 1945 but have since eroded or sunk, emphasizing coastal retreat from human or natural interference.
- Number of Pixels: 859,076;
- Resolution: 0.4 m × 0.4 m = 0.16 m2 per pixel.
Calculated Area:
- In square meters: 137,452.16 m2;
- In square kilometers: 0.1375 km2.
5. Riverbed Changes
This chapter focuses on the analysis of riverbed changes from two of the rivers in the broader of the city of Patras region. To achieve this, we describe the preprocessing steps necessary to harmonize the datasets, remove noise, and prepare the data for successful feature extraction. Following this, we present the methodology we used for feature extraction to capture meaningful textures related to river structures. Finally, we describe the classification techniques applied to distinguish between riverine and non-riverine areas, allowing an in-depth examination of riverbed dynamics over time.
5.1. Methodology
Having already separated the sea from the mainland, we were able to mask out the sea and work only with the mainland and rivers. Our main problem in this research article was the high computational load for the classification of the whole region. So, after experimentation, we decided to lower the data resolution by one-fifth, more specifically from 0.4 m to 2 m (Figure 10). This resolution balances computational feasibility with sufficient spatial detail for accurate classification. Previous studies in remote sensing and image analysis suggest that moderate resolution reduction can preserve essential spatial patterns while significantly improving efficiency [22]. Furthermore, our classification approach focuses on large-scale land cover changes rather than fine-grained textures, making the selected resolution appropriate for our objectives.

Figure 10.
Original images with the sea masked out and lower resolution for computational efficiency: (a) 1945 RAF aerial image; (b) 2011 Worldview-2 satellite imagery.
Then, we rotated both images 45 degrees to take a subset focused on the two Charadros and Selemnos, which are our rivers of interest, as shown in Figure 11.

Figure 11.
Rivers Charadros and Selemnos from 1945 (a) to 2011 (b).
In the old image, we performed an adaptive histogram equalization to achieve better contrast because it has faded through time (Figure 12a). The result appears in (Figure 12b).

Figure 12.
Rivers Charadros and Selemnos from 1945 before (a,b) after adaptive histogram equalization.
Finally, we applied thresholding to remove information that may be confusing and make the training of the classifier difficult (Figure 13).

Figure 13.
Final products after preprocessing the images (1945) (a) and (2011) (b), which were used for feature extraction.
Feature Extraction and Classification
To analyze riverbed changes in the Charadros and Selemnos rivers, we utilized a combination of feature extraction and classification techniques. The methodology involved the preprocessing of the two finally thresholded images representing historical and recent river conditions, as we presented in the previous subsection. Texture features were extracted using the Gray-Level Co-occurrence Matrix (GLCM) approach [23]
We computed the Gray-Level Co-occurrence Matrix (GLCM) for a sliding window of 11 × 11 pixels, centered around each pixel in the image. For each neighborhood, the energy (13) and contrast (14) were calculated from the GLCM. As stated in (13), the energy value increases when the elements of the matrix exhibit uniform or similar values. This can be determined using the following formula [24,25]:
Equation (14) defines contrast, also referred to as inertia, as a metric that quantifies the variation in intensity between different pixels in an image. A high contrast value signifies significant intensity variation, while a low value indicates minimal variation. The contrast is computed using the following formula [26,27]:
where and is co-occurrence matrix indices and is the element of the co-occurrence matrix at position .
These two statistical values, representing the texture characteristics of the neighborhood, were then assigned to the corresponding pixel as its features. The resulting feature maps were aggregated into a multidimensional dataset.
Regions of interest (ROIs) were manually selected to create a training dataset. Specifically, 15,000 pixels from both river and non-river areas in the old image (Figure 14a) and 5400 pixels from the new image (Figure 14b) were chosen to train a Support Vector Machine (SVM) classification model.

Figure 14.
Training datasets of river (with blue) and non-river (with red) areas in both old (a) and new (b) imageries.
The SVM model was configured using by default the Sequential Minimal Optimization (SMO) [28] solver, which is efficient for binary classification tasks. The training data consisted of two predictors (contrast and energy). The SVM identified 1074 support vectors in the new image dataset and 9760 in the old dataset. These support vectors are the data points that contribute to defining the decision boundary, as determined by the SVM using a linear kernel as shown in Figure 15.
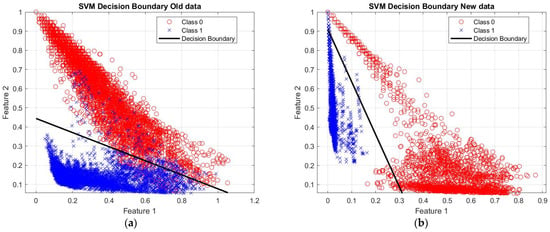
Figure 15.
SVM decision boundaries for the training pixels, for old imagery (a) and new imagery (b), described with two features. Class 1 (river) is represented with blue and class 0 (not river) with red.
The model also calculated the optimal weights (Beta) and bias terms to maximize the margin between classes. These parameters ensured a robust classification framework, as demonstrated by the SVM’s ability to predict river regions accurately in subsequent analysis.
After training, the feature maps of the entire image were reshaped into a vector format, allowing the trained SVM classification model to predict each pixel as either river (1) or non-river (0). These predictions were then reshaped back to the original image dimensions, resulting in a classification map that visually delineates river regions from non-river regions, as represented in Figure 16.

Figure 16.
Binary classification maps of Charadros and Selemnos from 1945 (a) and 2011 (b).
5.2. Results
To describe the accuracy of our model, knowing that we do not have a truth table for the entire study area, we decided to use some testing pixels (Figure 17) to check the accuracy. More specifically, our classifier achieved 92.5% accuracy for 5400 random known river and not river pixels for the new image and 92.6% for 60,000 random river and non-river pixels for the old imagery. Although the feature extraction and SVM classification method were quite promising, some challenges remain. As shown in Figure 16, both images contain many extra pixels predicted as river pixels (value 1) that are not actually part of the river.

Figure 17.
Testing datasets of river (with blue) and non-river (with red) areas in both old (a) and new (b) imageries.
This discrepancy, as depicted in Figure 15, does not necessarily indicate an inaccuracy in our model because the rivers we analyze are dry. They consist of gravel, rocks, and soil, which visually resemble other flat land surfaces. As a result, the classification process struggles to reliably distinguish these areas. In addition, some distinct areas in the 2011 image show no trace of the river at all. This absence is mainly due to the dense vegetation that overwhelms the riverbeds, which hides the river’s features in the images.
As presented in the confusion matrices (Figure 18) for the SVM classifier applied to both the old and new imagery, the diagonal values represent correctly classified pixels, while off-diagonal values correspond to misclassifications. The classifier performed well in both cases, showing a strong ability to distinguish between river and non-river pixels. However, as indicated by the false positives, some areas were incorrectly labeled as river, which is likely due to the visual similarity of dry riverbeds to the surrounding terrain.
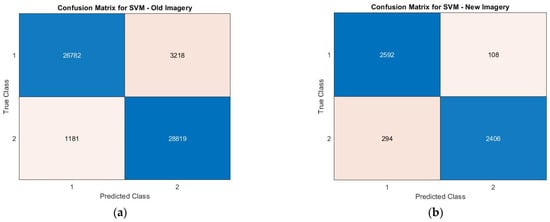
Figure 18.
Confusion matrices of testing pixels for both old (a) and new (b) imageries. Class one represents the non-river pixels, and class two represents pixels that are classified as river.
The ROC curves for both cases, providing further insight into the classifier’s performance, are depicted in Figure 19. The high AUC values (0.974 for the old imagery (Figure 19a) and 0.983 for the new imagery (Figure 19b)) indicate strong discriminative capability. Despite these high scores, the presence of misclassified pixels, particularly false positives, remains a challenge, as discussed earlier. These misclassifications are influenced by the natural appearance of dry riverbeds and dense vegetation covering certain sections of the river.
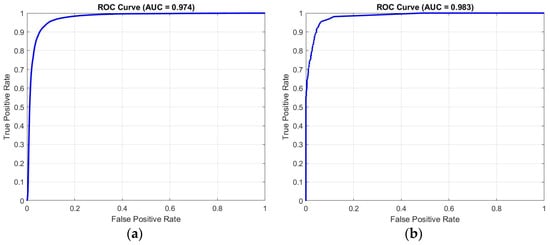
Figure 19.
ROC curve for testing pixel classification from both old (a) and new (b) imageries.
In the main body of Charadros, we observe a significant reduction in the diameter of the river’s core. In 1945, the core measured 388 m, but it has now been reduced to just 88 m—a dramatic reduction of approximately 77.3%. At the position of the river delta, the width has decreased even more drastically. From an initial width of 1180 m in 1945, human activities have reduced it to a mere 64 m, representing a reduction of 94.6% (Figure 20).

Figure 20.
Areas of interest that changed drastically over the years. The deltas of Charadros and Selemnos are depicted with the two left parallelograms and two main bodies at the right. The old image (1945) is depicted in (a) and the new image (2011) is depicted in (b).
Similarly, for Selemnos, we observe a reduction in the core of about 74 m. The core was 132 m in 1945 and shrank to just 58 m, a decrease of approximately 56.1%. At the river delta, the changes are even more pronounced. The width was reduced from 434 m to a very narrow 9 m stream, which constitutes a reduction of 97.9%.
These observations highlight the profound impact of human activities and natural changes in river dimensions over time. The significant narrowing of river deltas and cores could have ecological and hydrological implications, such as altered flow dynamics, reduced habitat availability, and increased vulnerability to flooding. Future work should consider these factors to better understand the consequences of such changes and explore potential mitigation strategies.
6. Discussion and Conclusions
To summarize, the results of this study highlight the significant geomorphological changes in the broader area of Patras over a period of 66 years. By utilizing historical aerial imagery from 1945 and high-resolution satellite data from 2011, we were able to quantify changes in both the coastal zone and the riverbeds of the Charadros and Selemnos rivers. The applied methodologies, including image registration, feature extraction, supervised classification, and NDWI-based water body delineation, proved to be effective in capturing and analyzing these changes.
6.1. Coastal Zone Changes
The coastline analysis revealed substantial modifications, particularly due to human activities such as the construction of the Rio-Antirio Bridge, breakwaters, and other modern additions such as the harbor at the city center and 2 Km northeast (Pelekaneika) of Patras, which consist of the docks for yachts and recreational areas. The study identified a net gain of approximately 0.5235 km2 of new land, primarily in the harbor expansion and protective coastal structures. On the contrary, approximately 0.1375 km2 of land has been lost due to natural coastal erosion and other human interventions due to urbanization. The comparison of our methodology with Google Earth Pro measurements demonstrated high accuracy, confirming the reliability of the NDWI-based approach in detecting coastal variations.
6.2. Riverbed Transformations
The river classification results indicate drastic reductions in riverbed widths, particularly in the deltas of Charadros and Selemnos. The Charadros River’s main body shrank from 388 m in 1945 to just 88 m in 2011, marking a 77.3% reduction, while its delta width decreased by 94.6%. Similarly, the Selemnos River experienced a 56.1% contraction in its main body and a 97.9% reduction at its delta. These changes are likely attributed to sediment deposition, urbanization, and the construction of flood control infrastructure. Despite the high classification accuracy achieved, challenges arose in distinguishing riverbeds from the surrounding land due to dry river conditions and vegetation cover, which obscured river features mainly in the 2011 imagery.
6.3. Comparison with Previous Studies
Among the most fascinating studies that align closely with our research are those by Feng et al. [11], Dewi et al. [4], Kuleli [2], Nikolakopoulos et al. [9], and Kundu and Mandal [16], each offering unique insights into coastal and riverine dynamics. Feng et al. [11] employed deep learning with a multi-branch convolutional neural network (MBCNN) for coastline classification in China’s Yellow River Delta, achieving a similar accuracy (93.78%), while our study also integrates machine learning via SVM, achieving 92.6% and 92.5% accuracy at new and old imagery, respectively. Incorporating deep learning could further enhance classification precision, especially in complex environments. Similarly, Dewi et al. [4] tackled shoreline uncertainty using fuzzy c-means classification, addressing the challenges of positional inaccuracies in Java, Indonesia. Our approach of image registration and NDWI-based water delineation serves a similar purpose but could benefit from uncertainty modeling to refine boundary detection. Kuleli [2] conducted a long-term assessment of shoreline retreat in Turkey’s Cukurova Delta, using edge detection and band ratioing to quantify erosion rates. In ours, this concept is advanced by incorporating pixel-wise classification and feature extraction, offering a finer-scale analysis. Nikolakopoulos et al. [9] analyzed river network transformations in the Greek river of Alfios using PCA and GIS-based mapping, highlighting human-induced morphological changes. Our research follows a similar trajectory, but with a greater emphasis on texture-based classification for detecting riverbed shrinkage. Finally, Kundu and Mandal [16] examined the Sundarban Delta’s rapid erosion, predicting future shoreline retreat through statistical modeling. While our study focuses on past changes, integrating predictive modeling could enhance its applicability for future coastal and riverine management. Overall, our methodology builds upon these innovative approaches while offering a unique contribution through the integration of high-resolution historical and modern imagery.
6.4. Methodological Strengths and Limitations
The integration of archive aerial imagery with modern high-resolution satellite data provided valuable insights into long-term landscape changes, allowing for a comprehensive analysis of coastal and riverbed modifications. The use of image registration techniques ensured the accurate alignment of datasets, minimizing spatial discrepancies between the 1945 and 2011 images. Additionally, GLCM-based feature extraction effectively captured texture variations, while the SVM classifier provided robust discrimination between river and non-river areas, achieving high classification accuracy. These methodological choices enabled a detailed assessment of geomorphological transformations, supporting reliable change detection.
However, certain limitations were encountered. One major challenge was the difficulty in detecting dry riverbeds due to vegetative overgrowth, particularly in the 2011 imagery. The dense vegetation obscured river features, leading to potential misclassification. Additionally, the visual similarity between dry riverbeds and the surrounding land posed challenges for classification, sometimes causing areas of bare land to be falsely identified as river pixels. Another significant constraint was the high computational cost of processing high-resolution data. To manage this, we had to reduce the spatial resolution of processed images, which, while improving efficiency, may have led to a loss of fine details.
6.5. Environmental Implications and Urban Planning Considerations
The detected changes reveal both coastal retreat and land expansion, emphasizing the dynamic nature of the study area. While erosion has reduced river widths and caused shoreline retreat in certain areas, sediment deposition—especially near the Charadros River delta—has led to the formation of new land. Notably, the area known today as Plaz Patras did not exist in 1945, highlighting the extent of coastal transformation over time. These changes have significant environmental implications, affecting sediment transport, ecosystem dynamics, and flood risks. From an urban planning perspective, the newly formed land presents opportunities for controlled development, but careful management is essential to prevent instability or unintended environmental consequences. Sustainable planning and conservation strategies should balance land use with ecological preservation to ensure long-term resilience.
Taking into consideration the results of our research, we could suggest some possible practical applications for coastal protection, flood risk management, and sustainable urban expansion. The narrowing of riverbeds, especially in Charadros and Selemnos, increases flood risks, requiring dredging or drainage improvements. Identifying erosion-prone zones can guide shoreline reinforcement and infrastructure planning, while newly formed land, like Plaz Patras, requires careful zoning policies to prevent environmental instability.
In conclusion, this study successfully quantified land cover changes in Patras’ coastline and riverine systems using a combination of remote sensing techniques and machine-learning-based classification. The findings emphasize the profound impact of anthropogenic interventions on coastal expansion and river morphology. Such insights are crucial for urban planning, coastal management, and environmental monitoring.
Future improvements could involve integrating additional spectral indices, deep learning approaches that would help to better distinguish similar land covers, or the incorporation of hydrological models for an in-depth understanding of the changes that took place through time and the enhancement of riverbed classification accuracy. Additionally, we recommend the incorporation of additional temporal datasets to analyze trends beyond 2011 and the development of hybrid models combining statistical and machine learning approaches for improved classification accuracy. Nevertheless, the accuracy of the method would be improved if we had other scenes with high-resolution data, which was not possible at this stage, and simultaneously, there are no high-resolution data before 1995. By advancing these methodologies, we can better understand and mitigate the environmental consequences of landscape alterations, ultimately contributing to more sustainable coastline and riverine management practices.
Author Contributions
Conceptualization, S.P., G.K. and V.A.; methodology, S.P., G.K. and V.A.; resources, S.P.; writing—original draft preparation, S.P.; writing—review and editing, G.K. and V.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
WorldView-2 imagery was freely downloaded after completing access authorization through the ESA TPM Map Catalogue—WorldView-2 European Cities collection data search (https://tpm-ds.eo.esa.int/smcat/WorldView-2/3/Greece/Patra/0/ accessed on 25 October 2024) with product name WV2_OPER_WV-110__2A_20110708T094541_N38-311_E021-758_4061.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zoran, M.; Anderson, E. The Use of Multi-Temporal and Multispectral Satellite Data for Change Detection Analysis of the Romanian Black Sea Coastal Zone. J. Optoelectron. Adv. Mater. 2016, 8, 252–256. [Google Scholar]
- Kuleli, T. Quantitative Analysis of Shoreline Changes at the Mediterranean Coast in Turkey. Environ. Monit. Assess. 2009, 167, 387–397. [Google Scholar] [CrossRef] [PubMed]
- Vassilakis, E.; Papadopoulou-Vrynioti, K. Quantification of Deltaic Coastal Zone Change Based on Multi-Temporal High Resolution Earth Observation Techniques. ISPRS Int. J. Geo-Inf. 2014, 3, 18–28. [Google Scholar] [CrossRef]
- Dewi, R.; Bijker, W.; Stein, A.; Marfai, M. Fuzzy Classification for Shoreline Change Monitoring in a Part of the Northern Coastal Area of Java, Indonesia. Remote Sens. 2016, 8, 190. [Google Scholar] [CrossRef]
- Xu, N. Detecting Coastline Change with All Available Landsat Data over 1986–2015: A Case Study for the State of Texas, USA. Atmosphere 2018, 9, 107. [Google Scholar] [CrossRef]
- Misra, A.; Ramakrishnan, B. Assessment of Coastal Geomorphological Changes Using Multi-Temporal Satellite-Derived Bathymetry. Cont. Shelf Res. 2020, 207, 104213. [Google Scholar] [CrossRef]
- Michałowska, K.; Głowienka, E. Multi-Temporal Analysis of Changes of the Southern Part of the Baltic Sea Coast Using Aerial Remote Sensing Data. Remote Sens. 2022, 14, 1212. [Google Scholar] [CrossRef]
- Zoysa, S.; Basnayake, V.; Samarasinghe, J.T.; Gunathilake, M.B.; Kantamaneni, K.; Muttil, N.; Pawar, U.; Rathnayake, U. Analysis of Multi-Temporal Shoreline Changes due to a Harbor Using Remote Sensing Data and GIS Techniques. Sustainability 2023, 15, 7651. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Vaiopoulos, D.A.; Skianis, G.A. Use of Multitemporal Remote Sensing Data for Mapping the Alfios River Network Changes from 1977 to 2000. Geocarto Int. 2007, 22, 251–271. [Google Scholar] [CrossRef]
- Li, X.; Damen, M.C.J. Coastline Change Detection with Satellite Remote Sensing for Environmental Management of the Pearl River Estuary, China. J. Mar. Syst. 2010, 82, S54–S61. [Google Scholar] [CrossRef]
- Feng, Q.; Yang, J.; Zhu, D.; Liu, J.; Guo, H.; Batsaikhan Bayartungalag; Li, B. Integrating Multitemporal Sentinel-1/2 Data for Coastal Land Cover Classification Using a Multibranch Convolutional Neural Network: A Case of the Yellow River Delta. Remote Sens. 2019, 11, 1006. [Google Scholar] [CrossRef]
- Chen, H.; Liang, Q.; Liang, Z.; Liu, Y.; Ren, T. Extraction of Connected River Networks from Multi-Temporal Remote Sensing Imagery Using a Path Tracking Technique. Remote Sens. Environ. 2020, 246, 111868. [Google Scholar] [CrossRef]
- Patel, K.; Jain, R.; Patel, A.N.; Kalubarme, M.H. Shoreline Change Monitoring for Coastal Zone Management Using Multi-Temporal Landsat Data in Mahi River Estuary, Gujarat State. Appl. Geomat. 2021, 13, 333–347. [Google Scholar] [CrossRef]
- El-Masry, E.A.; Magdy, A.; El-Gamal, A.; Mahmoud, B.; El-Sayed, M.K. Multi-Decadal Coastal Change Detection Using Remote Sensing: The Mediterranean Coast of Egypt between El-Dabaa and Ras El-Hekma. Environ. Monit. Assess. 2024, 196, 182. [Google Scholar] [CrossRef]
- da Silva, P.G.; Jara, M.S.; Medina, R.; Beck, A.-L.; Taji, M.A. On the Use of Satellite Information to Detect Coastal Change: Demonstration Case on the Coast of Spain. Coast. Eng. 2024, 191, 104517. [Google Scholar] [CrossRef]
- Kundu, K.; Mandal, J.K. Shoreline Change Detection and Future Prediction of Sundarban Delta Using Remote Sensing Data and Digital Shoreline Analysis System. J. Indian Soc. Remote Sens. 2024, 52, 485–503. [Google Scholar] [CrossRef]
- Bar, B.; Swain, R.; Das, P.; Sahoo, J.; Das, D.N. Spatial Analysis and Forecasting of Coastal Dynamics Using Optical and SAR Imageries: A Case Study of Contai Coastal Tract of Bay of Bengal. J. Indian Soc. Remote Sens. 2024, 52, 2783–2806. [Google Scholar] [CrossRef]
- Abhilash, G.; Rama Murthy, T.V.; Naidu, V.P.S. Image Fusion for Enhanced Vision System Using Laplacian Pyramid. Int. J. Eng. Res. Technol. 2015, V4, 507–512. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M.; da Vitoria Lobo, N.; Shah, M. Learning Affine Transformations. Pattern Recogn. 1999, 32, 1783–1799. [Google Scholar] [CrossRef]
- Affine Transformations, MathWorks Help Center. Available online: https://ch.mathworks.com/discovery/affine-transformation.html (accessed on 17 January 2025).
- Wolf, A.F. Using WorldView-2 Vis-NIR Multispectral Imagery to Support Land Mapping and Feature Extraction Using Normalized Difference Index Ratios. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Nternational Society for Optics and Photonics, Baltimore, MD, USA, 14 May 2012. [Google Scholar] [CrossRef]
- Liu, M.; Yu, T.; Gu, X.; Sun, Z.; Yang, J.; Zhang, Z.; Mi, X.; Cao, W.; Li, J. The Impact of Spatial Resolution on the Classification of Vegetation Types in Highly Fragmented Planting Areas Based on Unmanned Aerial Vehicle Hyperspectral Images. Remote Sens. 2020, 12, 146. [Google Scholar] [CrossRef]
- Kurniati, F.T.; Manongga, D.H.; Sediyono, E.; Prasetyo, S.Y.J.; Huizen, R.R. GLCM-Based Feature Combination for Extraction Model Optimization in Object Detection Using Machine Learning. arXiv 2024, arXiv:2404.04578. [Google Scholar] [CrossRef]
- Razali, N.F.; Isa, I.S.; Sulaiman, S.N.; Karim, N.K.A.; Osman, M.K. CNN-Wavelet Scattering Textural Feature Fusion for Classifying Breast Tissue in Mammograms. Biomed. Signal Process. Control 2023, 83, 104683. [Google Scholar] [CrossRef]
- Utaminingrum, F.; Sarosa, S.J.A.; Karim, C.; Gapsari, F.; Wihandika, R.C. The Combination of Gray Level Co-Occurrence Matrix and Back Propagation Neural Network for Classifying Stairs Descent and Floor. ICT Express 2021, 8, 151–160. [Google Scholar] [CrossRef]
- Park, Y.; Guldmann, J.-M. Measuring Continuous Landscape Patterns with Gray-Level Co-Occurrence Matrix (GLCM) Indices: An Alternative to Patch Metrics? Ecol. Indic. 2020, 109, 105802. [Google Scholar] [CrossRef]
- Guo, L.; Wang, W.; Zhong, L.; Guo, L.; Zhang, F.; Guo, Y. Texture Analysis of the Microstructure of Internal Curing Concrete Based on Image Recognition Technology. CSCM 2022, 17, e01360. [Google Scholar] [CrossRef]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. MSR-TR-98-14. Microsoft. 1998. Available online: https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/ (accessed on 1 October 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).