Towards Realistic Human Motion Prediction with Latent Diffusion and Physics-Based Models
Abstract
1. Introduction
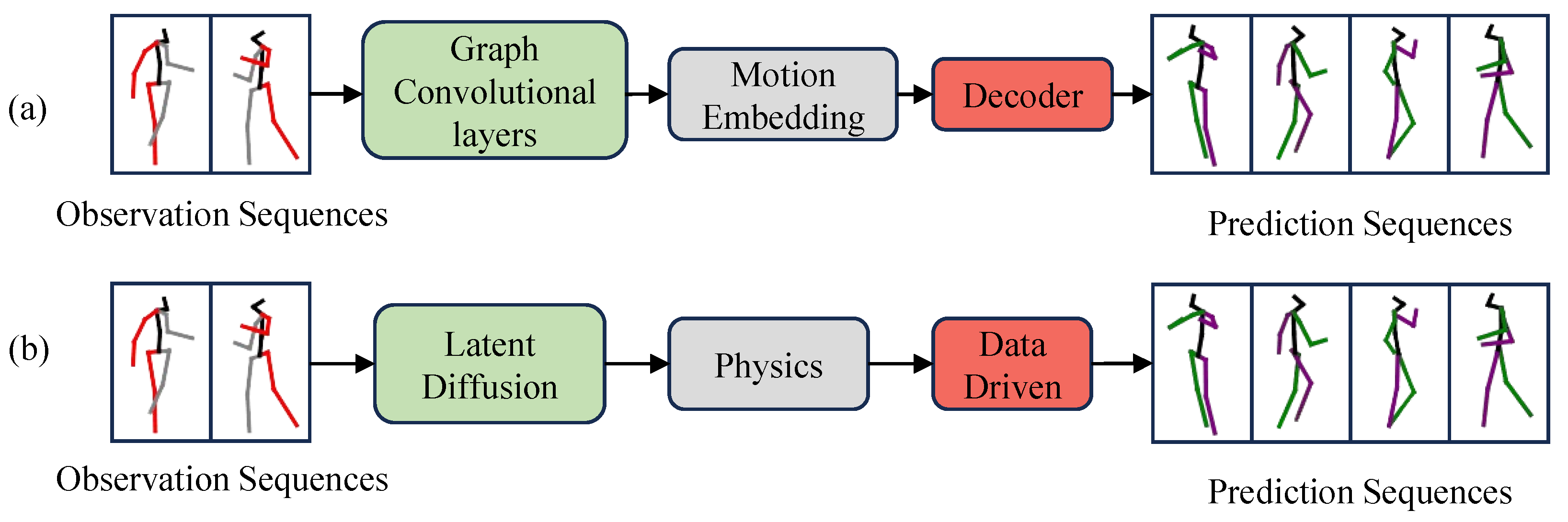
- To address the problems mentioned above, we propose a new framework. The diffusion-based and physically driven approach has the advantages of long-term prediction, high motion switching capability, and reduced error accumulation. The future motion is predicted by an efficient combination of physical principles and random noise.
- It is experimentally demonstrated that the proposed method obtains better performance and outperforms existing methods, providing a new perspective for future research.
2. Related Works
2.1. Human Motion Prediction
2.2. Latent Diffusion and Physically Driven Models
3. Proposed Framework
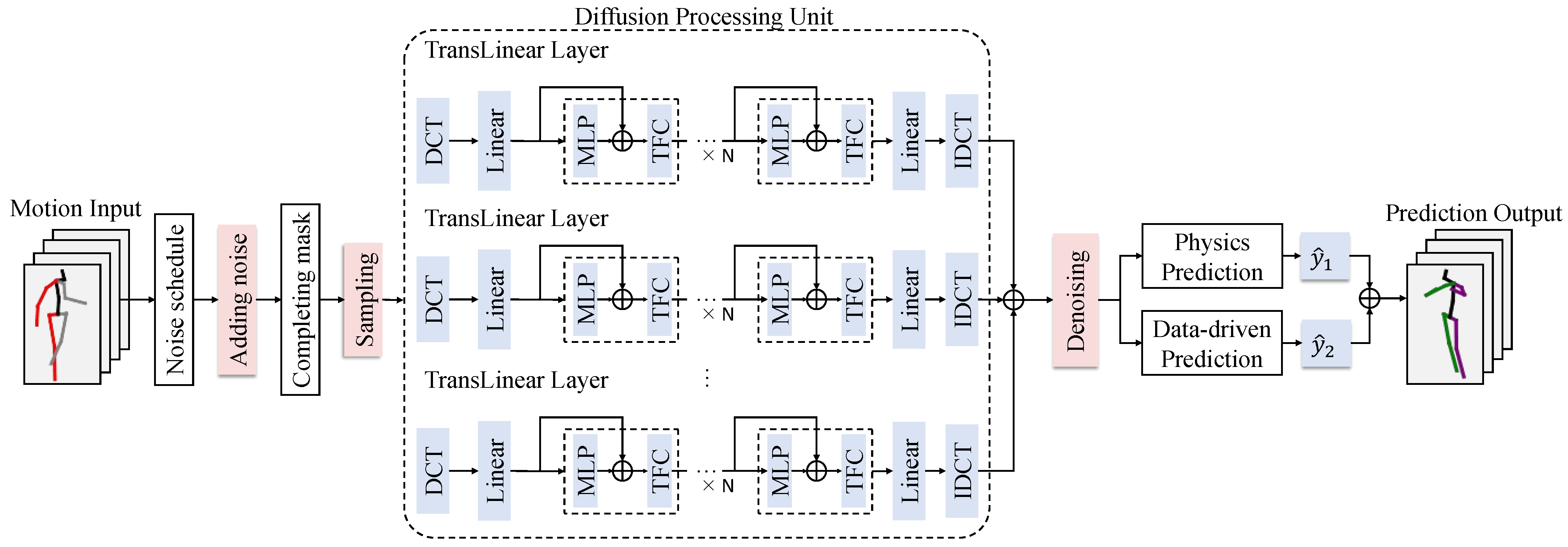
3.1. Potential Diffusion Model
| Algorithm 1 DCT and iDCT |
| Input: sequences: . Output: sequences: . 1: DCT transfer operation: 2: ; 3: ; 4: Generate sequences: 5: ; 6: ; 7: iDCT transfer operation: 8: ; 9: return . |
3.2. Physics-Based and Data-Driven Motion Prediction Model
| Algorithm 2 Training procedure of LDPM |
| Input: Observation sequences , time steps , physic feature and geometric feature . Output: Future sequences . 1: Extract feature: 2: Using MLP to obtain two features: 3: , 4: ; 5: Dynamic modeling: 6: 7: 8: 9: Data-driven: 10: Using the full connectivity layer: 11: ; 12: Fusion physic and data: 13: Addition weight to predict: 14: ; 15: return . |
3.3. Training of the Model
4. Experiments
4.1. Comparison to the State of the Art
4.2. Ablation Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, W.; Song, R.; Guo, X.; Zhang, C.; Chen, L. Genad: Generative end-to-end autonomous driving. In European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2025; pp. 87–104. [Google Scholar]
- Lu, G.; Zhang, S.; Wang, Z.; Liu, C.; Lu, J.; Tang, Y. Manigaussian: Dynamic gaussian splatting for multi-task robotic manipulation. In European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2025; pp. 349–366. [Google Scholar]
- Hu, L. Animate anyone: Consistent and controllable image-to-video synthesis for character animation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 8153–8163. [Google Scholar]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D gaussian splatting for real-time radiance field rendering. Acm Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Goto, T.; Ohzeki, M. Online calibration scheme for training restricted Boltzmann machines with quantum annealing. arXiv 2023, arXiv:2307.09785. [Google Scholar]
- Wei, D.; Sun, H.; Li, B.; Lu, J.; Li, W.; Sun, X.; Hu, S. Human joint kinematics diffusion-refinement for stochastic motion prediction. AAAI Conf. Artif. Intell. 2023, 37, 6110–6118. [Google Scholar] [CrossRef]
- Pearce, T.; Rashid, T.; Kanervisto, A.; Bignell, D.; Sun, M.; Georgescu, R.; Macua, S.V.; Tan, S.Z.; Momennejad, I.; Hofmann, K.; et al. Imitating human behaviour with diffusion models. arXiv 2023, arXiv:2301.10677. [Google Scholar]
- Adeli, V.; Ehsanpour, M.; Reid, I.; Niebles, J.C.; Savarese, S.; Adeli, E.; Rezatofighi, H. Tripod: Human trajectory and pose dynamics forecasting in the wild. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 13390–13400. [Google Scholar]
- Cai, Z.; Ren, D.; Zeng, A.; Lin, Z.; Yu, T.; Wang, W.; Liu, Z. Humman: Multi-modal 4D human dataset for versatile sensing and modeling. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 557–577. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar]
- Aliakbarian, S.; Saleh, F.S.; Salzmann, M.; Petersson, L.; Gould, S. A stochastic conditioning scheme for diverse human motion prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5223–5232. [Google Scholar]
- Bouazizi, A.; Holzbock, A.; Kressel, U.; Dietmayer, K.; Belagiannis, V. Motionmixer: Mlp-based 3D human body pose forecasting. arXiv 2022, arXiv:2207.00499. [Google Scholar]
- Li, B.; Zhao, Y.; Zhelun, S.; Sheng, L. Danceformer: Music conditioned 3D dance generation with parametric motion transformer. AAAI Conf. Artif. Intell. 2022, 36, 1272–1279. [Google Scholar] [CrossRef]
- Alexanderson, S.; Nagy, R.; Beskow, J.; Henter, G.E. Listen, denoise, action! audio-driven motion synthesis with diffusion models. Acm Trans. Graph. 2023, 42, 1–20. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, Y.; Bao, F.; Chen, J.; Li, C.; Zhu, J. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps. Adv. Neural Inf. Process. Syst. 2022, 35, 5775–5787. [Google Scholar]
- Gurumurthy, S.; Kiran Sarvadevabhatla, R.; Venkatesh Babu, R. Deligan: Generative adversarial networks for diverse and limited data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 166–174. [Google Scholar]
- Hong, F.; Zhang, M.; Pan, L.; Cai, Z.; Yang, L.; Liu, Z. Avatarclip: Zero-shot text-driven generation and animation of 3D avatars. arXiv 2022, arXiv:2205.08535. [Google Scholar] [CrossRef]
- Sun, B.; Yang, Y.; Zhang, L.; Cheng, M.M.; Hou, Q. Corrmatch: Label propagation via correlation matching for semi-supervised semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 3097–3107. [Google Scholar]
- Starke, S.; Mason, I.; Komura, T. Deepphase: Periodic autoencoders for learning motion phase manifolds. ACM Trans. Graph. 2022, 41, 1–13. [Google Scholar] [CrossRef]
- Ju, X.; Zeng, A.; Zhao, C.; Wang, J.; Zhang, L.; Xu, Q. Humansd: A native skeleton-guided diffusion model for human image generation. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 15988–15998. [Google Scholar]
- Tevet, G.; Gordon, B.; Hertz, A.; Bermano, A.H.; Cohen-Or, D.; Liu, Z. Motionclip: Exposing human motion generation to clip space. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 358–374. [Google Scholar]
- Cai, X.; Cheng, P.; Liu, S.; Zhang, H.; Sun, H. Human Motion Prediction Based on a Multi-Scale Hypergraph for Intangible Cultural Heritage Dance Videos. Electronics 2023, 12, 1–21. [Google Scholar] [CrossRef]
- Maeda, T.; Ukita, N. Motionaug: Augmentation with physical correction for human motion prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6427–6436. [Google Scholar]
- Xie, K.; Wang, T.; Iqbal, U.; Guo, Y.; Fidler, S.; Shkurti, F. Physics-based human motion estimation and synthesis from videos. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11532–11541. [Google Scholar]
- Yuan, Y.; Song, J.; Iqbal, U.; Vahdat, A.; Kautz, J. Physdiff: Physics-guided human motion diffusion model. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 16010–16021. [Google Scholar]
- Zhang, Z.; Zhu, Y.; Rai, R.; Doermann, D. Pimnet: Physics-infused neural network for human motion prediction. IEEE Robot. Autom. Lett. 2022, 7, 8949–8955. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Chen, L.H.; Zhang, J.; Li, Y.; Pang, Y.; Xia, X.; Liu, T. Humanmac: Masked motion completion for human motion prediction. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 9544–9555. [Google Scholar]
- Zhang, Y.; Kephart, J.O.; Ji, Q. Incorporating physics principles for precise human motion prediction. In Proceedings of the Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 6164–6174. [Google Scholar]
- Barquero, G.; Escalera, S.; Palmero, C. Belfusion: Latent diffusion for behavior-driven human motion prediction. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 2317–2327. [Google Scholar]
- Zhong, C.; Hu, L.; Zhang, Z.; Ye, Y.; Xia, S. Spatio-temporal gating-adjacency gcn for human motion prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6447–6456. [Google Scholar]
- Salzmann, T.; Pavone, M.; Ryll, M. Motron: Multimodal probabilistic human motion forecasting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6457–6466. [Google Scholar]
- Lucas, T.; Baradel, F.; Weinzaepfel, P.; Rogez, G. Posegpt: Quantization-based 3D human motion generation and forecasting. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 417–435. [Google Scholar]
- Blattmann, A.; Milbich, T.; Dorkenwald, M.; Ommer, B. Behavior-driven synthesis of human dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 12236–12246. [Google Scholar]
- Dang, L.; Nie, Y.; Long, C.; Zhang, Q.; Li, G. Diverse human motion prediction via gumbel-softmax sampling from an auxiliary space. In Proceedings of the ACM International Conference on Multimedia (ACM MM), Lisboa, Portugal, 10–14 October 2022; pp. 5162–5171. [Google Scholar]
- Xu, S.; Wang, Y.X.; Gui, L.Y. Diverse human motion prediction guided by multi-level spatial-temporal anchors. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 251–269. [Google Scholar]
- Dang, L.; Nie, Y.; Long, C.; Zhang, Q.; Li, G. Msr-gcn: Multi-scale residual graph convolution networks for human motion prediction. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11467–11476. [Google Scholar]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Symbiotic graph neural networks for 3D skeleton-based human action recognition and motion prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3316–3333. [Google Scholar] [CrossRef]
- Li, M.; Chen, S.; Zhang, Z.; Xie, L.; Tian, Q.; Zhang, Y. Skeleton-parted graph scattering networks for 3D human motion prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 18–36. [Google Scholar]
- Guo, W.; Du, Y.; Shen, X.; Lepetit, V.; Alameda-Pineda, X.; Moreno-Noguer, X. Back to mlp: A simple baseline for human motion prediction. In Proceedings of the Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 4809–4819. [Google Scholar]
- Xu, C.; Tan, R.T.; Tan, Y.; Chen, S.; Wang, Y.G.; Wang, X.; Wang, Y. Eqmotion: Equivariant multi-agent motion prediction with invariant interaction reasoning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 1410–1420. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Yu, Z.; Yin, Z.; Zhou, D.; Wang, D.; Wong, F.; Wang, B. Talking head generation with probabilistic audio-to-visual diffusion priors. In Proceedings of the International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 7645–7655. [Google Scholar]
- Ho, J.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video diffusion models. Adv. Neural Inf. Process. Syst. 2022, 35, 8633–8646. [Google Scholar]
- Xu, M.; Yu, L.; Song, Y.; Shi, C.; Ermon, S.; Tang, J. Geodiff: A geometric diffusion model for molecular conformation generation. arXiv 2022, arXiv:2203.02923. [Google Scholar]
- Xu, J.; Wang, X.; Cheng, W.; Cao, Y.P.; Shan, Y.; Qie, X.; Cao, S. Dream3d: Zero-shot text-to-3D synthesis using 3D shape prior and text-to-image diffusion models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 20908–20918. [Google Scholar]
- Popov, V.; Vovk, I.; Gogoryan, V.; Sadekova, T.; Kudinov, M. Grad-tts: A diffusion probabilistic model for text-to-speech. In Proceedings of the International Conference on Machine Learning (ICML), Virtal, 18–24 July 2021; pp. 8599–8608. [Google Scholar]
- Yang, J.; Wang, C.; Li, Z.; Wang, J.; Zhang, R. Semantic human parsing via scalable semantic transfer over multiple label domains. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 19424–19433. [Google Scholar]
- Mao, W.; Liu, M.; Salzmann, M. Generating smooth pose sequences for diverse human motion prediction. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 13309–13318. [Google Scholar]
- Zhang, Y.; Black, M.J.; Tang, S. We are more than our joints: Predicting how 3D bodies move. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3372–3382. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3. 6m: Large scale datasets and predictive methods for 3D human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef]
- Sigal, L.; Balan, A.O.; Black, M.J. Humaneva: Synchronized video and motion capture dataset and baseline algorithm for evaluation of articulated human motion. Int. J. Comput. Vis. 2010, 87, 4–27. [Google Scholar] [CrossRef]
- Mahmood, N.; Ghorbani, N.; Troje, N.F.; Pons-Moll, G.; Black, M.J. AMASS: Archive of motion capture as surface shapes. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5442–5451. [Google Scholar]
- Zhang, H.; Ning, X.; Wang, C.; Ning, E.; Li, L. Deformation depth decoupling network for point cloud domain adaptation. Neural Netw. 2024, 180, 106626. [Google Scholar] [CrossRef]
- Ning, E.; Wang, C.; Zhang, H.; Ning, X.; Tiwari, P. Occluded person re-identification with deep learning: A survey and perspectives. Expert Syst. Appl. 2024, 239, 122419. [Google Scholar] [CrossRef]
- Wang, C.; Ning, X.; Li, W.; Bai, X.; Gao, X. 3D person re-identification based on global semantic guidance and local feature aggregation. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 4698–4712. [Google Scholar] [CrossRef]
- Ning, E.; Wang, C.; Zhang, H.; Ning, X.; Tiwari, P. Pedestrian 3D shape understanding for person re-identification via multi-view learning. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 5589–5602. [Google Scholar]
- Ning, E.; Zhang, C.; Wang, C.; Ning, X.; Chen, H.; Bai, X. Pedestrian Re-ID based on feature consistency and contrast enhancement. Displays 2023, 79, 102467. [Google Scholar] [CrossRef]







| Method | Human3.6M | HumanEva-I | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| APD | ADE | FDE | MMADE | MMFDE | APD | ADE | FDE | MMADE | MMFDE | |
| MotionDiff [6] | 15.353 | 0.411 | 0.509 | 0.536 | 0.536 | 5.931 | 0.232 | 0.236 | 0.352 | 0.320 |
| Deligan [16] | 6.509 | 0.483 | 0.520 | 0.545 | 0.520 | 2.177 | 0.306 | 0.322 | 0.385 | 0.371 |
| HumanMAC [28] | 6.301 | 0.369 | 0.480 | 0.509 | 0.545 | 6.554 | 0.209 | 0.223 | 0.342 | 0.335 |
| BeLFusion [30] | 7.602 | 0.420 | 0.472 | 0.474 | 0.507 | 6.109 | 0.220 | 0.234 | 0.342 | 0.316 |
| Diversampling [35] | 15.310 | 0.370 | 0.480 | 0.482 | 0.509 | 6.109 | 0.220 | 0.234 | 0.342 | 0.316 |
| Gsps [50] | 14.757 | 0.389 | 0.496 | 0.476 | 0.525 | 5.825 | 0.233 | 0.240 | 0.344 | 0.331 |
| Mojo [51] | 12.579 | 0.412 | 0.497 | 0.497 | 0.538 | 4.181 | 0.234 | 0.244 | 0.369 | 0.347 |
| Ours | 13.158 | 0.319 | 0.410 | 0.430 | 0.473 | 10.119 | 0.234 | 0.229 | 0.369 | 0.372 |
| Step | Batch Time (s) | Total Time (s) |
|---|---|---|
| 1/2598 | 0.25 | 1 |
| 1001/2598 | 0.257 | 70 |
| 2001/2598 | 0.243 | 138 |
| 1/59 | 0.024 | 0 |
| 1/1141 | 0.103 | 0 |
| 1001/1141 | 0.149 | 25 |
| Scheduler | Human3.6M | HumanEva-I | ||||
|---|---|---|---|---|---|---|
| FDE | MMADE | MMFDE | FDE | MMADE | MMFDE | |
| Linear | 0.521 | 0.518 | 0.563 | 0.258 | 0.408 | 0.422 |
| Sqrt | 0.733 | 0.665 | 0.768 | 0.508 | 0.545 | 0.612 |
| Cosine | 0.410 | 0.430 | 0.473 | 0.229 | 0.369 | 0.372 |
| E | Human3.6M | ||
|---|---|---|---|
| FDE | MMADE | MMFDE | |
| 5.000 | 0.410 | 0.390 | 0.423 |
| 10.000 | 0.534 | 0.524 | 0.572 |
| 20.000 | 0.410 | 0.430 | 0.473 |
| E | HumanEva-I | ||
|---|---|---|---|
| FDE | MMADE | MMFDE | |
| 5.000 | 0.265 | 0.408 | 0.438 |
| 10.000 | 0.229 | 0.369 | 0.372 |
| 20.000 | 0.248 | 0.401 | 0.403 |
| Skip Connection | Human3.6M | HumanEva-I | ||||
|---|---|---|---|---|---|---|
| APD | ADE | FDE | APD | ADE | FDE | |
| N | 15.236 | 0.400 | 0.423 | 9.927 | 0.226 | 0.217 |
| Y | 13.158 | 0.319 | 0.410 | 10.119 | 0.234 | 0.229 |
| Layers | Human3.6M | HumanEva-I | ||||
|---|---|---|---|---|---|---|
| FDE | MMADE | MMFDE | FDE | MMADE | MMFDE | |
| 2 | 0.580 | 0.546 | 0.609 | 0.508 | 0.545 | 0.612 |
| 4 | 0.551 | 0.529 | 0.584 | 0.229 | 0.369 | 0.372 |
| 6 | 0.532 | 0.523 | 0.571 | 0.239 | 0.410 | 0.425 |
| 8 | 0.410 | 0.430 | 0.473 | 0.255 | 0.417 | 0.439 |
| 10 | 0.510 | 0.516 | 0.554 | 0.256 | 0.422 | 0.450 |
| Noising Steps | Human3.6M | HumanEva-I | ||||
|---|---|---|---|---|---|---|
| FDE | MMADE | MMFDE | FDE | MMADE | MMFDE | |
| 100.000 | 0.528 | 0.522 | 0.565 | 0.246 | 0.402 | 0.419 |
| 1000.000 | 0.410 | 0.430 | 0.473 | 0.229 | 0.369 | 0.372 |
| Method | Switch Ability | Independent Body Part Control |
|---|---|---|
| MotionDiff [6] | 0 | 0 |
| Deligan [16] | 0 | 0 |
| HumanMAC [28] | 1 | 1 |
| BeLFusion [30] | 1 | 0 |
| Diversampling [35] | 0 | 0 |
| Gsps [50] | 0 | 1 |
| Mojo [51] | 0 | 0 |
| Ours | 1 | 1 |
| MotionDiff [6] | Deligan [16] | HumanMAC [28] | BeLFusion [30] | Diversampling [35] | Gsps [50] | Ours | |
|---|---|---|---|---|---|---|---|
| One Stage | N | Y | Y | N | N | N | Y |
| Loss | 4 | 1 | 1 | 4 | 3 | 5 | 1 |
| FPS | 15 | 22 | 25 | 18 | 20 | 12 | 30 |
| MotionDiff [6] | HumanMAC [28] | BeLFusion [30] | Diversampling [35] | Gsps [50] | Ours | |
|---|---|---|---|---|---|---|
| Runtime (ms) | 15.2 | 12.3 | 18.1 | 14.5 | 16.7 | 10.8 |
| Parameter Size (M) | 45.3 | 30.1 | 35.8 | 28.7 | 40.2 | 25.9 |
| ADE | 0.411 | 0.369 | 0.420 | 0.370 | 0.389 | 0.319 |
| FDE | 0.509 | 0.480 | 0.472 | 0.480 | 0.496 | 0.410 |
| Model | APD | ADE | FDE | MMADE | MMFDE |
|---|---|---|---|---|---|
| Data-driven | 12.406 | 0.395 | 0.517 | 0.512 | 0.580 |
| Physics-based | 11.238 | 0.329 | 0.534 | 0.487 | 0.543 |
| Proposed hybrid | 13.158 | 0.319 | 0.410 | 0.430 | 0.473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Jin, M.; Nie, H.; Shen, J.; Dong, A.; Zhang, Q. Towards Realistic Human Motion Prediction with Latent Diffusion and Physics-Based Models. Electronics 2025, 14, 605. https://doi.org/10.3390/electronics14030605
Ren Z, Jin M, Nie H, Shen J, Dong A, Zhang Q. Towards Realistic Human Motion Prediction with Latent Diffusion and Physics-Based Models. Electronics. 2025; 14(3):605. https://doi.org/10.3390/electronics14030605
Chicago/Turabian StyleRen, Ziliang, Miaomiao Jin, Huabei Nie, Jianqiao Shen, Ani Dong, and Qieshi Zhang. 2025. "Towards Realistic Human Motion Prediction with Latent Diffusion and Physics-Based Models" Electronics 14, no. 3: 605. https://doi.org/10.3390/electronics14030605
APA StyleRen, Z., Jin, M., Nie, H., Shen, J., Dong, A., & Zhang, Q. (2025). Towards Realistic Human Motion Prediction with Latent Diffusion and Physics-Based Models. Electronics, 14(3), 605. https://doi.org/10.3390/electronics14030605







