ASFNOformer—A Superior Frequency Domain Token Mixer in Spiking Transformer

Abstract

As the third generation of neural networks, Spiking Neural Networks (SNNs) simulate the event-driven processing mode of the brain, offering superior energy efficiency and biological interpretability compared to traditional deep learning. Combining the architectural strengths of Transformers with SNNs has recently demonstrated high accuracy and significant potential. SNNs process binary spikes and rich temporal information, resulting in lower computational complexity and making them particularly suitable for neuromorphic datasets. However, neuromorphic data typically involve dynamic edges and high-frequency pixel intensity changes. Capturing this frequency information is challenging for traditional spatial methods but is critical for event-driven vision. To address this, we investigate the integration of the Fast Fourier Transform (FFT) into SNNs and propose the Adaptive Spiking Fourier Neural Operator Transformer (ASFNOformer). This architecture adapts the Adaptive Fourier Neural Operator (AFNO)—originally validated in Artificial Neural Networks (ANNs)—specifically for the spiking domain. Unlike standard AFNOs, our module applies FFT across both spatial (H, W) and temporal (T) dimensions, followed by a Multi-Layer Perceptron structure (MLP) mechanism with a block-diagonal weight matrix. This design effectively captures both spatial features and temporal dynamics inherent in event streams. Furthermore, we incorporate Leaky Integrate-and-Fire (LIF) neurons optimized with Learnable Weight Parameters (LWP-LIF) to enhance temporal feature extraction and adaptivity. Experimental results on standard benchmarks indicate that our method reduces the parameter count by approximately 25%. In terms of recognition accuracy, ASFNOformer is comparable to mainstream models on static datasets and demonstrates superior performance on neuromorphic datasets by efficiently capturing frequency features. Notably, ablation studies confirm the model’s generalizability, and when using QKformer as a baseline, our method achieves state-of-the-art (SOTA) performance on the CIFAR10-DVS dataset. This work advances frequency-domain analysis in SNNs, paving the way for efficient deployment on neuromorphic hardware.

1. Introduction

Spiking Neural Networks (SNNs) are considered the third generation of neural networks, evolving from the first-generation perceptrons and second-generation Artificial Neural Networks (ANNs) [1]. Characterized by temporal sparsity, event-driven processing, and biological plausibility, SNNs are well-suited for low-power neuromorphic hardware and have received widespread attention [2]. Meanwhile, ANNs, as a relatively mature technology [3], have provided SNNs with advanced architectural foundations and backpropagation algorithms. This has facilitated the rapid development of deep spiking architectures, such as ResNet-like SNNs [4]. Among these architectures, the Transformer—originally designed for natural language processing [5] and now widely applied in computer vision—shows particular promise. The effectiveness of Transformers is largely attributed to the efficient mixing of tokens. However, designing an optimal token mixer remains challenging; it must scale effectively with sequence size and generalize systematically to downstream tasks. This challenge is further compounded in SNNs by the unique characteristics of neuromorphic datasets.

Neuromorphic vision datasets [6,7,8] introduce a temporal dimension by adopting an event-driven processing approach. Generated by Dynamic Vision Sensors (DVS), these data consist of binary spikes triggered by spatiotemporal changes in pixel intensity. Consequently, these datasets possess rich spatiotemporal information. On the other hand, neurons in SNNs mimic biological processes, updating their membrane potentials based on temporal history and incoming inputs, and firing only when the potential exceeds a threshold. This discrete, spike-based communication contrasts with ANNs, which rely on continuous activation functions. In summary, the characteristics of neuromorphic data align naturally with the event-driven nature of SNNs, making them ideal benchmarks for validation [9,10]. Generally, these datasets fall into two categories: static datasets converted by scanning images with DVS cameras (e.g., N-MNIST [11] and CIFAR10-DVS [12]) and real-world recordings capturing moving objects (e.g., DVS-Gesture [11]).

While the precise mechanisms of neural information encoding remain a subject of ongoing research, there is compelling evidence that spike-based communication is biologically optimal for metabolic efficiency and information transmission. Although the event-driven nature of SNNs offers distinct advantages in processing the spatiotemporal dynamics of neuromorphic data [1,12], the question of how to efficiently extract these features remains.

From a biological perspective, the visual system does not merely process pixel intensities; it functions fundamentally as a frequency analyzer. Neurophysiological studies indicate that simple cells in the primary visual cortex (V1) possess receptive fields that resemble Gabor functions—effectively acting as local spatial frequency filters to extract orientation and texture information [13,14,15]. This suggests that the brain decomposes visual scenes into spectral components to perceive structure. Therefore, introducing frequency-domain analysis into SNNs is not only mathematically efficient but also biologically plausible. Motivated by this, we design ASFNO as a token mixer. This approach mimics the spectral decomposition capability of the visual cortex, making it highly suitable for processing neuromorphic datasets, and we verify its effectiveness on several established Spiking Transformers.

This paper primarily demonstrates that feature extraction in the frequency domain, via the Discrete Fourier Transform (DFT), offers distinct informational advantages for binary data compared to continuous data. We propose that frequency-domain analysis can significantly enhance SNN performance on neuromorphic datasets. Building on advancements in ANNs, we introduce a novel Adaptive Spiking Fourier Neural Operator (ASFNO). This module incorporates temporal information and serves as an efficient token mixer to improve SNN accuracy, thereby facilitating deployment on neuromorphic hardware. To validate our method, we conducted benchmarking tests using two established Spiking Transformer models as baselines. Extensive experiments on multiple neuromorphic datasets demonstrate high recognition rates, ultimately achieving state-of-the-art (SOTA) results. The main contributions of this paper are summarized as follows:

(1)

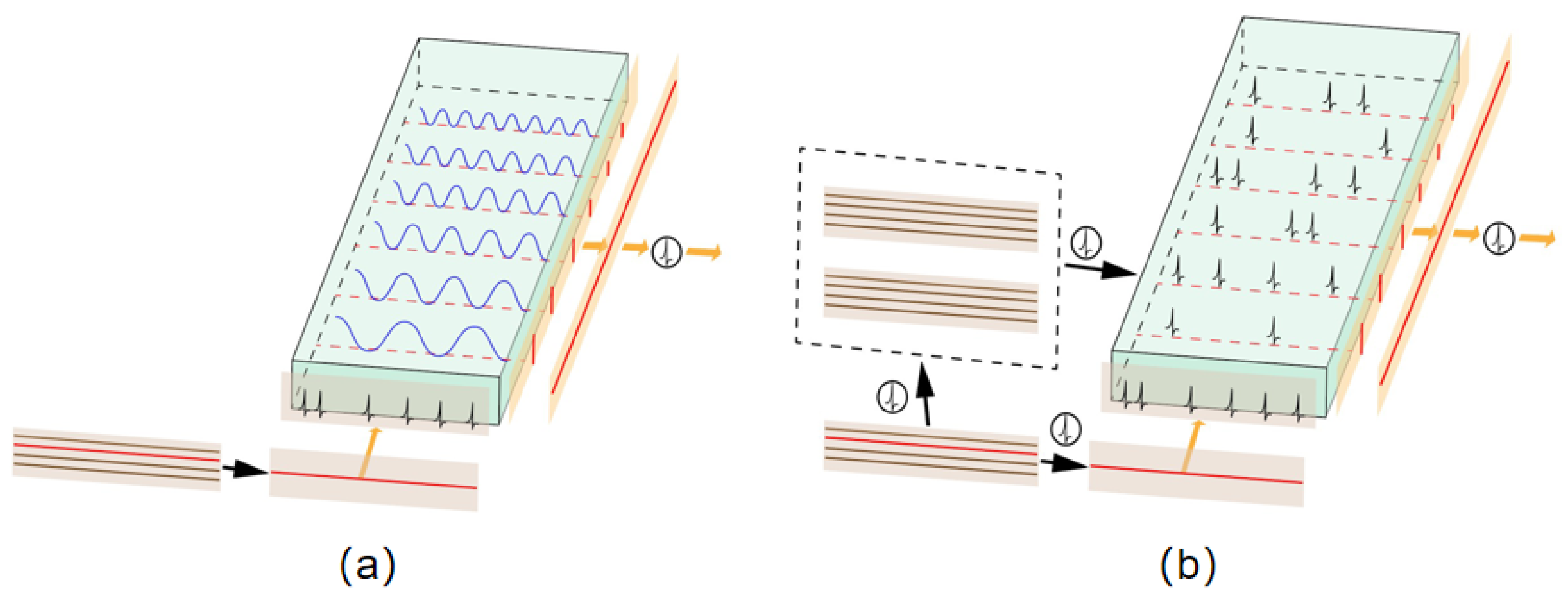
Theoretical Validation: We conducted a theoretical analysis of binary versus continuous signals using the Fourier transform to demonstrate the unique superiority of frequency-domain analysis for SNNs. We found that for binary spike signals, the Fourier transform effectively enhances signal intensity representation. Furthermore, signal analysis experiments confirm that this method efficiently extracts temporal features from dynamic datasets—a task that remains challenging for traditional spatial methods.

(2)

Novel Architecture: Based on the theoretical analysis and the inherent spatiotemporal nature of neuromorphic data, we designed the ASFNO module with weight sharing and weight block diagonal matrix. This module explicitly integrates temporal dimensions and employs LIF neurons with Learnable Weight Parameters (LWP-LIF) to further enhance network sparsity and adaptability.

(3)

SOTA Performance: We integrated the ASFNO module as a token mixer within Spiking Transformers. Experimental results on multiple neuromorphic datasets confirm that our model achieves state-of-the-art performance in classification tasks.

2. Related Works

2.1. Spiking Neural Networks

Unlike second-generation neural networks, SNNs utilize discrete spike sequences as information carriers rather than continuous values. This mechanism mimics biological neurons [2,16], which integrate inputs and generate binary outputs via spike activation. Prominent spiking neuron models include the Leaky Integrate-and-Fire (LIF) [17] and the Poisson-like Leaky Integrate-and-Fire (PLIF) [18]. Generally, deep SNN models are constructed using two primary paradigms: ANN-to-SNN conversion and direct training.

The ANN-to-SNN conversion method [19,20] replaces activation layers (e.g., ReLU) in pre-trained ANNs with spiking neurons. However, this approach often requires a large number of simulation time steps to approximate activation values, leading to significant inference latency [21]. Conversely, direct training [22,23] involves unrolling SNNs over time steps and employing backpropagation through time (BPTT). In this study, we adopt the direct training strategy to fully leverage the low power consumption and event-driven nature of SNNs.

The fundamental unit of SNNs is the spiking neuron, which accumulates membrane potential based on input spikes and fires when the potential exceeds a threshold. To ensure signal sparsity and effectively utilize temporal dynamics, we employ LIF neurons throughout this work. The dynamics of the LIF neuron are governed by the following equation:

$$\begin{array}{c}H\left[t\right]=V[t-1]+{\displaystyle \frac{1}{\tau }}\left(X\left[t\right]-\left(V[t-1]-V_{\mathrm{reset}}\right)\right),\hfill \\ S\left[t\right]=\mathsf{\Theta }\left(H\left[t\right]-V_{\mathrm{th}}\right),\hfill \\ V\left[t\right]=H\left[t\right](1-S\left[t\right])+V_{\mathrm{reset}}S\left[t\right],\hfill \end{array}$$

(1)

2.2. Token Mixer

In vision transformers, capturing long-range and multidirectional dependencies is crucial for understanding the compositionality and relationships among objects within a scene. Consequently, an efficient token mixer is essential for enhancing transformer performance. However, designing an effective mixer presents significant challenges, particularly for SNNs. Such a mixer must not only scale efficiently with sequence size and generalize to downstream tasks but also address the potential information loss inherent in binary spike signals. Furthermore, it must effectively extract temporal features—a task that remains difficult for conventional spatial methods. While some studies focus on optimizing the overall architecture [24], it is widely acknowledged that a well-designed token mixer is critical for superior performance.

Since the introduction of transformers in ANNs, numerous studies have explored alternatives to the standard self-attention mechanism. These include sparse transformers [25], image transformers [26], long-short transformers [27], Linformers [28], Reformers [29], routing transformers [30], and various clustering-based models. However, these approaches often achieve efficiency at the expense of accuracy.

The Fourier-Based Mixer serves as the primary inspiration for this work, employing the Fourier transform to mix tokens spatially. FNet [31] introduces a fixed Discrete Fourier Transform (DFT) into the MLP structure. Global Filter Networks (GFNs) [32] utilize learned Fourier filters for deep global convolution but often lack adaptability, leading to suboptimal generalization. Building on advances in Fourier Neural Operators (FNO) [33], the Adaptive Fourier Neural Operator (AFNO) [34] incorporates adaptivity and has emerged as a leading approach in this domain. Despite these advancements, there is a scarcity of research addressing the unique advantages of the frequency domain for binary sparse data within SNNs, and no studies have yet introduced such a mixer into spiking transformers. Moreover, existing work lacks specific frequency-domain analysis to support the optimization of token mixers for the rich temporal information present in SNNs and neuromorphic datasets. This work aims to bridge these gaps.

2.3. Frequency Domain Analysis

Frequency domain representation is particularly significant for neuromorphic datasets, as these datasets capture brightness changes that correspond to high-frequency signals. Consequently, a frequency-domain approach to token mixing offers a distinct advantage for SNNs, enabling the direct and efficient utilization of this information. However, research in this area remains limited. Existing studies have primarily focused on frequency representation within specific bandwidths, exploring concepts such as spiking band-pass filters [35] and resonant neurons tailored to specific frequencies [36]. While Lopez et al. [37,38] recently employed time-value mapping to achieve accurate Fourier transforms, their method introduces substantial latency (approximately 1024 time steps), limiting practical efficiency.

The Fourier unit serves as a fundamental building block for token mixing by applying the Fast Fourier Transform (FFT) to input signals. This mechanism transforms spatial domain signals into the frequency domain, effectively isolating the underlying frequency components that characterize the input data [31]. By assigning weights to these components, the Fourier unit captures essential features while mitigating noise, thereby enhancing representation quality. The efficacy of this approach lies in its ability to identify and emphasize critical frequency patterns—often indicative of significant signal variations—which is particularly advantageous for signal processing and image analysis tasks. Preliminary experiments have demonstrated that employing a Fourier unit not only improves feature extraction but also enhances overall model performance, providing a robust foundation for advanced token mixing architectures [31].

Motivated by the analysis above, we identified the need for a specialized token mixer tailored to SNNs. We selected the AFNO [39] as the basis for our adaptation. Recognized as a leading approach in ANNs, the AFNO effectively transforms data into the frequency domain for feature processing and integrates global context, achieving robust results on static datasets.

In this work, we conduct a comprehensive analysis of the advantages of frequency domain analysis for SNNs and neuromorphic datasets. We improved the original AFNO by incorporating the unique temporal dimension of SNNs and the dynamics of LIF neurons. This novel approach effectively combines binary spikes, event-driven processing, and temporal information to generate robust frequency representations. Furthermore, while spiking neurons can encode static images into spike trains, these converted datasets often lack the rich high-frequency temporal dynamics inherent in native neuromorphic data. Consequently, this paper primarily focuses on neuromorphic datasets to fully validate the superiority of our proposed method.

3. Materials and Methods

3.1. Signal Analysis

Figure 1 illustrates the distinct signal representations utilized in neural networks. When SNN signals are transformed into the frequency domain, the extraction and processing of spectral features are significantly emphasized. We hypothesize that this approach effectively captures key frequency components of the input signal, thereby enhancing feature expressivity.

In contrast, conventional SNN approaches predominantly rely on time-domain signals, achieving information transmission and attention mechanisms through the local interaction of spiking neurons. While this method is effective for capturing local spatial features, it may face limitations in processing global frequency information.

To demonstrate the superiority of frequency-domain analysis in SNNs, we first verify its positive impact on signal intensity representation. We begin by applying the Discrete Fourier Transform (DFT) to two-dimensional discrete images, as expressed by the following equation:

$$\begin{array}{c}F(\mu ,v)=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y)exp\left[-j2\pi \left({\displaystyle \frac{\mu x}{M}}+{\displaystyle \frac{vy}{N}}\right)\right]\\ \left\{\begin{array}{c}\mu =0,1,2,\dots ,M-1\hfill \\ v=0,1,2,\dots ,N-1\hfill \end{array}\right.\end{array}$$

(2)

where $f(x,y)$ is the spatial signal, $F(\mu ,v)$ is the signal in frequency domain, j is imaginary unit, $M,N$ are height, width of the 2D discrete digital signal, respectively. Based on this definition, we observe that frequency components serve as indicators of the magnitude of input variations, effectively representing gradients within the spatial domain. The correlation between signal gradients and frequency implies that higher frequency values correspond to sharper transitions in signal intensity. We can quantify this relationship by analyzing the squared differences between adjacent pixel values:

$$\begin{array}{c}\hfill F(M-1,N-1)\propto {\displaystyle \frac{1}{2}}\sum _{x=1}^{M-1}\sum _{y=1}^{N-1}\left({(f(x,y)-f(x-1,y))}^2\right.\\ \hfill \left.+{(f(x,y)-f(x,y-1))}^2\right)\end{array}$$

(3)

Taking the horizontal pixel change as a specific example, we can decompose this analysis into two components. Let $f(x,y)$ and $f(x-1,y)$ represent two distinct pixel values, while $f_s(x,y)$ and $f_s(x-1,y)$ denote the corresponding pulse signals generated in the SNN. We can then express the following probabilities:

$$\begin{array}{c}P(f_s(x,y)=1)=f(x,y)\hfill \\ P(f_s(x,y)=0)=1-f(x,y)\hfill \end{array}$$

(4)

As is well-known, convolution operations are integral to SNNs. Essentially, the convolution layer functions as a mechanism to transition the signal from the spatial domain to the frequency domain, akin to the Fourier transform process. However, given that the weights are represented as floating-point numbers, the resulting calculations yield a continuous signal. Consequently, we can formulate the high-frequency signal strength as follows:

$$I=F{(\mu ,v)}^2$$

(5)

Assuming $f(x,y)=a$ and $f(x-1,y)=b$ (with $0\le a\le 1$ and $0\le b\le 1$), we can derive strength formulas for both continuous and binary signals:

$$\begin{array}{cc}\hfill I_c\propto & {(a-b)}^2\hfill \\ \hfill I_s\propto & P\left(f\right(x,y)=1)·P\left(f\right(x-1,y)=0)\hfill \\ \hfill & +P\left(f\right(x-1,y)=1)·P\left(f\right(x,y)=0)\hfill \\ \hfill =& a(1-b)+b(1-a)\hfill \end{array}$$

(6)

where $I_c$ represents the intensity of the continuous signal, $I_s$ represents the intensity of the spiking signal, and $P(·)$ denotes the probability function governing spike activation. To compare the intensity magnitudes between these two representations, we define the difference function as

$$I_s-I_c=a(1-b)+b(1-a)-(a^2+b^2)$$

(7)

We present a simple numerical example. Suppose the values of two adjacent pixels are different, this represents an “edge” in the image. $a=0.2,b=0.8$ (for instance, an edge with a gradual gray gradient) Suppose a represents the probability that the pixel value is 1 as 0.2, and b represents the probability that the pixel value is 1 as 0.8. Continuous signal intensity $I_c$: $I_c={(a-b)}^2={(0.2-0.8)}^2=0.36$. Binary signal intensity $I_s$: $I_s=a(1-b)+b(1-a)=0.2(1-0.8)+0.8(1-0.2)=0.68$. Comparison: $I_s-I_c=0.68-0.36=0.32\ge 0$. Consequently, the intensity of the binary signal exceeds that of the continuous signal ($I_s>I_c$), indicating that binary representations retain higher information content when analyzed in the frequency domain. This amplification of high-frequency components enhances signal saliency, which is particularly beneficial for tasks relying on spectral feature analysis—such as edge detection and, in the context of this study, the Fourier-based Token Mixer. Thus, the inherent characteristics of binary signals make them highly sensitive to spatial variations, offering significant advantages for frequency-domain processing.

Finally, we conducted a comparative experiment using synthetic signals. We generated a composite multi-frequency signal comprising three distinct frequency components to serve as the baseline continuous data. Subsequently, this signal was converted into a binary spike stream using a dynamic thresholding mechanism analogous to the encoding method proposed in this paper. We then applied the Fast Fourier Transform (FFT) to both the continuous and binary signals to analyze their spectral characteristics. The time-domain waveforms and their corresponding frequency-domain representations are illustrated in Figure 2.

As illustrated in Figure 2, the spectral energy of the continuous raw data is concentrated in the low-frequency region. In contrast, the spectrum of the binary spike data exhibits significant high-frequency components. This phenomenon arises from the sharp transitions (step functions) inherent in binary switching (0 to 1 and 1 to 0), which effectively introduce high-frequency harmonics (edge effects). These high-frequency components are intrinsic to fast, asynchronous event-driven processing.

In the context of neuromorphic datasets, these spectral features encode the temporal dynamics of the signal—specifically, the rate of pixel intensity changes. The spatiotemporal locations of these changes represent the critical features that need to be prioritized, a task for which SNNs are uniquely optimized. For instance, a hand-waving gesture generates a stream of events along the motion trajectory, producing distinct spectral signatures in the frequency domain. Our proposed ASFNO module is designed to adaptively capture and preserve these relevant frequency features. This capability highlights the distinct advantage of ASFNO in processing neuromorphic data, addressing a challenge that remains difficult for traditional spatial attention mechanisms. The following section details the architecture and operational mechanism of the ASFNO.

3.2. AFNO in Spikingformer

To demonstrate the effectiveness of our proposed module, we designed ASFNOformer, a novel attention-free architecture for SNNs that seamlessly integrates time-frequency information with spikingformers. This architecture enables efficient feature perception across a broad frequency range in an event-driven manner, eliminating the need for multiplication operations. In the following sections, we will introduce our modules, progressing from an overview of the entire architecture to a detailed examination of its individual components.

Figure 3 illustrates the overall structure of our ASFNOformer. To minimize interference from other components, we retain the fundamental architecture of Spikeformer while optimizing the token mixer; specifically, we replace the original Spike Self-Attention (SSA) with our ASFNO module. The Spike Patch Splitting (SPS) module employs a biologically interpretable convolution kernel to linearly project the input image onto a D-dimensional pulse feature vector. This process compresses the original image into a series of N flat spike-form patches.

To ensure that position embeddings align with the principles of SNNs, we utilize the conditional position embedding generator to create Relative Position Embeddings (RPEs) in the form of peaks. These RPEs are added to the patch sequence x to produce $X_0$. The conditional position embedding generator consists of a two-dimensional convolution layer (Conv2d) with a kernel size of 3, followed by batch normalization (BN) and a Spiking Neuron layer (SN). Subsequently, as in the original model, $X_0$ is fed into the ASFNOformer encoding block L-block. However, instead of employing pulsed self-attention as in the original model, each encoding block incorporates a ASFNO token mixer along with an MLP multi-head perceptron.

In the next section, we will delve into the main innovation of this work: the ASFNO token hybrid module. Global Average Pooling (GAP) is then performed on the features processed by the ASFNOformer encoder, resulting in D-dimensional feature outputs that are directed to the fully connected layer Classification Header (CH) to produce the predicted value Y. Our model can be formally expressed as follows:

$$\begin{array}{cc}x=\mathrm{SPS}\left(I\right),\hfill & I\in {\mathbb{R}}^{T\times C\times H\times W},x\in {\mathbb{R}}^{T\times N\times D},\hfill \\ \mathrm{RPE}=\mathrm{SN}\left(\mathrm{BN}\left(\mathrm{Conv}2\mathrm{d}\left(x\right)\right)\right),\hfill & \mathrm{RPE}\in {\mathbb{R}}^{T\times N\times D},\hfill \\ X_0=x+\mathrm{RPE},\hfill & X_0\in {\mathbb{R}}^{T\times N\times D},\hfill \\ X_l^{\prime }=\mathrm{ASFNO}\left(X_{l-1}\right)+X_{l-1},\hfill & X_l^{\prime }\in {\mathbb{R}}^{T\times N\times D},l=1,\dots ,L,\hfill \\ X_l=\mathrm{MLP}\left(X_l^{\prime }\right)+X_l^{\prime },\hfill & X_l\in {\mathbb{R}}^{T\times N\times D},l=1,\dots ,L,\hfill \\ Y=\mathrm{CH}\left(\mathrm{GAP}\left(X_L\right)\right).\hfill \end{array}$$

(8)

ASFNO is an enhanced optimization module of the FNO, which emulates FNO’s three-step process: token mixing, channel mixing, and token decoupling. Our proposed ASFNO follows a similar process: it first employs the DFT to mix feature data, then introduces adaptive weights to complete the channel mixing, and finally applies the inverse Fourier transform to recover the data, as illustrated in Figure 2. To adapt this approach to the discrete binary signals characteristic of SNNs, along with their temporal information, we further transplant the ASFNO module.

$$\begin{array}{c}{z}_{m,n}={\left[\mathrm{DFT}\left(X\right)\right]}_{m,n},\hfill \\ {\tilde{z}}_{m,n}={\left[\mathrm{MLP}\left(X\right)\right]}_{m,n},\hfill \\ {\tilde{Z}}_{m,n}={\left[\mathrm{LWP}\text{-}\mathrm{LIF}\left(\tilde{z}\right)\right]}_{m,n},\hfill \\ y_{m,n}={\left[\mathrm{IDFT}\left(\tilde{Z}\right)\right]}_{m,n}.\hfill \end{array}$$

(9)

3.3. Weight Sharing and Weight Block Diagonal Matrix

Inspired by the principles of self-attention, we aim for the tokens to be adaptive. While traditional static weights function independently across tokens, our approach allows for token interaction, enabling the system to selectively emphasize specific low and high-frequency patterns. To achieve this, we employ a two-layer perceptron, which, with a sufficiently large hidden layer, can approximate any function. To ensure compatibility with SNNs, we substitute the activation function with an LIF layer. The mathematical formulation is as follows:

$$\begin{array}{c}\mathrm{MLP}\left(X\right):\hfill \\ X={\left[\mathrm{MatMul}(X,W_1)+b_1\right]}_{m,n},\hfill \\ X={\left[\mathrm{LWP}\text{-}\mathrm{LIF}\left(X\right)\right]}_{m,n},\hfill \\ X={\left[\mathrm{MatMul}(X,W_2)+b_2\right]}_{m,n}.\hfill \end{array}$$

(10)

To enhance computational efficiency, we employ a block-diagonal weight structure that partitions the weight matrix $W\in {\mathbb{C}}^{d\times d}$ into k independent blocks, each of size ${\displaystyle \frac{d}{k}}\times {\displaystyle \frac{d}{k}}$. This technique effectively reduces the parameter complexity from $O\left(d^2\right)$ to $O(d^2/k)$ and facilitates parallel processing. Within this architecture, each weight block operates independently. Conceptually, each block functions analogously to a head in a multi-head self-attention mechanism, projecting input features into corresponding subspaces. Therefore, selecting an optimal number of blocks k is critical to ensuring that each subspace maintains sufficient dimensionality for effective feature representation.

While the proposed structure shares conceptual similarities with Multi-Head Attention (MHA), their underlying mechanisms and functional roles differ significantly. Standard MHA enables the model to attend simultaneously to distinct segments of the input sequence, extracting information from various “representation subspaces.” Attention weights are dynamically computed based on Query-Key (Q-K) similarity to capture semantic dependencies and achieve global context modeling. In contrast, the Block-Partitioned MLP within the ASFNO Token Mixer operates via a frequency-domain paradigm. It first transforms time-domain signals into the frequency domain using the FFT, applies MLP-based learning and nonlinear processing to the spectral features, and finally reconstructs the signal via the Inverse FFT (IFFT). As established in our prior analysis, this approach focuses on decomposing and processing frequency components, which encode the dynamic transitions inherent in neuromorphic datasets. Consequently, our module extracts features based on spectral properties rather than by directly calculating element-wise dynamic correlations.

Regarding computational complexity, distinct trade-offs exist between the two approaches. MHA typically incurs a high computational cost of $O\left(N^2\right)$ due to the attention matrix calculation. Conversely, our method involves an FFT overhead with a complexity of $O(NlogN)$. To mitigate the computational load of high-dimensional channel mixing, we employ the block-diagonal weight matrix strategy, which significantly reduces the parameter complexity of matrix operations. Furthermore, leveraging the binary accumulation nature of SNNs results in a computational cost significantly lower than that of equivalent ANNs—a fundamental advantage of neuromorphic computing. By eliminating complex convolution operations and optimizing the weight structure, our method achieves a lower space complexity compared to MHA. In summary, our design effectively reduces parameter count while maintaining manageable computational complexity, ultimately improving recognition accuracy on neuromorphic datasets. Detailed validation of these claims is provided in the Section 4.4.

3.4. LIF Model with Learnable Weight Parameter (LWP-LIF)

Unlike traditional LIF models that rely on fixed decay constants, we propose an optimized variant: the LIF Model with LWP-LIF. In this architecture, the membrane potential leakage coefficient is treated as a learnable parameter, denoted as $k_{\tau }\left(a\right)$. From a computational perspective, the automatic optimization of $k_{\tau }\left(a\right)$ eliminates the need for manual hyperparameter tuning, thereby facilitating efficient end-to-end training. In our implementation, neurons within the same layer share the value of $k_{\tau }\left(a\right)$ to ensure parameter efficiency. From a biological perspective, this design offers significant interpretability. The leakage coefficient dictates the rate at which the membrane potential returns to the resting state without external input, simulating the varying availability and conductivity of ion channels. A reduced leakage coefficient prolongs the integration window for input signals—analogous to neurons with closed ion channels—thereby altering the neuron’s firing pattern and encoding capability. Therefore, dynamically adjusting this coefficient allows the model to better reflect the biological diversity of real neurons compared to fixed-parameter models. The dynamic equation of the proposed LWP-LIF is defined as follows:

$$\begin{array}{c}{u}^{t+1,n+1}\left(i\right)=k_{\tau }\left(a\right)u^{t,n+1}\left(i\right)\left(1-o^{t,n+1}\left(i\right)\right)+\sum _{j=1}^{l\left(n\right)}{w}_{ij}^n{o}^{t+1,n}\left(j\right),\hfill \\ o^{t+1,n+1}\left(i\right)=f\left(u^{t+1,n+1}\left(i\right)-V_{\mathrm{th}}\right).\hfill \end{array}$$

(11)

Furthermore, the leakage coefficients are independent across layers, endowing each layer with unique temporal encoding characteristics. By integrating this adjustable decay mechanism, the model can more accurately mimic the heterogeneous dynamic behaviors of biological neurons. Since this parameter is learnable, it is adaptively optimized via backpropagation based on the input data distribution. This flexibility allows the network to converge to optimal leakage profiles tailored to specific tasks, thereby maximizing performance. This biologically inspired design opens new avenues for constructing high-performance SNNs. Ultimately, by synergizing the LWP-LIF model with the ASFNO module, we significantly enhance the network’s temporal adaptability and efficiency, enabling it to address complex spatiotemporal learning challenges in the frequency domain.

3.5. The Temporal Information in ASFNO

The fundamental distinction and advantage of SNNs compared to ANNs lie in their inherent capability to process rich temporal dynamics, providing a natural superiority in handling neuromorphic datasets. Consequently, our ASFNO module explicitly incorporates this temporal dimension, marking a significant departure from the original ANN-based architecture.

Specifically, we encode temporal information by integrating spiking neurons prior to the FFT operation. While we have applied adaptive optimization to these units LWP-LIF, they retain the fundamental dynamics of the Leaky Integrate-and-Fire mechanism. The core characteristic of these neurons is the temporal integration of input currents into the membrane potential, which triggers a spike only when a threshold is breached. This integration process effectively functions as a mechanism for temporal sequence encoding. By deploying a layer of such neurons, the model can effectively capture and utilize the rich temporal information embedded within the input data.

On the other hand, ANNs typically process static inputs with dimensions denoted as $(B,C,H,W)$. SNNs, however, process time-series spike events characterized by the dimensions $(T,B,C,H,W)$, where T represents the number of time steps. This structure ensures that SNNs inherently contain temporal information. Consequently, in terms of data processing dimensions, our ASFNO diverges significantly from standard ANN implementations. In ANNs, the FFT is typically employed solely for global filtering of static images. In contrast, our ASFNO preprocesses the data dimensions prior to the FFT, effectively integrating the T and B dimensions to perform frequency-domain transformations across channels. In essence, our module operates simultaneously across the spatiotemporal dimensions ($T,H,W$). This allows it to perform global filtering while simultaneously retaining and highlighting effective frequency features within the temporal domain. This design aligns with the experimental validation and theoretical conclusions presented in the conclusion of Section 3.1.

4. Results

4.1. Setup

SNNs possess an inherent advantage in processing temporal tasks due to their intrinsic spatiotemporal characteristics. While static image classification can be achieved by repeatedly presenting the same input at each time step, this approach fails to leverage critical temporal information. Although increasing simulation time steps may marginally improve accuracy, it inevitably leads to higher latency, increased hardware requirements, and greater energy consumption during inference. Consequently, we contend that evaluating SNN performance solely on static datasets offers limited significance. In contrast, neuromorphic datasets exhibit inherent spatiotemporal dynamics, enabling SNNs to fully exploit their advantages in energy efficiency and temporal processing.

Furthermore, as discussed in Section 3.1, our proposed module is specifically optimized for binary high-frequency signals derived from pixel intensity changes. Therefore, this study focuses on established neuromorphic datasets to demonstrate the efficacy of our module in advancing SNN research.

Datasets: We evaluated our approach on a comprehensive suite of neuromorphic datasets, primarily focusing on CIFAR10-DVS and DVS128 Gesture [40]. Although we previously noted the limitations of static datasets in evaluating SNN dynamics, to demonstrate the versatility and robustness of our method across different data modalities, we also provided performance benchmarks on the static CIFAR10 dataset [41].

Implementation Details: Our implementation is developed using the Python programming language (version 3.10, Python Software Foundation, Wilmington, DE, USA) and built upon the PyTorch (version 2.0.1+cu118, Meta Platforms, Inc., Menlo Park, CA, USA) framework [39], utilizing the SpikingJelly library (version 0.0.0.0.14, Multimedia Learning Group, Peking University, Beijing, China) for neuromorphic components and the PyTorch Image Models (timm) library (version 0.9.12, Ross Wightman, Vancouver, BC, Canada). To validate the efficacy of our proposal, we integrated the ASFNO module into the baseline spikformer [40] as well as the state-of-the-art QKformer [42] architecture. We trained the proposed model alongside baseline comparisons, achieving State-of-the-Art (SOTA) performance across all tested benchmarks. Furthermore, to isolate the specific contributions of the ASFNO module, we conducted detailed ablation studies, which are discussed in Section 4.4.

4.2. Performance of Static Data Sets

Table 1. Performance on static datasets.

Method	CIFAR10
	Para (M)	Time Steps	Accuracy
TET [43]	12.63	6	94.50
tdBN [44]	12.63	4	92.92
TEBN [45]	12.63	6	94.71
Real Spike [46]	12.63	6	95.78
DSR [47]	11.20	20	95.40
SpikFormer [40]	9.32	4	95.51
SpikingFormer [48]	9.32	4	95.81
ASFNOFormer (ours)	9.12	4	96.04

Note: It can be seen that our model has achieved better performance with less accuracy on static datasets.

presents a comprehensive comparison between the proposed ASFNOformer and current State-of-the-Art (SOTA) SNN models on the CIFAR-10 benchmark. Notably, ASFNOformer surpasses all competing baselines in terms of Top-1 accuracy. Furthermore, it achieves this superior performance with greater efficiency, utilizing fewer parameters and reduced simulation time steps compared to existing architectures.

Compared to established methods such as TET, tdBN, and TEBN, ASFNOformer exhibits an average accuracy improvement of 2%. While the performance margin against some leading SNNs is narrow, it is crucial to note that ASFNOformer achieves these results with significantly fewer parameters. This implies that the model’s enhanced performance stems from the efficiency of its unique architectural design—specifically the frequency-domain token mixing—rather than merely from an increase in model capacity.

4.3. Performance of Dynamic Data Sets

The proposed ASFNOformer demonstrates significant effectiveness across various neuromorphic datasets, including CIFAR10-DVS [7], N-Caltech101, and DVS128 Gesture [40]. Specifically, the DVS128 Gesture dataset comprises 11 gesture categories recorded under three distinct lighting conditions, representing real-world dynamic capture. Conversely, datasets like CIFAR10-DVS represent static images converted into neuromorphic event streams via motion using event-based cameras.

As detailed in the methodology, we optimized the existing Spiking Transformer architecture by replacing the standard token mixer with the ASFNO, which is specifically tailored for neuromorphic data. This design facilitates effective global frequency-domain filtering. Compared to Standard Spiking Self-Attention (SSA), our method not only preserves a greater amount of feature information but also significantly enhances the extraction of high-frequency components associated with temporal dynamics. Consequently, ASFNOformer achieves impressive results across all evaluated benchmarks, as detailed in

Table 2. Performance on Cifar10-DVS and DVS128-Gesture.

Method	Cifar10-DVS			DVS128-Gesture
	Para (M)	Time Steps	Accuracy	Para (M)	Time Steps	Accuracy
tdBN [44]	12.63	10	67.80	12.63	10	96.90
TEBN [45]	12.63	10	75.10	12.63	10	97.50
CML [7]	2.57	16	80.90	2.57	16	98.30
S-Transformer [49]	2.57	16	80.00	2.57	16	99.30
Spikformer [40]	2.57	16	80.90	2.57	16	98.30
Spikingformer [48]	2.57	16	81.30	2.57	16	98.30
ASFNOformer (ours)	2.12	16	82.80	2.12	16	99.10

Note: It can be seen that our model has achieved better performance with less parameters on dynamic datasets.

.

Consistent with the theoretical analysis in the Methodology section, our model demonstrates a significant advantage in tasks involving dynamic datasets. This aligns with our ultimate goal of facilitating the deployment of SNNs on neuromorphic hardware for engineering applications. Regarding static datasets, the relatively marginal improvements can be attributed to two main factors: First, baseline models have already achieved saturation on these benchmarks, likely reaching a local optimum. Second, the intrinsic advantage of SNNs lies in processing temporal information; therefore, our research primarily focuses on enhancing performance on neuromorphic datasets.

While our method excels on dynamic data, it is not overly reliant on temporal dynamics. Experimental results confirm that the model remains robust on static datasets, achieving competitive performance. This versatility stems from the Adaptive Fourier Neural Operator (AFNO) itself. Unlike simple Fourier units, the AFNO acts as an efficient token mixer capable of global feature extraction even in the absence of the temporal dimension $\left[T\right]$.

Finally, regarding training stability, all experiments were conducted for 200 epochs regardless of dataset type. The models consistently achieved convergence, demonstrating structural stability across different random seeds, with the standard deviation of the error observed to be within 0.2%.

4.4. Ablation Experiment

To quantifiably evaluate the contribution of the ASFNO module, we conducted comprehensive ablation studies. The removal of the Adaptive Fourier Neural Operator from the baseline models resulted in a significant degradation in classification accuracy on the CIFAR10-DVS dataset. This finding underscores the critical importance of frequency-domain feature learning for processing neuromorphic data.

Specifically, when integrating ASFNO into the Spikformer architecture [40], classification accuracy on CIFAR10-DVS improved from 80.9% to 82.8% (see

Table 3. The ablation experiments of ASFNOformer based on spikeformer.

Model	Accuracy	FLOPS (G)
Spikeformer	80.9	2.79
ASFNO (ours)	82.8	3.19

). Notably, this performance gain was accompanied by a reduction in parameter count from 2.57 M to 2.12 M, demonstrating improved efficiency.

To further verify the generalizability of our approach and ensure that the improvements are not limited to a specific architecture (i.e., avoiding local optimization bias), we applied our method to a more advanced baseline: the QKFormer [42]. By optimizing its QK-attention module with our proposed method, the classification accuracy on CIFAR10-DVS increased from 84.0% to 85.5% (

Table 4. The ablation experiments of ASFNOformer based on QKformer.

Model	Accuracy
QKformer	84.0
ASFNO (ours)	85.5

), effectively establishing a new State-of-the-Art (SOTA) benchmark.

Furthermore, the significant reduction in parameter counts for both optimized models provides compelling evidence that our enhancements do not rely on merely increasing model capacity (i.e., stacking parameters) but rather offer distinct methodological advantages. These findings underscore the importance of accurate global filtering of frequency-domain features and the efficacy of the adaptive operators within the ASFNO module. Ultimately, this highlights the critical role of high-frequency components in optimizing SNNs for neuromorphic datasets.

Regarding computational complexity, our analysis acknowledges that ASFNO introduces a higher overhead compared to the traditional SSA method. To quantify this impact, we conducted ablation studies focusing on Floating Point Operations (FLOPs) using the standard model benchmarks, as presented in Table 3. The results indicate a marginal increase in computational cost of approximately $15\%$. However, we consider this trade-off to be justifiable. Given the inherent sparsity and binary computing characteristics of SNNs, their overall computational cost remains significantly lower than that of comparable ANNs. Therefore, considering the substantial gains in recognition accuracy and the reduction in parameter count, our method achieves a favorable balance between efficiency and performance, demonstrating significant practical value.

5. Discussion

In SNNs, the spectral characteristics of time series and spatial event patterns (i.e., spikes) constitute critical spatiotemporal information. The Fast Fourier Transform (FFT) serves as a powerful tool for analyzing these signals in the frequency domain, particularly for revealing temporal variations and spatial textures. For single-pixel time series in SNNs, FFT effectively performs spectral analysis on the event count within each time window. The rate of variation in spike events significantly influences the spectrogram: static states correspond to the low-frequency regions, while rapidly changing events occupy the high-frequency spectrum. Specifically, the frequency axis represents the rate of event changes; low-frequency components indicate relatively stable transitions, whereas high-frequency components correspond to rapid or abrupt dynamic events.

When prominent spectral peaks appear, they typically indicate a strong intensity of change at a specific frequency. The magnitude of these peaks is positively correlated with the rate of change, suggesting that the spiking activity of the neural network is highly active at this frequency point. This characteristic mirrors the dynamic nature of the signal, reflecting the time-varying response of SNNs to external stimuli. While existing Spiking Transformers utilize global operations to facilitate information exchange among non-overlapping patch tokens, spiking neurons inherently encode pixel-level intensity transitions. This mechanism enriches local image information, particularly regarding high-frequency components.

Therefore, to validate that the empirical success of our module aligns with our theoretical analysis, we aim to demonstrate that the ASFNO module effectively amplifies high-frequency signals (i.e., the dynamic components of the dataset). Given the necessity of spatiotemporal feature analysis for neuromorphic data, we prioritized the CIFAR10-DVS dataset over static benchmarks like ImageNet for this visualization. We visualized and compared the feature maps generated by the ASFNO module against those from the conventional Spiking Self-Attention (SSA) module, observing the representations both before and after processing. As illustrated in Figure 4, this comparison provides robust empirical support for our hypothesis.

In the CIFAR10-DVS classification task, following the SPS and RPE operations, the input is transformed into a sequence of $8\times 8$ patches. These patches serve as the primary inputs for feature extraction, processed by either the Spiking Self-Attention (SSA) module in the baseline architecture or the ASFNO module in our optimized framework. To visually demonstrate the specific contributions of these modules, we plotted the feature maps at three distinct stages: (a) the raw input prior to processing, (b) the output processed by the ASFNO module, and (c) the output processed by the SSA module, as illustrated in Figure 4. Through both 2D and 3D visualizations, it is evident that while both mechanisms are capable of feature extraction, the SSA module (c) tends to attenuate the intensity of the original signal compared to the input (a). In contrast, the ASFNO module (b) exhibits significantly higher activation values (represented by brighter regions), effectively enhancing signal intensity. This empirical observation corroborates our theoretical derivations regarding signal intensity enhancement presented in Section 3.1.

Finally, to validate the efficacy of our frequency-domain analysis, we performed an FFT on the temporal dimension of each channel to obtain its spectral representation. Figure 5 illustrates the global average spectral distribution. The proposed token mixer in ASFNOformer effectively captures specific frequency components, facilitating comprehensive feature learning within the spectral domain. Crucially, it preserves high-frequency information transmission into deeper network layers more effectively than the baseline Spiking Transformer. This capability enhances the model’s responsiveness to the rich temporal dynamics inherent in neuromorphic datasets. Consequently, this improved spectral learning capability results in more robust feature extraction, ultimately leading to superior recognition performance.

6. Conclusions

In this study, we explored the integration of frequency-domain adaptive operators into SNNs and proposed the ASFNOformer, a novel architecture that synergizes the ASFNO with frequency-aware transformers. This design explicitly addresses the unique characteristics of binary spike data, specifically leveraging the intrinsic correlation between luminance variations and frequency components in neuromorphic sensing. By adapting and optimizing the artificial neural network-based AFNO framework for the spiking paradigm, we achieved significant improvements in both efficiency and performance.

The key innovations of the ASFNOformer are threefold:

SNN-Specific Frequency Adaptation: We replaced traditional activation functions with LWP-LIF neurons and incorporated block-diagonal weight matrices for multi-head perception. This design effectively processes sparse spike data while maintaining spatiotemporal and frequency coherence across the $[T,H,W]$ dimensions.

Computational Efficiency: The sparsity-driven design reduces model parameters by approximately 24% compared to conventional AFNOs in ANNs, making the architecture inherently suitable for resource-constrained neuromorphic hardware.

Dual-Domain Generalization: Experimental validation on static datasets (e.g., CIFAR-10) demonstrates competitive accuracy against mainstream ANN-based models (e.g., ResNet, ViT). More importantly, on neuromorphic datasets (e.g., CIFAR10-DVS, DVS128-Gesture), our method exhibits a 2% performance improvement, confirming its superior adaptability to dynamic spatiotemporal patterns.

Comprehensive ablation studies on two state-of-the-art spiking transformers (Spikformer and QKFormer) validate that ASFNO demonstrates robust generalization capabilities, mitigating the risk of local optimization bias, and achieves new State-of-the-Art (SOTA) results when trained from scratch. Notably, the synergy between frequency-aware operators and spike-driven computation enables the efficient extraction of time-frequency features without compromising biological plausibility.

This work opens a new pathway for deploying transformer-based architectures in SNNs and provides critical insights into frequency-domain processing for neuromorphic computing. Future research will focus on hardware-software co-design to further compress model footprints and explore real-time deployment on emerging neuromorphic chips. We anticipate that the ASFNOformer will serve as a foundational framework for next-generation energy-efficient AI systems leveraging event-driven sensing.