Asymmetric Metamaterial Nanowire Structure for Selective Solar Absorption

Abstract

A novel wavelength-selective absorber is numerically designed and analyzed using a three-dimensional finite-difference time-domain method. The proposed solar thermal absorber consists of an array of asymmetric tungsten ring nanowires deposited on a tungsten thin film. This structure achieves high solar absorption efficiency (78.5%) and low thermal emissivity (5%) at 100 °C, resulting in a photothermal conversion efficiency of 73.55% under standard solar illumination. The selective absorption arises from the excitation of magnetic polaritons and surface plasmon polaritons. To further elucidate the physical mechanisms behind the spectral response, an equivalent inductor–capacitor circuit model is employed. The absorber also exhibits polarization-insensitive and angle-independent performance up to 50° for both transverse magnetic and transverse electric polarizations. These results demonstrate the potential of the proposed metamaterial absorber for advanced applications in solar energy harvesting, photothermal conversion, and thermal emission.

1. Introduction

Sunlight is a tremendous source of energy that radiates onto our planet daily. The amount of solar energy reaching Earth in a single hour exceeds the total annual energy consumption of human society [1]. Solar energy thus offers a practical alternative to help alleviate the energy crisis and mitigate greenhouse gas emissions. In this context, various approaches have been developed to harvest solar energy, such as photovoltaic (PV) systems, which convert solar energy into electricity [2,3,4].

However, the materials used in PV systems limit their efficiency due to the Shockley–Queisser limit. To overcome this limitation, a new approach known as solar thermophotovoltaics (STPV) has been explored [5,6,7,8,9]. STPV systems use solar energy to heat thermal absorbers, which then radiate energy toward a solar cell. This thermal radiation generates electron-hole pairs in the solar cell, resulting in a photocurrent.

For effective operation, STPV systems require thermal absorbers with high broadband absorption in the solar spectrum and low thermal emission losses at longer wavelengths. Spectrally and spatially selective thermal absorbers are especially desirable for increasing conversion efficiency. These characteristics can be achieved through the excitation of phonon polaritons or surface plasmons [10,11,12,13], resonance microcavities [14,15], Fabry–Pérot resonances [16,17,18], and photonic crystals [19,20].

Recently, metamaterial absorbers have gained significant attention for achieving wavelength-selective absorption through the excitation of magnetic polaritons [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Various nanostructure designs have been proposed, including nanowires [38], cut-wire arrays [23], fishnet structures [39], chiral metamaterials [40], and Dirac semimetal absorbers [41,42,43]. In this regard, Landy et al. [23] proposed a perfect metamaterial absorber composed of ring resonators that absorb incident radiation through a single unit cell layer. Selective absorbers and TPV emitters have also been investigated using nanostructures made of tungsten gratings and SiO₂ spacers [22].

Liu et al. [44] numerically demonstrated a refractory titanium nitride metasurface, while Wang et al. [45] introduced concave grating metamaterials capable of exciting multiple magnetic polariton resonances, resulting in selective absorption. An ultrathin metamaterial absorber using a single-sized disk and high $\epsilon ″$ metals was also reported [46]. Rana et al. [47] proposed a flat optical absorber based on tungsten, achieving an absorption efficiency of 99.3%. Furthermore, a broadband metamaterial absorber incorporating a phase-change material, Ge₂Sb₂Te₅ (GST), was experimentally demonstrated [48], achieving over 80% absorption in the 480–1020 nm range.

Zhou et al. [49] presented two types of absorbers based on Ti/Ge/Si₃N₄/Ti configurations, with absorption efficiencies of 92% and 87% in the spectral ranges of 14–30 μm and 8–30 μm, respectively. Another design featuring a periodic square array of iron film, separated by silica and a phase-change material, achieved absorption above 93% over the 400–2000 nm range [50]. A metal-free absorber using vanadium dioxide (a phase-change material) also demonstrated a broadband absorption bandwidth of 6.26 THz [51].

Despite these advancements, previously proposed thermal solar absorbers remain suboptimal. Achieving high photothermal conversion efficiency, along with polarization independence and insensitivity to the angle of incidence, continues to pose a significant design challenge.

In this study, a novel wavelength-selective thermal solar absorber is proposed to address these limitations. The design features a metamaterial structure composed of asymmetric ring nanowires deposited on a 200 nm-thick tungsten substrate. Tungsten is selected for its exceptionally high melting point (3420 °C), which makes it suitable for high-temperature applications. The absorber’s solar absorption and thermal emissivity are evaluated across a broad spectral range, from the ultraviolet to the mid-infrared. In addition, the photothermal conversion efficiency is calculated to assess overall performance. The effects of oblique incidence and polarization are also investigated to evaluate the design’s angle insensitivity and polarization independence.

2. Design Considerations

Figure 1 presents a schematic of the proposed asymmetric nanowire array metamaterial, designed as a selective solar thermal absorber. The structure consists of asymmetric tungsten ring nanowires arranged on a tungsten thin-film substrate. Tungsten is chosen due to its high melting point (3420 °C) and good corrosion resistance in the visible range.

The nanowire array includes two asymmetric rings with diameters set as follows: d₁ = 120 nm and d₂ = 300 nm for the first ring, and d₃ = 100 nm and d₄ = 200 nm for the second. Each nanowire has a height of L = 600 nm, and the spacing between nanowires is 500 nm. The optically opaque tungsten thin film, with a thickness of h = 200 nm, functions as a mirror, enhancing the interaction between the incident light and the nanostructures. The nanowires are arranged in a square lattice with a period of P = 1 μm.

The optical constants of tungsten are obtained from Palik [52]. The radiative properties are calculated using the finite-difference time-domain (FDTD) method by numerically solving Maxwell’s equations. The simulations are carried out using the Lumerical FDTD Solutions package(Ansys Lumerical 2025 R1.3, Lumerical Solutions, Inc., Vancouver, BC, Canada) [53]. The studied broadband spectral range extends from the ultraviolet to the mid-infrared (0.3 µm to 12 µm). A broadband polarized plane wave source, simulating sunlight, is placed above the structure, as illustrated in Figure 1.

Non-uniform mesh sizes of 5 nm are manually applied in the x, y, and z directions to minimize the computational domain and reduce the complexity of the 3D simulations. Periodic boundary conditions are applied in the x and y directions, while perfectly matched layer (PML) boundary conditions are used in the z direction to ensure reflection coefficients below 10⁻⁶. A simulation time of 1000 fs is selected to achieve accurate results. For oblique incidence cases, Bloch boundary conditions are applied to capture phase differences.

To measure reflectance (R), a frequency-domain field monitor is placed above the source. Due to the reflective tungsten backing, transmission (T) is negligible (T ≈ 0). Therefore, the spectral directional absorptance is calculated using Kirchhoff’s law: $A=1-R$ [54,55].

The absorber efficiency (${\eta }_{abs}$) describes the performance of the proposed thermal solar absorber and is defined as:

$${\eta }_{abs}={\displaystyle \frac{{\int }_{0.3\mu m}^{4\mu m}A\left(\lambda \right)I_{AM1.5}\left(\lambda \right)d\lambda }{{\int }_{0.3\mu m}^{4\mu m}{I}_{AM1.5}\left(\lambda \right)d\lambda }}$$

(1)

where $A\left(\lambda \right)$ is the spectral absorptance of the absorber, and $I_{AM1.5}$ is the solar spectral irradiance under AM1.5 (Global) conditions [56].

The performance of the solar absorber also depends on the total emissivity ($\epsilon$), which evaluates its thermal emitter characteristics. Total thermal emissivity is defined as [38,57,58]:

$$\epsilon ={\displaystyle \frac{{\int }_0^{\mathrm{\infty }}\epsilon \left(\lambda \right)I_{BB}\left(\lambda ,T_A\right)d\lambda }{{\int }_0^{\mathrm{\infty }}{I}_{BB}\left(\lambda ,T_A\right)}}$$

(2)

where $I_{BB}\left(\lambda ,T_A\right)$ is the blackbody radiation intensity at temperature $T_A$, and $\epsilon \left(\lambda \right)$ is the spectral emissivity of the proposed thermal absorber. Finally, the photon-to-heat conversion efficiency ($\eta$) of the thermal solar absorber, assuming 1-sun illumination and neglecting convective and conductive losses, is expressed as [3,59,60]:

$$\eta ={\displaystyle \frac{{\eta }_{abs}G-\epsilon G(\sigma T_A^4-\sigma T_{sky}^4)}{G}}$$

(3)

where $G$ is the incident solar flux, $\sigma$ is the Stefan–Boltzmann constant, and $T_A$ and $T_{sky}$ are the absorber and sky temperatures, respectively (with $T_{sky}$ = 0 °C).

3. Numerical Results and Optical Performance Analysis

The spectral directional absorption of the asymmetric nanowire array metamaterial absorber is illustrated in Figure 2a. Transverse magnetic polarizations (TM-polarized) waves are applied at normal incidence to evaluate the absorber’s performance across the ultraviolet to mid-infrared range. As shown in Figure 2a, four major absorption peaks are identified. The first significant peak reaches an absorption rate of 0.93 at a wavelength of λ = 300 nm. The subsequent peaks occur at λ = 600 nm (A = 0.94), λ = 880 nm (A = 0.98), and λ = 1545 nm (A = 0.92), indicating strong resonant behavior across the visible and near-infrared spectrum. Additionally, the inset of Figure 2a illustrates the absorption performance of the proposed thermal solar absorber at longer wavelengths. It is observed that the absorption falls below 0.09 beyond the mid-infrared region.

A validation procedure is studied and implemented to quantify the reliability of the FDTD simulations. First, a mesh-convergence study is conducted by systematically refining the spatial discretization from 10 nm down to 4 nm within the nanowire region. The absorption spectra are monitored at each refinement step. Convergence is confirmed when further mesh refinement produces changes of less than 0.03% in peak positions and amplitudes, as shown in

Table 1. Presents a comparison of the absorption results obtained using different mesh cell sizes.

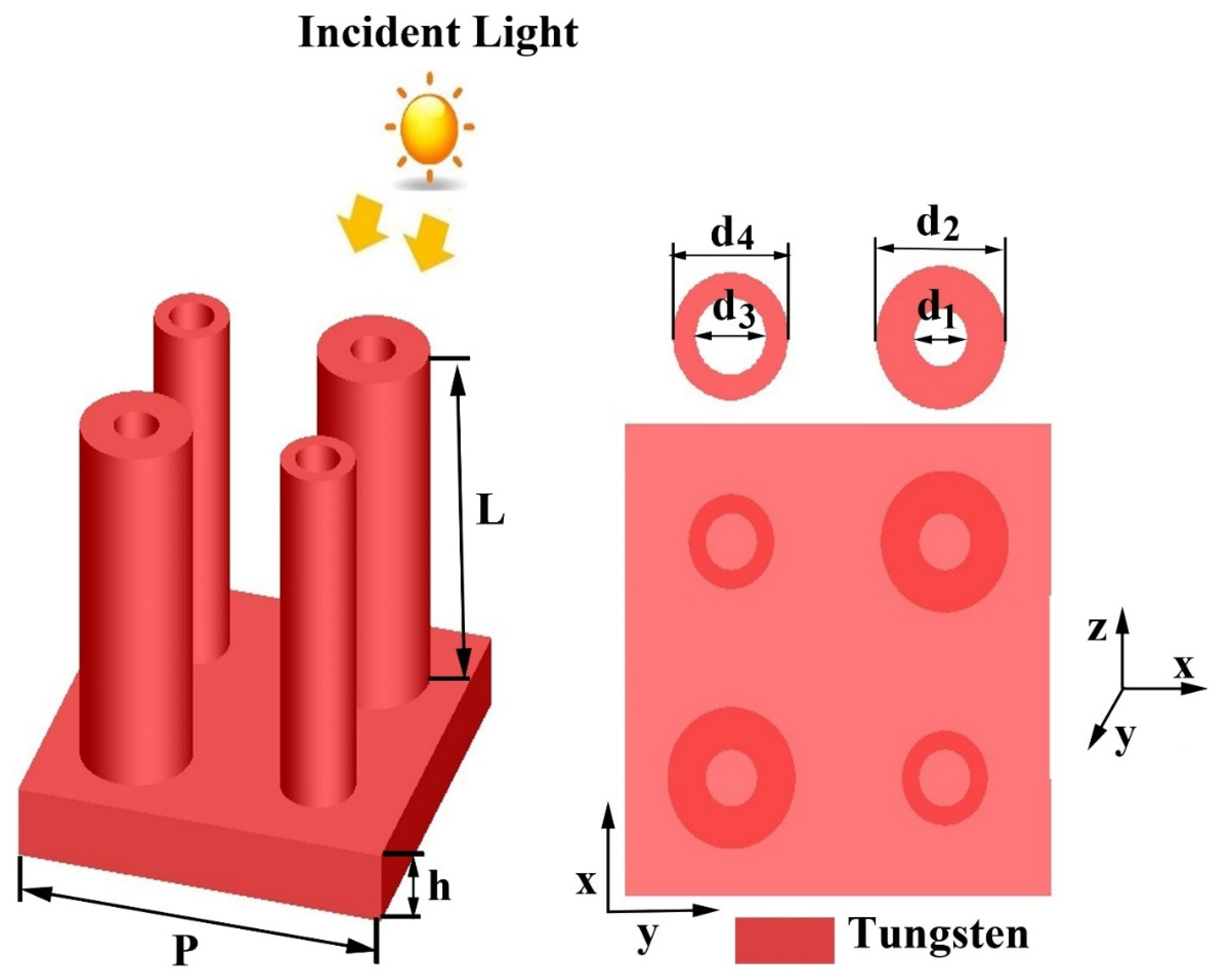
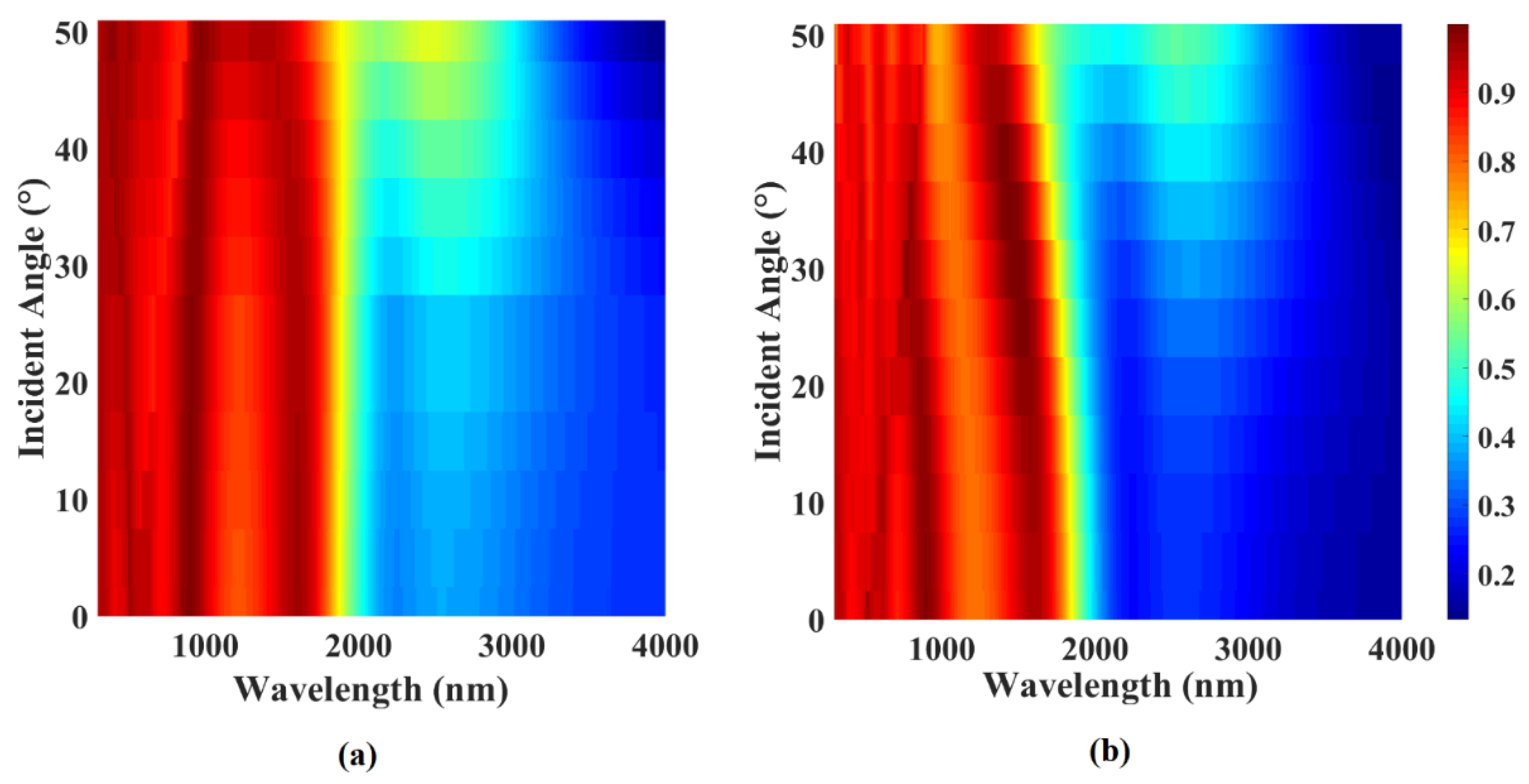
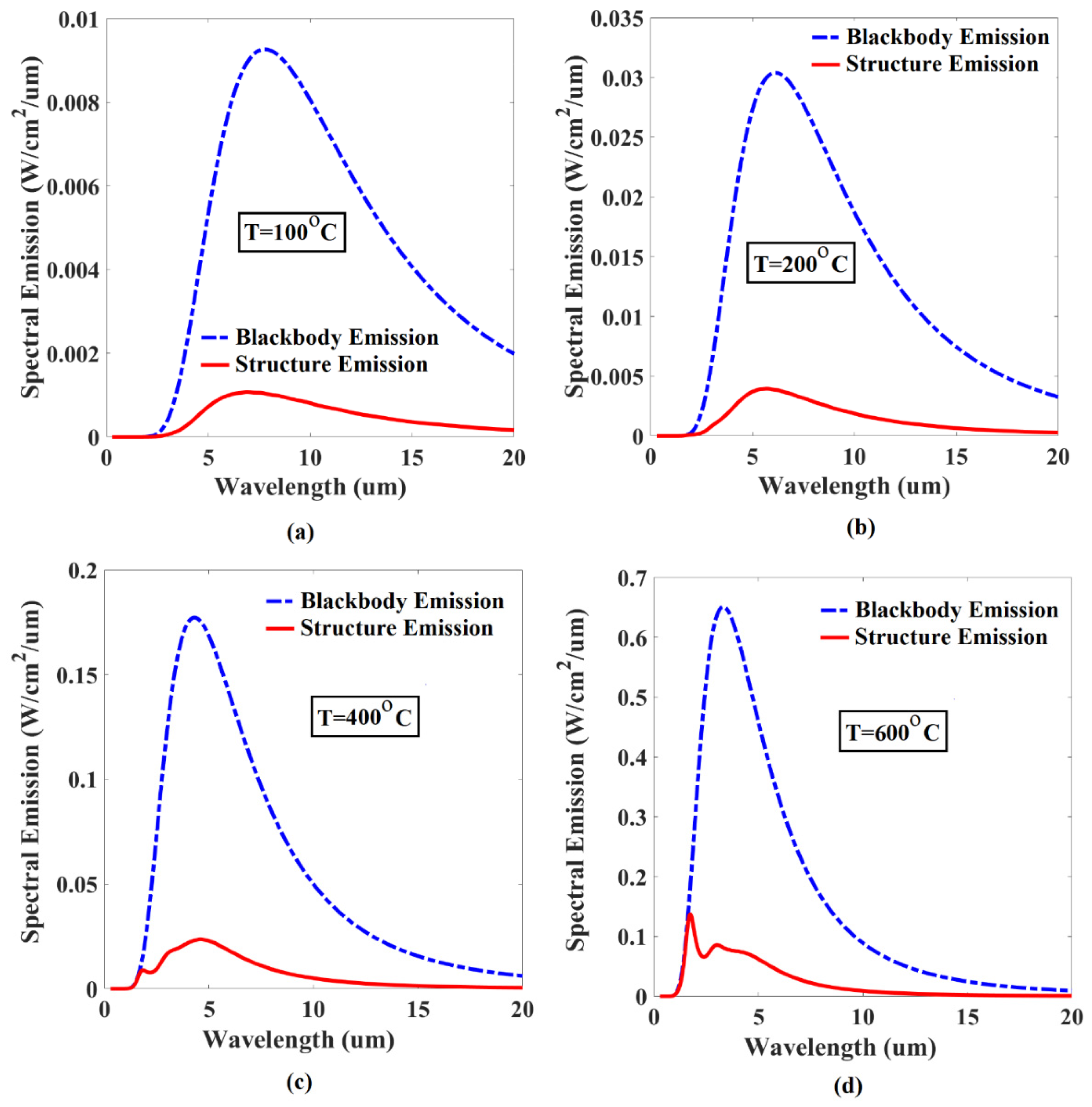
Mesh Cell Size (nm)	Peak Abs. 300 nm	Peak Abs. 600 nm	Peak Abs. 880 nm	Peak Abs. 1545 nm	Relative Change Compared to Finer Mesh (%)
10 nm	0.939	0.938	0.981	0.930	0.40%
7 nm	0.936	0.937	0.983	0.921	0.16%
5 nm	0.933	0.938	0.984	0.920	0.03%
4 nm	0.933	0.937	0.984	0.920	— (the finest mesh)

. A non-uniform mesh is employed with a minimum cell size of 5 nm in the x, y, and z directions around the nanowire region using mesh-override regions. This is due to the accurate resolution of the subwavelength geometric features of the asymmetric tungsten nanowire array. The spatial resolution is necessary due to the narrow ring widths (100–120 nm), the sharp metal–dielectric interfaces, and the presence of strongly localized electromagnetic fields. This approach ensures accurate resolution of rapidly varying electromagnetic fields without high computational cost. Second, perfectly matched layer (PML) boundary conditions are optimized by adjusting the layer thickness, polynomial grading order, and absorption strength to suppress numerical reflections, particularly at long wavelengths where evanescent decay lengths are larger. Finally, the numerical results are benchmarked against analytical estimates for surface plasmon polariton (SPP) dispersion at planar air–tungsten interfaces and the well-established inductor–capacitor (LC-type) resonance model for magnetic polaritons (MPs) in periodic metallic structures. The strong agreement between simulated and theoretical resonance wavelengths confirms the validity of the numerical model and supports the physical interpretation of the observed absorption peaks.

To elucidate the necessity of geometric asymmetry, the simulation of a symmetric nanoring array is presented in which both rings share a single averaged diameter. As shown in Figure 2a, the symmetric structure exhibits noticeably reduced absorption, characterized by a narrower bandwidth and weaker impedance matching relative to the asymmetric design. In contrast, the asymmetric configuration supports multiple, well-separated resonances arising from the two distinct ring sizes, resulting in four prominent absorption peaks at 300, 600, 880, and 1545 nm. This result demonstrates that the asymmetric design is essential for achieving strong broadband absorption, enhanced impedance matching, and selective low-emissivity performance.

The suitability of the proposed absorber for solar energy harvesting has been evaluated by comparing its absorption spectrum with the standard AM1.5 Global solar spectrum [56]. As presented in Figure 2b, the absorber demonstrates strong and broadband absorption across the visible and near-infrared regions, which closely aligns with the high-intensity portions of the solar spectrum. This spectral overlap confirms the potential of the proposed structure for efficient solar energy conversion.

To further investigate the resonance mechanisms responsible for these peaks, the electromagnetic (EM) field distributions at the corresponding wavelengths are shown in Figure 3. This figure illustrates cross-sectional views of the EM field distribution in the x–z plane along the normal direction. The analysis provides insight into the physical mechanisms responsible for the distinct absorption peaks observed in the spectral profile presented in Figure 2.

The primary resonance peaks are observed at the following wavelengths: (a) λ = 300 nm, (b) λ = 600 nm, (c) λ = 880 nm, (d) λ = 1545 nm, and (e) λ = 3370 nm. Figure 3a highlights the field distribution at λ = 300 nm (A = 0.94), attributed to the excitation of surface plasmon polaritons (SPPs) at the dielectric/metal (air–tungsten) interface. SPPs are generated by the coupling of incident electromagnetic radiation with collective oscillations of free electrons at the metal surface. This interaction leads to enhanced field localization near the interface, particularly at the top surfaces of the nanowires, where SPP excitation is strongest. The high field intensity at these locations indicates efficient energy coupling and absorption in the ultraviolet range.

The absorption peaks at λ = 600 nm, λ = 880 nm, and λ = 1545 nm—depicted in Figure 3b–d—are associated with the excitation of magnetic polaritons (MPs). In these cases, magnetic energy is strongly confined within the air gaps between adjacent nanowires. When incident light interacts with the nanowire surfaces, it induces oscillatory motion of free charges, generating closed-loop displacement currents between neighboring nanostructures. These currents excite localized magnetic responses characteristic of MP modes. The observed field patterns correspond to higher-order MP resonances, labeled as MP4, MP3, and MP2, resonating at progressively longer wavelengths within the visible to near-infrared spectrum.

Finally, Figure 3e shows the field distribution at λ = 3370 nm, corresponding to the longest-wavelength absorption peak. This resonance is attributed to the first magnetic polariton mode (MP1). At this wavelength, magnetic energy is intensely confined between the nanowires, indicating strong magnetic resonance that enhances absorption in the mid-infrared region.

Overall, these resonant modes—SPPs in the ultraviolet and MPs across the visible to mid-infrared spectrum—contribute to the broadband and selective absorption performance of the designed metamaterial. The coexistence of multiple resonant mechanisms enables efficient light harvesting, making the structure highly suitable for solar thermal applications that require spectral selectivity and thermal stability.

To further substantiate the physical origin of the resonant peaks, quantitative mode analyses have been added, as shown in Figure 4. Figure 4a and 4b present the absolute current-density distributions ($J$) at λ = 300 nm and λ = 600 nm, respectively. At λ = 300 nm, the antisymmetric surface-charge oscillation along the air–tungsten interface confirms the excitation of SPP. In contrast, at λ = 600 nm, the displacement-current distributions exhibit closed-loop current paths and pronounced magnetic-field confinement within the air gaps between adjacent nanowires—features characteristic of magnetic polariton (MP) modes. Additionally, the surface charge density ($rho$) shown in Figure 4c further supports this attribution, demonstrating charge localization at the metal edges as expected for these resonant conditions.

In the following analysis, the impedance matching theory of the proposed solar absorber is presented to explain its fundamental absorption mechanism. The optical impedance (real and imaginary parts) of the proposed thermal solar absorber is shown in Figure 5. The definitions of relative and absorption impedance are as follows [3,61]:

$$A\left(\omega \right)=1-R\left(\omega \right)=1-{\left|{\displaystyle \frac{Z-Z_o}{Z+Z_o}}\right|}^2=1-{\left|{\displaystyle \frac{Z_r-1}{Z_r+1}}\right|}^2$$

(4)

$$Z_r=\pm \sqrt{{\displaystyle \frac{{(1+S_{11})}^2-S_{21}^2}{{(1-S_{11})}^2-S_{21}^2}}}$$

(5)

$$A\left(\lambda \right)={\displaystyle \frac{4Re\left(z\right)}{{[1+4Re(z\left)\right]}^2+{\left[Im\right(z\left)\right]}^2}}$$

(6)

where $Z$ is the effective impedance of the proposed absorber, $Z_o$ is the free-space impedance as illustrated in Equation (4), and $S_{11}$ and $S_{21}$ are the reflection and transmission coefficients as introduced in Equation (5), respectively. Since any transmitted light is blocked by the tungsten thin film, the transmission coefficient $S_{21}$ is zero.

According to Equation (6), the spectral absorption $A\left(\lambda \right)$ approaches unity when the effective impedance satisfies $Re\left(z\right)\approx 1$ and $Im\left(z\right)\approx 0$. As illustrated in Figure 5, within the wavelength range of 300 to 1800 nm, the real part of the impedance remains close to 1, while the imaginary part remains near 0, indicating excellent impedance matching between the absorber and the surrounding medium. This aligns with Figure 2, which shows high spectral absorption in the same wavelength range, further confirming effective impedance matching.

Beyond 1800 nm, Figure 5 shows that both $Re\left(z\right)$ and $Im\left(z\right)$ vary significantly and decline sharply. As the wavelength approaches 4000 nm, $Re\left(z\right)$ tends toward zero, leading $A\left(\lambda \right)$ to also approach zero, as predicted by Equation (6). Thus, the absorber demonstrates selective wavelength absorption, maximizing energy harvesting at desired spectral regions.

The effect of the polarization angle $\psi$ on the directional absorption spectra is illustrated in Figure 6. This study is conducted under normal incidence. As shown in Figure 6, the absorber maintains high absorption across the 0.3 to 2 μm wavelength range. Notably, the absorption spectra remain nearly unchanged for polarization angles from 0° to 90°, indicating polarization insensitivity. Since incident light includes both transverse magnetic and transverse electric polarizations (TM and TE) components at any polarization wave, the absorption characteristics remain consistent for all angles within this range.

As previously discussed, the proposed metamaterial absorber achieves near-unity absorption under TM polarization at normal incidence across the specified wavelength range. However, the angle of incidence significantly affects the spectral response. To explore this, the absorption behavior is analyzed for various angles. Figure 7a,b present the absorption spectra under both TE and TM polarizations for incident angles ranging from 0° to 50° in 5° increments. The results indicate consistently high absorption from 300 nm to 2000 nm for both polarizations within this angular range. Beyond 50°, notable spectral oscillations emerge, and resonance excitation becomes less effective, reducing absorption efficiency. Therefore, the proposed absorber maintains optimal performance for incident angles up to 50°.

The inductor–capacitor (LC model) is introduced in the subsequent investigation to further explain the absorption enhancement of the proposed selective absorber. This model also helps optimize the absorber geometry. The equivalent LC model is shown in Figure 8. Due to the curvature of the nanowire surface, direct quantification of inductance and capacitance is challenging. To simplify this, a modified LC model treats the nanowire as an effective plate, as shown in Figure 8a, based on the equivalent distribution of localized magnetic fields.

The circuit representation of the LC model is shown between two vertically aligned and closely spaced nanowires in Figure 8b. $C_1$ and $C_2$ are the cavity capacitances for NW1 and NW2, respectively. A gap capacitor, $C_g$, is formed between the two adjacent nanowires. Additionally, inductors are formed by the parallel plates: $L_{m1}$ and $L_{m2}$ represent the magnetic inductance of NW1 and NW2, respectively. Drift current induced by charge movement also leads to kinetic inductance, denoted $L_{k1}$ and $L_{k2}$. Finally, drifting electrons in the substrate and nanowires contribute to an additional inductance, $L_{Sub}$.

Accordingly, Equation (7) presents the total impedance of the LC circuit as given by

$$Z_{total}={\displaystyle \frac{\left(L_{m1}+L_{k1}\right)}{1-{\omega }^2{C}_1\left(L_{m1}+L_{k1}\right)}}+{\displaystyle \frac{\left(L_{m2}+L_{k2}\right)}{1-{\omega }^2{C}_2\left(L_{m2}+L_{k2+}\right)}}-{\displaystyle \frac{1}{{\omega }^2{C}_g}}+L_{Sub}+\left(L_{m1}+L_{k1}\right)+\left(L_{m2}+L_{k2}\right)$$

(7)

To identify the magnetic resonance wavelength (${\lambda }_{MP}$), the overall impedance is set to zero. The wavelength is then expressed by Equation (8) as

$${\lambda }_{MP}=2\pi c\sqrt{C_g\left[\right(2\left(L_{m1}+L_{k1}\right)+2\left(L_{m2}+L_{k2}\right)+L_{Sub}]}$$

(8)

where $c$ is the speed of light in vacuum.

To provide a quantitative validation of the LC model, the dominant capacitive and inductive components of the asymmetric nanowires are estimated separately. Using the effective-plate approximation (Figure 7a), the cavity capacitances of NW1 and NW2 are computed as $C_1$ = 9.55 × 10⁻¹⁹ F and $C_2$ = 5.31 × 10⁻¹⁹, respectively. The gap capacitance between the nanowires is $C_g$ = 7.43 × 10⁻¹⁹ F. The magnetic inductances are $L_{m1}$ = 1.73 × 10⁻¹² H and $L_{m2}$ = 1.63 × 10⁻¹² H, while the kinetic inductances are $L_{k1}$ = 1.73 × 10⁻¹³ H and $L_{k2}$ = 1.63 × 10⁻¹³ H. The substrate-induced inductance is $L_{sub}$ = 5.0 × 10⁻¹³ H.

Using Equation (8) with these separate LC values, the predicted resonance wavelengths for MP1–MP4 are 3330 nm, 1660 nm, 1110 nm, and 830 nm, which closely match the simulated absorption peaks at 3370 nm, 1545 nm, 880 nm, and 600 nm, respectively. The detailed comparison is presented in

Table 2. Comparison between the LC predicted and simulated results.

Mode	${\mathit{C}}_1$(F)	${\mathit{C}}_2$(F)	${\mathit{C}}_{\mathit{g}}$(F)	${\mathit{L}}_{\mathit{m}1}$(H)	${\mathit{L}}_{\mathit{m}2}$(H)	${\mathit{L}}_{\mathit{k}1}$(H)	${\mathit{L}}_{\mathit{k}2}$(H)	${\mathit{L}}_{\mathit{s}\mathit{u}\mathit{b}}$	LC-Predicted λ (nm)	Simulated λ (nm)	Error (%)
MP4	9.55 × 10−19	5.31 × 10−19	7.43 × 10−19	1.73 × 10−12	1.63 × 10−12	1.73 × 10−13	1.63 × 10−13	5.0 × 10−13	830	600	8%
MP3	9.55 × 10−19	5.31 × 10−19	7.43 × 10−19	1.73 × 10−12	1.63 × 10−12	1.73 × 10−13	1.63 × 10−13	5.0 × 10−13	1110	880	6%
MP2	9.55 × 10−19	5.31 × 10−19	7.43 × 10−19	1.73 × 10−12	1.63 × 10−12	1.73 × 10−13	1.63 × 10−13	5.0 × 10−13	1660	1545	3%
MP1	9.55 × 10−19	5.31 × 10−19	7.43 × 10−19	1.73 × 10−12	1.63 × 10−12	1.73 × 10−13	1.63 × 10−13	5.0 × 10−13	3330	3370	0.3%

, confirming that the LC model effectively captures the resonant physics of the asymmetric nanowire array and provides a reliable basis for absorber design and optimization.

The proposed structure can also function effectively as a thermal emitter, as thermal radiation can be emitted or absorbed by thermodynamic sources. In this context, the thermal emission characteristics of the proposed absorber are analyzed at $T=100 °\mathrm{C}$ and $T=200 °\mathrm{C}$, as illustrated in Figure 9a and Figure 9b, respectively. Using Equation (2), the total emissivity of the proposed absorber is estimated to be 4.6% at $100 °\mathrm{C}$ and 12.07% at $200 °\mathrm{C}$. Correspondingly, the photothermal conversion efficiency, calculated using Equation (3), is 73.55% and 44.3% at 100 °C and 200 °C, respectively. These results indicate that while total emissivity increases with temperature, the associated rise in radiative energy losses leads to a reduction in photothermal conversion efficiency.

To assess the thermal robustness of the design, the temperature-dependent emissivity is further evaluated at 400 °C and 600 °C, as shown in Figure 9c and Figure 9d, respectively. Because the absorption spectrum is temperature-invariant for metallic nanostructures, emissivity at each temperature is obtained by multiplying the spectral absorptance by the corresponding Planck distribution. As shown in Figure 9c,d, the emissivity curves at 400 °C and 600 °C closely resemble those at lower temperatures, indicating minimal spectral distortion and stable mid-infrared suppression. This confirms that the asymmetric tungsten nanowire absorber can maintain its selective emission behavior at high temperatures, making it a promising candidate for solar-thermal and STPV systems.

To further evaluate the material versatility of the proposed selective absorber, a comparative analysis is performed by substituting tungsten (W) with other refractory plasmonic materials, including titanium (Ti), titanium nitride (TiN), chromium (Cr), and nickel (Ni), as illustrated in Figure 10. As shown in Figure 10a, W demonstrates nearly ideal selective absorption characteristics—exhibiting near-unity absorption across the ultraviolet to near-infrared spectrum, followed by a sharp drop to near-zero absorption at longer wavelengths. The absorption efficiency for each material is calculated using Equation (1) under consistent geometric and simulation conditions, as presented in Figure 10b.

While Ti shows a slightly higher solar absorption efficiency (78.9%) compared to W (78.6%), its extended absorption in the long-wavelength region (λ > 2 µm) may lead to increased thermal re-radiation losses, thereby diminishing its effectiveness in solar thermal applications. In contrast, W offers a pronounced spectral cutoff and negligible absorption in the mid- to far-infrared range, which is essential for minimizing thermal losses. Combined with its superior thermal and mechanical stability, these attributes make W the most suitable candidate for the proposed design, despite the marginal difference in solar absorption efficiency.

Table 3. Comparative evaluation of the proposed solar absorber with previously reported selective absorber.

Reference	Design	Number of Sheets	Materials		Absorption Performance
			Metal	Dielectric
Xu et al. [62]	Nanodisk array	3	Al	SiO2	Two peaks (0.92 and 0.99)
Rana et al. [63]	Cross-shaped	3	Cr	SiO2	0.9 (300–1200 nm)
Wu et al. [50]	Square array	6	Fe	SiO2	0.93 (400–2000 nm)
Cai et al. [64]	Square grating	6	W	SiO2	0.97 (300–2000 nm)
Ye et al. [65]	Sphere array	3	W	SiO2	0.95 (300–1777 nm)
Liang et al. [66]	Fishnet-shaped	2	W	SiO2	0.935 (400–1200 nm)
Zhou et al. [67]	Nanodisk array	4	TiN	Si3N4	0.97 (400–2500 nm)
Chang et al. [38]	Nanowire array	1	W	air	≈0.93 (300–1500 nm)
This study	Asymmetric ring	1	W	air	0.95 (300–2000 nm)

presents a comparative analysis of the proposed thermal solar absorber against previously reported selective absorbers. The comparison considers structural design, number of layers, constituent materials, and broadband absorption characteristics. The proposed asymmetric ring-based absorber, utilizing only a single tungsten layer with air as the dielectric, achieves an average absorption of 0.95 across the 300–2000 nm spectral range. Compared to more complex multilayered designs, the current structure offers high performance with a simpler and potentially more manufacturable configuration, making it an attractive candidate for efficient and scalable solar thermal applications.

The etching of tungsten is challenging when using standard wet, dry chemical, or plasma methods. However, several established nanofabrication techniques are capable of producing asymmetric tungsten nanoring structures such as the proposed structure. One practical approach is lift-off lithography, in which the asymmetric ring pattern is first defined in a resist using electron-beam lithography (EBL) or nanoimprint lithography, followed by tungsten deposition via sputtering or electron-beam evaporation and subsequent lift-off, thereby avoiding tungsten etching. Alternatively, the second approach is atomic layer deposition–assisted templating (ALD-assisted), where tungsten or tungsten nitride is conformally deposited onto an asymmetric polymer or hydrogen silsesquioxane (HSQ) mold, followed by directional etching and template removal. A third viable route is a Damascene-style process: asymmetric ring trenches are patterned into a dielectric layer, filled with chemically vapor-deposited tungsten, and then planarized by chemical–mechanical polishing, again eliminating the need for tungsten etches. For laboratory-scale prototypes, focused ion beam milling (FIB) or FIB–induced tungsten deposition provides a direct-write method capable of producing complex asymmetric ring geometries. Together, these approaches demonstrate that the proposed structures are compatible with existing nanofabrication capabilities [68,69,70].

In practical implementations, the performance of the proposed nanowire absorber may be influenced by fabrication tolerances and thermal effects. Dimensional variations on the order of ±5–10 nm can introduce slight shifts in the resonance wavelengths; however, our analysis indicates that such perturbations do not substantially degrade the broadband absorption performance, owing to the intrinsically wide resonance bandwidth of the design.

Tungsten offers excellent thermal stability due to its high melting point (3420 °C) and strong corrosion resistance. Nevertheless, oxidation may occur at elevated temperatures in oxygen-containing environments, potentially modifying the surface optical properties and thereby affecting the absorber’s spectral response. To mitigate these effects and enhance long-term durability, thin protective coatings—such as silica (SiO₂)—can be applied to the nanowires. These coatings act as effective diffusion barriers against oxidation while preserving the strong optical absorption, ensuring stable operation of the absorber under realistic high-temperature solar-thermal conditions.

4. Conclusions

A novel structure of an asymmetric ring nanowire array metamaterial has been numerically studied and analyzed using FDTD. The proposed thermal solar absorber exhibits high absorption in the range of 300–1800 nm, with values below 0.09 at longer wavelengths. Selective spectral absorption is achieved through the excitation of SPP and MP modes. As a result, a notable photothermal conversion efficiency of 73.55% is obtained within the studied range. Additionally, the emittance in the mid-infrared spectrum remains below 0.05 at 100 °C. The physical mechanisms underlying the enhanced absorption are explained by impedance matching and an equivalent LC model. Furthermore, the proposed absorber demonstrates angular independence up to 50° for both TM and TE polarization waves. The absorption spectra of the asymmetric ring nanowire array metamaterial using various refractory metals also reflect its high material tolerance.