Beyond “One-Size-Fits-All”: Estimating Driver Attention with Physiological Clustering and LSTM Models
Abstract
1. Introduction
1.1. Similar Studies
1.1.1. Research Gap and Contributions
1.1.2. Approach
1.1.3. Research Questions and Hypotheses
- R1: Does clustering of physiological time series using time-series k-means offer an advantage in predicting the level of attention compared to global or random clustering?
- R2: Can it be shown that membership in the obtained clusters does not directly depend on demographic variables such as age, gender, or years of experience, but instead on the observed physiological and behavioral dynamics?
- H1: Cluster-specialized models, defined using time-series k-means, achieve higher predictive performance than global models and models trained with random clustering.
- H2: Participant assignment to clusters is not explained by demographic characteristics, but by physiological and behavioral patterns.
2. Methodology
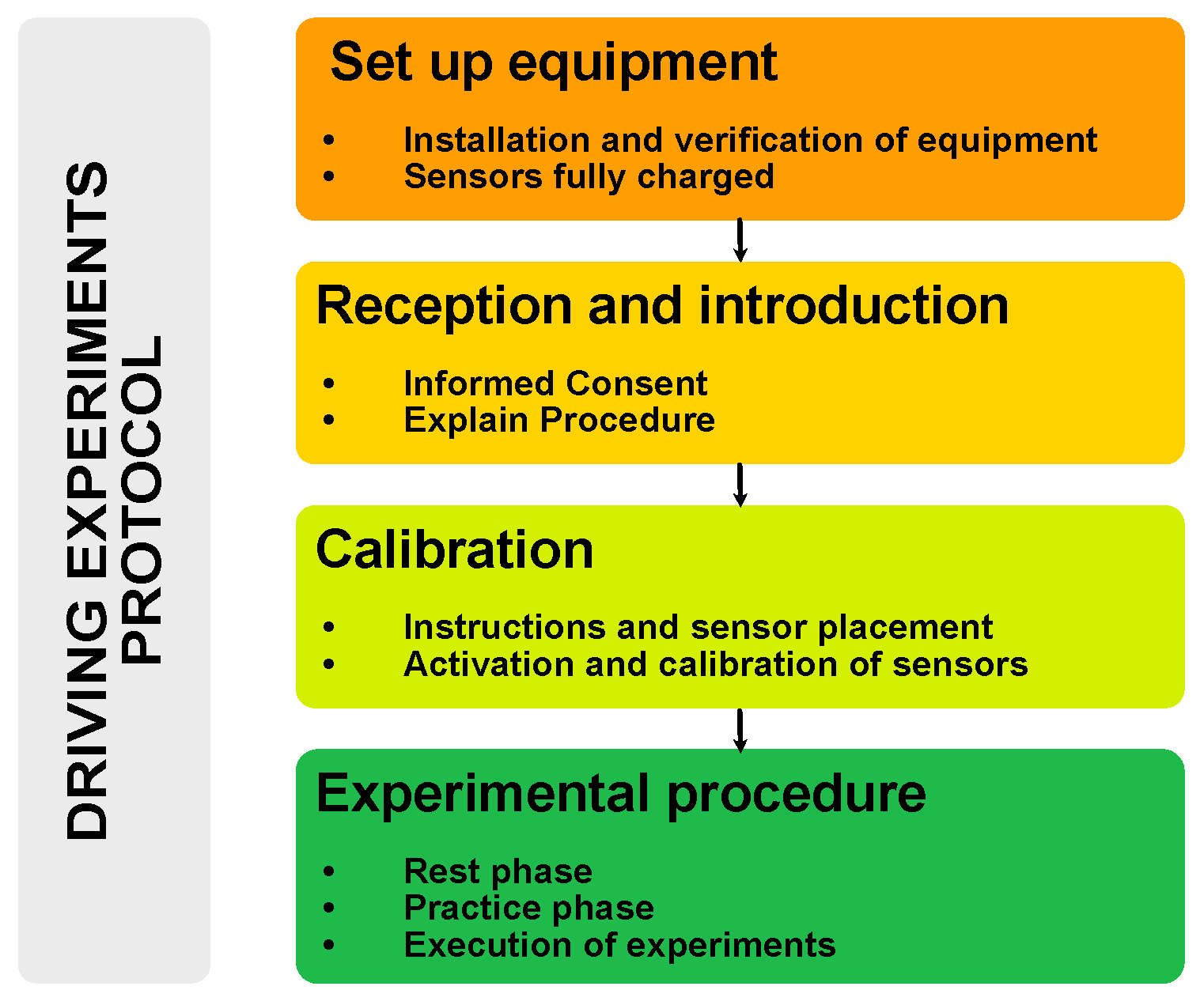
2.1. Structure of the Test Protocol
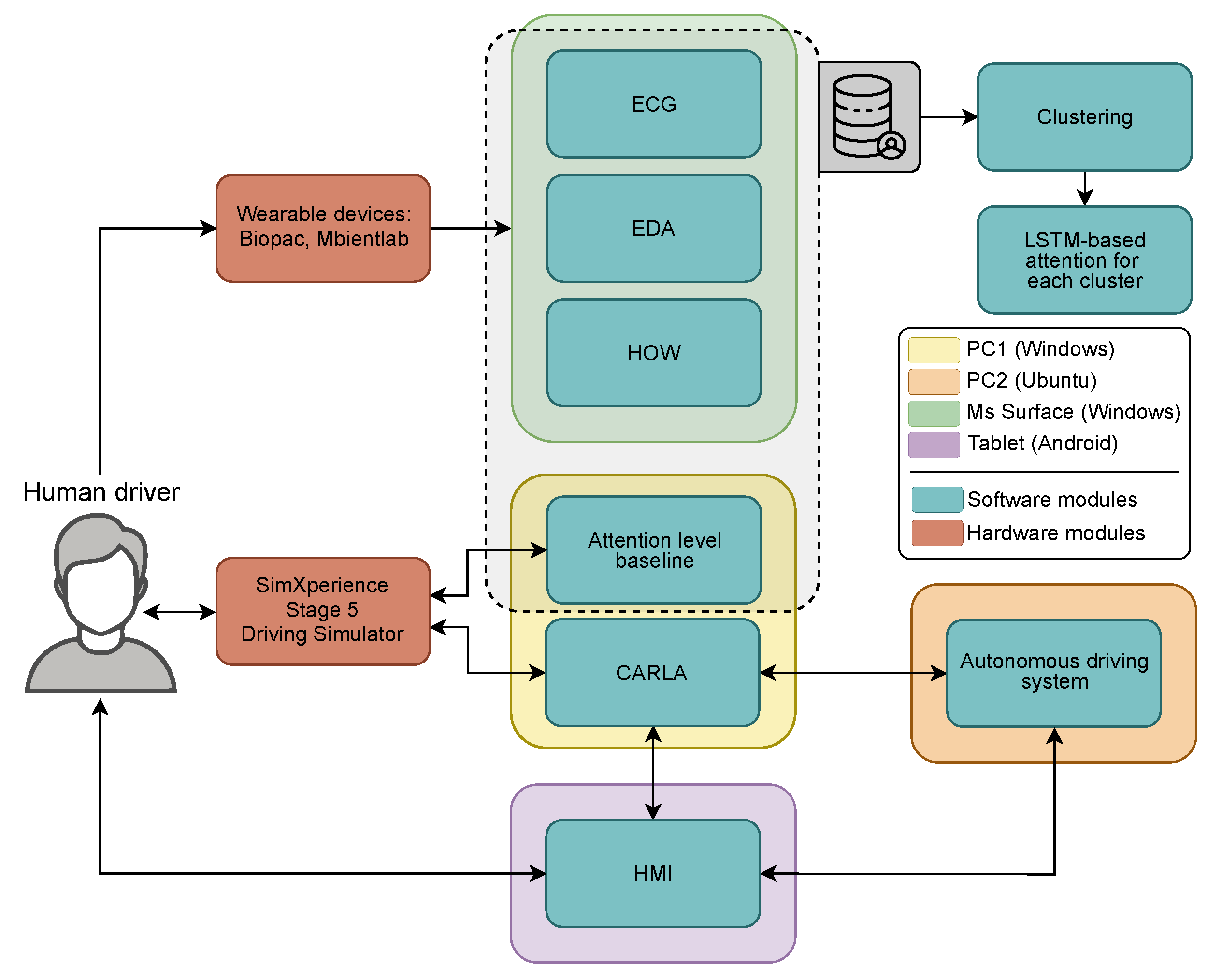
2.2. Technologies and Equipment Used
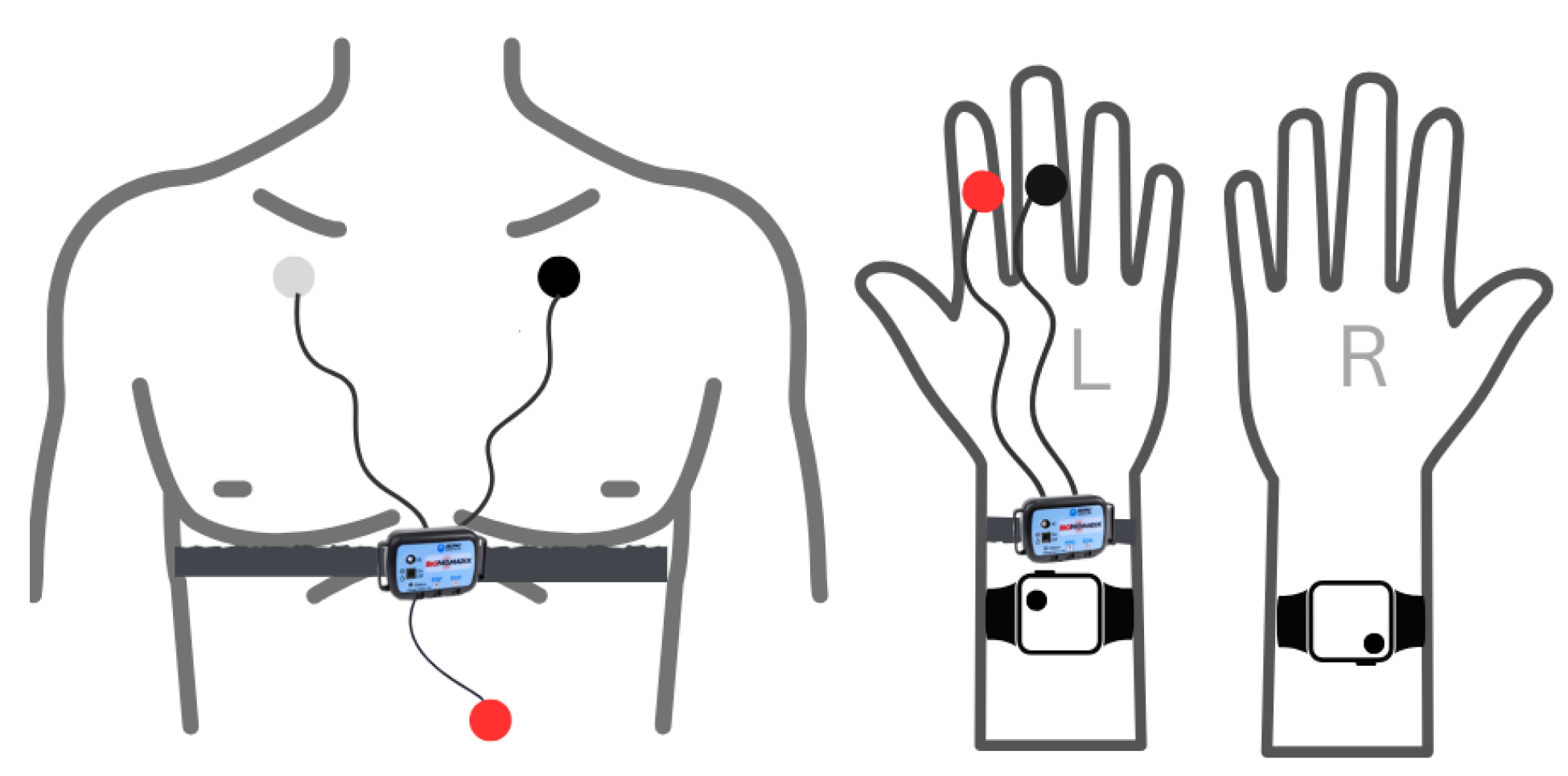
- Electrocardiogram (ECG): Data were acquired using Biopac Bionomadix wireless device RSP&ECG (Model BN-RSPEC-TGED-T) sensors, placed on the chest in a Lead I configuration. These sensors were connected via BN-EL45-LEAD3 cables to electrodes pre-gelled with conductive gel. The red, black, and white electrodes corresponded to the positive (E+), negative (E−), and ground (GND) inputs, respectively (Figure 6 chest placement).
- Electrodermal Activity (EDA): Measurements were taken using a Bionomadix PPG&EDA (Model BN-PPGED-T) sensor. This sensor, connected via a BN-EDA25-LEAD2 cable, utilized electrodes affixed to the index and middle fingers of the left hand (Figure 6 hand placement).
2.3. Description of Data Acquisition and Computational Equipment
- Physiological Signals (ECG and EDA): The signals were acquired in real time. Data were streamed continuously during the experiment and stored in raw .csv format for offline analysis. A custom-designed graphical interface was used for live monitoring, buffering, and data export.Signal processing and feature extraction were performed using NeuroKit2 (v0.2.11) (Python) and supplementary MATLAB (R2020b, Update 7) routines. The preprocessing pipeline included noise reduction, signal normalization, and event detection—specifically R-peak identification for ECG and skin conductance response (SCR) peak detection for EDA. Signals were segmented into fixed-length windows (1 min), and features were extracted to quantify physiological states associated with stress, arousal, and cognitive workload.The extracted features include widely used psychophysiological metrics. For example, RMSSD (Root Mean Square of Successive Differences) and SDNN (Standard Deviation of NN intervals) are time-domain indicators of heart rate variability (HRV), commonly associated with parasympathetic nervous system activity and emotional regulation. Similarly, the LF/HF ratio (Low-Frequency to High-Frequency power ratio) is a frequency-domain HRV metric frequently used as a marker of sympathetic–vagal balance. In electrodermal activity, SCL (skin conductance level) reflects tonic arousal, while SCR (skin conductance response) quantifies phasic responses to discrete stimuli or cognitive shifts. These features serve as core inputs for downstream modeling of driver attention and state classification. For a more detailed overview of the physiological metrics and their interpretation, see [29,30,31].
- Inertial Motion Data (IMU): MetaWear sensors (MbientLab Inc., San Jose, CA, USA) on both wrists recorded accelerometer, gyroscope, and quaternion values from both wrists at 10 Hz. This data enabled hands-on-wheel detection, processed via LSTM-based deep learning models. The IMU logs were labeled with binary contact states and exported as structured CSV files. More details on this model can be found in [32].
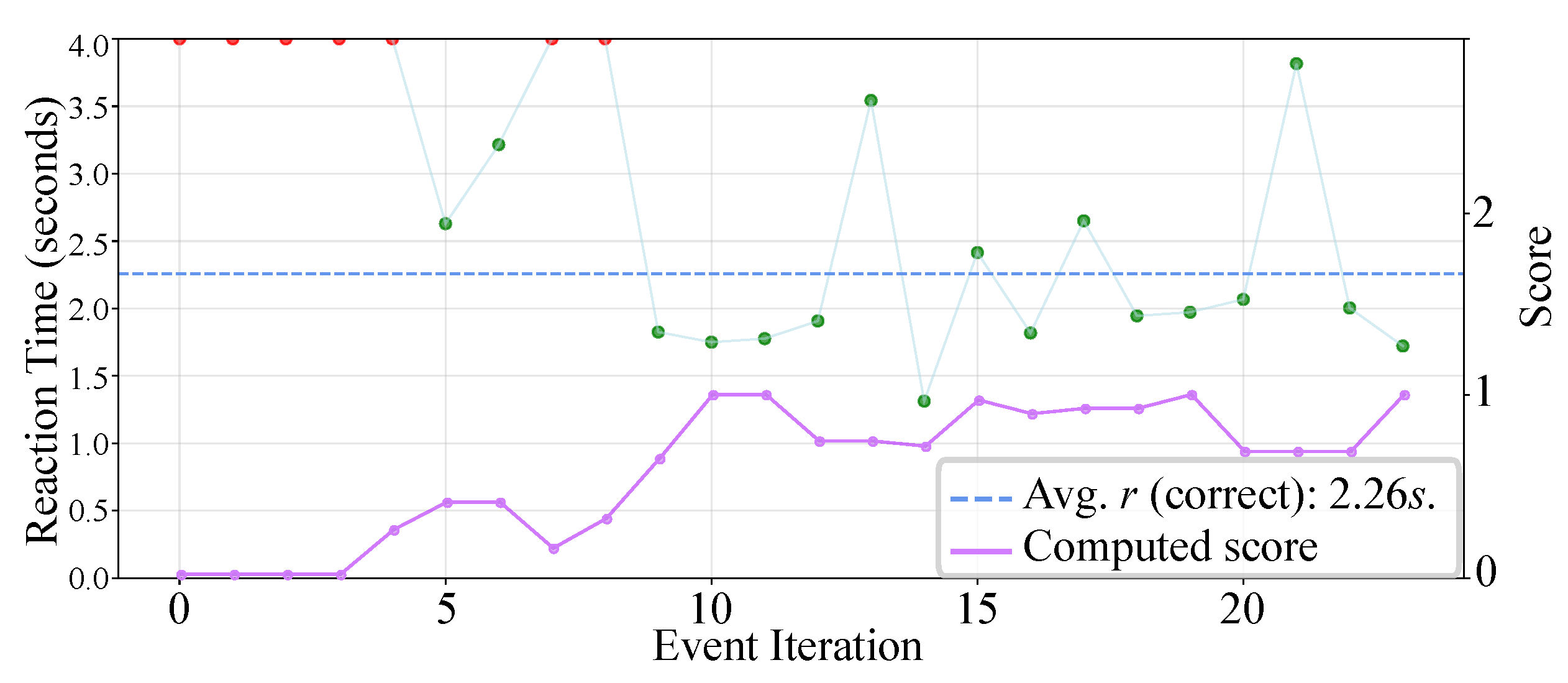
- Attention Logs: As illustrated in Figure 3, participants responded to visual stimuli through a gear-shift lever, with each interaction automatically recorded in .json files including both response time and accuracy. Each recorded response was subsequently scored and categorized into discrete attention levels—focused, semi-distracted, or distracted. These attention labels were then resampled and temporally synchronized with the physiological signals at 1s intervals to facilitate data fusion and training processes.
- Simulator and Vehicle State Logs: The simulator environment recorded continuous data on vehicle trajectory, speed, TOR events, traffic objects, and user control inputs. These logs were structured via a Lightweight Communications and Marshaling (LCM) framework and timestamped for alignment.
2.4. Participants
3. Data Processing and Modeling Framework
3.1. Physiological Feature Preprocessing
3.2. ANOVA
3.3. Feature Selection
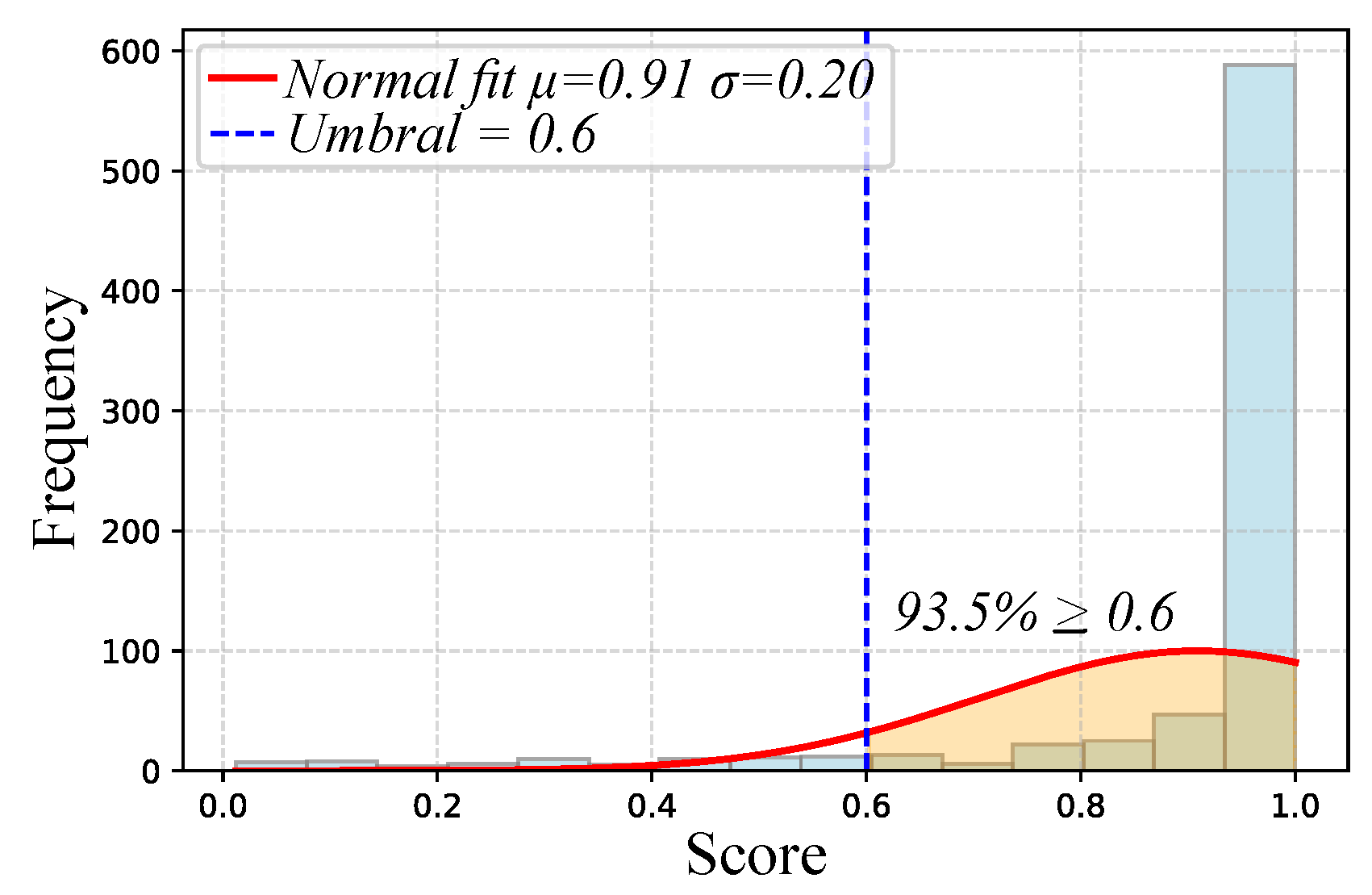
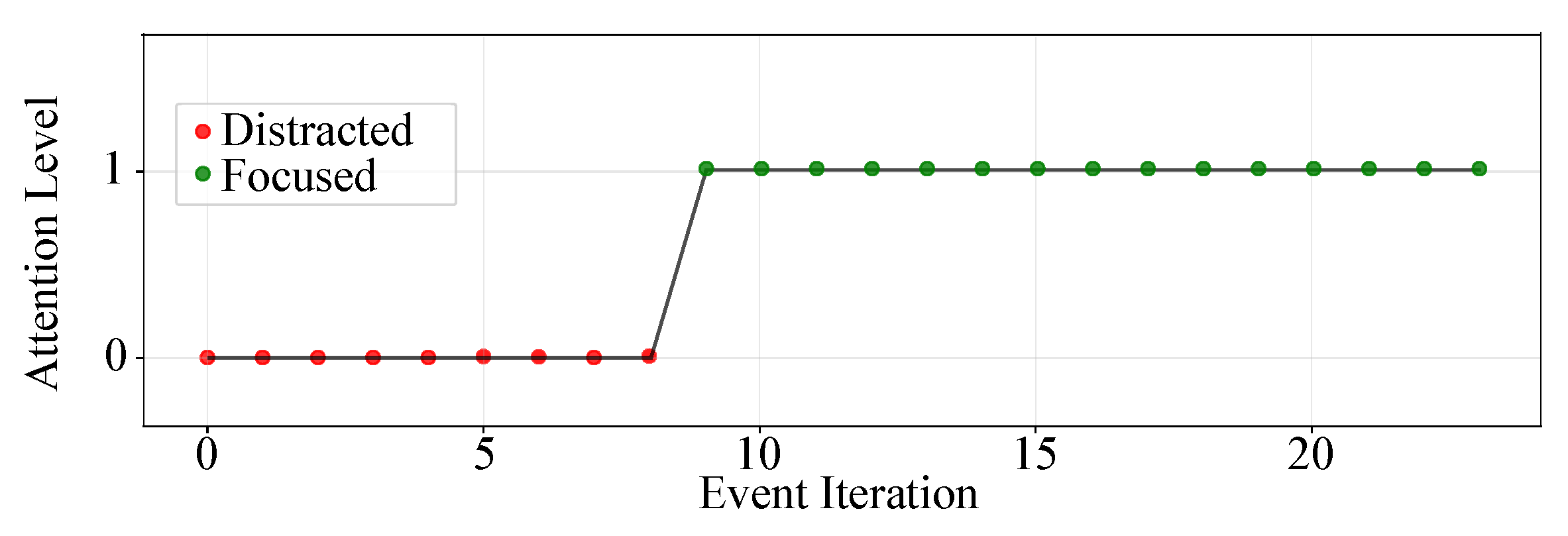
3.4. Attention Level Preprocessing
Hands-on-Wheel Prediction Feature Preprocessing
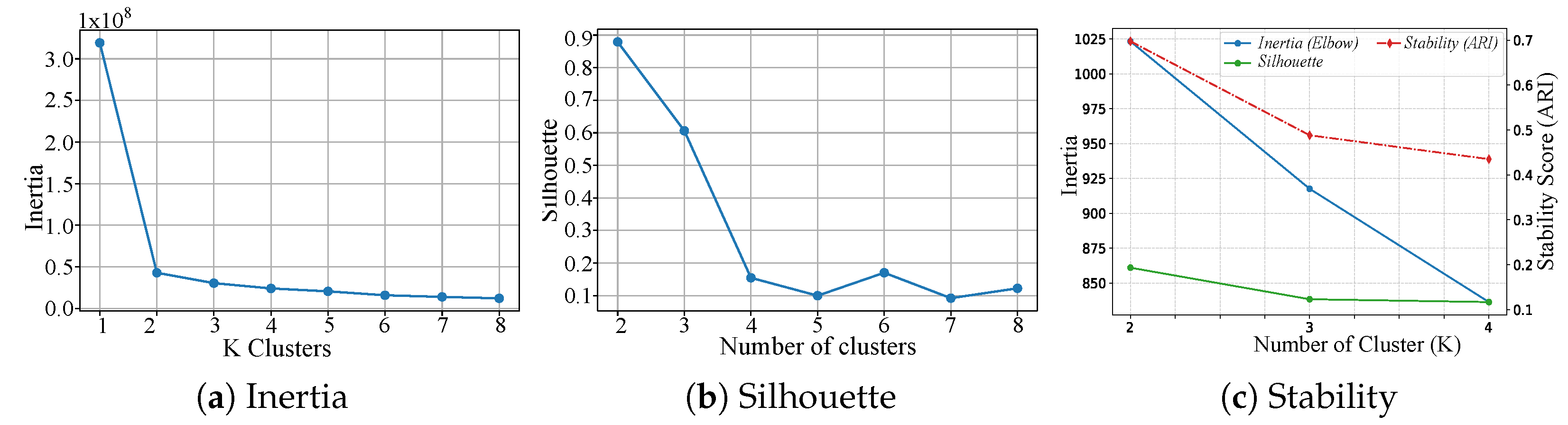
3.5. Time-Series k-Means Clustering
3.6. Model Architecture and Hyperparameter Optimization
3.6.1. Random Forest and Support Vector Machine
3.6.2. Long Short-Term Memory Architecture
3.6.3. Bayesian Optimization
4. Results
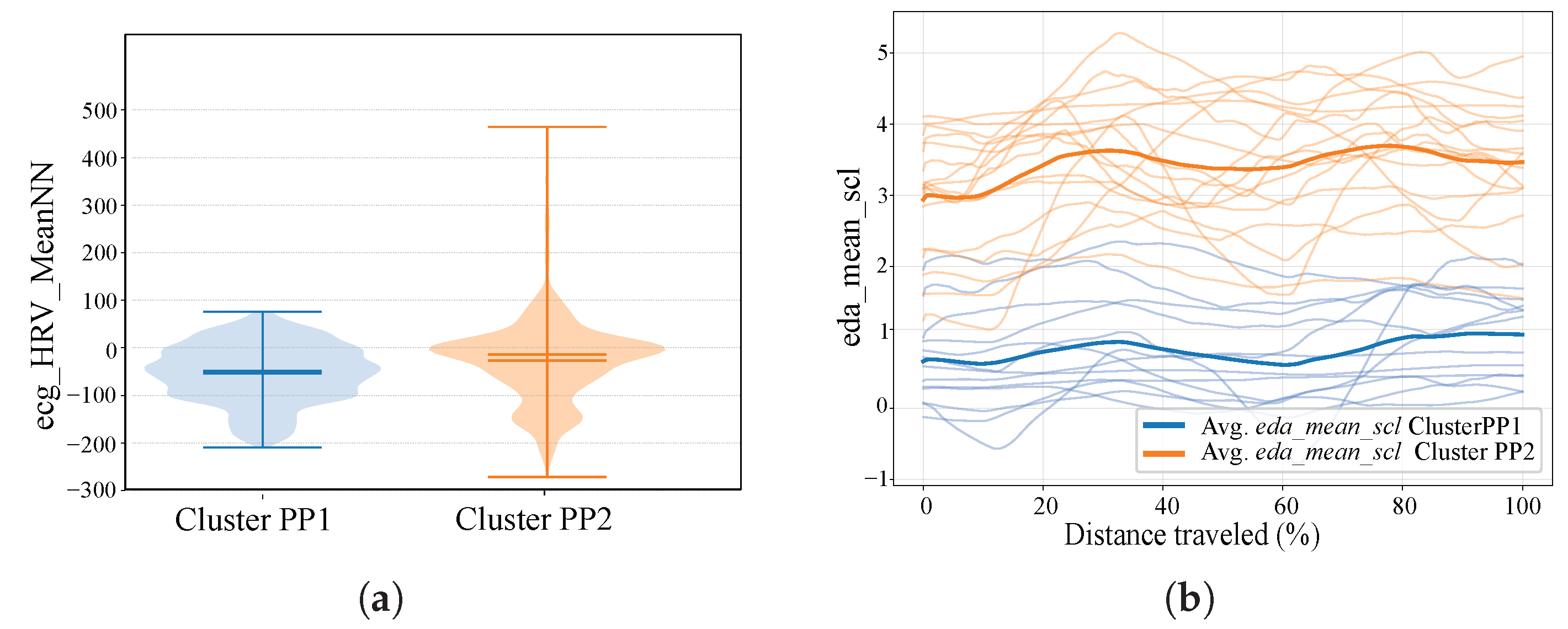
4.1. Clustering
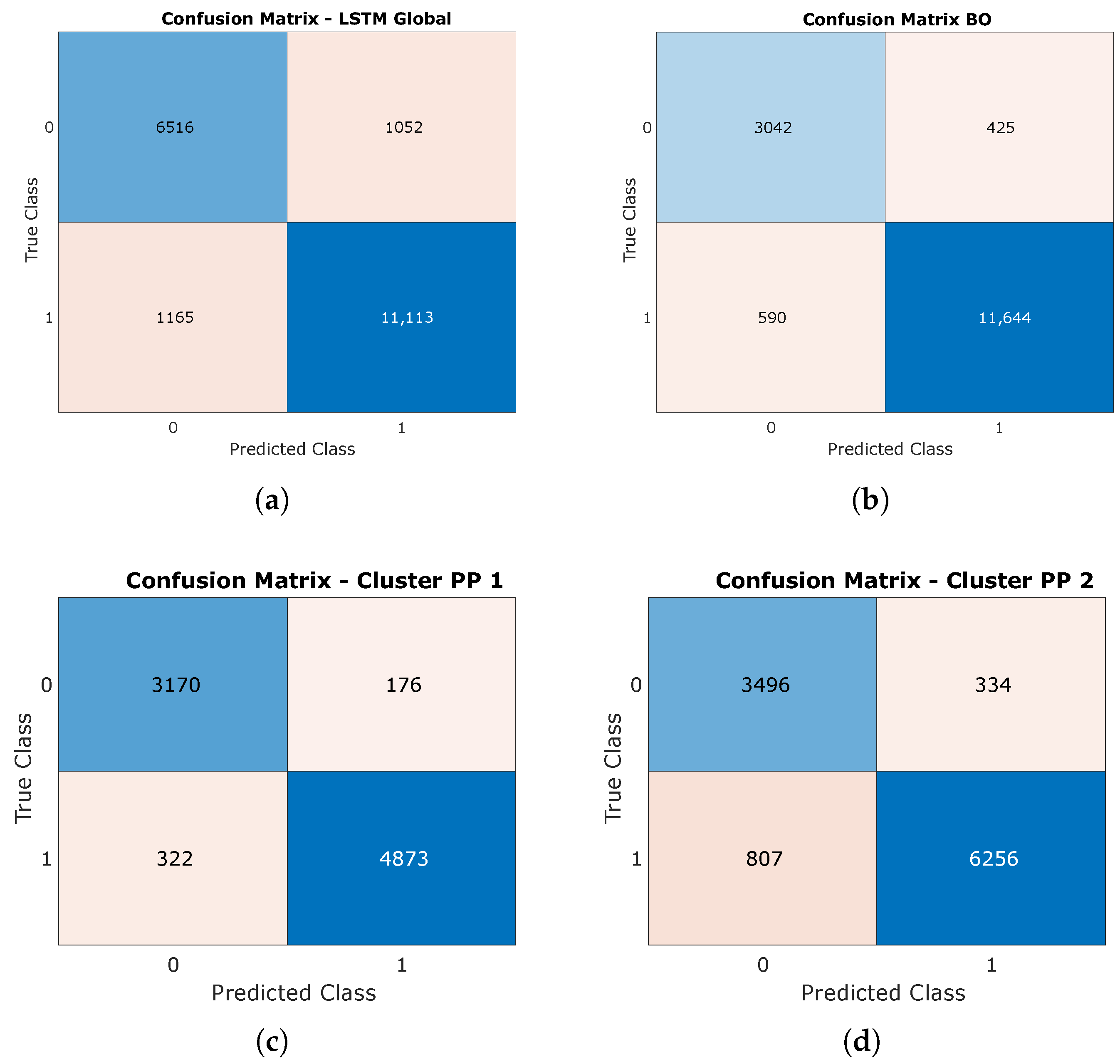
4.2. Results of Bayesian Optimization
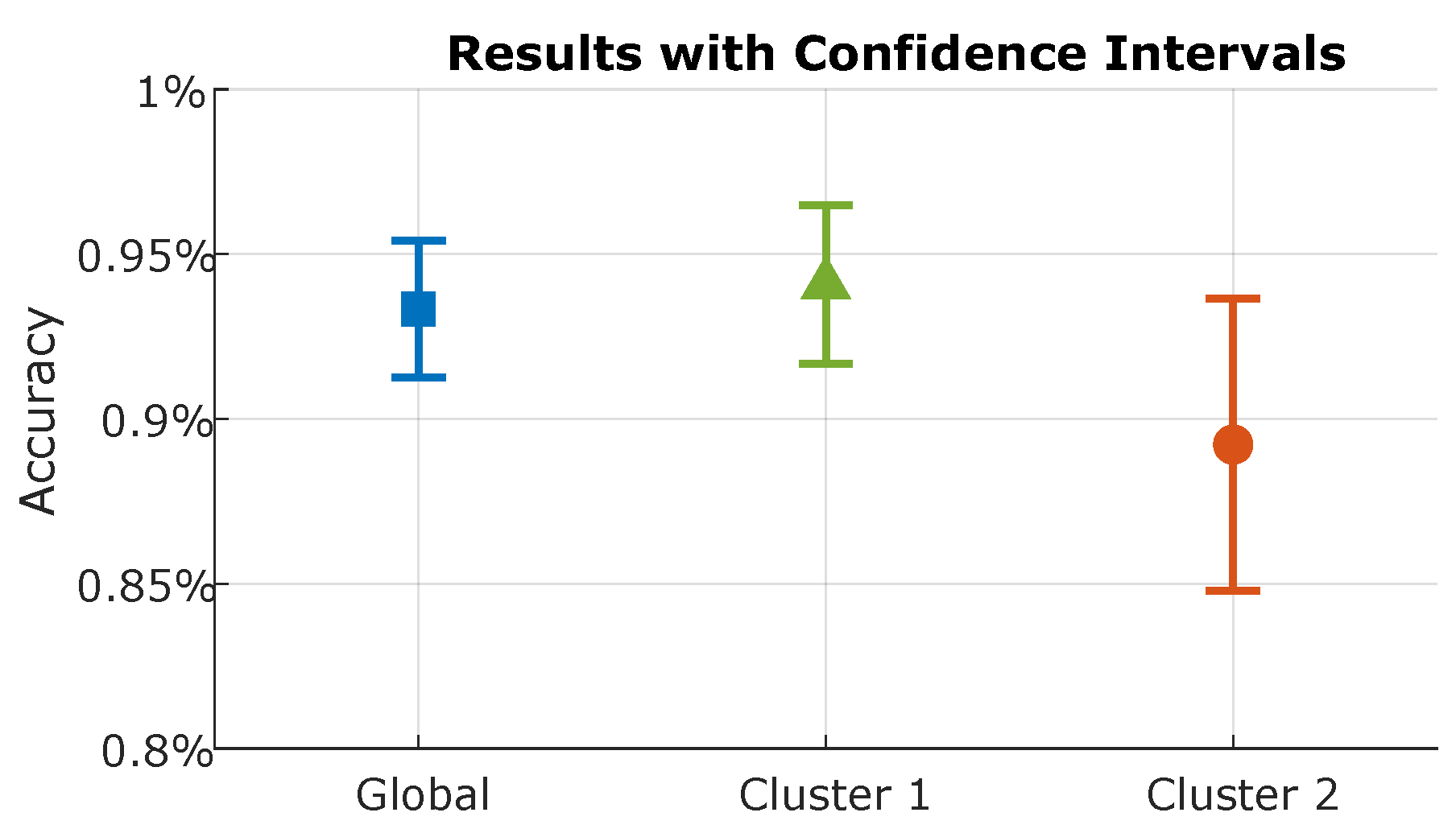
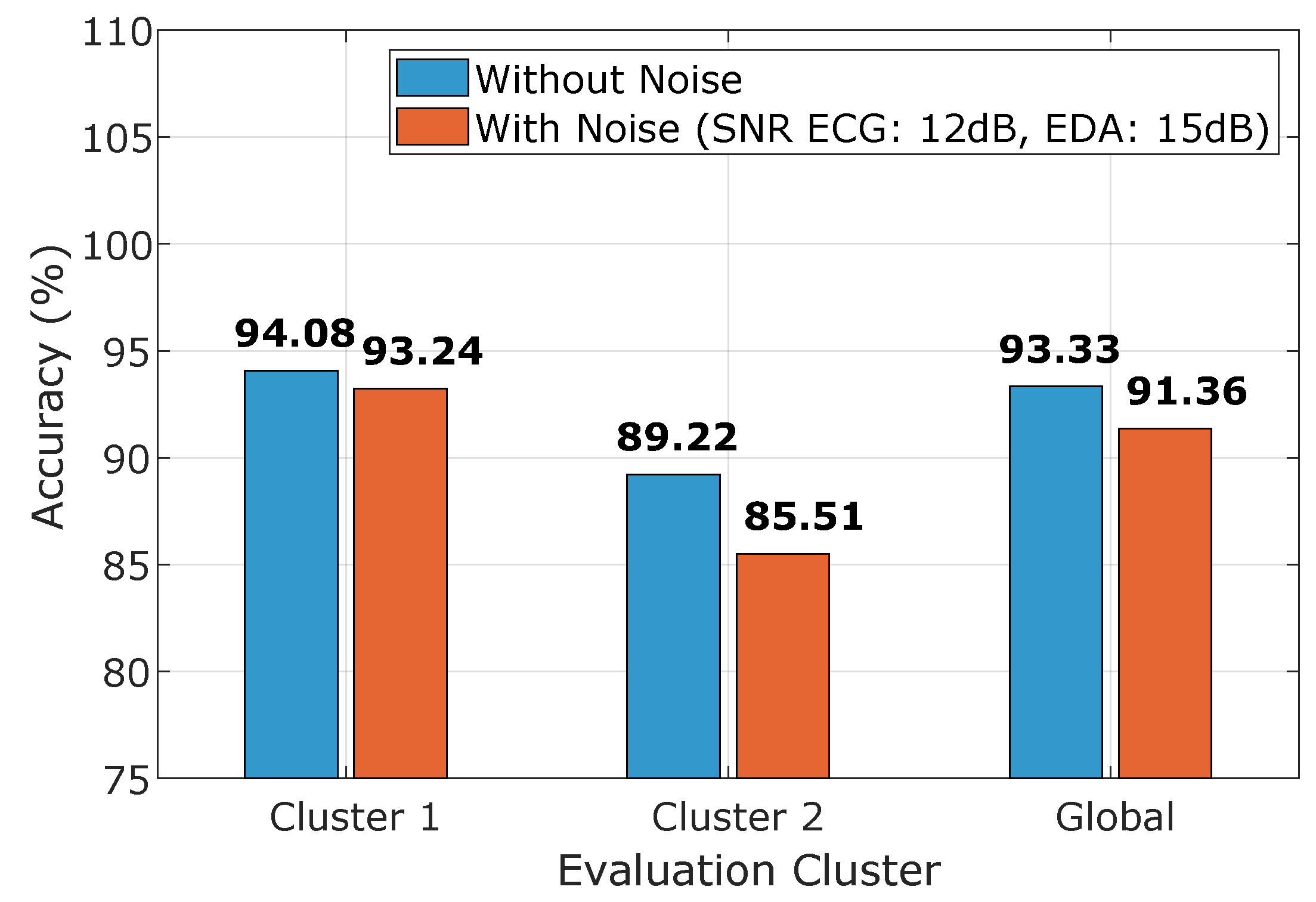
4.3. LSTM Results
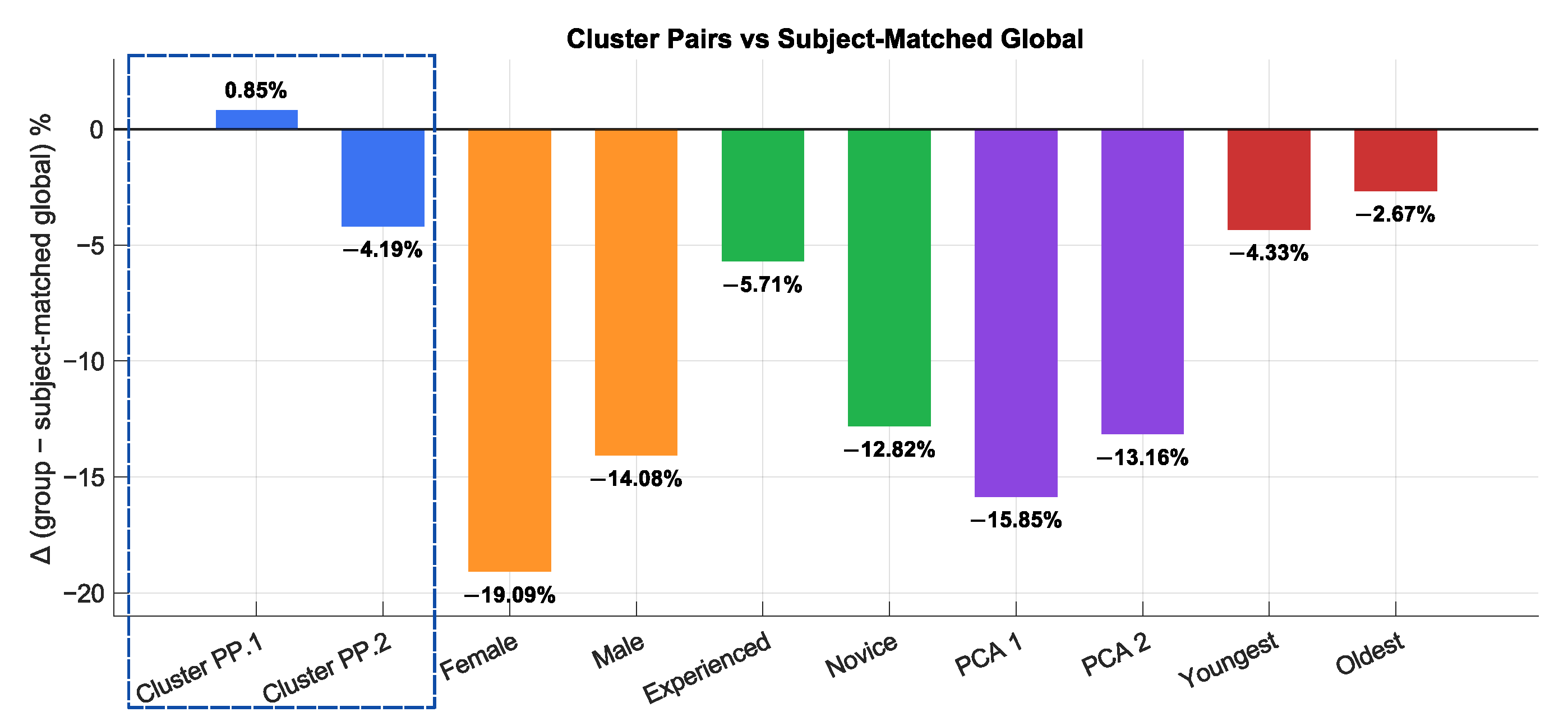
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BILSTM | Bidirectional LSTM |
| BO | Bayesian optimization |
| CARLA | Car Learning to Act |
| DTW | Dynamic time warping |
| ECG | Electrocardiogram |
| EDA | Electrodermal activity |
| FR | Frequency |
| HF | High frequency |
| HMI | Human–machine interface |
| HOW | Hands on wheel |
| HRV | Heart rate variability |
| IMU | Inertial motion data |
| LCM | Lightweight Communications and Marshaling |
| LF | Low frequency |
| LSTM | Long Short-Term Memory |
| LOSO | Leave-One-Subject-Out |
| PCA | Principal component analysis |
| PP | Physiological parameter |
| RMSSD | Root Mean Square of Successive Differences |
| SCL | Skin conductance level |
| SCR | Skin conductance response |
| SDNN | Standard deviation of NN intervals |
| TOR | Takeover requests |
References
- Aminosharieh Najafi, T.; Affanni, A.; Rinaldo, R.; Zontone, P. Driver attention assessment using physiological measures from EEG, ECG, and EDA signals. Sensors 2023, 23, 2039. [Google Scholar] [CrossRef] [PubMed]
- Veluchamy, S.; Michael Mahesh, K.; Muthukrishnan, R.; Karthi, S. HY-LSTM: A new time series deep learning architecture for estimation of pedestrian time to cross in advanced driver assistance system. J. Vis. Commun. Image Represent. 2023, 97, 103982. [Google Scholar] [CrossRef]
- Kashevnik, A.; Lashkov, I.; Ponomarev, A.; Teslya, N.; Gurtov, A. Cloud-based driver monitoring system using a smartphone. IEEE Sens. J. 2020, 20, 6701–6715. [Google Scholar] [CrossRef]
- Schwarz, C.; Gaspar, J.; Miller, T.; Yousefian, R. The detection of drowsiness using a driver monitoring system. Traffic Inj. Prev. 2019, 20, S157–S161. [Google Scholar] [CrossRef]
- Daza, I.G.; Bergasa, L.M.; Bronte, S.; Yebes, J.J.; Almazán, J.; Arroyo, R. Fusion of optimized indicators from Advanced Driver Assistance Systems (ADAS) for driver drowsiness detection. Sensors 2014, 14, 1106–1131. [Google Scholar] [CrossRef]
- SAE International. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles (Surface Vehicle Recommended Practice: Superseding J3016 sep 2016); Technical report; SAE International: Warrendale PA, USA, 2016. [Google Scholar]
- Gold, C.; Körber, M.; Lechner, D.; Bengler, K. Taking Over Control From Highly Automated Vehicles in Complex Traffic Situations: The Role of Traffic Density. Hum. Factors 2016, 58, 642–652. [Google Scholar] [CrossRef]
- Kumar, M.; Weippert, M.; Vilbrandt, R.; Kreuzfeld, S.; Stoll, R. Fuzzy evaluation of heart rate signals for mental stress assessment. IEEE Trans. Fuzzy Syst. 2007, 15, 791–808. [Google Scholar] [CrossRef]
- Noh, Y.; Kim, S.; Jang, Y.J.; Yoon, Y. Modeling individual differences in driver workload inference using physiological data. Int. J. Automot. Technol. 2021, 22, 201–212. [Google Scholar] [CrossRef]
- Nezamabadi, K.; Sardaripour, N.; Haghi, B.; Forouzanfar, M. Unsupervised ECG Analysis: A Review. IEEE Rev. Biomed. Eng. 2023, 16, 208–224. [Google Scholar] [CrossRef]
- Collet, C.; Clarion, A.; Morel, M.; Chapon, A.; Petit, C. Physiological and behavioural changes associated to the management of secondary tasks while driving. Appl. Ergon. 2009, 40, 1041–1046. [Google Scholar] [CrossRef]
- Shajari, A.; Asadi, H.; Alsanwy, S.; Nahavandi, S.; Lim, C.P. Leveraging Motion Platform Simulator for Detecting Driver Distraction: A CNN-LSTM Approach Integrating Physiological Signal and Head Motion Analysis. In Proceedings of the Neural Information Processing. ICONIP 2024, Auckland, New Zealand, 2–6 December 2024; Mahmud, M., Doborjeh, M., Wong, K., Leung, A.C.S., Doborjeh, Z., Tanveer, M., Eds.; Communications in Computer and Information Science. Springer Nature: Singapore, 2025; Volume 2284. [Google Scholar] [CrossRef]
- Papakostas, M.; Das, K.; Abouelenien, M.; Mihalcea, R.; Burzo, M. Distracted and Drowsy Driving Modeling Using Deep Physiological Representations and Multitask Learning. Appl. Sci. 2021, 11, 88. [Google Scholar] [CrossRef]
- Chen, L.; Li, D.; Wang, T.; Chen, J.; Yuan, Q. Driver Takeover Performance Prediction Based on LSTM-BiLSTM-ATTENTION Model. Systems 2025, 13, 46. [Google Scholar] [CrossRef]
- Li, H.; Lin, Z.; An, Z.; Zuo, S.; Zhu, W.; Zhang, Z.; Mu, Y.; Cao, L.; Prades García, J.D. Automatic electrocardiogram detection and classification using bidirectional long short-term memory network improved by Bayesian optimization. Biomed. Signal Process. Control 2022, 73, 103424. [Google Scholar] [CrossRef]
- Kumar, P.S.; Ramasamy, M.; Kallur, K.R.; Rai, P.; Varadan, V.K. Personalized LSTM Models for ECG Lead Transformations Led to Fewer Diagnostic Errors Than Generalized Models: Deriving 12-Lead ECG from Lead II, V2, and V6. Sensors 2023, 23, 1389. [Google Scholar] [CrossRef]
- Riboni, A.; Ghioldi, N.; Candelieri, A.; Borrotti, M. Bayesian Optimization and Deep Learning for Steering Wheel Angle Prediction. Sci. Rep. 2022, 12, 8739. [Google Scholar] [CrossRef]
- Amre, S.M.; Steelman, K.S. Keep your hands on the wheel: The effect of driver supervision strategy on change detection, mind wandering, and gaze behavior. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Washington, DC, USA, 23–27 October 2023; Volume 67, pp. 1214–1220. [Google Scholar] [CrossRef]
- Wu, Y.; Hasegawa, K.; Kihara, K. How to request drivers to prepare for takeovers during automated driving. Transp. Res. Part F Traffic Psychol. Behav. 2025, 109, 938–950. [Google Scholar] [CrossRef]
- Ariff, N.M.; Bakar, M.A.A.; Lim, H.Y. Prediction of PM10 concentration in Malaysia using k-means clustering and LSTM hybrid model. Atmosphere 2023, 14, 853. [Google Scholar] [CrossRef]
- Masood, Z.; Gantassi, R.; Ardiansyah; Choi, Y. A Multi-Step Time-Series Clustering-Based Seq2Seq LSTM Learning for a Single Household Electricity Load Forecasting. Energies 2022, 15, 2623. [Google Scholar] [CrossRef]
- Kubota, K.; Togo, R.; Maeda, K.; Ogawa, T.; Haseyama, M. Balancing generalization and personalization by sharing layers in clustered federated learning. In Proceedings of the International Workshop on Advanced Imaging Technology (IWAIT), Douliu City, Taiwan, 5 February 2025; SPIE: Douliu City, Taiwan, 2025; Volume 13510, pp. 112–116. [Google Scholar]
- Benedetto, S.; Pedrotti, M.; Minin, L.; Baccino, T.; Re, A.; Montanari, R. Driver workload and eye blink duration. TRansportation Res. Part F Traffic Psychol. Behav. 2011, 14, 199–208. [Google Scholar] [CrossRef]
- Kazemi, M.; Rezaei, M.; Azarmi, M. Evaluating Driver Readiness in Conditionally Automated Vehicles From Eye-Tracking Data and Head Pose. IET Intell. Transp. Syst. 2025, 19, e70006. [Google Scholar] [CrossRef]
- Sahayadhas, A.; Sundaraj, K.; Murugappan, P. Driver inattention detection methods: A review. In Proceedings of the 2012 IEEE Conference on Sustainable Utilization and Development in Engineering and Technology (STUDENT), Kuala Lumpur, Malaysia, 6–9 October 2012; Volume 10, pp. 1–6. [Google Scholar] [CrossRef]
- CARLA Team. CARLA Simulator. 2025. Available online: https://carla.org/ (accessed on 5 August 2025).
- Poggenhans, F.; Pauls, J.H.; Janosovits, J.; Orf, S.; Naumann, M.; Kuhnt, F.; Mayr, M. Lanelet2: A high-definition map framework for the future of automated driving. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1672–1679. [Google Scholar] [CrossRef]
- Medina-Lee, J.; Artuñedo, A.; Godoy, J.; Villagra, J. Merit-based motion planning for autonomous vehicles in urban scenarios. Sensors 2021, 21, 3755. [Google Scholar] [CrossRef] [PubMed]
- Benedek, M.; Kaernbach, C. A continuous measure of phasic electrodermal activity. J. Neurosci. Methods 2010, 190, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, F.; Ginsberg, J.P. An overview of heart rate variability metrics and norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Martinez, A.; Chen, S. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 53, 1689–1696. [Google Scholar] [CrossRef]
- Peña, J.C.; Negroni Santiago, A.; Martínez García, D.; Vásquez, E.; Medina Lee, J.F. Comparative Study of Hands-on-Wheel Detection Using Wearable LSTM and Camera-Based Vision Models for Driver Monitoring. IEEE Int. Conf. Veh. Electron. Saf. 2025, accepted. [Google Scholar]
- Ayata, D.; Yaslan, Y.; Kamasak, M.E. Emotion Recognition from Multimodal Physiological Signals for Emotion Aware Healthcare Systems. J. Med. Biol. Eng. 2020, 40, 149–157. [Google Scholar] [CrossRef]
- Mishra, V.; Sen, S.; Chen, G.; Hao, T.; Rogers, J.; Chen, C.H.; Kotz, D. Evaluating the Reproducibility of Physiological Stress Detection Models. NPJ Digit. Med. 2020, 3, 125. [Google Scholar] [CrossRef]
- Huang, X.; Ye, Y.; Xiong, L.; Lau, R.Y.; Jiang, N.; Wang, S. Time series k-means: A new k-means type smooth subspace clustering for time series data. Inf. Sci. 2016, 367–368, 1–13. [Google Scholar] [CrossRef]
- Maharaj, E.A.; D’Urso, P.; Caiado, J. Time Series Clustering and Classification, 1st ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Von Luxburg, U. Clustering stability: An overview. Found. Trends® Mach. Learn. 2010, 2, 235–274. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ebrahimian, S.; Nahvi, A.; Tashakori, M.; Salmanzadeh, H.; Mohseni, O.; Leppänen, T. Multi-Level Classification of Driver Drowsiness by Simultaneous Analysis of ECG and Respiration Signals Using Deep Neural Networks. Int. J. Environ. Res. Public Health 2022, 19, 10736. [Google Scholar] [CrossRef]
- Mattern, E.; Jackson, R.R.; Doshmanziari, R.; Dewitte, M.; Varagnolo, D.; Knorn, S. Emotion Recognition from Physiological Signals Collected with a Wrist Device and Emotional Recall. Bioengineering 2023, 10, 1308. [Google Scholar] [CrossRef]
- Gholamiangonabadi, D.; Kiselov, N.; Grolinger, K. Deep Neural Networks for Human Activity Recognition With Wearable Sensors: Leave-One-Subject-Out Cross-Validation for Model Selection. IEEE Access 2020, 8, 133982–133994. [Google Scholar] [CrossRef]
- Kunjan, S.; Grummett, T.S.; Pope, K.J.; Powers, D.M.W.; Fitzgibbon, S.P.; Bastiampillai, T.; Battersby, M.; Lewis, T.W. The Necessity of Leave One Subject Out (LOSO) Cross Validation for EEG Disease Diagnosis. In Proceedings of the Brain Informatics, Virtual Event, 17–19 September 2021; Mahmud, M., Kaiser, M.S., Vassanelli, S., Dai, Q., Zhong, N., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 558–567. [Google Scholar]
- Masuda, N.; Yairi, I.E. Multi-Input CNN-LSTM deep learning model for fear level classification based on EEG and peripheral physiological signals. Front. Psychol. 2023, 14, 1141801. [Google Scholar] [CrossRef] [PubMed]
- Dhake, H.; Kashyap, Y.; Kosmopoulos, P. Algorithms for Hyperparameter Tuning of LSTMs for Time Series Forecasting. Remote Sens. 2023, 15, 2076. [Google Scholar] [CrossRef]
- Vo, H.T.; Ngoc, H.T.; Quach, L.D. An Approach to Hyperparameter Tuning in Transfer Learning for Driver Drowsiness Detection Based on Bayesian Optimization and Random Search. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 828–837. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- MathWorks. Bayesian Optimization Algorithm—Statistics and Machine Learning Toolbox; MathWorks, Inc.: Natick, MA, USA, 2025. [Google Scholar]
- Greco, A.; Valenza, G.; Scilingo, E. Advances in Electrodermal Activity Processing with Applications for Mental Health; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Mohd Apandi, Z.F.; Ikeura, R.; Hayakawa, S.; Tsutsumi, S. An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance. Bioengineering 2020, 7, 53. [Google Scholar] [CrossRef]
- Moody, G.B.; Muldrow, W.; Mark, R.G. A noise stress test for arrhythmia detectors. Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
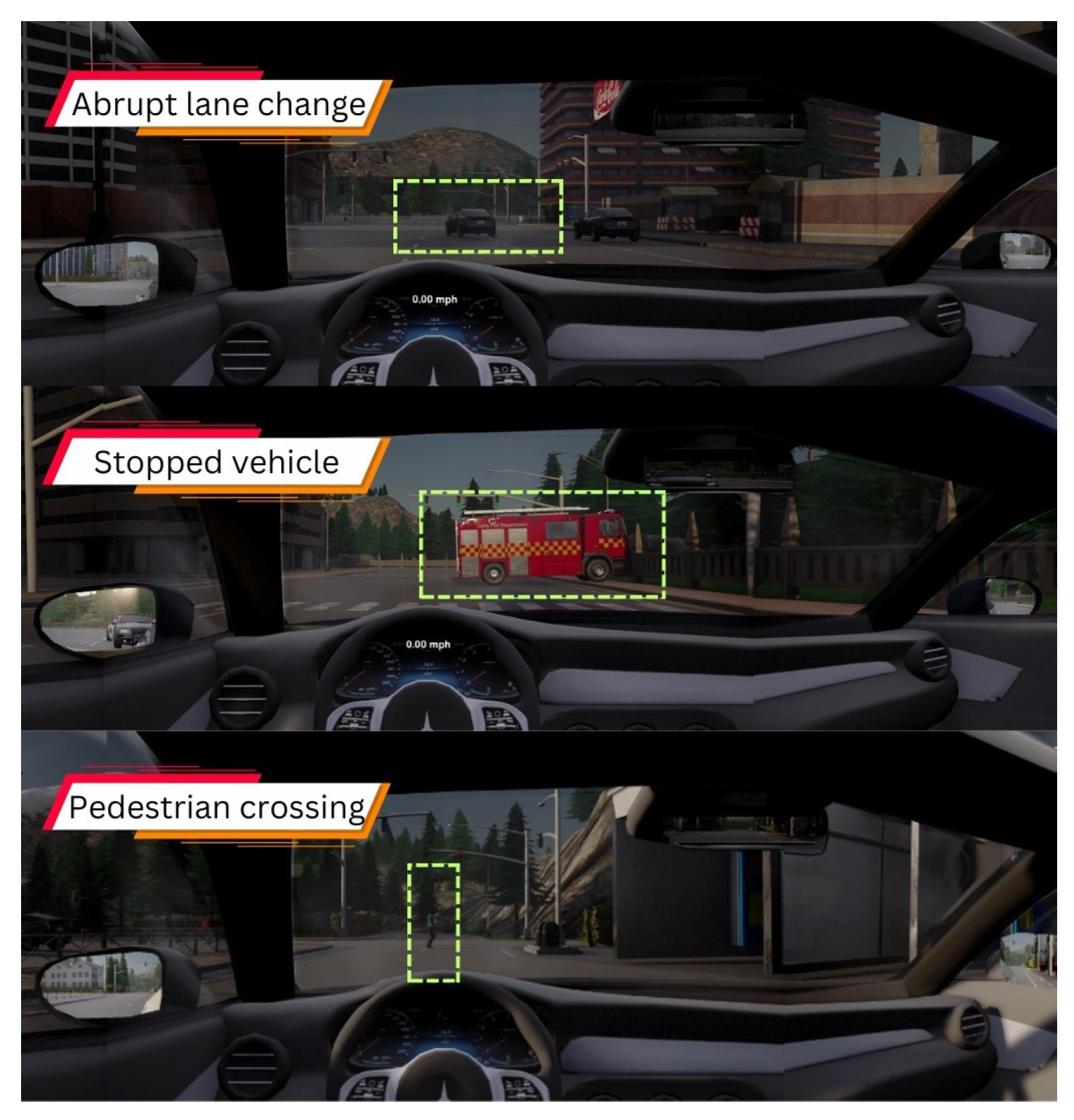



| Exp. | CARLA Town | Environment | TOR Urgency Level | Concentration Level | Scenarios | TOR Time | EXP. Time |
|---|---|---|---|---|---|---|---|
| 1 | 4 | Semi-urban | Low/high | Focused/distracted | Abrupt lane change, pedestrian crossing, obstacle in the road/stopped vehicle | ||
| 2 | 5 | Urban | Low/high/critical | Focused/distracted | Obstruction by stopped vehicle, traffic accident, dynamic obstacle in lane |
| Signal Type | Feature Category | Extracted Features |
|---|---|---|
| ECG | HRV–Time Domain | MeanNN, SDNN, RMSSD, MedianNN, MadNN, MinNN, MaxNN, pNN50 |
| HRV–Frequency Domain | LF, HF, LF/HF ratio | |
| HRV–Nonlinear | SD1, SD2, SD1/SD2 ratio, Approximate Entropy (ApEn) | |
| EDA | Tonic (SCL) | Mean SCL, Max SCL, Min SCL, SCL Slope, SCL Std, Variance, Energy |
| Phasic (SCR) | SCR Count, SCR Rate, Mean Amplitude, Max Amplitude, Amplitude Std | |
| Statistical | Mean Diff, Max Diff between successive values | |
| IMU (MetaWear) | Raw Motion Data | Linear Acceleration (X, Y, Z), Angular Velocity (X, Y, Z), Quaternion (W, X, Y, Z) |
| Behavioral State Label | Hands-on-Wheel binary label (1 = contact, 0 = no contact) | |
| Attention Logs | Attentional Score | Coded values based on visual stimulus (0 = distracted, [0.6–1.0] = semi-distracted, 2 = focused) |
| Simulator Logs | Vehicle and Scenario State | Speed, Control Mode, Planner State, Obstacle Proximity, TOR trigger timestamps |
| Variable | Category | General (100%) | GR1 | GR2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FR# | % | Stats | FR# | % | Stats | FR# | % | Stats | ||
| Gender | Male (M) | 19 | 63.3 | – | 10 | 66.7 | – | 9 | 60 | – |
| Female (F) | 11 | 36.7 | – | 5 | 33.3 | – | 6 | 40 | – | |
| Age (years) | Min | - | - | 22 | - | - | 23 | - | - | 22 |
| Max | - | - | 71 | - | - | 71 | - | - | 70 | |
| Mean | - | - | 36 | - | - | 36.33 | - | - | 35.87 | |
| Median | - | - | 33.5 | - | - | 33 | - | - | 34 | |
| SD | - | - | 12.7 | - | - | 12.73 | - | - | 12.62 | |
| Driving Experience (Years) | Min | - | - | 0.6 | - | - | 1 | - | - | 0.6 |
| Max | - | - | 55 | - | - | 50 | - | - | 55 | |
| Mean | - | - | 14.95 | - | - | 14.13 | - | - | 15.77 | |
| Median | - | - | 8.5 | - | - | 7 | - | - | 13 | |
| SD | - | - | 14.33 | - | - | 13.81 | - | - | 14.78 | |
| Previous Autonomous Driving Experience | Yes (Y) | 4 | 13.3 | – | 2 | 13.3 | – | 2 | 13.3 | – |
| No (N) | 26 | 86.7 | – | 13 | 86.7 | – | 13 | 86.7 | – | |
| Group | Experiment | Attention Configuration |
|---|---|---|
| 1 | 1 | FOCUSED → DISTRACTED → DISTRACTED (FDD) |
| 2 | DISTRACTED → FOCUSED → FOCUSED (DFF) | |
| 2 | 1 | DISTRACTED → DISTRACTED → FOCUSED (DDF) |
| 2 | FOCUSED → FOCUSED → DISTRACTED (FFD) |
| Feature | p-Value |
|---|---|
| prediction | 1.88 × |
| eda_energy | 9.39 × |
| ecg_HRV_MinNN | 2.60 × |
| eda_min_scl | 4.12 × |
| eda_max_diff | 1.00 × |
| eda_mean_scl | 7.41 × |
| ecg_HRV_MedianNN | 1.54 × |
| eda_max_scl | 5.63 × |
| ecg_HRV_RMSSD | 5.75 × |
| ecg_HRV_SD1 | 9.79 × |
| ecg_HRV_HF | 2.67 × |
| ecg_HRV_SD1SD2 | 8.28 × |
| ecg_HRV_SDNN | 1.17 × |
| eda_mean_diff | 2.94 × |
| ecg_HRV_SD2 | 6.26 × |
| eda_scr_rate | 2.20 × |
| eda_scr_count | 2.20 × |
| ecg_HRV_MeanNN | 7.06 × |
| ecg_HRV_MaxNN | 4.81 × |
| ecg_HRV_LF | 2.80 × |
| eda_scl_slope | 1.09 × |
| ecg_HRV_ApEn | 6.18 × |
| eda_scl_std | 3.46 × |
| eda_scr_amplitude_mean | 3.97 × |
| eda_variance | 5.18 × |
| ecg_HRV_MadNN | 1.18 × |
| ecg_HRV_LFHF | 2.11 × |
| eda_scr_amplitude_max | 2.28 × |
| eda_scr_amplitude_std | 4.34 × |
| ecg_HRV_pNN50 | 8.54 × |
| LSTM | 24 Features | 27 Features | 30 Features |
|---|---|---|---|
| Global | 95.34% | 94.50% | 95.15% |
| Cluster 1 | 75.58% | 78.47% | 94.08% |
| Cluster 2 | 68.17% | 75.05% | 89.22% |
| K | Silhouette | Inertia | Mean ARI | Null Mean | Gap | Z-Score |
|---|---|---|---|---|---|---|
| 2 | 0.193 | 1023.26 | 0.697 | 0.0049 | 0.692 | 8.66 |
| 3 | 0.123 | 917.55 | 0.488 | 0.0004 | 0.488 | 6.62 |
| 4 | 0.117 | 836.34 | 0.435 | 0.0042 | 0.431 | 5.52 |
| Cluster | Subjects | Demographic | ecg_HRV_MeanNN | eda_mean_scl | ||||
|---|---|---|---|---|---|---|---|---|
| Age | Gender | Exp | Mean | Std | Mean | Std | ||
| Cluster PP 1 | S03 | 44 | M | 4 | −51.61 | ±41.51 | 0.14 | ±0.27 |
| S05 | 35 | F | 20 | −20.05 | ±25.29 | 1.99 | ±0.3 | |
| S07 | 42 | M | 24 | −87.08 | ±30.49 | 0.63 | ±0.25 | |
| S10 | 30 | M | 4 | −136.74 | ±24.98 | 1.15 | ±0.15 | |
| S12 | 24 | M | 7 | −38.74 | ±13.67 | 0.14 | ±0.17 | |
| S13 | 33 | M | 1 | −17.34 | ±27.96 | 1.52 | ±0.24 | |
| S15 | 31 | F | 3 | −91.11 | ±37.76 | 3.04 | ±0.36 | |
| S16 | 36 | M | 19 | −63.42 | ±44.58 | 0.69 | ±0.13 | |
| S18 | 22 | M | 0.6 | 31.16 | ±29.16 | 0.71 | ±0.67 | |
| S20 | 40 | M | 15 | 0.62 | ±26.97 | 0.39 | ±0.03 | |
| S25 | 70 | M | 55 | −36.85 | ±59.78 | 0.08 | ±0.19 | |
| S19 | 23 | M | 7 | −9.24 | ±28.52 | 1.03 | ±0.29 | |
| S29 | 24 | M | 7 | 24.79 | ±29.37 | 0.73 | ±0.26 | |
| Cluster PP 2 | S01 | 24 | M | 8 | −9.75 | ±27.6 | 4.0 | ±0.64 |
| S02 | 23 | M | 7 | −20.24 | ±28.5 | 3.57 | ±0.2 | |
| S04 | 49 | F | 33 | 77.95 | ±15.42 | 4.31 | ±0.31 | |
| S06 | 25 | F | 1 | 1.44 | ±31.64 | 3.84 | ±0.5 | |
| S08 | 31 | M | 11 | −58.55 | ±18.56 | 2.45 | ±0.25 | |
| S11 | 35 | M | 5 | −67.06 | ±23.52 | 4.24 | ±0.11 | |
| S14 | 29 | M | 13 | 16.04 | ±44.02 | 3.02 | ±0.21 | |
| S17 | 25 | M | 9 | −13.65 | ±23.63 | 3.3 | ±0.3 | |
| S21 | 35 | F | 15 | 106.31 | ±74.8 | 3.29 | ±0.28 | |
| S22 | 56 | M | 40 | 20.45 | ±12.05 | 3.16 | ±0.47 | |
| S23 | 28 | M | 7 | −100.08 | ±36.36 | 1.89 | ±0.25 | |
| S24 | 30 | F | 3 | −109.87 | ±65.33 | 1.23 | ±0.26 | |
| S26 | 39 | F | 23 | −8.4 | ±27.52 | 2.09 | ±0.28 | |
| S27 | 34 | F | 1 | −2.96 | ±20.54 | 3.32 | ±0.21 | |
| S28 | 71 | F | 50 | −149.21 | ±29.44 | 3.18 | ±0.9 | |
| S29 | 51 | F | 30 | 1.85 | ±14.07 | 2.75 | ±0.99 | |
| S30 | 44 | F | 26 | 111.02 | ±292.66 | 4.53 | ±0.56 | |
| Parameter | Global | Global BO | Cluster PP 1 | Cluster PP 2 | Young | Old | Male | Female | PCA 1.1 | PCA 1.2 | Novice | Experienced |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Window size | 5 | 15 | 13 | 11 | 10 | 14 | 5 | 9 | 11 | 10 | 5 | 14 |
| LSTM units | 64 | 80 | 117 | 127 | 120 | 48 | 102 | 114 | 37 | 120 | 101 | 115 |
| Dropout | 0.3 | 0.31278 | 0.33888 | 0.22343 | 0.49752 | 0.3815 | 0.22298 | 0.23995 | 0.20032 | 0.49752 | 0.28891 | 0.38473 |
| Fully Connected Layers | 64 | 114 | 84 | 24 | 99 | 123 | 116 | 33 | 93 | 99 | 49 | 86 |
| Learning rate | 1.0 × | 5.3 × | 1.0 × | 9.3 × | 4.2 × | 9.8 × | 9.3 × | 9.6 × | 9.1 × | 4.2 × | 8.1 × | 6.5 × |
| Metric | Global | Cluster 1 | Cluster 2 |
|---|---|---|---|
| Total parameters | 83,446 | 79,406 | 83,446 |
| Model size (KB) | 325.96 | 310.18 | 325.96 |
| FLOPs per sample | 2,415,012 | 1,821,636 | 1,772,660 |
| Avg. inference time per sample (ms) | 0.099 | 0.104 | 0.103 |
| Throughput (samples/s) | 10,148.1 | 9621.5 | 9703.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña, J.C.; Vásquez, E.; Feo-Cediel, G.A.; Negroni, A.; Medina-Lee, J.F. Beyond “One-Size-Fits-All”: Estimating Driver Attention with Physiological Clustering and LSTM Models. Electronics 2025, 14, 4655. https://doi.org/10.3390/electronics14234655
Peña JC, Vásquez E, Feo-Cediel GA, Negroni A, Medina-Lee JF. Beyond “One-Size-Fits-All”: Estimating Driver Attention with Physiological Clustering and LSTM Models. Electronics. 2025; 14(23):4655. https://doi.org/10.3390/electronics14234655
Chicago/Turabian StylePeña, Juan Camilo, Evelyn Vásquez, Guiselle A. Feo-Cediel, Alanis Negroni, and Juan Felipe Medina-Lee. 2025. "Beyond “One-Size-Fits-All”: Estimating Driver Attention with Physiological Clustering and LSTM Models" Electronics 14, no. 23: 4655. https://doi.org/10.3390/electronics14234655
APA StylePeña, J. C., Vásquez, E., Feo-Cediel, G. A., Negroni, A., & Medina-Lee, J. F. (2025). Beyond “One-Size-Fits-All”: Estimating Driver Attention with Physiological Clustering and LSTM Models. Electronics, 14(23), 4655. https://doi.org/10.3390/electronics14234655






