Certificateless Proxy Re-Encryption Scheme for the Internet of Medical Things

Abstract

With the rapid development of the Internet of Medical Things (IoMT), the data generated and collected by various sensors and medical devices are gradually increasing. How to realize flexible, efficient, and secure data sharing while ensuring data confidentiality and patient privacy has become a critical research challenge. The traditional Public Key Infrastructure (PKI) must deal with the complicated certificate management problem. An identity-based cryptosystem has the inherent key-escrow risk. These concerns make them unsuitable for resource-constrained and dynamic IoMT environments. To address it, this paper introduces a cloud data sharing protocol for IoMT using a Certificateless Proxy Re-encryption (CL-PRE) scheme that integrates an efficient access-list-based user revocation mechanism. In our system, a patient’s data can be encrypted and securely stored in a semi-trusted third party like the cloud server. When the patient wants to grant the access to designated users, e.g., doctors or medical institutions, a delegated proxy server will re-encrypt the ciphertext to a new one, which is decryptable by the designators. The proxy server also learns nothing during the re-encryption process, so as to maintain the end-to-end confidentiality. As for the security, the authors formally prove that the proposed CL-PRE mechanism for IoMT achieves Type-I and Type-II indistinguishability against adaptive chosen-identity and chosen-ciphertext attacks (IND-PrID-CCA) under the Decisional Bilinear Diffie–Hellman (DBDH) assumption. Moreover, the functional and computational comparisons with previous studies reveal the qualitative advantage of simultaneously achieving certificateless properties and user revocation, and the quantitative advantage of an optimized encryption cost (requiring only one bilinear pairing and two scalar multiplications), making it a theoretically efficient solution for resource-constrained IoMT devices.

1. Introduction

The advancement of information technology and the increasing demand for healthcare have promoted the emergence of profound IoT applications [1,2,3,4,5] in the medical field, known as the Internet of Medical Things (IoMT) [6,7,8]. It utilizes various wearable devices, embedded sensors, remote monitoring systems, and other smart medical equipment to enable the real-time collection, transmission, and analysis of patients’ vital data (such as heart rate, blood glucose, and blood oxygen saturation.) These data not only provide unprecedented convenience for personal health management and chronic disease tracking, but also constitute valuable information assets for remote medical care, precise diagnosis, and clinical research.

However, the processed data in IoMT systems are highly sensitive and private. Any unauthorized access, compromise, or alteration may pose serious threats to patients’ privacy and even to their life safety. Hence, ensuring the confidentiality, integrity, and availability of such sensitive medical data during transmission over open and complex network environments has become a key issue for the widespread adoption and success of IoMT applications.

To realize a secure, flexible, and efficient medical data-sharing model that treats patients as the center, the technique of Proxy Re-encryption (PRE) [9,10,11,12,13] provides a promising solution. It allows a data owner (such as a patient) to generate a special re-encryption key and give it to a semi-trusted proxy server (such as the cloud). The proxy server is therefore able to use this key to convert a ciphertext encrypted with a patient’s public key into another one that is able to be decrypted by the private key of authorized user (such as a doctor). In particular, during the entire transformation process, the proxy server is unable to learn anything about the original data. This property perfectly matches the requirements of medical data sharing [14,15,16].

While various PRE schemes have been proposed, they often suffer from issues such as the key-escrow problem in identity-based systems, the lack of user revocation mechanisms, or insufficient security guarantees (e.g., only achieving CPA security). These limitations hinder their practical application in sensitive IoMT environments.

Motivated by the demand for secure data sharing in IoMT applications, we propose a new CL-PRE scheme with user revocation. Our main contributions are as follows:

• We design a secure data sharing framework for IoMT using the CL-PRE mechanism that eliminates the key-escrow problem inherent in identity-based cryptosystems and avoids the complex certificate management of traditional PKI.
• The proposed scheme supports a flexible user revocation without incurring extra computational cost. This property is essential for managing user access rights in dynamic IoMT systems.
• The proposed CL-PRE scheme appeals to resource-constrained IoMT devices, as the encryption cost is specifically optimized.
• We formally prove that our scheme achieves indistinguishability against adaptive chosen-identity and chosen-ciphertext attacks (IND-PrID-CCA) under the Decisional Bilinear Diffie–Hellman (DBDH) assumption.

The remainder of this paper is organized as follows. Section 2 reviews related works. We present the proposed CL-PRE scheme for IoMT in Section 3. The formal security proof and comparison will be given in Section 4. Finally, we provide a conclusion with the future work in Section 5.

2. Related Works

In recent years, many Proxy Re-encryption (PRE) schemes have been developed for facilitating secure data sharing. In 2010, Wang et al. [17] introduced an identity-based PRE (IB-PRE) scheme that does not rely on the assumption of a semi-trusted proxy. In other words, their scheme is secure against collusion attacks. Moreover, their scheme has the property of no ciphertext expansion, meaning that the re-encrypted ciphertext and the original one have the same size. In 2013, Seo et al. [18] came up with a type-based PRE (TB-PRE) scheme in which a proxy could only re-encrypt those ciphertexts with a special type designated by the data owner. Additionally, their scheme has the proxy-invisible property, which prevents an adversary from distinguishing an original ciphertext from a re-encrypted one. They also proved that their scheme achieves chosen-ciphertext attacks (CCA) security in the standard model.

In 2018, a so-called sender-specified PRE (SS-PRE) scheme was addressed by Zeng et al. [19]. An SS-PRE scheme is a special kind of conditional Proxy Re-Encryption (C-PRE) schemes [20,21,22,23] and it allows the delegator to authorize the decryption right of a ciphertext from a designated sender to their delegatee. They formalized the definition and security model of the SS-PRE scheme and provided a concrete CCA-secure construction that supports both unidirectionality and single-use.

To address the key-escrow problem in identity-based systems, in 2020, Zhang et al. [24] employed an anonymous key generation technique and PRE to present an ID-based data storage protocol for fog computing. Although their scheme offers certain computational advantages, several security weaknesses have been identified by [25]. Considering data sharing in IoT environments, Lin and Chen [26] proposed a revocable and fog-enabled PRE scheme that uses a periodically updated time key to achieve user revocation.

In 2022, Zhou et al. [27] addressed a backdoor-resistant IB-PRE scheme for cloud-assisted wireless body area networks. Specifically, their scheme integrates a cryptographic reverse firewall and can withstand exfiltration attacks in multi-access telemedicine data sharing scenarios. Nevertheless, both the Lin-Chen [26] and their systems are identity-based and fail to address the inherent key-escrow problem.

Leveraging the advantages of certificateless public key systems, Ren et al. [28] presented an autonomous path PRE (AP-PRE) scheme for cloud data sharing. In their design, a data owner is in charge of the entire delegation path in a multi-hop delegation procedure. Yet, their scheme does not include a revocation mechanism, which is essential for data sharing in the cloud. More recently, Eltayieb et al. [29] proposed a certificateless PRE (CL-PRE) scheme with cryptographic reverse firewalls for secure cloud data sharing. Although their scheme provides a flexible revocation mechanism to prevent privacy leakage, it only achieves chosen plaintext attack (CPA) security.

2.1. Revocation Mechanism in PRE

A critical function for practical data sharing in dynamic IoMT environments is user revocation. As mentioned the above, several schemes, such as Ren et al. [28], do not include this essential mechanism. Existing revocable schemes utilize several main approaches. The time-based approach, such as Lin and Chen [26], achieves revocation by combining ciphertexts with specific time periods. The key/ciphertext evolution approach, used by Eltayieb et al. [29] and Yao et al. [30], links revocation to key updates. In this approach, an update-key is generated, allowing the proxy to evolve either existing ciphertexts or re-encryption keys to be compatible with the new key, thus automatically revoking old keys. Hybrid system-level approaches have also been proposed; for example, Worapaluk and Fugkeaw [31] integrated blockchains to manage revocation transactions. Our proposed scheme adopts an efficient access-list-based revocation mechanism, where the cloud server simply checks a revocation list (RVL) during a query process. The advantage of the list-based approach lies in its flexibility and cost-free nature, although the storage cost increases linearly with the number of revoked users.

2.2. Post-Quantum Secure PRE

Beyond the above works, a noticeable direction in recent cryptographic research is to develop post-quantum secure (PQC) schemes. Traditional pairing-based schemes cannot resist attacks from large-scale quantum computers. Therefore, researchers have begun exploring PRE schemes based on PQC-hard problems, such as lattices. For example, in 2023, Liang et al. [32] addressed a lattice-based PRE with keyword search (PRES), which is proven to be secure under the LWE hard assumption. Zhang et al. [33] introduced an IB-PRE scheme using the LWE problem with short public parameters. In particular, their scheme utilizes the blocking operation to decrease the public parameters and can be proved secure in the standard model. While PQC-PRE represents a crucial direction for long-term security, these schemes often present different trade-offs in computational and communication overhead. Our work, therefore, focuses on enhancing the security and functionality of the highly efficient and practical (though non-PQC) pairing-based paradigm for current IoMT environments.

3. Proposed CL-PRE System for IoMT

We first present preliminaries, the system party, algorithm definition, and security models of the proposed CL-PRE system for IoMT and then give a concrete construction.

3.1. Preliminaries

Before formally introducing the proposed scheme, we first describe the utilized mathematical operations and related cryptographic assumption.

• Bilinear Pairing
  Assume that the notations of G₁ and G_T denote two multiplicative groups. The order of both groups is a prime p. The symbol g represents a generator of G₁. We can express a bilinear pairing as e: G₁ × G₁ → G_T, satisfying the characteristics outlined below:
  • Bilinearity: Given u, v ∈ Z_p, the value e(g^u, g^v) equals e(g, g)^uv.
  • Non-degeneracy: The value e(g, g) does not equal 1 for some generator g ∈ G₁.
  • Computability: There is an efficient algorithm to calculate the value e(X, Y) for all X, Y ∈ G₁.
• Decisional Bilinear Diffie–Hellman (DBDH) Problem
  To determine whether W ∈ G_T equals the value e(g, g)^abc from a given tuple (g, g^a, g^b, g^c, W).
• Decisional Bilinear Diffie–Hellman (DBDH) Assumption
  The advantage is negligible for any probabilistic attacker to solve a given DBDH instance in polynomial time.

3.2. System Party

In general, a CL-PRE scheme for IoMT is composed of four parties as follows:

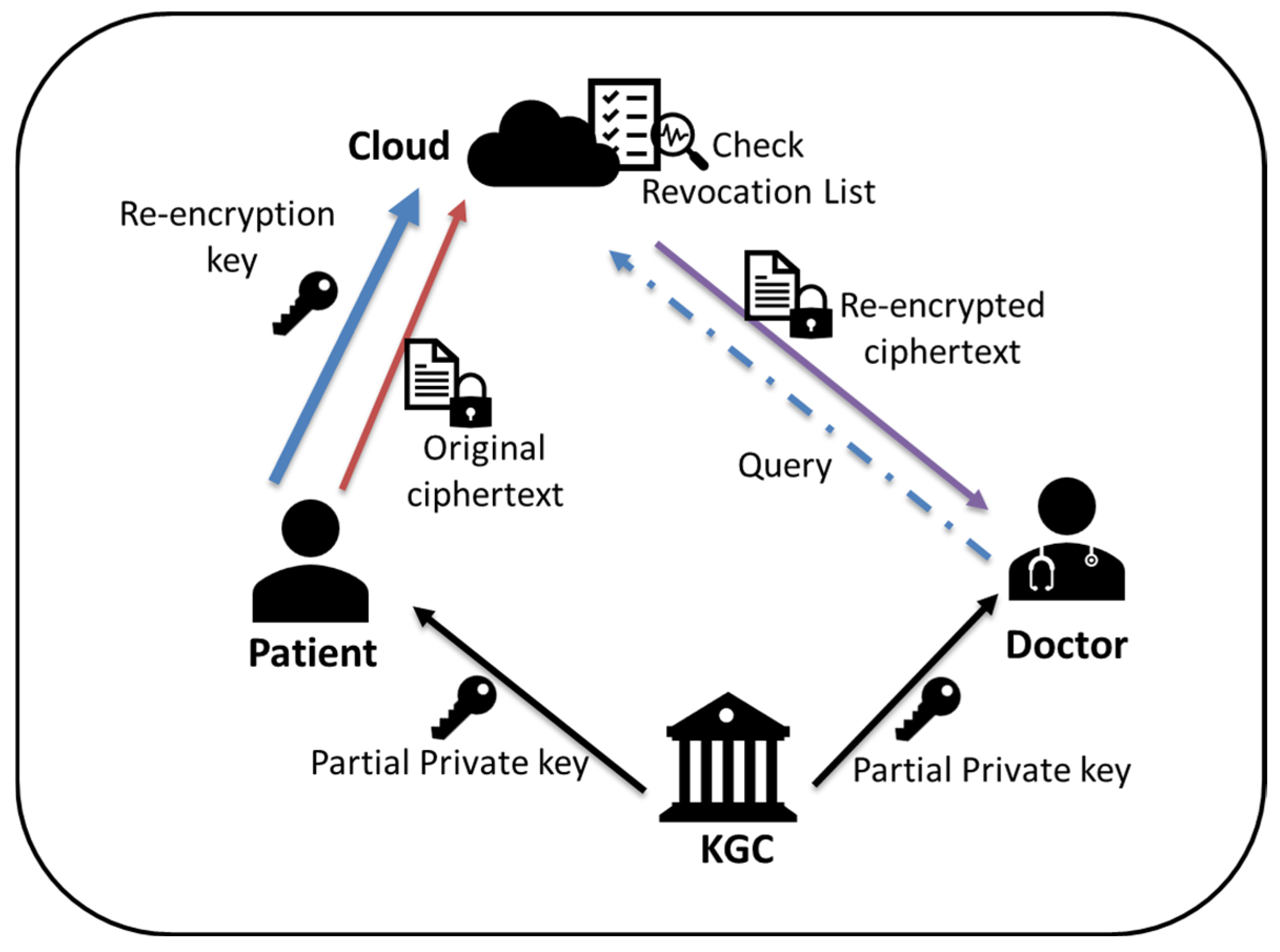
• Key Generator Center (KGC): The KGC is in charge of creating system’s public parameters and issuing the partial private key for all system parties. However, the KGC will be unable to learn the genuine private key of any user due to the secret value chosen by the user themselves.
• Data Owner (DO): A data owner is a patient who produces their health data via all kinds of wearable IoMT devices. These IoMT devices will encrypt sensed data with the data owner’s public key and then transmit the ciphertext to the cloud. If someone requests the encrypted health data in the cloud, the data owner/patient can authorize a re-encryption key to the cloud for performing ciphertext transformation.
• Data User (DU): A data user is an institution or medical staff who attempt to access the encrypted health data stored in the cloud. If access request is granted, they will receive the re-encrypted ciphertext that is decryptable by their own private keys.
• Cloud Server (CS): The CS is viewed as a semi-trusted proxy responsible for storing the encrypted health data as well as maintaining the obtained re-encryption keys authorized by the data owner. It also performs ciphertext re-encryption process without learning the content of health data.

3.3. Algorithm Definitions

The following are definitions of the algorithms used in this paper:

• Setup: The KGC utilizes a security parameter l as its input to generate a master secret key (Msk) and initializes the system public parameters (PP).
• PPKeyGen: The KGC utilizes PP and Msk to produce a partial private key (d_u) for the user ID_u.
• Set-Secret-Value: Each user ID_u determines a secret value (ss_u) for themselves.
• Set-Private-Key: Each user ID_u sets their full private key (sk_u).
• Set-Public-Key: Each user ID_u sets their full public key (pk_u).
• Encryption: The DO creates a ciphertext (CT) by taking the inputs of PP, a plaintext (M), an identity (ID_o), a symmetric key (K), and a secret value (ss_o).
• Query: The DU creates a query token W by taking the input of an identity (ID_u) and a random number.
• ReKeyGen: The DO creates a re-encryption key (Rk) by taking the inputs of PP, an identity (ID_u), a query token (W), the public key (pk_u) of ID_u, and a secret value (ss_o) of the DO.
• Re-encryption: The CS generates a re-encrypted ciphertext (CT’) by taking the inputs of a re-encryption key and a ciphertext (CT).
• Decryption: The DU recovers the original plaintext (M) by taking the inputs of a transformed ciphertext (CT’), a token seed together with a private key (sk_u). Similarly, the DO can also recover the original plaintext (M) by taking the inputs of a ciphertext (CT) and a private key (sk_o).
• Revocation: The KGC creates a renewed revocation list (RVL) by taking the input of a revoked identity ID_ru.

3.4. Security Model

The essential security notion of a CL-PRE scheme for IoMT is indistinguishability against adaptive chosen-identity and chosen-ciphertext attacks (IND-PrID-CCA). To satisfy such a security notion, we consider two types of adversaries. A type-I adversary is an outsider who does not know any information about legitimate user’s private key but is able to replace the public key of legitimate users. A type-II adversary is a malicious KGC who controls the partial private key of legitimate users but cannot replace the public key of legitimate users. Our security model for IND-PrID-CCA is based on the standard definitions used in certificateless cryptography, similar to the model presented in [28]. We present the corresponding definitions below.

Definition 1.

(Type-I IND-PrID-CCA):

A CL-PRE scheme is considered secure against adaptive chosen-identity and chosen-ciphertext attacks (IND-PrID-CCA) by a Type-I adversary if no probabilistic polynomial-time (PPT) adversary  𝒜 has a non-negligible advantage in the following game played with a challenger $ℬ$:

• Initialization: At first, $ℬ$ performs the Setup algorithm to obtain PP as well as the Msk. The former is given to 𝒜.
• Phase 1: 𝒜 is permitted to adaptively make the following queries:

• PPKeyGen Queries: 𝒜 submits an identity ID_u to $ℬ$ who returns the corresponding partial private key d_u.
• Full Private Key Queries: 𝒜 submits an identity ID_u to $ℬ$ who returns the corresponding full partial private key sk_u.
• Public Key Queries: 𝒜 submits an identity ID_u to $ℬ$ who returns the corresponding full public key pk_u.
• Replace Public Key Queries: 𝒜 submits an identity ID_u and a public key pk’_u1 to $ℬ$ who replaces the corresponding public key pk_u1 with pk’_u1. Note that after the public key of ID_u has been replaced, 𝒜 cannot query the corresponding full private key.
• Re-encryption Key Queries: 𝒜 submits two legitimate identities (ID_o, ID_u) to $ℬ$ who outputs a related transformation key Rk.
• Decryption Queries: 𝒜 submits a re-encrypted ciphertext CT’ to $ℬ$ who returns either a plaintext M or an error symbol ⊥.

• Challenge: 𝒜 submits a chosen identity ID*, two plaintexts (M₀*, M₁*) of equal lengths to $ℬ$ who creates a challenge ciphertext CT* by internally generating a symmetric key K*, flipping a coin λ ∈ {0, 1}, and encrypting M_λ* using K* under ID*. The challenge ciphertext is then given to 𝒜. This challenge is valid only under the condition that ID* was not the subject of any PPKeyGen, Full Private Key, or Re-encryption Key queries during Phase 1.
• Phase 2: 𝒜 makes new queries as those stated in Phase 1 under the constraints below:

• A PPKeyGen query for ID* is disallowed.
• A Full Private Key query for ID* is disallowed.
• A Re-encryption key query with respect to ID* would be disallowed.
• A Decryption query with respect to (ID*, CT*) is disallowed.
• The maximum query times for PPKeyGen, Full Private Key, Public Key, Replace Public Key, Re-encryption Key, and Decryption queries are bounded by q_psk, q_sk, q_pk, q_rpk, q_rek, and q_d.

• Guess: After Phase 2 ends, 𝒜 guesses a bit λ’. As long as λ’ = λ, 𝒜 succeeds in the game. We therefore express the advantage of 𝒜 as Adv(𝒜) = |Pr[λ’ = λ] − 1/2|.

Definition 2.

(Type-II IND-PrID-CCA):

A CL-PRE scheme is secure against a Type-II adversary (a malicious KGC) if no PPT adversary 𝒜 has a non-negligible advantage in the following game:

• Initialization: At first, $ℬ$ performs the Setup algorithm to obtain PP and the Msk and then gives both to 𝒜.
• Phase 1: The adversary 𝒜 is permitted to adaptively ask the following queries:

• Full Private Key Queries: 𝒜 submits an identity ID_u to $ℬ$ who returns the corresponding full partial private key sk_u.
• Public Key Queries: 𝒜 submits an identity ID_u to $ℬ$ who returns the corresponding full public key pk_u.
• Re-encryption Key Queries: 𝒜 submits two legitimate identities (ID_o, ID_u) to $ℬ$ who outputs the related transformation key Rk.
• Decryption Queries: 𝒜 submits a re-encrypted ciphertext CT’ to $ℬ$ who outputs either a plaintext M or an error symbol ⊥.

Since 𝒜 possesses the Msk, it can compute any user’s partial private key at will, thus PPKeyGen Queries are unnecessary for this adversary type.

• Challenge: 𝒜 sends a chosen identity ID*, two plaintexts (M₀*, M₁*) of equal lengths to $ℬ$ who creates a challenge ciphertext CT* by internally generating a symmetric key K*, flipping a coin λ ∈ {0, 1}, and encrypting M_λ* using K* under ID*. The challenge ciphertext is then given to 𝒜. This challenge is valid only under the condition that ID* was not the subject of any Full Private Key or Re-encryption Key queries during Phase 1.
• Phase 2: The adversary 𝒜 makes new queries as those stated in Phase 1 under the constraints below:

• A Full Private Key query for ID* is disallowed.
• A Re-encryption Key query with respect to ID* is disallowed.
• A Decryption query with respect to (ID*, CT*) is disallowed.
• The maximum query times for Full Private Key, Public Key, Re-encryption Key, and Decryption queries will be bounded by q_sk, q_pk, q_rek, and q_d.

• Guess: After Phase 2 ends, 𝒜 guesses a bit λ’. As long as λ’ = λ, 𝒜 succeeds in the game. We therefore express the advantage of 𝒜 as Adv(𝒜) = |Pr[λ’ = λ] − 1/2|.

3.5. Construction

We present a concrete CL-PRE scheme for IoMT according to previous definition of algorithms. The system model is shown as Figure 1. Some used symbols are defined as shown in

Table 1. Definition of notations.

Symbol	Description
l	security parameter
PP	system-wide public parameters
p	large prime
G1, GT	multiplicative group
g	generator
e	bilinear pairing
H1, H2	one-way hash function
α	Msk
N (= gα)	Mpk
SE, SD	symmetric encryption and decryption functions
di	partial private key of IDi
ssi	secret value of IDi
ski	full private key of IDi
Yi (= gssi)	partial public key of IDi
pki	full public key of IDi
K	symmetric key
M = (M1, M2, …, Mn)	message
CT = (CT1, CT2)	ciphertext
CT1 = (EO, 1, EO, 2)	partial ciphertext
EO, 1, EO, 2	partial ciphertext components
FM	File index of message M
v	secret query number
V	query token component
W	query token
h, z, r	random numbers
Rk = (Rk1, Rk2, Rk3)	re-encryption key
CT′ = (CT′1, CT2)	re-encrypted ciphertext
CT′1 = (E′O, 1, E′O, 2, E′O, 3, E′O, 4)	re-encrypted partial ciphertext
E′O, 1, E′O, 2, E′O, 3, E′O, 4	re-encrypted partial ciphertext components
X	intermediate decryption value
RVL	revocation list

.

• Setup(1^ζ) → (PP, Msk)
  Taking the security parameter l as an input, the KGC chooses α ∈ _R Z_p to be the Msk and produces PP = (e, G₁, G_T, g, H_1~2, Mpk, SE, SD) as follows. Here, PP stands for the set of all system-wide public parameters, which includes the Master Public Key (Mpk) as one of its components.

  (1)

  Two multiplicative groups are separately expressed as G₁ and G_T. Each of them has prime order p and let g be a generator of G₁. A symmetric bilinear pairing could be written as e: G₁ × G₁ → G_T.

  (2)

  Two collision-resistant cryptographic hash functions are denoted as H₁ and H₂. The former accepts variable-length inputs and maps the result to an element in G₁ while the latter also maps the result to an element in G₁ but only accepts an element from G_T.

  (3)

  The master public key Mpk is derived as N = g^α.

  (4)

  A symmetric encryption and decryption functions are denoted as SE and SD, respectively.

• PPKeyGen(PP, Msk, ID_u) → (d_u)
  A user can request his partial private key by the following processes with the KGC:

  (1)

  A user transmits his identity ID_u to the KGC.

  (2)

  The KGC calculates d_u = H₁(ID_u || ID_KGC)^α and sends d_u back to ID_u.

  (3)

  The correctness of generated partial private key could be verified if

  e(d_u, g) = e(H₁(ID_u || ID_KGC), N)
• Set-Secret-Value(PP, ID_u) → (ss_u)
  A user ID_u designates his secret value as ss_u ∈ _R Z_p.
• Set-Private-Key(PP, ID_u, d_u, ss_u) → (sk_u)
  A user ID_u sets sk_u = (d_u, ss_u) as his/her full private key.
• Set-Public-Key(PP, ID_u, ss_u) → (pk_u)
  A user ID_u first calculates Y_u = g^ss_u and then sets pk_u = (Y_u, H₁(ID_u || ID_KGC)) as his/her full public key.
• Encryption(PP, ID_o, K, M, ss_o) → (CT)
  To create a ciphertext CT = (CT₁, CT₂) for the data M composed of (M₁, M₂, …, M_n), the DO, with identity ID_o, uses PP, a symmetric key K, along with his secret value ss_o to perform the following processes. The DO first selects h ∈ Z_p and derives

              E_{O, 1} = K · e(N, H₁(ID_o || ID_KGC)^hss_o)

  E_{O, 2} = g^h

      CT₁ = (E_{O, 1}, E_{O, 2})

             CT₂ = (SE(K, M₁)…, SE(K, M_n))
  Here, the ciphertext CT = (CT₁, CT₂), an associated file index F_M, and the identity ID_o are delivered to the CS for storage.
• Query(PP, ID_u, F_M) → (W)
  To retrieve the ciphertext for a given file index F_M, the DU, with identity ID_u, first chooses a query number v ∈ Z_p and then derives

  V = g^v
  The query token W = (V, ID_u, F_M) will be sent to the CS who will check whether ID_u is in the revocation list RVL. If it does, the CS will reject the request. Otherwise, the CS forwards the token W to the DO. The component V (derived from the user’s secret v) serves a dual purpose: it is first used by the data owner (DO) in the ReKeyGen algorithm to generate the re-encryption key, and the corresponding secret v is later required by the data user (DU) to perform the final decryption.
• ReKeyGen(PP, W, sk_o) → (Rk)
  The DO first chooses z, r ∈ Z_p and then calculates

  Rk₁ = N^z

                     Rk₂ = (d_o)^ss_o · Rk₁/H₂(e(N, H₁(ID_u || ID_KGC)V^rY_u))

                       = ((d_o)^ss_o · N^z)/H₂(e(N, H₁(ID_u || ID_KGC)g^vrY_u))

    Rk₃ = e(g^r, N)
  Here, the ciphertext transformation key Rk composed of Rk₁, Rk₂, and Rk₃ will be forwarded to the CS.
• Re-encryption(PP, ID_u, Rk, CT) → CT′
  To re-encrypt the ciphertext CT for DU, the CS uses the authorized re-encryption key Rk to compute

      E′_{O, 1} = E_{O, 1} · e(Rk₁, E_{O, 2})

                  = K · e(N^ss_o, H₁(ID_o || ID_KGC)^h)e(N^z, g^h)

  E′_{O, 2} = E_{O, 2} = g^h

                      E′_{O, 3} = Rk₂ = ((d_o)^ss_o · N^z)/H₂(e(N, H₁(ID_u || ID_KGC)g^vrY_u))

     E′_{O, 4} = Rk₃ = e(g^r, N)

          CT′₁ = (E′_{O, 1}, E′_{O, 2}, E′_{O, 3}, E′_{O, 4})
  Finally, the CS sends the re-encrypted ciphertext CT’ = (CT’₁, CT₂) to the DU.
• Decryption(CT, sk_u) → (M = M₁, M₂, …, M_n)
  If the DO wants to decrypt their own ciphertext CT, they can use their partial private key d_o to recover the symmetric key K as

  $$K={\displaystyle \frac{E_{O, 1}}{e({E_{O, 2}}^{{ss}_o}, { d}_o)}}$$

  and then decrypt {M_i = SD(K, SE(K, M_i))}_{i = 1, …, n}.
  For the DU to decrypt a requested ciphertext CT’, they first use their full private key sk_u = (d_u, ss_u) and the previously selected query number v to compute

  $$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} X={{E^{\prime }}_{O, 3}·H}_2\left({{E^{\prime }}_{O,4}}^{v}e\right(d_u{N}^{{ss}_u}, g\left)\right)$$

    = (d_o)^ss_o · N^z

            = (H₁(ID_o || ID_KGC)^α)^ss_o · N^z

  $$K={\displaystyle \frac{{E^{\prime }}_{O,1}}{e\left(X, { E^{\prime }}_{O,2}\right)}}$$

  and then decrypt {M_i = SD(K, SE(K, M_i))}_{i = 1, …, n}. The correctness for the derivation of the symmetric key K can be confirmed as follows:

  $${\displaystyle \frac{{E^{\prime }}_{O,1}}{e\left(X, { E^{\prime }}_{O,2}\right)}}={\displaystyle \frac{K · e(N^{{ss}_o}, { H_1\left({ID}_o\right|\left|{ID}_{KGC}\right)}^h)e(N^z, g^h)}{e({H_1\left({ID}_o\right|\left|{ID}_{KGC}\right)}^{{\alpha ss}_o}{N}^z,{ g}^h)}}=K$$
• Revocation(ID_ru) → RVL

The KGC is responsible for maintaining the system’s revocation list (RVL). To revoke a user ID_ru, the KGC updates the list as RVL ← RVL ∪ {ID_ru} and securely distributes this updated list to the CS. The CS is responsible for enforcing this revocation. As described in the Query algorithm, the CS will check this list upon receiving a query request and reject any request from an identity present in the RVL.

4. Security Proof and Comparison

In this section, we provide the formal security proof for our proposed CL-PRE scheme for IoMT according to previous security models and evaluate its computational performance.

4.1. Security Proof

In this subsection, we first prove that the proposed scheme achieves IND-PrID-CCA security in the random oracle model under the DBDH assumption.

Theorem 1.

(Proof of Type-I IND-PrID-CCA)

The designed CL-PRE system for IoMT fulfills the security requirement of IND-PrID-CCA provided that any Type-I adversary 𝒜 cannot own a non-negligible advantage ε to defeat a challenger $ℬ$ who tries to break the DBDH problem in the following game.

Proof. 

We utilize the random oracle model (ROM) in this proof and treat H₁ as a random oracle. Assume that the Type-I adversary 𝒜 has a non-negligible advantage ε to break ciphertext indistinguishability of the proposed system under adaptive chosen-ciphertext attacks and the challenger $ℬ$ is given a DBDH instance of (g, g^a, g^b, g^c, Q), in which a, b, c ∈ Z_p and Q ∈ G_T. The purpose of $ℬ$ is to distinguish Q from e(g, g)^abc by using the advantage of 𝒜.

• Initialization: By performing the Setup(1^l) algorithm, $ℬ$ first sets Mpk to be N = g^a, which implicitly defines the Msk to be the integer a that $ℬ$ does not know. Then, $ℬ$ sends PP = (e, G₁, G_T, g, p, H₂, Mpk, SE, SD) to 𝒜.
• Phase 1: $ℬ$ responds the queries 𝒜 made below:

• H₁ Oracles: To respond to an H₁(ID_u || ID_KGC) query, the challenger $ℬ$ searches the stored H₁-list for previous records. If no matched entry exists, $ℬ$ tosses a coin cc with Pr[cc = 1] = π. When cc equals 0, $ℬ$ derives the return value O_h1 = ${\left(g^b\right)}^{h_1}$, in which h₁ ∈_R Z_p. Otherwise, $ℬ$ sets O_h1 = $g^{h_1}$. The entry (ID_u, cc, h₁, O_h1) is also added to the H₁-list.
• PPKeyGen Queries: To respond to a PPKeyGen query of ID_i, the challenger $ℬ$ first makes an H₁(ID_i || ID_KGC) query and then aborts as long as cc equals 0. Otherwise, $ℬ$ derives the return value d_i = $N^{h_1}$
• Full Private Key Queries: To respond to a Full Private Key query of ID_i, the challenger $ℬ$ first makes an H₁(ID_i || ID_KGC) query and then aborts as long as cc equals 0. Otherwise, $ℬ$ obtains the secret value ss_i by the Set-Secret-Value(PP, ID_i) algorithm and sets the return value sk_i = ($N^{h_1}$, ss_i).
• Public Key Queries: To respond to a Public Key query of ID_i, the challenger $ℬ$ obtains O_h1 and the secret value ss_i by H₁(ID_i || ID_KGC) oracle and the Set-Secret-Value(PP, ID_i) algorithm, respectively. Then $ℬ$ and sets the return value pk_i = (O_h1, Y_i = g^ss_i).
• Replace Public Key Queries: To respond to a Replace Public Key query of (ID_i, Y_i, Y_i’), in which the Full Private Key query of ID_i has never been made, the challenger $ℬ$ replaces the associated public key Y_i with Y_i’.
• Re-encryption Key Query: To respond to a Re-encryption Key query of (ID_o, ID_u, F_M), in which ID_u ∉ RVL, $ℬ$ first makes an H₁(ID_o || ID_KGC) query and might abort if cc equals 0. If not, $ℬ$ obtains the secret value ss_o by the Set-Secret-Value(PP, ID_o) algorithm and derives full private key sk_o = ($N^{h_1}$, ss_o). Next, $ℬ$ calculates the token W by performing the Query(PP, ID_u, F_M) algorithm and finally derives the returned ciphertext transformation key Rk composed of (Rk₁, Rk₂, Rk₃) with the algorithm of ReKeyGen(PP, W, sk_o).
• Decryption Query: To respond to a Decryption query of (ID_u, CT’), in which ID_u ∉ RVL, $ℬ$ first makes an H₁(ID_u || ID_KGC) query and might abort if cc equals 0. If not, $ℬ$ obtains the secret value ss_u by the Set-Secret-Value(PP, ID_u) algorithm and derives full private key sk_u = ($N^{h_1}$, ss_u). Next, $ℬ$ outputs the result of Decryption(CT’, sk_u) process.

• Challenge: 𝒜 submits a chosen identity, say ID*, two plaintexts (M₀*, M₁*) of equal lengths to $ℬ$ who creates a challenge ciphertext CT* = (E_{O, 1}*, E_{O, 2}*, CT₂*) by internally generating a symmetric key K*, flipping a coin λ ∈ {0, 1}, and encrypting M_λ* using K* under ID* as follows. The challenge ciphertext is then given to 𝒜.

• Without loss of generality, it is assumed that the H₁(ID* || ID_KGC) oracle has been made by 𝒜. In this case, whenever the value cc* equals 1, the challenger $ℬ$ directly aborts.
• Otherwise, the associated value h₁ could be fetched from the H₁-list. Then $ℬ$ sets the secret value of ID* to be ss* ∈_R Z_p and computes

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {E_{O, 1}}^{*}=K^{*}{Q}^{h_1{ss}^{*}} \mathrm{where} H_1({ID}^{*} || {\mathit{ID}}_{\mathit{PKG}})={{(g}^b)}^{h_1}$$

E_{O, 2}^* = g^c

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{{\mathit{CT}}_2}^{*}=\left(\mathit{SE}\right(K^{*}, {M_{\lambda 1}}^{*}), \dots , \mathit{SE}(K^{*}, {M_{\lambda n}}^{*}\left)\right)$$

3.

Here, the challenge ciphertext CT* = (E_{O, 1}*, E_{O, 2}*, CT₂*) is given to 𝒜.

• Phase 2: 𝒜 makes new queries as those described in previous phase under the limits outlined in Definition 1.
• Guess: After Phase 2 ends, 𝒜 guesses a bit λ’. Provided that λ’ = λ, $ℬ$ outputs 1 implying that Q equals e(g, g)^abc. If Q ≠ e(g, g)^abc, $ℬ$ outputs 0.
• Analysis: Based on the ciphertext CT* properly simulated in the challenge phase, it will be valid if only Q equals e (g, g)^abc. In this case, the adversary 𝒜 owns an assumed advantage to break our scheme, meaning that Adv(𝒜) = | Pr[λ’ = λ] $-$ ${\displaystyle \frac{1}{2}}$ | ≥ ε. On the contrary, as long as Q is inequivalent to e (g, g)^abc, the formed ciphertext CT* will be invalid, which denotes that 𝒜 owns no better advantage, and we get | Pr[λ’ = λ] | = ${\displaystyle \frac{1}{2}}$. To obtain a reliable estimation, we use Pr[¬AT] to stand for the probability that $ℬ$ will not abort during the entire game. We can thus describe the success advantage for $ℬ$ to solve the given DBDH instance as

                           |Pr[$ℬ$ returns 1| Q = e (g, g)^abc] − Pr[$ℬ$ returns 1 |Q ∈_R G_T]|

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\ge |\left({\displaystyle \frac{1}{2}}+\mathsf{\epsilon }\right)-{\displaystyle \frac{1}{2}}|·\mathrm{P}\mathrm{r}[\neg \mathrm{A}\mathrm{T}]$$

$$=\epsilon ·\mathrm{P}\mathrm{r}[\neg \mathrm{A}\mathrm{T}]$$

To further analyze Pr[¬AT], we define some probability events to evaluate the query process that will be aborted by the challenger $ℬ$ as follows:

F₁: For any PPKeyGen query, $ℬ$ will not abort throughout the game.

F₂: For any Full Private Key query, $ℬ$ will not abort throughout the game.

F₃: For any Re-encryption Key query, $ℬ$ will not abort throughout the game.

F₄: For any Decryption query, $ℬ$ will not abort throughout the game.

F₅: For the challenge phase, $ℬ$ will not abort.

Given that events F₁ to F₅ are mutually independent, we could express Pr[¬AT] as Pr[F₁] ∙ Pr[F₂] ∙ Pr[F₃] ∙ Pr[F₄] ∙ Pr[F₅]. In addition, in PPKeyGen, Full Private Key, Re-encryption Key, and Decryption queries, a termination occurs whenever cc associated with the asked identity equals 0, meaning that Pr[F₁] ≤ ${\left(\pi \right)}^{q_{psk}}$, Pr[F₂] ≤ ${\left(\pi \right)}^{q_{sk}}$, Pr[F₃] ≤ ${\left(\pi \right)}^{q_{rek}}$, and Pr[F₄] ≤ ${\left(\pi \right)}^{q_d}$.

As for the challenge phase, a termination occurs if only cc* associated with the chosen identity ID^*equals 1, meaning that Pr[F₅] ≤ (1 − $\pi$). Accordingly, we can further obtain

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Pr}[\neg \mathrm{AT}] \le {\left(\pi \right)}^{q_{psk}}{\left(\pi \right)}^{q_{sk}}{\left(\pi \right)}^{q_{rek}}{\left(\pi \right)}^{q_d}(1-\pi )$$

$$={\left(\pi \right)}^{q_{psk}+q_{sk}+q_{rek}+q_d}(1-\pi )$$

In this inequality, when we maximize the value $\pi$ at 1 − 1/(q_psk + q_sk + q_rek + q_d + 1), Pr[¬AT] is at least 1/e(q_psk + q_sk + q_rek + q_d + 1), in which the symbol e represents the base of natural logarithm. Therefore, we know that the advantage for the challenger $ℬ$ to solve the provided DBDH instance can derived as

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{{e(q}_{psk}+q_{sk}+q_{rek}+q_d+1)}}.\square$$

Theorem 2.

(Proof of Type-II IND-PrID-CCA)

The designed CL-PRE system for IoMT fulfills the security requirement of IND-PrID-CCA provided that any Type-II adversary 𝒜 cannot own a non-negligible advantage ε to defeat a challenger $ℬ$ who tries to break the DBDH problem in the following game.

Proof. 

We utilize the random oracle model (ROM) in this proof and treat H₁ as a random oracle. Assume that the Type-II adversary 𝒜 has a non-negligible advantage ε to break ciphertext indistinguishability of the proposed scheme under adaptive chosen-ciphertext attacks and the challenger $ℬ$ is given a DBDH instance of (g, g^a, g^b, g^c, Q), in which a, b, c ∈ Z_p and Q ∈ G_T. The goal of $ℬ$ is to distinguish Q from e(g, g)^abc by using the advantage of 𝒜.

• Initialization: By performing the Setup(1^l) algorithm, $ℬ$ first sets Mpk to be N = g^α, which defines the Msk to be the integer α chosen by $ℬ$. Then, $ℬ$ sends PP = (e, G₁, G_T, g, p, H₂, Mpk, SE, SD) and the Msk α to 𝒜.
• Phase 1: $ℬ$ responds the queries 𝒜 made below:

• H₁Oracles: To respond an H₁(ID_u || ID_KGC) query, the challenger $ℬ$ searches the stored H₁-list for previous records. If no matched entry exists, $ℬ$ tosses a coin cc with Pr[cc = 1] = π. When cc equals 0, $ℬ$ derives the return value O_h1 = ${\left(g^b\right)}^{h_1}$, in which h₁ ∈_R Z_p. Otherwise, $ℬ$ sets O_h1 = $g^{h_1}$ The entry (ID_u, cc, h₁, O_h1) is also added to the H₁-list.
• Full Private Key Queries: To respond a Full Private Key query of ID_i, the challenger $ℬ$ first makes an H₁(ID_i || ID_KGC) query and then aborts as long as cc equals 0. Otherwise, $ℬ$ obtains the secret value ss_i by the Set-Secret-Value(PP, ID_i) algorithm and sets the return value sk_i = ($N^{h_1}$, ss_i).
• Public Key Queries: To respond a Public Key query of ID_i, the challenger $ℬ$ obtains O_h1 and the secret value ss_i by H₁(ID_i || ID_KGC) oracle and the Set-Secret-Value(PP, ID_i) algorithm, respectively. Then $ℬ$ and sets the return value pk_i = (O_h1, Y_i = g^ss_i).
• Re-encryption Key Query: To respond a Re-encryption Key query of (ID_o, ID_u, F_M), in which ID_u ∉ RVL, $ℬ$ first makes an H₁(ID_o || ID_KGC) query and might abort if cc equals 0. If not, $ℬ$ obtains the secret value ss_o by the Set-Secret-Value(PP, ID_o) algorithm and derives full private key sk_o = ($N^{h_1}$, ss_o). Next, $ℬ$ calculates the token W by performing the Query(PP, ID_u, F_M) algorithm and finally derives the returned ciphertext transformation key Rk composed of (Rk₁, Rk₂, Rk₃) with the algorithm of ReKeyGen(PP, W, sk_o).
• Decryption Query: To respond a Decryption query of (ID_u, CT’), in which ID_u ∉ RVL, $ℬ$ first makes an H₁(ID_u || ID_KGC) query and might abort if cc equals 0. If not, $ℬ$ obtains the secret value ss_u by the Set-Secret-Value(PP, ID_u) algorithm and derives full private key sk_u = ($N^{h_1}$, ss_u). Next, $ℬ$ outputs the result of Decryption(CT’, sk_u) process.

• Challenge: 𝒜 submits a chosen identity, say ID*, two plaintexts (M₀*, M₁*) of equal lengths to $ℬ$ who create a challenge ciphertext CT* = (E_{O, 1}*, E_{O, 2}*, CT₂*) by internally generating a symmetric key K*, flipping a coin λ ∈ {0, 1}, and encrypting M_λ* using K* under ID* as follows. The challenge ciphertext is then given to 𝒜.

• Without loss of generality, it is assumed that the H₁(ID* || ID_KGC) oracle has been made by 𝒜. In this case, whenever the value cc* equals 1, the challenger $ℬ$ directly aborts.
• Otherwise, the associated value h₁ could be fetched from the H₁-list. Then $ℬ$ sets the public key Y* of ID* to be g^a, which implicitly defines the secret value ss* to be a and then computes

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {E_{O, 1}}^{*}=K^{*}{Q}^{h_1\alpha } \mathrm{where} H_1({ID}^{*} || {ID}_{PKG})={(g^b)}^{h_1}$$

E_{O, 2}^* = g^c

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{{CT}_2}^{*}=\left(SE\right(K^{*}, {M_{\lambda 1}}^{*}), \dots , \mathrm{SE}(K^{*}, {M_{\lambda n}}^{*}\left)\right)$$

3.

Here, the challenge ciphertext CT* = (E_{O, 1}*, E_{O, 2}*, CT₂*) is given to 𝒜.

• Phase 2: 𝒜 makes new queries as those described previous phase under the limits outlined in Definition 2.
• Guess: After Phase 2 ends, 𝒜 guesses a bit λ’. Provided that λ’ = λ, $ℬ$ outputs 1 implying that Q equals e(g, g)^abc. If Q ≠ e(g, g)^abc, $ℬ$ outputs 0.
• Analysis: Based on the ciphertext CT* properly simulated in the challenge phase, it will be valid if only Q equals e(g, g)^abc. In this case, the adversary 𝒜 owns an assumed advantage to break our scheme, meaning that Adv(𝒜) = |Pr[λ’ = λ] $-$ ${\displaystyle \frac{1}{2}}$| ≥ ε. On the contrary, as long as Q is inequivalent to e(g, g)^abc, the formed ciphertext CT* will be invalid, which denotes that 𝒜 owns no better advantage, and we get |Pr[λ’ = λ]| = ${\displaystyle \frac{1}{2}}$. To obtain a reliable estimation, we use Pr[¬AT] to stand for the probability that $ℬ$ will not abort during the entire game. We can thus describe the success advantage for $ℬ$ to solve the given DBDH instance as

                       |Pr[$ℬ$ returns 1| Q = e (g, g)^abc] − Pr[$ℬ$ returns 1 |Q ∈_R G_T]|

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\ge |\left({\displaystyle \frac{1}{2}}+\mathsf{\epsilon }\right)-{\displaystyle \frac{1}{2}}|·\mathrm{P}\mathrm{r}[\neg \mathrm{A}\mathrm{T}]$$

$$=\epsilon ·\mathrm{P}\mathrm{r}[\neg \mathrm{A}\mathrm{T}]$$

To further analyze Pr[¬AT], we define some probability events to evaluate the query process that will be aborted by the challenger $ℬ$ as follows:

J₁: For any Full Private Key query, $ℬ$ will not abort throughout the game.

J₂: For any Re-encryption Key query, $ℬ$ will not abort throughout the game.

J₃: For any Decryption query, $ℬ$ will not abort throughout the game.

J₄: For the challenge phase, $ℬ$ will not abort.

Given that events J₁ to J₄ are mutually independent, we could express Pr[¬AT] as Pr[J₁] · Pr[J₂] · Pr[J₃] · Pr[J₄]. In addition, in Full Private Key, Re-encryption Key, and Decryption queries, a termination occurs whenever cc associated with the asked identity equals 0, meaning that Pr[J₁] ≤ ${\left(\pi \right)}^{q_{sk}}$, Pr[J₂] ≤ ${\left(\pi \right)}^{q_{rek}}$, and Pr[J₃] ≤ ${\left(\pi \right)}^{q_d}$.

As to the challenge phase, a termination occurs if only cc* associated with the chosen identity ID* equals 1, meaning that Pr[J₄] ≤ (1 − $\pi$). Accordingly, we can further obtain

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Pr}[\neg \mathrm{AT}] \le {\left(\pi \right)}^{q_{sk}}{\left(\pi \right)}^{q_{rek}}{\left(\pi \right)}^{q_d}(1-\pi )$$

$$={\left(\pi \right)}^{q_{sk}+q_{rek}+q_d}(1-\pi )$$

In this inequality, when we maximize the value $\pi$ at 1 − 1/(q_sk + q_rek + q_d + 1), Pr[¬AT] is at least 1/e(q_sk + q_rek + q_d + 1), in which the symbol e represents the base of natural logarithm. Therefore, we know that the advantage for the challenger $ℬ$ to solve the provided DBDH instance can calculated as

$${\epsilon }^{\prime }\ge {\displaystyle \frac{\epsilon }{{e(q}_{sk}+q_{rek}+q_d+1)}}.\square$$

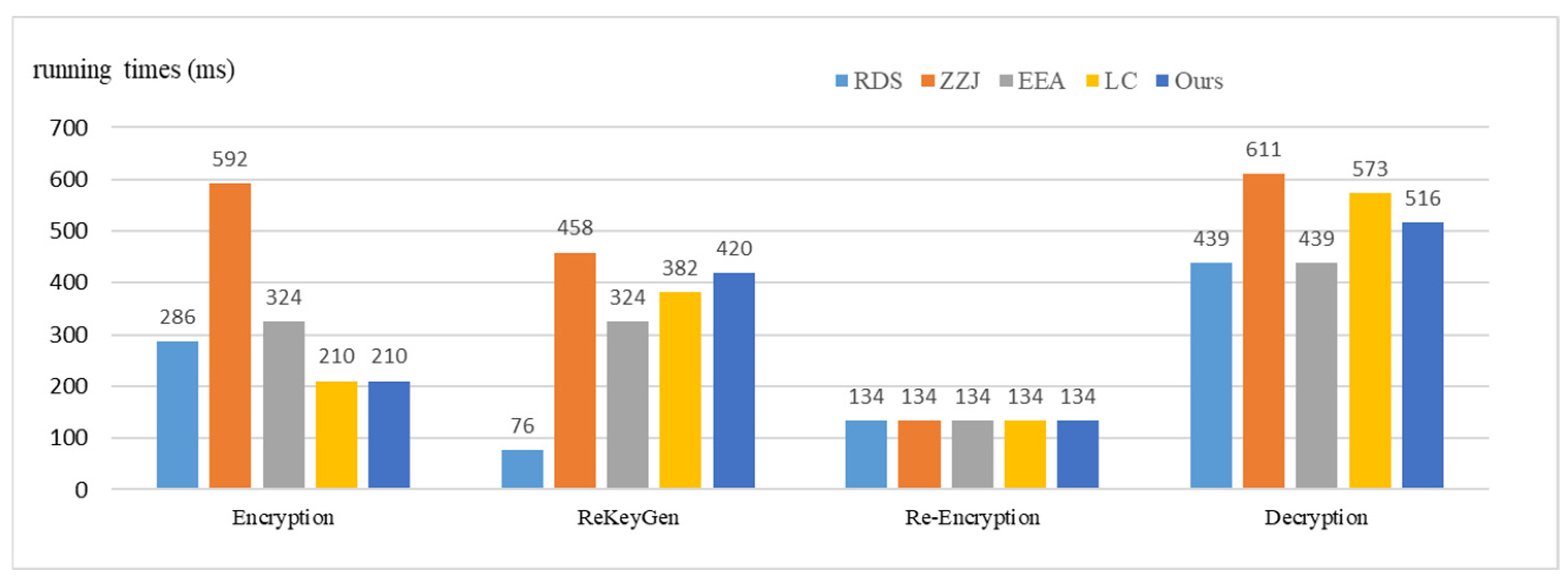
4.2. Comparison

We compare the proposed CL-PRE scheme for IoMT with some previous studies [26,27,28,29] in

Table 2. Comparative analysis of several PRE systems.

	RDS	ZZJ	EEA	LC	Ours
Encryption	B + 4M	3B + 3M + 2E	B + 4M + E	B + 2M	B + 2M
ReKeyGen	2M	2B + 3M + 2E	B + 5M	2B + 3M	2B + 4M
Re-encryption	B	B	B	B	B
Decryption	3B + M	4B + 2M	3B + M	4B + E	3B + 2M + E
Ciphertext Size	>>4096 bits	≈2048 bits	≈3072 bits	≈2048 bits	≈2048 bits
Re-encryption Key Size	>>4096 bits	≈3072 bits	≈3072 bits	≈3072 bits	≈3072 bits
Re-encrypted Ciphertext Size	>>4096 bits	≈4096 bits	≈4096 bits	≈4096 bits	≈4096 bits
Certificateless	√	×	√	×	√
Revocation	×	×	√	√	√
Security Level	CPA	CPA	CPA	CPA	CCA

Remark: “√” indicates that the feature is supported, and “×” means not supported.

. To evaluate the computational costs, we focus on the relatively time-consuming computations such as bilinear pairing (B), scalar multiplication in G₁ (M), and modular exponentiation in G_T (E). From the comparison results shown in this table, one can learn that the Lin–Chen scheme (LC) [26] and ours have better performance in the Encryption process, which is B + 2M. In the ReKeyGen phase, Ren et al.’s scheme (RDS) [28] only takes 2M, which is the best. All compared mechanisms have identical computational costs in the re-encryption process, which is one bilinear pairing. As for the decryption process (including both DO and DU), the computational cost of the proposed scheme is slightly higher than that of Ren et al.’s (RDS) [28] and Eltayieb et al.’s (EEA) [29] schemes, but is still lower than that of the Lin–Chen (LC) [26] and Zhou et al.’s (ZZJ) [27] schemes. Regarding the functionality, only the proposed one and Eltayieb et al.’s (EEA) [29] scheme simultaneously support the certificateless system and revocation. However, we notice that Eltayieb et al.’s scheme (EEA) [29] only achieves CPA security. Hence, the proposed CL-PRE for IoMT is a better alternative among the compared systems in terms of practical applications.

To further provide a theoretical cost comparison, we estimate the computational overhead based on the benchmarked execution times for the four algorithms on the compared systems, as shown in Figure 2. The communication overhead is estimated in terms of bit-length of ciphertexts and keys based on a standard 80-bit security level (equivalent to 1024-bit RSA). At this level, typical element sizes for bilinear pairings are |G₁| ≈ |G_T| ≈ 1024 bits. Since the RDS scheme utilizes multilinear maps, the implementation of their scheme is computationally impractical and requires magnitude larger size to achieve the same security. It is widely recognized that current multilinear map constructions are significantly less practical than bilinear pairings, often involving far larger element sizes (i.e., higher communication costs) and much slower operations to achieve an equivalent security level. Our performance estimation is not based on a new implementation, but is calculated theoretically using the benchmarked execution times for fundamental cryptographic operations reported in a recent peer-reviewed study by Zhu et al. [34]. This approach provides a transparent estimation based on publicly available benchmarks, allowing for a fair comparison of the theoretical efficiency. This comparison is relevant because the benchmark in [34] utilized an identical hardware platform (Raspberry Pi Zero, ARM1176JZF-S Single-Core CPU @ 1.0 GHz, 512 MB RAM) and the same Pairing-Based Cryptography (PBC) library (v0.5.14) that we assume for our IoMT environment. The technical parameters from the benchmark [34] used for these calculations are as follows:

(1)

Implementation Language: C.

(2)

Pairing Type: MNT224 curve (a Type 3 pairing).

(3)

Security Level: 96-bit.

The specific benchmark values from [34] used for our calculations are B ≈ 0.133663 s, E ≈ 0.038339 s, and M ≈ 0.038108 s. Our Figure 2 is plotted based on the formulas in Table 2 and these benchmarked values.

Based on the computational cost estimation provided in Table 2 and Figure 2, we can observe the theoretical efficiency trade-offs among the compared schemes. The Encryption phase, which is critical for resource-constrained IoMT devices, is the most optimized in our scheme, achieving the minimum computational cost (210 ms) alongside the LC scheme. In contrast, the re-encryption phase requires only one bilinear pairing (B) and is uniform across all compared schemes (134 ms). Although the RDS scheme exhibits the lowest cost for the ReKeyGen phase (76 ms), and its decryption cost (439 ms) is the minimum alongside the EEA scheme, our proposed scheme still maintains a competitive decryption overhead (516 ms), which is theoretically lower than both the LC and ZZJ schemes. Overall, these results show the computational advantage of our optimized encryption cost, while simultaneously achieving certificateless properties and CCA security.

5. Conclusions

In this paper, we address the security issues of medical data sharing in IoMT environments and propose a cloud data sharing system based on CL-PRE. The proposed system, which integrates the advantages of PRE and certificateless public key cryptosystems, resolves the complicated certificate management problem in traditional PKI as well as the key-escrow risk inherent in identity-based systems. By employing a semi-trusted cloud server, patients can flexibly authorize specific medical staff or institutions to access encrypted data without compromising the original information, thereby achieving end-to-end protection of confidentiality. From a security perspective, the proposed scheme is based on the DBDH assumption and is formally proven to satisfy the IND-PrID-CCA security requirement against both Type-I and Type-II adversaries. The comparison results demonstrate that our proposed system not only provides stronger security and better functionality, but also achieves theoretically lower computational costs in the encryption process. For future work, several avenues remain. First, we analyze the revocation properties of our scheme. The proposed revocation mechanism is an access-list-based approach. Although it is efficient, this approach lacks forward security, because it cannot prevent a revoked user from decrypting ciphertexts obtained before revocation. However, our scheme guarantees backward security since a new user cannot decrypt any ciphertext until the data owner explicitly generates a re-encryption key for them. Therefore, designing a stronger, time-based revocation mechanism to achieve forward security is an important direction. Furthermore, our scheme is based on Pairing-Based Cryptography, which is known to be vulnerable to attacks from large-scale quantum computers. Therefore, exploring the construction of post-quantum secure (PQC) CL-PRE variants is another critical research direction to ensure the long-term security of IoMT data sharing. Finally, the performance evaluation of this work is based on a theoretical estimation of computational costs. Another important direction for future work is to implement a practical prototype of the proposed scheme and conduct extensive experiments on resource-constrained devices to validate its real-world performance, overhead, and practicality for IoMT environments.