Physics-Informed Reinforcement Learning for Multi-Band Octagonal Fractal Frequency-Selective Surface Optimization
Abstract
1. Introduction
2. Problem Formulation and Methodology
2.1. Octagonal Fractal Frequency-Selective Metasurface
2.1.1. The Structure of the Designed OF-FSS
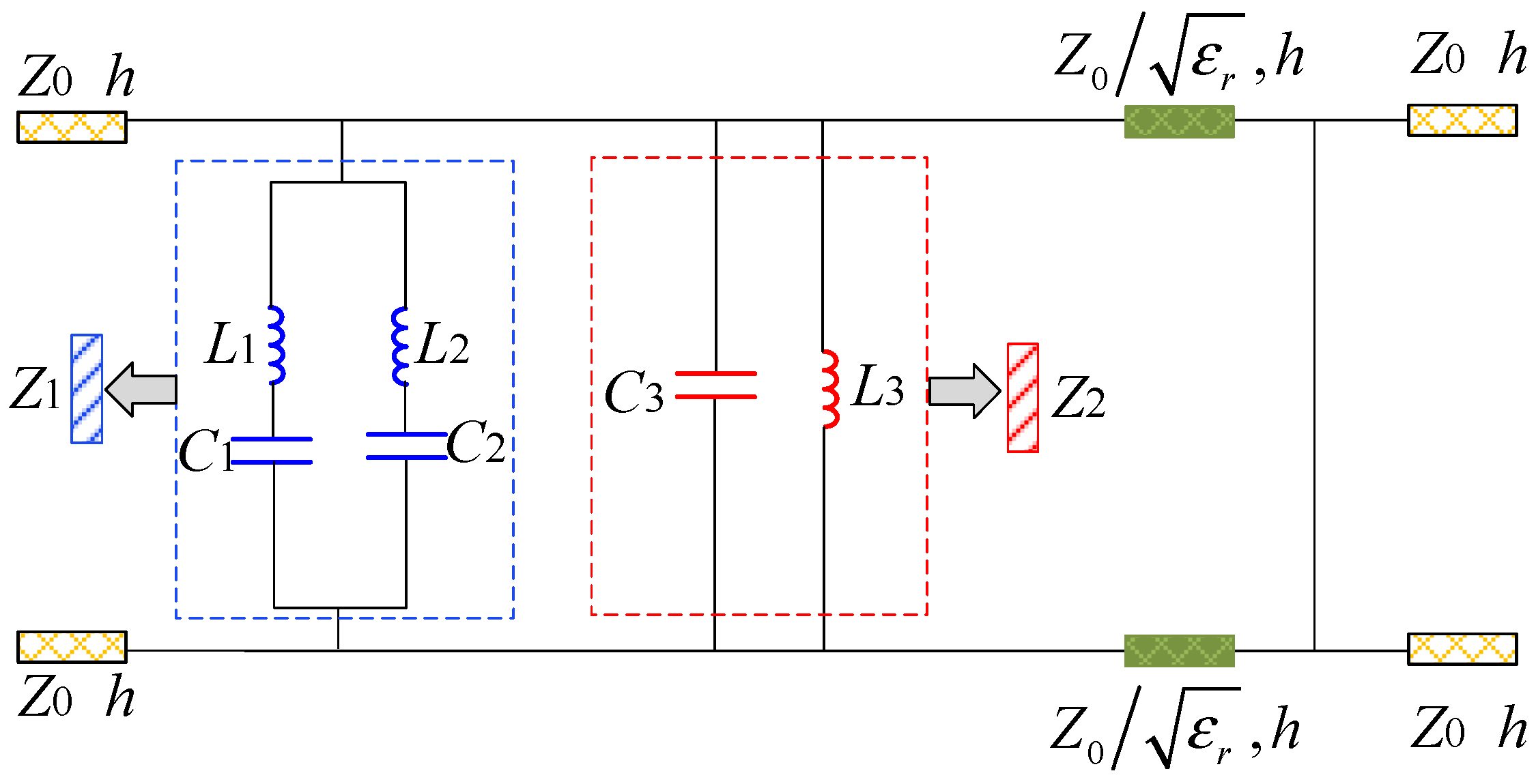
2.1.2. The Operating Mechanism of the Designed OF-FSS
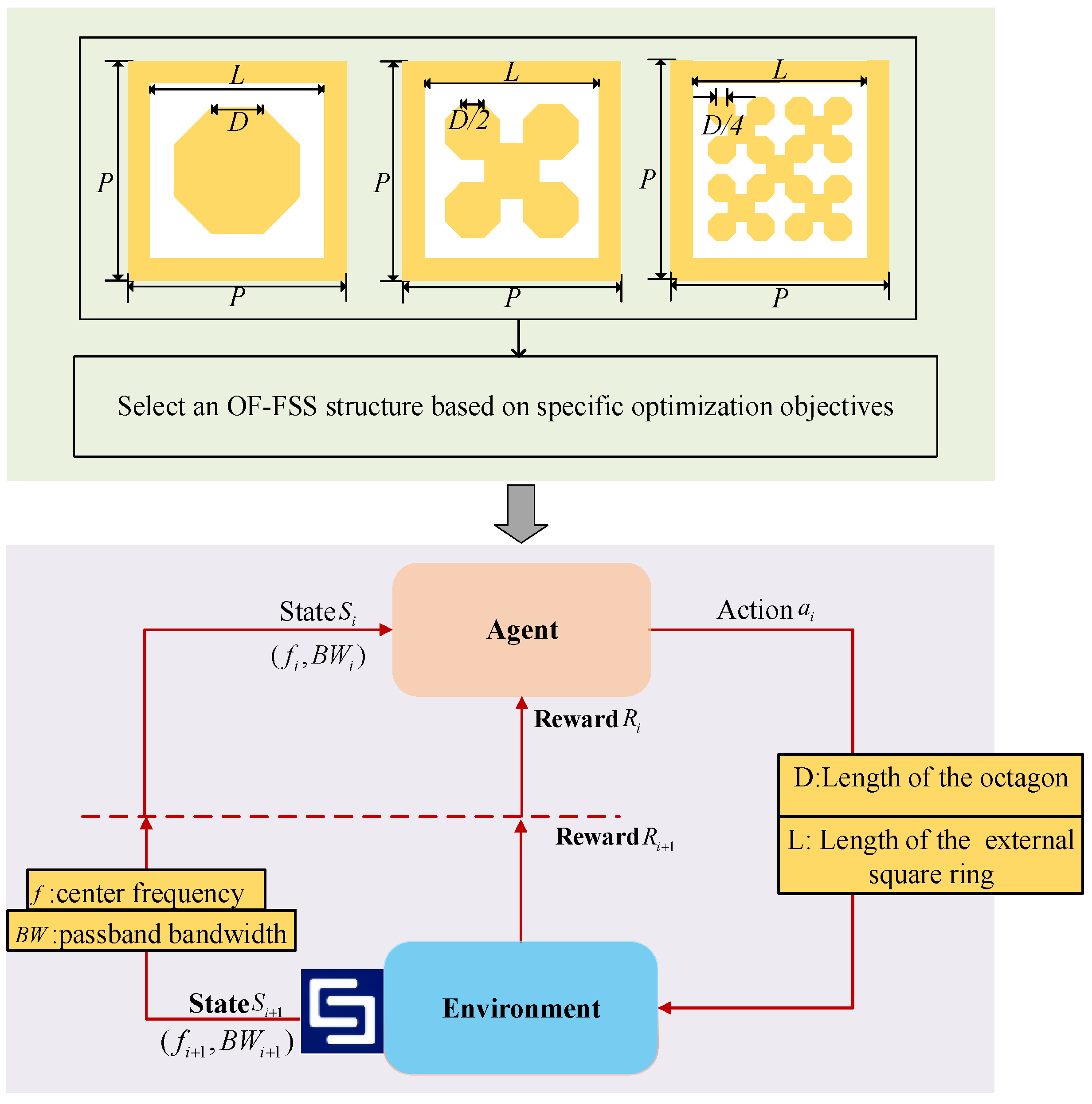
2.2. Physics-Informed Reinforcement Learning for OF-FSS
2.2.1. Environment (CSTEnv)
2.2.2. State Space
2.2.3. Action Space
2.2.4. Reward Function
2.2.5. Agent Implementation and Training Process
| Algorithm 1: PIRL for OF-FSS Optimization |
| Initialization: Learning rate , discount factor , -greedy (Epsilon), Epsilon_min, Epsilon_decay, Q-table arbitrarily for all state-action pairs. Process: For episode = 1 to M do: Reset the environment CSTEnv and get initial state For step t = 1 to T do: With probability : choose a random action from the full action space A. Otherwise: choose action End if Execute action and obtain reward Store {} in Q-table If meets | − | < and | − | < then break (Exit step loop for this episode) End if End for End for |
3. Optimization Results
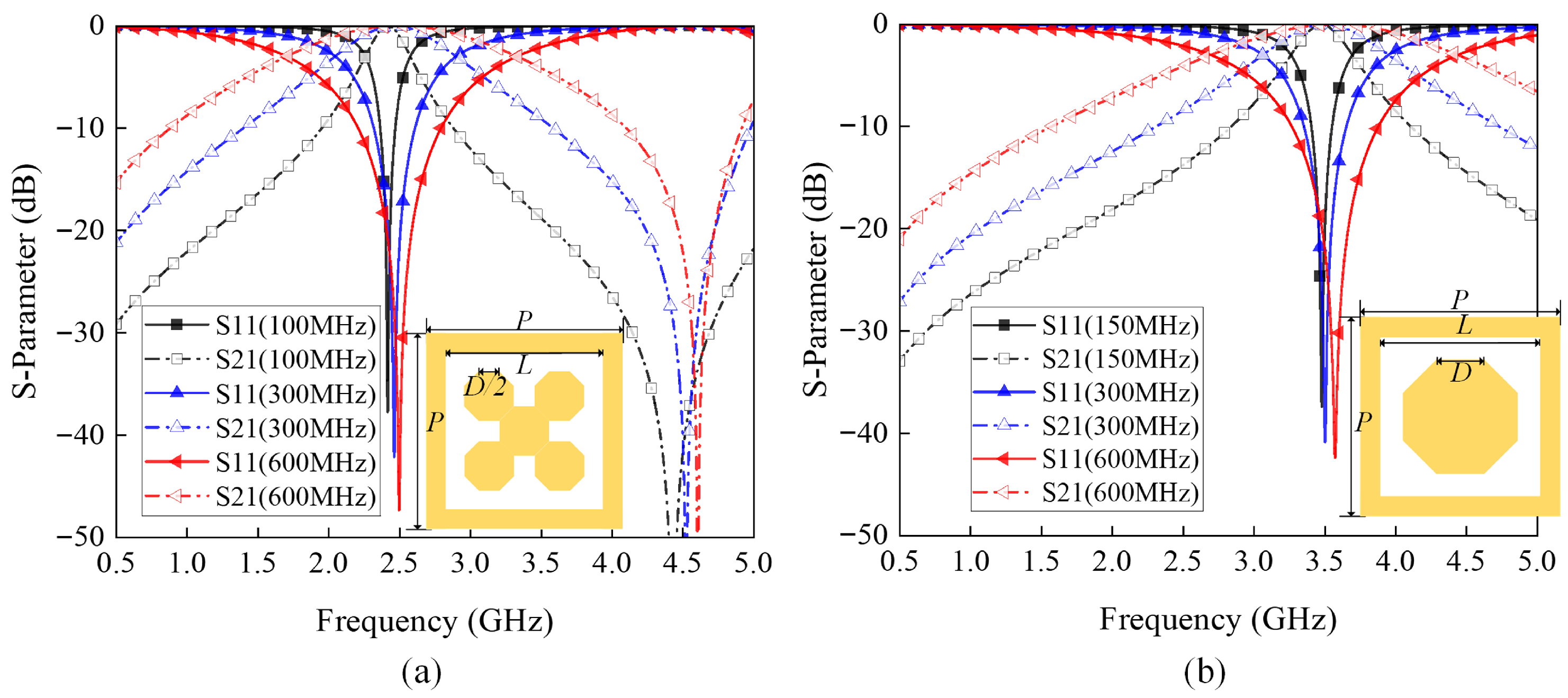
3.1. Single Band Optimization at 2.4 GHz and 3.5 GHz
3.2. Dual-Band Optimization at 1.8 GHz/3.5 GHz
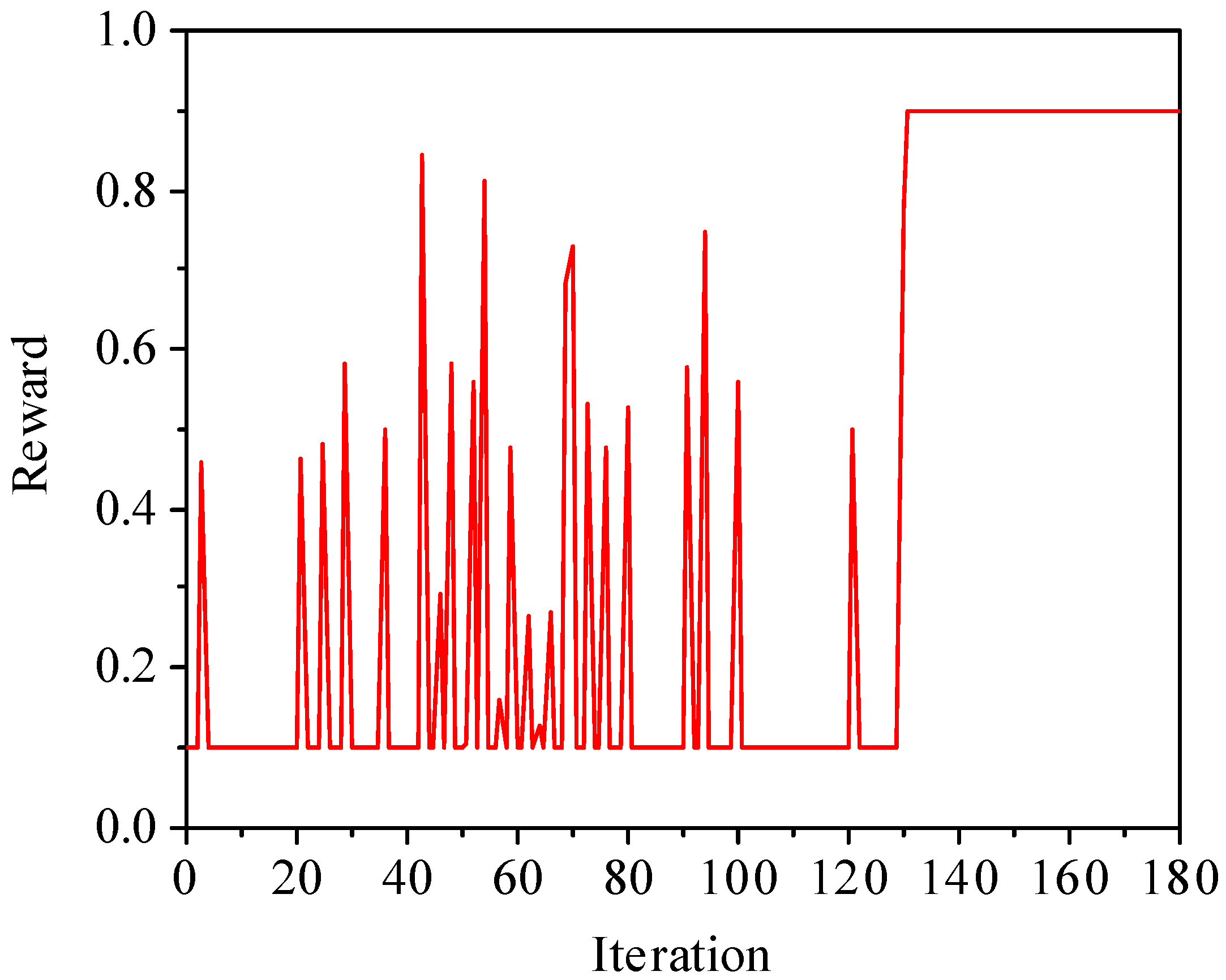
3.3. Analysis of Simulation Time and Convergence Characteristics
4. Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CST | Computer Simulation Technology |
| HFSS | High-Frequency Structure Simulator |
| OF-FSS | Octagonal fractal frequency-selective surface |
| PIRL | Physics-informed reinforcement learning |
| FSSs | Frequency-selective surfaces |
| FSAs | Frequency-selective absorbers |
| ML | Machine learning |
| SVMs | Support vector machines |
| VAE | Variational autoencoder |
| DNN | Deep neural network |
| RL | Reinforcement learning |
| KBDRL | Knowledge-based deep reinforcement learning |
| RINN | Relational induction neural network |
| DDPG | Deterministic policy gradient |
References
- Xiao, T.; Liao, Q.; Tang, G.; Huang, L.; Wang, H.; Liu, C.; Lin, F. A Novel Frequency-Selective Polarization Converter and Application in RCS Reduction. Electronics 2025, 14, 1280. [Google Scholar] [CrossRef]
- Zhang, H.; Si, L.; Ma, T.; Dong, L.; Niu, R.; Bao, X.; Sun, H.; Ding, J. Triple-band terahertz chiral metasurface for spin-selective absorption and reflection phase manipulation. Electronics 2022, 11, 4195. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zeng, Y.; Liu, X. Explainable Encoder–Prediction–Reconstruction Framework for the Prediction of Metasurface Absorption Spectra. Nanomaterials 2024, 14, 1497. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, L.; Zhao, X.; Gao, R.X.-K. An ultrawideband frequency selective surface absorber with high polarization-independent angular stability. IEEE Antennas Wirel. Propag. Lett. 2022, 22, 789–793. [Google Scholar] [CrossRef]
- Guo, C.; Li, J. Polarization-Multiplexed Transmissive Metasurfaces for Multifunctional Focusing at 5.8 GHz. Electronics 2025, 14, 1774. [Google Scholar] [CrossRef]
- Ren, X.; Liu, Y.; Ji, Z.; Zhang, Q.; Cao, W. Ultra-Wideband Passive Polarization Conversion Metasurface for Radar Cross-Section Reduction Across C-, X-, Ku-, and K-Bands. Micromachines 2025, 16, 292. [Google Scholar] [CrossRef]
- Xu, J.; Liu, J.; Hao, R.; Chen, G.; Wang, W.; Li, H.; Sheng, P.; Li, Y.; Kong, J.; Zhao, J. Simulation of Circular Dichroism in a Three-Layer Complementary Chiral Metasurface. Photonics 2025, 12, 228. [Google Scholar] [CrossRef]
- Zhang, S.; Qin, Q.; Hua, M. A Wideband Polarization-Insensitive Bistatic Radar Cross-Section Reduction Design Based on Hybrid Spherical Phase-Chessboard Metasurfaces. Coatings 2024, 14, 1130. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Y.; Xu, R.; Ren, P.; Xiang, Z. Design of a multi-passband metasurface with ultra-high angular stability based on complementary frequency selective surfaces. Opt. Express 2025, 33, 32862–32880. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Y.; Ren, P.; Xu, B.; Xu, R.; Xiang, Z. Design of angle-selective surface with narrow-angle filtering for variable frequency. IEEE Antennas Wirel. Propag. Lett. 2025, 24, 1487–1491. [Google Scholar] [CrossRef]
- Li, Y.; Ren, P.; Chen, R.; Xu, B.; Xiang, Z.; Wang, M. Design of miniaturized frequency selective rasorber based on complementary bandpass FSS for 5G applications. IEEE Trans. Electromagn. Compat. 2024, 66, 636–639. [Google Scholar] [CrossRef]
- Prado, D.R.; Lopez-Fernandez, J.A.; Arrebola, M.; Goussetis, G. Support vector regression to accelerate design and crosspolar optimization of shaped-beam reflectarray antennas for space applications. IEEE Trans. Antennas Propag. 2018, 67, 1659–1668. [Google Scholar] [CrossRef]
- Prado, D.R.; López-Fernández, J.A.; Arrebola, M.; Pino, M.R.; Goussetis, G. Wideband shaped-beam reflectarray design using support vector regression analysis. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2287–2291. [Google Scholar] [CrossRef]
- Abdullah, M.; Koziel, S. Supervised-learning-based development of multibit RCS-reduced coding metasurfaces. IEEE Trans. Microw. Theory Tech. 2021, 70, 264–274. [Google Scholar] [CrossRef]
- Koziel, S.; Abdullah, M. Machine-learning-powered EM-based framework for efficient and reliable design of low scattering metasurfaces. IEEE Trans. Microw. Theory Tech. 2021, 69, 2028–2041. [Google Scholar] [CrossRef]
- Hodge, J.A.; Mishra, K.V.; Zaghloul, A.I. RF metasurface array design using deep convolutional generative adversarial networks. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; pp. 1–6. [Google Scholar]
- Fan, J.A. Generating high performance, topologically-complex metasurfaces with neural networks. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; pp. 1–2. [Google Scholar]
- Naseri, P.; Goussetis, G.; Fonseca, N.J.G.; Hum, S.V. Inverse design of a dual-band reflective polarizing surface using generative machine learning. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–5. [Google Scholar]
- Xiao, L.Y.; Jin, F.L.; Wang, B.Z.; Liu, Q.H. Efficient inverse extreme learning machine for parametric design of metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 992–996. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, J.; Han, Y.; Sui, S.; Qiu, T.; Jia, Y.; Feng, M.; Wang, X.; Zheng, L.; Qu, S. Design of aperture-multiplexing metasurfaces via back-propagation neural network: Independent control of orthogonally-polarized waves. IEEE Trans. Antennas Propag. 2022, 70, 4569–4575. [Google Scholar] [CrossRef]
- Wei, Z.; Zhou, Z.; Wang, P.; Ren, J.; Yin, Y.; Pedersen, G.F.; Shen, M. Equivalent circuit theory-assisted deep learning for accelerated generative design of metasurfaces. IEEE Trans. Antennas Propag. 2022, 70, 5120–5129. [Google Scholar] [CrossRef]
- Naseri, P.; Hum, S.V. A generative machine learning-based approach for inverse design of multilayer metasurfaces. IEEE Trans. Antennas Propag. 2021, 69, 5725–5739. [Google Scholar] [CrossRef]
- Naseri, P.; Pearson, S.; Wang, Z.; Hum, S.V. A combined machine-learning/optimization-based approach for inverse design of nonuniform bianisotropic metasurfaces. IEEE Trans. Antennas Propag. 2021, 70, 5105–5119. [Google Scholar] [CrossRef]
- Nadell, C.C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep learning for accelerated all-dielectric metasurface design. Opt. Express 2019, 27, 27523–27535. [Google Scholar] [CrossRef]
- Liu, H.; Zong, Z.; Li, Y.; Jin, D. NeuroCrossover: An intelligent genetic locus selection scheme for genetic algorithm using reinforcement learning. Appl. Soft Comput. 2023, 146, 110680. [Google Scholar] [CrossRef]
- Zhu, E.; Wei, Z.; Xu, X.; Yin, W.-Y. Fourier subspace-based deep learning method for inverse design of frequency selective surface. IEEE Trans. Antennas Propag. 2021, 70, 5130–5143. [Google Scholar] [CrossRef]
- Cong, R.; Liu, N.; Li, X.; Wang, H.; Sheng, X. Design of wideband frequency selective surface based on the combination of the equivalent circuit model and deep learning. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2110–2114. [Google Scholar] [CrossRef]
- Zhu, E.; Li, E.; Wei, Z.; Yin, W.-Y. Adversarial-network regularized inverse design of frequency-selective surface with frequency-temporal deep learning. IEEE Trans. Antennas Propag. 2022, 70, 9460–9469. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, H.; Wang, J.; Yuan, S.; Feng, W. LSTM-GAN-AE: A promising approach for fault diagnosis in machine health monitoring. IEEE Trans. Instrum. Meas. 2021, 71, 1–13. [Google Scholar] [CrossRef]
- Wei, Z.; Zhou, Z.; Wang, P.; Ren, J.; Yin, Y.; Pedersen, G.F.; Shen, M. Fully automated design method based on reinforcement learning and surrogate modeling for antenna array decoupling. IEEE Trans. Antennas Propag. 2022, 71, 660–671. [Google Scholar] [CrossRef]
- Peng, F.; Chen, X. An antenna optimization framework based on deep reinforcement learning. IEEE Trans. Antennas Propag. 2024, 72, 7594–7605. [Google Scholar] [CrossRef]
- Wei, Z.; Zhou, Z.; Wang, P.; Ren, J.; Yin, Y.; Pedersen, G.F.; Shen, M. Automated antenna design via domain knowledge-informed reinforcement learning and imitation learning. IEEE Trans. Antennas Propag. 2023, 71, 5549–5557. [Google Scholar] [CrossRef]
- Liu, H.; Li, T.; Jiang, F.; Su, W.; Wang, Z. Coverage optimization for large-scale mobile networks with digital twin and multi-agent reinforcement learning. IEEE Trans. Wirel. Commun. 2024, 23, 18316–18330. [Google Scholar] [CrossRef]
- Liu, H.; Huang, W.; Kim, D.I.; Sun, S.; Zeng, Y.; Feng, S. Towards efficient task offloading with dependency guarantees in vehicular edge networks through distributed deep reinforcement learning. IEEE Trans. Veh. Technol. 2024, 73, 13665–13681. [Google Scholar] [CrossRef]
- Liu, H.; Su, W.; Li, T.; Huang, W.; Li, Y. Digital twin enhanced multi-agent reinforcement learning for large-scale mobile network coverage optimization. ACM Trans. Knowl. Discov. Data 2024, 19, 1–23. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.X.; Dong, W.H.; Wang, X.; Shi, J.; Teng, H.-L.; Dai, X.-W.; Yau, S.S.-T.; Liang, C.-H.; Feng, P.-F. Microwave integrated circuits design with relational induction neural network. arXiv 2019, arXiv:1901.02069. [Google Scholar] [CrossRef]
- Su, Y.; Yin, Y.; Li, S.; Zhao, H.; Yin, X. Bandwidth Improvement for Patch Antenna via Knowledge-Based Deep Reinforcement Learning. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 4094–4098. [Google Scholar] [CrossRef]
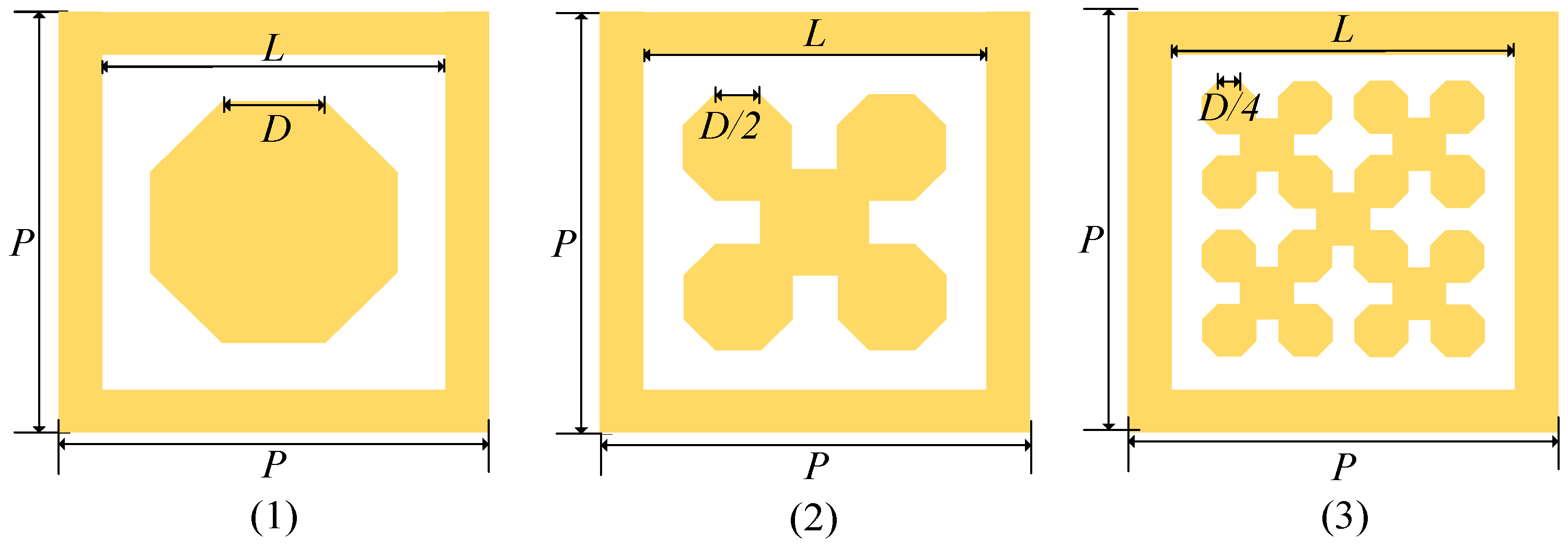
| Variable | Value |
|---|---|
| Learning rate | 0.0001 |
| Discount factor | 0.99 |
| -greedy (Epsilon) | 0.1 |
| Epsilon_min | 0.05 |
| Epsilon_decay | 0.92 |
| Maximum episode M | 1 |
| Maximum steps of each episode T | 700 |
| Target Bandwidth | 100 MHZ | 300 MHZ | 600 MHZ |
|---|---|---|---|
| Actual Bandwidth | 106 MHz | 301 MHz | 598 MHz |
| L (mm) | 22.44 | 28.94 | 32.80 |
| D (mm) | 7.39 | 8.49 | 7.88 |
| Target Bandwidth | 150 MHZ | 300 MHZ | 600 MHZ |
|---|---|---|---|
| Actual Bandwidth | 146 MHz | 300 MHz | 599 MHz |
| L (mm) | 17.30 | 21.11 | 25.42 |
| D (mm) | 5.41 | 6.63 | 6.58 |
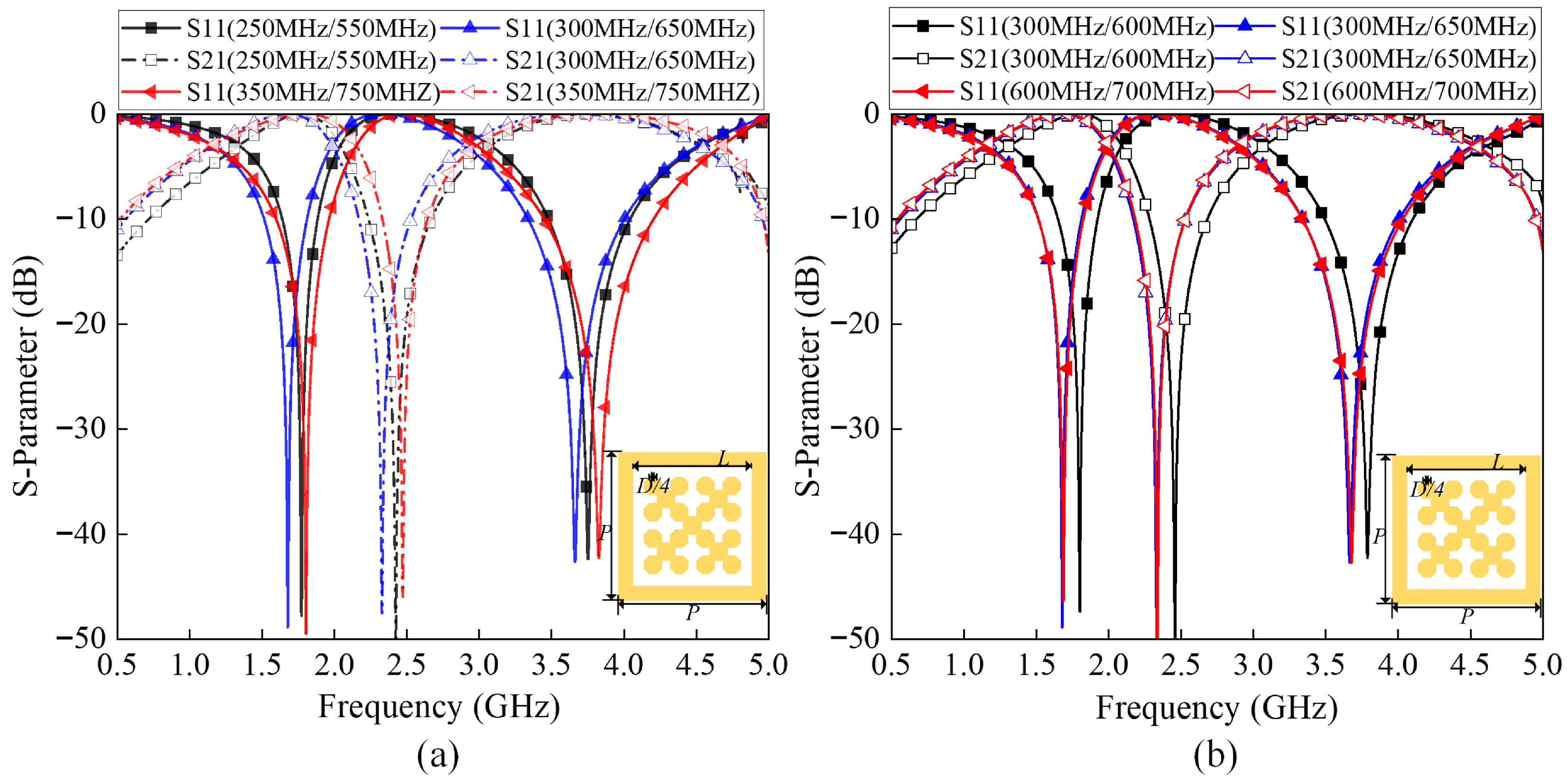
| Target Bandwidth | 250/550 MHz | 300/600 MHz | 300/650 MHz | 300/700 MHz | 350/750 MHz |
|---|---|---|---|---|---|
| Actual Bandwidth | 245/566 MHz | 273/609 MHz | 297/668 MHz | 312/694 MHz | 367/758 MHz |
| L (mm) | 51.29 | 52.32 | 55.05 | 55.51 | 56.19 |
| D (mm) | 10.18 | 10.01 | 10.68 | 10.66 | 9.84 |
| Literature | Core Technology | Operating Frequency | Frequency Migrability | Polarization Sensitive | Physical Interpretability |
|---|---|---|---|---|---|
| [26] | FS-BDLM + FSS | Dual Band | N | N | N |
| [27] | ECM + CNN + FSS | Three Band | N | N | Y |
| [28] | AR-FTDL + FSS | Single Band | N | N | N |
| Baseline | PSO | Single Band | N | N | N |
| This work | PIRL + OF-FSS | Single and Dual Band | Y | N | Y |
| Objective BW | 150 MHz | 300 MHz | 600 MHz | |
|---|---|---|---|---|
| PSO | ΔBW | 66 MHz | 4 MHz | 6 MHz |
| Iteration | 700 | 533 | 430 | |
| PIRL | ΔBW | 4 MHz | 0 MHz | 1 MHz |
| Iteration | 42 | 169 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, G.; Liu, M.; He, X. Physics-Informed Reinforcement Learning for Multi-Band Octagonal Fractal Frequency-Selective Surface Optimization. Electronics 2025, 14, 4656. https://doi.org/10.3390/electronics14234656
Dong G, Liu M, He X. Physics-Informed Reinforcement Learning for Multi-Band Octagonal Fractal Frequency-Selective Surface Optimization. Electronics. 2025; 14(23):4656. https://doi.org/10.3390/electronics14234656
Chicago/Turabian StyleDong, Gaoya, Ming Liu, and Xin He. 2025. "Physics-Informed Reinforcement Learning for Multi-Band Octagonal Fractal Frequency-Selective Surface Optimization" Electronics 14, no. 23: 4656. https://doi.org/10.3390/electronics14234656
APA StyleDong, G., Liu, M., & He, X. (2025). Physics-Informed Reinforcement Learning for Multi-Band Octagonal Fractal Frequency-Selective Surface Optimization. Electronics, 14(23), 4656. https://doi.org/10.3390/electronics14234656







