A Blockchain-Based Architecture for Energy Trading to Enhance Power Grid Stability

Abstract

The integration of renewable energy sources (RES) and distributed energy resources (DER) into local energy markets is transforming modern power grids toward a decentralized architecture. To enhance the efficiency of decentralized energy trading, blockchain technology has been widely adopted in constructing peer-to-peer energy trading platforms, providing incentives for renewable energy generation and utilization. However, the rapid growth of small-scale suppliers and intermittent DERs introduces significant challenges to grid stability, including supply–demand imbalances and voltage fluctuations. To address these challenges, we propose a blockchain-based energy trading system architecture designed to enable a self-regulating, sustainable, and resilient grid. The proposed system architecture achieves grid stability through three key components: (i) precise endpoint control via AI Agents with lightweight forecasting models integrated into existing hardware systems, (ii) flexible distributed control through an efficient incentive mechanism, named Proof of Prediction, based on a blockchain-based automated trading process, and (iii) macro-level coordination via global regulation roles. We implemented a prototype of the proposed architecture on the Ethereum Blockchain and applied it to a microgrid-scale distributed automated trading environment. Our evaluation results show that using the architecture we proposed achieves a peak-shaving rate of up to 29.6%, while maintaining the overall supply–demand deviation of around 5% on average, demonstrating its strong potential as a foundation for building stable and modern power grids.

1. Introduction

Traditional energy markets operate under a centralized and fossil-fuel-dominated model, where electricity is generated by large power plants and delivered unidirectionally to end users through local power distributors (LPDs) and distributed system operators (DSOs) [1], as illustrated in Figure 1 (left). With the increasing penetration of renewable energy sources (RES) and distributed energy resources (DERs) [2], many consumers become capable of both producing and consuming electricity, named “prosumers” [3], resulting in complex bidirectional peer-to-peer (P2P) energy flows inside local energy markets (LEMs), as shown in Figure 1 (right). Under this transformation, traditional centralized market mechanisms lack the flexibility and efficiency needed to support P2P energy trading, leading to inefficient coordination and limited economic motivation for prosumers, which ultimately slows down the energy transition [4,5,6]. In this context, blockchain, as an advanced decentralized distributed ledger technology (DLT), has been adopted as a cutting-edge technology to support the prosperity of local energy markets [7]. The application of blockchain has enabled effective decentralized market operations, strengthened grid decentralization, and facilitated the integration of RES and DERs, thus reducing the dependence of power grids on fossil fuel-based centralized generation [8,9,10,11]. In addition, smart contracts automate the energy trading process and provide price transparency, fostering a free trading scheme and unlocking the full potential of local energy markets [12]. However, the large-scale integration of RES and DERs, such as smart meters, solar panels, and electric vehicles (EVs), has gradually transformed the modern power grid into a highly dynamic, decentralized, and heterogeneous system. The increasing uncertainty introduced by flexible loads and intermittent generation makes maintaining grid stability a critical challenge, one that is indispensable for ensuring the continuity of daily life and economic activities [11].

To fill this gap, this paper systematically analyzes the operational characteristics of modern power grids and examines the challenges and requirements for maintaining grid stability under high penetration of dynamic loads such as RES and DERs. Building on this analysis, we propose a modular and general blockchain-based energy trading architecture that provides a fundamental platform for decentralized local energy markets, aiming to ensure both efficient P2P energy trading and the preservation of power grid stability. The main contributions of this paper are as follows:

• We systematically analyze the inefficiencies of modern power grid management and operational models under large-scale adoption of dynamic loads, and identify the fundamental structures and requirements for building stable modern power grids, while also outlining the challenges in fulfilling these requirements.
• We propose a modular blockchain-based energy trading architecture that flexibly integrates existing hardware and power grid technologies as fundamental components. The architecture enables efficient end-user management through precise forecasting and real-time monitoring at grid endpoints, while leveraging blockchain consensus mechanisms and smart contracts to achieve highly efficient global distributed control and automated trading. Furthermore, it allows the integration of regulators to realize dynamic system-wide coordination without a centralized monopoly.
• We implement a prototype at the microgrid scale. By integrating forecasting models for energy trading simulation and analysis, we demonstrate that the proposed architecture demonstrates strong capability in enabling self-management at grid endpoints, supporting distributed control and facilitating system-wide dynamic regulation, such as peak-shaving, energy market activity monitoring, and balancing energy supply and demand within the power grid.

The remainder of this paper is organized as follows. Section 2 analyzes the role and impact of blockchain in the structural and business model transformation of modern power grids, and outlines the key challenges and technical requirements for grid stability. Section 3 presents the framework of the proposed blockchain-based trading architecture. Section 4 analyzes the security of the proposed architecture. Section 5 discusses the evaluation results of the prototype. Section 6 concludes the paper and outlines directions for future work.

2. Blockchain in Modern Power Grids

The emergence of prosumers has disrupted the traditional unidirectional energy flow of power grids, giving rise to the demand for P2P energy trading. Blockchain technology has fulfilled this demand by enabling decentralized and trustless transactions, thereby laying the foundation for decentralized business models in modern power grids and fostering the growth of RESs and DERs. In this section, we draw on existing projects and research to analyze the distinct development path of blockchain applications in power grids, highlighting the impacts and emphasizing how modern power grids must continuously optimize their technical architectures to meet the increasingly diverse stability demands of users and society, while addressing the challenges that arise in this process in the Web3 era.

2.1. Stage I: Boosting P2P Energy Trading

In the initial phase, the application of blockchain technology in power grids focused primarily on facilitating transparent, efficient, and automated energy trading. On the one hand, blockchain offers a platform that enables efficient P2P trading and supports multidirectional energy flows; on the other hand, its traceability and data transparency capabilities facilitate price referencing, thereby encouraging the implementation of diverse trading mechanisms, such as energy auctions.

The Brooklyn Microgrid in New York served as a pioneering example of blockchain application in energy systems [13]. Initiated by LO3 Energy, the project enabled residents to generate, store, and trade energy locally on a blockchain platform, thereby reducing reliance on centralized utilities and promoting the adoption of renewable energy. Mengelkamp et al. [14] conducted a seminal study on the Brooklyn Microgrid, demonstrating how blockchain facilitated P2P energy trading within a community and improved local energy resilience and autonomy. Besides, during the Quartierstrom research project in Switzerland, a test environment was established in Walenstadt and real-world tests were performed [15,16]. Power Ledger, an Australian company, implemented blockchain-based energy trading platforms in several locations, including Australia, Thailand, and the United States [17], which enabled consumers to buy and sell excess solar power directly, improving trading efficiency and supporting renewable energy integration. Other pilot programs, such as the Enerchain project in Europe [18], explored blockchain for wholesale energy trading, demonstrating its potential to streamline processes and reduce transaction costs. Building on these practical experiences, Andoni et al. [19] provided a comprehensive review of blockchain applications in the energy sector, highlighting its potential to enhance transparency, security, and efficiency in energy transactions. In parallel, theoretical models were also proposed; for example, researchers developed blockchain-based frameworks for decentralized energy markets, using smart contracts to automate transactions and establish trust among participants [20]. Collectively, these studies underscored the transformative potential of blockchain in modernizing the power grids [14].

In this stage, the integration of blockchain technology primarily served to steer the local energy market’s evolution from conventional centralized structures toward more efficient decentralized trading structures, thereby improving consumer engagement with RES and DERs. However, most projects and related research at this stage neglected grid stability considerations. As demonstrated by several pilot implementations, the intermittency of solar generation, the midday production peak, and the evening demand surge introduced substantial volatility and underscored the lack of dynamic distributed control mechanisms, which ultimately hindered large-scale deployment. The inherent tension between market liberalization and operational stability that emerged during this period established a crucial basis for the subsequent refinement of blockchain integration within power grid operations.

2.2. Stage II: Limited Distributed Control Mechanism

In the second stage, the volatility introduced by RES and DERs increasingly came into focus due to its impact on daily life and industrial activities. Subsequent studies introduced distributed control mechanisms aimed at mitigating the potential effects of grid imbalances and instability on both daily and economic operations.

Existing research on distributed control in local energy markets generally follows two directions. One research line integrates blockchain directly into smart-meter or energy-management systems to enhance demand-side management through transparent data sharing [21]. For instance, Boumaiza [22] demonstrates that blockchain-enhanced demand-side management can improve energy efficiency, user engagement, and operational flexibility. Smart contracts have also been used to support autonomous scheduling and state monitoring of distributed energy resources (DERs) [23,24]. Danzi et al. [25] propose a proportional-fairness control scheme for microgrids, where smart contracts selectively reduce DERs output to prevent voltage violations and dynamically determine participating nodes based on historical control contributions. Yang et al. [26] model DERs interaction as a distributed optimization problem deployed on blockchain to ensure transparent and verifiable scheduling decisions. In parallel, machine-learning-based approaches have recently emerged to improve demand-side management. MAS-DR [27] introduces an ML-based consumer segmentation and aggregation framework that clusters residential users to support targeted demand–response programs. Michalakopoulos et al. [28] present a large-scale load-profiling pipeline that compares multiple clustering algorithms and then applies explainable classification to emulate the clustering decisions for scalable DR targeting. Sarmas et al. [29] propose an explainable ensemble clustering method for residential load profiles, combining hierarchical clustering with a follow-the-leader mechanism to avoid predefining the number of clusters and to improve interpretability for DR program design.

In this stage, the increasing uncertainty caused by the massive integration of DERs and RES has attracted widespread concern, making the design of a stable grid architecture a critical research focus. However, existing blockchain-based control methods follow an integrated, “all-in-one” paradigm, but latency, throughput, and integration overhead prevent real-time, fine-grained control at smart-meter granularity. Conversely, ML-based demand-side management techniques achieve local efficiency but lack global coordination and hardware-level interaction, limiting their applicability in highly decentralized and dynamic environments.

2.3. Challenges and Requirements

As the power grid transitions toward a highly distributed structure, maintaining grid stability has become increasingly complex. Our objective in this paper is to develop a blockchain-based energy trading architecture that can achieve a decentralized, dynamic, and stable power grid ecosystem. To achieve this, we outline the key challenges and corresponding requirements as follows.

• The intermittent and unstable characteristics of RES and DERs lead to increased fluctuations in the modern power grid. Accurate forecasting of energy production and consumption at grid endpoints (definition in Section 3.1) is a fundamental prerequisite for maintaining grid stability.
• The composition and activities of endpoints in modern power grids are increasingly complex. Incorporating incentive mechanisms into blockchain-based transaction logic to strengthen demand-side management is fundamental to enhancing the controllability of grid endpoints.
• Modern power grids are more sensitive to environmental conditions because of DERs. Meanwhile, the immediacy of energy demand often conflicts with the latency of energy transactions. Therefore, energy trading architecture must retain the capacity for effective macro-level regulation while preventing third parties from monopolization.
• The high manufacturing and installation costs of existing hardware systems necessitate that the energy trading architecture be complementary, providing coverage and adaptability to integrate with existing setups.
• A blockchain-based energy trading architecture must ensure the transparency of transaction data, while simultaneously safeguarding privacy-sensitive information from potential leakage in anonymous environments.

We refer to the energy trading architecture that meets the above requirements as the foundational infrastructure of “Stage III”, which we denote as “Towards a Stable, Controllable, and Decentralized Era”, and propose a comprehensive design framework for its construction in the following section.

3. A Blockchain-Based Architecture for Power Grid Stability

With the integration of RES and DERs, the composition, trading structure, and commercial activities of modern local energy markets have undergone substantial changes compared to traditional centralized models. In order to improve the generalizability of the proposed energy trading architecture, this section begins by defining a generic business model tailored for modern local energy markets. Based on this model, we propose a structured framework of our blockchain-based energy trading architecture that provides fine-grained component interfaces to enable efficient real-time energy trading while ensuring the overall stability of the power grid.

3.1. Business Model

In this paper, we focus on medium-scale local energy markets, such as city-level markets defined by geographic boundaries, and treat them as subunits of the broader energy market, which serves as the primary research focus of most research and practical projects [1,6]. We abstract the business model of modern local energy markets into four essential components: market roles, market assets, market ownership and objectives, and market trading mechanisms.

Definition 1 

(Market Roles). Market roles in a local energy market refer to various entities that perform distinct functions.

In our model, there are four important market roles:

• Prosumer: A prosumer is an entity that both produces and consumes energy. Unlike the central power grid, a prosumer generates energy through distributed generation units. Prosumers are primary production units in a modern local energy market.
• Consumer: A consumer is an entity that purchases and uses electricity without participating in production.
• Local Power Distributor, LPD: An LPD is an entity responsible for distributing electricity within a specific geographic area. In a centralized local energy market, it is typically operated by an authoritative third party. In our model, LPDs offload most of their transactional functions and primarily assume the role of grid regulator.
• Distributed System Operator, DSO: A DSO is an entity responsible for managing the grid infrastructure, such as providing smart meters.

Definition 2 

(Market Assets). Market assets in a local energy market refer to the physical and digital resources involved in the production, storage, consumption, and distribution activities conducted by different market roles.

In our model, there are four key market assets:

• Household Assets: Devices that do not directly participate in market trading but indirectly influence the activities of market roles.
• Battery: A decentralized energy storage device that stores electricity for later use, enhancing grid stability, demand response, and energy arbitrage in local energy markets.
• Electric Vehicles, EVs: Mobile energy assets equipped with batteries.
• Smart Meters: An advanced metering device that enables real-time measurement, monitoring, and communication of electricity consumption and generation.

In this context, the term battery refers to grid public assets that serve as hardware for power buffering and stability maintenance. Household assets may also include privately owned home batteries, which belong to individual users. Due to their mobility, EVs can directly participate in grid activities such as smart charging and are therefore not classified as household assets. Moreover, at the current stage, smart meters are centrally managed by the DSO. Since our design in the following section builds upon the existing hardware infrastructure, we classify smart meters as grid public assets.

Definition 3 

(Market Ownership and Objectives). Market ownership refers to the structure and control of the local energy market, defining the key stakeholders responsible for operation, regulation, and benefiting from market transactions. Market ownership of a local energy market directly determines the market’s optimization objectives.

In our model, we define the local energy market as collectively owned [1], with dynamic supply-demand balancing as its primary objective:

$$min\sum _{t=1}^T\left|P_g^t+P_b^t+P_{ev}^t+P_{LPD}^t-P_d^t-L^t\right|+\lambda \sum _{t=1}^T{P}_{LPD}^t,$$

(1)

where t denotes the discrete time period (e.g., hourly or daily), and T is the total number of time periods considered. $P_g^t$ denotes power generated by DERs, $P_b^t$ denotes power charged/discharged from the battery, $P_{ev}^t$ denotes the power exchanged with electric vehicles, which is equal to mobile batteries, $P_{LPD}^t$ denotes power supplied by the LPD (imported from the external grid), $P_d^t$ denotes power demand, $\lambda$ denotes the weighted factor that penalizes external grid reliance, $\alpha$ is the loss coefficient of the power transmission, $L^t$ denotes transmission loss,

$$L^t=\alpha {(P_g^t+P_b^t+P_{ev}^t+P_{LPD}^t)}^2.$$

(2)

with the following constraints:

$$P_{LPD}^t\ge 0,\mathrm{only}\mathrm{if}{P}_g^t+P_b^t+P_{ev}^t<P_d^t,$$

$$\forall t,0\le P_b^t\le P_{b,max},0\le P_{ev}^t\le P_{ev,max}.$$

Definition 4 

(Market Trading Mechanism). The trading mechanism of a local energy market refers to the structured process of energy exchange among market roles, including transaction flows, price setting, and energy flows.

In our model, we adopt a P2P trading network, where any role in the local energy market can act as a buyer or seller and directly trade energy through a digital platform. To incentivize energy production, sellers use an auction-based approach [1] to determine energy prices and allocation. Buyers and sellers submit bids, and the market clears at a price that balances supply and demand regularly according to the setting.

3.2. Summary of the Implementation Framework

As described in Section 3.1, we regard the power grid composed of medium-sized local energy markets as an independent unit within the overall energy market, which is collectively owned and primarily aims to maintain grid stability. Given that prosumers, serving as the primary energy producers in the grid, rely heavily on DERs, their production is significantly influenced by environmental factors. Therefore, to better reflect real-world conditions, the macro-level power plants (mainly composed of production units fueled by fossil fuel) need to exist within the whole energy market, but primarily serve as a supportive coordinator.

As shown in Figure 2 (left), the macro energy market consists of different power grids and power plants [1], which together form a regulatory platform for system-wide coordination (i.e., another macro blockchain). The framework of the internal energy trading architecture of a single power grid is illustrated in Figure 2 (right), which is the primary focus of the design proposed in this paper. We refer to participants directly involved in power grid activities as grid endpoints or endpoints, which include any market role or large mobile market assets mentioned in Section 3.1, such as EVs. In a power grid, our proposed energy trading architecture consists of three components: Endpoint Mini Server, Blockchain Trading Platform, and LEM Management Platform. The Endpoint Mini-Server (EMS) is deployed at each grid endpoint and maintained by the household corresponding user (i.e., consumer or prosumer). The primary function of the EMS is to encapsulate the operational logic of the endpoint and interface with the underlying hardware. We implement the EMS as a workflow-driven AI agent that integrates predictive models to accurately forecast the production and consumption of each endpoint. EMS is used to enhance endpoint controllability, reduce uncontrollable fluctuations, and improve the overall predictability of supply and demand in the grid through data exchange between the endpoint and LPD. The Blockchain Trading Platform (BTP), jointly maintained by all grid endpoints, facilitates automated energy trading via smart contracts. We employ an advanced token-based incentive mechanism, named Proof of Prediction, rewarding accurate forecasts and penalizing deviations, thereby encouraging self-management at endpoints and achieving efficient distributed control in coordination with the EMS to reinforce system-wide management. The Local Energy Market Management Platform (LEMMP) is operated by DSOs and LPDs and functions as a blockchain node. LEMMP performs macro-level coordination by leveraging endpoint forecasts to adjust the supply–demand balance of the whole power grid, for instance, by importing external energy, thus mitigating imbalances caused by exogenous factors such as weather variability.

In summary, the core design of our energy trading architecture is as follows, and we will introduce each component in detail in the subsequent parts.

• Propose a component-based architecture to encapsulate existing hardware, enabling compatible and portable upgrades for the whole grid infrastructure.
• Integrate AI agents at grid endpoints to accurately forecast production and consumption activities, and incorporate these agents into the proposed architecture to enable accurate hardware management.
• Embed user-oriented incentive mechanisms within the blockchain trading platform to enhance market engagement and strengthen demand-side management, thereby enabling efficient distributed control while reducing global coordination overhead.
• Reconfigure third-party platforms as macro-level coordinators and grid endpoints to reduce their monopolistic influence while improving overall resource allocation efficiency and macro-level regulation of the grid.
• Introduce advanced cryptographic techniques, such as zero-knowledge proofs, as foundational modules to ensure data availability and privacy in an open and anonymous environment.

3.3. Endpoint Mini-Server, EMS

Since the operational logic of a consumer is relatively straightforward within the power grid, we take a prosumer household as an example to illustrate the detailed design of the Endpoint Mini-Server. Currently, device monitors (DMs) and smart meters (SMs) are already widely deployed and centrally managed by the DSOs; large-scale hardware replacement would be prohibitively costly. To ensure compatibility, we retain the legacy smart meter system and introduce an additional control layer, named the Smart Meter Controller (SMC) as shown in Figure 2, which extracts, filters, and preprocesses hardware data to fuel EMS. The data flow from the hardware proceeds as follows. Device monitors generate real-time consumption and production data from individual household devices (e.g., a heating pump or solar panels). The smart meter aggregates data from all DMs, and the SMC further processes the aggregated stream, for example, by generating verifiability proofs based on the smart meter’s calculation logic for validation in anonymous environments, and by bridging the processed data to the EMS.

The EMS assists each endpoint in achieving intelligent prediction, local decision-making, and self-management. An EMS consists of three modules: a local forecasting component, a self-controller component (SC), and a transaction controller component (TC). The overall workflow of the EMS is illustrated in Figure 3, which is very simple and makes it easy to deploy EMS. The forecasting component is triggered by a daily timer, acquires inputs via the SMC, and applies lightweight AI models to predict future consumption and production, thereby enhancing the global coordinator’s visibility into endpoint variability and strengthening macro-level control. Based on these predictive data, the SC component and TC component, triggered by an hourly timer (The timer triggers of the SC and TC components are configured according to the frequency of the experimental dataset, which can be changed into other time intervals depending on different scenarios). They respectively execute local self-management actions and on-chain operational decisions, interacting with both the hardware and blockchain. The SC refers to the forecasted data to detect the status of local hardware and implement automated demand-side management, for example, turning off high consumption devices when detecting real consumption overtaking the forecasted data. Meanwhile, the TC periodically conducts state and profit analysis at predefined intervals and selectively generates different types of transactions (e.g., selling/Ask or purchasing/Bid energy), which are submitted to the blockchain through Web3 tools. As an integrated and automatic agent, the EMS reduces user workload while preserving endpoint controllability. In addition, users can monitor real-time data and manually adjust or intervene through user interfaces (UI).

3.4. Blockchain Trading Platform, BTP

To improve the efficiency of P2P trading and enhance distributed control, we adopt blockchain as the energy trading platform, which is jointly maintained by all EMSs in the grid. We propose using a permissioned blockchain to construct the trading platform, where identity restrictions strengthen the security of participating entities, thereby maximizing scalability and decentralization while ensuring security [30]. Endpoints equipped with EMS can first register their identities to get access to the trading network, for example, by obtaining digital certificates through a Public Key Infrastructure (PKI) [31] and registering the smart meter identity, and then establish an Identity Smart Contract (ISC) on the blockchain to store personal data, which they should keep transparent. The ISC, together with the corresponding EMS, can establish secure private communication channels based on cryptographic protocols such as the Diffie–Hellman protocol [32], thereby preventing personal information leakage caused by potential network attacks.

In addition to the identity smart contract, two further sets of smart contracts are deployed on the blockchain platform to serve as the information billboard: Trading Smart Contracts (TSC) and Consensus Smart Contracts (ConsensusSC). The TC within each EMS can use Web3 tools to publish energy sales and purchase information to the TSC. The TSC automatically conducts price-based matching between buyers and sellers to enable energy auctions and performs periodic market clearing (e.g., on a daily basis), as outlined in Section 3.2. The ConsensusSC monitors the forecasting accuracy of each EMS and issues self-management scores for different endpoints, thereby strengthening demand-side management and incentivizing reliable predictions. The interaction between the EMS and the blockchain is described in detail in Algorithms 1 and 2.

As illustrated by the red line in Algorithm 2, we propose a highly efficient consensus mechanism based on Proof-of-Stake, which we name Proof-of-Prediction (PoP). In the following, we will describe how the PoP mechanism is realized based on the consumption sequence of each endpoint, and how it incentivizes endpoints to achieve self-management. Assume at the beginning of each day (corresponding to the daily timer trigger shown in Figure 3), for each endpoint, the forecast component produces a predicted consumption sequence for the next day: $L_{pc}=\{{\widehat{c}}_1,{\widehat{c}}_2,\dots ,{\widehat{c}}_{24}\}$, where ${\widehat{c}}_t$ denotes the predicted consumption at hour t. To alleviate peak demand, a peak cleaner operator $\mathcal{P}$ is applied, which redistributes a fixed percentage $\alpha$ of the predicted load from peak hours to off-peak intervals, giving the adjusted forecast sequence: $L_{pc}^{\prime }=\mathcal{P}\left(L_{pc}\right)$. In parallel, the DSO observes the real consumption sequence of the endpoint: $L_c=\{c_1,c_2,\dots ,c_{24}\}$.

Then, for each endpoint, the prediction deviation is computed as the mean absolute error (or another proper scoring rule, e.g., CRPS [33]):

$$E_i^{\mathrm{dev}}={\displaystyle \frac{1}{24}}\sum _{t=1}^{24}\left|c_t-{\widehat{c}}_t^{\prime }\right|.$$

(3)

To further encourage stable and less fluctuating consumption patterns, we introduce a vibration factor, defined as the cumulative squared variation of the actual sequence:

$$E_i^{\mathrm{vib}}={\displaystyle \frac{1}{23}}\sum _{t=1}^{23}\left({(c_{t+1}-c_t)}^2\right).$$

(4)

Based on the above two factors, the final evaluation score of a grid endpoint i is then obtained as a weighted combination of the two components:

$$E_i=\lambda E_i^{\mathrm{dev}}+(1-\lambda )E_i^{\mathrm{vib}},\lambda \in [0, 1],$$

(5)

where $\lambda$ controls the relative importance of accuracy versus stability. The consensus mechanism is defined by selecting the endpoint with the smallest overall score $i^{*}=arg{min}_i{E}_i$ as the leader for the next block proposal. The winning endpoint $i^{*}$ is granted the right to append the block to the chain for the next day. In addition to selecting a single leader, the PoP mechanism is inherently extensible and compatible with a wide range of consensus designs. Specifically, PoP can also elect the set of endpoints attaining the minimum score, $\mathcal{L}{s}^{*}=\left\{i\in endpoints|E_i={min}_{j\in k}{E}_j\right\}$, thereby forming a k-sized committee that can be seamlessly integrated with committee-based BFT consensus protocols (e.g., [34]). Alternatively, the set $\mathcal{L}{s}^{*}$ may be interpreted as a multi-leader group, enabling PoP to naturally extend toward parallel-proposer or multi-leader consensus families (e.g., [35]).

Algorithm 1 Simulator 1 of Blockchain Trading Architecture $S_{BT{A}_1}$ (Part 1)

Algorithm 2 Simulator 1 of Blockchain Trading Architecture $S_{BT{A}_1}$ (Part 2)

In Algorithms 1 and 2, we assign the task of scoring all grid endpoints to the DSO for privacy-preserving purposes. While the blockchain is jointly maintained by all EMS nodes, directly submitting true consumption and production data into the smart contract would lead to information leakage, which could further expose the system to a range of off-chain attacks (e.g., electricity theft). Nevertheless, calculating prediction accuracy and fluctuation requires access to the actual data of all grid endpoints. To address this tension, we employ the DSO as a trusted intermediary for PoP computation. Similar to conventional smart meter networks, the DSO has access to all smart meter data. Accordingly, the DSO verifies the submitted predictions against actual measurements, computes the final scores, and publishes the next leader. This approach both preserves privacy and reduces blockchain computational overhead. However, to prevent either the DSO or endpoints from submitting falsified data, the entire computation process is supervised through zero-knowledge proofs (zk-proofs) [36], as shown in Algorithms 1 and 2.

3.5. LEM Management Platform, LEMMP

The LEM Management Platform (LEMMP) is jointly operated by the LPD and DSO and is responsible for grid supervision, dispute arbitration, and macro-level coordination through comprehensive data monitoring. As an information hub, the LEMMP stores the identity information of grid participants to enhance security control and aggregates prediction data from all endpoints to construct a global energy landscape and enable macro-level capacity forecasting. Based on these insights, the LEMMP can intervene in cases of supply–demand imbalance. For example, during an energy shortage, it can procure electricity from external grids and participate in energy auctions as a grid endpoint, and vice versa in times of surplus, as illustrated in Algorithm 3. Furthermore, given the instantaneous nature of energy trading and potential delays in transaction clearing, the LEMMP can act as an intermediary to facilitate real-time and flexible energy reallocation within the power grid.

4. Security Analysis

In this section, we analyze the security properties of the proposed architecture. Because the system is deployed in a permissioned blockchain environment, all participants possess registered identities, preventing Sybil entities [37] from joining the power grid. We consider a realistic Byzantine setting in which all parties may deviate arbitrarily from the prescribed protocol in order to increase their economic benefit. We assume the system consists of n grid endpoints and a single DSO/LPD node that manages the smart meters and calculates scores for the leader election. In the following, we examine the major attack strategies available to different roles and analyze how the architecture defends against them.

Algorithm 3 Simulator 2 of Blockchain Trading Architecture $S_{BT{A}_2}$

• Security Against Malicious Grid Endpoints. The PoP consensus mechanism selects leaders based on the deviation and vibration metrics, rather than hash power or stake. Therefore, the core security requirement is to ensure that grid endpoints cannot manipulate their consumption or prediction traces to gain an unfair advantage. We analyze several concrete attack strategies and explain why they fail:

(a) Submitting fake real consumption sequences: A malicious endpoint i may attempt to fabricate $L_c^{\left(i\right)}$ so that it closely matches its prediction ${L_{pc}^{\left(i\right)}}^{\prime }$, thereby reducing $E_i^{\mathrm{dev}}$ and increasing its chance of becoming leader. However:

• The consumption trace must be accompanied by a valid ZK-proof ${\pi }_i$, as shown in Appendix A, demonstrating correctness with respect to the smart meter’s hardware logic and raw measurements.
• All smart meters under the same DSO share the same hardware logic, preventing endpoint-specific manipulation.
• Any fake $L_c^{\left(i\right)}$ will fail verification and be excluded from the eligible set $\mathcal{V}$.

Thus, an adversary cannot fake its daily consumption to bias PoP consensus.

(b) Submitting falsified predicted consumption sequences. Since prediction sequences ${L_{pc}^{\left(i\right)}}^{\prime }$ must be submitted to the ISC smart contract before the day begins, predictions are immutable once posted, publicly auditable, and chronologically anchored on-chain. Therefore, sending false predictions does not improve PoP scores, and predictions cannot be retroactively adjusted once the day starts.

(c) Delaying the submission of prediction or consumption sequences: An endpoint might try to delay its submission to tailor predictions to early parts of the day. However:

• Each ISC contract only accepts predictions before the beginning of the day.
• The consumption proof must be submitted at the end of the day.
• Missing either value leads to being automatically excluded from the candidate set $\mathcal{V}$.

Therefore, instead of benefiting from it, delayed submission strictly reduces the adversary’s probability of being selected to be the next leader.

(d) DDoS-style flooding against the ISC contract: A malicious endpoint that realizes it has little chance of becoming the next proposer may attempt to overload the ISC contract by submitting large volumes of irrelevant or malformed transactions, aiming to degrade the availability of the blockchain service. However,

• Each ISC and ConsensusSC processes at most one update per endpoint per day.
• Additional writes are rejected at the smart-contract level.
• Gas cost disincentivizes spamming.

Thus, flooding does not affect the liveness of smart contracts.

• Security Against a Malicious DSO. As discussed in Section 3, to avoid the cost and compatibility issues associated with large-scale hardware upgrades, our architecture retains the existing smart-meter infrastructure, in which all meters are accessed by a single DSO. Moreover, to preserve user privacy, real consumption traces are never posted on-chain; instead, the DSO collects metering data and participates in PoP leader selection on behalf of the grid, and the blockchain is only responsible for verifying data submitted by the DSO. Consequently, DSO’s behaviors must be carefully examined. We consider two classes of adversarial strategies relevant to the DSO’s capabilities:

(a) Forging smart meters or injecting fake high-accuracy meters: A malicious DSO may attempt to increase its probability of being selected as leader by creating additional “fake meters” or artificially precise consumption traces that reduce its PoP error score. However, this attack is mitigated by two mechanisms in our architecture:

• On-chain smart-meter identity binding. Every endpoint must register a unique SM_ID in the ISC contract when entering the power grid, and all consumption proofs must reference this identity, as shown in Appendix A. The DSO cannot introduce new meters without violating the contract’s uniqueness constraint.
• ZK-supervised metering computation. As detailed in Appendix A, each consumption trace must be accompanied by a proof showing that it was computed by the legitimate smart meter following the specified hardware logic. Any forged meter or fabricated trace will fail verification and be excluded from the candidate set $\mathcal{V}$.

Thus, DSO-generated fake meters or artificially optimized consumption data cannot join the PoP leader selection process.

(b) Manipulating users’ consumption measurements for strategic gain. A more subtle attack is collusion between the DSO and a subset $\mathcal{A}$ of endpoints, in which the DSO alters the real consumption sequences ${\left\{L_c^i\right\}}_{i\in \mathcal{A}}$ to artificially reduce their PoP error score. Unlike the previous “submitting fake real consumption sequences”, here the DSO is dishonest even toward legitimate users. Our architecture prevents this manipulation through two constraints:

• Each endpoint is required to submit a zero-knowledge proof of its own real consumption sequence to its ISC smart contract, certifying that the sequence used in PoP is consistent with the output of its registered smart meter, as shown in Appendix A.
• The leader-selection computation is defined over these certified real consumption sequences X and is itself subject to ZK verification under ${\mathcal{R}}_{\mathrm{calc}}$.

If the DSO attempts to alter any real consumption value in X, the modified data will no longer be consistent with the corresponding metering proof on-chain. During verification, the consensus contract detects this mismatch between the announced input and the user-provided proof, and the PoP proof for that round would be rejected. As a result, the current leader selection is invalidated, and the manipulated outcome cannot be accepted by other honest participants.

5. Evaluation

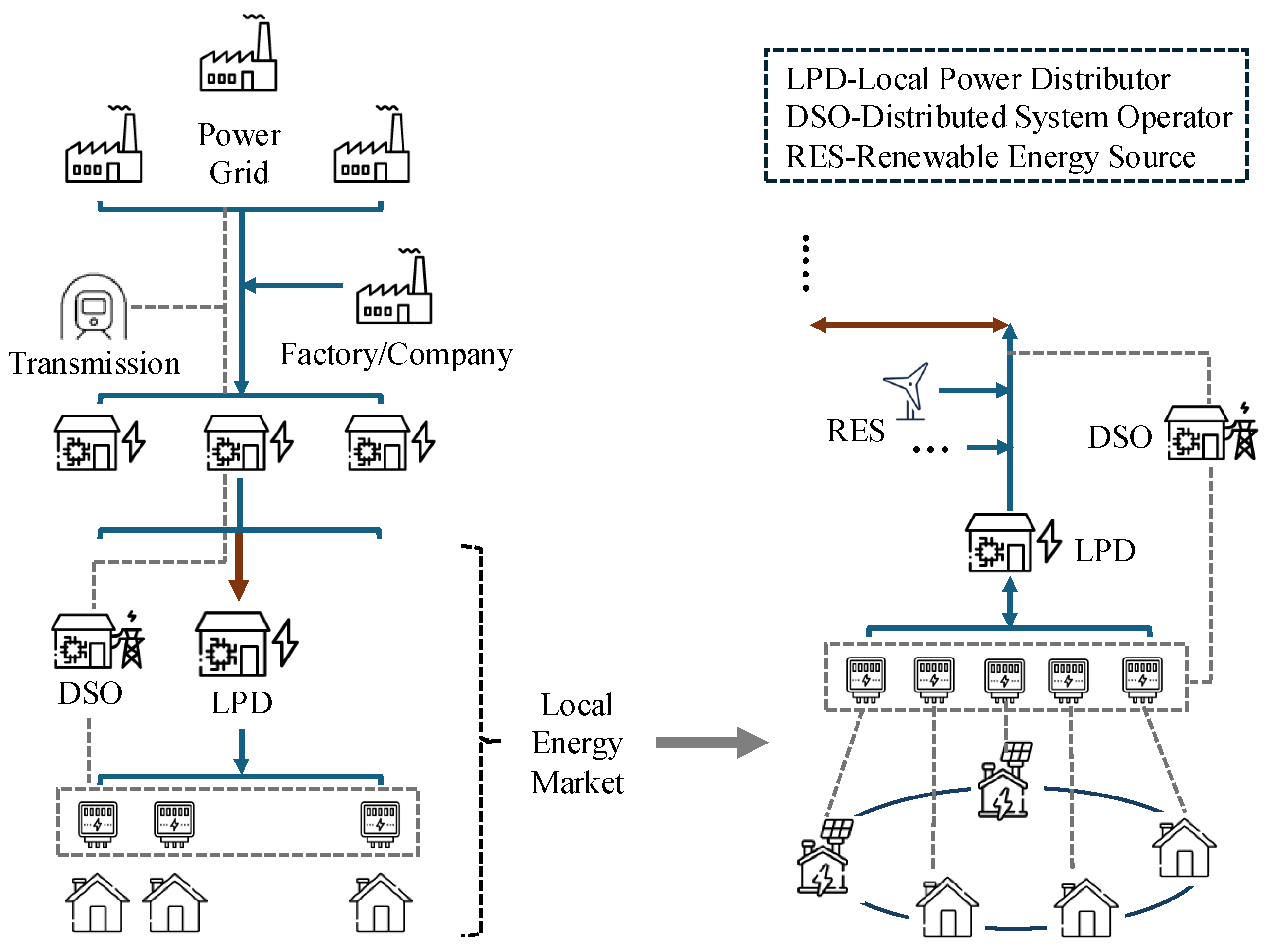
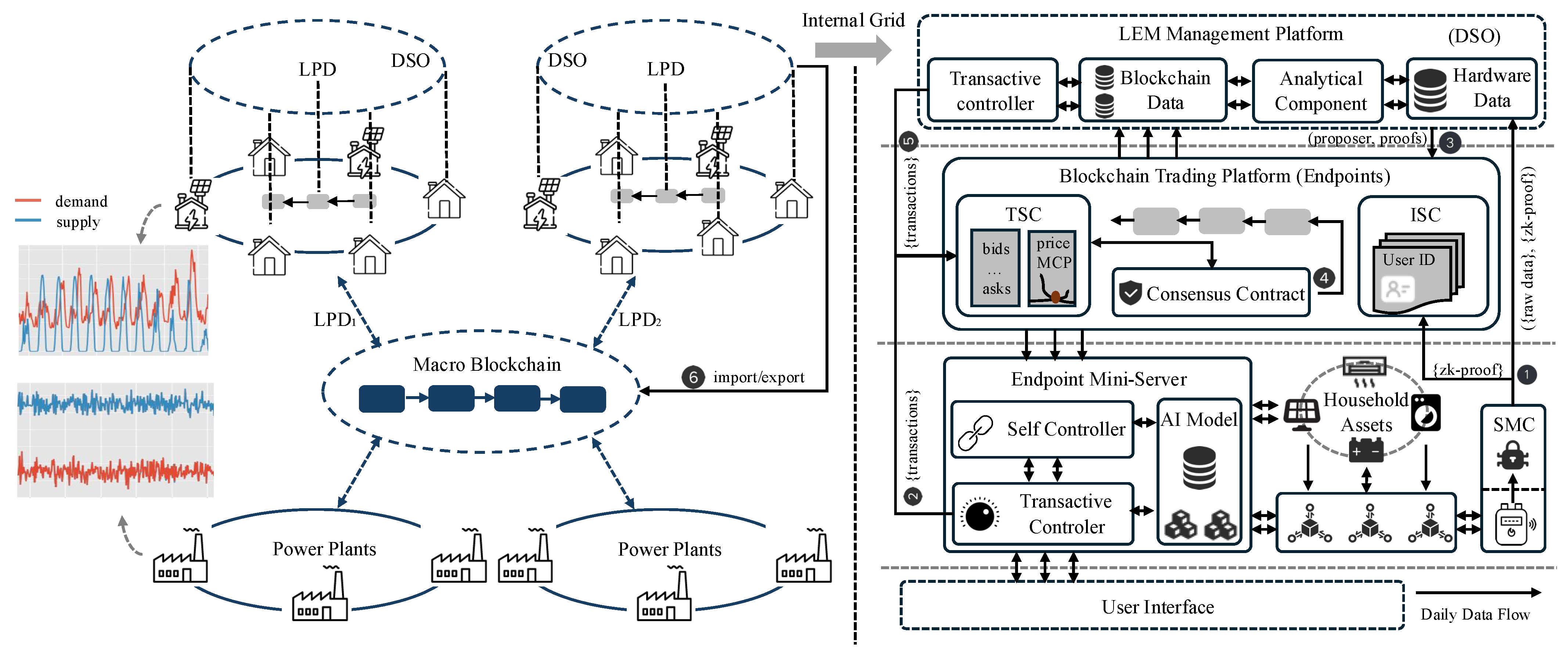
In this section, we implement a microgrid-scale prototype consisting of 16 grid endpoints, based on the design proposed in Section 3.2. To enhance the realism of the simulation, the endpoints include 5 consumers with heterogeneous energy consumption capacities, 10 prosumers with varying generation capacities and one national grid endpoint that jointly represents the roles of the LPD and the DSO. The selected market assets comprise the household asset of each grid endpoint, of which prosumers employ solar panels as their primary generation units, supplemented by batteries and smart meters. The energy trading market is collectively owned and maintained by all grid endpoints, with the optimization objectives defined in Section 3.1. In the implementation, we configure 16 grid endpoint threads, each encapsulating the EMS logic associated with its designated role (consumer, prosumer, or LPD/DSO). We design a main thread to coordinate all endpoint threads and simulate the overall system workflow. To avoid excessive computational load on individual execution threads, we only store essential data in smart contracts without letting it execute complex calculation logic, thereby avoiding the resource exhaustion and high gas costs that would otherwise arise from running smart contracts at each endpoint. All on-chain functionalities are implemented on a private Ethereum blockchain [38]. Next, we analyze the proposed trading infrastructure from two perspectives, the EMS and the on-chain level, in terms of their contribution and optimization effects on grid stability. The EMS perspective illustrates the local view of an individual grid endpoint, while the on-chain perspective evaluates the interaction processes among all grid endpoints.

5.1. EMS Perspective: Local Contribution for Grid Stability

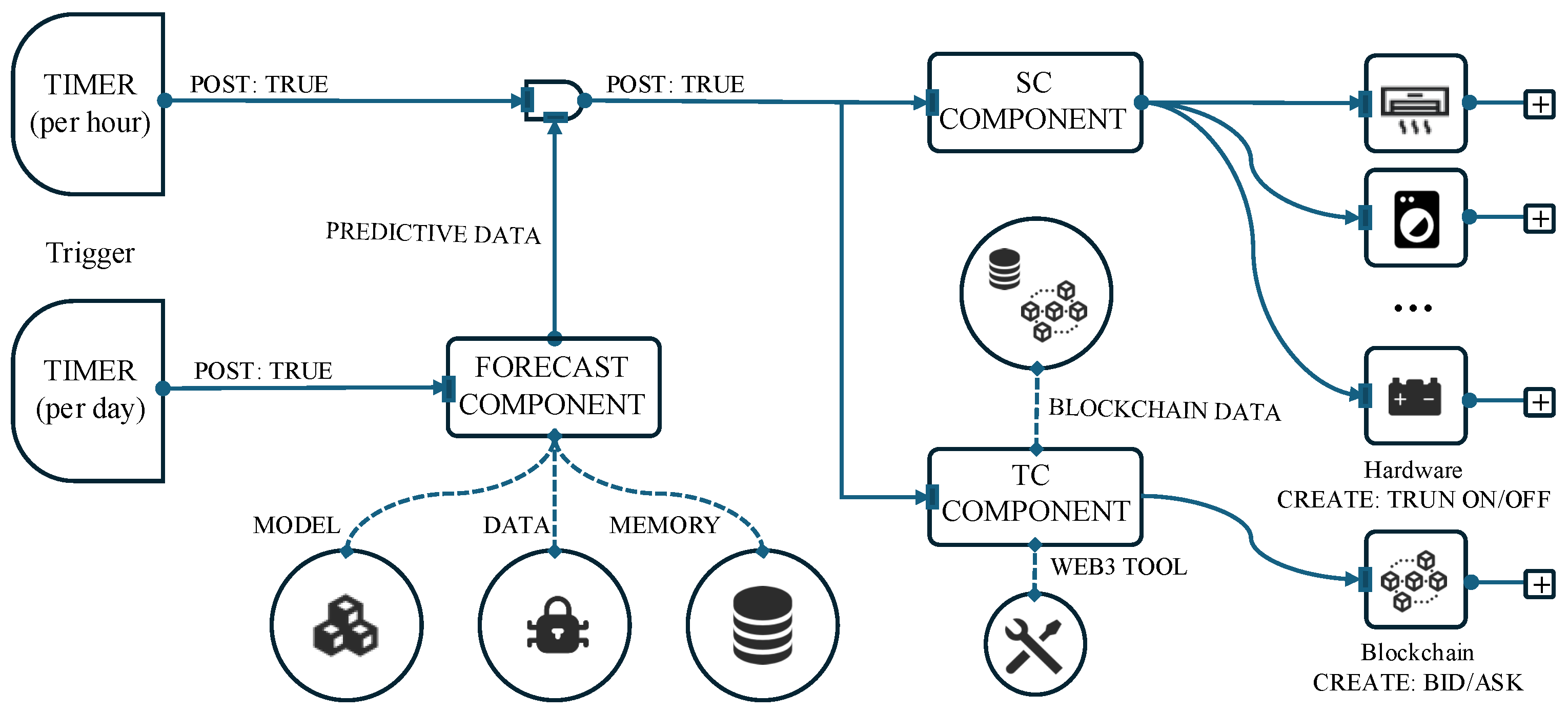
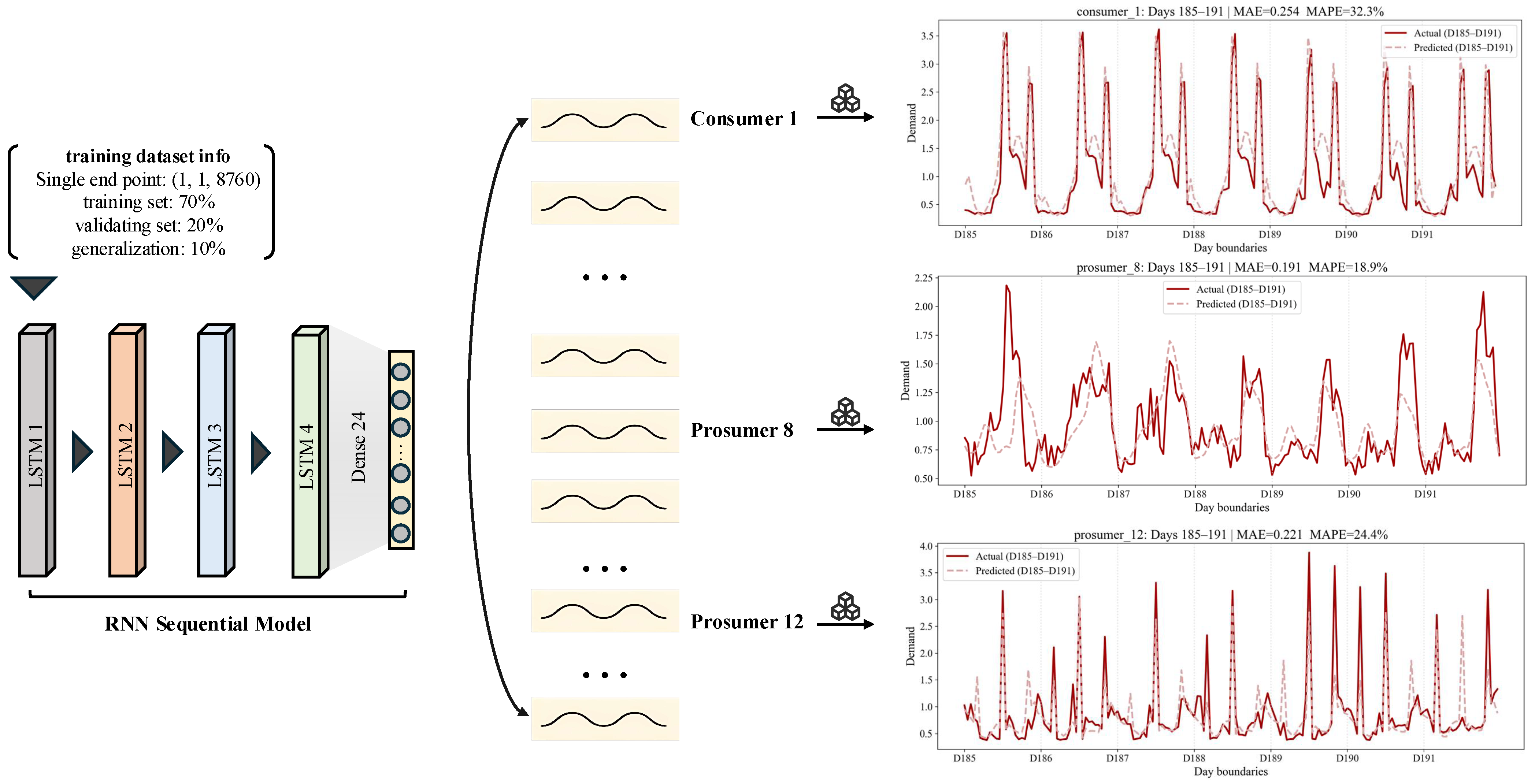
In Section 3.2, we describe the detailed workflow of the EMS deployed at each grid endpoint and explain how self-management is achieved through blockchain-based incentive mechanisms. The EMS logic consists primarily of a forecasting component, an SC component, and a TC component. To improve prediction accuracy under noisy data while minimizing thread overhead, we implement a lightweight predictive model based on a deep recurrent neural network with Long Short-Term Memory (LSTM) units to forecast the 24-h electricity consumption of the following day. The model consists of four stacked LSTM layers, each with 50 hidden units, as shown in the Figure 4 (left part). To mitigate overfitting, we apply a dropout rate of 0.2 after the first LSTM layer. A fully connected dense layer maps the learned temporal representations to the predicted consumption values. Each EMS thread first reads one year of simulation data to train its local model, which is subsequently adopted as part of the forecasting component. We split one year of load and generation traces per endpoint into 80% training and 20% validation, and train for 50 epochs with a batch size of 32 and a learning rate of ${10}^{-3}$. The model consists of only four LSTM layers with 50 hidden units and a dropout rate of 0.2, which is a compact architecture suitable for embedded environments. Despite its small size, the model converges efficiently: the final training loss reaches approximately $5^{-4}$ on average, while the validation loss stabilizes around $6^{-4}$ on average, indicating good generalization performance. 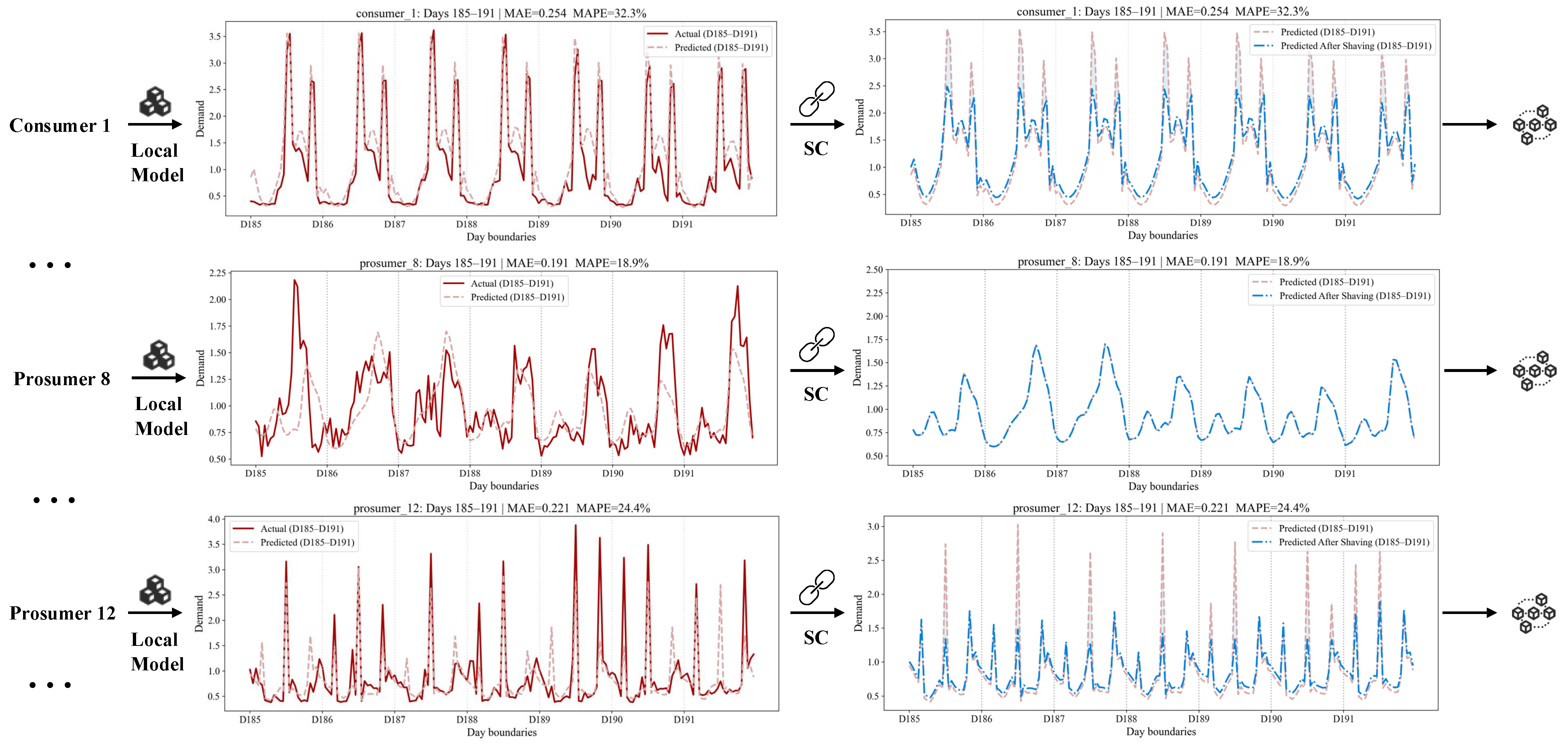As shown in Figure 4 (right part), we evaluate the locally trained models for each endpoint. The light red dashed lines represent the predicted 24-h load profiles generated by the predictive model, while the dark red solid lines indicate the actual consumption data for the corresponding day. The model achieves reliable feature extraction, maintaining a mean absolute percentage error (MAPE) in the range of 10–35% across daily forecasts.

To mitigate voltage fluctuations in the power grid, we adopt a rule-based peak shaving mechanism within the SC component to enforce the self-management objectives of each endpoint. Specifically, based on the data output of the forecasting component, the SC component identifies two typical peak demand windows in each daily load curve, corresponding to 11:00–13:00 and 17:00–21:00. During these intervals, if the consumption of a single hour exceeds 10% of the total daily demand [39], the forecasted demand values are proportionally reduced by a shaving factor $\alpha \in [0.1, 0.3]$. The curtailed energy is then redistributed uniformly across the remaining non-peak hours, thereby alleviating load peaks while preserving the total daily consumption. This mechanism avoids a degradation of prediction accuracy while ensuring sufficient energy availability for endpoint production activities. The adjusted forecasted values are subsequently output to the blockchain as the endpoint’s prediction for the following day. The peak-shaving optimization effect of the SC component on the forecasted values is illustrated in the Figure 5. As shown in the right part, the red dashed line represents the 24-h electricity consumption generated by the forecasting component, while the blue dashed line denotes the optimized 24-h forecasted values produced by the SC component and submitted to the blockchain’s corresponding ISC smart contracts. For endpoints with highly uneven consumption distributions, such as consumer 1 and prosumer 12 in the Figure 5, the SC component effectively redistributes consumption during rush hours. This adjustment establishes a self-management goal that contributes to grid voltage stability and reduces power fluctuations at the endpoints.

5.2. On-Chain Perspective: Global Interaction and Grid Stability

In the last section, we describe the detailed dataflow and workflow of each grid endpoint equipped with an EMS. Once the daily timer is triggered, the TC component of each EMS submits the optimized forecasted data for the following day to the blockchain. At the start of the next day, all grid endpoints adjust their behavior according to their actual consumption patterns in order to increase their probability of being elected as the next day’s block proposer (or leader) and to participate in energy trading. At each EMS endpoint, we configure 11 household devices that can be controlled and adjusted through the SC component to enable self-management of grid endpoints, including television, heat pump, lamps, dishwasher, washing machine, microwave, oven, electric water heater, vacuum cleaner, laptop, and tumble dryer.

As mentioned earlier, we use one-year data to train the built-in forecasting model of each EMS, and employ the subsequent year’s data as a reference to evaluate and illustrate the internal dynamics of our proposed blockchain energy trading architecture (hereinafter referred to as BTA), including supply–demand fluctuations, pricing, and trading activity. For demonstration purposes, we select two time periods for simulation: Days 91–105 (corresponding to hour index 2161–2496) as Period 1 and Days 321–335 (corresponding to hour index 7681–8016) as Period 2. 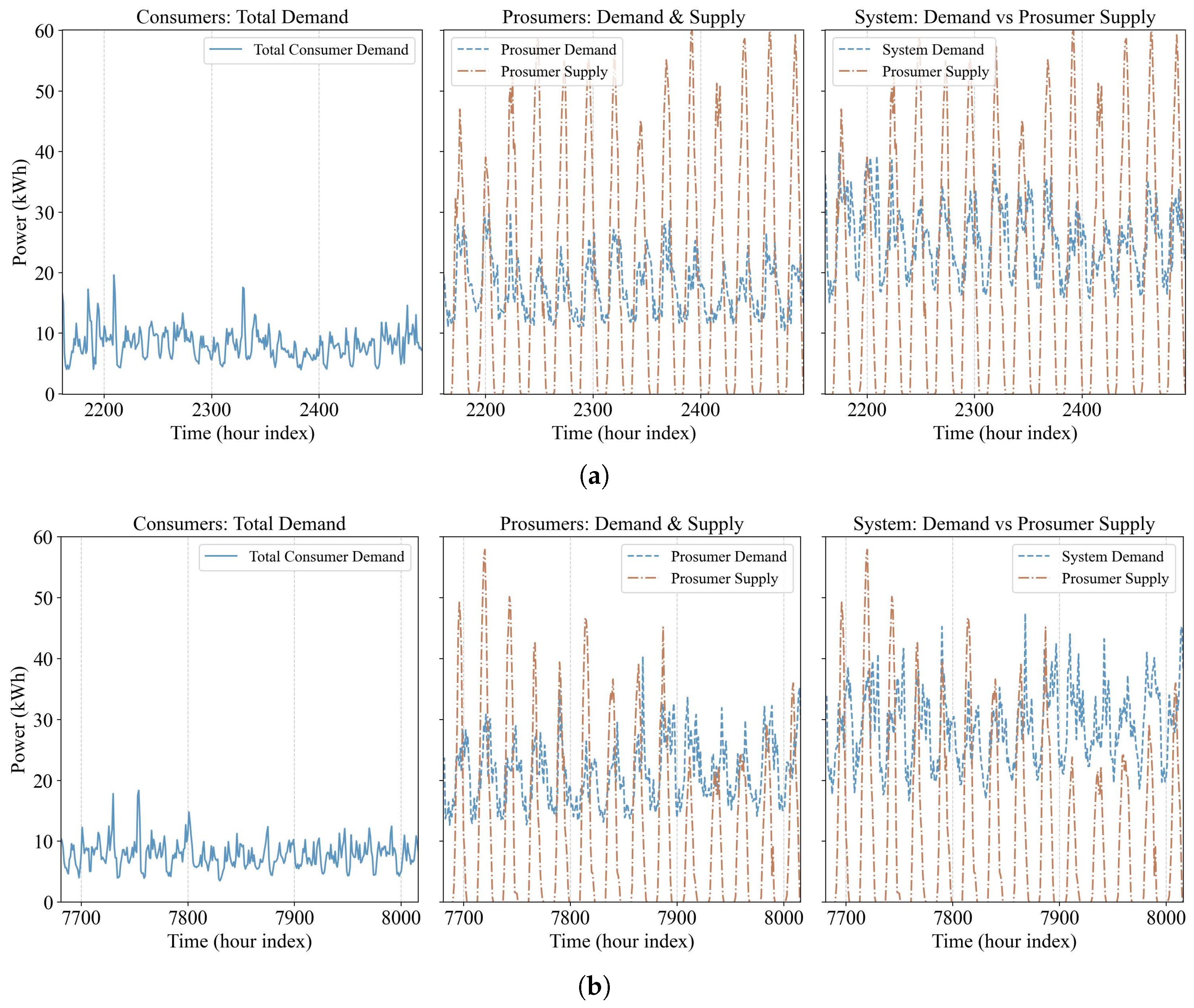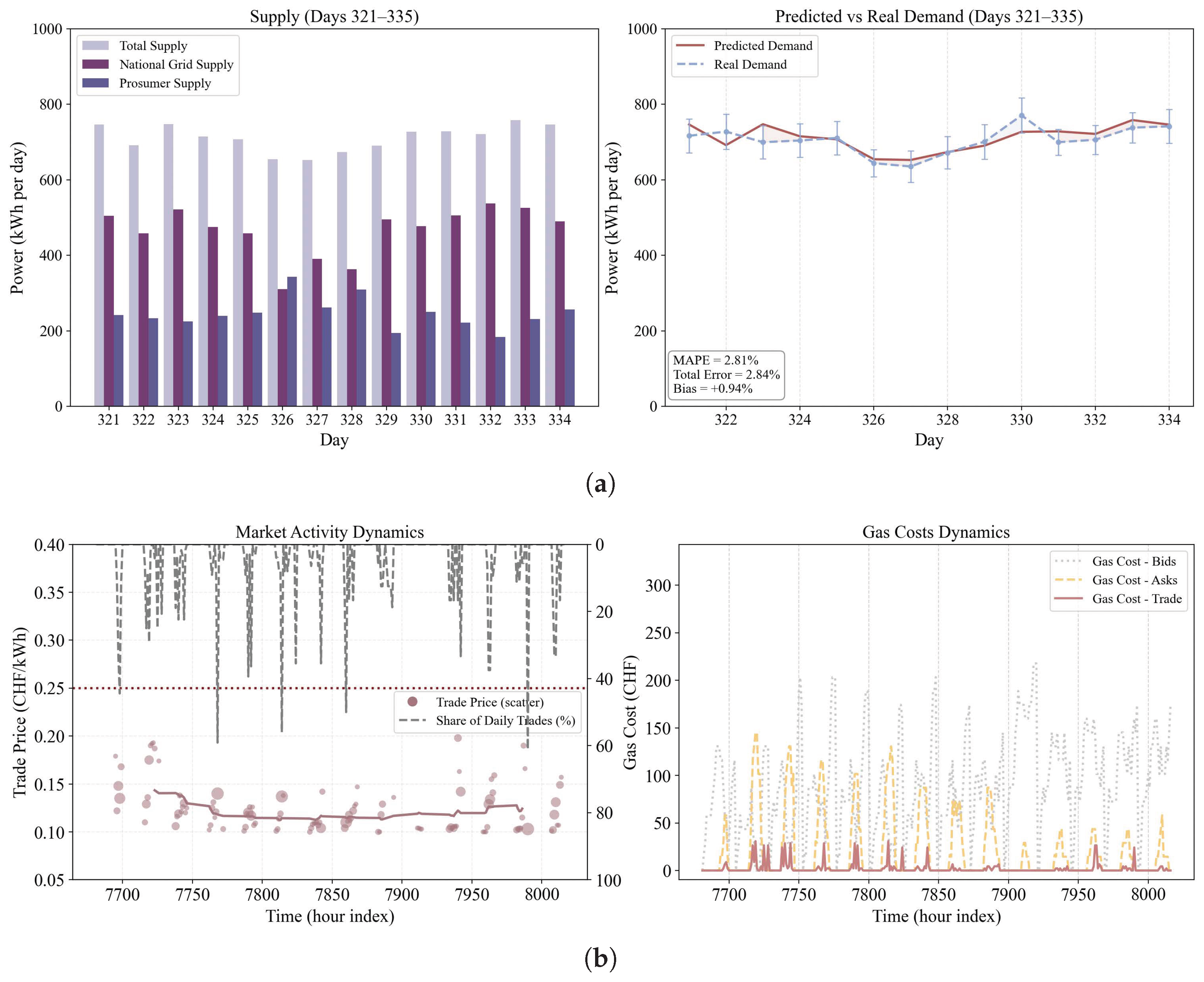Figure 6a illustrates the supply–demand pattern of the grid during Period 1. This period corresponds to Condition ${\mathcal{C}}_1$ in Algorithms 1 and 2, where solar irradiance is relatively abundant and the aggregate supply from prosumers is high. In contrast, as shown in Figure 6b, the total prosumer supply in Period 2 is substantially lower, corresponding to Condition ${\mathcal{C}}_2$ in Algorithm 3. It should be noted that although the Sundance dataset originates from a region with highly favorable geographic conditions, a microgrid with a large number of consumers cannot rely solely on solar panel-based supply to meet the total demand [40,41]. In our experimental setting, the ratio between consumers and prosumers is 1:2, and the overall level of consumption is relatively high. As a result, unlike the Algorithms 1 and 2, both conditions require active participation from the national grid to balance supply and demand. We select these two time periods primarily to evaluate whether the proposed BTA can maintain grid stability under different dynamic conditions while simultaneously monitoring the activity of the energy trading market.

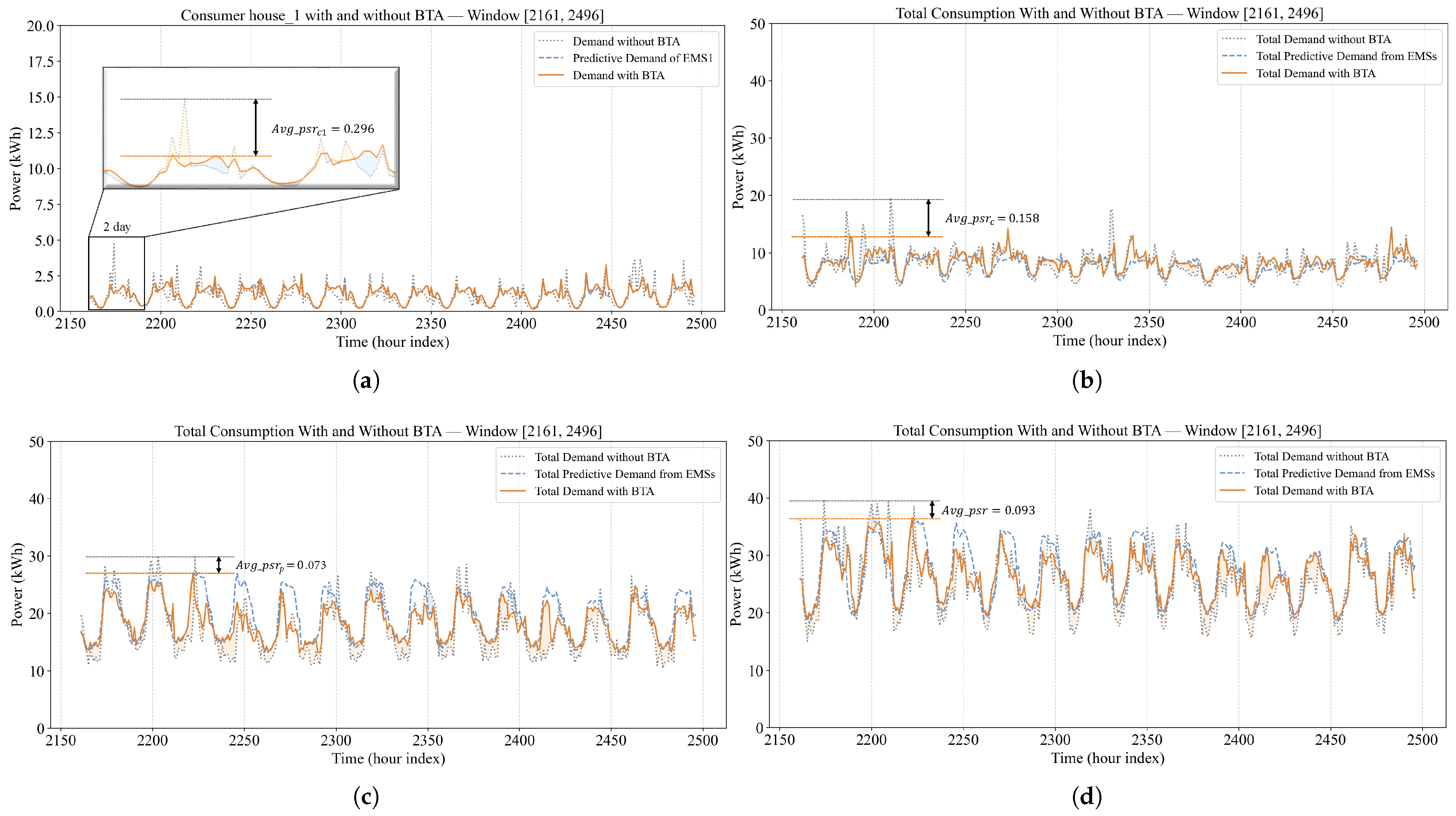
Pattern 1: Figure 7 illustrates the dynamic energy consumption within the grid during Period 1. Subfigure (a) presents the consumption behavior of a selected individual endpoint (Consumer 1), (b) shows the aggregated consumption of all consumers, (c) depicts the aggregated consumption of all prosumers, and (d) displays the overall grid consumption. In each subplot, the gray dashed line represents the consumption trend from the original dataset at the corresponding time, the blue dashed line denotes the forecasted values submitted by the EMSs to the blockchain, and the orange solid line indicates the actual consumption dynamics of the power grid, which we refer to as the output of the BTA.

We conceptualize the BTA as a “power transformer” that converts highly fluctuating, single-endpoint consumption inputs into a stabilized aggregate output with reduced peak amplitudes. As shown in Figure 7a, the BTA exhibits strong distributed control capability for a single endpoint: the average peak shaving rate ($Avg\_psr$ in Figure 7) of an individual endpoint can reach up to 30%. Since the consumption patterns vary across grid endpoints and some endpoints naturally exhibit low volatility, the average peak shaving rate across all consumers is approximately 15%, while that of all prosumers is around 7.3%. From a power-system perspective, peak-load reduction has direct implications for distribution-grid stability. Under the linearized DistFlow model for radial distribution feeders [42,43], nodal voltage drops scale approximately with the active power flowing through each line. A peak-shaving rate, therefore, corresponds to a proportional reduction in the worst-case voltage drop, increasing the system’s voltage margin relative to statutory limits and reducing thermal stress on feeder conductors and transformers. Peak-load reduction is also closely related to economic performance. Lower system peaks typically reduce demand-related capacity charges and can defer network reinforcement investments, which constitute a major portion of distribution-grid operational expenditures [44,45]. Moreover, endpoint-side management at each grid endpoint cannot always enforce consumption precisely within the forecasted range. In our simulation, household machines support only a limited number of operating modes (2 modes of high-power and energy-saving). When the actual demand exceeds the forecasted one, the SC of the EMS may switch the refrigerator to an energy-saving mode, but would not turn it off entirely. As a result, the actual consumption slightly deviates from the forecasted demand. Nevertheless, due to the influence of the incentive mechanism, the overall deviation remains small, and the average peak shaving rate of the entire grid remains around 10%.

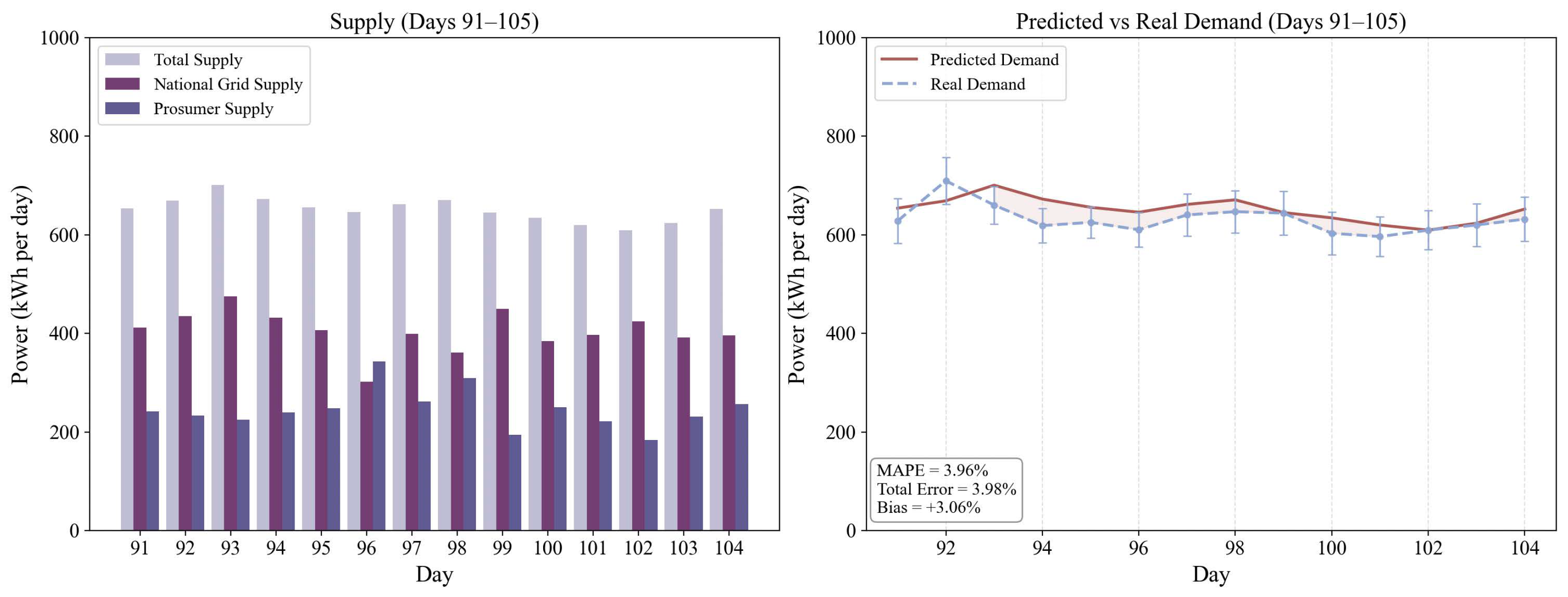
Figure 8 presents the overall supply–demand levels of the power grid during Period 1. Although prosumers generate a relatively high amount of electricity during this period, as also shown in Figure 6a, their actual contribution to the market is impacted by the energy price, self-demand, and battery status. In our simulation, if the lowest bid price in the market on a given day falls below the previous day’s market-clearing price, prosumers may deem the profit insufficient and choose not to sell their energy. Instead, they store it in their batteries and wait for a more favorable selling opportunity, which aligns with realistic market behavior. As a result, the national grid ultimately supplies slightly more electricity than prosumers during Period 1. However, thanks to the forecasting component in EMS and the PoP incentivized mechanism, the overall prediction error between the forecasted consumption and actual consumption in the power grid remains around 3.98%, which enables the national grid to accurately determine the amount of power that needs to be imported by comparing the forecasted demand with the prosumers’ generation capacity, thereby maintaining a stable balance between supply and demand within the power grid.

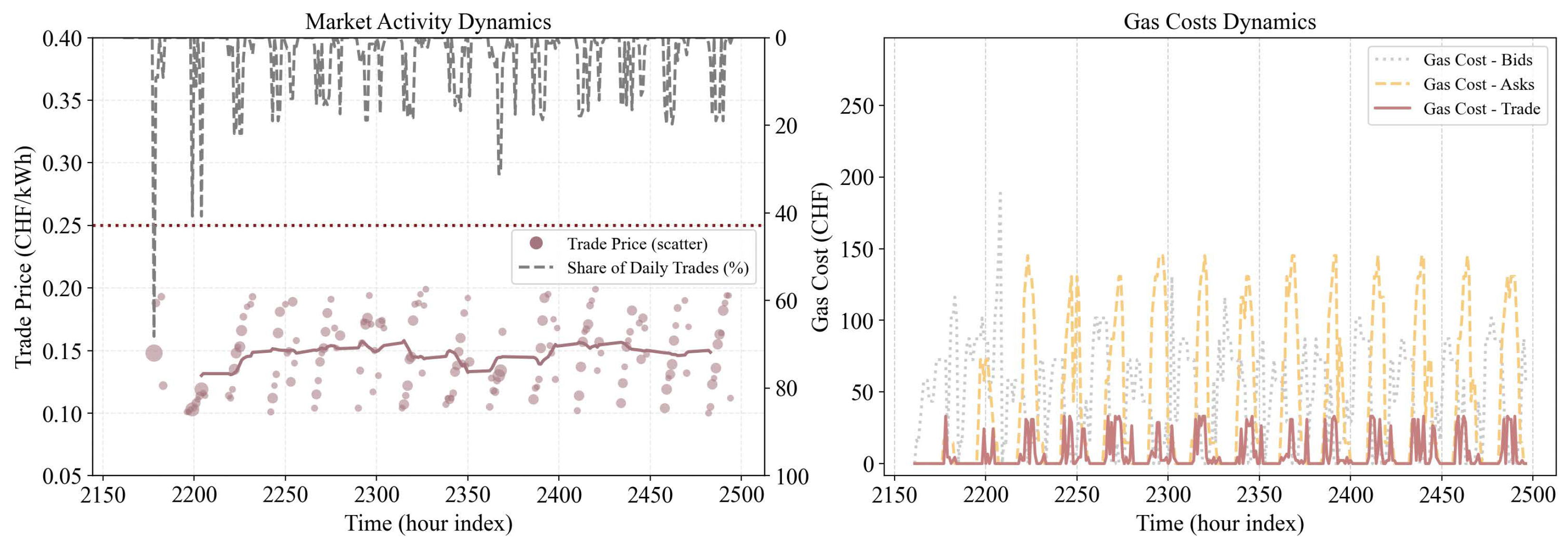
Finally, to evaluate the trading activity of the on-chain energy auction market, we analyze the transaction dynamics during Period 1, including the average auction price at each hour index and the gas cost incurred by EMSs–blockchain interactions, as shown in Figure 9. We set the electricity price of the national grid to 0.25 CHF/kWh (based on the electricity tariff published by Zug Canton, Switzerland: https://www.wwz.ch/de/privatpersonen/energie/strom/tarife, accessed on 17 October 2025), which is approximately 0.31 USD/kWh. The pricing strategy for energy selling requires the price to be higher than the previous day’s market-clearing price but lower than the lowest bid price in the current hour index. The purchasing price of energy is determined based on the transaction prices of the previous seven days. As shown in Figure 9 (left), the auction price in the energy market ranges between 0.10 and 0.20 CHF/kWh, exhibiting relatively stable fluctuations while consistently remaining below the national grid electricity price (0 means no energy flow between consumers and prosumers). This price advantage helps sustain the activity of the energy trading market. Moreover, since each grid endpoint is equipped with a battery for self-management in our simulation, most energy trading occurs in the middle of the day, as shown in Figure 9 (left) with the gray dashed line. To minimize the computational and energy overhead associated with blockchain execution, we design the smart contract in a lightweight, information-oriented form that avoids any intensive state changes or iterative on-chain logic, which significantly reduces the energy cost of blockchain participation for EMS, making our architecture environment-friendly. The Figure 9 (right) reports the gas cost required for on-chain transactions. For each time index, we aggregate the gas consumption of all on-chain transactions of a given type and convert the total gas cost from ETH to CHF (The ETH-CHF conversion is computed using real-time exchange rates from CoinGecko: https://www.coingecko.com, accessed on 17 October 2025). Therefore, each point in the figure represents the total gas expenditure of that transaction type within the corresponding hour. As shown in the Figure 9 (right), even during periods of intensive market activity, the resulting costs remain moderate and are primarily driven by simple data-registration operations, since all computation-intensive logic is kept off-chain.

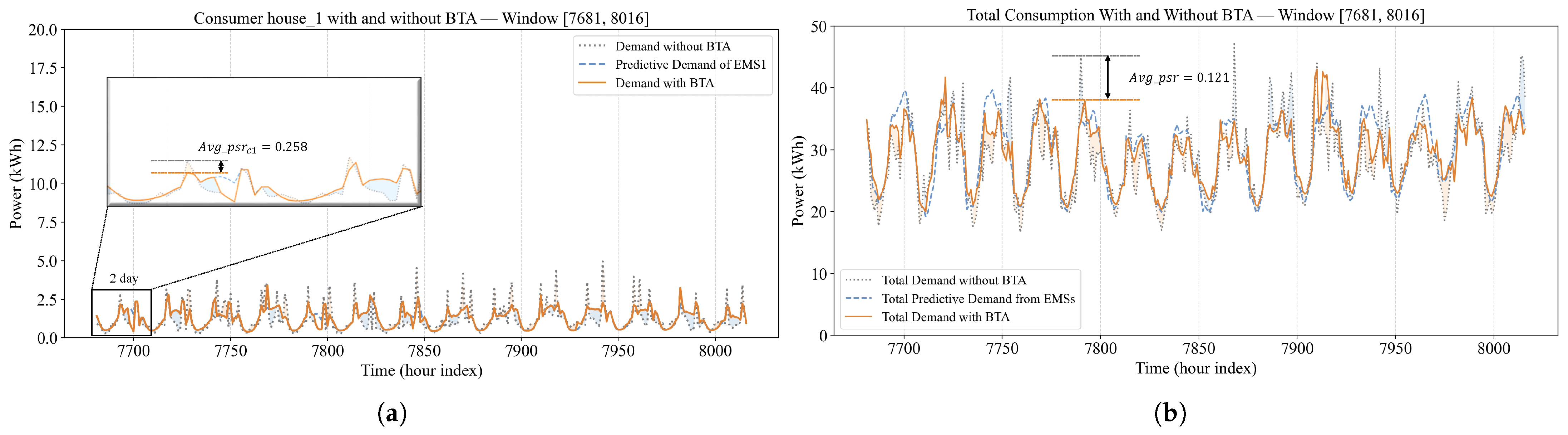
Pattern 2: The dynamic consumption pattern of the grid in Period 2 is shown in Figure 10. Subfigure (a) presents the consumption dynamics of Endpoint 1 (Consumer 1), and subfigure (b) illustrates the overall consumption dynamics of all endpoints during Period 2. Similar to Period 1, the BTA achieves an average peak-shaving rate of 25.8% for Endpoint 1 and 12.1% for the entire grid. In comparison, existing blockchain-based energy trading and demand-side management frameworks typically report peak-demand reductions on the order of 10–25% under different settings. For example, Ouyang et al. [46] report about a 10% peak reduction in a blockchain-based new energy trading system, while Boumaiza [22] achieves a 25% highest reduction in peak demand in a blockchain-enhanced DSM case study. Our results therefore fall within the upper range of peak-shaving performance of 29.6% in the pattern 1 reported for blockchain-enabled schemes, while relying only on an incentive-driven, distributed control architecture without centralized optimization. As shown in Figure 6, Period 2 exhibits stronger consumption volatility compared to Period 1, which imposes higher requirements on the self-management capability of individual endpoints. Nevertheless, as seen in Figure 10b, the overall fluctuation in consumption during Period 2 remains comparable to that of Period 1, as shown in Figure 7d, demonstrating the flexibility and robustness of the BTA’s distributed control capability.

Similar to the dynamic monitoring performed for Period 1, we also analyze the supply–demand behavior of the grid during Period 2, including the distribution of supply between prosumers and the national grid, as well as the resulting supply–demand gap. As shown in Figure 11a, the total supply from prosumers during Period 2 is lower than in Period 1, leading to a significant increase in the national grid’s contribution. Nevertheless, due to the EMS-based forecasting mechanism, the average supply–demand gap in Period 2 remains as low as approximately 2.84%, ensuring that overall grid balance of supply and demand is maintained. In addition, as illustrated in Figure 11b (left), the energy market price continues to remain within the range of 0.10–0.20 CHF/kWh, indicating price stability. However, market activity is noticeably lower than in Period 1, particularly among prosumers, as reflected by the yellow dashed line in the Figure 11b (right).

Based on the observations from the above figures and tables, our proposed BTA integrates bottom-up EMS-driven self-management with top-down blockchain-based incentive coordination, thereby exhibiting strong distributed control capability to maintain grid stability. At the local level, each EMS autonomously smooths its own consumption profile to reduce single-point volatility and leverages accurate forecasting to minimize local unpredictability. At the global level, the blockchain and the regulator enable efficient distributed coordination across all endpoints, thereby stabilizing overall power grid voltage and balancing supply and demand.

6. Conclusions and Future Work

Blockchain technology offers unprecedented opportunities for advancing modern power grid development and has significantly accelerated the adoption of clean and distributed energy resources. However, the rapid proliferation of RES and DERs also introduces severe challenges to maintaining grid stability under dynamic and heterogeneous operational conditions. To address these challenges, this paper systematically analyzes the inefficiencies inherent in existing power grid management models under large-scale integration of dynamic loads and identifies the fundamental structural requirements for achieving stability in modern energy systems. Building on this analysis, we further develop a generalized business model applicable to small- and medium-scale power grids, which clarifies the key organizational components and operational interactions within modern power systems. Based on this business model, we propose a modular blockchain-based energy trading architecture that flexibly integrates existing hardware infrastructures and grid control technologies as core components, maintaining grid stability through three essential capabilities: endpoint-level self-management, distributed control enabled by blockchain-based incentive mechanisms, and global coordination facilitated by regulatory entities. We further implemented and evaluated a prototype of the proposed architecture. Experimental results demonstrate that it effectively supports self-management at grid endpoints, achieving peak-shaving improvements of up to 29.6%, and maintains supply–demand balance through distributed regulation, with a deviation of only 5% in average. In addition, the architecture enables system-wide coordination across distributed entities. Overall, the findings indicate that the proposed architecture provides a viable pathway toward a stable, transparent, and autonomously managed power grid, effectively bridging the gap between market liberalization and operational reliability.

To enhance compatibility and reduce infrastructure upgrade costs, our architecture is designed to integrate existing hardware and software while primarily upgrading the management and operational logic. Accordingly, our future work will focus on advancing key technical components within the proposed architecture. One direction is to integrate more accurate AI models and a more efficient training framework into the EMS component. A promising extension is to incorporate federated learning frameworks that identify consumption patterns at grid endpoints [47], together with recent ML-based demand-side modeling techniques—such as MAS-DR for consumer segmentation and aggregation [27]. For the trading platform component, we aim to integrate scalable and high-performance blockchain systems to improve transaction throughput while keeping blockchain maintenance overhead at the endpoints minimal. Potential solutions include adopting DAG-based blockchain architectures [35,48]. In addition, expanding access to high-quality datasets and real-world experimental environments remains an important direction for future work. Due to privacy regulations and geographical constraints, publicly available household-level renewable generation datasets are limited, and comprehensive open datasets, including the Sundance dataset used in this work, generally do not provide corresponding distribution network models. As a result, we are able to assess grid-level phenomena such as nodal voltage stability or power-flow constraints only at a theoretical level rather than through full power-flow simulations. Beyond data availability, realistic hardware test environments are also difficult to access, which are typically deployed under strict utility control, and their firmware, measurement logic, and security modules (such as trusted execution environments for ZK-proof generation) are rarely open for experimental validation. Consequently, the privacy-preserving components of our architecture, such as zero-knowledge proofs for metering correctness, are demonstrated using software-based abstractions rather than genuine hardware-backed metering systems. We view this as an important opportunity for future work. Establishing a controlled testbed with real smart meters and programmable EMS hardware, together with a distribution-level network models and field-grade measurement systems would enable comprehensive validation of both the privacy-preserving metering pipeline and the full-grid stability impacts of PoP-based coordination.

Ultimately, our goal is to combine advanced analytics, scalable distributed computing, and a global coordination platform to strengthen grid stability and reliability, laying the foundation for the next generation of sustainable, resilient, and efficient energy trading infrastructures.