End-to-End Camera Pose Estimation with Camera Ray Token
Abstract
1. Introduction
2. Related Works
3. Method
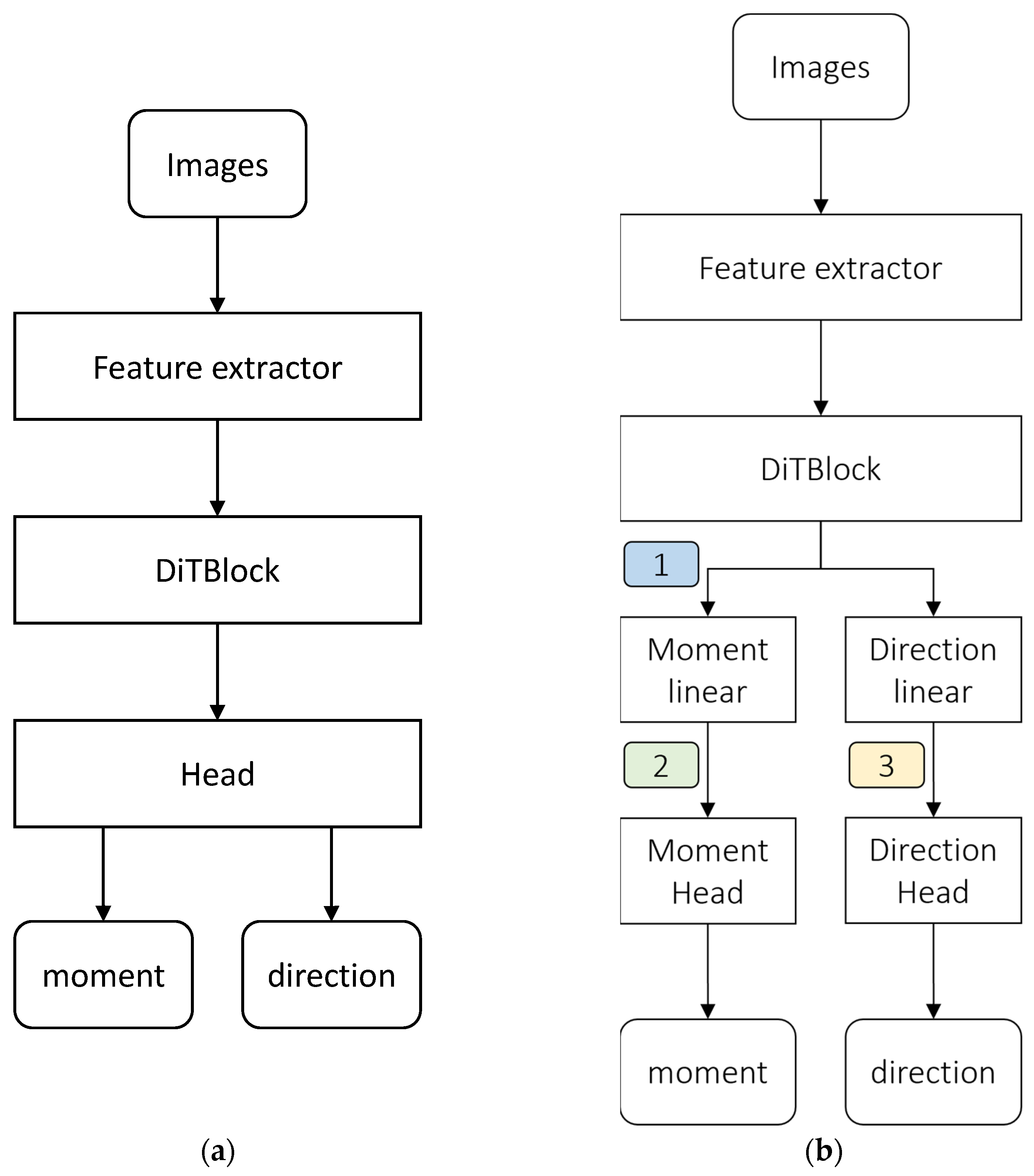
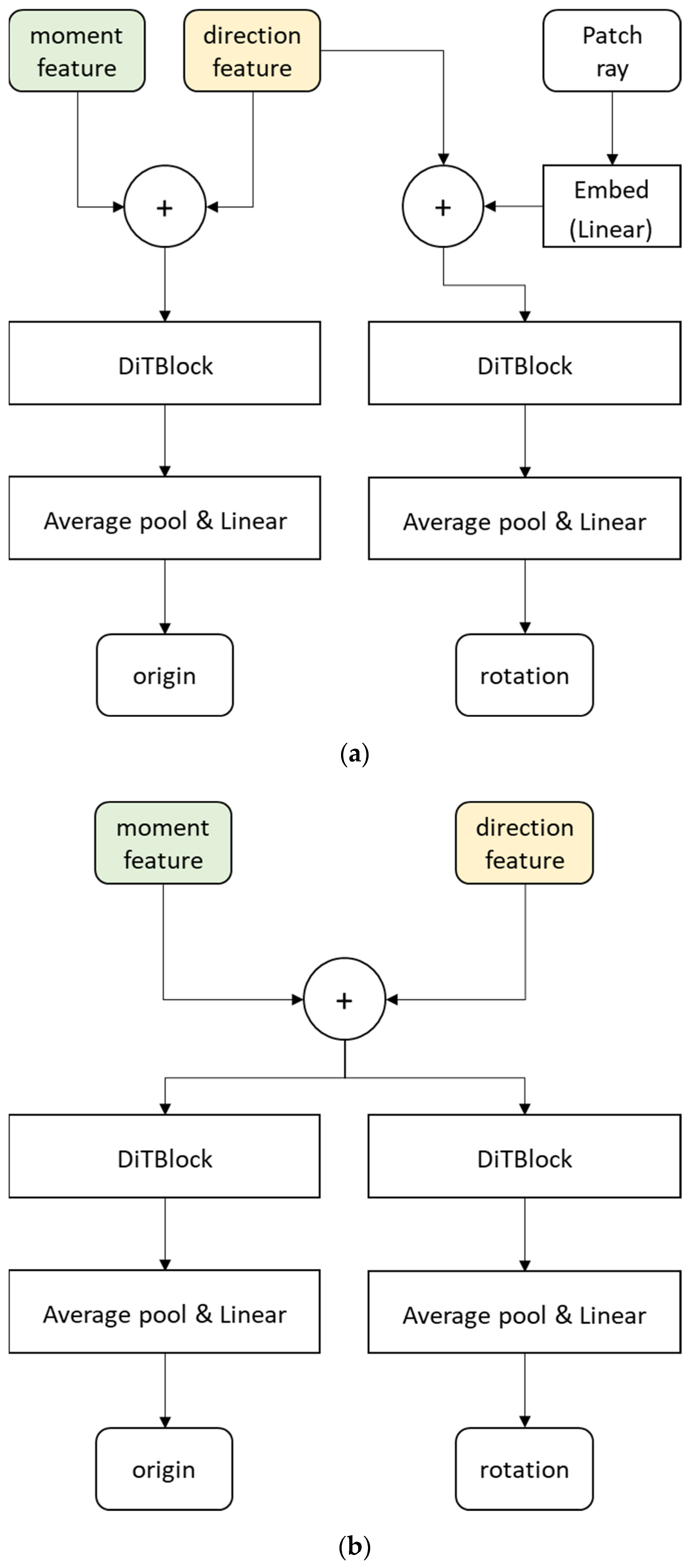
3.1. Pose Estimation Network
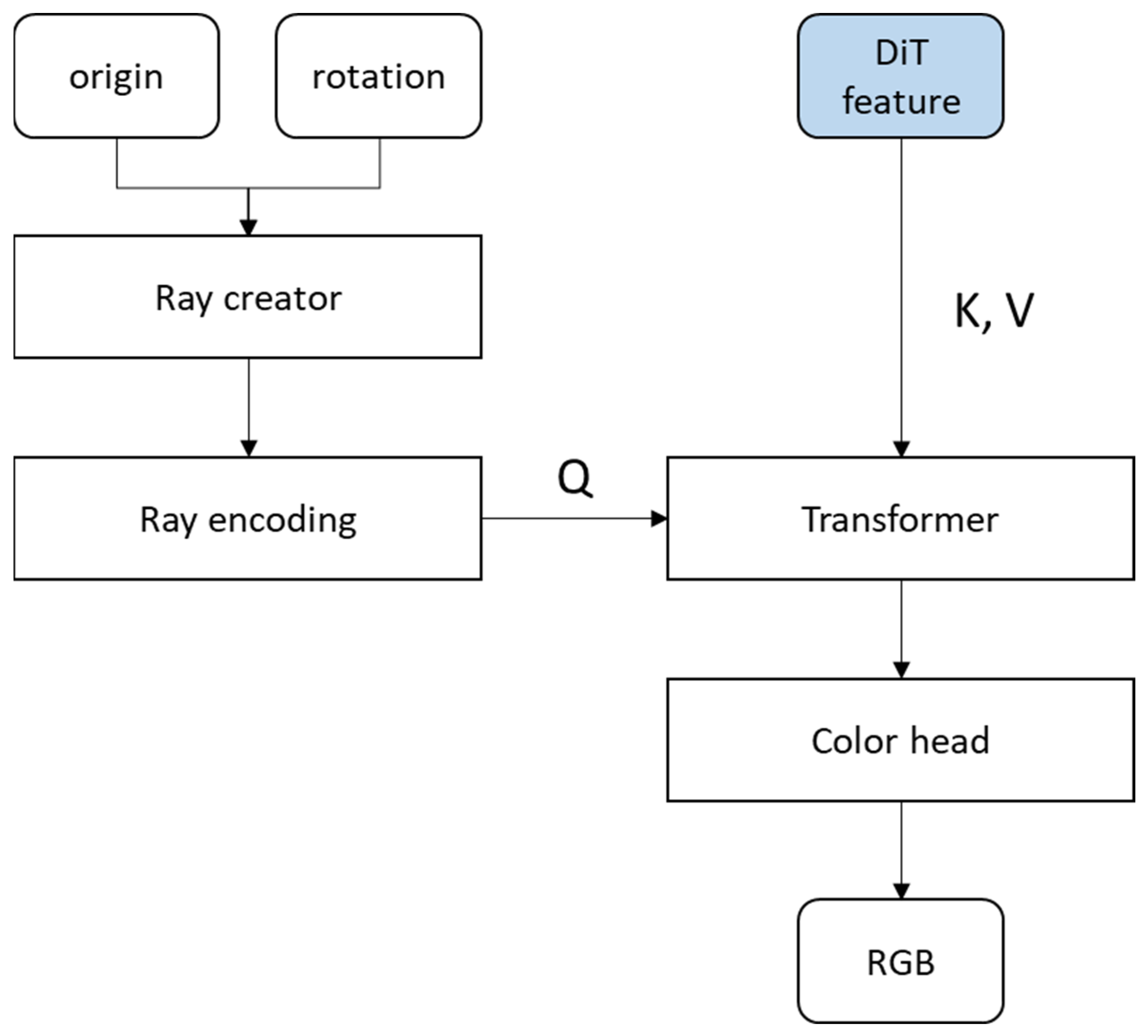
3.2. Image Rendering Network
3.3. Loss Terms
4. Experimental Results
4.1. Datasets and Implementation Details
4.2. Experimental Results and Discussions
4.3. Ablation Studies
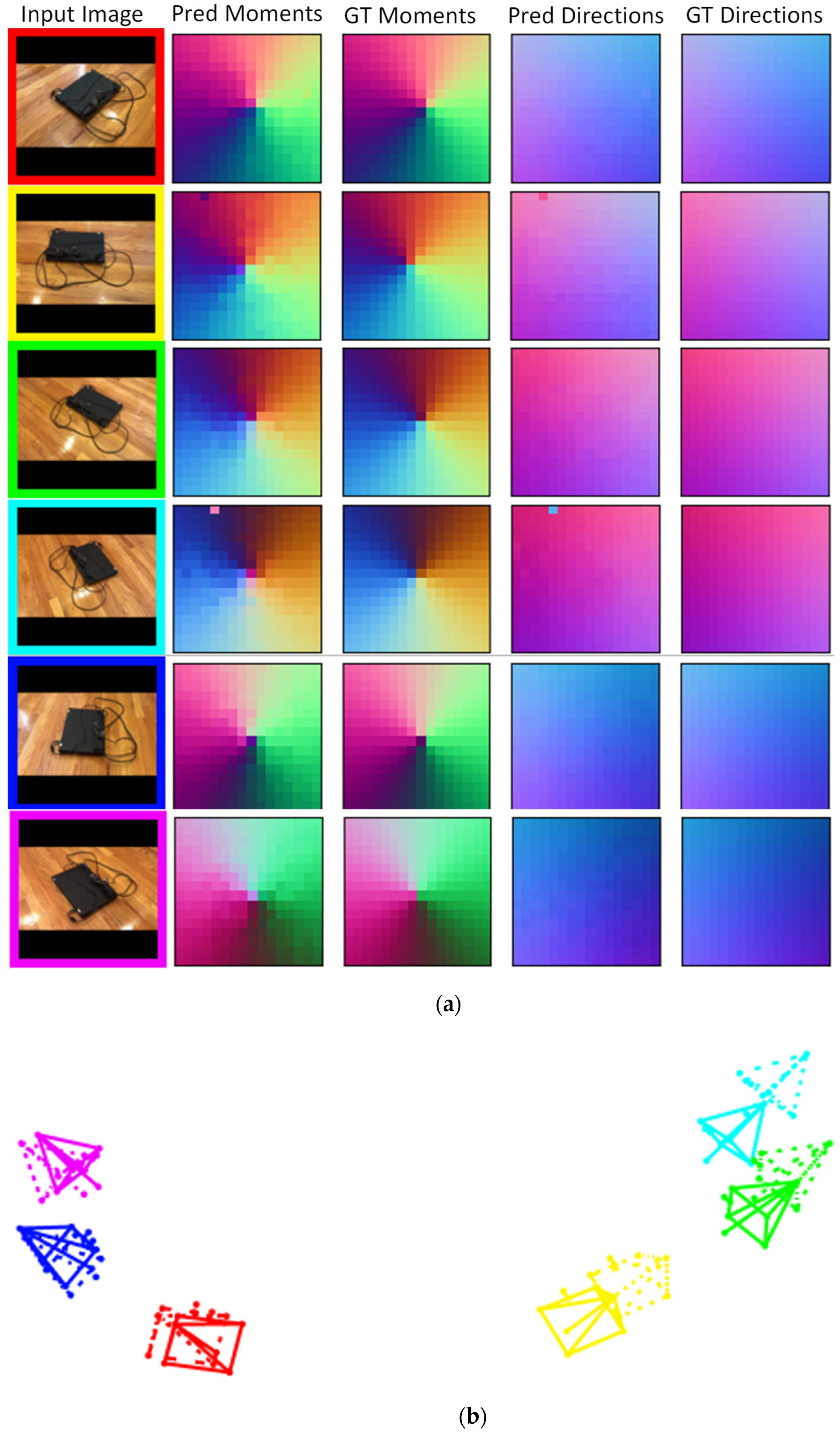
4.4. Rendering Quality Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.-N.; Zhang, F.-F.; Mai, Q. Robot adoption and laber demand: A new interpretation from external completion. Technol. Soc. 2023, 74, 102310. [Google Scholar] [CrossRef]
- Kojima, T.; Zhu, Y.; Iwasawa, Y.; Kitamura, T.; Yan, G.; Morikuni, S.; Takanami, R.; Solano, A.; Matsushima, T.; Murakami, A.; et al. A comprehensive survey on physical risk control in the era of foundation model-enabled robotics. arXiv 2025, arXiv:2505.12583v2. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Lin, A.; Kumar, M.; Yang, T.-H.; Ramanan, D.; Tulsiani, S. Camera as rays: Pose estimation via ray diffusion. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing scenes as neural radiance fields for view synthesis. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Sarlin, P.-E.; Cadena, C.; Siegwart, R.; Dymczyk, M. From coarse to fine: Robust hierarchical localization at large scale. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12716–12725. [Google Scholar]
- Zhang, J.Y.; Ramanan, D.; Tulsiani, S. Relpose: Predicting probabilistic relative rotation for single objects in the wild. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 592–611. [Google Scholar]
- Wang, J.; Rupprecht, C.; Novotny, D. Posediffusion: Solving pose estimation via diffusion-aided bundle adjustment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 9773–9783. [Google Scholar]
- Lin, A.; Zhang, J.Y.; Ramanan, D.; Tulsiani, S. Relpose++: Recovering 6d poses from sparse-view observations. In Proceedings of the 2024 International Conference on 3D Vision (3DV), Davos, Switzerland, 18–21 March 2024; pp. 106–115. [Google Scholar]
- Johari, M.M.; Lepoittevin, Y.; Fleuret, F. Geon erf: Generalizing nerf with geometry priors. In Proceedings of the IEEE/ CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18365–18375. [Google Scholar]
- Wang, P.; Chen, X.; Chen, T.; Venugopalan, S.; Wang, Z. Is attention all that nerf needs? arXiv 2022, arXiv:2207.13298. [Google Scholar]
- Plücker, J. Analytisch-Geometrische Entwicklungen, 2nd ed.; GD Baedeker: Essen, Germany, 1828. [Google Scholar]
- Abdel-Aziz, Y.I.; Karara, H.M.; Hauck, M. Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry. Photogramm. Eng. Remote Sens. 2015, 81, 103–107. [Google Scholar] [CrossRef]
- Peebles, W.; Xie, S. Scalable diffusion models with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 4195–4205. [Google Scholar]
- Paszke, A. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Reizenstein, J.; Shapovalov, R.; Henzler, P.; Sbordone, L.; Labatut, P.; Novotny, D. Common objects in 3d: Large-scale learning and evaluation of real-life 3d category reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10901–10911. [Google Scholar]
- Oquab, M.; Darcet, T.; Moutakanni, T.; Vo, H.; Szafraniec, M.; Khalidov, V.; Fernandez, P.; Haziza, D.; Massa, F.; El-Nouby, A.; et al. Dinov2: Learning robust visual features without supervision. arXiv 2023, arXiv:2304.07193. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.-Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Shi, S.; Wang, X.; Li, H. Pointrcnn: 3d object proposal generation and detection from point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 770–779. [Google Scholar]
- Wang, P.; Liu, Y.; Chen, Z.; Liu, L.; Liu, Z.; Komura, T.; Theobalt, C.; Wang, W. F2-nerf: Fast neural radiance field training with free camera trajectories. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 4150–4159. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Kim, J.W. Intergrated Enhancement of SLAM Components Using Deep Learning and Its Applicability. Ph.D. Thesis, Seoul National University of Science & Technology, Seoul, Republic of Korea, August 2025. [Google Scholar]

| Number of images | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Seen Categories | |||||||
| Ray Diffusion [3] | 92.9 | 93.7 | 94.0 | 94.2 | 94.4 | 94.5 | 94.7 |
| Ray Regression [3] | 90.2 | 90.3 | 90.5 | 90.9 | 91.2 | 91.2 | 91.1 |
| Ray Regression* | 79.1 | 80.3 | 80.4 | 80.9 | 80.5 | 80.5 | 80.5 |
| Ours (R + T) | 87.4 | 86.7 | 86.5 | 86.7 | 86.7 | 86.7 | 86.5 |
| Ours (R + T + Render) | 80.9 | 81.3 | 80.8 | 80.7 | 80.7 | 80.7 | 80.3 |
| Unseen Categories | |||||||
| Ray Diffusion [3] | 84.8 | 87.3 | 88.4 | 89.0 | 89.0 | 89.4 | 89.6 |
| Ray Regression [3] | 81.2 | 82.7 | 83.4 | 84.0 | 84.1 | 84.4 | 84.5 |
| Ray Regression* | 64.4 | 65.1 | 64.0 | 64.3 | 64.2 | 64.9 | 65.0 |
| Ours (R + T) | 84.0 | 83.3 | 83.3 | 83.2 | 83.1 | 83.0 | 82.7 |
| Ours (R + T + Render) | 79.2 | 78.2 | 78.3 | 77.8 | 77.5 | 77.2 | 76.5 |
| Number of images | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Seen Categories | |||||||
| Ray Diffusion [3] | 100 | 95.0 | 91.5 | 88.9 | 87.5 | 86.3 | 85.3 |
| Ray Regression [3] | 100 | 92.3 | 86.8 | 83.2 | 81.0 | 79.0 | 77.4 |
| Ray Regression* | 100 | 85.5 | 75.4 | 69.5 | 65.3 | 63.2 | 60.5 |
| Ours (R + T) | 100 | 99.7 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| Ours (R + T + Render) | 100 | 99.8 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| Unseen Categories | |||||||
| Ray Diffusion [3] | 100 | 88.5 | 83.1 | 79.0 | 75.7 | 74.6 | 72.4 |
| Ray Regression [3] | 100 | 85.5 | 76.7 | 72.4 | 69.1 | 66.1 | 64.9 |
| Ray Regression* | 100 | 72.9 | 58.5 | 51.8 | 48.1 | 45.1 | 43.9 |
| Ours (R + T) | 100 | 99.3 | 98.9 | 98.9 | 98.5 | 98.3 | 98.2 |
| Ours (R + T + Render) | 100 | 99.4 | 98.9 | 98.8 | 98.5 | 98.4 | 98.3 |
| Number of images | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Seen Categories | |||||||
| 1.—Our block1 (R + T) | 84.5 | 83.7 | 83.6 | 83.7 | 83.9 | 83.9 | 83.9 |
| 2.—Rotation w/tanh | 87.4 | 86.7 | 86.5 | 86.7 | 86.7 | 86.7 | 86.5 |
| 3.—ConvNext encoder all freeze * | 59.5 | 58.9 | 59.0 | 58.9 | 59.1 | 58.7 | 58.6 |
| 4.—ConvNext encoder all freeze | 50.6 | 49.5 | 49.4 | 49.4 | 49.6 | 49.8 | 49.7 |
| 5.—ConvNext encoder 0, 1 freeze | 60.8 | 60.3 | 60.6 | 60.9 | 61.0 | 60.9 | 60.8 |
| 6.—Our block1 (R + T + Render) | 80.9 | 81.3 | 80.8 | 80.7 | 80.7 | 80.7 | 80.3 |
| 7.—Our block2 (R + T) | 87.8 | 87.2 | 86.9 | 86.9 | 86.8 | 86.7 | 86.7 |
| 8.—Our block2 (R + T + Render) | 85.9 | 85.3 | 85.7 | 85.5 | 85.6 | 85.5 | 85.3 |
| Unseen Categories | |||||||
| 1.—Our block1 (R + T) | 82.1 | 80.7 | 80.4 | 80.6 | 80.2 | 80.3 | 80.3 |
| 2.—Rotation w/tanh | 84.0 | 83.3 | 83.3 | 83.2 | 83.1 | 83.0 | 82.7 |
| 3.—ConvNext encoder all freeze * | 45.0 | 43.4 | 42.0 | 42.0 | 41.9 | 41.3 | 40.8 |
| 4.—ConvNext encoder all freeze | 26.0 | 24.5 | 24.5 | 24.4 | 24.1 | 23.8 | 23.5 |
| 5.—ConvNext encoder 0, 1 freeze | 51.2 | 51.1 | 51.8 | 52.3 | 52.7 | 52.8 | 52.9 |
| 6.—Our block1 (R + T + Render) | 79.2 | 78.2 | 78.3 | 77.8 | 77.5 | 77.2 | 76.5 |
| 7.—Our block2 (R + T) | 84.6 | 83.3 | 82.6 | 81.6 | 81.8 | 81.5 | 81.8 |
| 8.—Our block2 (R + T + Render) | 82.3 | 81.2 | 81.5 | 81.0 | 81.1 | 81.0 | 80.6 |
| Number of images | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Seen Categories | |||||||
| 1.—Our block1 (R + T) | 100 | 99.7 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| 2.—Rotation w/tanh | 100 | 99.7 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| 3.—ConvNext encoder all freeze * | 100 | 99.7 | 99.3 | 99.1 | 98.9 | 98.7 | 98.6 |
| 4.—ConvNext encoder all freeze | 100 | 99.6 | 99.2 | 98.9 | 98.6 | 98.4 | 98.2 |
| 5.—ConvNext encoder 0, 1 freeze | 100 | 99.4 | 99.0 | 98.7 | 98.4 | 98.3 | 98.1 |
| 6.—Our block1 (R + T + Render) | 100 | 99.8 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| 7.—Our block2 (R + T) | 100 | 99.8 | 99.7 | 99.6 | 99.4 | 99.5 | 99.5 |
| 8.—Our block2 (R + T + Render) | 100 | 99.6 | 99.2 | 98.9 | 98.6 | 98.4 | 98.2 |
| Unseen Categories | |||||||
| 1.—Our block1 (R + T) | 100 | 99.3 | 98.9 | 98.9 | 98.5 | 98.3 | 98.2 |
| 2.—Rotation w/tanh | 100 | 99.7 | 99.6 | 99.6 | 99.5 | 99.5 | 99.4 |
| 3.—ConvNext encoder all freeze * | 100 | 98.8 | 98.2 | 97.6 | 97.2 | 99.5 | 99.4 |
| 4.—ConvNext encoder all freeze | 100 | 98.6 | 97.3 | 96.7 | 95.9 | 95.5 | 94.9 |
| 5.—ConvNext encoder 0, 1 freeze | 100 | 99.0 | 98.1 | 97.7 | 96.8 | 96.8 | 96.5 |
| 6.—Our block1 (R + T + Render) | 100 | 99.4 | 98.9 | 98.8 | 98.5 | 98.4 | 98.3 |
| 7.—Our block2 (R + T) | 100 | 99.1 | 98.6 | 98.6 | 98.5 | 98.4 | 98.2 |
| 8.—Our block2 (R + T + Render) | 100 | 99.1 | 98.9 | 99.0 | 98.6 | 98.5 | 98.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-W.; Ha, J.-E. End-to-End Camera Pose Estimation with Camera Ray Token. Electronics 2025, 14, 4624. https://doi.org/10.3390/electronics14234624
Kim J-W, Ha J-E. End-to-End Camera Pose Estimation with Camera Ray Token. Electronics. 2025; 14(23):4624. https://doi.org/10.3390/electronics14234624
Chicago/Turabian StyleKim, Jin-Woo, and Jong-Eun Ha. 2025. "End-to-End Camera Pose Estimation with Camera Ray Token" Electronics 14, no. 23: 4624. https://doi.org/10.3390/electronics14234624
APA StyleKim, J.-W., & Ha, J.-E. (2025). End-to-End Camera Pose Estimation with Camera Ray Token. Electronics, 14(23), 4624. https://doi.org/10.3390/electronics14234624







