Experimentally-Based Circuit Modeling Validation of a DC-Electrified Railway System for Rail Voltage and Stray-Current Evaluation
Abstract
1. Introduction
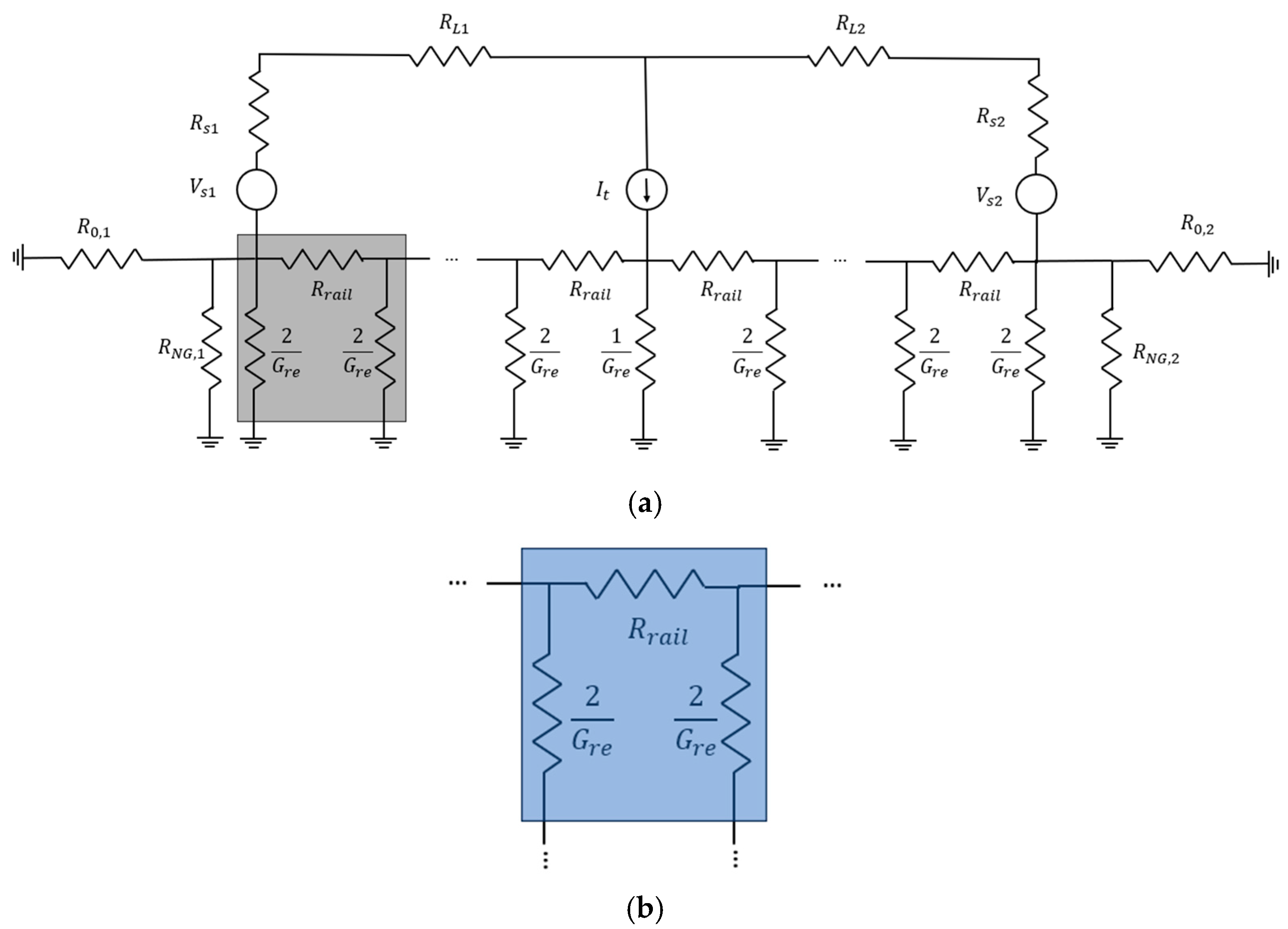
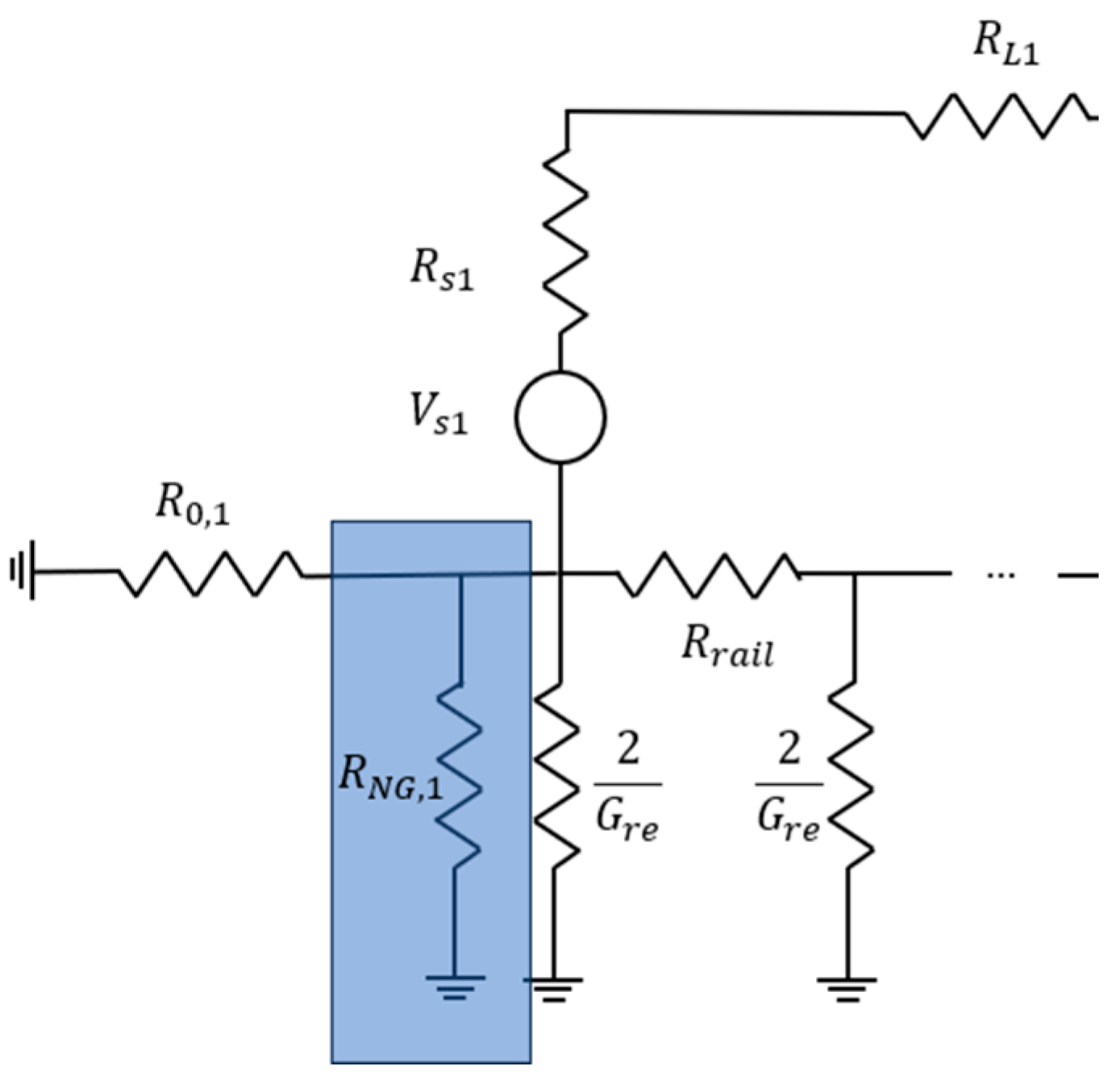
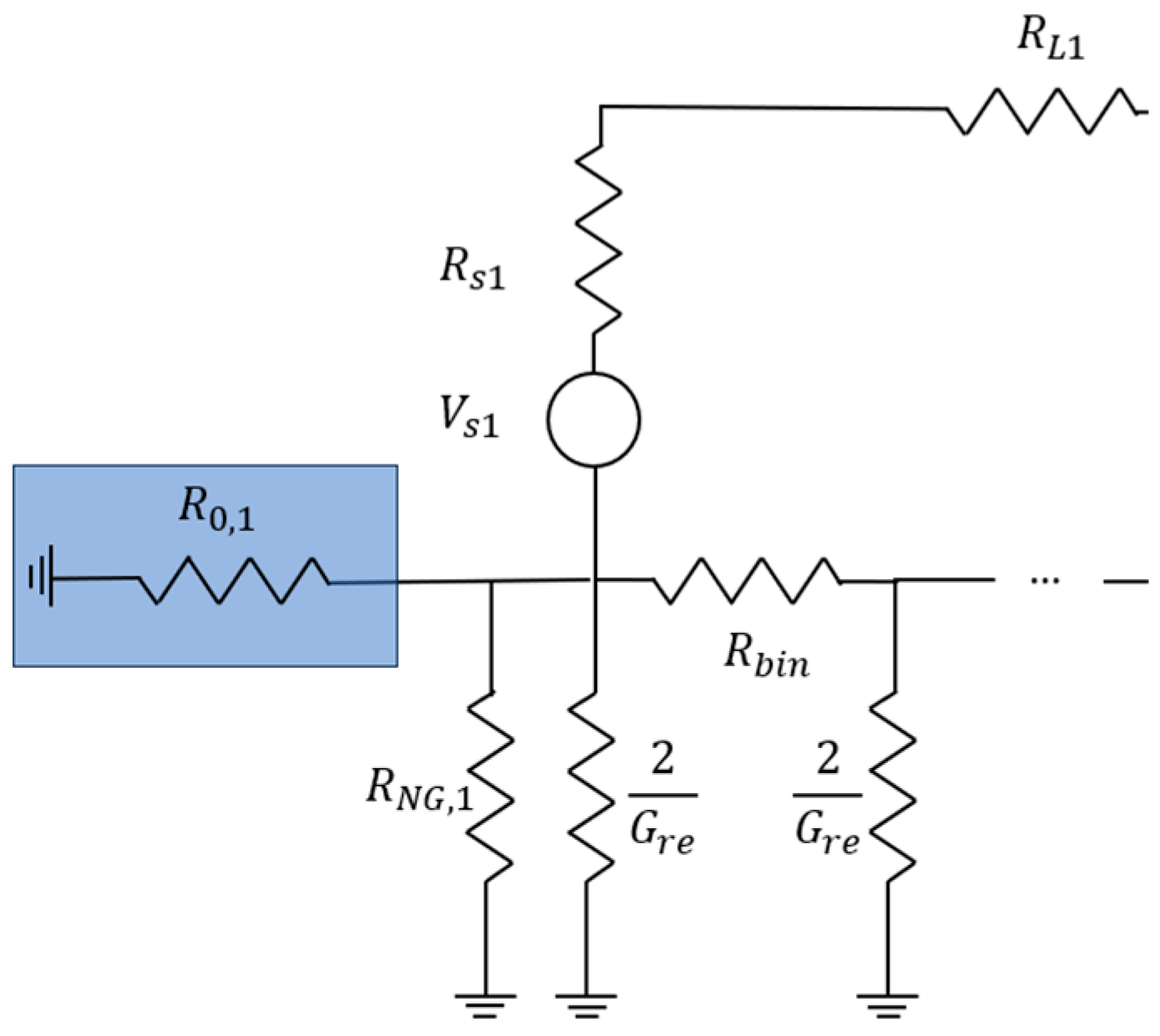
2. Railway Circuit Modeling
3. Experimental Validation
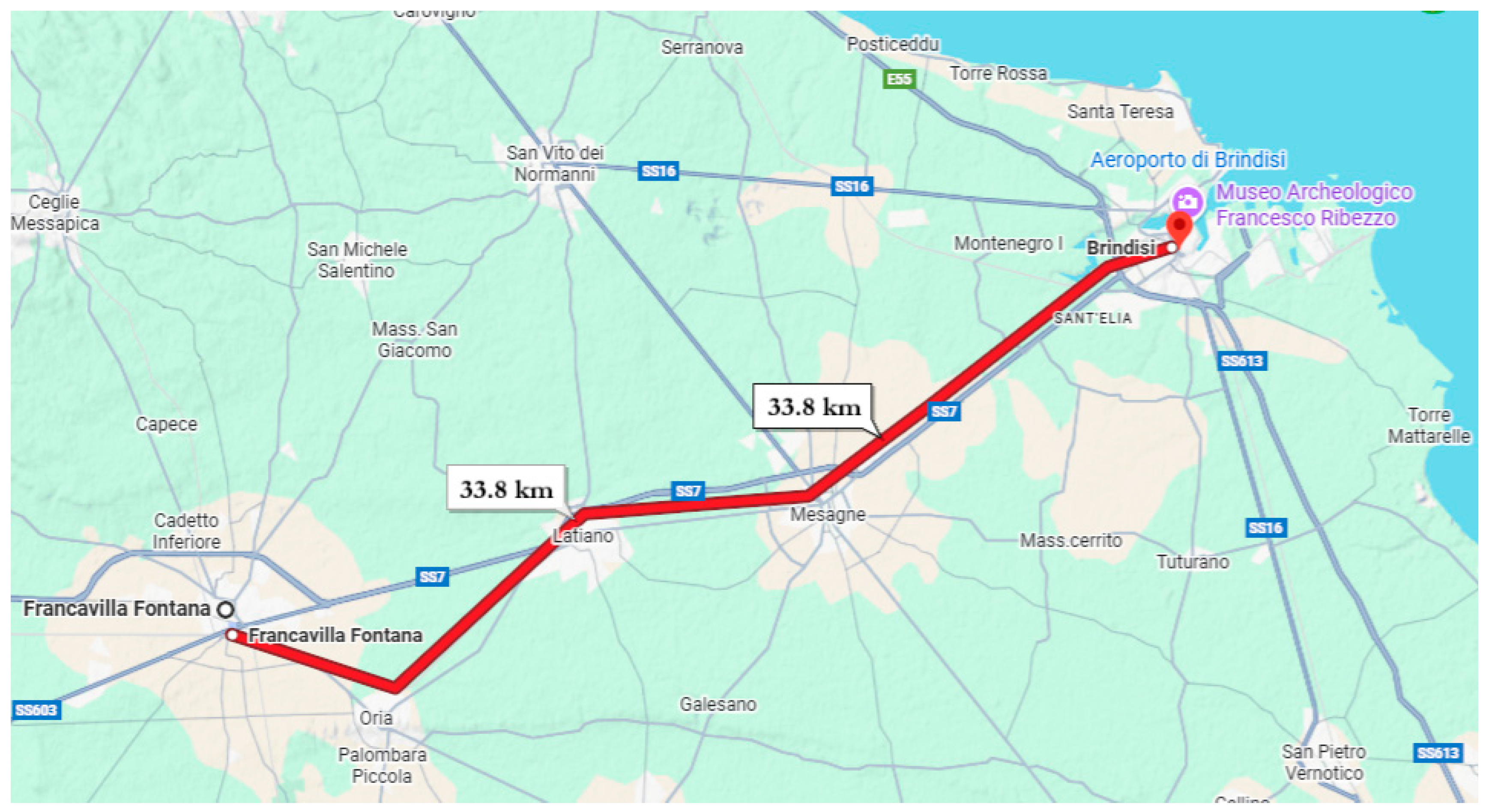
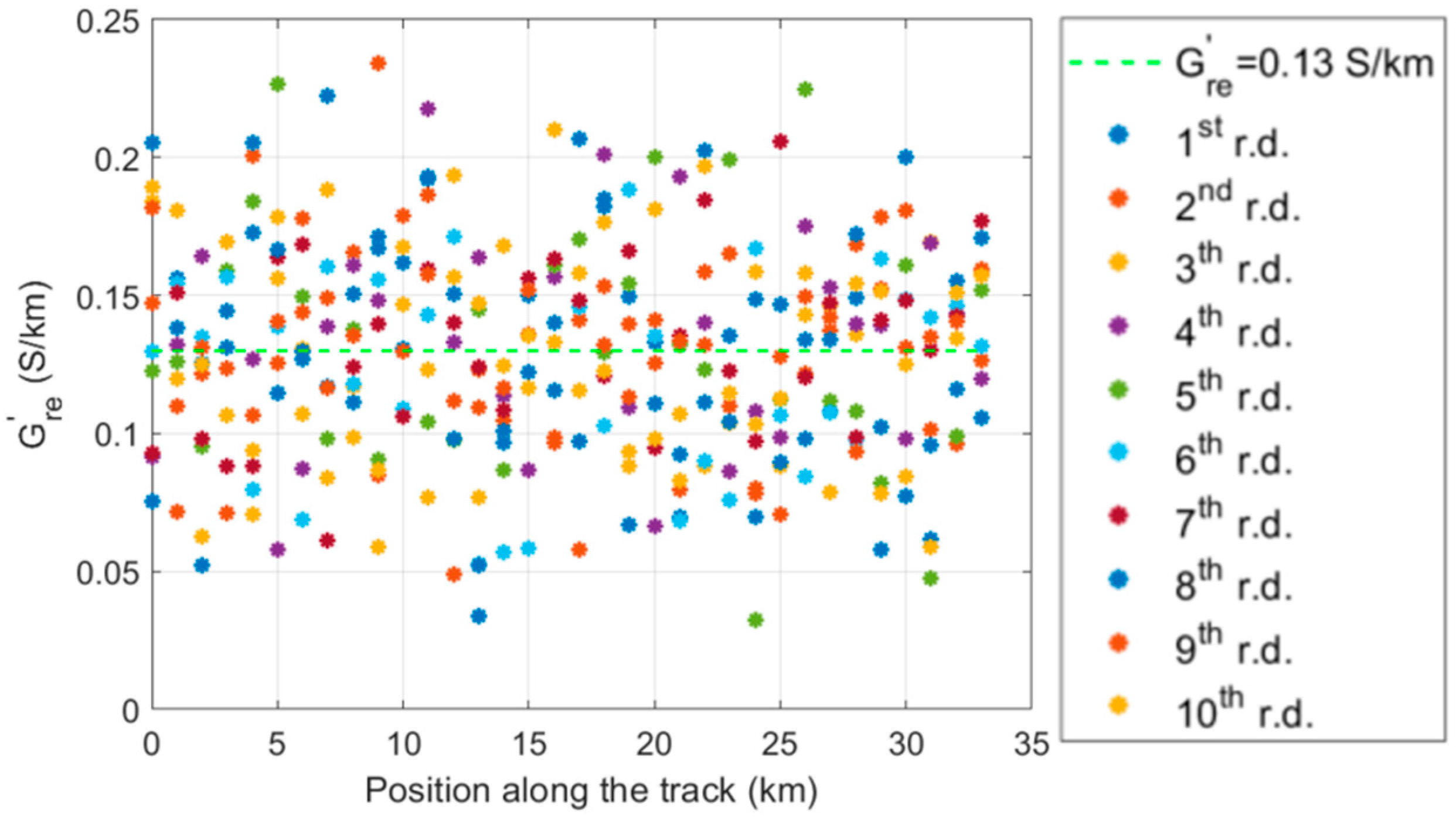
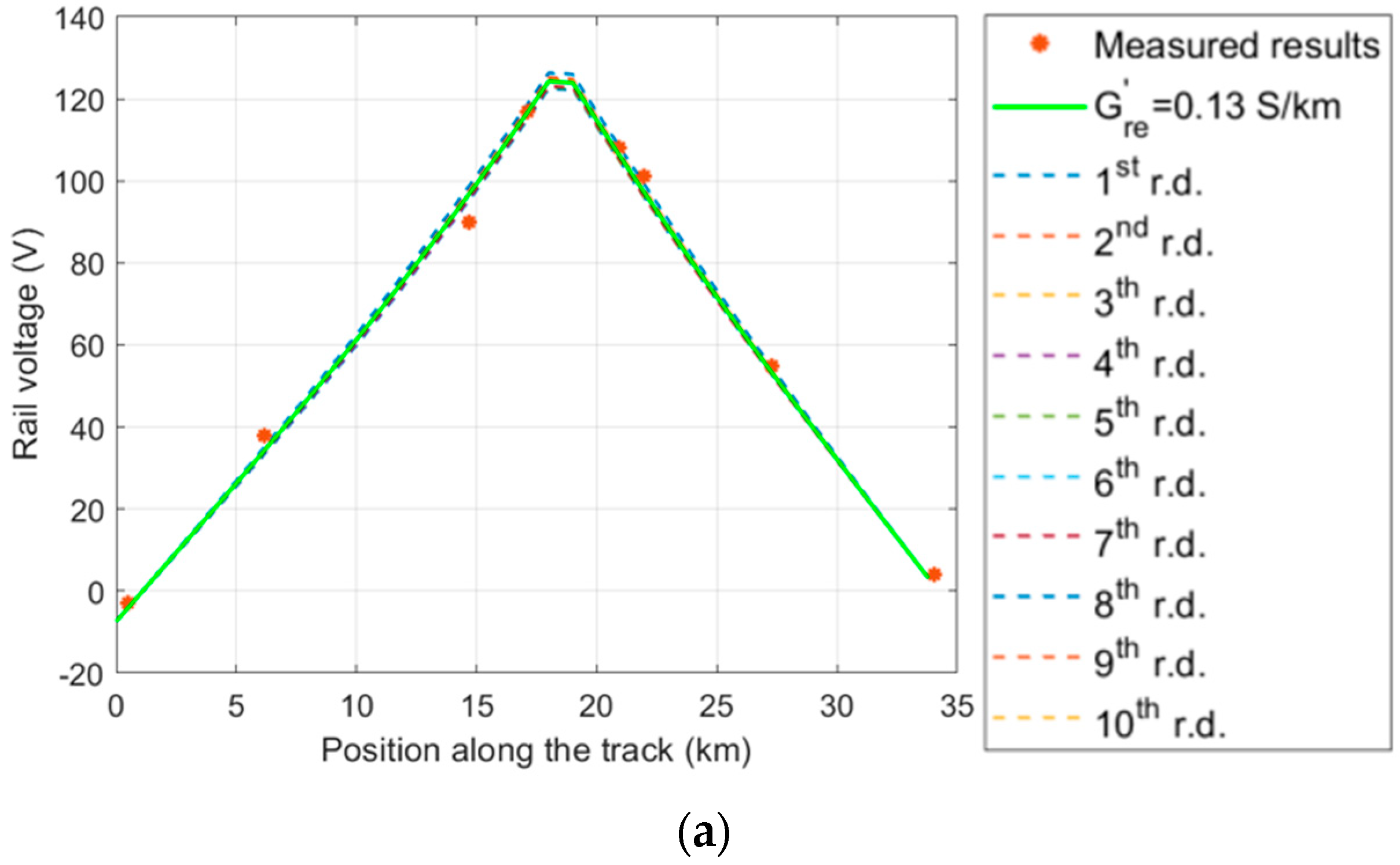
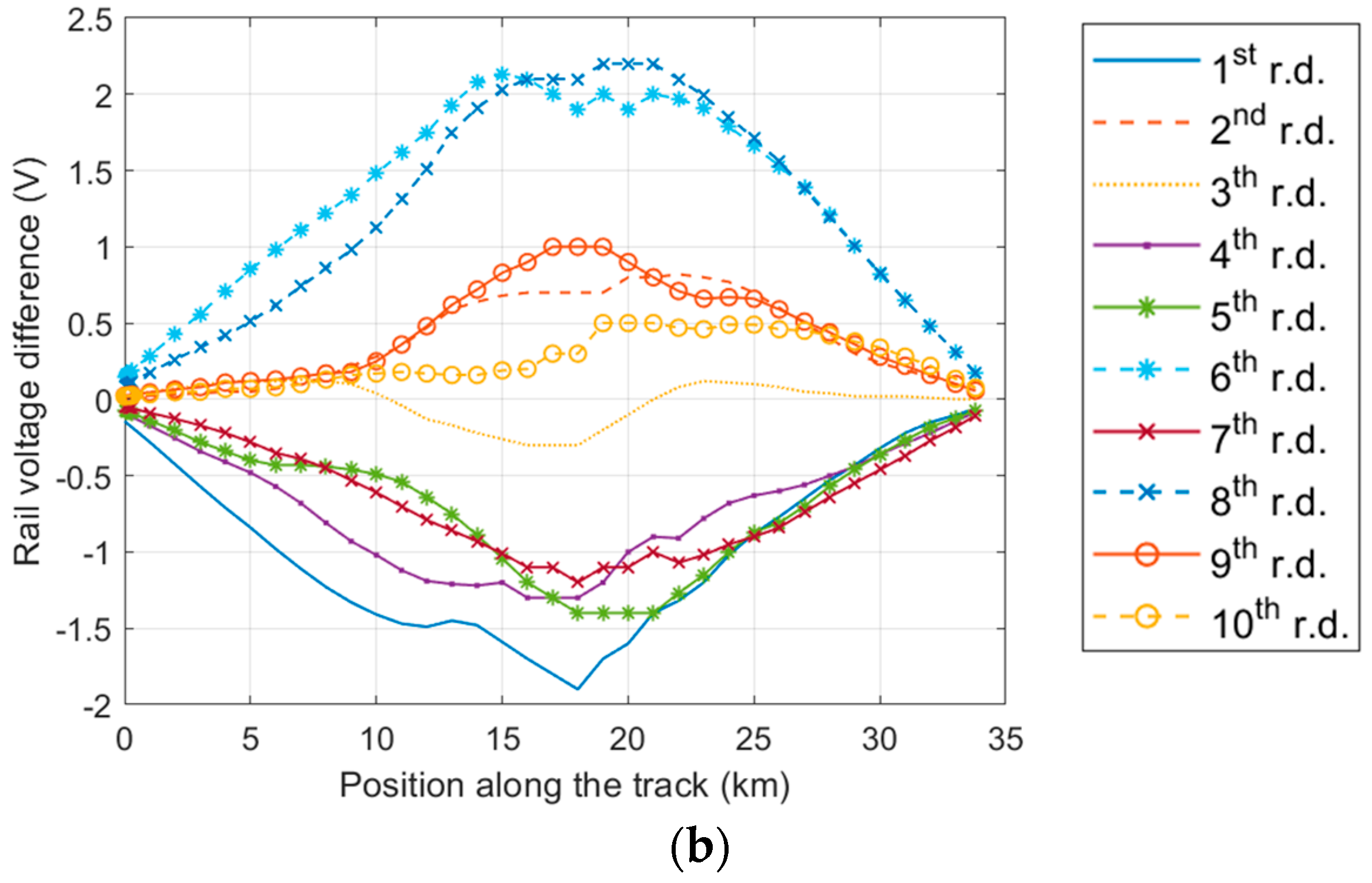
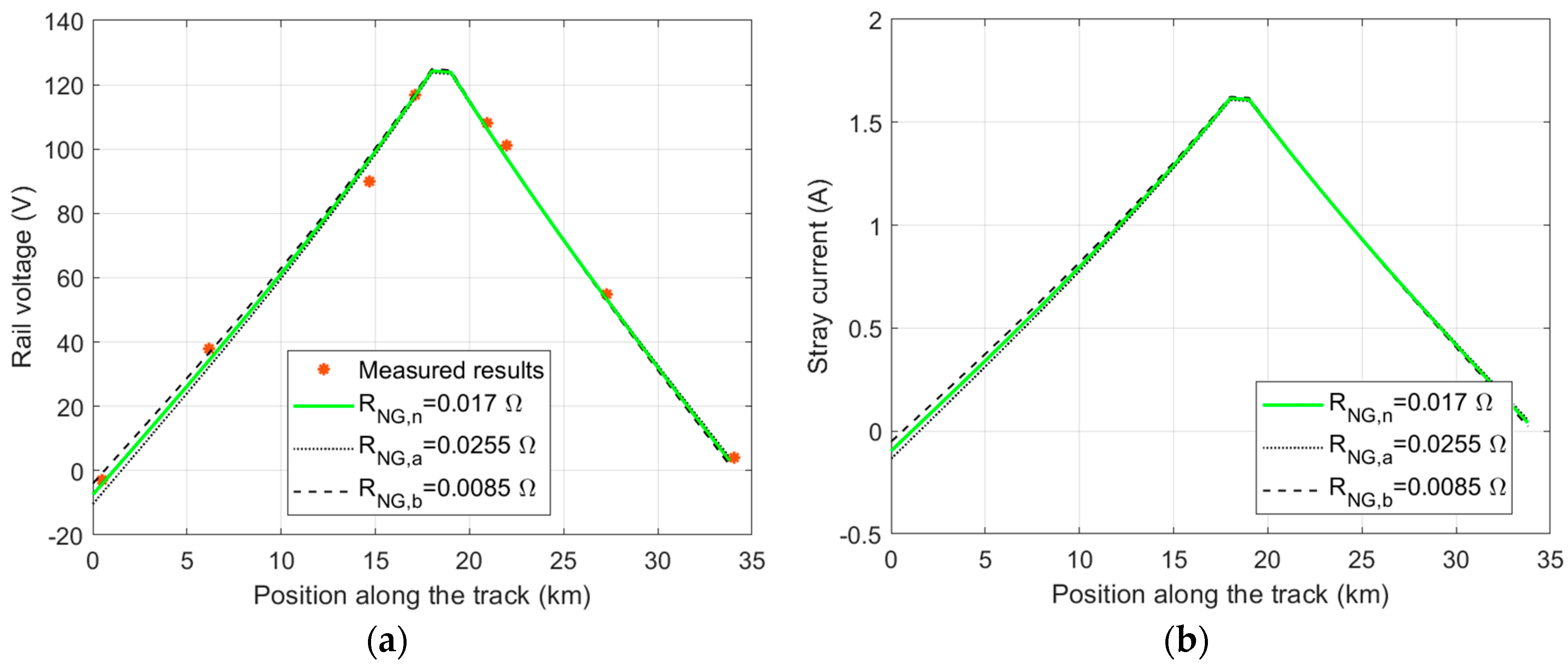
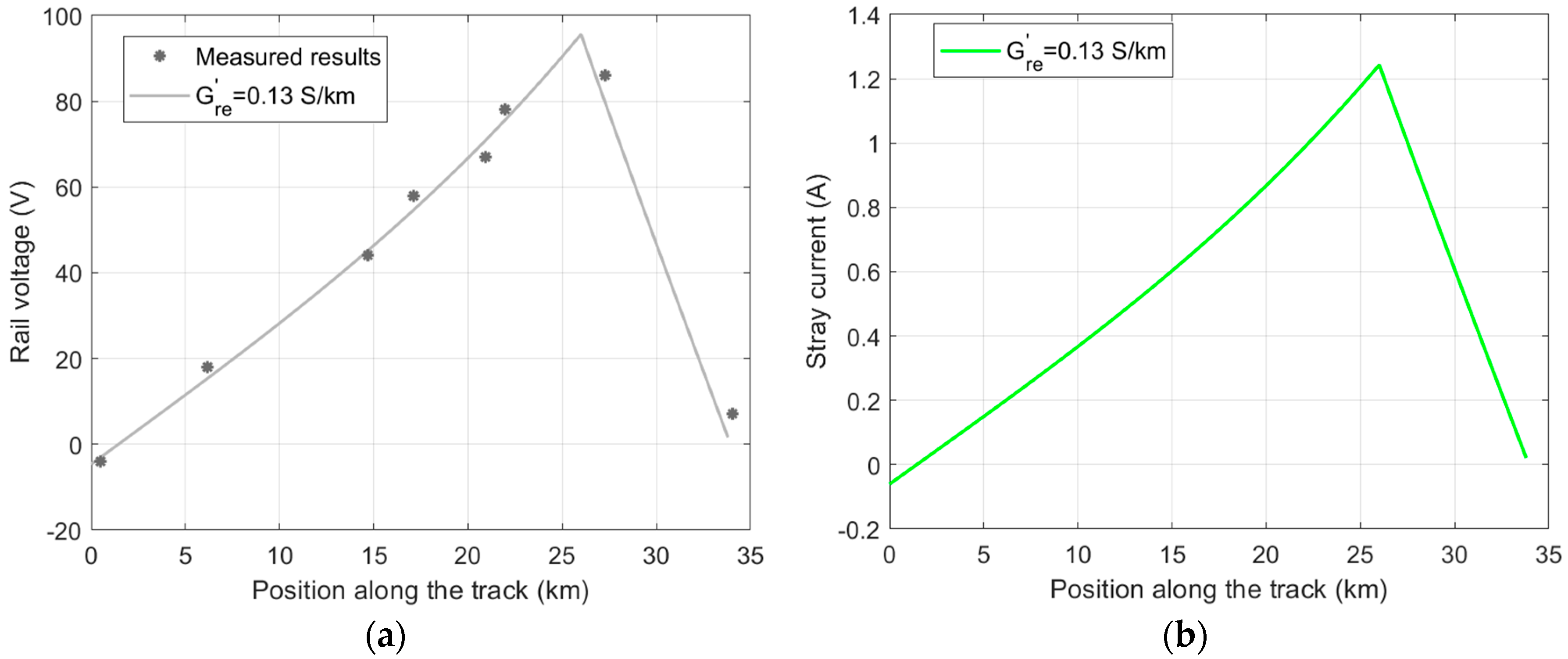
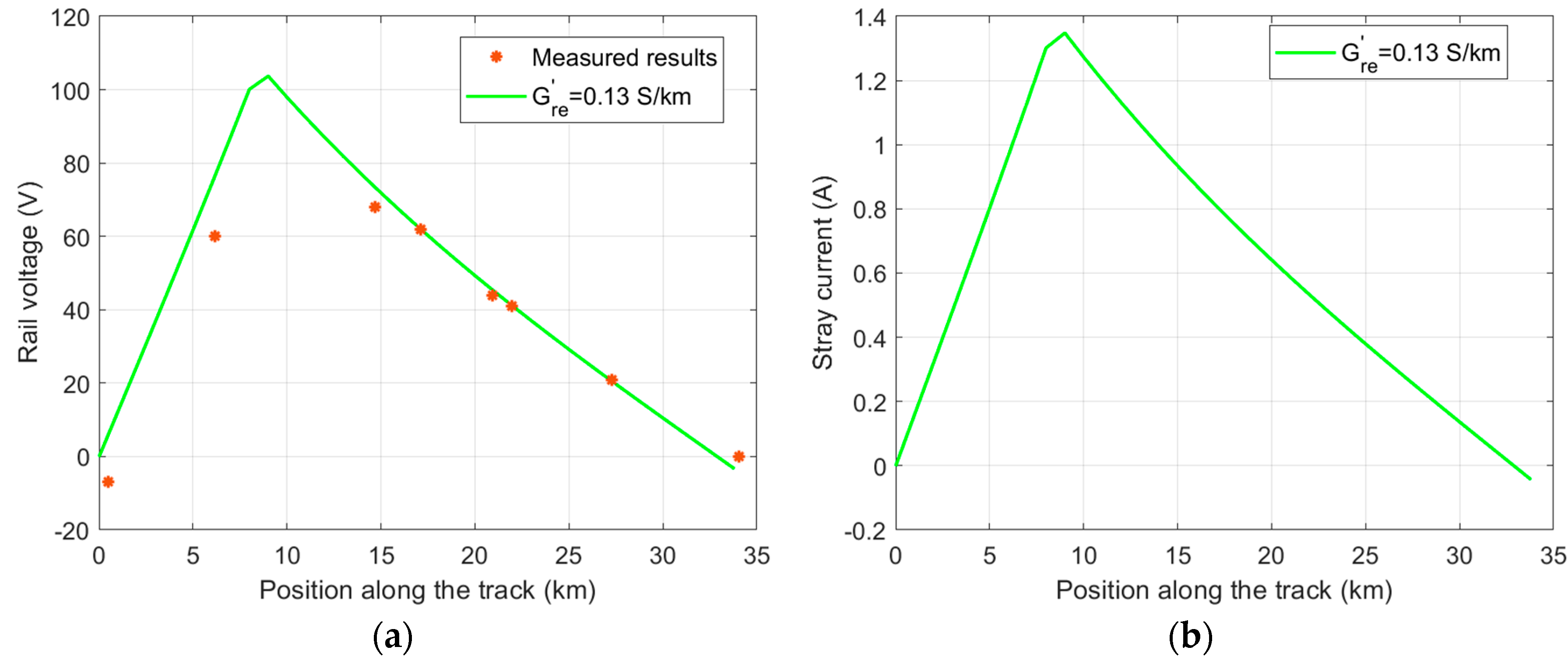
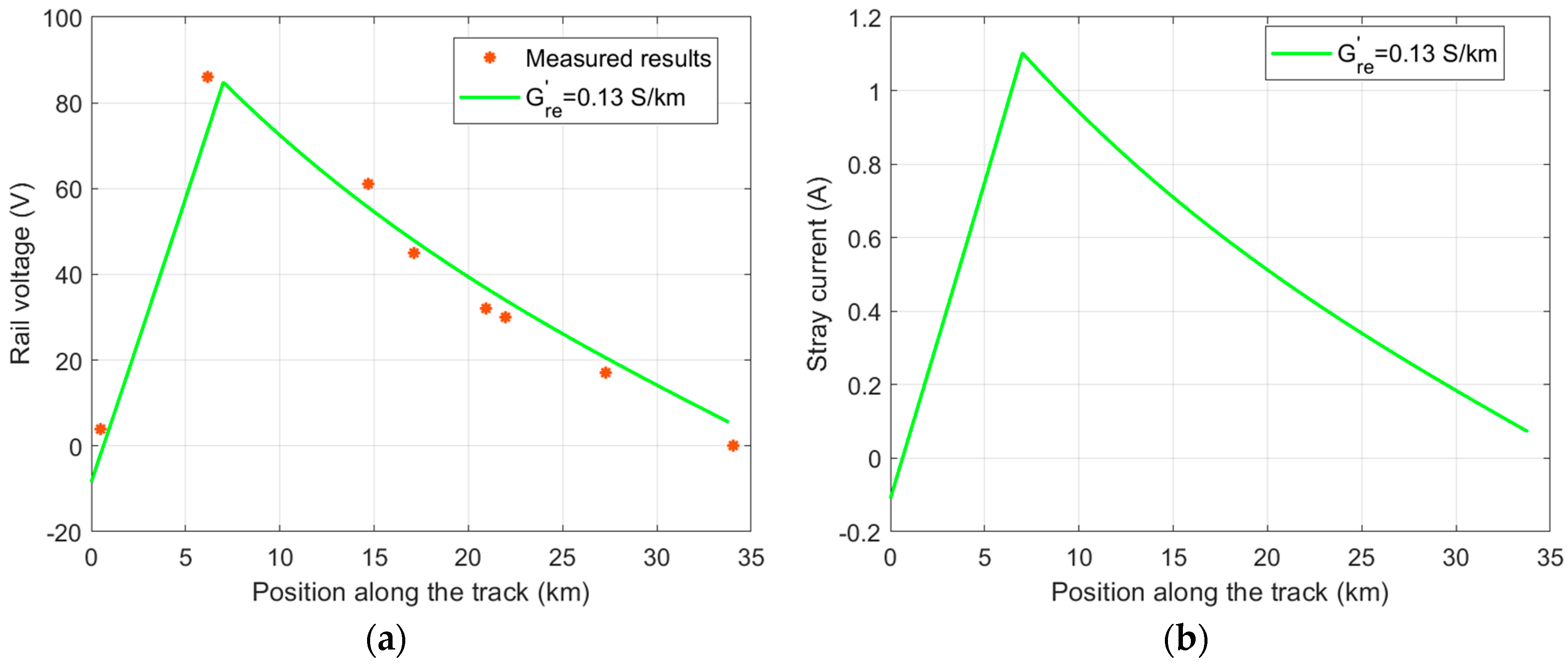
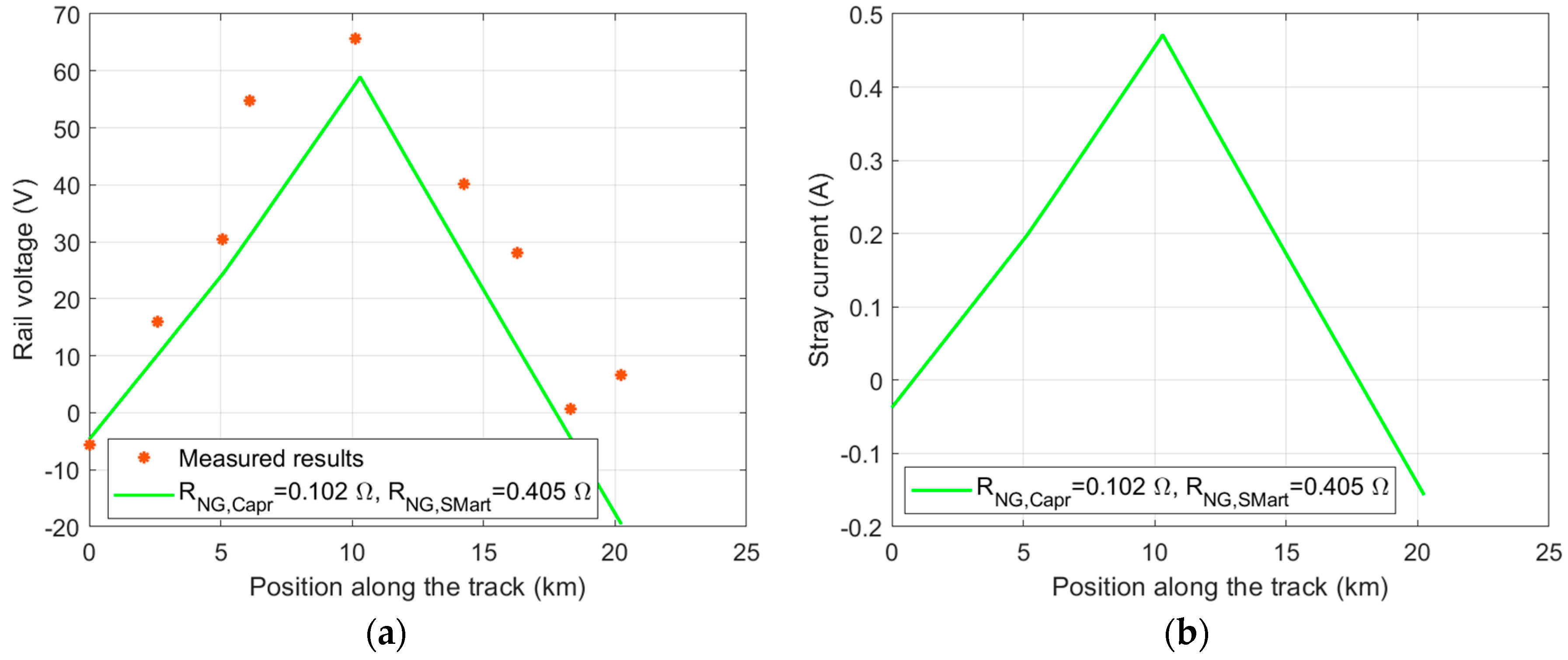
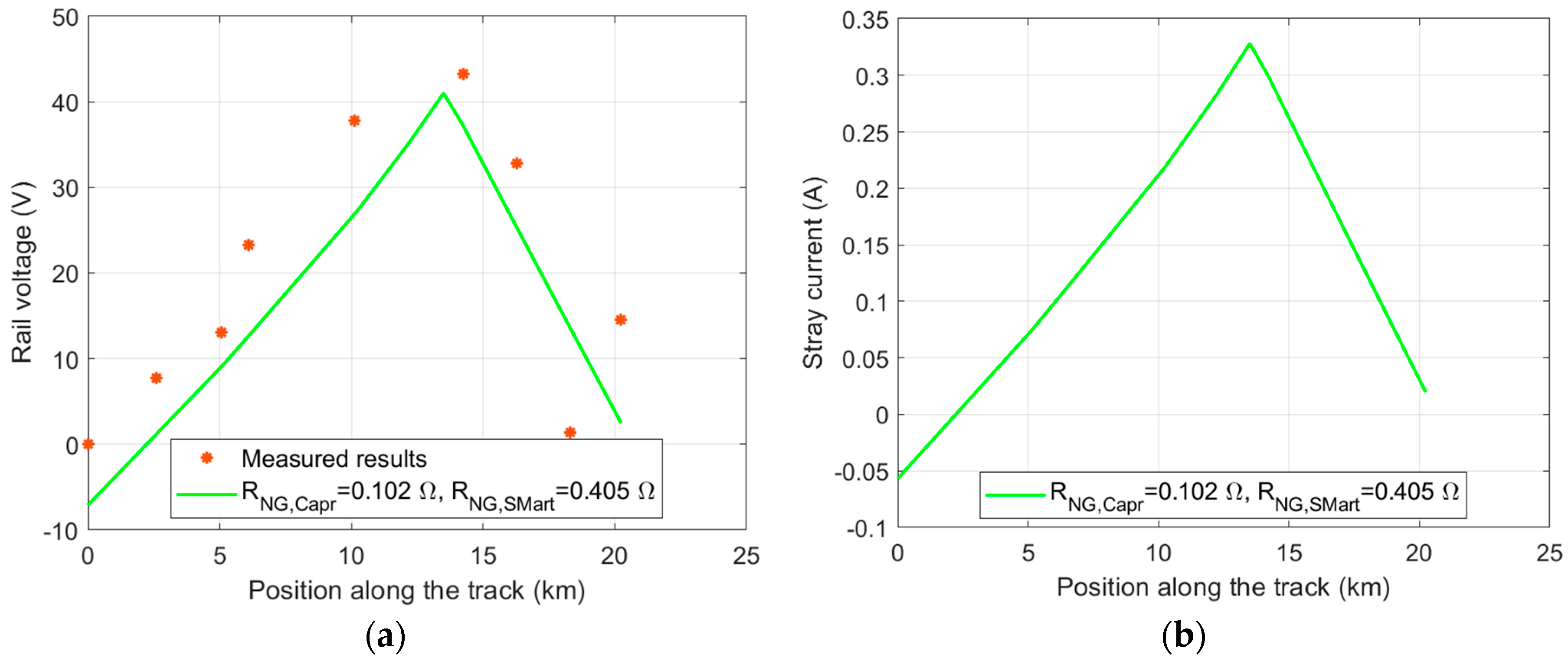
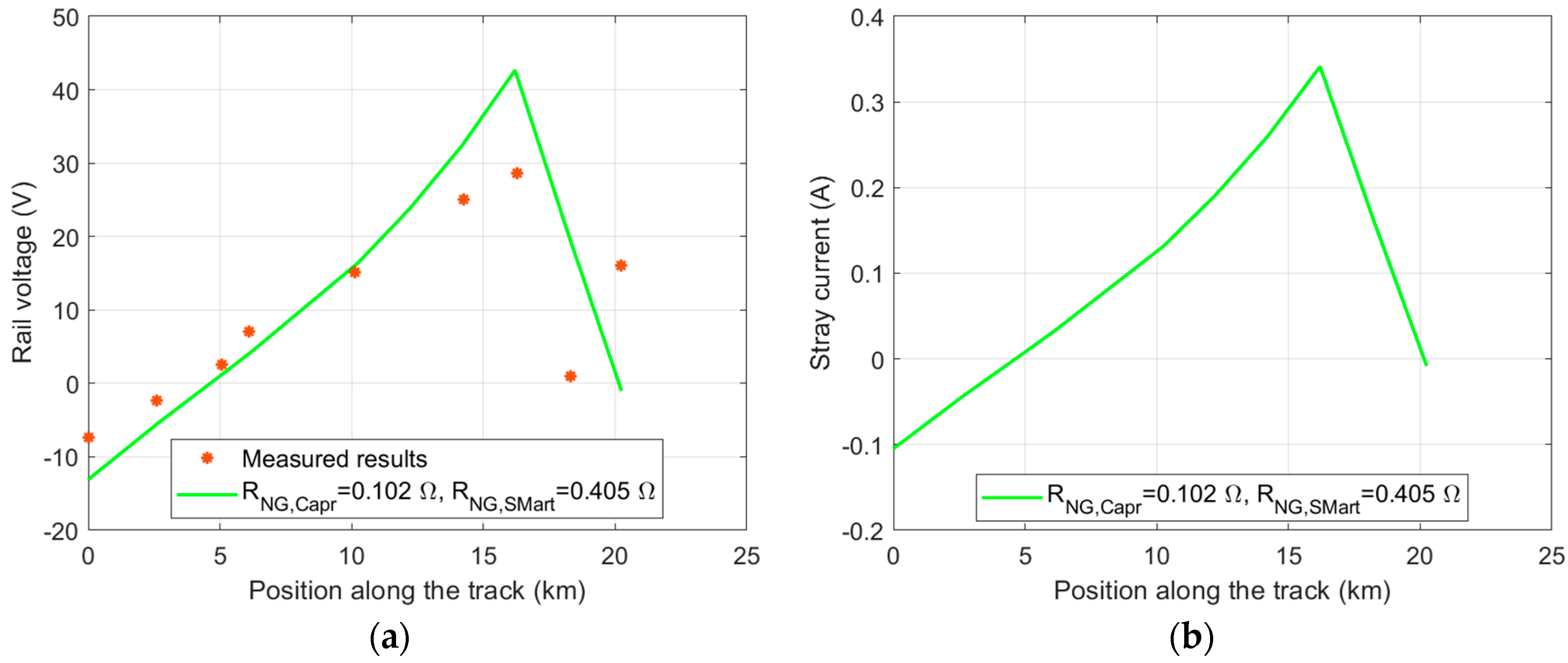
3.1. Assessment of Rail Voltage and Stray Current in the Francavilla Fontana–Brindisi Railway Section
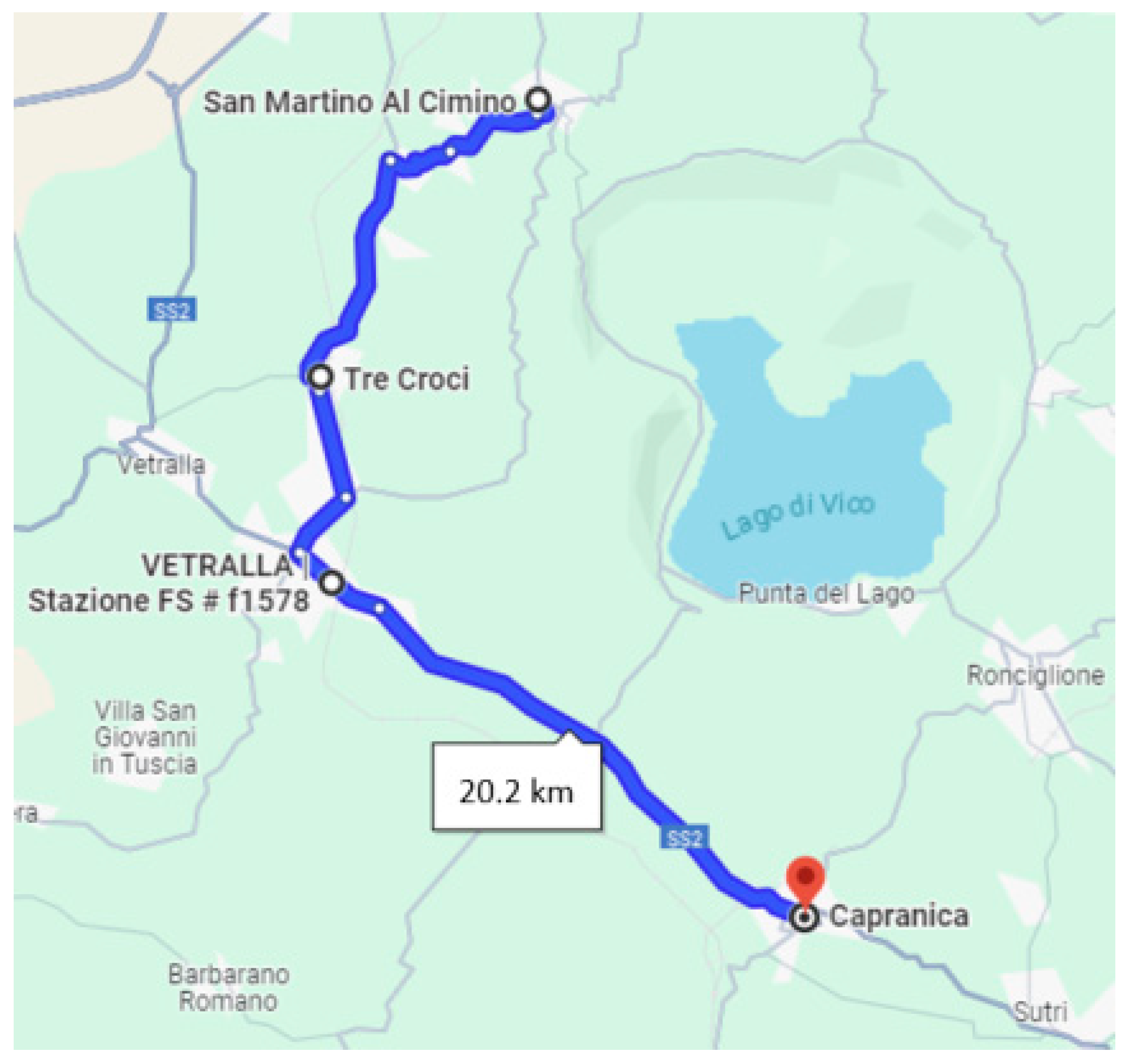
3.2. Assessment of Rail Voltage and Stray Current in the S. Martino al Cimino–Capranica Railway Section
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Regula, M.; Siranec, M.; Otcenasova, A.; Hoger, M. Possibilities of the stray current measurement and corrosive risk evaluation. Electr. Eng. 2022, 104, 2497–2513. [Google Scholar] [CrossRef]
- Siranec, M.; Regula, M.; Otcenasova, A.; Altus, J. Measurement and Evaluation of the Stray Currents from the DC Electric Traction Systems. In Proceedings of the 2020 ELEKTRO, Taormina, Italy, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Höger, M.; Reguľa, M.; Roch, M. Investigating the impacts of high voltage powerlines on ground current fields. Transp. Res. Procedia 2023, 74, 900–907. [Google Scholar] [CrossRef]
- Aatif, S.; Hu, H.; Rafiq, F.; He, Z. Analysis of rail potential and stray current in MVDC railway electrification system. Railw. Eng. Sci. 2021, 29, 394–407. [Google Scholar] [CrossRef]
- Wieczorek, G.; Bernacki, K.; Rymarski, Z.; Oliwa, W. Gathering Energy of the Stray Currents in Electrified Railways Environment for Power Supply. Energies 2021, 14, 6206. [Google Scholar] [CrossRef]
- Mariscotti, A. Stray Current Protection and Monitoring Systems: Characteristic Quantities, Assessment of Performance and Verification. Sensors 2020, 20, 6610. [Google Scholar] [CrossRef] [PubMed]
- Charalambous, C.A.; Cotton, I.; Aylott, P. A Simulation Tool to Predict the Impact of Soil Topologies on Coupling Between a Light Rail System and Buried Third-Party Infrastructure. IEEE Trans. Veh. Technol. 2008, 57, 1404–1416. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, B.; Wei, K.; Fang, D.; Zou, Q. Analysis of Leakage Current Characteristics of Rail Insulation Fasteners Based on ANSYS. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 2640–2643. [Google Scholar] [CrossRef]
- Zaboli, A.; Vahidi, B.; Yousefi, S.; Hosseini-Biyouki, M.M. Evaluation and Control of Stray Current in DC-Electrified Railway Systems. IEEE Trans. Veh. Technol. 2017, 66, 974–980. [Google Scholar] [CrossRef]
- Huang, K.; Lin, G.; Liu, Z. Prediction Approach of Negative Rail Potentials and Stray Currents in Medium-Low-Speed Maglev. IEEE Trans. Transp. Electrif. 2022, 8, 3801–3815. [Google Scholar] [CrossRef]
- Liu, W.; Li, T.; Jie, Z.; Weiguo, P.; Yichen, Y. Evaluation of the Effect of Stray Current Collection System in DC-Electrified Railway System. IEEE Trans. Veh. Technol. 2021, 70, 6542–6553. [Google Scholar] [CrossRef]
- Zhu, C.; Zheng, Z.; Du, G.; Hu, J.; Kang, C.; Hu, J.; Yang, Y. Simulation Method of DC Traction Power Systems with Complex Operation Conditions Based on Unified Chain Model. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 846–852. [Google Scholar] [CrossRef]
- Jamali, S.; Alamuti, M.M.; Savaghebi, M. Effects of different earthing schemes on the stray current in rail transit systems. In Proceedings of the 2008 43rd International Universities Power Engineering Conference, Padua, Italy, 1–4 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Fichera, F.; Mariscotti, A.; Ogunsola, A.; Sandrolini, L. Comparison of distributed and lumped parameters stray current models. In Proceedings of the 2013 Africon, Pointe aux Piments, Mauritius, 9–12 September 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Li, C.; Du, Q.; Guo, Y.; Liu, Y.; Yang, F.; Chen, L.; Zhang, X.; Huang, G.; Gao, G.; Wu, G. Modeling of Stray Currents from Metro Intruding into Power System Considering the Complex Geological Conditions in Modern Megacities. IEEE Trans. Transp. Electrif. 2023, 9, 1653–1663. [Google Scholar] [CrossRef]
- Tang, M.; Zhong, H.; Zhu, T.; Zhang, J.; Yan, J.; Xiao, S.; Guo, Y.; Wu, G. The Distribution Analysis of the Ground Potential and Stray Current in Power Grid Under the Operation of Metro System. In Proceedings of the 2023 2nd International Conference on Power Systems and Electrical Technology (PSET), Milan, Italy, 25–27 August 2023; pp. 158–162. [Google Scholar] [CrossRef]
- Zhou, Q.; Lin, S.; Lin, X.; Wang, A. A Uniform Model for Stray Current of Long-Line DC Metro Systems. IEEE Trans. Transp. Electrif. 2022, 8, 2915–2927. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Wang, Y.; Xu, S.; Fan, M. Stray Current Distributing Model in the Subway System: A review and outlook. Int. J. Electrochem. Sci. 2018, 13, 1700–1727. [Google Scholar] [CrossRef]
- Arboleya, P.; Mayet, C.; Mohamed, B.; Aguado, J.A.; de la Torre, S. A review of railway feeding infrastructures: Mathematical models for planning and operation. eTransportation 2020, 5, 100063. [Google Scholar] [CrossRef]
- Tzeng, Y.-S.; Lee, C.-H. Analysis of Rail Potential and Stray Currents in a Direct-Current Transit System. IEEE Trans. Power Deliv. 2010, 25, 1516–1525. [Google Scholar] [CrossRef]
- Ogunsola, A.; Sandrolini, L.; Mariscotti, A. Evaluation of Stray Current From a DC-Electrified Railway with Integrated Electric–Electromechanical Modeling and Traffic Simulation. IEEE Trans. Ind. Appl. 2015, 51, 5431–5441. [Google Scholar] [CrossRef]
- Vranešić, K.; Haladin, I.; Lakušić, S.; Burnać, K. Convenient Procedure for Measuring the Electrical Resistance of Fastening Systems in Urban Railway Tracks. Energies 2023, 16, 1990. [Google Scholar] [CrossRef]
- Bhagat, S.; Bongiorno, J.; Mariscotti, A. Uncertainty of Standardized Track Insulation Measurement Methods for Stray Current Assessment. Sensors 2023, 23, 5900. [Google Scholar] [CrossRef] [PubMed]
- Ku, B.-Y. Rail-to-Earth Resistance Assessment: A Medium Capacity Transit System with Continuous Negative Rails by Potential Measurement. IEEE Veh. Technol. Mag. 2016, 11, 29–35. [Google Scholar] [CrossRef]
- Alamuti, M.; Nouri, H.; Jamali, S. Effects of earthing systems on stray current for corrosion and safety behaviour in practical metro systems. IET Electr. Syst. Transp. 2011, 1, 69–79. [Google Scholar] [CrossRef]
- Liu, N.; Du, G.; He, F.; Li, Q.; Xu, F.; Huang, W.; Jiang, X.; Zhu, Z. Optimization of grounding resistance in multitrain DC subway system based on MOEA/D-DE. IET Intell. Transp. Syst. 2023, 17, 1675–1689. [Google Scholar] [CrossRef]
- Chuchit, T.; Kulworawanichpong, T. Stray current assessment for DC transit systems based on modelling of earthing and bonding. Electr. Eng. 2019, 101, 81–90. [Google Scholar] [CrossRef]
- Soylemez, M.T.; Acikbas, S.; Kaypmaz, A. Controlling rail potential of DC supplied rail traction systems. Turk. J. Electr. Eng. 2006, 14, 475–484. [Google Scholar]
- Keysight Pathwave Advanced Design System, ADS 2023. Available online: https://www.keysight.com/us/en/products/software/pathwave-design-software/pathwave-advanced-design-system.html (accessed on 2 December 2022).
- EN 50122-1:2022; Railway Applications—Fixed Installations—Electrical Safety, Earthing and the Return Circuit—Part 1: Protective Provisions Against Electric Shock. CENELEC: Brussels, Belgium, 2022.
- EN 50122-2:2022; Railway Applications—Fixed Installations—Electrical Safety, Earthing and the Return Circuit—Part 2: Provisions Against the Effects of Stray Current Caused by DC Traction Systems. CENELEC: Brussels, Belgium, 2022.
- EN 50163:2022; Railway Applications—Supply Voltages of Traction Systems. CENELEC: Brussels, Belgium, 2022.
- Fluke. A3003 FC, Operating Manual; Fluke: Everett, WA, USA, 2024. [Google Scholar]
- Fluke. V3001AC, Operating Manual; Fluke: Everett, WA, USA, 2023. [Google Scholar]
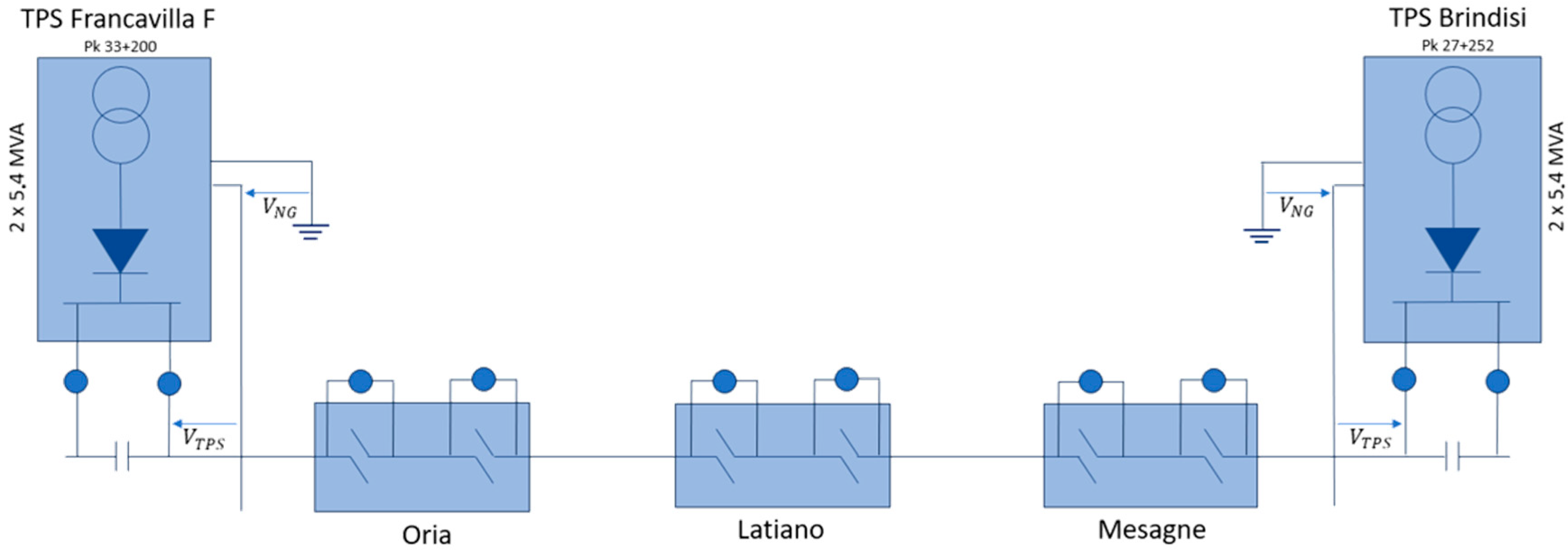


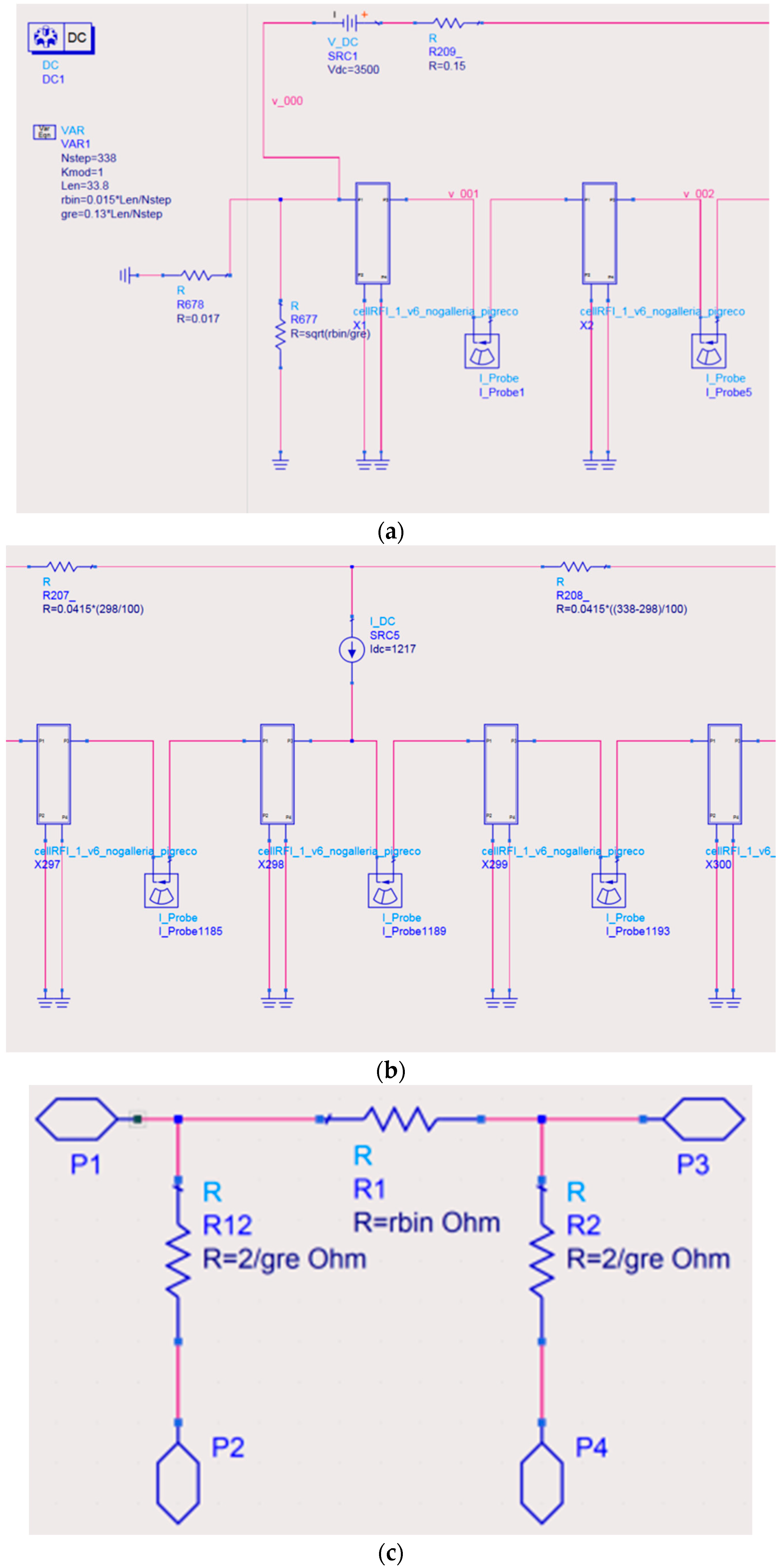
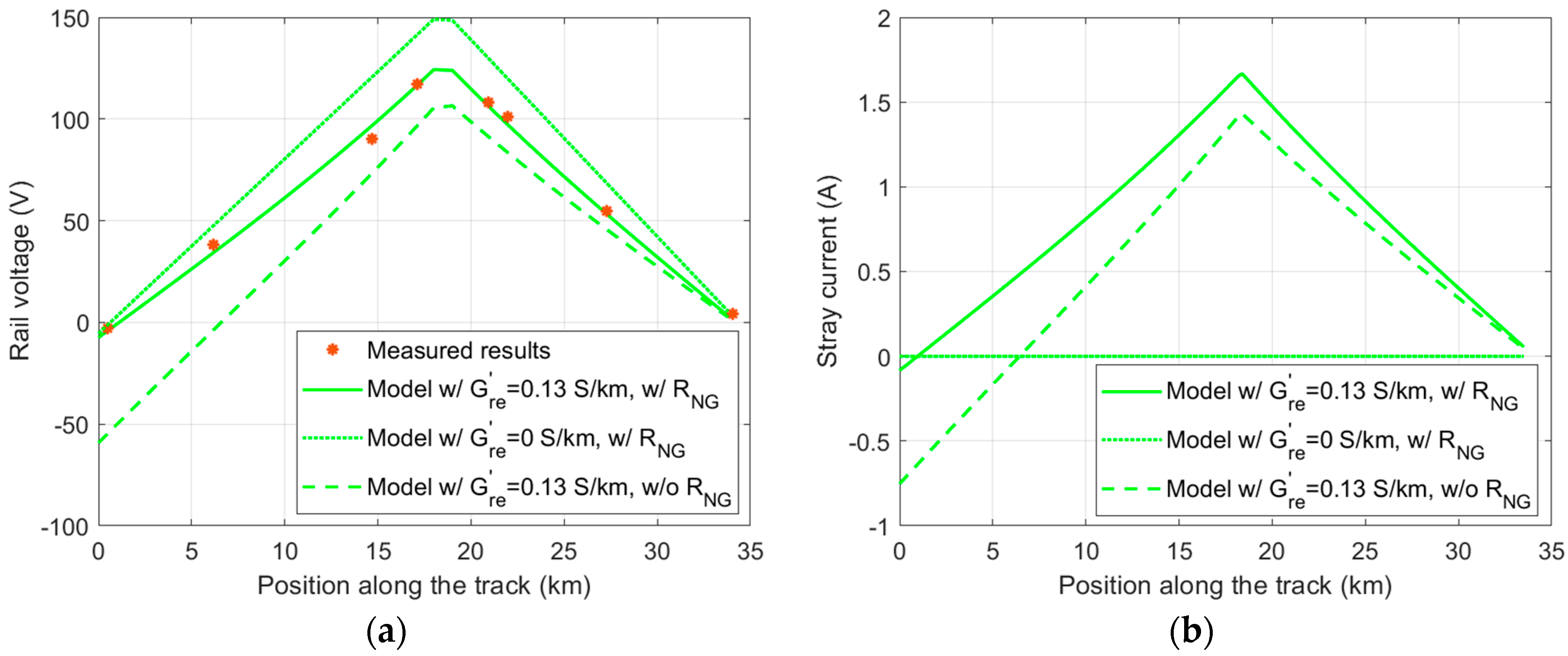
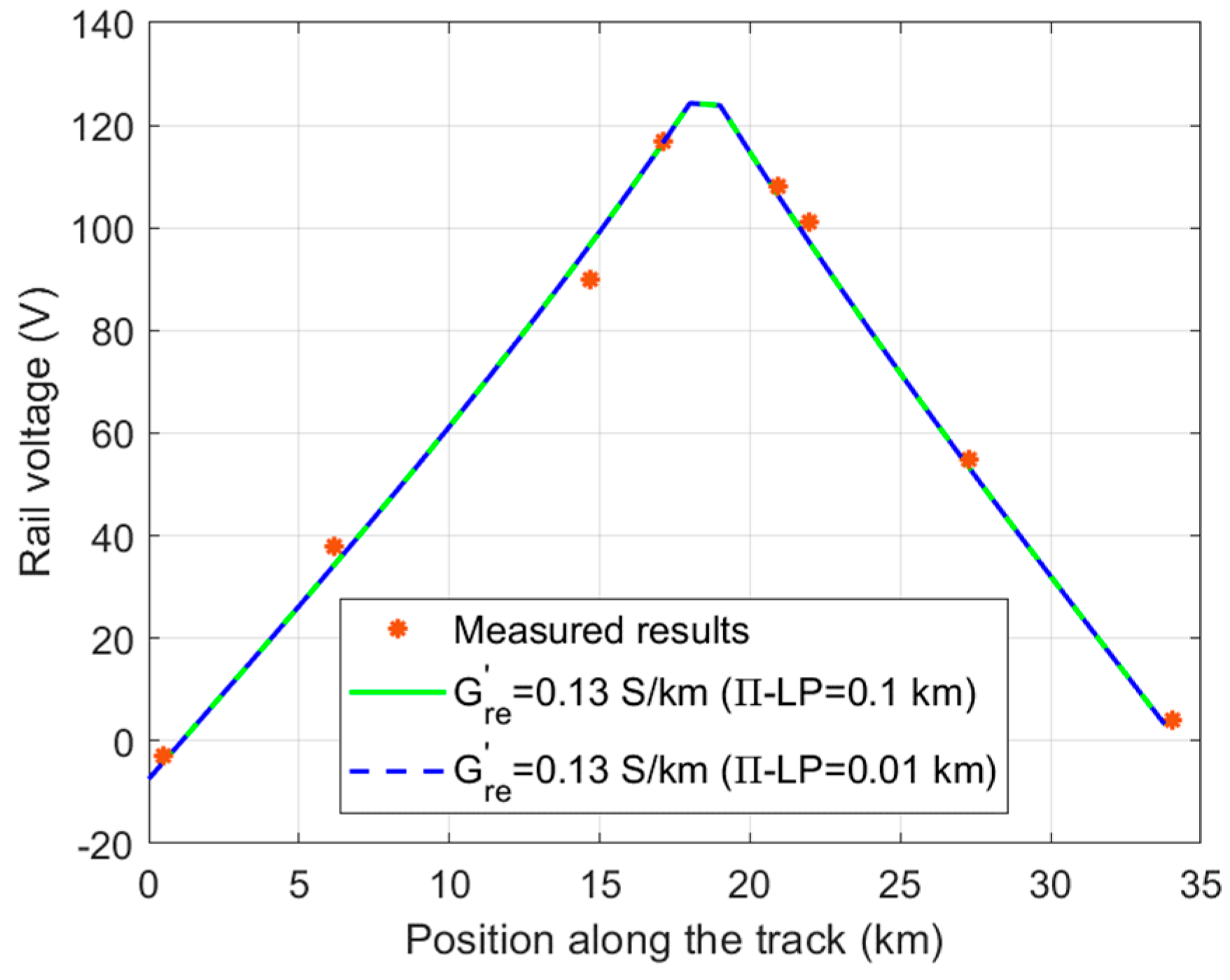
| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| TPS source voltages | ) | 3500 | V |
| TPS internal resistance | ) | 0.15 | Ω |
| Longitudinal resistance of the contact line per kilometer | 0.0415 | Ω/km | |
| Resistance of the rail per kilometer | 0.015 | Ω/km | |
| Conductance of the rail per kilometer | 0.13 | S/km | |
| Termination resistance | ) | 0.34 | Ω |
| Neutral-to-ground resistance TPS | ) | 0.017 | Ω |
| (Ω) | Rail Voltage at Francavilla Fontana Substation (0 km) (V) | Rail Voltage at Brindisi Substation (33.8 km) (V) |
|---|---|---|
| ) | −7.42 | 3.14 |
| ) | −10.4 | 4.21 |
| ) | −4.00 | 1.78 |
(Ω) | Stray Current at Francavilla Fontana Substation (0 km) (A) | Stray Current at Brindisi Substation (33.8 km) (A) |
|---|---|---|
| ) | −0.096 | 0.041 |
| ) | −0.13 | 0.054 |
| ) | −0.052 | 0.023 |
| Subsection—Figure | RMSE (V) |
|---|---|
| Mesagne–Brindisi—Figure 14 | 4.39 |
| Oria–Latiano—Figure 15 | 7.90 |
| Francavilla Fontana–Oria—Figure 16 | 6.09 |
| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| TPS Source voltages | ) | 3500 | V |
| TPS internal resistance | ) | 0.15 | Ω |
| Longitudinal resistance of the contact line per kilometer | 0.05725 | Ω/km | |
| Resistance of the rail per kilometer | 0.015 | Ω/km | |
| Conductance of the rail per kilometer | 0.08 | S/km | |
| Termination resistance | ) | 0.43 | Ω |
| Neutral-to-ground resistance TPS Capranica | 0.017 | Ω | |
| Neutral-to-ground resistance TPS S. Martino Al Cimino | 0.450 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivieri, C.; Di Leonardo, L.; de Paulis, F.; Orlandi, A.; Sbarra, F.; Camomilla, M. Experimentally-Based Circuit Modeling Validation of a DC-Electrified Railway System for Rail Voltage and Stray-Current Evaluation. Electronics 2025, 14, 4541. https://doi.org/10.3390/electronics14224541
Olivieri C, Di Leonardo L, de Paulis F, Orlandi A, Sbarra F, Camomilla M. Experimentally-Based Circuit Modeling Validation of a DC-Electrified Railway System for Rail Voltage and Stray-Current Evaluation. Electronics. 2025; 14(22):4541. https://doi.org/10.3390/electronics14224541
Chicago/Turabian StyleOlivieri, Carlo, Lino Di Leonardo, Francesco de Paulis, Antonio Orlandi, Fabio Sbarra, and Marco Camomilla. 2025. "Experimentally-Based Circuit Modeling Validation of a DC-Electrified Railway System for Rail Voltage and Stray-Current Evaluation" Electronics 14, no. 22: 4541. https://doi.org/10.3390/electronics14224541
APA StyleOlivieri, C., Di Leonardo, L., de Paulis, F., Orlandi, A., Sbarra, F., & Camomilla, M. (2025). Experimentally-Based Circuit Modeling Validation of a DC-Electrified Railway System for Rail Voltage and Stray-Current Evaluation. Electronics, 14(22), 4541. https://doi.org/10.3390/electronics14224541










