A 16-GHz 6.56-mW Slew-Rate-Tolerant Integrating-Mode Phase Interpolator in 12-nm FinFET

Abstract

This study presents a high-speed, 9-bit integrating-mode phase interpolator (IMPI) in a 12 nm FinFET process. The proposed slew-rate-tolerant design accepts bandwidth-limited inputs, relaxing the stringent need for high-slew-rate clocks found in prior research. This is primarily achieved through an optimized switch design that converts the sinusoidal voltage input into a quasi-square-wave current. A detailed theoretical model identifies asymmetrical clock feedthrough as the dominant nonlinearity, which is suppressed by a cancellation circuit. Furthermore, an adaptive biasing loop is employed to compensate for Process, Voltage, and Temperature (PVT)-induced P/N mismatch. This work is validated through comprehensive post-layout simulations; operating from a 0.8 V supply at 16 GHz, the PI achieves a peak-to-peak Integral Nonlinearity (INL) of 4.3 LSB (530 fs) while consuming 6.56 mW.

1. Introduction

The insatiable demand for higher bandwidth in data communication, driven by the growth of data-intensive applications like large language models (LLMs) and cloud computing, has accelerated the evolution of high-speed serializer/deserializer (SerDes) technologies [1,2].

In a typical high-speed SerDes, data is transmitted as a single, continuous stream, often without an accompanying forwarded clock to save power and I/O pins. This presents a fundamental challenge to the receiver: it must determine the precise timing (i.e., when to sample) from the data stream itself. This function is performed by the Clock and Data Recovery (CDR) circuit. The CDR’s core task is to extract the embedded clock timing directly from the data transitions, generate a local clock, and precisely align its phase with the incoming data to sample at the optimal point, thereby minimizing the bit error rate (BER).

The Phase Interpolator (PI)-based CDR architecture is widely adopted due to its fast frequency acquisition and better jitter performance [3,4,5]. The PI functions as a digitally controlled phase shifter. Its inputs are multi-phase clocks (e.g., quadrature I/Q phases) and a digital control code. Its output is a clock signal whose phase is precisely interpolated between the reference phases based on the digital code. Ideally, this input-to-output transfer function—from digital code to output clock phase—should be perfectly linear. Any deviation from this ideal linear relationship constitutes phase nonlinearity, typically characterized by Differential and Integral Nonlinearity (DNL/INL).

The PI’s phase nonlinearity (characterized by DNL/INL) is a primary source of sampling deterministic jitter (DJ). This jitter degrades system performance by shrinking the data sampling timing margin, which ultimately increases the system’s BER. Therefore, designing highly linear PIs is critical for reliable, high-speed communication.

Although Current-Mode PIs (CMPIs) are widely used, they ideally require complex sinusoidal weighting to achieve strictly linear phase interpolation. Practical designs often resort to linear weighting for simplicity, but this approximation introduces a deterministic sinusoidal phase error [6,7]. The Integrating-Mode PI (IMPI) is selected here because it inherently supports linear weighting, offering the potential for better linearity with standard quadrature inputs [8].

This study presents a high-resolution, 9-bit IMPI in a 12 nm FinFET process that features a high tolerance to slew-rate-limited inputs, significantly relaxing the input bandwidth requirements of prior research and thereby enabling higher frequency operation. We systematically analyze primary sources of nonlinearity—including an asymmetrical clock feedthrough mechanism, finite output impedance, and P/N mismatches—and introduce targeted design techniques to mitigate them. The main contributions of this work are summarized as follows:

• A slew-rate-tolerant IMPI architecture is proposed without requiring complex control logic, relaxing input bandwidth requirements for high-frequency operation.
• Systematic analysis of key nonlinearity sources is presented, along with targeted design solutions to enhance PVT robustness.
• The proposed PI, implemented in a 12 nm FinFET process, achieves a simulated INL of 4.3 LSB at 16 GHz from a 0.8 V supply, while consuming 6.56 mW.

The remainder of this paper is organized as follows. Section 2 introduces the proposed architecture and provides a detailed theoretical analysis of the key nonlinearity sources. Section 3 describes the specific circuit implementation techniques used to enhance linearity. Section 4 presents the post-layout simulation results and a comparison with prior research. Finally, Section 5 concludes the paper.

2. Proposed IMPI and Linearity Analysis

Phase interpolators are essential building blocks in modern high-speed communication systems, and are broadly classified into three main topologies: current-mode (CMPI), voltage-mode (VMPI), and integrating-mode (IMPI) [8].

A typical current-mode PI, as shown in Figure 1a, employs an I-Q phase mixer architecture where the output phase is determined by the weighted sum of input currents. While capable of high-speed operation, CMPIs often require a subsequent low-pass filter to reduce harmonic distortion and can suffer from degraded linearity with large input swings [6,7,9]. Furthermore, their significant static current consumption makes them less suitable for low-power applications.

Voltage-mode PI, depicted in Figure 1b, have gained popularity due to their simple, inverter-based structure and low static power consumption. They operate by selecting a digitally weighted number of inverter slices to perform a voltage-domain summation at the output node. However, they require slew control circuits at the inputs [10].

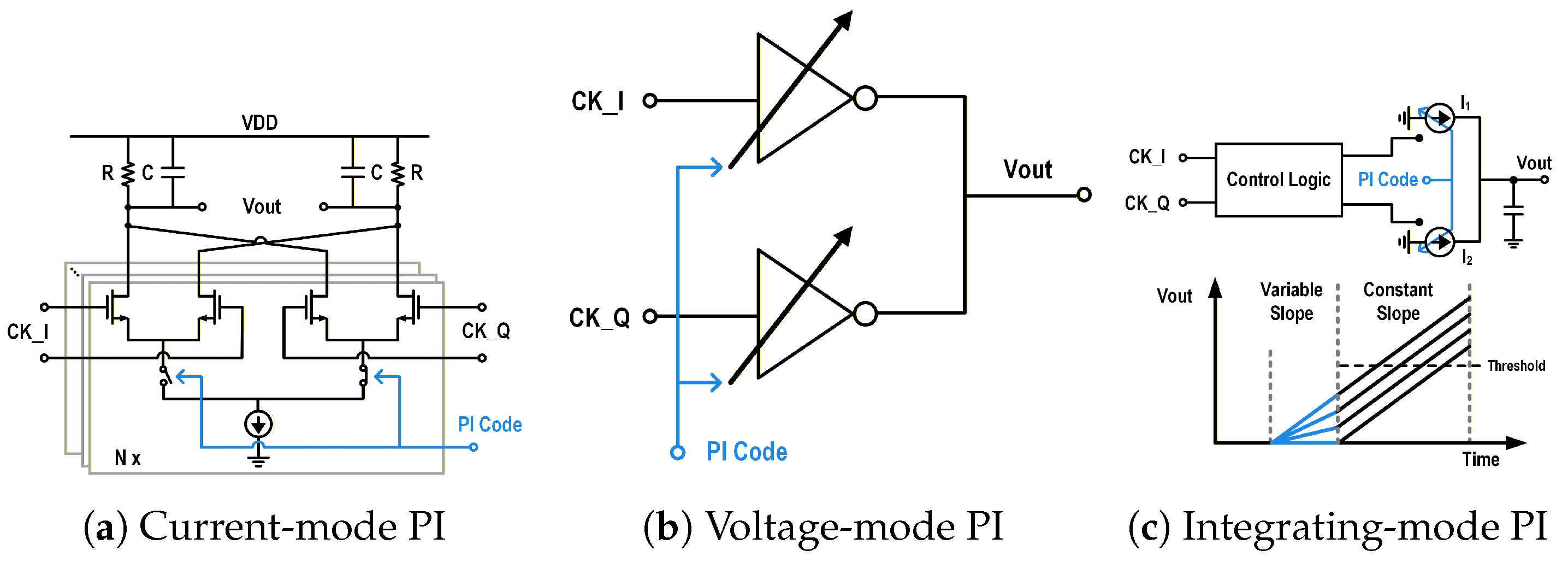
The integrating-mode PI (IMPI) presents a promising alternative. As shown in the generic architecture in Figure 1c, the IMPI operation toggles between a variable region and a constant region, governed by the input clocks (CK_I and CK_Q). In the variable-slope region, the digital PI code modulates the integration current magnitude, charging (or discharging) the load capacitor $C_L$ at different rates to establish a code-dependent linear voltage level. Subsequently, in the constant-slope region, $C_L$ is charged (or discharged) by a fixed current. This constant slew rate translates the previously established linear voltage difference into a linear time delay. This mechanism offers the potential for fundamentally better linearity with only quadrature inputs, typically leading to lower power consumption and a smaller area compared to its counterparts. For these reasons, the IMPI topology is chosen for this work.

Recent research has focused on improving the speed and resolution of IMPIs. While early architectures were often limited by complex control logic and feedback loops, a significant advancement presented in [8] achieved an impressive 14 GHz operation by removing these elements. However, this performance is predicated on a critical prerequisite: high slew-rate input clocks (i.e., “square-wave-like” waveforms with a rise/fall time of less than $0.25T$, where T is the period of input clocks). Preserving such fast transitions requires wide signal bandwidths, which is challenging and power-intensive to maintain in multi-gigahertz distribution networks. This requirement has become a major bottleneck limiting the application of high-speed IMPIs in even higher frequency domains. Furthermore, to achieve lower INL change from the process variation, Ref. [8] has employed slice architectures using transistor and resistor stacking (as shown in Figure 2). While this topology is effective for stabilizing output impedance, it requires a resistor value comparable to the transistor’s $r_o$. This large resistance consumes significant voltage headroom ($I\times R$), which is a critical concern in modern low-voltage FinFET processes.

This work is therefore motivated by the need to overcome this fundamental limitation. The primary goal is to develop an IMPI architecture that can achieve high-speed, low-jitter performance while releasing the stringent requirement on input bandwidth, enabling it to operate with more practical slew-rate-limited inputs. A pure sine-wave, having a continuously varying and limited slew rate, is considered as the representative worst-case for the following theoretical analysis.

2.1. Proposed Circuit Architecture and Operation

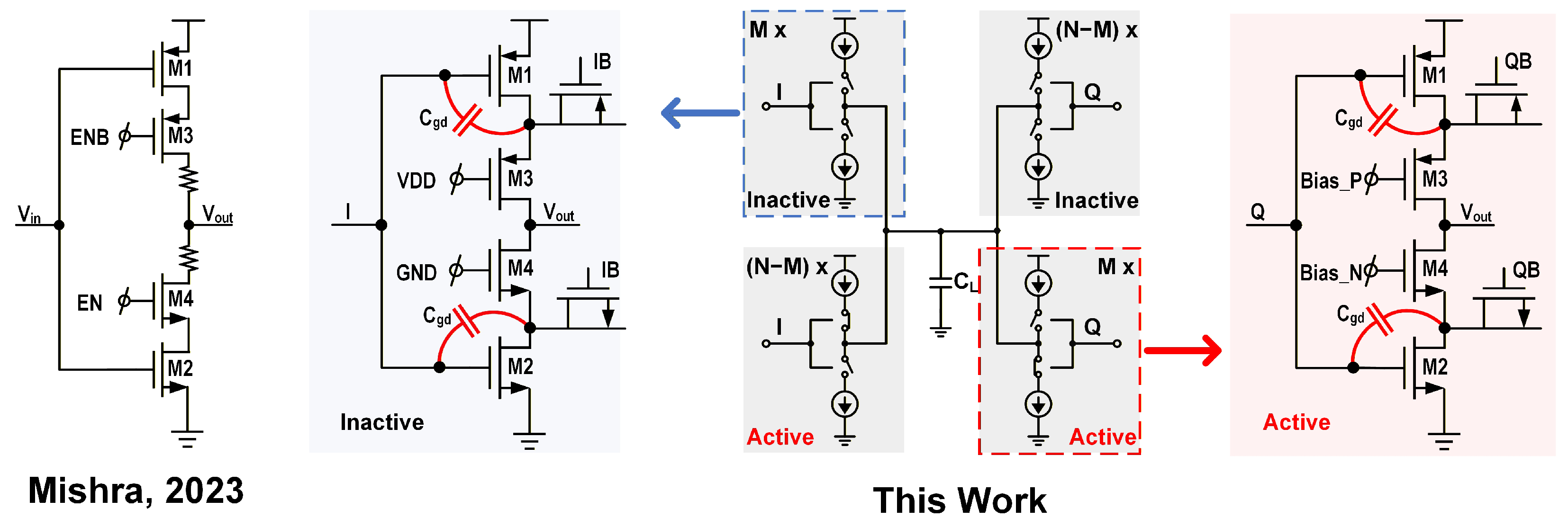
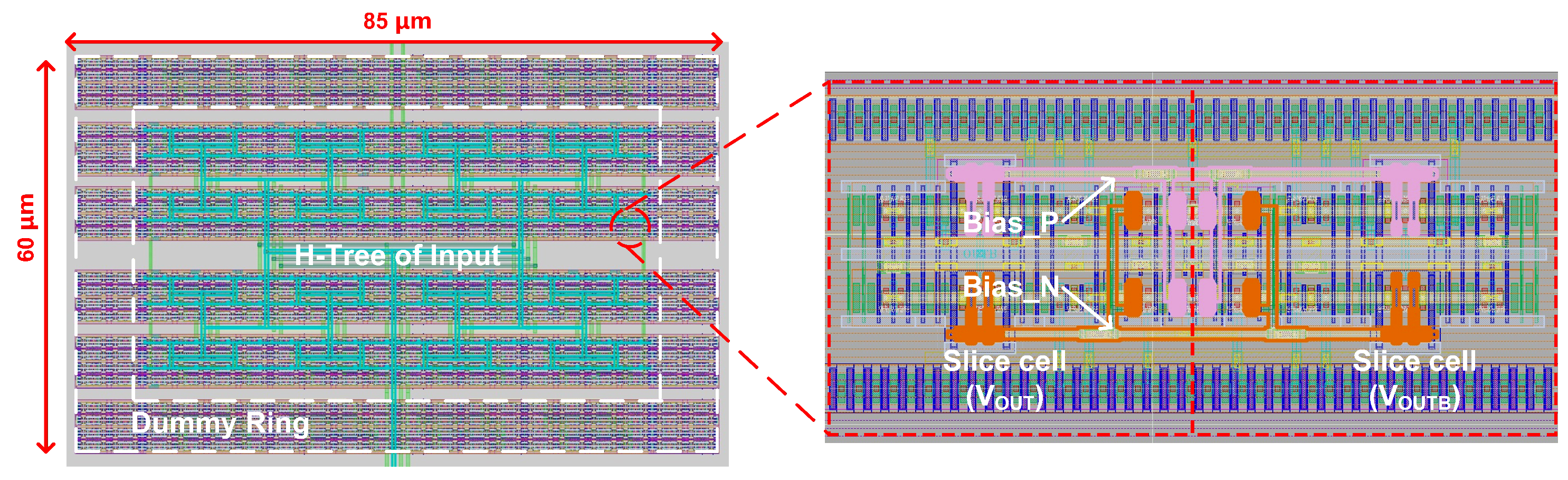
The proposed 9-bit PI is implemented using a coarse-fine architecture consisting of a 2-bit MUX and a 7-bit PI core. The interpolation process begins with the MUX, which receives the quadrature clocks and performs a coarse 2-bit interpolation by selecting two adjacent phases. These selected phases are subsequently sharpened by an inverter-based buffer to generate steeper edges. Finally, the edge-sharpened clocks are fed into the 7-bit PI core, which performs the fine-grained 7-bit interpolation. This hierarchical structure combines the 2-bit coarse and 7-bit fine stages to achieve the full 9-bit resolution.

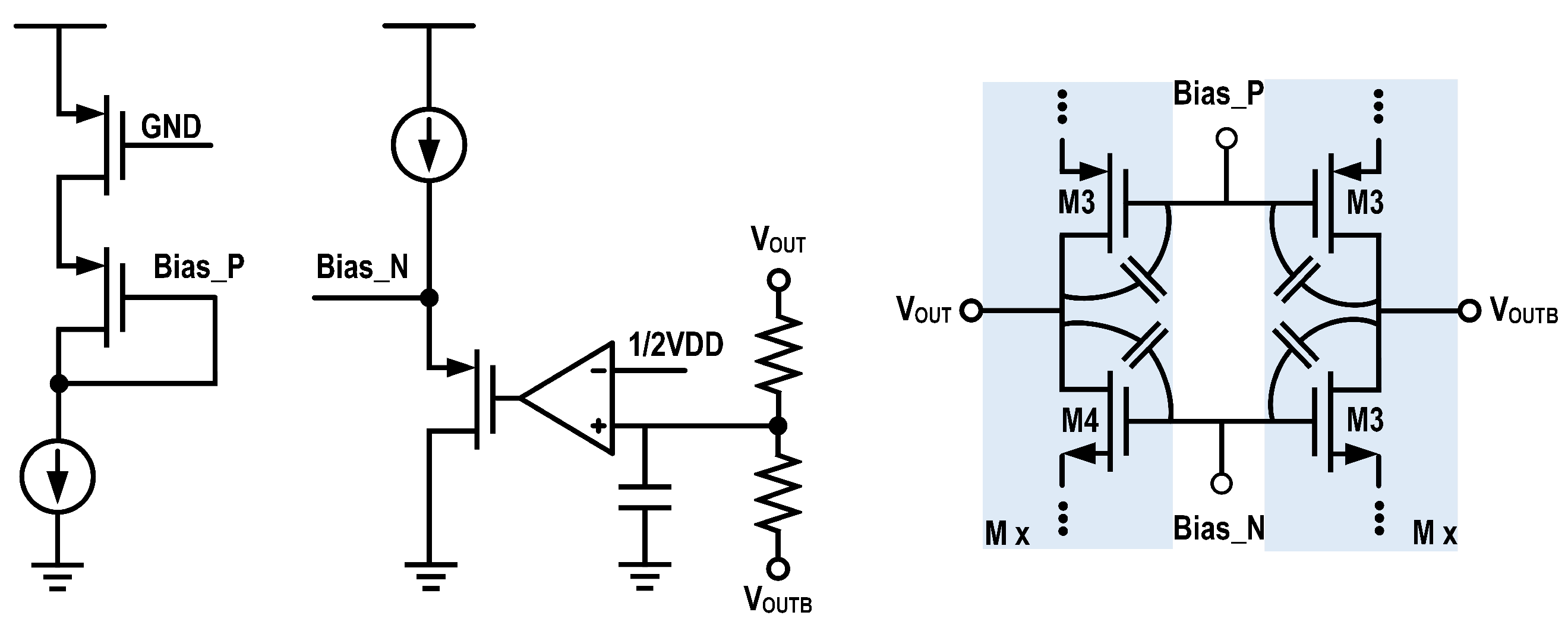
The 7-bit PI core architecture and the schematic of its unit slice are shown in Figure 2. The core consists of arrays of identical unit slices connected to a shared load capacitor, $C_L$. As depicted in the central part of the figure, the 7-bit fine-interpolation code M partitions the total N (where N $=2^7=128$) slices within the core into groups of M and (N-M), which are then selectively activated to perform a weighted current integration.

Each unit slice is based on a compact 4-transistor cell designed for high-speed operation. The mechanism for activating and deactivating a slice is also illustrated in Figure 2. In the “Active” state, the gates of the current-source transistors (M3 and M4) are connected to the analog bias voltages “Bias_P” and “Bias_N”. In this state, M3/M4 function as a current source/sink pair, while M1/M2 act as input switches, allowing the slice to contribute its unit current to the output node ‘Vout’. Conversely, in the “Inactive” state, the gates of M3 and M4 are connected to VDD and GND, respectively, which reliably turns the current sources off and disconnects the slice from the interpolation operation.

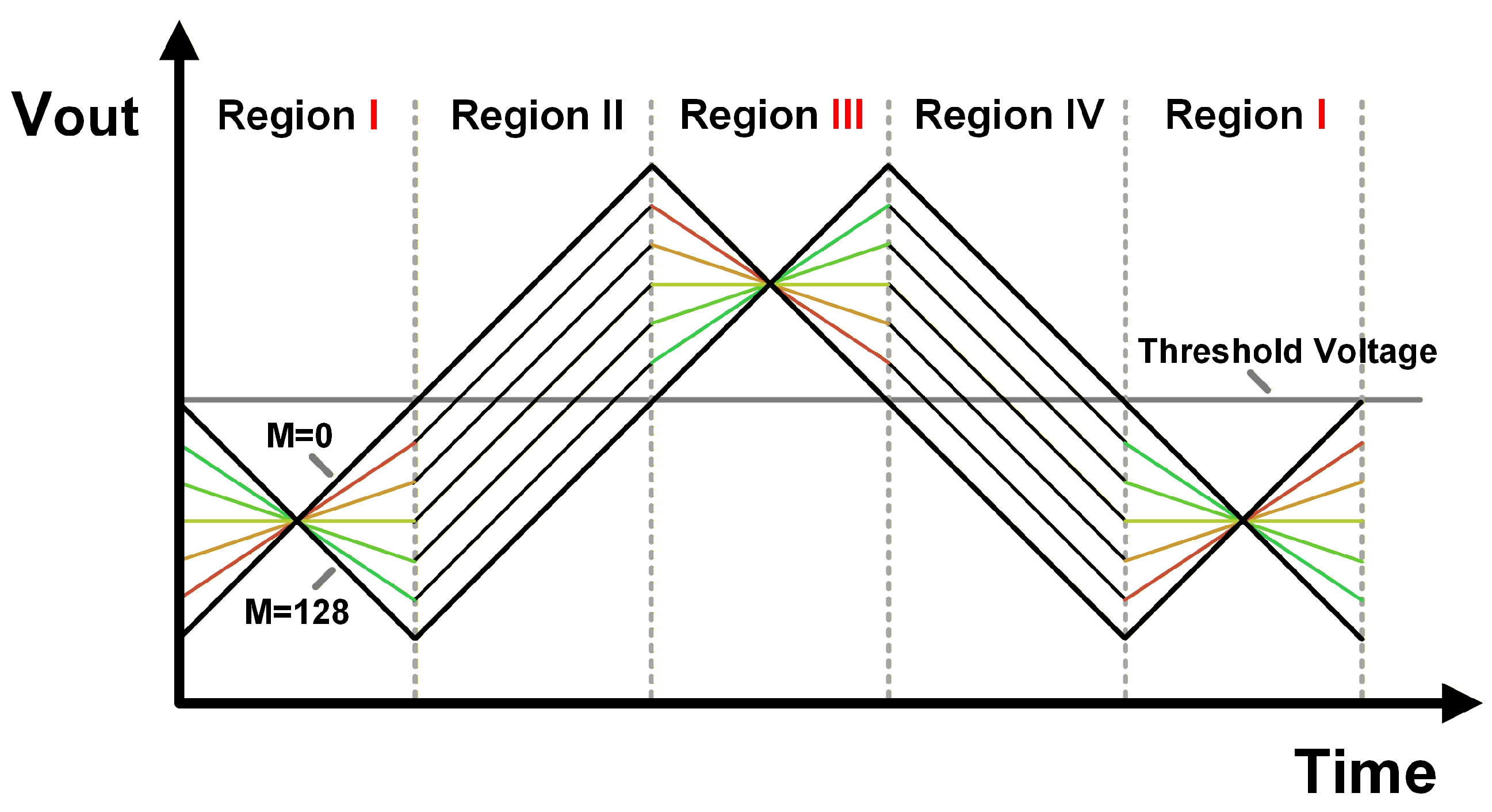
This architecture, controlled by the quadrature input clocks, sequentially activates different combinations of slices. This generates the ideal triangular voltage waveform across the load capacitor ($C_L$), as shown in Figure 3. In the variable-slope regions (Regions I and III), the integration slope is dependent on the digital code M, establishing a code-dependent voltage level. In the subsequent constant-slope regions (Regions II and IV), this voltage level is translated into a precise time delay, thus completing the phase interpolation.

2.2. Nonlinearity Analysis and Modeling

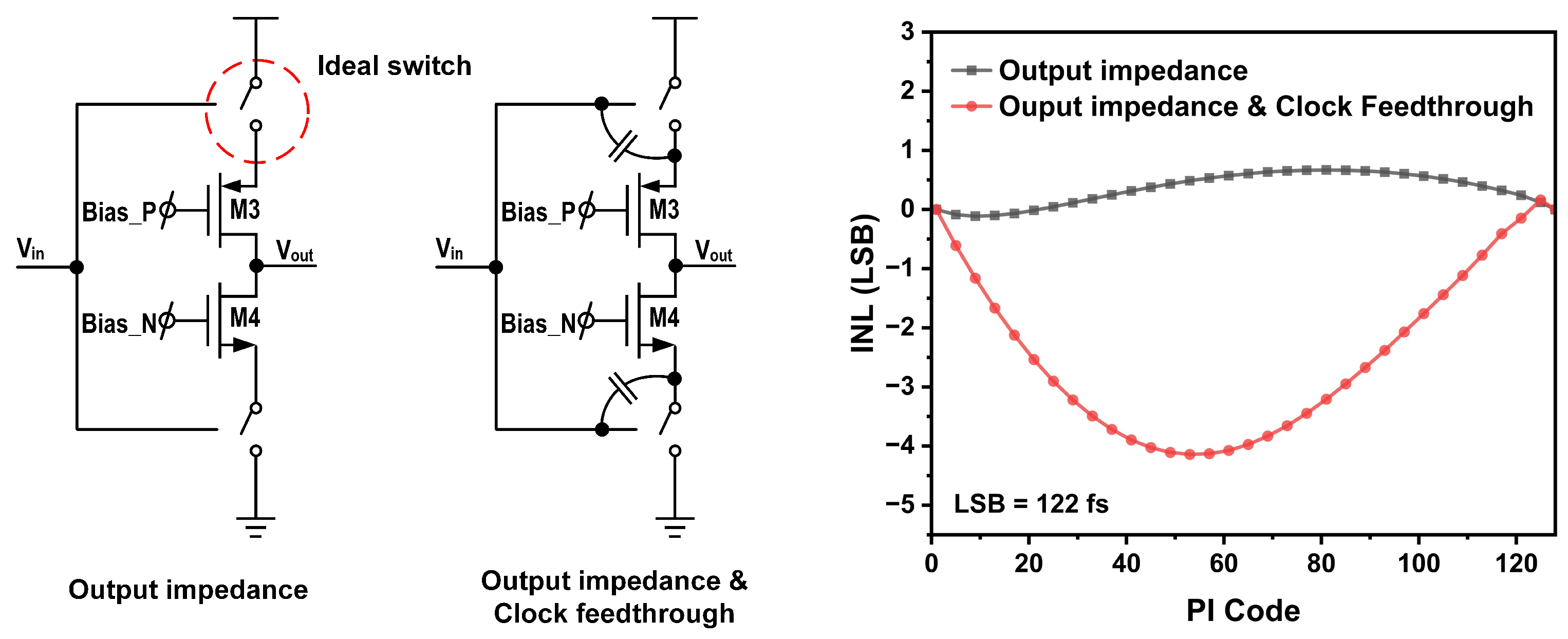
Having established the architecture and ideal operation of the proposed IMPI, this section provides a detailed analysis of the key non-idealities that degrade its linearity. To identify and decompose the dominant sources of nonlinearity, a specific transient simulation methodology was used, as illustrated in Figure 4. The goal was to isolate nonlinearities from the current sources (M3/M4) versus the switches (M1/M2).

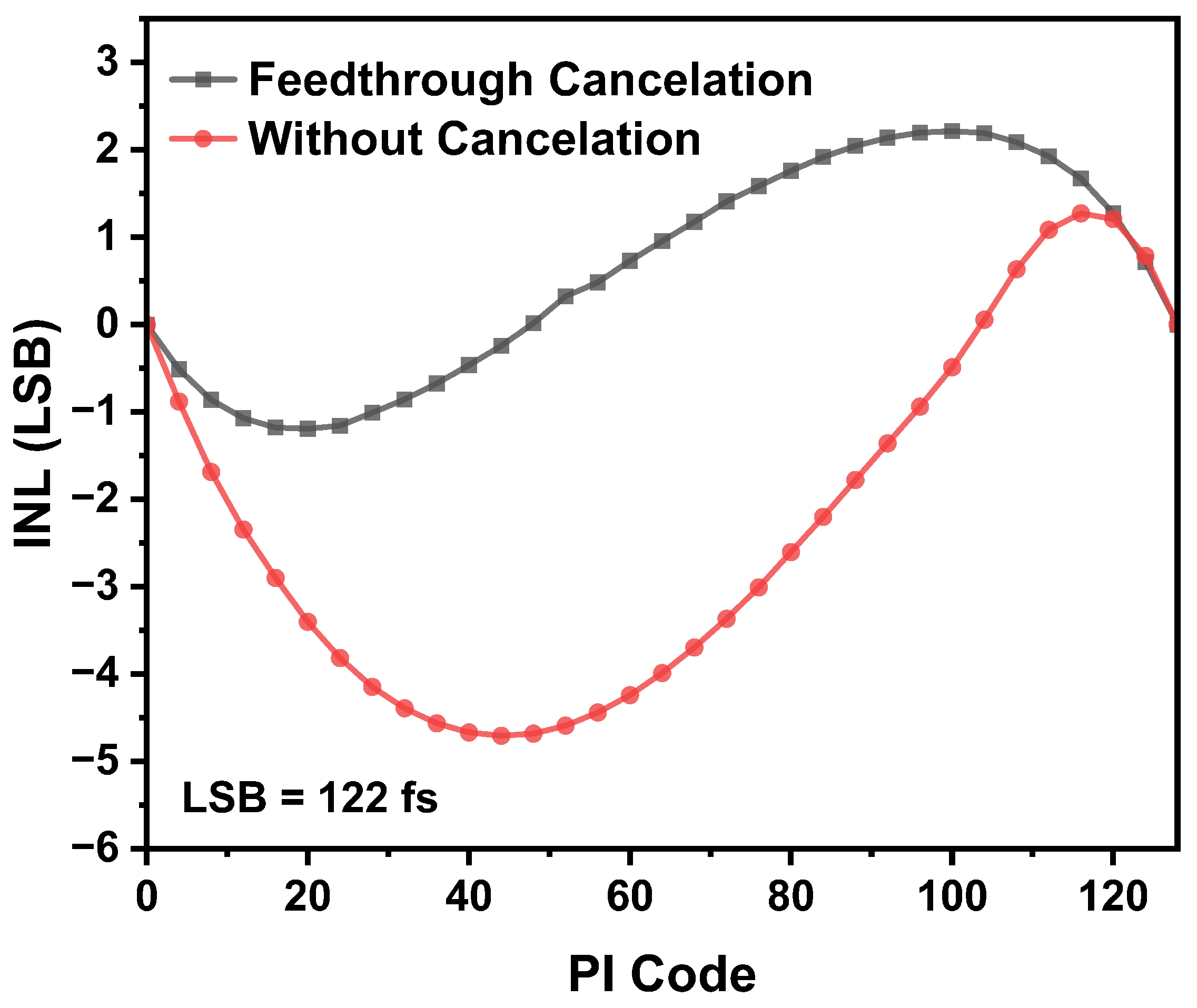
First, to isolate the “Output impedance” contribution, the real M1/M2 FinFET switches were replaced with ideal voltage-controlled switches (e.g., from the analogLib library) configured with near-zero on-resistance, infinite off-resistance, and zero parasitic capacitance. The INL was then simulated by sweeping the digital code M and measuring the output phase. The result, plotted as the “Output impedance” curve, isolates the INL contribution originating solely from the finite output impedance of the current sources (M3/M4).

Next, to this same setup, ideal capacitors were added between the switch control input (clock) and the switch output node. These capacitors were sized to match the estimated gate-drain capacitance ($C_{gd}$) of the original M1/M2 transistors. The INL simulation was repeated. The resulting “Output impedance & Clock Feedthrough” curve shows a dramatic increase in nonlinearity.

This comparative simulation clearly demonstrates that the asymmetrical clock feedthrough is the dominant source of nonlinearity in this architecture. The following subsections will provide a rigorous theoretical model for each of these key effects, with a primary focus on the clock feedthrough mechanism.

2.2.1. Modeling of Asymmetrical Clock Feedthrough

A comprehensive analysis reveals that the clock feedthrough nonlinearity is a composite effect. The physical mechanism is dynamic: taking a rising edge at the gate of the PMOS switch (M1) as an example, the feedthrough path evolves in two stages. In the initial phase of the transition, while M1 is still conductive, it provides a low-impedance path to VDD. Consequently, the majority of the current coupled through $C_{gd1}$, the gate-drain capacitance of M1, is shunted to the supply rail, having a minimal impact on the output. As the input voltage rises further and M1 enters the cutoff region, this shunting path disappears. The primary path for the feedthrough current now becomes the injection into the source of the current-source transistor, M3. It is this latter phase of the transition that is the dominant contributor to the nonlinearity. This two-stage mechanism underscores the sensitivity to the input slew rate; a slower edge, such as that of a sine wave, prolongs the duration of the harmful injection phase, leading to a larger total injected error charge. 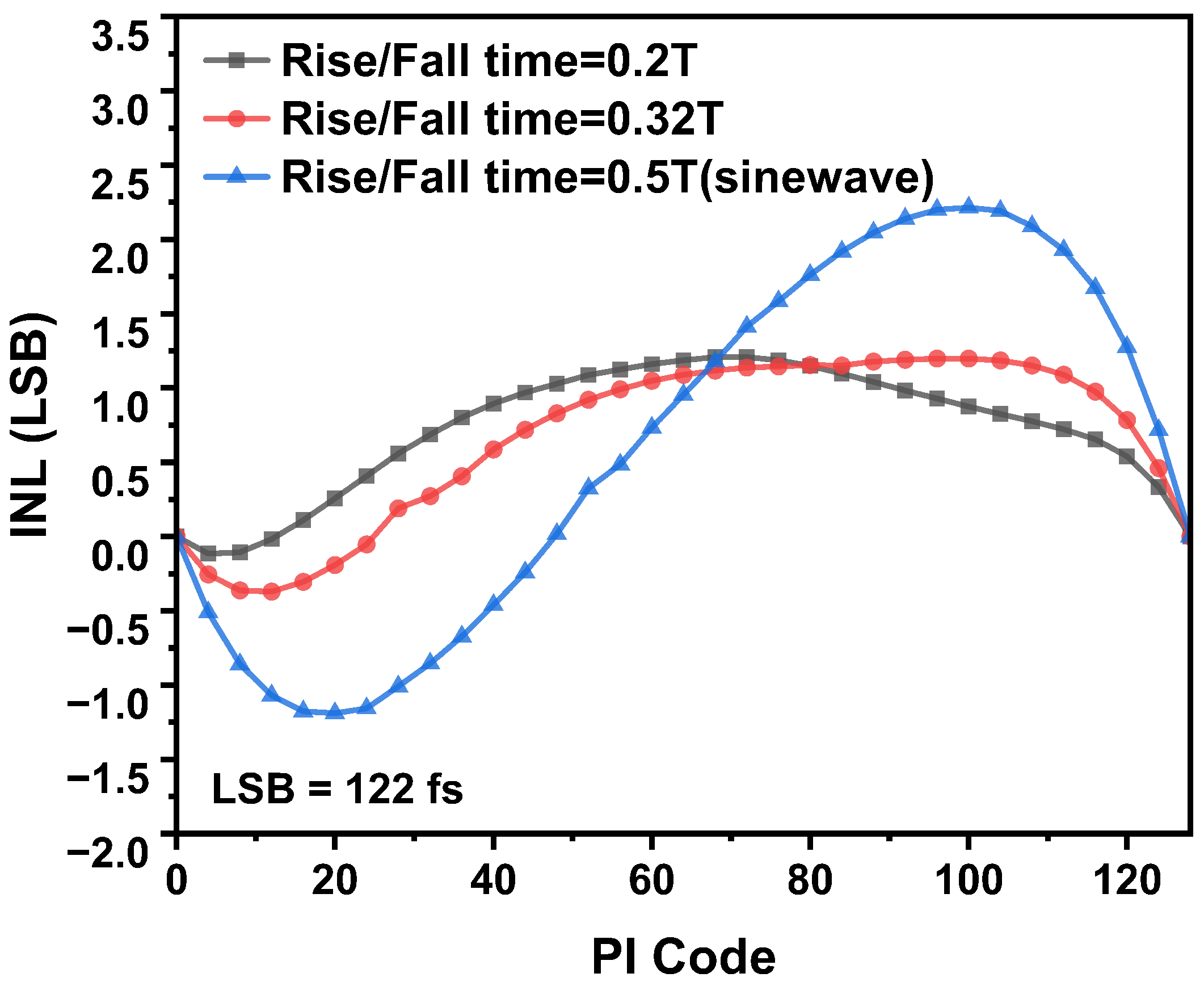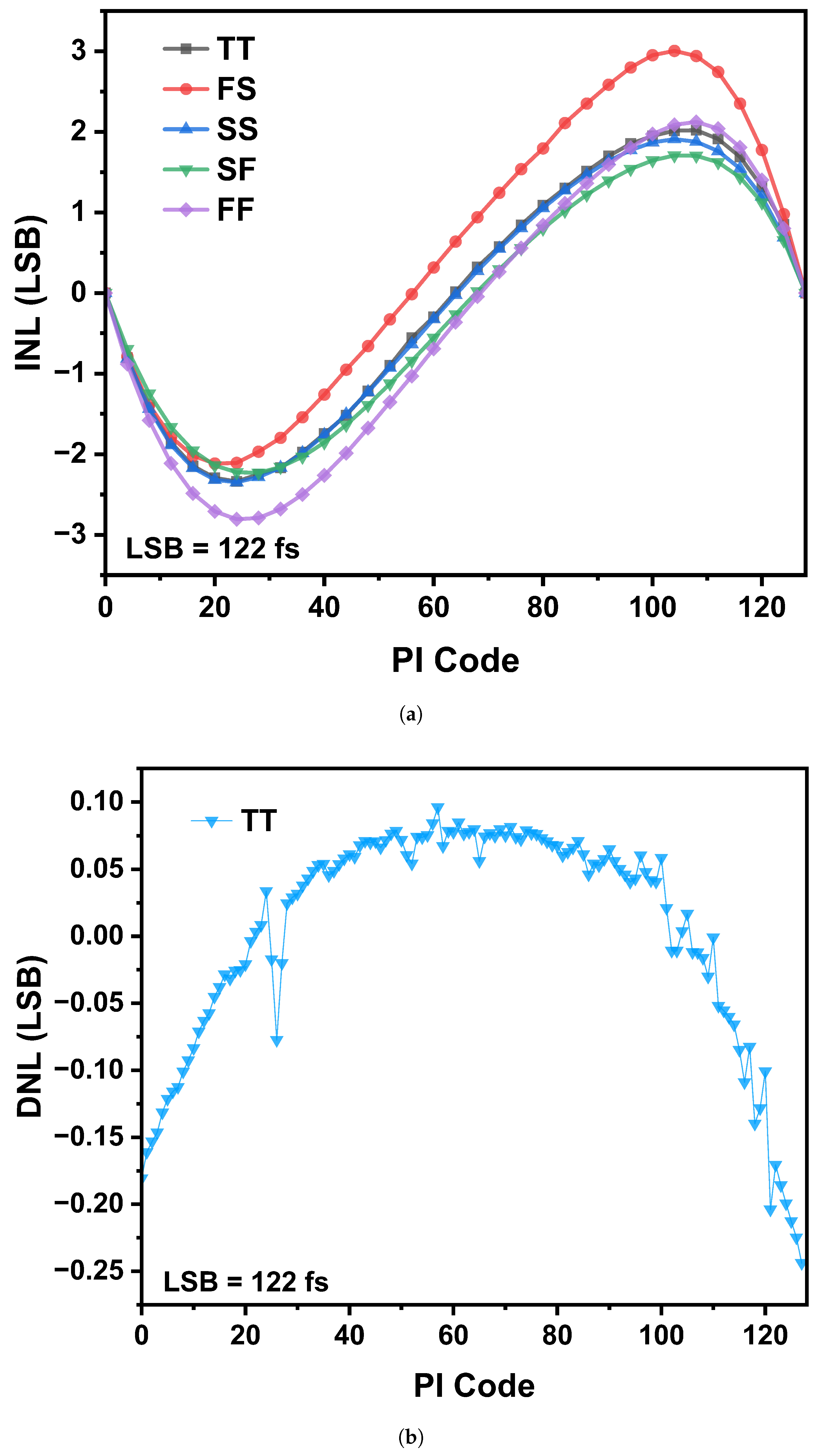Figure 5 validates the model’s dependency on the input slew rate. The pre-layout simulation, run at 16 GHz (where the input clock period $T=62.5$ ps), shows that sharpening the input edge from a pure sine-wave (0.5T rise/fall time) to 0.2T reduces the peak-to-peak INL by more than 50%, from approximately 3.5 LSB to 1.3 LSB. This result confirms the nonlinearity is fundamentally linked to the input transition duration, as predicted by our model.

This physical process can be modeled by considering the confluence of the code-dependent number of switching slices and the time-varying nature of the parasitic current. For a sinusoidal input $V_{in}\left(t\right)=V_{DD}sin\left(2\pi f_{in}t\right)$, the feedthrough current generated by a single PI slice, $i_{ft,unit}\left(t\right)$, is proportional to the input’s slew rate. This can be modeled using an effective gate-drain capacitance, $C_{gd,eff}$. Here, $C_{gd,eff}$ is an effective parameter that accounts for both the physical gate-drain capacitance of the switch and the “shielding effect” provided by the source impedance of the current-source transistors (M3/M4). This shielding can be understood by analyzing the feedthrough path when the switch (e.g., M1) is off. The physical $C_{gd}$ of the switch is effectively in series with the low source-impedance (approximately $1/g_{m,M3}$) of the current-source transistor (M3). This series combination increases the total impedance of the feedthrough path. Therefore, the resulting feedthrough current $i_{ft,unit}$ (and thus the total injected charge) is significantly reduced compared to a case where $C_{gd}$ would couple directly to the output node. The feedthrough current is thus given by:

$$i_{ft,unit}\left(t\right)\approx C_{gd,eff}·{\displaystyle \frac{d{V}_{in}}{dt}}=C_{gd,eff}·V_{DD}·2\pi f_{in}·cos\left(2\pi f_{in}t\right)$$

(1)

where $f_{in}$ is the input clock frequency and $V_{DD}$ is the power supply voltage (assume input clock is rail to rail). The charge injected by a single slice, $q_{inj}\left(t\right)$, is the integral of $i_{ft,unit}\left(t\right)$ over the code-dependent time window, resulting in:

$$q_{inj}\left(t\right)={\int }_0^t{i}_{ft,unit}\left(t\right)dt=C_{gd,eff}{V}_{DD}sin\left(2\pi f_{in}t\right)$$

(2)

In this design, the interpolation range spans one clock quadrant ($T/4$), where T is the input clock period, which is divided into N steps (e.g., $N=2^7=128$). The time resolution per code, LSB, is thus defined as:

$$\mathrm{LSB}={\displaystyle \frac{T}{4N}}={\displaystyle \frac{1}{4N·f_{in}}}$$

(3)

The integration duration, $T_{var}$, is then a direct linear function of the PI code $M\in [0,N]$:

$$T_{var}\left(M\right)=M·\mathrm{LSB}$$

(4)

Crucially, the number of slices that are actively switching at the region transition is also determined by the PI code M. The total injected charge, $Q_{inj,total}\left(M\right)$, is the product of these two effects:

$$Q_{inj,total}\left(M\right)=M·q_{inj}\left(T_{var}\right)\propto M·sin(2\pi f_{in}·M·\mathrm{LSB})$$

(5)

The resulting physical phase error, $T_{error}\left(M\right)$, is proportional to this total injected charge. We can model the error term as:

$$T_{error}\left(M\right)=c_2·M·sin(2\pi f_{in}·M·\mathrm{LSB})$$

(6)

where $c_2\approx {\displaystyle \frac{C_{gd,eff}·V_{DD}}{I_{const}}}$ and $I_{const}$ is the integration current in the constant-slope region. This model starkly contrasts with the case of a square-wave input. For an idealized square-wave with a very fast slew rate, the two-stage injection process is completed within a very short, fixed time interval at the beginning of the clock transition. The resulting injected charge, $Q_{inj,square}$, becomes a constant value, independent of the subsequent integration time $T_{var}\left(M\right)$ and thus independent of the PI code M. This code-independent charge injection manifests as a fixed DC offset on the output waveform, which does not degrade the PI’s integral nonlinearity. This complex, code-dependent nonlinearity therefore arises from two combined factors. The first is the continuous, time-varying slew rate of the sinusoidal input, and the second is the code-dependent integration window.

2.2.2. INL Formulation and Interpretation

The final INL observed in simulations is not the raw physical error, $T_{error}\left(M\right)$, but rather the form this error takes when subjected to the PI’s fundamental boundary conditions. This distinction is critical for correctly interpreting the results. The formulation can be understood in two steps:

First, we acknowledge the raw physical error source, $T_{error}\left(M\right)$, as modeled in the previous sections. This term represents the underlying nonlinearity from effects like clock feedthrough and has a non-zero value at the end of the range, $T_{error}\left(N\right)$.

Second, we must apply the system’s physical constraint. The PI is designed to interpolate between two fixed phase points (e.g., 0° and 90°). Therefore, regardless of any internal nonlinearities, the total accumulated phase at the end of the code range ($M=N$) must precisely equal the ideal total phase; i.e., $T_{out,real}\left(N\right)=N·T_{LSB}$. This implies that the net observable error at $M=N$ must be zero. To satisfy this boundary condition, the raw physical error, $T_{error}\left(M\right)$, must be inherently counteracted by a linear error component that represents a simple gain error of the overall transfer function. This linear correction term must be exactly equal to $-T_{error}\left(N\right)$ at the endpoint. Its form is therefore $-M·{\displaystyle \frac{T_{error}\left(N\right)}{N}}$.

The final, observable INL is the superposition of the raw physical error and this system-level linear correction term. This leads to the final INL formula:

$$\mathrm{INL}\left(M\right)=T_{error}\left(M\right)-M·{\displaystyle \frac{T_{error}\left(N\right)}{N}}$$

(7)

This physically derived formula is mathematically equivalent to the standard metrological definition of INL: the deviation of a transfer curve from a straight line drawn between its start and end points. This final equation explains the observed simulation results. The subtraction of the linear ramp term from the underlying physical error curve mathematically forces the INL at $M=0$ and $M=N$ to be zero and creates the characteristic arch-shaped or S-shaped INL curve.

2.2.3. Finite Output Impedance and Signal Swing Limitations

While the proposed architecture mitigates several sources of nonlinearity, its linearity is still fundamentally limited by the non-ideal characteristics of the current-source transistors (M3/M4). An ideal integrator requires a current source with infinite output impedance ($r_{out}$). However, practical MOS transistors exhibit a finite $r_{out}$ that is also dependent on the output signal swing, which introduces timing errors. This section provides a detailed model of this effect.

First, we consider the current source as an ideal source $I_0$ in parallel with a finite, but constant, output resistance $r_{out}$. This parallel resistance creates a path for current to leak from the load capacitor $C_L$, making the effective charging current dependent on the output voltage $V_x$. The behavior of this circuit is described by the following first-order differential equation, derived from Kirchhoff’s current law at the output node:

$$I_0=C_L{\displaystyle \frac{d{V}_x\left(t\right)}{dt}}+{\displaystyle \frac{V_x\left(t\right)}{r_{out}}}$$

(8)

Solving this equation with the initial condition $V_x\left(0\right)=0$, we find that the output voltage is not a linear ramp but an exponential function:

$$V_x\left(t\right)=I_0{r}_{out}\left(1-e^{-{\displaystyle \frac{t}{r_{out}{C}_L}}}\right)$$

(9)

To quantify the deviation from an ideal linear ramp, $V_{ideal}\left(t\right)=(I_0/C_L)t$, we can use a Taylor series expansion for small t:

$$V_x\left(t\right)\approx {\displaystyle \frac{I_0}{C_L}}t-{\displaystyle \frac{I_0}{2r_{out}{C}_L^2}}{t}^2+O\left(t^3\right)$$

(10)

The equation reveals a second-order error term that is proportional to $-t^2$ and inversely proportional to $r_{out}$. This term causes the voltage ramp to “droop” or bend downwards over time. Since the duration of the variable-slope integration phase, t, is determined by the PI’s digital code M, the accumulated voltage error at the end of this phase is a nonlinear function of the code. This code-dependent error directly translates into integral nonlinearity (INL).

The model above assumes a constant $r_{out}$. In reality, the output impedance of the MOS current source varies significantly with its drain-source voltage ($V_{ds}$), which is directly related to the output voltage swing $V_x$. This dependency is especially pronounced with large signal swings.

The output impedance is relatively high and stable only when the transistor is in the deep saturation region. However, as the output voltage $V_x$ swings towards the supply rails, the $V_{ds}$ across the current-source transistor decreases. If the swing is excessively large, the saturation condition ($V_{ds}>V_{gs}-V_{th}$) is violated, and the transistor enters the triode region. In this region, the device no longer acts as a current source, and its output impedance drops drastically.

This sharp decline in $r_{out}$ at the extremes of the voltage swing means that the nonlinearity described by our model is significantly exacerbated at the beginning and end of the integration ramps. The error term proportional to $1/r_{out}$ becomes much larger, causing severe distortion of the triangular waveform and further degrading the PI’s linearity.

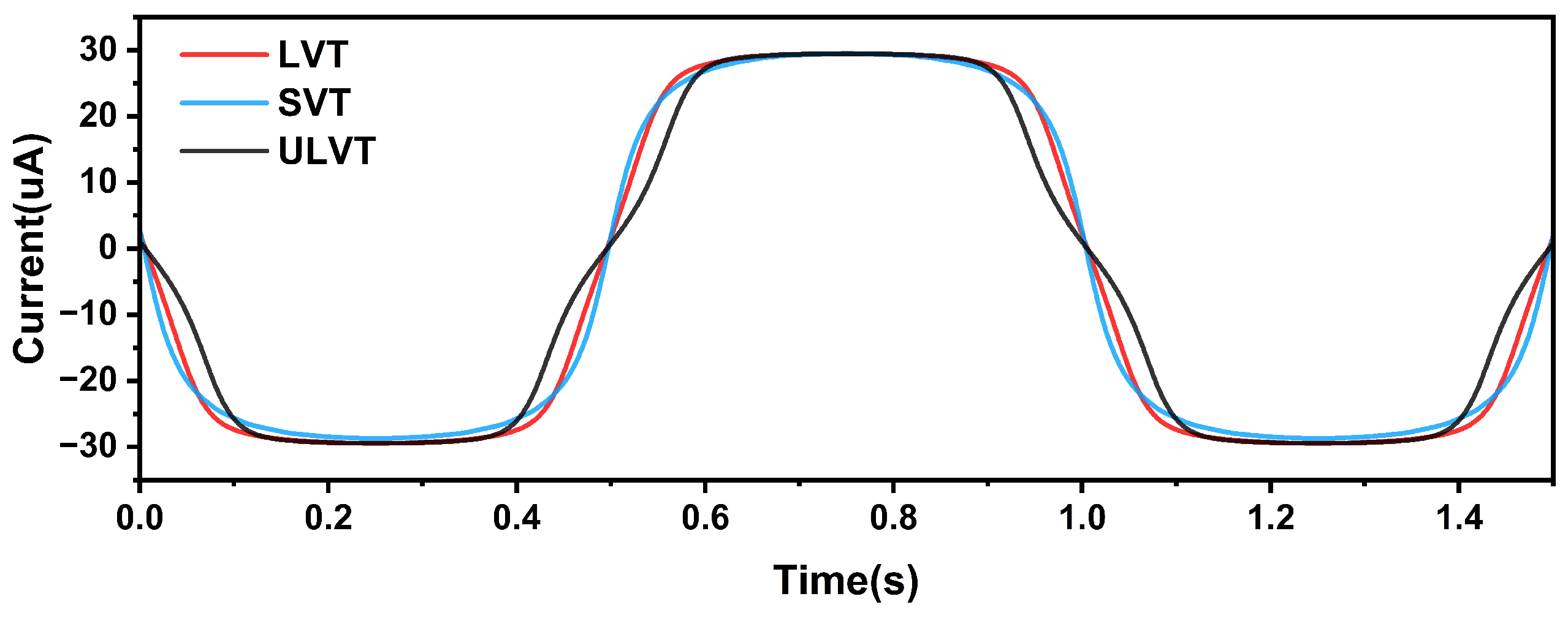
This detailed analysis provides direct theoretical justification for the design choices made in this work. To ensure high linearity, it is critical to both maximize the baseline $r_{out}$ and prevent the current-source transistors from entering the triode region. Therefore, a longer channel length of 36 nm is chosen to increase the intrinsic output impedance by mitigating channel length modulation. Simultaneously, the overdrive voltage is carefully optimized to be less than 0.1 V, which lowers the required saturation voltage ($V_{ds,sat}$) and maximizes the available linear signal swing before $r_{out}$ begins to drops drastically.

2.2.4. P/N Mismatch

In advanced FinFET processes, achieving precise matching between PMOS and NMOS devices is challenging due to the quantization of fin/gate dimensions. This inherent P/N mismatch is highly sensitive to process, voltage, and temperature (PVT) variations, leading to an imbalance between the pull-up and pull-down current networks.

For the IMPI to maintain a stable DC operating point over a full clock cycle, the net charge sourced to the output capacitor must equal the net charge sunk from it. If a P/N mismatch exists, the circuit will automatically seek a new equilibrium by shifting its output common-mode DC level. This shift alters the $V_{ds}$ of the current-source transistors, modulating their currents via channel length modulation until the net charge is balanced to zero over one period.

The critical issue arises when a simple, fixed biasing scheme is used. Under significant PVT variations, the P/N mismatch can become severe, forcing the output DC level to shift substantially to maintain this charge balance. A large DC shift can dangerously reduce the available drain-source voltage for either the PMOS or NMOS current-source transistors. This can force the devices into the triode region, where they no longer behave as stable current sources but rather as low-impedance resistors. Operation in the triode region fundamentally violates the principle of linear integration, leading to severe nonlinearity.

Therefore, this analysis concludes that a fixed biasing strategy is not robust against PVT-induced P/N mismatch. It is essential to employ an adaptive biasing scheme that actively regulates the output DC level, ensuring the current-source transistors remain in the saturation region across all operating conditions.

2.2.5. Dynamic Errors from Asymmetrical Settling Time

Beyond static nonlinearities, dynamic errors arising from finite settling times are critical at 16 GHz. The core issue is the asymmetrical settling behavior at the internal parasitic nodes of the PI slices.

As an example, we analyze the transition from a variable-slope region (e.g., Region I) to a constant-slope region (e.g., Region II), where M of the N active NMOS switches must turn off. We focus on the internal node X, located between the NMOS switch (M2) and the current source (M4).

When M2 turns off, node X loses its low-impedance path to ground. However, it is not immediately isolated; the output voltage $V_{out}$ continues to drive a leakage current, $I_{leak}\left(t\right)$, through M4 into node X. We make two key assumptions: (1) M2 provides a near-ideal discharge path when on, so the initial voltage is $V_x\left(0\right)\approx 0\mathrm{V}$; (2) The current source M4 follows a square-law model during this transient. The voltage at node X thus follows:

$$C_x{\displaystyle \frac{d{V}_x\left(t\right)}{dt}}=I_{leak}\left(t\right)\approx {\displaystyle \frac{g_{m0,M4}}{2V_{ov0,M4}}}{\left(V_{ov0,M4}-V_x\left(t\right)\right)}^2$$

(11)

where $C_x$ is the parasitic capacitance at node X, $V_{ov0,M4}=(V_{Bias\_N}-V_{th,M4})$ is the initial overdrive voltage of M4, and $g_{m0,M4}$ is its corresponding initial transconductance. Solving this yields:

$$V_x\left(t\right)=V_{ov0,M4}·{\displaystyle \frac{t}{t+{\tau }_{eff}}},\mathrm{with}{\tau }_{eff}={\displaystyle \frac{2C_x}{g_{m0,M4}}}$$

(12)

The total error charge is the sum of charge accumulated on these nodes across all M switching slices. Crucially, the leakage duration t depends on the time the output ramp takes to cross the threshold, which is linearly related to the code: $t\left(M\right)\approx M·\mathrm{LSB}$. Substituting this into the solution yields:

$$Q_{err\_total}\left(M\right)=M·C_x{V}_x\left(t\left(M\right)\right)=M·C_x{V}_{ov0,M4}{\displaystyle \frac{M·\mathrm{LSB}}{M·\mathrm{LSB}+{\tau }_{eff}}}$$

(13)

For typical operation ($M·\mathrm{LSB}\ll {\tau }_{eff}$), this error approximates to a quadratic term ($Q_{err}\propto M^2$). Finally, INL is defined after removing the ideal linear transfer function (zero-based end-point correction):

$$INL\left(M\right)\propto Q_{err\_total}\left(M\right)-{\displaystyle \frac{M}{N}}{Q}_{err\_total}\left(N\right)\approx k·(M^2-N·M)$$

(14)

This mathematical form represents a symmetric, parabolic (arch-shaped) curve.

3. Circuit Implementation

The proposed IMPI is designed to relax the requirement for input bandwidth, enabling it to accept sine-wave inputs and extend to higher operating frequencies. A key advantage of this architecture is its ability to achieve high-speed, dual-edge interpolation without the need for complex control logic or feedback loops.This section details the circuit implementations designed to overcome the nonlinearity challenges analyzed in Section 2.

3.1. Current Source Design (M3/M4)

As analyzed in Section 2, maintaining high output impedance ($r_{out}$) and sufficient voltage headroom for the current-source transistors is critical for linearity. To achieve this, several design choices have been made. First, to maximize the available output voltage swing, conventional source degeneration resistors are avoided, as they would consume valuable voltage headroom. Second, the overdrive voltage of M3 and M4 is optimized to be less than 0.1 V. This ensures the devices remain in the saturation region even during large signal swings, preventing them from entering the highly nonlinear triode region. Finally, the channel length of M3 and M4 is set to 36 nm to increase the intrinsic output impedance of the devices, directly counteracting the linearity degradation from a finite $r_{out}$.

3.2. Switch Design for Slew-Rate Tolerance (M1/M2)

The design of the switches M1/M2 is critical as it involves balancing multiple, competing nonlinearity sources, primarily through the optimization of transistor sizing (W/L) and threshold voltage ($V_{th}$).

The first consideration is transistor sizing. A trade-off exists between settling-time nonlinearity and clock feedthrough. If the switches are too small, their on-resistance ($R_{on}$) becomes significant. This creates a large RC time constant with the load capacitor, causing a slow voltage settling at the output which introduces nonlinearity. Conversely, increasing the switch size reduces this settling error but also increases the parasitic gate-drain capacitance ($C_{gd}$). As analyzed in Section 2, this exacerbates clock feedthrough, which is the dominant source of nonlinearity in this design. Therefore, an optimal size for M1/M2 has been chosen through simulation to balance these two effects.

The second consideration is the threshold voltage, $V_{th}$. To find the optimal $V_{th}$, a comparative simulation is performed using Standard-$V_{th}$ (SVT), Low-$V_{th}$ (LVT), and Ultra-Low-$V_{th}$ (ULVT) devices. The resulting net current waveforms, shown in Figure 6, demonstrate that all three device types successfully convert the sinusoidal voltage input into a quasi-square-wave current via the “clipping” effect. However, the ULVT device, due to its very low threshold, causes the PMOS and NMOS switches to be simultaneously conductive for a longer duration, which slows down the transition of the net output current. In contrast, the LVT and SVT devices exhibit nearly identical and significantly faster transition speeds.

Based on this comprehensive analysis, LVT is selected as the optimal choice for the switch implementation. It provides a lower on-resistance than SVT (beneficial for the clipping action) without the penalty of a slower current transition speed and higher short-circuit power associated with ULVT.

3.3. Clock Feedthrough Cancellation Circuit

As established by the theoretical model in Section 2, the asymmetrical clock feedthrough is the primary source of nonlinearity in the proposed IMPI. To mitigate this dominant effect, a feedthrough cancellation technique is implemented directly within the PI core slice. The implementation involves adding a set of dummy transistors that mirror the main switching transistors (M1/M2) but are driven by the inverted input clocks.

The effectiveness of this technique is demonstrated by the pre-layout simulation results shown in Figure 7. The plot compares the INL with and without the cancellation circuit. Without cancellation, the peak-to-peak INL reaches nearly 6.0 LSB. With the cancellation enabled, the peak-to-peak INL is reduced to less than 3.36 LSB. This result validates the effectiveness of the proposed cancellation scheme.

3.4. Biasing for P/N Mismatch Compensation

As analyzed in Section 2, P/N device mismatch, especially when exacerbated by PVT variations, can force the PI’s current sources into the nonlinear triode region. To overcome this, an adaptive biasing scheme is essential.

To counteract the effects of P/N mismatch and enhance PVT robustness, an adaptive biasing circuit is implemented. As shown in the schematic in Figure 8, this feedback loop actively stabilizes the output common-mode voltage. The circuit works by sensing the DC level of the PI’s output and comparing it against a stable $V_{DD}/2$ reference. The resulting error signal is then used to adjust the bias voltage of the NMOS current sources (Bias_N). This negative feedback forces the output DC level to remain close to $V_{DD}/2$, effectively compensating for the current imbalance caused by P/N mismatch across all PVT corners. This prevents the output common-mode voltage from drifting and ensures that the current-source transistors are kept in their high-impedance saturation region rather than entering the non-linear triode region, thus maintaining stable INL performance.

In addition to static mismatch, the analog bias nodes (Bias_P/Bias_N) are highly susceptible to noise coupled from the fast-switching differential output nodes ($V_{OUT}$/$V_{OUTB}$). A robust, low-impedance bias generation circuit would traditionally require power-hungry, wide-bandwidth buffers. To address this efficiently, a shared biasing architecture is employed, as illustrated in the overall biasing schematic in Figure 8.

As shown in the connection diagram on the right, the Bias_P and Bias_N nodes are shared between the two differential PI cores that generate $V_{OUT}$ and $V_{OUTB}$. Noise coupled from the $V_{OUT}$ node is largely canceled by the anti-phase noise coupled from the $V_{OUTB}$ node at these shared bias lines. This occurs because the $V_{OUT}$ and $V_{OUTB}$ nodes are differential, causing the noise currents they couple to $\mathrm{Bias}\_\mathrm{N}/\mathrm{Bias}\_\mathrm{P}$ to be anti-phase. These anti-phase currents then largely cancel each other out at $\mathrm{Bias}\_\mathrm{N}/\mathrm{Bias}\_\mathrm{P}$. This cancellation mechanism significantly suppresses the noise seen by the bias generation circuits—a current mirror for Bias_P and an adaptive feedback loop for Bias_N. This shared architecture relaxes the design requirements of the biasing loop, leading to substantial savings in both power and area while maintaining high stability.

4. Simulation Results and Comparison

The PI is designed in a 12 nm FinFET technology, with the final layout shown in Figure 9. In the layout, special care is taken to ensure symmetry. For instance, a tree-like (H-tree) clock distribution network is employed for the quadrature input signals to guarantee matched routing and minimize phase errors, and the core arrays are surrounded by dummy cells. The core area of the PI is 0.0051 mm².

This section presents the post-layout simulation results, which are obtained with a 0.8 V supply voltage at a 16-GHz clock frequency unless otherwise specified. The key performance metrics of this work are summarized in

Table 1. Performance Summary of the Proposed IMPI.

Parameter	Value (Post-Layout Simulation)
Technology	12 nm FinFET
Supply Voltage	0.8 V
Resolution	9-bit (2-bit coarse, 7-bit fine)
Max. Frequency	16 GHz
Input Condition	Sine-wave (0.5 T rise/fall time)
INL (peak-to-peak, @ 16 GHz)	4.3 LSB (530 fs)
DNL (peak-to-peak, @ 16 GHz)	0.35 LSB (43 fs)
Output Jitter (RMS, @ 16 GHz)	46 fs
Power Consumption (@ 16 GHz)	6.56 mW
Power Efficiency	0.41 mW/GHz
Core Area	0.0051 mm2

.

The presented linearity results focus on the 7-bit fine-interpolation core, which operates over 128 codes within a selected clock quadrant. This fine-interpolation stage is the dominant contributor to the overall nonlinearity of the 9-bit PI. The post-layout simulated linearity of the PI is shown in Figure 10. Figure 10a plots the INL across five process corners (TT, FF, SS, FS, SF), demonstrating the design’s robustness. The worst-case peak-to-peak INL is observed at the FS corner, reaching approximately 5.1 LSB, while the best case in SF is 3.9 LSB. It is worth noting that this result is under the worst-case sine-wave input condition. To demonstrate the design’s performance scalability with input signal quality, a post-layout simulation was also performed with a faster 0.32T rise/fall time input at the typical corner, which shows the peak-to-peak INL improves significantly to 2.45 LSB. At the typical-typical (TT) corner, the peak-to-peak INL is 4.3 LSB. At 16 GHz, this corresponds to a timing error of approximately 530 fs, which is only 0.85% of the 62.5 ps clock period. Figure 10b shows the DNL for the typical (TT) corner, which has a value between 0.1 LSB and −0.25 LSB, ensuring monotonic operation across the entire code range.

The robustness of the proposed PI was verified against both global process variations and local random mismatch. The design’s resilience to global variations is demonstrated in Figure 10a, which shows stable INL performance across five process corners.

To evaluate the impact of local random mismatch, a Monte Carlo simulation was performed. The simulation for the peak to peak INL, shown in Figure 11a, yields a standard deviation of 76 fs. Similarly, the simulation for the DNL, shown in Figure 11b, yields a mean of 117 fs (LSB = 122 fs) with a standard deviation of 37 fs. These low variations in both INL and DNL demonstrate the design’s high robustness against random device mismatch effects.

In addition, two key dynamic performance metrics, output jitter and power-supply rejection ratio (PSRR), were evaluated. The intrinsic random jitter was evaluated using Periodic Steady State (PSS) and Periodic Noise (PNoise) analysis. At 16 GHz with a clean supply, the simulated integrated RMS jitter is 46 fs.

The circuit’s sensitivity to supply noise (PSRR) was also considered. Superimposing a 100 MHz, 20 mV (peak-to-peak) sinusoidal ripple on the 0.8 V supply resulted in a peak-to-peak deterministic output jitter of 268 fs. This corresponds to a timing sensitivity of approximately 13 fs/mV, which may degrade the system’s timing margin significantly with a noisy supply. This value reflects the core topology’s intrinsic sensitivity to supply ripple, particularly at high frequencies. This is because such frequencies are outside the correction bandwidth of the low-frequency adaptive biasing loop. In practical implementations, this high-frequency noise is intended to be suppressed by a dedicated Low-dropout regulator (LDO) supply and sufficient on-chip decoupling capacitance. This system-level approach is consistent with other high-performance PI designs, such as the 7 nm FinFET PI in [11], which also operates under a regulated supply. These components were not included in this block-level validation.

The total power consumption is 6.56 mW. A breakdown of the total 6.56 mW power consumption at 16 GHz is provided in

Table 2. Power Consumption Breakdown (@ 16 GHz).

Block	Power (mW)	Percentage (%)
PI Core	3.07	46.8
Clock Buffers	2.41	36.7
Biasing Circuits	1.08	16.5
Total	6.56	100.0

. The power is dominated by the core PI arrays and the high-speed clock buffers. The adaptive biasing circuits, including the shared common-mode feedback loop, consume only 1.08 mW (less than 17% of the total), demonstrating the efficiency of this scheme.

Comparison with State-of-the-Art

Table 3. Performance Comparison with State-of-the-Art Phase Interpolators.

	[12]	[13]	[8]	This Work
PI architecture	CMPI	VMPI	IMPI	IMPI
Technology	28 nm CMOS	8 m FINFET	5 nm FINFET	12 nm FINFET
Input phase	4	4	4	4
Power supply (V)	1	0.85	0.75	0.8
Resolution (bit)	7	8	9	9
Input clock Requirement	Sine-wave (via slew control)	-	rise/fall time ≤0.25T *	rise/fall time ≤0.5T *
INL (LSB)	1.20	-	3.66 @ 0.18T *	4.34 @ 0.5T * 2.45 @ 0.32T *
DNL (LSB)	0.27	0.39	2.08	0.32
Frequency (GHz)	14	2	14	16
Power (mW)	8.48	1.24	6	6.56
Area (mm2)	-	0.035	0.006	0.005

* Input rise/fall time specified as a fraction of the input clock period (T).

compares this work with several recently published high-speed PIs. Compared to the state-of-the-art IMPI in [8], this work achieves a higher operating frequency of 16 GHz while maintaining a comparable INL and power consumption. Crucially, this performance is achieved with an architecture specifically optimized for slew-rate-limited (e.g., sinusoidal) inputs, relaxing the stringent requirement for high-slew-rate, “square-wave-like” clocks often needed in prior studies. When compared with other architectures, such as the CMPI in [12] and the VMPI in [13], the proposed IMPI operates at a significantly higher frequency than [13] while achieving competitive linearity against [12]. Overall, the proposed PI demonstrates a strong combination of high-speed operation, high resolution, and excellent linearity, with the key advantage of tolerating bandwidth-limited inputs, making it well-suited for modern SerDes applications.

5. Conclusions

This study presented the design, analysis, and simulation of a high-linearity, 9-bit IMPI in a 12 nm FinFET process, focusing on overcoming the challenge of using practical sine-wave inputs at high frequencies. A systematic analysis identified asymmetrical clock feedthrough as dominant nonlinearity source. To address these issues, a suite of co-optimized circuit solutions is implemented: an optimized LVT switch enables slew-rate tolerance, a feedthrough cancellation circuit suppresses the dominant asymmetrical clock feedthrough caused by this slew-rate-limited input, and an adaptive biasing loop is used to mitigate PVT-induced P/N mismatch. The proposed PI achieves a simulated peak to peak INL of 4.3 LSB and a power consumption of 6.56 mW at 16 GHz, demonstrating that high-performance phase interpolation is achievable without requiring power-intensive, high-bandwidth input clock signals and making the proposed design a robust solution for SerDes. The performance of the PI proposed in this work was validated through post-layout simulations; experimental verification of the proposed architecture, while a critical next step, was outside the scope of this study and is left for future work.