Abstract
In wireless sensor networks (WSNs), node localization technology serves as a critical foundation for Internet of Things (IoT) applications such as environmental monitoring and ecological protection. High-precision localization has long been a key challenge in IoT applications. However, traditional multi-hop localization algorithms suffer from insufficient localization accuracy in complex environments due to path tortuosity and error accumulation. To address this issue, this paper proposes DV-Hop-HLPT, a multi-hop localization algorithm based on a tortuosity model and a hierarchical strategy for reliable anchor nodes. The algorithm employs a hierarchical localization strategy to expand the anchor node set, incorporating high-precision localized nodes into the anchor node collection through received signal strength indication (RSSI) calibration and evaluating their reliability. To address the multi-hop path tortuosity problem, the algorithm constructs a tortuosity weight model by analyzing path information between anchor nodes, enabling dynamic correction of multi-hop path lengths. Combined with an incremental shortest path first (ISPF) algorithm to limit search depth, the approach enhances adaptability to dynamic networks. Finally, utilizing the tortuosity model and anchor node reliability, the unknown node coordinates are solved through regularized weighted least squares method. Experimental results demonstrate that under square and C-shaped network topologies, DV-Hop-HLPT reduces average normalized localization error by 50.15% and 70.95%, respectively, compared with DV-Hop, and shows significant improvements over other enhanced algorithms, effectively addressing the localization accuracy degradation problem caused by sparse anchor nodes in complex environments.
1. Introduction
With the continuous development of technology, Wireless Sensor Networks (WSNs), as a vital component of the Internet of Things (IoT), have gained widespread application driven by the demand for intelligent systems [1]. WSNs constitute wireless multi-hop communication network systems composed of sensor nodes featuring low cost, low power consumption, and self-reconfiguration capability, with capabilities for sensing, collecting, and transmitting physical or chemical environmental parameters [2]. In recent years, they have been extensively deployed in various domains including environmental monitoring, healthcare, smart buildings, and industrial automation [3], with their working structure shown in Figure 1. Furthermore, accurate monitoring and tracing of information sources in WSNs are crucial for ensuring efficient network operation. Location information serves not only as a prerequisite for the validity of sensed data, but also as the foundation for efficient resource scheduling and optimization. Therefore, the development of localization technologies is of paramount importance.
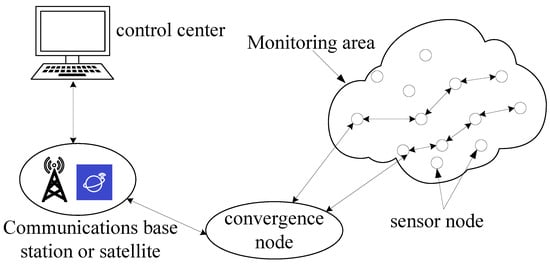
Figure 1.
WSN working structure diagram.
Currently, node localization algorithms are primarily classified into two categories: range-based and range-free approaches. Range-based localization algorithms generally estimate node coordinates by directly measuring the distance or time difference between target nodes and anchor nodes in combination with localization algorithms. Common algorithms include Time of Arrival (TOA) [4], Time Difference of Arrival (TDOA) [5], and Received Signal Strength Indicator (RSSI) [6]. However, range-based algorithms are highly sensitive to environmental interference, significantly affected by environmental factors, and require additional hardware equipment, resulting in relatively high costs.In contrast, range-free localization algorithms do not require precise inter-node distance measurements but instead utilize network connectivity information for localization, offering advantages of low cost and flexible deployment. In WSNs, multi-hop localization algorithms, as typical representatives of range-free methods, leverage network topology structures to propagate anchor node coordinate information to unknown nodes through multi-hop communication, establishing distance estimation models based on parameters such as hop count, received signal strength, or link delay. Multi-hop algorithms such as DV-Hop [7,8] and DV-Distance [9], through cooperative information transmission among neighboring nodes, can address global localization challenges in scenarios with absent or sparse anchor nodes, demonstrating significant advantages in terms of low power consumption and cost-effectiveness [10].
However, in practical deployment scenarios, Non-Line-Of-Sight (NLOS) signal propagation [11] is prevalent in complex geographical environments such as urban streets and forested valleys. Propagation characteristics are significantly interfered by factors including multipath effects, shadow fading, and obstacle occlusion, leading to signal strength attenuation, delay spreading, and nonlinear transmission path loss, which greatly increases localization complexity. Therefore, effectively addressing interference factors in complex regions to achieve high-precision robust localization algorithm design and optimization has become one of the important research directions in node localization technology. To address these issues, research by domestic and international scholars has mainly focused on two aspects: hardware improvement and algorithm optimization [12]. In hardware development, multi-sensor fusion techniques are employed, such as integrating information from accelerometers, gyroscopes, and Inertial Measurement Units (IMU), to achieve more precise spatial location estimation [13]. However, such methods typically increase system complexity and energy consumption. In algorithm optimization, researchers tend to enhance localization accuracy and stability by improving the mathematical models, computational processes, or parameter adaptation mechanisms of localization algorithms. These methods require no additional hardware support and possess higher portability and application flexibility [14], thus becoming the primary direction of node localization algorithm research and optimization in recent years.
To address the aforementioned challenges, this manuscript proposes an enhanced multi-hop localization framework aimed at improving localizationing accuracy and robustness in complex WSN environments. The major contributions of this work are summarized as follows:
- A hierarchical anchor extension strategy is proposed to enhance network coverage and localization stability in sparse-anchor scenarios.
- A path tortuosity weighting model is developed to dynamically correct multi-hop distances and mitigate the impact of irregular propagation paths.
- An incremental shortest path first (ISPF) algorithm is introduced to limit hop propagation depth and improve adaptability to dynamic network structures.
- A regularized weighted least-squares method is employed to integrate tortuosity correction and anchor reliability for achieving stable and high-precision localization.
The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 elaborates on the proposed DV-Hop-HLPT algorithm model and its specific steps. Section 4 presents the experimental setup and provides an in-depth analysis and discussion of the results. Finally, Section 5 concludes the paper and outlines future research directions.
2. Related Work
In recent years, significant progress has been made in multi-hop localization algorithm research, with research directions covering algorithm improvements, error analysis, and other aspects. In terms of anchor node selection, Liu et al. [15] proposed a hybrid localization algorithm combining Approximate Point-In-Triangulation Test (APIT) with DV-Hop, which preliminarily determines unknown node locations through angular information and achieves hierarchical localization using triangular region division: the APIT algorithm is applied to unknown nodes within triangular regions formed by anchor nodes, while the DV-Hop algorithm is employed for unknown nodes outside these regions. However, the hierarchical boundaries of this algorithm are fixed, and when nodes are at region edges, accuracy tends to decrease due to exceeding the division range. Cao et al. [16] proposed the OANS DV-Hop algorithm, which constructs an optimal anchor node subset through binary particle swarm optimization, to replace all anchor nodes in localization, significantly reducing distance estimation errors caused by hop count accumulation, and further optimizes localization results by combining continuous Particle Swarm Optimization (PSO). However, performance degrades significantly when anchor nodes are sparsely or unevenly distributed. Zhang et al. [17] proposed an improved DV-Distance algorithm that reduces multi-hop routing arc errors by statically selecting nodes near the network center as auxiliary anchor nodes. However, auxiliary anchor nodes are pre-selected and cannot adapt to node mobility or dynamic topology changes. Sankaranarayanan et al. [18] proposed a node localization algorithm combining Crow Search with Weighted Centroid Localization (CS-WCL), which effectively reduces average localization error and energy consumption by optimizing anchor node selection and weighted centroid calculation. This method features simple computation and low energy overhead, making it suitable for resource-constrained scenarios, but localization accuracy decreases under conditions of uneven anchor node distribution or high RSSI noise.
In terms of distance estimation correction, Sun et al. [19] proposed a differential DV-Distance localization algorithm by considering the varying correction coefficients of unknown nodes and adopting an unknown node-based correction model. However, its correction coefficients depend on fixed path distance difference calculations and do not consider dynamic environmental factors such as NLOS interference. Jia et al. [20] proposed an adaptive step-size varying chaotic fruit fly optimization algorithm (CAFOA-DV-Hop) for anisotropic networks (AN), demonstrating high localization accuracy under different communication radii and anchor node ratios, with its weighting logic focusing on the optimization efficiency of intelligent algorithms. Cui et al. [21] proposed the WRCDV-Hop algorithm, which treats hop counts as continuous values and combines RSSI to estimate average hop distance, while limiting anchor beacon forwarding to reduce energy consumption and using the Whale Optimization Algorithm (WOA) for refined localization. This algorithm achieves a good balance between accuracy and energy consumption but has strong dependence on network density and RSSI stability. Zhang et al. [22] addressed the cumulative error problem in the traditional DV-Distance algorithm under multipath propagation by proposing a path-based improvement method. This method reduces the impact of single-path errors on localization results by applying a weighted average of distances from multiple paths, combined with trilateration and multipath fusion mechanisms. Wang et al. [23] proposed the SIC-DV-Hop algorithm, which introduces inverse distance weighting and anchor node inclusion checking mechanisms and employing an improved centroid method for location estimation. Experimental results show that this algorithm has significantly lower localization errors than traditional DV-Hop under different network topologies while reducing network resource consumption. However, this method still depends on the rationality of anchor node geometric distribution, and with degraded performance under sparse networks or unstable channels.
In terms of error accumulation control, Tian et al. [24] proposed a DV-MDS-SA fusion localization algorithm to address the large localization errors of DV-Hop and MDS-MAP algorithms in concave regions. This algorithm first employs the DV-Hop algorithm to obtain estimated distances from unknown nodes to anchor nodes, then applies the DV-Hop localization algorithm to derive shortest distances between nodes for use in the MDS-MAP algorithm to obtain estimated locations of unknown nodes, and finally utilizes simulated annealing algorithm to optimize estimated locations to reduce localization errors. Wang et al. [25] presented a multi-objective DV-Hop localization algorithm based on NSGA-II, named NSGA-II-DV-Hop. This algorithm establishes a new multi-objective model and utilizes an enhanced constraint strategy based on all anchor nodes to enhance DV-Hop localization estimation accuracy, focusing on solution space optimization of localization results. Table 1 compares key differences between the classical method, representative improvement schemes, and the proposed algorithm in this paper, including anchor node utilization strategies and distance correction mechanisms, demonstrating how the proposed solution addresses these challenges.

Table 1.
Comparison of Representative Localization Algorithms.
3. Proposed Work on Algorithm Based on Hierarchical Localization Strategies and Path Tortuosity Correction
In the node localization process, traditional hop-count or hop-distance based localization methods typically rely on key information such as hop counts of optimal paths and single-hop distance estimation between target nodes and anchor nodes to estimate distances and calculate target node locations. However, in practical application scenarios, the complexity and non-uniformity of geographical environments pose significant challenges to signal propagation, such as signal reflection and refraction phenomena. These factors cause significant deviations between the cumulative length of communication paths and Euclidean distances between target nodes and anchor nodes, leading to substantial increases in localization errors and affecting the overall localization performance of algorithms, as shown in Figure 2.
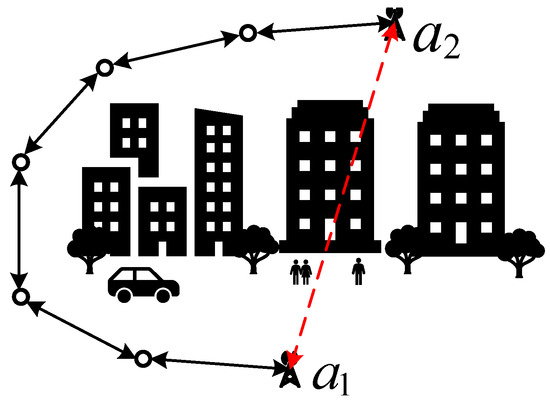
Figure 2.
Shortest communication path affected by interference factors.
To address the aforementioned issues and overcome the limitations of existing multi-hop localization methods, this paper proposes an improved DV-Hop-HLPT algorithm. By systematically enhancing anchor node utilization, path distance estimation, and coordinate calculation, it improves the accuracy and robustness of multi-hop localization. The overall framework of this localization algorithm is shown in Figure 3:
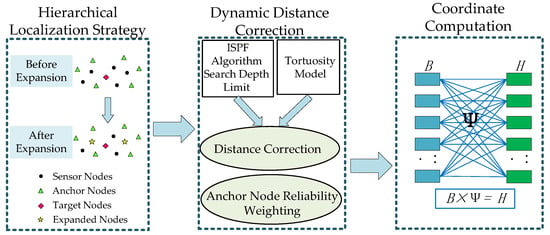
Figure 3.
The overall architecture of the algorithm.
3.1. Hierarchical Localization Strategy
Existing localization methods generally rely on a known set of anchor nodes; however, the initial proportion of anchor nodes is often limited. To make fuller use of the effective information provided by anchor nodes, this paper proposes a hierarchical localization strategy. In this strategy, intermediate nodes that can directly communicate with multiple anchor nodes are first localized and incorporated into the anchor node set, after which the reliability of each extended anchor node is evaluated. Unlike traditional hierarchical anchor expansion methods, DV-Hop-HLPT expands only those nodes localized through the original anchors, thereby avoiding the propagation of localization errors that may arise from multiple iterative expansions. Since noise interference in direct node-to-node communication is significantly smaller than that in multi-hop communication [26], the extended anchor nodes exhibit high reliability. During the initial network formation phase, this strategy identifies and integrates available intermediate node resources within the network, expands the anchor node set, fully exploits the available information, and effectively enhances the network’s adaptability and robustness in dynamic environments [27].
Assume a simulation region contains N nodes, where nodes are anchor nodes with known locations and the remaining nodes are ordinary nodes with unknown locations. The communication radius of all nodes is R and each node has a unique . During the initial flooding phase, an neighbor relationship matrix can be obtained by exchanging information between nodes. This matrix records the connections between each node and its neighboring nodes.
where indicates that node i can communicate directly with node j, while indicates that node i is unable to communicate directly with node j.
As shown in Figure 4, nodes that can maintain direct single-hop communication with at least three original anchor nodes are first selected. The RSSI calibration model is then used to estimate the distances between the selected node and the three anchor nodes. Subsequently, based on these distances and the corresponding anchor coordinates, the location of the extended anchor node is calculated using the least squares method. The reliability of the extended anchor node’s estimated location is further evaluated using the Root Mean Square Residual. The resulting hybrid anchor node set is thus not only expanded in quantity but also capable of distinguishing the credibility of different anchors during localization, effectively controlling potential error propagation introduced by the extended anchor nodes.Use the following residual formula to evaluate the reliability of the anchor node.
where k is the number of original anchor nodes used to locate the unknown node. are the calculated coordinates of the unknown node U. are the known coordinates of anchor node . is the estimated distance from unknown node U to anchor node . A smaller value indicates higher node quality, and the node’s Reliability Score approaches 1.
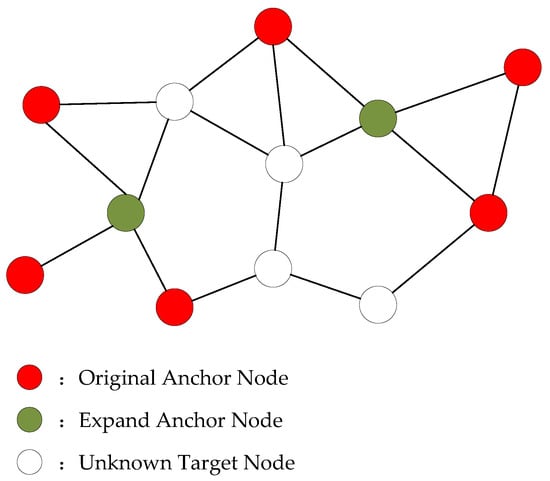
Figure 4.
Anchor node expansion.
The following two scenarios illustrate how the hierarchical localization strategy improves target node localization accuracy. As shown in Figure 5, in Scenario 1, target node communicates with anchor nodes and via multi-hop paths, with minimum hop counts of and , corresponding to estimated distances of and , respectively. The feasible region of is constrained to the intersection of two circles centered at and with radii and , respectively. In Scenario 2, intermediate node is promoted to an anchor node through the hierarchical localization strategy. With now serving as a closer reference point, is localized using anchor nodes and with minimum hop counts of and , corresponding to estimated distances of and , respectively. The feasible region of is then constrained to the intersection of two circles centered at and with radii and , respectively, resulting in a smaller and more precise constraint region.Comparing these two scenarios reveals that the hierarchical localization strategy can effectively enhance localization accuracy, which is further validated by simulation results.
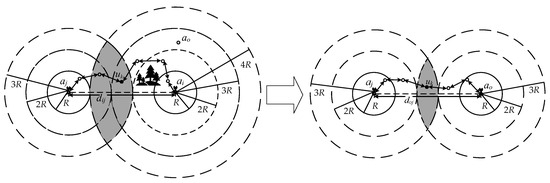
Figure 5.
Comparison of anchor node expansion before and after.
3.2. Path Database Construction and Tortuosity Model Correction
Research has revealed that the node localization process primarily consists of two stages: the distance estimation stage between anchor nodes and target nodes, and the coordinate determination stage for target nodes. During the distance estimation stage, minimizing the discrepancy between the estimated distance and the Euclidean distance between anchor and target nodes is a critical factor in enhancing localization accuracy. Traditional multi-hop localization algorithms often employ fixed weights or simplistic path models [28]. Some algorithms even directly use the cumulative length of communication paths between nodes as their Euclidean distance, which can easily lead to significant localization errors. Therefore, to mitigate errors in the distance estimation phase, this paper proposes a tortuosity model correction mechanism. First, a path database PathDB is constructed using known anchor node pairs to store samples of path geometric characteristics. Each sample consists of a triplet (, , ), representing the number of hops, the cumulative communication distance, and the true Euclidean distance between anchor nodes, respectively. For anchor nodes and , the path database entry can be represented as:
As shown in Figure 6, the curvature of each path sample in the PathDB is characterized by the path tortuosity , which is calculated as:
where denotes the cumulative length of the path, and represents the Euclidean distance between the two end nodes. To more accurately characterize the tortuosity features of paths with different hop counts, this paper designs a Tortuosity Statistical Model, indexed by the path hop count h. For each hop count h, the model collects the set of tortuosity samples corresponding to all paths with h hops, and calculates their mean and standard deviation as follows:
where reflects the average tortuosity of paths at a given hop count, while quantifies the variability and uncertainty in path morphology, enabling more effective suppression of irregular path errors during distance correction. Subsequently, based on this statistical model, a dynamic path correction mechanism is proposed. For an unknown path with hop count h, the algorithm calculates a tortuosity-weighted factor . is the conservation coefficient, and serves as the deviation adjustment factor. When path tortuosity exhibits significant fluctuations at a given hop count, this correction factor automatically reduces its weight to mitigate the negative impact of highly uncertain paths on localization accuracy. This correction method effectively integrates path geometric characteristics with statistical robustness, ensuring reliable and resilient localization distance estimation under complex topologies. Consequently, the corrected distance estimate between target node u and anchor node is calculated as follows:
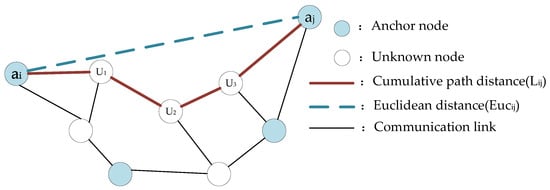
Figure 6.
Path curvature diagram.
3.3. ISPF Algorithm and Search Depth Limit
3.3.1. Search Depth Limit
During node localization, the localization algorithm must explore the network to acquire sufficient localization information. However, when the search depth increases, computational load grows exponentially, resulting in a significant decrease in computational efficiency and severely compromising the timeliness and practicality of localization. Therefore, establishing a reasonable search depth threshold is critical. Moreover, the search depth threshold should be closely correlated with factors including the number and spatial distribution of anchor nodes and network connectivity, and should be adaptively adjusted to accurately reflect the actual communication characteristics of the network [29]. This study utilizes the average hop distance among anchor node pairs to estimate the effective communication radius for computing the search depth threshold, instead of directly using the predefined communication radius R. The calculation formula for the effective communication radius is given as follows:
where represents the node communication radius used when calculating the threshold for the search depth; denotes the number of anchor nodes whose locations are known; represents the cumulative length of the communication path between anchor node i and j; represents the number of hops between anchor node i and j; and k represents the number of pairs of anchor nodes in the network that can communicate with each other.
By comparing the communication coverage area with a radius of to the area of the simulation region, the following formula is derived:
where t represents the minimum number of anchor nodes required to complete node localization within the region; represents the threshold for the search depth; and S represents the area of the simulation region. denotes the number of anchor nodes whose locations are known.
The aforementioned calculation of the search depth threshold is theoretical. However, in practical application scenarios, due to various influencing factors, the value of is generally set slightly higher than the theoretical value to meet normal requirements.
By imposing reasonable limits on the search depth, the communication frequency among nodes within the network can be effectively reduced, thereby improving transmission efficiency. By comparing simulation experiment results with and without search depth limits, it is evident that setting an appropriate search depth has a positive effect on enhancing node localization accuracy.
3.3.2. ISPF Algorithm
In WSNs, nodes may leave or join the network due to energy depletion, failures, or other reasons, and link states can change with the environment [30]. Traditional distance vector routing protocols update routing tables via periodic neighbor exchanges, resulting in slow convergence and potential suboptimal paths or routing loops in dynamic topologies, which affect communication stability. In contrast, the ISPF algorithm uses an incremental update mechanism with a stored shortest path tree, recalculating only affected paths and adjusting part of the routing table without recomputing the entire network. This reduces computational overhead, avoids routing loops, and accurately reflects link states to identify precise optimal paths. Regional partitioning and hierarchical routing further allow the algorithm to adapt to large-scale networks.
Therefore, this paper employs ISPF to replace traditional protocols for finding communication paths, enabling the localization algorithm to efficiently respond to dynamic node changes. Although ISPF requires higher processing and storage capacity, advances in modern network hardware mitigate these limitations.
The ISPF algorithm is an optimization algorithm in the Open Shortest Path First (OSPF) routing protocol, used to update routing information more efficiently when the network topology changes. In the context of WSN node localization, the algorithm implementation steps are shown in Figure 7.
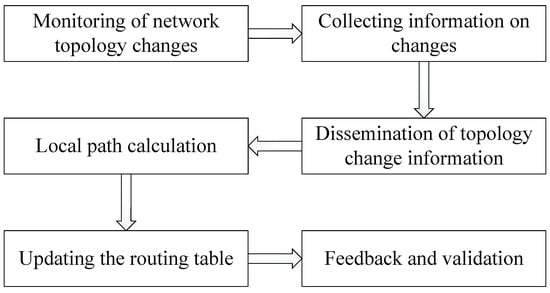
Figure 7.
Steps of ISPF algorithm implementation.
Figure 8 clearly shows the advantages of the ISPF algorithm in solving routing loop problems when the links between nodes are suddenly disconnected, forming a dynamic network topology. The simple network topology is as follows: there are nodes A, B, C, and D, where D is the destination node. Figure 8a depicts a simple network in its initial stable state, where the link costs between adjacent nodes are all 1.
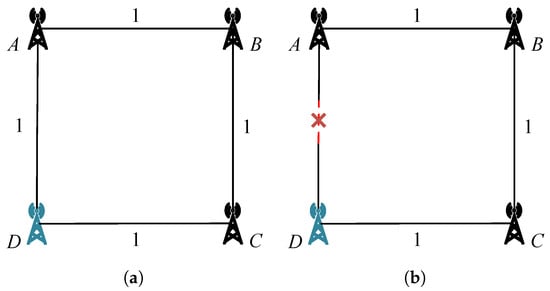
Figure 8.
Simple Topological Structure. (a) Initial state. (b) State after a link failure.
When the link between nodes A and D fails, as depicted in Figure 8b, traditional distance-vector protocols suffer from the count-to-infinity problem, leading to persistent routing loops. In contrast, the ISPF algorithm resolves this by performing a localized update: only the affected node A recalculates its path to the target node D via the new path , while nodes B and C retain their existing routing tables. This mechanism eliminates the need for global recomputation and significantly improves the efficiency and reliability of path updates.
3.4. Solving Node Coordinates Based on Regularized Least Squares Method
To further enhance localization accuracy and stability, this paper proposes the use of weighted regularized least squares to solve target node coordinates, based on thorough consideration of data validity and noise effects. Compared to traditional least squares methods [31,32], regularized least squares overcome potential overfitting issues in localization by incorporating a regularization term into the loss function. This approach not only improves localization accuracy but also enhances the model’s generalization capability.
During the hierarchical expansion phase of anchor nodes, Each extended anchor node carries a reliability weight , with the original anchor node assigned a weight of 1. During the final localization phase, anchor reliability weights are introduced to solve for the locations of unknown nodes. By assigning different weight values to original and extended anchor nodes, the coordinate calculation process relies more heavily on high-confidence anchor information, thereby suppressing the propagation of errors from extended anchor nodes. The following content provides a more direct observation of the process of solving for target node coordinates using regularized least squares weighting. Assume that three anchor nodes , , and exist in a two-dimensional space, and the coordinates of the target node are denoted as . According to the distance formula between two points, the measured distances from the target node to the three anchor nodes are , , and , respectively. The resulting system of equations is constructed as follows:
Express it in the form of , where:
For an overdetermined system of equations , the goal of the least squares method is to find that minimizes . On this basis, the regularized least squares method adds a regularization term, and its objective function becomes , where W denotes the weight matrix, and is the regularization parameter. Calculate the specific value of , which is the estimated coordinates of the target node.
4. Experimental Simulation and Result Analysis
In real-world scenarios, wireless signals often bypass or penetrate obstacles, resulting in non-circular and anisotropic radio ranges [33]. To capture this complexity in simulations, the Degree of Irregularity () is introduced as a parameter that quantifies variations in signal propagation across different directions [34,35]. Higher values correspond to stronger anisotropy and increased localization uncertainty. In our simulations, represents moderately irregular indoor or urban propagation conditions. The probability of successful communication between two nodes separated by distance d is defined as:
where represents the communication success probability between two nodes at distance d, R is the communication radius, and quantifies the degree of signal irregularity in wireless propagation.
The experiment utilizes MATLAB R2023a for simulation. To evaluate the performance of the proposed DV-Hop-HLPT algorithm, it is compared with four related multi-hop localization algorithms: DV-HOP, ICFP-PM, SIC-DV-Hop, and OANS DV-Hop. Table 2 shows the key experimental parameters of the simulation experiments in this section, such as the number of simulations, the anchor node ratio and the communication radius.

Table 2.
Simulation parameters for performance evaluation of the proposed algorithm.
To more realistically simulate the complexity of WSN deployment in practical scenarios, this paper conducts simulation experiments in two typical structural regions: a square regular area and a C-shaped irregular area. The C-shaped structure is highly representative and typical in real-world applications, as it commonly appears in complex environments such as building corners, industrial plant corridors, and indoor turning hallways. This type of structure easily causes signal propagation path deviation and error amplification, making it a typical scenario in which traditional multi-hop localization algorithms suffer from large errors due to path bending and signal attenuation. Figure 9 illustrate example node deployments and network topologies.
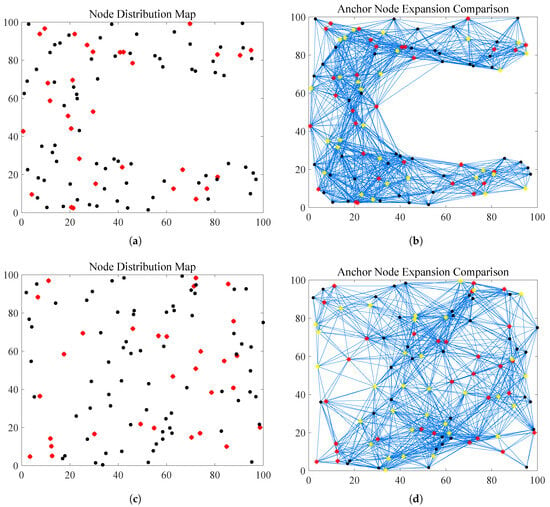
Figure 9.
Node deployment and network topologies, with all axes in meters (m) (a) Node deployment in a C-shaped area. (b) Network topology in a C-shaped area. (c) Node deployment in a square area. (d) Network topology in a square area.
To evaluate the localization performance of the algorithm, this paper employs the normalized average localization error (N-ALE) [36] as the performance metric, defined as follows:
where is the number of target nodes; are the true coordinates of the target node ; are the estimated coordinates of the target node obtained using the algorithm; and R is the communication radius of the nodes.
4.1. Effect of Search Depth Limitation and the Parameter on the Algorithm Localization Performance
In WSNs, properly setting the search depth not only allows more effective use of anchor node information for localizing target nodes but also enhances the algorithm’s adaptability and robustness. As shown in the experimental results in Figure 10a, we explored the impact of the search depth limit on the error in the estimated distance between nodes, using the multiple of the current communication radius as the evaluation indicator. However, when different search depths are set, the error exhibits a trend of first decreasing and then increasing. Therefore, selecting an appropriate search depth limit can effectively reduce the error in estimated distance and improve localization accuracy. Through multiple simulation experiments, it has been found that the error in estimated distance is minimized when the threshold for search depth is set to .
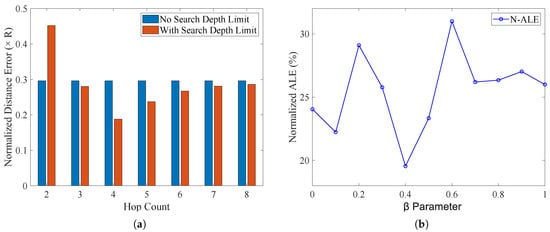
Figure 10.
(a) Effect of hop count on estimated distance error. (b) Effect of the Parameter on Localization Error.
To determine the optimal value of , a systematic scanning experiment was conducted under fixed network parameters, with varying from 0 to 1 in increments of 0.1. As shown in Figure 10b, the algorithm achieves the best localization performance when . This indicates that moderately considering the standard deviation in the weight calculation can effectively suppress the negative impact of path length fluctuations on distance estimation, thereby improving localization accuracy. When is too small, path variability is insufficiently accounted for; when is too large, the influence of the standard deviation is overly amplified. Therefore, in all subsequent experiments, is adopted as the adjustment parameter for the weighting coefficient.
4.2. Effect of Hierarchical Localization on Inter-Node Localization Error
This section focuses on investigating the effect of hierarchical localization strategies on algorithm localization performance through two comparative experiments to validate the effectiveness of hierarchical strategies. Experiment 1: Total nodes of 100, anchor ratio ranging from 15% to 40% with 5% increments, communication radius of 30 m; Experiment 2: Total nodes of 100, anchor ratio of 30%, communication radius ranging from 15 m to 40 m with 5 m increments.
As shown in Figure 11, in the C-shaped region experiments, when the anchor ratio is below 25%, the localization performance of hierarchical and non-hierarchical strategies is comparable, as the hierarchical strategy struggles to fully leverage its structural advantages under sparse anchor node conditions. However, when the anchor ratio exceeds 25%, the hierarchical localization strategy begins to significantly outperform the non-hierarchical strategy, with continuous improvement in localization accuracy as the anchor ratio increases, achieving an average improvement of 12.5% in localization precision. In the communication range variation experiments, when the communication radius exceeds 25 m, the hierarchical localization strategy starts to significantly outperform the non-hierarchical strategy, with continuous enhancement as the communication radius increases, achieving an average improvement of 17.3% in localization precision. In the square region experiments, the hierarchical algorithm demonstrates superior performance, achieving an average improvement of 17.8% in localization precision for anchor ratio variations and an average improvement of 24.7% for communication range variations. The experimental results indicate that under reasonable conditions of anchor ratio and communication radius, adopting hierarchical localization strategies can significantly enhance the overall localization effectiveness of the algorithm.
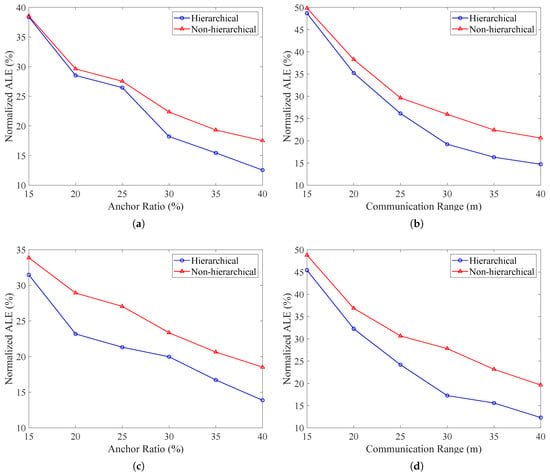
Figure 11.
Performance comparison of Hierarchical and Non-hierarchical localization methods under different network conditions. (a) C-shaped area: N-ALE versus Anchor Ratio. (b) C-shaped area: N-ALE versus Communication Range. (c) Square area: N-ALE versus Anchor Ratio. (d) Square area: N-ALE versus Communication Range.
4.3. Effect of Anchor Node Ratio on Localization Error Among Nodes
This section primarily analyzes the influence of different anchor node ratios on the localization performance of various algorithms under two network topologies: square and C-shaped. The main experimental parameters are set as follows: communication radius of 30 m, anchor node ratio ranging from 15% to 40% with a step size of 5%.
As shown in Table 3 and Figure 12, the localization error of all algorithms decreases as the anchor node ratio increases. The proposed DV-Hop-HLPT algorithm demonstrates the best average localization performance in both topological environments. In the C-shaped topology, its average error is reduced by 72.0%, 40.1%, 42.1%, and 4.2% compared with the DV-Hop, OANS, SIC-DV-Hop, and ICFP-PM algorithms, respectively. In the square topology, the average error of the DV-Hop-HLPT algorithm decreases by 48.6%, 26.9%, 24.6%, and 11.2% relative to the DV-Hop, OANS, SIC-DV-Hop, and ICFP-PM algorithms, respectively. As the anchor ratio increases, more unknown nodes can be promoted to high-reliability extended anchors, leading to a higher anchor node utilization efficiency. This provides more proximate and accurate reference points for the remaining nodes, thereby rapidly reducing localization error. The DV-Hop-HLPT algorithm exhibits faster error convergence and higher anchor node utilization efficiency across both topologies.

Table 3.
Algorithm comparison by anchor ratio (N-ALE%).
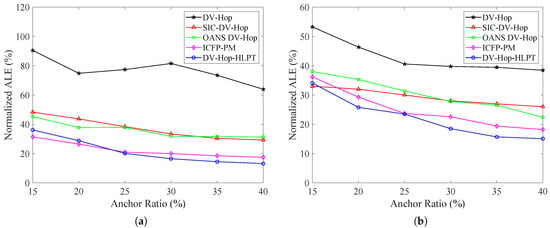
Figure 12.
Comparison of N-ALE for different localization methods under different anchor node ratios. (a) C-shaped area. (b) Square area.
4.4. Effect of Communication Radius on Localization Error Between Nodes
This section primarily analyzes the influence of different communication radii on the localization performance of various algorithms under two network topologies: square and C-shaped. The main experimental parameters are set as follows: anchor node ratio of 30%, and communication radius ranging from 15 m to 40 m with a step size of 5 m.
As shown in Table 4 and Figure 13, the localization accuracy of the proposed DV-Hop-HLPT algorithm gradually improves with the increase in communication radius. In the C-shaped region, the average localization error of the DV-Hop-HLPT algorithm is reduced by 71.4%, 37.7%, 47.1%, and 6.9% compared with the DV-Hop, OANS DV-Hop, SIC-DV-Hop, and ICFP-PM algorithms, respectively. In the square region, the average error is reduced by 51.4%, 22.2%, 15.0%, and 11.4%, respectively. A larger communication radius results in a denser network with shorter hop-count paths between nodes. This provides the tortuosity model with a richer and more reliable statistical basis for correcting distance estimations, thereby more effectively mitigating the errors caused by irregular paths. The DV-Hop-HLPT algorithm effectively reduces localization error under different communication radius conditions, indicating that the proposed method is sensitive to overall network connectivity.

Table 4.
Algorithm comparison by communication range (N-ALE%).
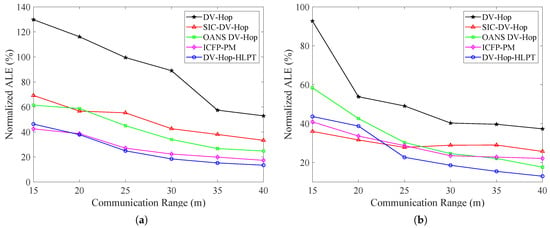
Figure 13.
Comparison of N-ALE for different localization methods under different communication ranges. (a) C-shaped area. (b) Square area.
4.5. Effect of Node Density on Localization Error Between Nodes
This section primarily analyzes the influence of different node densities on the localization performance of various algorithms under two network topologies: square and C-shaped. The main experimental parameters are set as follows: anchor node ratio of 30%, communication radius of 30 m, and node density ranging from 0.004 to 0.014 with a step size of 0.002.
As shown in Table 5 and Figure 14, as node density increases, the proposed DV-Hop-HLPT algorithm can acquire and utilize more effective information, resulting in a corresponding increase in the number of expandable anchor nodes. This change leads to a gradual reduction in average localization error and significant improvement in localization performance. The N-ALE of the proposed algorithm, compared with the other four algorithms, decreases consistently with increasing node density. In the C-shaped region, the average error of DV-Hop-HLPT is reduced by 69.4%, 34.4%, 49.9%, and 8.6% compared with DV-Hop, OANS DV-Hop, SIC-DV-Hop, and ICFP-PM, respectively, achieving the best performance among all compared algorithms. In the square region, the corresponding reductions are 50.2%, 33.6%, 37.5%, and 18.3%, respectively. The outstanding performance under high density demonstrates that DV-Hop-HLPT can effectively utilize additional network information, making it suitable for diverse deployment scenarios where node density may vary. In WSNs, deploying excessive nodes not only increases costs but may also impose a heavier computational burden on the network. To meet localization requirements while optimizing resource utilization, it is generally preferable to minimize the number of deployed nodes. Considering multiple factors, including cost and localization accuracy, the DV-Hop-HLPT algorithm demonstrates a more significant advantage compared with other methods.

Table 5.
Algorithm comparison by node density (N-ALE%). Density unit: .
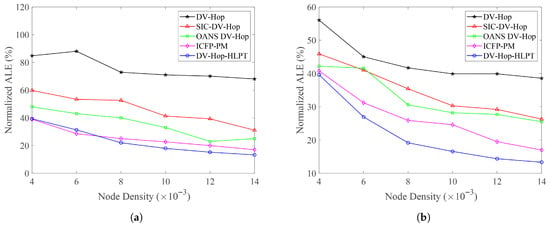
Figure 14.
Comparison of N-ALE for different localization methods under different node densities. (a) C-shaped area. (b) Square area.
4.6. Algorithm Stability Analysis
To evaluate the reliability of the algorithms, multiple independent experiments were conducted under fixed parameter settings, including an anchor ratio of 30%, a communication range of 30 m, and a total of 100 nodes. The standard deviation of each algorithm was then computed. As shown in Figure 15, the error-band plots indicate that the standard deviation decreases as algorithm performance improves, suggesting that advanced algorithms enhance both localization accuracy and stability. The DV-Hop-HLPT algorithm maintains consistently low standard deviations in both topologies, demonstrating robustness to topological variations and confirming its reliability for practical wireless sensor network deployments.
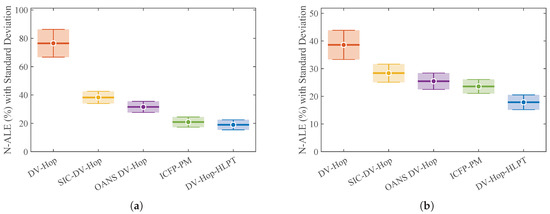
Figure 15.
Normalized Average Localization Error with stability analysis. (a) C-shaped area. (b) Square area.
5. Summary
With the rapid development of the IoT, range-free localization algorithms have shown great potential in practical applications. To address the problem of insufficient localization accuracy of traditional multi-hop localization algorithms in complex environments of WSNs, this paper proposes a multi-hop localization algorithm named DV-Hop-HLPT, based on a path tortuosity modeling and a reliable anchor node hierarchical strategy. The proposed algorithm expands the anchor node set through hierarchical localization, constructs a tortuosity-weighted model to correct multi-hop path lengths, and incorporates an ispf algorithm to optimize the search process, and estimates the coordinates of unknown nodes using a regularized weighted least squares method. Simulation results demonstrate that the DV-Hop-HLPT algorithm achieves significant performance improvements in both C-shaped and square network topologies. In the C-shaped topology, the proposed algorithm reduces the average normalized localization error by 70.95%, 37.40%, 46.66%, and 6.65% compared with DV-Hop, OANS DV-Hop, SIC-DV-Hop, and ICFP-PM, respectively. In the square topology, the average normalized localization error is reduced by 50.15%, 27.59%, 26.34%, and 13.59%, respectively. These results indicate that the proposed algorithm not only performs well in regular network topologies but also exhibits more pronounced advantages in challenging irregular topologies, demonstrating strong robustness and adaptability to complex network environments.
Although the proposed DV-Hop-HLPT algorithm significantly enhances localization accuracy and robustness in complex environments, certain limitations remain. The current design is primarily oriented toward static network scenarios, and its ability to accommodate node mobility is still limited. When the network topology changes rapidly, the reliability of hierarchical anchor nodes and the timeliness of the path database may be difficult to maintain. Moreover, the improvement in localizationing accuracy comes at the cost of increased computational and storage overhead, which could constrain its applicability in resource-limited sensor nodes. Future work will focus on developing a mobility-adaptive localization mechanism and designing a dynamic, data-driven correction framework. In particular, emerging machine learning methods such as Graph Neural Networks (GNNs) will be explored to learn complex mappings between local network topology and path tortuosity, enabling a more precise and environment-aware localization system.
Author Contributions
Conceptualization, L.W. and X.L.; methodology, X.L.; software, X.L.; validation, L.W., X.L. and D.Z.; formal analysis, X.L.; investigation, L.W. and X.L.; resources, L.W.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, L.W. and X.L.; visualization, X.L.; supervision, L.W. and D.Z.; project administration, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research on multi-scene deep compressed sensing technology for edge-cloud cooperative industrial Internet of Things, Science and Technology Tackling Project of Henan Province, grant number 242102211104.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the first author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, S.; Liu, J.; He, B.; Lin, C.; Yang, J.; Wei, W. An enhanced DV-hop localization algorithm based on hop distance correction and multi-strategy modified aquila optimizer in HWSNs. Clust. Comput. 2025, 28, 106. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.; Zheng, A.; Zheng, Z.; Jiang, X.; Zhang, S. DV-hop algorithm based on multi-objective salp swarm algorithm optimization. Sensors 2023, 23, 3698. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Chen, L.; Feng, C.; Fang, D.; Xiong, J.; Wang, Z. Sensing our world using wireless signals. IEEE Internet Comput. 2019, 23, 38–45. [Google Scholar] [CrossRef]
- Pan, M.; Liu, P.; Liu, S.; Qi, W.; Huang, Y.; You, X.; Jia, X.; Li, X. Efficient joint DOA and TOA estimation for indoor positioning with 5G picocell base stations. IEEE Trans. Instrum. Meas. 2022, 71, 1–19. [Google Scholar] [CrossRef]
- Hua, C.; Zhao, K.; Dong, D.; Zheng, Z.; Yu, C.; Zhang, Y.; Zhao, T. Multipath map method for TDOA based indoor reverse positioning system with improved chan-taylor algorithm. Sensors 2020, 20, 3223. [Google Scholar] [CrossRef] [PubMed]
- Fabris, A.; Kerusauskas Rayel, O.; Luiz Rebelatto, J.; Luiz Moritz, G.; Demo Souza, R. AoA and RSSI-based BLE indoor positioning system with kalman filter and data fusion. IEEE Internet Things J. 2025, 12, 15348–15359. [Google Scholar] [CrossRef]
- Liu, G.; Qian, Z.; Wang, X. An improved DV-hop localization algorithm based on hop distances correction. China Commun. 2019, 16, 200–214. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, X.; Xu, J. Improved DV-hop localization algorithm based on variable communication radius for wireless sensor networks. Wirel. Pers. Commun. 2024, 138, 1703–1725. [Google Scholar] [CrossRef]
- Chen, S.; An, M. Research on control strategy in wireless location system. In Proceedings of the 2018 IEEE International Conference of Intelligent Robotic and Control Engineering (IRCE), Lanzhou, China, 24–27 August 2018; pp. 208–212. [Google Scholar]
- Diaz-Roman, J.; Mederos, B.; Sifuentes, E.; Gonzalez-Landaeta, R.; Cota-Ruiz, J. A weighted and distributed algorithm for range-based multi-hop localization using a newton method. Sensors 2021, 21, 2324. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Chen, Y.; Guan, J. INS/UWB multi-sensor integrated localization scheme in indoor LOS/NLOS environment based on MEF-GPDAF. Comput. Electr. Eng. 2024, 120, 109693. [Google Scholar] [CrossRef]
- Jin, Y.; Zhou, L.; Zhang, L.; Hu, Z.; Han, J. A novel range-free node localization method for wireless sensor networks. IEEE Wirel. Commun. Lett. 2022, 11, 688–692. [Google Scholar] [CrossRef]
- Leitch, S.G.; Ahmed, Q.Z.; Abbas, W.B.; Hafeez, M.; Laziridis, P.I.; Sureephong, P.; Alade, T. On Indoor Localization Using WiFi, BLE, UWB, and IMU Technologies. Sensors 2023, 23, 8598. [Google Scholar] [CrossRef]
- Li, N.; Liu, L.; Zou, D.; Liu, X. Node localization algorithm for irregular regions based on particle swarm optimization algorithm and reliable anchor node pairs. IEEE Access Pract. Innov. Open Solut. 2024, 12, 37470–37482. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Zhang, W.; Zhao, D. Hybrid localization algorithm based on APIT and DV-HOP in Wireless Sensor Networks. In Proceedings of the 2015 IEEE/CIC International Conference on Communications in China—Workshops (CIC/ICCC), Shenzhen, China, 2–4 November 2015; pp. 164–168. [Google Scholar]
- Cao, Y.; Xu, J. DV-hop-based localization algorithm using optimum anchor nodes subsets for wireless sensor network. Ad Hoc Netw. 2023, 139, 103035. [Google Scholar] [CrossRef]
- Zhang, Y.; Ben, W. An improved DV-distance algorithm with assistant anchor for nodes localization in WSNs. In Proceedings of the 2014 11th International Joint Conference on Computer Science and Software Engineering (JCSSE), Chonburi, Thailand, 14–16 May 2014; pp. 182–187. [Google Scholar]
- Sankaranarayanan, S.; Vijayakumar, R.; Swaminathan, S.; Almarri, B.; Lorenz, P.; Rodrigues, J.J.P.C. Node localization method in wireless sensor networks using combined crow search and the weighted centroid method. Sensors 2024, 24, 4791. [Google Scholar] [CrossRef]
- Sun, L.; Chen, T. Difference DV_Distance localization algorithm using correction coefficients of unknown nodes. Sensors 2018, 18, 2860. [Google Scholar] [CrossRef]
- Jia, W.; Qi, G.; Liu, M.; Zhou, J. A high accuracy localization algorithm with DV-hop and fruit fly optimization in anisotropic wireless networks. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8102–8111. [Google Scholar] [CrossRef]
- Cui, H.; Wang, S.; Zhou, C. A high-accuracy and low-energy range-free localization algorithm for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2023, 2023, 37. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, S.; Chen, J. New dv-distance method based on path for wireless sensor network. Intell. Autom. Soft Comput. 2017, 23, 219–225. [Google Scholar] [CrossRef]
- Wang, J.; Hou, A.; Tu, Y.; Yu, H. An improved DV-hop localization algorithm based on selected anchors. Comput. Mater. Contin. 2020, 65, 977–991. [Google Scholar] [CrossRef]
- Tian, E. A non-ranging Fusion Location Algorithm for Concave Regions. Wirel. Pers. Commun. 2022, 124, 2537–2551. [Google Scholar] [CrossRef]
- Wang, P.; Xue, F.; Li, H.; Cui, Z.; Xie, L.; Chen, J. A multi-objective DV-hop localization algorithm based on NSGA-II in internet of things. Mathematics 2019, 7, 184. [Google Scholar] [CrossRef]
- Khedr, A.M.; Rani, S.S.; Saad, M. Hybridized dragonfly and jaya algorithm for optimal sensor node location identification in mobile wireless sensor networks. J. Supercomput. 2023, 79, 16940–16962. [Google Scholar] [CrossRef]
- Sekhar Rao Rayavarapu, V.C.; Mahapatro, A.; Kanti, R.D. Design and development of mobile anchor assisted node localization strategy using a hybrid electric-coyote optimization. Evol. Intell. 2024, 17, 1405–1423. [Google Scholar] [CrossRef]
- Feng, X.; Chen, Z.; Liu, Z. A new range-free algorithm based on hop correction of RSSI. J. Intell. Fuzzy Syst. 2018, 34, 1205–1212. [Google Scholar] [CrossRef]
- Sesyuk, A.; Ioannou, S.; Raspopoulos, M. A Survey of 3D Indoor Localization Systems and Technologies. Sensors 2022, 22, 9380. [Google Scholar] [CrossRef]
- Yu, X.; Peng, W.; Zhou, Z.; Zhang, K.; Liu, Y. An IMOA DV-Hop localization algorithm in WSN based on hop count and hop distance correction. Peer-to-Peer Netw. Appl. 2024, 17, 2637–2650. [Google Scholar] [CrossRef]
- Zhao, W.; Shao, F.; Ye, S.; Zheng, W. LSRR-LA: An Anisotropy-Tolerant Localization Algorithm Based on Least Square Regularized Regression for Multi-Hop Wireless Sensor Networks. Sensors 2018, 18, 3974. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Xu, Z.; Yang, L. An improvement of DV-hop localization algorithm based on cyclotomic method in wireless sensor networks. Appl. Sci. 2023, 13, 3597. [Google Scholar] [CrossRef]
- Kuhn, F.; Wattenhofer, R.; Zollinger, A. Ad-hoc networks beyond unit disk graphs. In Proceedings of the 2003 Joint Workshop on Foundations of Mobile Computing, San Diego, CA, USA, 19 September 2003; pp. 69–78. [Google Scholar]
- Zhang, S.; Liu, X.; Wang, J.; Cao, J.; Min, G. Accurate range-free localization for anisotropic wireless sensor networks. ACM Trans. Sens. Netw. 2015, 11, 1–28. [Google Scholar] [CrossRef]
- Jiang, J.; Han, G.; Xu, H.; Shu, L.; Zhang, Y. A two-hop localization scheme with radio irregularity model in wireless sensor networks. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1–4 April 2012; pp. 1704–1709. [Google Scholar]
- Zhang, W.; Yang, X. DV-hop location algorithm based on RSSI correction. Electronics 2023, 12, 1141. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).