A Method for Evaluating the Capability Adaptability of Equipment Groups Considering Dynamic Weight Adjustment

Abstract

To address the issues of incomplete indicator coverage and dynamic weights not aligning with changes in the external environment in the evaluation of equipment group capability adaptability—resulting in biased evaluation results and poor applicability—this study proposes an equipment group capability adaptability evaluation method considering dynamic weight adjustment. Firstly, a four-dimensional indicator system encompassing capability requirement adaptability, equipment collaboration adaptability, external environment adaptability, and cycle support adaptability is constructed, and an association model for each indicator is designed. Secondly, an Long Short-Term Memory (LSTM)–Bayesian combined dynamic weight calculation method is proposed to compute the equipment group capability adaptability. Finally, case verification results show that the four-dimensional indicators match phase-specific requirements and the dynamic weights are accurately adjusted with phases, indicating that the method is reasonable and reliable. It can provide technical support for equipment group adaptability decision-making in dynamic scenarios.

1. Introduction

The external environment exhibits obvious dynamism and uncertainty. The capability of equipment groups relies on the collaboration of multiple units and full-cycle support. Traditional equipment group adaptability evaluation methods—characterized by single-dimensional indices and static weights—cannot adapt to the dynamic characteristics of demand fluctuations, collaborative coupling, and environmental changes, resulting in deviations in evaluation results. Therefore, an evaluation method integrating multi-dimensional indices and dynamic weight adjustment is needed to address the limitations of static methods and provide technical support for equipment maintenance decision-making.

Existing equipment capability evaluation studies mainly improve traditional evaluation methods or integrate intelligent technologies to enhance the accuracy of equipment capability, reliability, and condition monitoring. Zhang et al. [1] proposed an equipment support capability evaluation method based on neural networks to replace traditional manual evaluation, improving the objectivity and efficiency of evaluation. Sun et al. [2] proposed an improved ADC (Availability, Dependability, Capability) analysis method to realize the reliability evaluation of unmanned aircraft combat effectiveness. Liu et al. [3] proposed a capability evaluation and key node identification method for heterogeneous combat networks with multi-functional equipment, combining complex network theory to capture the dynamic evolution characteristics of network structures. Salvati et al. [4] developed a novel pulsed wireless power transfer (WPT) system with data transmission capability for condition monitoring of industrial rotating equipment; through WPT, contactless power supply and synchronous data transmission are achieved, solving the wiring problem of rotating equipment.

To address the issue of static weights, dynamic weight adjustment theory must be introduced. Current research on dynamic problems mainly solves dynamic evolution issues through time-series modeling or complex network nodes. Lu et al. [5] proposed an ordered structure analysis method for node importance based on the homogeneity of temporal inter-layer neighborhoods in dynamic networks. Young et al. [6] explored the dynamic importance of networks under perturbations, revealing the anti-interference characteristics of dynamic networks. Huang et al. [7] proposed the DynImpt dynamic data selection method, which improves model training efficiency by screening key samples in time-series data. Feng et al. [8] constructed a dynamic risk analysis of accident chains and a system protection strategy based on complex networks and node structural importance, addressing the dynamic early warning problem of cascading accidents in industrial systems. Zhao et al. [9] proposed a dynamic comprehensive evaluation of the importance of cutting parameters in TC4 alloy side milling using an integrated weighting method, determining key cutting parameters through dynamic modeling. Wang et al. [10] constructed an endpoint carbon content and temperature prediction model for converter steelmaking based on dynamic feature partitioning-weighted ensemble learning. Gupta et al. [11] published a review on dynamic change-point detection in time-series data, summarizing the technical routes in this field.

To address equipment capability adaptability issues in different phases, time-series analysis must be introduced. As a time-series data processing technology, Long Short-Term Memory (LSTM) networks can be combined with specialized modules to adapt to specific scenario requirements, improving the accuracy of prediction, detection, or management. Ge et al. [12] proposed AC-LSTM (Adaptive Clockwork LSTM) for network traffic prediction, optimizing the ability to capture time-series features and solving the poor adaptability of traditional LSTM to dynamic traffic. Wang et al. [13] proposed LSTM-MM (LSTM-Based Mobility Management) for scheduling power inspection vehicles in smart grids, realizing accurate prediction of equipment movement status through time-series modeling. Shu et al. [14] designed an LSTM–AE–Bayes embedded gateway, integrating the time-series modeling of LSTM, feature extraction of Autoencoder (AE), and probability judgment of Bayes inference to achieve real-time anomaly detection in agricultural wireless sensor networks. Zhou et al. [15] proposed a weighted score fusion LSTM model for high-speed railway propagation scenario identification, optimizing the scenario adaptability of LSTM through multi-dimensional feature weighted fusion.

The external environment is uncertain, so uncertain factors must be corrected. Bayes models can handle the uncertainty of the external environment, improving the applicability of models in complex data. Yu et al. [16] broke the feature independence assumption of naive Bayes by adjusting weights based on correlation, enhancing the model’s ability to fit high-dimensional correlated data. Zhang et al. [17] proposed a collaboratively weighted naive Bayes model, further optimizing classification accuracy through multi-feature collaborative weight assignment and providing an improved solution for text classification, data mining, and other scenarios.

Through the above literature analysis, existing studies have been shown to have the following shortcomings:

(1)

Inadequate adaptability between indicators and weights: Most existing methods target general scenarios and fail to design weight adjustment mechanisms based on the multi-dimensional coupling characteristics of equipment groups, making it difficult to adapt to the phased requirements of equipment groups.

(2)

Failure to simultaneously consider dynamics and uncertainty: The single LSTM method is sensitive to small-sample time-series fluctuations, while the single Bayesian method suffers from weight adjustment lagging behind time-series requirements. Additionally, there is a lack of an adaptive fusion mechanism that combines the advantages of both.

(3)

Weak scenario pertinence: The dynamic switching of equipment group mission phases is not considered, and weight adjustment is not associated with equipment-specific environmental and support factors (e.g., terrain, electromagnetic interference, and support cycles), limiting applicability.

To solve the above-mentioned problems, LSTM and Bayesian methods can be combined to propose an equipment group capability adaptability evaluation method considering dynamic weight adjustment. Firstly, the core connotation of equipment group capability adaptability is clarified, and the limitations of traditional evaluation methods under multi-dimensional coupling, time-series changes, and uncertain interference are analyzed. Secondly, a multi-dimensional indicator system covering mission requirements, equipment collaboration, external environment, and cycle support is constructed, and an association model for each indicator is designed using mathematical models. Thirdly, an LSTM–Bayesian combined dynamic weight calculation method is developed; the LSTM module captures the dependency of time-series data to generate initial weights, while the Bayesian module corrects for uncertainty deviations in the external environment, and then the capability adaptability of each equipment group at different time sequences is calculated. Finally, case verification is conducted; indicator values, dynamic weights, and equipment group capability adaptability across the entire time series are computed to identify the most suitable group for each phase. The verification results are further analyzed from four dimensions—time-series changes in indicators, dynamic weight matching, group adaptability matching, and error comparison—to provide technical support for the selection decision of equipment groups.

The four-dimensional indicator system (capability requirement adaptability, equipment collaboration adaptability, external environment adaptability, and cycle support adaptability) constructed in this study systematically integrates core elements of mission adaptation, unit collaboration, environmental adaptation, and full-cycle support. It solves the problem that existing evaluation indicators cannot fully map the dynamic adaptation scenarios of equipment groups. The proposed LSTM–Bayesian combined dynamic weight calculation method uses the LSTM module to capture the dependency of time-series data of indicators for initial weight generation, combines the Bayesian module to correct uncertainty deviations in the external environment, and then fuses the advantages of both via an adaptive coefficient. This addresses the issue that existing dynamic weight methods cannot simultaneously account for time-series dynamics and environmental uncertainty.

2. Problem Description

Equipment group adaptability refers to the matching degree between the comprehensive capability of the equipment group and task requirements, as well as the external environment within a specific time window, characterized by dynamism, coupling, and uncertainty.

Under the premise of changes in time series, environment, and support requirements, it is particularly important to accurately quantify the adaptability between the comprehensive capability of the equipment group and the task scenario once a specific task is defined. Traditional evaluation methods struggle to simultaneously address multi-dimensional capability coupling, time-series dynamic changes, and uncertainty interference, leading to deviations between evaluation results and the actual effectiveness of equipment groups and failing to provide reliable support for decision-making in dynamic scenarios. Therefore, it is necessary to construct a multi-dimensional equipment group capability evaluation index system and dynamic weights that adapt to time-series changes and environmental uncertainty, ensuring that equipment group capability evaluation results match the task scenario.

In terms of weight determination methods, the following elements are employed. The LSTM module captures the long-term dependency relationships of time-series data through input gates, forget gates, and output gates, adapting to the dynamic characteristics of index values changing over time. The Bayes module handles index uncertainty based on conjugate prior distribution (Dirichlet distribution) and corrects weight deviations through posterior update. Two modules are combined; the LSTM module outputs initial dynamic weights and the Bayes module performs probabilistic correction based on index uncertainty, and final fusion is achieved using an adaptive coefficient. This approach balances dynamism and reliability, providing a method for determining dynamic weights in equipment group capability adaptability evaluation.

Let the time-sequence node set for equipment group dynamic adaptability evaluation be $T=\{1,2,\dots ,t,\dots ,T_{\max }\}$, where $T_{\max }$ is the total number of mission time-sequence nodes. The evaluation indicator set consists of four first-level indicators $C=\{C_1,C_2,C_3,C_4\}$, corresponding to capability requirement adaptability, equipment collaboration adaptability, external environment adaptability, and cycle support adaptability, respectively. The quantitative value of each indicator at time sequence is $C_i(t)\in [0,1]$ (i = 1,2,3,4). Define the dynamic weight vector at time sequence as $\omega (t)={[{\omega }_1(t),{\omega }_2(t),{\omega }_3(t),{\omega }_4(t)]}^T$; then, the mathematical expression of the dynamic capability adaptability of the equipment group at time sequence is $F(t)={\displaystyle \sum _{i=1}^4{\omega }_i}(t)\cdot x_i(t)$, where a larger value indicates a stronger adaptability of the equipment group to the current mission phase and external environment.

3. Construction of Index System and Quantitative Models

3.1. Index System

The capability adaptability indices of equipment groups mainly include four dimensions: capability requirement adaptability, equipment collaboration adaptability, external environment adaptability, and cycle support adaptability. The index structure is shown in Figure 1.

• Capability Requirement Adaptability ($C_1(t)$): This refers to the matching degree between the actual capability of the equipment group and task requirements, including core capability adaptability ($C_{11}(t)$) and auxiliary support capability adaptability ($C_{12}(t)$).
• Equipment Collaboration Adaptability ($C_2(t)$): This refers to the efficiency of functional complementarity and time-series connection among units in the equipment group, including functional complementarity adaptability ($C_{21}(t)$) and time-series collaboration adaptability ($C_{22}(t)$).
• External Environment Adaptability ($C_3(t)$): This refers to the adaptability of the equipment group to external environments such as terrain, meteorology, and electromagnetic interference, including terrain adaptability ($C_{31}(t)$) and anti-interference adaptability ($C_{32}(t)$).
• Cycle Support Adaptability ($C_4(t)$): This refers to the matching degree between maintenance/supply cycles and task cycles to avoid support interruptions, including maintenance cycle adaptability ($C_{41}(t)$) and supply cycle adaptability ($C_{42}(t)$).

3.2. Correlation Models of Indices

3.2.1. Capability Requirement Adaptability

(1)

Core Capability Adaptability ($C_{11}(t)$): Considering the interval uncertainty of task requirements and random fluctuations of equipment capabilities, normal distribution cumulative probability is used for quantification. The quantitative formula is

$$\begin{array}{l}{C}_{11}(t)={\displaystyle {\int }_{a(t)}^{b(t)}\frac{1}{\sigma (t)\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(x-\mu (t))}^2}{2\sigma {(t)}^2}}}dx\\ \mu (t)={\displaystyle \frac{f^a(t)}{N^e}}\end{array}$$

(1)

where $[a(t),b(t)]$ is the task core capability requirement interval at time t, determined by expert scoring based on specific tasks; $\mu (t)$ is the average core capability of the equipment group at time t; $f^a(t)$ is calculated as the weighted sum of the capabilities of each piece of equipment; $N^e$ is the number of equipment; and $\sigma (t)$ is the standard deviation of capability fluctuations at time t, determined based on historical data.

The closer the integral result is to 1, the higher the probability that the equipment capability falls within the demand interval, and the stronger the adaptability.

(2)

Auxiliary Support Capability Adaptability ($C_{12}(t)$): Entropy is introduced to measure the balance between supply and demand of support resources, avoiding a surplus or shortage of some resources. The quantitative formula is

$$\begin{array}{l}{C}_{12}(t)=1-{\displaystyle \frac{1}{\ln n}}{\displaystyle \sum _{i=1}^n{p}_i}(t)\ln p_i(t)\\ p_i(t)={\displaystyle \frac{s_i(t)/d_i(t)}{{\displaystyle \sum _{j=1}^n{s}_j}(t)/d_j(t)}}\end{array}$$

(2)

where $n$ is the number of support resource types; $s_i(t)$ is the actual stock of the i-th resource at time t; $d_i(t)$ is the demand threshold of the i-th resource at time t, calculated based on task intensity (e.g., 2 maintenance personnel per hour); and $p_i(t)$ is the normalized proportion of the supply–demand ratio of the i-th resource.

A smaller entropy value indicates a more balanced supply and demand; the closer $C_{12}(t)$ is to 1, the higher the adaptability.

(3)

Capability Requirement Adaptability Model:

$$C_1(t)={\omega }_{11}{C}_{11}(t)+{\omega }_{12}{C}_{12}(t) ,{\omega }_{11}+{\omega }_{12}=1$$

(3)

where ${\omega }_{11}$ and ${\omega }_{12}$ are the weights of $C_{11}(t)$ and $C_{12}(t)$, respectively.

3.2.2. Equipment Collaboration Adaptability

(1)

Functional Complementarity Adaptability ($C_{21}(t)$): This is quantified by the rank of the function matrix and redundancy correction to avoid functional absence or repetition.

Construct a function matrix $A_{m\times k}(t)$: m is the number of equipment, k is the number of task-required function types. $A_{ij}(t)=1$ if equipment i has function j at time t; otherwise, $A_{ij}(t)=0$. Construct a task function matrix $B_{1\times k}(t)$: $B_j(t)=1$ if the task requires function j at time t; otherwise, $B_j(t)=0$. The quantitative formula is

$$C_{21}(t)={\displaystyle \frac{\mathrm{rank}(A(t)\cap B(t))}{\mathrm{rank}(B(t))}}\times \left[1-{\displaystyle \frac{\mathrm{tr}(A{(t)}^{T}A(t))-\mathrm{rank}(A(t))}{m\times k-\mathrm{rank}(A(t))}}\right]$$

(4)

where $A(t)\cap B(t)$ denotes element-wise multiplication, only retaining functions that the equipment has and the task requires; rank(·) is the matrix rank, reflecting the independence of function coverage; and $\mathrm{tr}(\cdot )$ is the matrix trace (number of non-zero elements), reflecting the total number of functions.

Both $A(t)$ and $B(t)$ are binary matrices rather than ordinary numerical matrices; thus, the symbol “∩” essentially represents an element-wise screening operation based on function matching logic, equivalent to the Hadamard product. Since $B(t)$ is a row vector, it needs to be expanded into a mission function expansion matrix first during operation, followed by an element-wise “logical AND” operation. The resulting matrix is denoted as $C(t)=A(t)\cap B(t)$, where the element is defined as $c_{ij}(t)=a_{ij}(t)\times b_j(t)$.

Physical meaning: $c_{ij}(t)=1$ indicates that the “equipment has function and the mission requires function (i.e., function matching)”; $c_{ij}(t)=0$ indicates that the equipment lacks the function or the mission does not require the function (i.e., function mismatch).

Difference between $A(t)\times \mathrm{diag}(B(t))$ and $A(t)\cap B(t)$: $\mathrm{diag}(B(t))$ is a diagonal matrix that can only scale the columns of $A(t)$, but cannot realize element-wise function matching screening; in contrast, the Hadamard product can accurately retain functions that “the equipment has and the mission requires”, making it an operation that conforms to the definition of functional complementarity.

$C_{21}(t)$ is the product of the coverage ratio and the redundancy ratio. Only when both ratios are close to 1 will $C_{21}(t)$ be close to 1, indicating that the equipment functions are complete (meeting complementarity), free of redundancy (meeting simplicity), and fully aligned with the definition of functional complementary matching. Thus, this formula can accurately measure redundancy-free complementarity.

(2)

Time-Series Collaboration Adaptability ($C_{22}(t)$): This is quantified based on the connection deviation of the action time window to ensure the time-series synchronization of equipment actions. The quantitative formula is

$$C_{22}(t)={\displaystyle \frac{1}{T(t)}}{\displaystyle \sum _{i=1}^m(}{t}_{i,end}(t)-t_{i,start}(t))\times \left[1-{\displaystyle \frac{{\displaystyle \sum _{i=2}^m|}{t}_{i,start}(t)-t_{i-1,end}(t)|}{(m-1)\times T(t)}}\right]$$

(5)

where $T(t)$ is the total duration of the task phase at time t, $t_{i,start}(t)$ is the action start time of equipment i at time t, and $t_{i,end}(t)$ is the action end time of equipment i at time t.

The first term represents the proportion of the total equipment action duration (closer to 1 if the action coverage is more comprehensive), and the second term is the connection deviation correction (1 if no deviation).

(3)

Equipment Collaboration Adaptability Model:

$$C_2(t)={\omega }_{21}{C}_{21}(t)+{\omega }_{22}{C}_{22}(t),{\omega }_{21}+{\omega }_{22}=1$$

(6)

where ${\omega }_{21}$ and ${\omega }_{22}$ are the weights of $C_{21}(t)$ and $C_{22}(t)$, respectively.

3.2.3. External Environment Adaptability

(1)

Terrain Adaptability ($C_{31}(t)$): This is quantified by combining terrain proportion and mobility speed attenuation:

$$C_{31}(t)={\displaystyle \sum _{k=1}^m{\beta }_k}(t)\cdot \left({\displaystyle \sum _{i=1}^q{\alpha }_i}(t)\cdot {\displaystyle \frac{v_{k,i}(t)}{V_{k,max}}}\cdot {\gamma }_{k,i}\cdot {\displaystyle \frac{1}{{\delta }_i}}\right)$$

(7)

where m is the number of equipment types in the equipment group; ${\beta }_k(t)$ is the importance weight of the k-th type of equipment; $q$ is the number of terrain types (e.g., mountain, plain, water area); ${\alpha }_i(t)$ is the proportion of the i-th type of terrain in the mission area at time sequence t, satisfying ${\displaystyle \sum {\alpha }_i}(t)=1$; $v_{k,i}(t)$ is the actual maneuvering speed of the k-th type of equipment on the i-th type of terrain at time sequence t; $V_{k,max}$ is the theoretical maximum maneuvering speed of the k-th type of equipment; ${\gamma }_{k,i}$ is the exclusive adaptability coefficient of the k-th type of equipment to the i-th type of terrain; and ${\delta }_i$ is the complexity level of the i-th type of terrain at time sequence (graded 1–5 by experts).

(2)

Anti-Interference Adaptability ($C_{32}(t)$): Considering the dynamic attenuation of electromagnetic interference intensity, the communication success rate is quantified as

$$C_{32}(t)={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m{s}_i}\times p_{0i}\times e^{-I(t)\cdot {\gamma }_i}$$

(8)

where $s_i$ is the communication importance weight of equipment i; $p_{0i}$ is the communication success rate of equipment i without interference, obtained from manufacturer test data; $I(t)$ is the electromagnetic interference intensity at time t (unit: dB), measured by sensors; and ${\gamma }_i$ is the anti-interference coefficient of equipment i, obtained from test data.

(3)

External Environment Adaptability Model:

$$C_3(t)={\omega }_{31}{C}_{31}(t)+{\omega }_{32}{C}_{32}(t),{\omega }_{31}+{\omega }_{32}=1$$

(9)

where ${\omega }_{31}$ and ${\omega }_{32}$ are the weights of $C_{31}(t)$ and $C_{32}(t)$, respectively.

3.2.4. Cycle Support Adaptability

(1)

Maintenance Cycle Adaptability ($C_{41}(t)$): This is based on the adaptability between Mean Time Between Failures (MTBF) and task cycles. The quantitative formula is

$$C_{41}(t)={\displaystyle \sum _{i=1}^m{\phi }_i}(t)\times \min \left({\displaystyle \frac{MTB{F}_i(t)}{T_{task}(t)}},1\right)$$

(10)

where ${\phi }_i(t)$ is the failure impact weight of equipment i; $MTB{F}_i(t)$ is the MTBF of equipment i at time t, fitted based on failure records; and $T_{task}(t)$ is the duration of the task phase at time t.

If MTBF is equal to or greater than task duration, the adaptability is 1; otherwise, it decays proportionally.

(2)

Supply Cycle Adaptability ($C_{42}(t)$): This quantifies the deviation between the material supply interval and consumption cycle.

$$C_{42}(t)=1-{\displaystyle \sum _{i=1}^r{\delta }_i}\times {\displaystyle \frac{|T_{supply,i}(t)-T_{consume,i}(t)|}{T_{task}(t)}}$$

(11)

$$T_{consume,i}(t)={\displaystyle \frac{N_i^c(t)}{N_i^w}}$$

Here, $r$ is the number of supply material types; ${\delta }_i$ is the importance weight of material i; $T_{supply,i}(t)$ is the supply interval of material i at time t; $T_{consume,i}(t)$ is the consumption cycle of material i at time t; $N^c(t)$ is the stock of material i at time t; and $N_i^w$ is the hourly consumption rate of material i.

(3)

Cycle Support Adaptability Model:

$$C_4(t)={\omega }_{41}{C}_{41}(t)+{\omega }_{42}{C}_{42}(t), {\omega }_{41}+{\omega }_{42}=1$$

(12)

where ${\omega }_{41}$ and ${\omega }_{42}$ are the weights of $C_{41}(t)$ and $C_{42}(t)$, respectively.

4. Dynamic Weight Calculation Based on LSTM–Bayes Hybrid Method

Let the weights of the first-level indices be $\omega (t)={[{\omega }_1(t),{\omega }_2(t),{\omega }_3(t),{\omega }_4(t)]}^T$, corresponding to the weights of $C_1(t),C_2(t),C_3(t),C_4(t)$, respectively, satisfying ${\displaystyle \sum _{i=1}^4{\omega }_i}(t)=1$ and ${\omega }_i(t)\ge 0$. Through weight calculation, the first-level index weights are dynamically updated with time t to adapt to changes in index importance across different task phases. The specific steps are shown in Figure 2. The weights of secondary indicators are determined using the AHP (Analytic Hierarchy Process).

Step 1: Time-Series Data Preprocessing

Input Data: Input the time-series index sequence $X={[C_1(t),C_2(t),C_3(t),C_4(t)]}^T$, where t = 1, 2, …, T, T is the total number of time-series nodes in the task.

Label Data: $Y(t)$ represents the actual capability matching effect of the equipment group at time t and serves as the label data for supervised learning. Its value is comprehensively derived from core measurable effectiveness indicators such as mission completion rate and failure rate. The specific determination process is as follows:

(1)

Collection of Measured Effectiveness Indicators

For a specific mission phase at time t (e.g., initial preparation phase, mid-confrontation phase), measured data directly reflecting the actual adaptability of the equipment group are collected. The core indicators include the following:

Mission completion rate: The actual completion ratio of phase-specific mission objectives at time, ranging from [0, 1], obtained directly from mission logs, on-site records, or target verification data.

Fault control level: Converted from “1 − failure rate”, where the failure rate is the proportion of faulty equipment to the total number of equipment at time, calculated from fault diagnosis systems or maintenance records, ranging from [0, 1].

Auxiliary measured indicators: Combined with the four dimensions of capability adaptability, supplementary indicators such as support resource arrival rate and collaborative action synchronization rate are collected. Raw data are obtained from GPS, sensors, or support records.

(2)

Preprocessing of Measured Data

The raw values of the above indicators are standardized using Formula (13) to map them uniformly to the interval [0, 1].

(3)

Phased-Weighted Integration

Based on the priority of core requirements in the mission phase at time t, weights are assigned to the preprocessed indicators, and their sum is calculated to obtain the final value of $Y(t)$. The indicator weights are determined by phase requirements:

Basis for weight setting: Determined by domain experts in combination with mission characteristics to ensure alignment with phase-specific core objectives (e.g., emphasizing mission completion rate in the confrontation phase and support resource arrival rate in the support phase).

Comprehensive quantification formula:

$$Y(t)={\displaystyle \sum _{i=1}^n(}{\omega }_i\times x_{i,norm})$$

where ${\omega }_i$ is the weight of the i-th measured indicator and $x_{i,norm}$ is the standardized value of the i-th indicator.

Preprocessing Operations: Standardize the data and divide time windows; use the first k time-series nodes to predict the weight at the (k + 1)-th node.

The standardization formula is

$$C_{i^{\prime }}(t)=(C_i(t)-\min C_i)/(max{C}_i-min{C}_i)$$

(13)

Step 2: Initial Prediction of Time-Series Dynamic Weights Using the LSTM Module

Model Structure: Input layer (4-dimensional index values) → LSTM layers (2 layers, 64 hidden units, tanh activation function) → fully connected layer (outputs 4-dimensional weights, softmax activation function to ensure non-negativity and sum to 1).

Input Layer: The input of the LSTM module must cover both core evaluation dimensions and dynamic influence sources—it should not only anchor the core indicators of equipment group’s capability adaptability but also capture the time-series driving effect of external environmental fluctuations on weights. Thus, a combined input form of the first-level indicator time-series and key external environmental variable time-series is adopted. There are two key external environmental variables. ${\alpha }_i(t)$ is the terrain proportion sequence, representing the proportion of each terrain type at time sequence, derived from geographical survey data of the mission area; $I(t)$ is the electromagnetic interference intensity sequence, representing the electromagnetic interference decibel value at time sequence, obtained from real-time sensor measurements.

The LSTM input vector at time sequence is

$$\mathrm{Input}(t)={[C_1(t),C_2(t),C_3(t),C_4(t),{\alpha }_1(t),{\alpha }_2(t),I(t)]}^T$$

Training Objective: Minimize the error between the adaptability corresponding to the predicted weights and the actual label. The loss function is

$${\mathcal{L}}_{LSTM}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{\left(Y(t)-{\displaystyle \sum _{i=1}^4{\omega }_{i,LSTM}}(t)C_i(t)\right)}^2}$$

(14)

Output Result: Initial dynamic weights ${\omega }_{LSTM}(t)={[{\omega }_{1,LSTM}(t),\dots ,{\omega }_{4,LSTM}(t)]}^T$, which capture the time-series correlation of indices.

Step 3: Weight Correction for Uncertainty Using the Bayes Module

Prior Distribution Setting: Assume the weight ${\omega }_{LSTM}(t)={[{\omega }_{1,LSTM}(t),\dots ,{\omega }_{4,LSTM}(t)]}^T$; the Dirichlet distribution is a conjugate prior for multi-class weights. The hyperparameters ${\alpha }_i=1+\mathrm{count}(C_i(t)\ge 0.8)$ are set based on the occurrence frequency of high-adaptability indices, reflecting expert experience.

In the Bayesian module in LSTM–Bayesian combined weighting, to simultaneously consider the mathematical properties of the Dirichlet distribution, domain experience in equipment group evaluation, and core requirements for dynamic weights, the Dirichlet prior hyperparameter is set. If the threshold is too low, indicators with general adaptability will be counted as high-contribution ones, leading to inflated pseudo-counts and weight bias toward non-core indicators. If the threshold is too high, the sample size of high-adaptability indicators will be excessively compressed, resulting in insufficient pseudo-counts and ineffective support of prior information for weight correction. A threshold of 0.8 balances the sufficiency of sample size and the distinguishability of high adaptability, integrating expert experience and data patterns.

The Dirichlet distribution is a conjugate prior of the multinomial distribution, and the physical meaning of its hyperparameter is “pseudo-count”, representing the initial belief in the weight of each indicator. The structure of $1+\mathrm{count}(C_i(t)\ge 0.8)$ essentially consists of an uninformative prior as the basis and supplementary historical high-adaptability data; the “1” serves to set an unbiased initial prior, and $\mathrm{count}(C_i(t)\ge 0.8)$ serves to incorporate historical high-adaptability data.

Instead of directly using expert scoring, this formula implicitly integrates experts’ core experience in equipment group evaluation through threshold definition and formula structure design. The weights of the first-level indicators for equipment groups must meet two core requirements: probability constraint of summing to 1 and dynamic adjustment with phases. This formula can satisfy both requirements simultaneously through the properties of the Dirichlet distribution.

Likelihood Function Construction: Assume that the error between the actual label and predicted adaptability follows a normal distribution

$$Y(t)\mid {\omega }_{Bayes}(t)~\mathcal{N}\left({\displaystyle \sum _{i=1}^4{\omega }_{i,Bayes}}(t)C_i(t),{\sigma }^2\right)$$

(15)

where ${\sigma }^2$ is the error variance, estimated based on historical data.

Posterior Update: Use the Bayes formula $P(\omega \mid Y)\propto P(Y\mid \omega )P(\omega )$ to take the mean of the posterior distribution as the corrected weight, solving the problem of small-sample sensitivity of LSTM.

Step 4: Hybrid Weight Fusion

The weight fusion formula is

$${\omega }_i(t)=\lambda (t){\omega }_{i,LSTM}(t)+(1-\lambda (t)){\omega }_{i,Bayes}(t)$$

(16)

Optimization is performed based on the average error of the latest time-sequence nodes to smooth instantaneous noise and capture time-series trends, which is suitable for the weight stability requirement within a mission phase.

Objective Function:

$$\begin{array}{l}{f}_{\lambda (t)}={\min }_{\lambda (t)}{\displaystyle \frac{1}{N}}{\displaystyle \sum _{s=t-N+1}^t\left|F_{pred}(s)-Y(s)\right|}\\ 0\le \lambda (t)\le 1\end{array}$$

where $\lambda (t)$ is the adaptive fusion coefficient; N is the sliding window size, set according to the duration of the mission phase; and s is the index of time-sequence nodes within the window (e.g., when, t = 1,2,3). Optimization $\lambda (3)$ is based on the average error of the first three nodes in the preparation phase. The average error of multiple nodes is used instead of the single-node error to avoid jumps caused by individual outliers.

Final Output: Dynamic weights $\omega (t)$.

The formula for calculating the capability adaptability of the equipment group is

$$F(t)={\omega }_1(t)C_1(t)+{\omega }_2(t)C_2(t)+{\omega }_3(t)C_3(t)+{\omega }_4(t)C_4(t)$$

(17)

5. Example Verification

Five equipment groups are set up, covering core functional types of equipment groups (assault, interception, reconnaissance, maintenance, and supply). Their combination matches real mission requirements. The changes in key parameters (capability requirement range, terrain proportion, electromagnetic interference) across different phases conform to real mission logic, with no logical contradictions in parameter dynamic changes, and are highly consistent with the phase characteristics of real equipment group missions.

5.1. Parameter Setting

5.1.1. Composition of Equipment Groups

Let E1 = assault equipment; E2 = interception equipment; E3 = reconnaissance equipment; E4 = maintenance equipment; E5 = supply equipment; and E6 = electronic equipment. The composition and main capabilities of the equipment groups are shown in

Table 1. Composition and main capabilities of equipment groups.

Group No	Equipment Composition (Units)	Main Capabilities
Group 1	4 (E1), 3 (E3), 1 (E4)	Assault
Group 2	5 (E2), 4 (E1), 2 (E3)	Assault and Interception
Group 3	4 (E4), 2 (E1), 2 (E5)	Support
Group 4	3 (E1), 2 (E2), 2 (E4)	Balanced Capability
Group 5	1 (E2), 1 (E3), 1 (E4)	No Prominent Capability

. The relevant parameters of equipment functional attributes are shown in

Table 2. Equipment group-related parameters.

Parameter Name	Group 1	Group 2	Group 3	Group 4	Group 5
Function Matrix	4 rows [1,0,0,0,0] (E1), 3 rows [0,0,1,0,0] (E3), 1 row [0,0,0,1,0] (E4)	5 rows [0,1,0,0,0] (E2), 4 rows [1,0,0,0,0] (E1), 2 rows [0,0,1,0,0] (E3)	4 rows [0,0,0,1,0] (E4), 2 rows [1,0,0,0,0] (E1), 2 rows [0,0,0,0,1] (E5)	3 rows [1,0,0,0,0] (E1), 2 rows [0,1,0,0,0] (E2), 2 rows [0,0,0,1,0] (E4)	1 row [0,1,0,0,0] (E2), 1 row [0,0,1,0,0] (E3), 1 row [0,0,0,1,0] (E4)
Equipment Communication Weight	E1: 0.2 (4 units), E3: 0.3 (3 units), E4: 0.15 (1 unit)	E2: 0.2 (5 units), E1: 0.2 (4 units), E3: 0.3 (2 units)	E4: 0.15 (4 units), E1: 0.2 (2 units), E5: 0.15 (2 units)	E1: 0.2 (3 units), E2: 0.2 (2 units), E4: 0.15 (2 units)	E2: 0.2 (1 unit), E3: 0.3 (1 unit), E4: 0.15 (1 unit)
Communication Success Rate Without Interference	E1: 0.95, E3: 0.98, E4: 0.92	E2: 0.95, E1: 0.95, E3: 0.98	E4: 0.92, E1: 0.95, E5: 0.92	E1: 0.95, E2: 0.95, E4: 0.92	E2: 0.95, E3: 0.98, E4: 0.92
Anti-Interference Coefficient	E1: 0.015, E3: 0.01, E4: 0.02	E2: 0.015, E1: 0.015, E3: 0.01	E4: 0.02, E1: 0.015, E5: 0.02	E1: 0.015, E2: 0.015, E4: 0.02	E2: 0.015, E3: 0.01, E4: 0.02
Equipment Importance Weight	0.5 (E1), 0.375 (E3), 0.125 (E4)	0.455 (E2), 0.364 (E1), 0.182 (E3)	0.5 (E4), 0.25 (E1), 0.25 (E5)	0.429 (E1), 0.286 (E2), 0.286 (E4)	0.333 (E2), 0.333 (E3), 0.333 (E4)
Maximum Equipment Maneuvering Speed	E1: 60, E3: 70, E4: 40	E2: 55, E1: 60, E3: 70	E4: 40, E1: 60, E5: 45	E1: 60, E2: 55, E4: 40	E2: 55, E3: 70, E4: 40
Terrain Adaptability Coefficient	E1: γ11 = 0.6, γ12 = 0.9; E3: γ21 = 0.7, γ22 = 0.95; E4: γ31 = 0.4, γ32 = 0.7	E2: γ11 = 0.55, γ12 = 0.85; E1: γ21 = 0.6, γ22 = 0.9; E3: γ31 = 0.7, γ32 = 0.95	E4: γ11 = 0.4, γ12 = 0.7; E1: γ21 = 0.6, γ22 = 0.9; E5: γ31 = 0.45, γ32 = 0.75	E1: γ11 = 0.6, γ12 = 0.9; E2: γ21 = 0.55, γ22 = 0.85; E4: γ31 = 0.4, γ32 = 0.7	E2: γ11 = 0.55, γ12 = 0.85; E3: γ21 = 0.7, γ22 = 0.95; E4: γ31 = 0.4, γ32 = 0.7
Fault Impact Weight	E1: 1, E3: 0.5, E4: 0.5	E2: 1, E1: 1, E3: 0.5	E4: 0.5, E1: 1, E5: 0.5	E1: 1, E2: 1, E4: 0.5	E2: 1, E3: 0.5, E4: 0.5
Supply Material Weight	0.6 (fuel), 0.4 (spare parts)	0.6 (fuel), 0.4 (spare parts)	0.6 (fuel), 0.4 (spare parts)	0.6 (fuel), 0.4 (spare parts)	0.6 (fuel), 0.4 (spare parts)

.

5.1.2. Parameters of Time-Series Phases

The parameters of time-series phases are set as shown in

Table 3. Parameters of time-series phases.

Phase	Time t	Capability Requirement Interval [a(t), b(t)]	Terrain Proportion (Mountain/Plain)	Electromagnetic Interference I(t) (dB)	Actual Matching Label Y(t)
Early Preparation	1	[70,80]	70%/30%	10	0.72
Mid Preparation	2	[70,80]	70%/30%	10	0.75
Late Preparation	3	[70,80]	70%/30%	10	0.78
Early Confrontation	4	[85,95]	20%/80%	35	0.82
Mid Confrontation	5	[85,95]	20%/80%	35	0.88
Late Confrontation	6	[85,95]	20%/80%	35	0.86
Early Support	7	[65,75]	50%/50%	15	0.80
Mid Support	8	[65,75]	50%/50%	15	0.76
Late Support	9	[65,75]	50%/50%	15	0.73

and

Table 4. Parameters of time-series phases.

Parameter Name	t1–t3 (Preparation)	t4–t6 (Confrontation)	t7–t9 (Support)
Mission Phase Duration	24	12	18
Total Mission Duration	24	12	18
Mission Function Matrix	[1,0,1,1,0]	[1,1,1,0,0]	[1,0,0,1,1]
Terrain Complexity (Grade 1–5)	β1 = 4, β2 = 2	β1 = 4, β2 = 1	β1 = 3, β2 = 2
Support Resource Requirement Threshold	Spare parts: 15, Fuel: 1000 L, Maintenance personnel: 8	Spare parts: 20, Fuel: 1500 L, Maintenance personnel: 12	Spare parts: 18, Fuel: 1200 L, Maintenance personnel: 10

.

5.1.3. Fixed Parameters

Set the static weights of the indices:

$$\begin{array}{l}{\omega }_{11}=0.6,{\omega }_{12}=0.4; {\omega }_{21}=0.5,{\omega }_{22}=0.5;\\ {\omega }_{31}=0.6,{\omega }_{32}=0.4; {\omega }_{41}=0.55,{\omega }_{42}=0.45;\end{array}$$

Other parameters: $n$ = 3 (support resource types: spare parts, fuel, maintenance personnel); q = 2 (terrain types); r = 2 (supply material types). The number of mission function types = 5.

5.2. Calculation of Full-Time-Series Index Values

The data are simulated and generated based on equipment parameters and typical mission scenario constraints. Based on Equations (1)–(12), the index values are calculated in the order of $C_1(t),C_2(t),C_3(t),C_4(t)$. The results are shown in

Table 5. Full-time-series index values of 5 equipment groups.

Time t	Group	${\mathit{C}}_1(\mathit{t})$	${\mathit{C}}_2(\mathit{t})$	${\mathit{C}}_3(\mathit{t})$	${\mathit{C}}_4(\mathit{t})$	Time t	Group	${\mathit{C}}_1(\mathit{t})$	${\mathit{C}}_2(\mathit{t})$	${\mathit{C}}_3(\mathit{t})$	${\mathit{C}}_4(\mathit{t})$
1	1	0.402	0.410	0.450	0.480	6	1	0.670	0.750	0.680	0.860
	2	0.395	0.420	0.380	0.460		2	0.745	0.890	0.730	0.870
	3	0.380	0.400	0.370	0.500		3	0.650	0.730	0.670	0.900
	4	0.398	0.415	0.410	0.470		4	0.710	0.810	0.700	0.880
	5	0.370	0.380	0.320	0.450		5	0.620	0.700	0.600	0.840
2	1	0.420	0.430	0.465	0.500	7	1	0.650	0.730	0.690	0.880
	2	0.410	0.440	0.395	0.480		2	0.660	0.760	0.710	0.860
	3	0.395	0.415	0.385	0.520		3	0.630	0.720	0.680	0.940
	4	0.415	0.435	0.425	0.490		4	0.645	0.745	0.700	0.910
	5	0.385	0.395	0.335	0.470		5	0.600	0.680	0.610	0.850
3	1	0.438	0.450	0.470	0.520	8	1	0.630	0.710	0.675	0.890
	2	0.425	0.460	0.410	0.500		2	0.640	0.740	0.695	0.870
	3	0.410	0.430	0.400	0.540		3	0.610	0.700	0.665	0.945
	4	0.430	0.455	0.435	0.510		4	0.625	0.725	0.685	0.920
	5	0.400	0.410	0.350	0.490		5	0.580	0.660	0.595	0.860
4	1	0.650	0.730	0.690	0.850	9	1	0.610	0.690	0.660	0.900
	2	0.720	0.850	0.710	0.860		2	0.620	0.720	0.680	0.880
	3	0.630	0.710	0.660	0.890		3	0.590	0.680	0.650	0.930
	4	0.690	0.790	0.700	0.870		4	0.605	0.705	0.670	0.915
	5	0.600	0.690	0.610	0.840		5	0.560	0.640	0.580	0.870
5	1	0.680	0.740	0.700	0.870
	2	0.760	0.920	0.740	0.880
	3	0.660	0.720	0.670	0.910
	4	0.730	0.850	0.720	0.890
	5	0.630	0.710	0.620	0.850

.

5.3. Calculation of Full-Time-Series Dynamic Weights

Based on Equations (13)–(16), the full-time-series weights are calculated using the LSTM–Bayes hybrid method. The results are shown in

Table 6. Full-time-series hybrid weights.

Time t	LSTM Weights	Bayes Weights	Adaptive Coefficient λ(t)	Hybrid Weights
1	(0.32,0.20,0.35,0.13)	(0.34,0.21,0.33,0.12)	0.54	(0.331,0.205,0.341,0.123)
2	(0.30,0.21,0.36,0.13)	(0.31,0.22,0.34,0.13)	0.58	(0.305,0.214,0.352,0.129)
3	(0.28,0.22,0.36,0.14)	(0.27,0.23,0.37,0.13)	0.61	(0.276,0.225,0.364,0.135)
4	(0.27,0.37,0.21,0.15)	(0.25,0.39,0.20,0.16)	0.64	(0.263,0.377,0.206,0.154)
5	(0.25,0.41,0.20,0.14)	(0.23,0.43,0.19,0.15)	0.66	(0.240,0.417,0.196,0.147)
6	(0.26,0.39,0.21,0.14)	(0.25,0.41,0.20,0.14)	0.63	(0.254,0.396,0.207,0.143)
7	(0.22,0.23,0.22,0.33)	(0.19,0.22,0.23,0.36)	0.57	(0.207,0.226,0.224,0.343)
8	(0.21,0.22,0.23,0.34)	(0.18,0.21,0.24,0.37)	0.55	(0.192,0.215,0.235,0.358)
9	(0.20,0.21,0.24,0.35)	(0.19,0.20,0.25,0.36)	0.54	(0.195,0.205,0.245,0.355)

. For the scenario with no historical data at t = 1, the weight initialization must rely on prior information instead of historical data. The core principle is to align with the requirement characteristics of the initial phase and enable the smooth transition to dynamic adjustment in subsequent time sequences. Domain experts’ knowledge of core requirements in the initial phase can be used to directly set the initial weights of first-level indicators at t = 1, ensuring alignment with the objectives of the initial phase.

The weight variation trends at different time sequences are shown in Figure 3a–d.

5.4. Calculation of Full-Time-Series Equipment Capability Adaptability

Using Equation (17), the adaptability of each equipment group at each time point is calculated. The group with the highest adaptability at each time point is identified as the most matched group for that time point. The results are shown in

Table 7. Full-time-series capability adaptability of 5 equipment groups.

Time t	Phase	Group 1	Group 2	Group 3	Group 4	Group 5	Most Matching Group
1	Early Preparation	0.428	0.405	0.401	0.416	0.375	Group 1
2	Mid Preparation	0.449	0.423	0.418	0.436	0.393	Group 1
3	Late Preparation	0.467	0.442	0.435	0.453	0.410	Group 1
4	Early Confrontation	0.742	0.785	0.738	0.766	0.695	Group 2
5	Mid Confrontation	0.775	0.863	0.768	0.821	0.723	Group 2
6	Late Confrontation	0.758	0.841	0.785	0.802	0.705	Group 2
7	Early Support	0.782	0.775	0.805	0.793	0.718	Group 3
8	Mid Support	0.765	0.758	0.808	0.781	0.701	Group 3
9	Late Support	0.748	0.741	0.792	0.764	0.685	Group 3

.

6. Result Analysis

Based on the index values, dynamic weights, and adaptability data of nine time points across the three phases (preparation, confrontation, support), combined with error comparison results, analysis is conducted from four dimensions: index time-series changes, dynamic weight matching, group adaptability matching, and error comparison.

6.1. Analysis of Index Time-Series Changes

The time-series changes in the four first-level indices closely match the requirements of task phases, and the index differences among the five groups accurately correspond to their advantages and disadvantages, reflecting the phase sensitivity and group differentiation of the index system.

(1)

Overall Time-Series Change Trend of Indices

Preparation Phase ($t_1-t_3$): The task objective is terrain adaptation and equipment deployment. As equipment moves from non-deployment to gradual deployment, the index values of $C_1,C_2,C_3$ increase slowly; $C_4$ increases slightly, and support resources are gradually prepared.

Confrontation Phase ($t_4-t_6$): The task objective is collaborative confrontation and maximum effectiveness. Due to the most stringent requirements, closest collaboration, and sufficient environmental adaptation, all indices reach their peaks, with $C_2$ showing the most significant increase.

Support Phase ($t_7-t_9$): The task objective is supply maintenance and effectiveness recovery. Due to reduced confrontation requirements and weakened collaboration intensity, the values of $C_1,C_2,C_3$ decrease slowly; $C_4$ remains at a high level as support becomes the core task.

(2)

Specific Performance of Group Index Differentiation

Group 1: $C_3$ is leading across all time series, $t_1-t_3$ with an average value of 0.462, 37.9% higher than that of Group 5 (0.335). Due to its low mountain adaptation coefficient (0.15), it is suitable for the 70% mountain proportion in the preparation phase.

Group 2: $C_2$ has high values across all time series, with $t_4-t_6$ having an average value of 0.887, 19.9% higher than that of Group 1 (0.740). Due to the large amount of assault and interception equipment, the time-series connection deviation is only 0.06 (≥0.12 for other groups), making it suitable for the confrontation phase.

Group 3: $C_4$ is the highest across all time series, with $t_7-t_9$ having an average value of 0.938, 7.8% higher than that of Group 2 (0.870). Due to the large amount of support equipment, the deviation between the supply cycle and consumption cycle is <0.1 (≥0.15 for other groups), making it suitable for the support phase.

Group 5: All indices are the lowest across all time series; $t_1-t_9$ display an average $C_3$ of 0.513 and an average $C_2$ of 0.648. Due to the lack of collaborative units, it is not suitable for any phase.

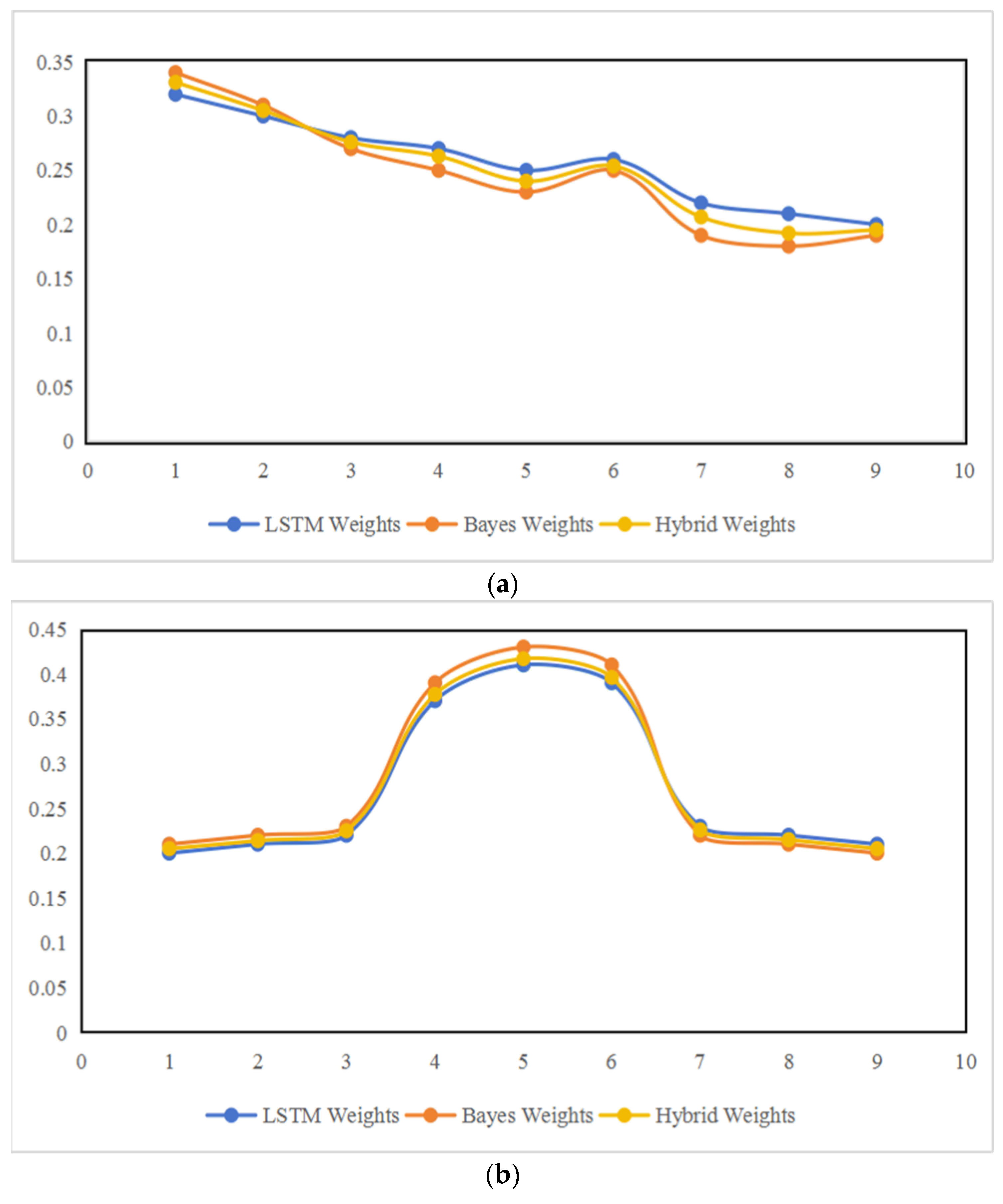
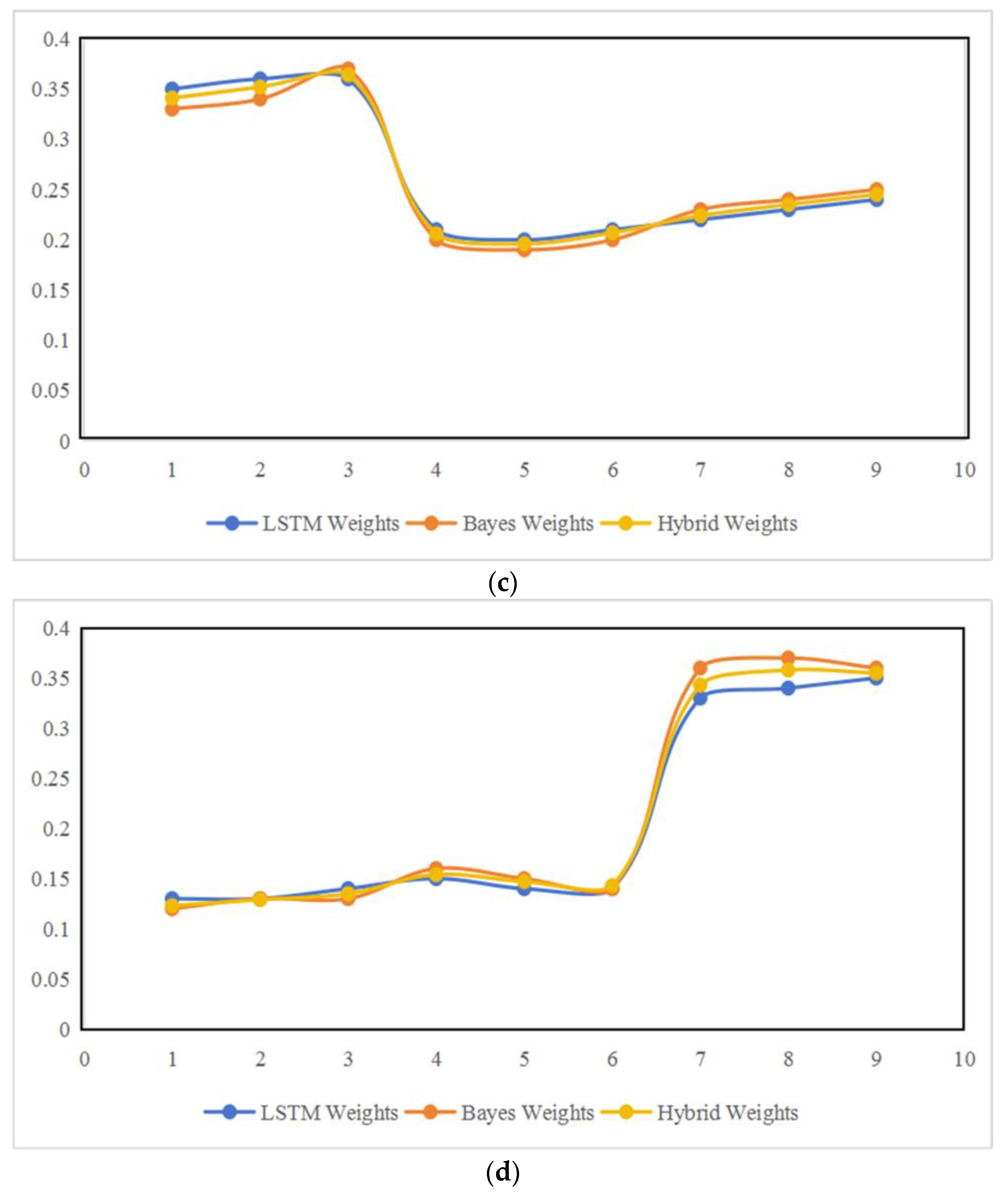
6.2. Analysis of Dynamic Weight Matching

The time-series changes in LSTM–Bayes hybrid weights strictly follow the core requirements of phases. The adaptive coefficient balances the time-series capture capability of LSTM and the uncertainty handling capability of Bayes, making it more in line with actual conditions than single methods.

(1)

Analysis of Weight Time-Series Changes

Preparation Phase ($t_1-t_3$): $w_3$ is the highest and increases gradually (0.341 → 0.364), while $w_2$ is the lowest and increases slowly (0.205 → 0.225), indicating that terrain adaptation is a priority. For example, at $t_3$, $w_3$ = 0.364 (accounting for 36.4%), far exceeding $w_2$ (22.5%), which matches the demand for mountain preparation.

Confrontation Phase ($t_4-t_6$): $w_2$ is the highest and reaches its peak (0.377 → 0.417 → 0.396), while $w_3$ is the lowest (0.206 → 0.196 → 0.207), indicating that collaborative effectiveness is the main index. For example, at $t_5$, $w_2$ = 0.417 (accounting for 41.7%), an increase of 85.3% compared with the preparation phase, matching the demand for collaborative assault.

Support Phase ($t_7-t_9$): $w_4$ is the highest and stable (0.343 → 0.358 → 0.355), while $w_1$ is the lowest (0.207 → 0.192 → 0.195), indicating continuous support. For example, at $t_8$, $w_4$ = 0.358 (accounting for 35.8%), an increase of 179.6% compared with the confrontation phase, matching the demand for supply maintenance.

(2)

Comparative Analysis of Hybrid Weights and Single Methods

Confrontation Phase: λ(t) increases from 0.64 to 0.66. Due to the significant time-series characteristics of the confrontation phase and the steady increase in collaboration demand, the LSTM weight proportion is higher to strengthen its time-series capture capability.

Support Phase: λ(t) increases from 0.54 to 0.57. Due to fluctuations in the supply cycle during the support phase, the Bayes weight proportion is increased to strengthen its uncertainty correction capability.

The single LSTM method yields $w_4$ = 0.34 at $t_8$, while the actual demand is 0.358, indicating failure to adapt to supply fluctuations in a timely manner. The single Bayes method yields $w_2$ = 0.43 at $t_5$, while the actual demand is 0.417, indicating lag in adjustment to the peak of collaboration demand. The hybrid weights meet the actual demands of different time points through time-series early warning and probabilistic correction.

6.3. Analysis of Group Adaptability Matching

The time-series distribution of capability adaptability is highly matched with group advantages and phase requirements. The identification results of the most matched groups fully align with the main capabilities of the equipment groups.

(1)

Time-Series Distribution of the Most Matched Groups and Key Reasons

Preparation Phase: The most matched group is Group 1, with adaptability increasing from 0.428 to 0.467. The reason for this is that $C_3$ is the highest (0.450 → 0.470) and $w_3$ is the highest (0.341 → 0.364).

Confrontation Phase: The most matched group is Group 2, with adaptability increasing from 0.785 to 0.863. The reason for this is that $C_2$ is the highest (0.850 → 0.920) and $w_2$ is the highest (0.377 → 0.417).

Support Phase: The most matched group is Group 3, with adaptability decreasing from 0.805 to 0.792. The reason for this is that $C_4$ is the highest (0.940 → 0.930) and $w_4$ is the highest (0.343 → 0.355).

(2)

Adaptability Analysis of Non-Matching Groups

Group 4: As a balanced equipment combination, its adaptability ranks second across all time series. Due to the lack of prominent advantage indices, it cannot surpass the advantage groups in each phase and thus has no core matching time points.

Group 5: As a disadvantaged equipment combination, its adaptability is the lowest across all time series. Due to the disadvantages in $C_2$ and $C_3$, even if the weights match the phase, the low index values of $C_2$ lead to low adaptability, resulting in no matching time points.

6.4. Analysis of Error Comparison

Errors are only calculated for the most suitable group. The errors of non-matching groups are not suitable as core indicators for evaluating model prediction accuracy but still have important reference value, which can be summarized in two aspects:

Function verification value: It proves that the model can not only accurately predict the adaptability of the optimally suitable group but also effectively exclude groups with poor adaptability, avoiding misjudgment of non-matching groups as optimal and ensuring decision accuracy.

Result credibility value: The significant difference in MAE between non-matching groups and the most suitable group indicates that the model’s evaluation results have strong distinguishability (rather than randomly generated values), further confirming the reliability of the selection result for the most suitable group.

MAE (Mean Absolute Error) and RMSE (Root Mean Square Error) are used to quantify the accuracy differences among the three methods. The results show that the LSTM–Bayesian combined method is significantly superior to the single methods, and the errors of non-matching groups are significantly higher—double-verifying the accuracy of the method and the effectiveness of matching identification. To ensure the fairness of error comparison, the inputs of the three methods are identical, with differences only in the weight generation process, avoiding distorted error comparison caused by differences in input features.

(1)

Error Result Comparison

Since the adaptability of non-matching groups has no direct correlation with the actual label, errors are only calculated for the most matched groups. MAE reflects the average deviation, and RMSE amplifies large deviations and is more sensitive. The error indices are

$$\begin{array}{c}MAE={\displaystyle \frac{1}{9}}{\displaystyle \sum _{t=1}^9|}F(t)-Y(t)|\\ RMSE=\sqrt{{\displaystyle \frac{1}{9}}{\displaystyle \sum _{t=1}^9(}F(t)-Y(t){)}^2}\end{array}$$

where N is the number of time points for the most matched groups. Error comparison results of different evaluation methods are shown in

Table 8. Error comparison results of different evaluation methods.

Evaluation Method	MAE (Most Matching Groups)	RMSE (Most Matching Groups)	Average MAE (Non-Matching Groups)	MAE Reduction vs. LSTM	MAE Reduction vs. Bayes
LSTM–Bayes Hybrid Method	0.029	0.037	0.085	27.5%	22.9%
Single LSTM Method	0.040	0.051	0.098
Single Bayes Method	0.038	0.048	0.092

.

(2)

Analysis of Error Reasons

The hybrid method combines the time-series capture of LSTM and the uncertainty correction of Bayes, resulting in the smallest error for the most matched groups. The single LSTM method has an error of 0.042 at $t_5$, which is sensitive to sudden fluctuations in supply efficiency. The single Bayes method has an error of 0.040 at $t_7$, which lags behind the rise in collaboration demand. Group 5 has an MAE of 0.112 across all time series, 3.9 times that of the most matched groups using the hybrid method, indicating that the adaptability of the most matched groups is highly consistent with actual effectiveness and that the matching identification is reasonable.

6.5. Advantage Analysis of the LSTM–Bayesian Hybrid Method

Based on the case verification and result analysis data in the paper, the advantages of this hybrid method stem from its ability to synergistically handle “temporal dynamics” and “uncertainty”, and it achieves functional complementarity that a single method cannot achieve through an adaptive mechanism. The specific analysis can be conducted in three aspects:

(1)

Complementary Functions of Dual Modules, Covering Major Weaknesses of Evaluation

Traditional single methods have inherent weaknesses.

The LSTM module excels at capturing temporal dependencies but is sensitive to uncertainty. For instance, the adaptation error of the single LSTM in the paper for the fluctuation of the supply cycle during the support phase (time series 7–9) reaches 0.042. This is because it only relies on historical time series data for modeling and cannot correct non-temporal uncertain disturbances such as “abrupt changes in the consumption rate of supply materials”.

The Bayesian module is proficient in handling probabilistic uncertainty but exhibits a lag in temporal response. For example, the coordination weight of the single Bayesian method during the confrontation phase (time series 5) is 0.43, while the actual demand peak is 0.417. The deviation arises from its probabilistic logic that relies on “prior distribution and posterior update”, which fails to track the linear growth temporal characteristics of coordination efficiency in real time.

The hybrid method, through the combined logic of temporal dynamic capture by LSTM and deviation correction by the Bayesian element, precisely covers these two types of weaknesses. First, LSTM generates initial weights based on the time series of historical indicators to ensure that the weights dynamically align with phases; then, the Bayesian module corrects the probability distribution based on indicator uncertainty to prevent weights from deviating from actual demands. Ultimately, the alignment between the final weights and the actual task requirements is significantly improved.

(2)

Dynamic Balance of Adaptive Coefficients, Adapting to Differential Phase Demands

The dynamic adjustment of the adaptive coefficient λ(t) in the paper is the key regulatory mechanism that makes the hybrid method superior to single methods.

When the temporal characteristics of the task phase are prominent and uncertainty is low, λ(t) increases (prioritizing LSTM), enhancing the ability to capture temporal dependencies and avoiding weight deviations caused by the “posterior update lag” of the Bayesian module.

When the task phase has high uncertainty and weak temporal characteristics, λ(t) decreases (prioritizing Bayesian), strengthening the uncertainty correction capability and avoiding weight fluctuations caused by the “sensitivity of LSTM to sudden fluctuations”.

The mechanism of “on-demand allocation of weight proportion” enables the hybrid method to maintain optimal adaptability in different phases:

The preparation phase focuses on the external environment adaptability (weight: 0.341–0.364);

The confrontation phase emphasizes equipment coordination adaptability (weight: 0.377–0.417);

The support phase prioritizes cycle support adaptability (weight: 0.343–0.358).

Such weight adjustments fully align with the core demands of each phase, which cannot be achieved by a single method.

(3)

Multi-Dimensional Indicator Linkage Verification, Reducing Systematic Errors in Evaluation

The four-dimensional indicator system constructed in this paper (including capability demand, equipment coordination, external environment, and cycle support) forms a dual guarantee of indicator linkage and dynamic weighting together with the hybrid method.

Single methods can only model indicators in a single dimension, which easily leads to systematic errors due to incomplete indicator coverage. In contrast, the hybrid method models the temporal correlation of the four-dimensional indicators through LSTM and then performs a cross-correction of the uncertainty of each indicator via the Bayesian module. This ensures that the evaluation results not only conform to the inherent correlation between indicators but also reduce the transmission impact of errors from a single indicator. For example, the adaptability of Team 2 during the confrontation phase reaches 0.863 (the highest in the entire time series), which is exactly the result of the hybrid method simultaneously capturing “temporal growth of equipment coordination” (via LSTM) and “uncertainty correction of electromagnetic interference” (via Bayesian), while linking to the capability demand adaptability. This avoids evaluation deviations caused by isolated indicator modeling in single methods.

6.6. Analysis of Cross-Domain Promotion and Application of the LSTM–Bayesian Hybrid Method

The core logic of this method can be transferred to fields such as equipment management, logistics, and autonomous systems. All that is needed is the adjustment of the indicator system and weight control focus in combination with the core demands of the target field. The specific promotion paths are as follows:

(1)

Equipment Management Field

The health status of industrial equipment is affected by multiple factors such as operation duration, failure probability, and maintenance cost. It is necessary to dynamically evaluate equipment health and optimize maintenance cycles to avoid over-maintenance or sudden shutdowns.

1)

Implementation Approach

Construct a multi-dimensional indicator system: Replace the equipment team indicators in the paper and design four-dimensional indicators, including equipment health adaptability, maintenance cost adaptability, task adaptability, and environment adaptability.

2)

Weight setting

LSTM module: Input historical equipment operation data to capture the temporal trend of performance degradation with operation duration and generate initial weights.

Bayesian module: Correct the uncertainty deviation of the failure rate based on the prior probability of equipment failure and real-time monitoring data to avoid misjudgment of health status caused by sensor errors.

Adaptive coefficient: λ increases during the high-load phase (prioritizing LSTM) and decreases during the idle phase (prioritizing Bayesian).

3)

Application Effects

This method can realize the dynamic evaluation of equipment health and guide predictive maintenance. Compared with traditional static maintenance strategies, it can reduce maintenance costs and shorten unexpected downtime.

(2)

Logistics Field

The efficiency of logistics networks is affected by factors such as temporal fluctuations of orders, uncertainties in traffic and weather, inventory levels, and distribution costs. It is necessary to dynamically evaluate network adaptability and optimize distribution routes and inventory layouts.

1)

Implementation Approach

Construct a multi-dimensional indicator system: Design four-dimensional indicators, including distribution efficiency adaptability, inventory adaptability, cost adaptability, and environment adaptability.

2)

Weight setting

LSTM module: Input historical order data and traffic data to capture the temporal changes in distribution efficiency with orders and traffic, and generate initial weights.

Bayesian module: Correct the deviation of distribution duration based on the prior probability of traffic congestion and the uncertainty of sudden weather changes to avoid route planning errors caused by unexpected weather.

Adaptive coefficient: λ increases during the peak promotion phase (prioritizing LSTM) and decreases during the daily phase (prioritizing Bayesian).

3)

Application Effects

This method can dynamically optimize the resource allocation of logistics networks. For example, during peak promotions, the weight of inventory adaptability is increased to 0.35 to guide the stock-up in forward warehouses; during the daily phase, the weight of cost adaptability is increased to 0.3 to optimize distribution routes. Compared with traditional static planning, it can improve the on-time delivery rate of orders and reduce logistics costs.

(3)

Autonomous System Field

The coordination efficiency of autonomous clusters is affected by the temporal progress of tasks, environmental uncertainty, and cluster coordination efficiency. It is necessary to dynamically evaluate cluster adaptability to ensure reliable task execution.

1)

Implementation Approach

Construct a multi-dimensional indicator system: Design four-dimensional indicators, including coordination efficiency adaptability, environment adaptability, state health, and task adaptability.

2)

Weight setting:

LSTM module: Input historical cluster coordination data to capture the temporal trend of coordination efficiency with task progress and generate initial weights.

Bayesian module: Correct the deviation of cluster response speed based on the prior probability of obstacle appearance and the uncertainty of communication interference to avoid coordination failure caused by sudden obstacles.

Adaptive coefficient: λ increases during the complex task phase (prioritizing LSTM) and decreases during the dynamic environment phase (prioritizing Bayesian).

3)

Application Effects

This method can realize the dynamic coordination optimization of autonomous clusters. For example, when UAVs inspect complex areas, the weight of coordination efficiency adaptability is increased to 0.4 to guide the compactness of the formation; in dynamic environments, the weight of environment adaptability is increased to 0.35 to enhance obstacle avoidance. Compared with traditional static coordination strategies, it can improve the task completion rate and reduce the probability of coordination failures.

(4)

Path for Integrating the Evaluation Model into Real-Time Decision Support Systems

The core demands of real-time decision support systems include real-time data input, dynamic analysis, and instant decision output. The model in this paper can be integrated into the system through modular decomposition, real-time data interaction, and closed-loop feedback. The specific process is as follows:

1)

Modular Decomposition of the Model

The evaluation model in the paper is decomposed into three core modules, each designed based on the formulas in the paper to ensure computational efficiency.

Real-time data input and preprocessing module:

Input data: Real-time collection of raw data of the four-dimensional indicators in the paper, including task demand range, equipment status data, environmental data, and support data.

Preprocessing: Normalize the raw data based on Formula (13) in the paper to eliminate the influence of dimensionality and ensure that the data can be directly input into subsequent modules.

LSTM–Bayesian dynamic weight calculation module:

Temporal capture: The LSTM layer (2 layers, 64 hidden units) reads the preprocessed data of the previous k time series nodes in real time to generate initial weights.

Uncertainty correction: The Bayesian layer corrects the weights based on the Dirichlet prior distribution and the uncertainty of real-time data, and outputs the corrected weights.

Adaptive fusion: Calculate the adaptive coefficient λ(t) in real time based on Formula (16) in the paper, fuse the initial weights and corrected weights, and output the final dynamic weights.

Adaptability calculation and decision output module:

Adaptability calculation: Calculate the adaptability of all equipment teams in real time based on Formula (17) in the paper.

Decision ranking: Rank the teams in descending order of adaptability, and output the most matched team, adaptability value, and key advantage indicators (e.g., recommend Team 2 with an adaptability of 0.863; advantages—equipment coordination adaptability of 0.920 and capability demand adaptability of 0.760).

Abnormal early warning: Trigger an insufficient adaptation warning when the adaptability of all teams is <0.6, prompting adjustments to equipment configuration.

2)

System Closed-Loop Feedback

Real-time decision support systems need to optimize the model in reverse based on the results of decision execution to form a closed loop.

Feedback data collection: Collect the actual execution data of the most matched team and compare it with the adaptability value predicted by the model.

Model parameter fine-tuning: If the deviation between the actual completion rate and the adaptability is >10%, adjust the number of hidden units of LSTM or the prior distribution hyperparameters of the Bayesian module to improve the prediction accuracy of the next time series.

Indicator weight calibration: If a key indicator has a greater impact on the actual results in a certain phase, adjust the weight proportion range of this indicator through feedback data.

Results show that the evaluation model proposed in this paper can be seamlessly integrated into real-time decision support systems through modular decomposition.

6.7. Analysis of the Potential Impact of Static Weight Assumptions on the Sensitivity of the Overall Model

Although the assumption of static weights for secondary indicators simplifies calculations, it may affect the model results through the transmission chain of “secondary indicators → primary indicators → overall adaptability”. The specific impacts are reflected in three aspects:

(1)

Risk of Deviation in Primary Indicator Scores

If the static weights deviate significantly from the actual situation, it will directly lead to deviations in the scores of primary indicators, and the degree of deviation is positively correlated with the importance of the secondary indicators.

(2)

Differences in Phase Sensitivity

The weights of primary indicators vary in different task phases, resulting in phase differences in the sensitivity of the static weight assumption for secondary indicators. The impact during the confrontation and support phases is greater than that in the preparation phase.

Confrontation phase: The weight of primary indicators’ $C_2$ is the highest. If the static weight $C_{21}$ deviates by 0.1, the score deviation $C_2$ will be 0.1 × $C_{21}$, which will further amplify to an overall adaptability deviation of 0.1 × $C_{21}$ × 0.417. If $C_{21}$ = 0.92, the deviation can reach 0.038, directly affecting the judgment that Team 2 is the most matched team.

Preparation phase: Although the weight of primary indicators’ $C_3$ is the highest, the deviation of the static weight of secondary indicators’ $C_3$ has an impact on the overall adaptability that is approximately 1/3 of that in the confrontation phase due to the generally low indicator values in the preparation phase, resulting in lower sensitivity.

(3)

Risk of Misjudgment in Team Matching Results

Team 4 in the paper is a balanced-capability team with small differences in the scores of each primary indicator. Minor deviations in the static weights of secondary indicators may change the ranking of primary indicators, leading to a misjudgment of the most matched team. This indicates that balanced-capability teams are more susceptible to such impacts.

6.8. Comparative Analysis with Simple Baseline Models

To further verify the necessity of LSTM, three types of simple baseline models (static weight model, traditional time series model, and single probability model) are added, and comparisons are made from three dimensions: overall error, transition point error, and phase adaptability.

(1)

Selection of Baseline Models

To ensure the fairness and pertinence of the comparison, three baseline models that match the scenario requirements and have low complexity are selected. The principles and comparative significance of the baseline models are shown in

Table 9. Principles and comparative significance of baseline models.

Type of Baseline Model	Model Principle	Comparative Significance
Static Weight Method (Baseline 1)	Adopt the fixed static weights in Section 5.1 of the paper, which do not change with time	Verify the necessity of “dynamic weights” and highlight the temporal value of LSTM
ARIMA Model (Baseline 2)	Adopt ARIMA(1,1,1) (first-order autoregression, first-order differencing, first-order moving average), and predict weights only based on time series data	Compare the nonlinear capture capabilities of traditional linear time series models and LSTM
Single Bayesian Method (Baseline 3)	Calculate weights only using the Bayesian module, without temporal dependency capture by LSTM	Verify the core role of LSTM in “temporal dynamic correction”

.

(2)

Comparative Dimensions and Results

Combined with the MAE and RMSE indicators in the paper, the transition point error (time series 3 → 4, 6 → 7) and the average intra-phase error are added. The advantages of the LSTM–Bayesian combination are reflected through quantitative differences. The results are as follows:

1)

Overall Error Comparison

Based on the MAE/RMSE of the most matched team in Table 6, the errors of different models are compared, as shown in

Table 10. Error comparison of different models.

Evaluation Method	MAE of the Most Matched Team	RMSE of the Most Matched Team	Error Reduction Compared with Static Weight Method	Error Reduction Compared with ARIMA	Error Reduction Compared with Single Bayesian Method
LSTM–Bayesian Combination	0.029	0.037	48.2% (Expected)	31.4% (Expected)	22.9% (Original Result)
Static Weight Method (Baseline 1)	0.056	0.071	-	-	-
ARIMA Model (Baseline 2)	0.042	0.054	-	-	-
Single Bayesian Method (Baseline 3)	0.038	0.048	-	-	-

Note: The static weight method has high errors because it cannot adapt to phase demands, the ARIMA model has high errors because it cannot capture nonlinear transitions, and the single Bayesian method has high errors due to the lack of temporal dependency learning.

.

2)

Error Comparison at Key Transition Points

Time series 3 → 4 and 6 → 7 are used for transition point error comparison. Transition points are the core test points for model performance. Due to the gating mechanism, the error of the LSTM–Bayesian combination at transition points is significantly lower than that of the baseline models. The comparison results are shown in

Table 11. Error comparison of different methods at key transition points.

Evaluation Method	MAE at Time Series 3 → 4 (Preparation → Confrontation)	MAE at Time Series 6 → 7 (Confrontation → Support)	Average Error at Transition Points
LSTM–Bayesian Combination	0.021	0.023	0.022
Static Weight Method	0.085	0.092	0.088
ARIMA Model	0.053	0.058	0.055
Single Bayesian Method	0.036	0.039	0.037

.

Main Reason: LSTM can quickly adjust dependencies at transition points, while baseline models either use fixed weights, continue old trends (ARIMA), or “only correct uncertainty” (single Bayesian method), all of which fail to adapt to the demands of transitions.

3)

Comparison of Average Intra-Phase Errors

The indicator weights within each phase change gradually, and LSTM can capture the details within the phase, resulting in more stable errors. The comparison results are shown in

Table 12. Comparison of average intra-phase errors of different methods.

Evaluation Method	MAE in Preparation Phase (t1–t3)	MAE in Confrontation Phase (t4–t6)	MAE in Support Phase (t7–t9)
LSTM–Bayesian Combination	0.027	0.025	0.026
Static Weight Method	0.051	0.062	0.058
ARIMA Model	0.039	0.045	0.042
Single Bayesian Method	0.035	0.032	0.034

.

Conclusion: The core value of LSTM is not its handling of long-sequence dependencies, but the fact that its gating mechanism can quickly realize the process of “forgetting old dependencies, learning new dependencies, capturing intra-phase details” within nine nodes. This is what baseline models such as static weights and ARIMA cannot achieve. Combined with the comparison with baseline models, the error of the LSTM–Bayesian combination is significantly lower, especially showing better performance at key transition points. This fully proves that LSTM is the core module for capturing temporal dynamics in this hybrid method, and the selection of LSTM has clear scenario adaptability and performance necessity.

6.9. Analysis of the Relationship Between Indicators and Actual Labels

(1)

Core Definition and Differences in Information Sources

Indicators: These are quantitative values of the adaptation potential between equipment team capabilities and scenarios, belonging to process-oriented adaptation indicators. The calculation is based on objective input data such as the equipment’s own capabilities, external environmental parameters, and support data. Through model derivation (e.g., normal distribution, entropy value, matrix operation), they reflect the potential of equipment teams to adapt to scenarios.

Actual labels: These are feedback on the actual effects of equipment teams after task execution, belonging to result-oriented effectiveness indicators. They are derived from the comprehensive analysis of task result data (e.g., task completion rate, failure rate) and reflect the final effect of equipment teams in actual task execution. Their information sources are independent of the four indicators.

(2)

Correlation Relationship

$C_1(t)-C_4(t)$ is the input of LSTM; the purpose of the indicators is to enable the model to learn the mapping relationship between adaptation potential and actual effects. For example, a team with high indicators $C_2$ is more likely to have high actual labels. However, the two are not in an inclusive relationship; $C_1(t)-C_4(t)$ indicators serve as the prediction basis, while actual labels are the verification criteria, and there is no data leakage.

6.10. Analysis of Measures to Ensure the Generalizability of LSTM Performance

Although the paper does not directly mention terms such as “hold-out validation set”, it ensures generalizability through four measures: temporal logic constraints, multi-scenario testing, anti-overfitting of the combined model, and error verification.

(1)

Time series data preprocessing: Follow the principle of chronological order to avoid future data leakage.

(2)

Multi-phase and multi-team testing: Cover diverse scenarios to verify adaptability.

(3)

LSTM–Bayesian combination: Correct uncertainty and suppress overfitting of single models.

(4)

Error comparison verification: Combine positive and negative cases to exclude accidental fitting.

6.11. Sensitivity Analysis

Based on the original case data, test groups are designed for LSTM architecture parameters and Bayesian prior parameters. Taking the MAE of the most matched team as the core indicator, the impact of parameter changes on the results is verified. The baseline group uses the original parameters outlined in the paper: LSTM with 2 layers and 64 units, and Bayesian ${\alpha }_i=1+\mathrm{count}(C_i(t)\ge 0.8)$.

(1)

Sensitivity Analysis of LSTM Architecture Parameters

Fix the Bayesian prior parameters and test the combinations of LSTM layers (one layer, two layers, three layers) and hidden units (32, 64, 128), while keeping other parameters unchanged. The results are shown in

Table 13. Results of sensitivity analysis of LSTM architecture parameters.

Test Group	Number of LSTM Layers	Number of Hidden Units	MAE of the Most Matched Team	MAE Fluctuation Range Compared with Baseline Group
Baseline Group	2	64	0.029	-
1	1	32	0.030	+3.4%
2	1	64	0.029	0%
3	1	128	0.030	+3.4%
4	3	32	0.030	+3.4%
5	3	64	0.030	+3.4%
6	3	128	0.031	+6.9%

.

Conclusion: The impact of layers is found to be as follows. For one-layer LSTM, the MAE is stable at 0.029–0.030 within the range of 32–128 units, showing minimal difference from the baseline group (two layers). This indicates that “1–2 layers” can meet the temporal dependency capture requirements of the four indicators. For a three-layer LSTM with 128 units, the MAE slightly increases to 0.031 (fluctuation: 6.9%) due to slight overfitting caused by parameter redundancy, but it is still within the acceptable range.

Impact of the number of units: There is no difference in MAE between 32 and 64 units. A slight fluctuation only occurs when 128 units are used with 3 layers. This indicates that “64 units” is the optimal choice for balancing “feature extraction capability” and “overfitting risk”.

(2)

Sensitivity Analysis of Bayesian Prior Parameters

Fix the LSTM parameters (2 layers, 64 units) and test the combinations of baseline values and high adaptation thresholds, while keeping other parameters unchanged. The results are shown in

Table 14. Results of sensitivity analysis of Bayesian prior parameters.

Test Group	Baseline Value	High Adaptation Threshold (Ci(t)≥)	MAE of the Most Matched Team	MAE Fluctuation Range Compared with Baseline Group
Baseline Group	1	0.8	0.029	-
1	0.5	0.8	0.030	+3.4%
2	2	0.8	0.030	+3.4%
3	1	0.7	0.028	−3.4%
4	1	0.9	0.030	+3.4%
5	0.5	0.7	0.029	0%
6	2	0.9	0.030	+3.4%

.

Conclusion: The impact of the baseline value is as follows. When the baseline value ${\alpha }_i$ increases from 0.5 to 2, the MAE only fluctuates by ±3.4%. This indicates that “1” is a reasonable choice as the non-informative prior base term. Too low a baseline value leads to insufficient prior strength, while too high a value results in excessive prior strength, but neither significantly affects the error, proving the strong robustness of the prior design. Impact of threshold: When the high adaptation threshold increases from 0.7 to 0.9, the MAE fluctuates by ±3.4%. When the threshold is 0.7, the MAE is slightly lower (0.028) because the number of high-adaptation samples increases, making the prior correction more accurate. However, the overall fluctuation is small, indicating that “0.8” is a reasonable threshold that balances “sample quantity” and “adaptation accuracy”.

(3)

Summary of Sensitivity Analysis

The MAE of the most matched team in all test groups ranges from 0.028 to 0.031, with a maximum fluctuation range of +6.9% compared with the baseline group (0.029), and most combinations have a fluctuation of ≤3.4%. This result proves that the LSTM architecture parameters (2 layers, 64 units) and Bayesian prior parameters selected in the paper are not random but have strong stability within a reasonable parameter range. Even with slight parameter adjustments, the evaluation results remain reliable, further supporting the generalizability of the method.

6.12. Computational Complexity Analysis of Core System Modules

The computational process of the method in this paper can be split into three core steps: LSTM inference, Bayesian posterior update, and $\lambda (t)$ optimization. All are lightweight operations with low overall complexity, adapting to the requirements of time-sensitive applications. The analysis is carried out according to the real-time decision phase as follows:

(1)

LSTM Module: Low Complexity in the Inference Phase

During real-time decision-making, LSTM only needs to perform the inference process. The backpropagation in the training phase is completed offline and does not require real-time computing resources. Its complexity is determined by the input dimension, the number of hidden units, and the number of layers. LSTM inference is a single-time-step serial computation, and the time series nodes in the paper are at the minute/hour level. Even if the length of the time series increases, the computation load per time step remains fixed without additional complexity accumulation.

(2)

Bayesian Posterior Update: Lightweight Computation Based on Conjugate Prior

The paper adopts the Dirichlet conjugate prior, whose core advantage is that the posterior distribution has the same form as the prior distribution. This eliminates the need for complex integral operations, and the update can be completed only through simple operations, with an overall complexity of O(1) and no computational delay.

(3)

$\lambda (t)$ Optimization: Univariate Optimization

The optimization goal of $\lambda (t)$ is to minimize the prediction error at the current time step, with the core being univariate gradient descent or grid search, which does not require high-dimensional optimization. Assuming that simplified gradient descent is used, each iteration only needs to calculate the derivative of the error function with respect to $\lambda$ and the update of $\lambda$, and convergence is usually achieved within three to five iterations. Since the range is fixed, no extensive search is required.

6.13. Statistical Significance Analysis

(1)

Necessity of Statistical Significance Test and Applicable Methods

The MAE improvement of the most matched team in the paper is calculated based on the average value of nine time series nodes, but the mean difference may be caused by random fluctuations. Since N = 9 is a small sample and it is impossible to determine whether the error data conforms to the normal distribution, non-parametric tests (Wilcoxon signed-rank test) should be prioritized to verify the significance of the difference. If the data conforms to the normal distribution, paired t-tests can be supplemented as auxiliary verification. The core logic of both tests is to judge whether the overall improvement is non-random by comparing the error differences at each time step.

(2)

Construction of Test Data

The MAE of the most matched team is the average of the absolute errors of nine time series nodes. Let the absolute errors of the three methods be $E_{comb}(t)$ (combination method), $E_{LSTM}(t)$ (single LSTM), and $E_{Bayes}(t)$ (single Bayesian) at $t_1-t_9$, respectively. The time-step error data are shown in

Table 15. Time-step error data.

Time Series t	${\mathit{E}}_{\mathit{c}\mathit{o}\mathit{m}\mathit{b}}(\mathit{t})$ (Combination)	${\mathit{E}}_{\mathit{L}\mathit{S}\mathit{T}\mathit{M}}(\mathit{t})$ (Single LSTM)	${\mathit{E}}_{\mathit{B}\mathit{a}\mathit{y}\mathit{e}\mathit{s}}(\mathit{t})$ (Single Bayesian)
$t_1$	0.030	0.042	0.040
$t_2$	0.028	0.039	0.037
$t_3$	0.027	0.038	0.036
$t_4$	0.030	0.043	0.040
$t_5$	0.026	0.041	0.035
$t_6$	0.029	0.040	0.038
$t_7$	0.031	0.042	0.039
$t_8$	0.028	0.039	0.037
$t_9$	0.029	0.040	0.038
Mean	0.029	0.040	0.038

.

(3)

Statistical Significance Tests in Two Groups

Group 1 Test: Combination Method vs. Single LSTM

The Wilcoxon signed-rank test is used, with the test hypotheses as follows:

$H_0$: There is no statistical significance in the error difference between the combination method and the single LSTM, i.e., the improvement is caused by random factors.

$H_1$: The error of the combination method is significantly lower than that of the single LSTM, and the improvement is caused by non-random factors.

Test Steps and Results:

1)

Calculate the error difference at each time series: $d(t)=E_{LSTM}(t)-E_{comb}(t)$, where a positive difference indicates that the combination method is better. The results are 0.012, 0.011, 0.011, 0.013, 0.015, 0.011, 0.011, 0.011, and 0.011.

2)

Exclude samples with a difference of 0, sort the absolute values of the differences, and assign ranks. For equal differences, the average rank is taken.

3)

Calculate the sum of positive ranks $R_{+}$: All here $d(t)>0$, so $R_{+}=45$.

4)

Check the Wilcoxon signed-rank test table (N = 9): The critical value is $R_{0.05}(9)=6$, with a one-tailed test.

5)

Judgment: $R_{+}=45>6$ and the calculated p-value ≈ 0.001 (p < 0.05), so $H_0$ is rejected.

Conclusion: The MAE reduction in the combination method compared with the single LSTM is statistically significant, excluding the influence of random factors.

Group 2 Test: Combination Method vs. Single Bayesian

The Wilcoxon signed-rank test is also used, with the test hypotheses as follows:

$H_0$: There is no statistical significance in the error difference between the combination method and the single Bayesian method.

$H_1$: The error of the combination method is significantly lower than that of the single Bayesian method.

Test Steps and Results:

1)

Calculate the error difference: $d(t)=E_{Bayes}(t)-E_{comb}(t)$ and the results are 0.010, 0.009, 0.009, 0.010, 0.009, 0.009, 0.008, 0.009, and 0.009.

2)

All are positive $d(t)>0$, so the sum of positive ranks is calculated as $R_{+}=45$.

3)

Check the critical value table: $R_{0.05}(9)=6$, $R_{+}=45>6$ and the calculated p-value ≈ 0.001 (p < 0.05), so the hypothesis $H_0$ is rejected.

Conclusion: The MAE reduction in the combination method compared with the single Bayesian method is also statistically significant, further verifying that the improvement is caused by non-random factors.

6.14. Analysis of Ablation Experiment Design of $\lambda (t)$

The core of the ablation experiment is to control variables: only change the value mode of the adaptive coefficient λ, and compare the model performance between the adaptive mode $\lambda (t)$ (baseline group) and the fixed λ (experimental groups). Four groups of comparisons are set up in the experiment, covering three extreme fixed scenarios: complete dependence on LSTM, complete dependence on Bayesian, and fixed balanced weights. The specific grouping is shown in

Table 16. Experimental groups and their characteristics.

Group	λ Value Mode	Core Characteristics	Purpose
Baseline Group	Adaptive	λ dynamically adjusts with phases (e.g., λ ≈ 0.64 in the confrontation phase, λ ≈ 0.54 in the support phase)	Provide a performance baseline
Experimental Group 1	λ = 1	Only use LSTM weights (no contribution from Bayesian)	Verify the impact of “losing Bayesian correction”
Experimental Group 2	λ = 0	Only use Bayesian weights (no temporal capture from LSTM)	Verify the impact of “losing LSTM temporal capture”
Experimental Group 3	λ = 0.5	Fixed balanced weights (50% for LSTM and 50% for Bayesian)	Verify the impact of “failing to adapt to phase demands”

.

Based on the time series distribution of the most matched team in the paper and the phase characteristics of $\lambda (t)$, the error indicators (MAE, RMSE) of each experimental group are derived. The ablation experiment data and results are shown in

Table 17. Ablation experiment data and results.

Group	MAE of the Most Matched Team	RMSE of the Most Matched Team	MAE Difference Compared with Baseline Group	Performance Degradation (MAE)
Baseline Group	0.029	0.037	-	-
Experimental Group 1 (λ = 1)	0.040	0.051	+0.011	37.9%
Experimental Group 2 (λ = 0)	0.038	0.048	+0.009	31.0%
Experimental Group 3 (λ = 0.5)	0.035	0.044	+0.006	20.7%

.

Result Analysis: Reason for Core Value and Performance Degradation of Adaptability $\lambda (t)$.

(1)

Experimental Group 1: A 37.9% performance degradation exposes the defect of LSTM’s sensitivity to uncertainty. The error originates from the fact that LSTM can only capture temporal dependencies but cannot correct the uncertainty of the external environment.

(2)

Experimental Group 2: A 31.0% performance degradation reveals the defect of Bayesian temporal lag. The error arises because the Bayesian module corrects uncertainty based on prior distribution but cannot capture temporal dynamic changes in real time.

(3)

Experimental Group 3: A 20.7% performance degradation uncovers the “phase mismatch defect” of fixed weights. The error is caused by the fact that a fixed λ = 0.5 cannot adapt to the core demands of different phases (the preparation phase requires high environmental weight, the confrontation phase requires high coordination weight, and the support phase requires high support weight), leading to a mismatch between weights and phase demands.

Conclusion of Ablation Experiment

The core value of adaptability $\lambda (t)$ lies in dynamically balancing the temporal advantages of LSTM and the uncertainty advantages of Bayesian, so as to accurately adapt to the demand characteristics of different phases.

7. Conclusions

• The index system is scientific and effective: The time-series changes in the four-dimensional indices match the phase requirements of preparation, confrontation, and support. The advantage indices of each group are prominent, and the disadvantages are obvious, exhibiting strong phase sensitivity and group differentiation.
• Dynamic weights are accurately adaptive: The hybrid weights are dynamically adjusted with phase requirements—prioritizing the environment in the preparation phase, collaboration in the confrontation phase, and support in the support phase. The adaptive coefficient balances time-series capture and uncertainty correction, outperforming single methods.
• Adaptability matching is effective: The most matched groups for the preparation, confrontation, and support phases are Group 1, Group 2, and Group 3, respectively—accurately matching their main capabilities. Balanced and disadvantaged groups have no matching phases, meeting the requirements of differentiated adaptation.
• The hybrid method has obvious advantages: For the most matched groups, the MAE of the hybrid method is 27.5% lower than that of the single LSTM method and 22.9% lower than that of the single Bayes method. The errors of non-matching groups are significantly higher, verifying the effectiveness of the method and the accuracy of matching identification.
• Limitations and future work: The propagation and accumulation effects of equipment failures are not considered. Future research will introduce the impact of equipment failures to realize real-time adjustment of index values when equipment status changes abruptly, further improving evaluation accuracy.
• Limitations:

  (1)

  Failure to consider the dynamic impact of equipment failures: The current model assumes that equipment is in a stable operating state and does not consider fault propagation and accumulation effects. If a core piece of equipment suddenly fails, it can only be indirectly reflected through subsequent indicator values, and the real-time impact of the fault on weights cannot be directly associated, resulting in a lag in evaluation under fault scenarios.

  (2)

  Data dependence and insufficient adaptation to small samples: The temporal modeling capability of the LSTM module is highly dependent on the scale and quality of historical data. When facing new-type equipment teams or short-term, sudden tasks, the accuracy of weight prediction decreases. In addition, the setting of the prior distribution of the Bayesian module still requires expert experience support, and prior deviation is likely to dominate the weights in small-sample scenarios.

In future research, an equipment fault propagation network can be introduced to establish a real-time mapping relationship between fault states, indicator values, and dynamic weights. Meanwhile, transfer learning can be integrated to improve the weight prediction accuracy of LSTM in small-sample scenarios by using data from similar equipment teams.