Improvement of Frequency Responses of MSBL-Based Approximate Fractional-Order Derivative Operator and Its Digital Realization with FPGA

Abstract

Fractional calculus has emerged as an important research area for the analysis and solution of complex engineering problems. However, because exact implementation of fractional-order (FO) operators is not possible, various integer-order approximations are used for implementation. Agreement of the time and frequency responses obtained with these approximation methods with the analytical responses of the FO models is critical for application accuracy and performance. This study aims to reduce the difference between analytical and approximation-based frequency responses through optimization for better implementation performance. After the success of the proposed method was proved for an FO operator, it was applied to an FOPID controller and an FO filter. Notable improvements were observed in both frequency and time response. To test the practicality of the method, the proposed method and other approximation methods were tested on an FPGA using the Vitis Model Composer Hub system generator block within the MATLAB Simulink environment. Also, the proposed method was experimentally implemented for an FO operator on a Nexys 4 DDR Artix-7 FPGA. It was observed that FPGA implementation and simulation results were in good agreement with each other.

1. Introduction

In recent years, fractional calculus has been increasingly used to solve and more precisely model the dynamic behaviors of the systems [1]. Therefore, fractional calculus has found widespread application in solving real-world problems across various fields such as power and energy systems, materials science, electronics, signal processing, and control systems. This broad range of applications has been clearly demonstrated in recent studies. For example, fractional calculus has been employed in diverse areas, ranging from the investigation of adsorption phenomena and complex fluids in physics [2] to the analysis of efficiency behavior in system dynamics environments [3]. In the context of power and energy systems, the advantages of fractional calculus have been utilized in intelligent controller designs for wind energy applications [4,5] and in the generalized modeling of electrohydraulic systems [6]. In the field of signal processing, it has been applied to fundamental image-processing tasks [7] and the analysis of non-stationary signals [8]. Furthermore, in materials science, it has been used to describe the rheological models of viscoelastic materials [9], while in electronics, it has provided effective solutions for thermal impedance modeling of IGBT devices [10] and for the control of electric springs [11]. Fractional calculus is also used in real-world applications, especially in cases where sensitivity and accuracy are essential. For example, I. Pataro et al. developed a fractional-order PID controller based on fractional calculus to control a solar collector field system [12]. Another example from the health domain is the fractional-order SEIHR-M model proposed by Rui Hu et al. for investigating the transmission dynamics of COVID-19 in Malaysia [13]. Fractional calculus is used to solve complex mathematical models in disciplines such as physics, chemistry, and biology, to improve the accuracy of deep learning models, and to simulate system behavior in electrical engineering. To illustrate the efficiency of fractional calculus on neural networks, C. Coelho et al. presented a survey of neural network-based computer vision techniques for denoising, enhancement, object detection, segmentation, and restoration [14]. Also, X. Zhang et al. address the discrepancies in electric spring (ES) models by establishing a fractional-order ES model based on the fractional-order characteristics of inductors and capacitors, analyzing its operational features, and proposing a fuzzy adaptive fractional-order PI^λD^μ control strategy to enhance the system’s control performance [15]. Moreover, M. Higazy et al. construct a novel 6D fractional-order chaotic model, analyze its complex dynamics and fundamental properties, and propose an active fractional-order controller for chaos control, with potential applications in data encryption [16]. In addition, AF. Mohammed et al. propose a novel Hybrid Intelligent Fractional-Order Proportional Derivative2+Integral (FOPDD+I) controller for Automatic Voltage Regulation (AVR) systems, which leverages Adaptive Neuro-Fuzzy Inference System (ANFIS) to optimize performance and achieve superior transient response compared to conventional methods [17]. The success of fractional calculus in real-world applications depends on how well these applications minimize errors and how realistically accurate models can be created.

Fractional-order (FO) operators generalize classical integer-order derivatives and integrals by allowing the order to take non-integer values. FO derivative operator introduces a frequency-dependent phase lead, which enables finer tuning of phase margin and damping, reducing overshoot while preserving amplitude characteristics. FO integral operator provides frequency-dependent gain and phase lag, improving low-frequency response and steady-state performance compared to classical integer-order integrals. These properties make FO operators highly effective for frequency–response shaping and precise control design, offering flexibility not achievable with integer-order operators alone. For example, in practical control applications, FO derivative operators can improve phase margin, reduce overshoot, and provide better frequency–response shaping compared to classical integer-order derivatives.

Although FO modeling provides more accurate results, one of the most important problems encountered is that FO derivative/integral operators cannot be realized directly [18,19]. To realize an FO derivative/integral operator, the FO transfer function is approximately converted into an integer-order approximate model in a defined frequency interval, and for this, approximation methods such as Oustaloup, Matsuda, Modified Stability Boundary Locus (MSBL), etc., are used [18,20,21,22,23,24]. However, since each of these methods is an approximation method, it is inevitable that a difference, i.e., an error, will occur between the real responses and the time and frequency response obtained by the approximation method during the realization. It is crucial to minimize the error for more accurate realization performance [25,26].

In this study, it is aimed at increasing the accuracy and efficiency in the realization of FO operators. Thus, an optimization method is applied to minimize the nonlinear multi-variable error functions which are based on the difference between the approximate frequency response obtained by the MSBL method and the analytical frequency response in a defined frequency range. In the first stage, analytical frequency response and MSBL approximation method-based frequency response are obtained for the FO derivative operator in a defined frequency interval. In the second stage, the cost function, which includes the difference between the analytically obtained frequency response and the approximation-based frequency response, is minimized by using FMINCON optimization algorithms, and an optimized integer-order transfer function is obtained. FMINCON minimizes an objective function under certain persistence, finds the minimum of constrained nonlinear multi-variable optimization function and optimizes the approximate integer-order transfer function obtained by MSBL method. The optimization algorithm used in FMINCON method was Sequential Quadratic Programming (SQP) in this study. In the third stage, considering an FO derivative operator, to evaluate the performance of the optimization results, the frequency and time responses based on approximation methods and the proposed method are analyzed in comparison with those of analytical responses. The RMSE and MAPE error comparisons are presented in tables. Furthermore, the real-world applicability and accuracy of the optimized transfer function for an FO derivative operator are successfully simulated in Vitis Model Composer Hub and experimentally implemented on an FPGA.

As a result, the proposed method provides a notable improvement in the frequency accompanying with a slight enhancement in the time response in general. The FMINCON method is employed for the first time in this study to enhance the approximate integer-order transfer function of an FO operator. The coefficients of the approximate transfer function obtained by the MSBL method for the derivative operator in a defined frequency range are taken as initial values, and then these coefficients are optimized using the FMINCON method. The proposed method minimizes the cost function and obtains a slightly modified approximate integer-order transfer function that exhibits more accurate convergence performance in the frequency response. It is observed that FMINCON is an applicable and promising method to optimize the frequency responses of approximate integer-order transfer function of the MSBL approximation method. However, one can apply this optimization to any other approximation method to improve the approximation performance. The proposed approach was applied to an FOPID controller and an FO low pass filter to compare the performance of the method with other approximation methods. The frequency and time responses are obtained, and comparative graphical analysis is performed. According to the comparative analysis, it has been concluded that the frequency-based optimization yielded satisfactory results in the realization of FO circuits. The main contribution of the study can be explained briefly as follows: to the authors’ knowledge, this study is the first to implement a frequency response-based optimization method for FO functions. This method can be generalized to other approximation methods, and more effective FO circuit performance can be observed, especially in applications where frequency response accuracy is important.

2. Materials and Methods

In this study, the fifth-order approximate continuous-time transfer function for FO derivative operator was obtained in a defined frequency interval by using MSBL approximation method. Then, the exact frequency response and frequency response based on MSBL approximation method were graphically illustrated. To minimize the difference between the exact and approximate frequency responses, a cost function based on the error between exact and approximate response was obtained. Then, the coefficients of the approximate transfer function were optimized and slightly modified using FMINCON nonlinear-constrained optimization method. The frequency response based on the proposed method is compared with exact frequency response and approximation-based frequency responses. RMSE and MAPE error values are presented as tables. In addition, it has been checked whether the improvement in the frequency response causes any deviation in the time response. Then, the optimized transfer function was realized on an FPGA board to check the applicability. Also, the specified method was applied to an FO low pass filter and an FOPID controller, and the results were analyzed comparatively.

2.1. Determination of Approximate Transfer Functions for Derivative Operator

In this study, the proposed optimization is applied to the integer-order transfer function obtained by MSBL approximation method in a defined frequency range. So, this approximation method was briefly explained. The MSBL approximation method provides a systematic approach for representing FO operators with integer-order transfer functions. The MSBL approximation process begins by selecting the desired frequency interval, typically denoted as [ω_min, ω_max], over which the approximation is to be valid. The order of the approximation, n, is then chosen based on the required accuracy and implementation complexity. For an n^th order approximation, the method systematically places the poles and zeros of the integer-order transfer function on the real axis in the complex frequency domain. These poles and zeros are distributed logarithmically across the selected frequency range to ensure a uniform approximation quality.

Mathematically, the approximate transfer function for the fractional derivative operator $s^{\alpha }$ using the MSBL approximation method can be expressed as

$$s^{\alpha }=K\ast {\displaystyle \frac{\left(s+z_1\right)\left(s+z_2\right)\dots \left(s+z_n\right)}{\left(s+p_1\right)\left(s+p_2\right)\dots \left(s+p_n\right)}}$$

(1)

where $K$ is a gain factor, and $z_i$ and $p_i$ represent the zeros and poles, respectively. The poles are typically determined as

$$p_i=w_{min}\ast r^{i-1}$$

(2)

$$r={\left({\displaystyle \frac{w_{max}}{w_{min}}}\right)}^{{\displaystyle \frac{1}{n}}}$$

(3)

The zeros are then calculated as

$$z_i=p_i\ast r^{\alpha }$$

(4)

The gain K is adjusted to ensure that the magnitude of the approximate transfer function matches the original operator at a reference frequency, often chosen as the geometric mean of the frequency range [18].

Additionally, in-depth information about FO approximation methods such as MSBL, Oustaloup, and Matsuda is presented in the literature [27]. To provide a clear comparison, the core principles of the MSBL, Oustaloup, and Matsuda methods, which are also considered in this study, are briefly introduced. The Oustaloup approximation, often implemented as the Oustaloup Recursive Approximation (ORA) filter, also approximates the sα operator using a filter of N poles and N zeros within the specified frequency range [ω_min, ω_max]. Its defining characteristic is the use of a recursive geometric progression to determine the locations of these poles and zeros. This recursive placement is specifically designed to achieve a transfer function that approximates the constant magnitude slope (in dB/decade) and, critically, the constant phase (in degrees) of the ideal fractional operator within the specified band [27,28]. The Matsuda method, in contrast, is a frequency-domain fitting technique. It approximates the operator by logarithmically spacing several frequency points within the target range and performing a least squares fit to match the gain and phase of the ideal operator, sα. This method systematically determines the poles, zeros, and overall gain of the integer-order transfer function (Equation (5)) to best match the frequency–response characteristics of the ideal operator, and it is often noted for its high accuracy in the frequency domain [27].

Therefore, while all three methods (MSBL, Oustaloup, and Matsuda) aim to produce a stable, rational integer-order transfer function, their core difference lies in the pole–zero placement strategy: MSBL uses a direct logarithmic distribution, Oustaloup uses a recursive geometric progression to maintain a flat phase response, and Matsuda uses a direct frequency–response fitting algorithm. As noted, in-depth analyses and derivations of these methods are available in the literature.

Using the mentioned FO approximation methods, different integer-order transfer functions can be obtained. The general expression of the approximate transfer function for an FO operator can be written as follows:

$$s^{\alpha }\cong {\displaystyle \frac{r_n{s}^n+r_{n-1}{s}^{n-1}+r_{n-2}{s}^{n-2} +\dots +r_2{s}^2 +r_{1}s +r_0 }{p_n{s}^n +p_{n-1}{s}^{n-1} +p_{n-2}{s}^{n-2} +\dots +p_2{s}^2 +p_{1}s +p_0}}$$

(5)

where the FO of the operator is α, and it is a real number between 0 and 1. The derivative operator takes a positive value in the notation; on the other hand, the integer operator takes the negative value. Also, n is the order of approximation method. The numerator polynomial coefficients A = [r_n r_n−1 r_n−2…r₂ r₁ r₀] and the denominator polynomial coefficients B = [p_n p_n−1 p_n−2…p₂ p₁ p₀] are calculated by several FO approximation methods to achieve a band limited frequency domain approximation to the FO element $s^{\alpha }$.

The 5th order approximate transfer functions for the FO derivative operator s^0.5 were obtained for the frequency interval of [0.01, 100) rad/s by considering the MSBL, Oustaloup, and Matsuda approximation methods as follows:

$$T_{msbl }\left(s\right)={\displaystyle \frac{21.62 s^5 +1186 s^4 +5877 s^3 +3516 s^2 +233.1 s +1}{1s^5 +233.1 s^4 +3516 s^3 +5877 s^2 +1186 s +21.62 }}$$

(6)

$$T_{oustaloup }\left(s\right)={\displaystyle \frac{31.66 s^5 +4249 s^4 +3.389\times {10}^4 s^3 +1.698\times {10}^4 s^2 +534.9 s +1}{1s^5 +534.9 s^4 +1.698\times {10}^4 s^3 +3.389\times {10}^4 s^2 +4249 s +31.66 }}$$

(7)

$$T_{matsuda }\left(s\right)={\displaystyle \frac{26.93 s^5 +1462 s^4 +7194 s^3 +4255 s^2 +279.4 s +1}{1s^5 +279.4 s^4 +4255 s^3 +7194 s^2 +1462 s +26.93 }}$$

(8)

2.2. Application of FMINCON Method to Optimize the Transfer Function Coefficients for Frequency Response Optimization

Optimization methods are crucial for improving transfer functions to ensure that the system model behaves as closely as possible to its intended dynamics. Especially in FO complicated systems, coefficients derived from theoretical approximations may not directly provide the desired performance due to numerical rounding errors and practical implementation limitations. In these cases, optimization algorithms minimize the error function and enable the most appropriate coefficients to be found in terms of amplitude, phase, and stability criteria.

The approximate error functions denoting the difference between the analytical and approximate values for phase ($\phi$) and magnitude ($H$) responses are defined, respectively, as

$$E_{phase}\left(\theta \right)={\sum }_{i=1}^m{\left({\phi }_{app}\left({\omega }_i,\theta \right)-{\phi }_{exact}\left({\omega }_i\right)\right)}^2$$

(9)

$$E_{mag}\left(\theta \right)={\sum }_{i=1}^m{\left(H_{app}\left({\omega }_i,\theta \right)-H_{exact}\left({\omega }_i\right)\right)}^2$$

(10)

where $\theta$ is the numerator and denominator coefficient vector that is optimized, m represents the number of sampling points in the defined frequency range. To obtain an accurate model, a logarithmic distribution of 1000 different solution points in the frequency range of 0.01 rad/s to 100 rad/s was considered. In this expression, ${\phi }_{exact}$ is calculated in degree as $\alpha ·\pi /2$, and $H_{exact}$ is calculated in dB as ${\omega }^{\alpha }$. ${\phi }_{app}$ is the approximate phase value calculated based on the 5th order FO approximation method, and $H_{app}$ is the approximate magnitude value calculated based on the 5th order FO approximation method.

The cost function, which will be minimized by using FMINCON method, is written as

$$J\left(\theta \right)=w_{phase}\ast E_{phase}\left(\theta \right)+w_{mag}\ast E_{mag}\left(\theta \right)$$

(11)

where $w_{phase}$ and $w_{mag}$ are the weight coefficients for phase and magnitude, respectively. The weight coefficients were selected empirically; $w_{phase}$ was set to 0.1 and $w_{mag}$ was set to 2.

The FMINCON function in MATLAB 2025b is a powerful tool for solving constrained optimization problems. This function can handle nonlinear constraints and generally find solutions using different algorithms such as the Interior Point Algorithm, the SQP algorithm, the Active Set Algorithm, and the Trust Region Reflective Algorithm [29,30,31,32]. The FMINCON-based optimization refines the coefficients of the 5th order transfer function through constrained nonlinear minimization of a weighted multi-objective cost function that combines magnitude and phase errors. By iteratively adjusting the pole–zero locations within feasible physical boundaries, the algorithm ensures that the approximated model reproduces the true system’s dynamic behavior more accurately. This process enhances the alignment between the model’s and the exact system’s natural frequencies and damping ratios, resulting in a more physically consistent frequency response.

In this study, the SQP algorithm, which is based on a quadratic approach to solving the optimization problem iteratively, is used because it is one of the most effective methods aimed at solving nonlinear problems in constraints [30,33]. The nonlinear multi-variable cost function combines weighted magnitude and phase errors, both of which depend nonlinearly on the model parameters through the polynomial structure of the transfer function. Consequently, the cost surface is smooth but nonconvex, with multiple local minima corresponding to different pole–zero configurations. FMINCON’s SQP approach efficiently explores this landscape and converges to the parameter set that yields the minimum combined error while maintaining the system’s physical realizability. MATLAB’s FMINCON function with the SQP algorithm was employed to solve the constrained nonlinear optimization problem for the frequency response of the approximate FO operator. SQP iteratively approximates the problem by solving a quadratic subproblem at each step, linearizing constraints, and updating the coefficients along a search direction that reduces a combined merit function [34]. This process continues until convergence to a solution that satisfies the Karush–Kuhn–Tucker (KKT) conditions, resulting in the optimized coefficients of the fifth-order transfer function [35].

To optimize the frequency response of the FO operator, firstly, the cost function given in Equation (11) is determined. Then, this cost function is optimized by FMINCON method. Following the multi-variable optimization based on a weighted multi-objective cost function, the coefficients of the 5th-order transfer function are fine-tuned in a coupled manner to minimize magnitude and phase errors. This coordinated correction reshapes the pole–zero distribution rather than merely altering numerical values, leading to a model that more accurately reproduces the system’s natural frequencies, damping ratios, and overall dynamic response. Thus, both amplitude and phase characteristics are improved while ensuring the stability and physical realizability of the system. At the end of the optimization, a new transfer function, whose coefficients have slightly changed compared to the transfer function obtained by MSBL approximation method, is obtained.

As a result, the optimized approximate MSBL transfer function was obtained as follows:

$$T_{opt.-msbl }\left(s\right)={\displaystyle \frac{23.77 s^5 +1173 s^4 +5913 s^3 +3462 s^2 +228.9 s +1.15}{1.15 s^5 +228.9 s^4 +3462 s^3 +5913 s^2 +1173 s +23.77 }}$$

(12)

Also, this transfer function can be decomposed by using the partial fraction expansion (PFE) method as

$$T_{opt.-msbl }\left(s\right)={\displaystyle \frac{-3052}{s+182.7}}+{\displaystyle \frac{-37.4}{s+14.4}}+{\displaystyle \frac{-1.504}{s+1.701}}+{\displaystyle \frac{-0.06172}{s+0.202}}+{\displaystyle \frac{-0.002583}{s+0.02287}}+20.6626$$

(13)

Each rational expression in this equation represents a first-order LPF, and the rightmost constant represents the gain factor. To improve numerical stability and minimize coefficient quantization effects, the continuous-time 5th order transfer function was expressed as the sum of five first-order components using partial fraction expansion. Each first-order section was converted to discrete-time function via the Tustin method and implemented in parallel on the FPGA. This approach significantly enhances numerical robustness, as the stability of each section can be individually verified and maintained within the unit circle.

2.3. Digital Realization on FPGA

To realize the continuous-time transfer function on an FPGA in digital form, it is necessary to convert the continuous-time transfer function to a discrete-time transfer function. Various conversion methods are available for this purpose, including zero-order hold (ZOH), first-order hold (FOH), impulse-invariant mapping, Tustin approximation (bilinear transform), zero–pole matching, and least squares approaches. Each method offers its own set of strengths and limitations, and the choice of a suitable method is governed by the particular requirements of the system under study and the characteristics of the input signals [36,37,38,39]. In this study, all the methods mentioned above were tested in MATLAB. It was found that, for the transfer function under consideration, the Tustin method with a sample time of 10 ms yields relatively better error rates within the defined frequency range.

When the optimized continuous-time approximate transfer function given in Equation (13), which represents the main transfer function as a sum of first-order low pass filter form, is converted into a discrete-time transfer function using the Tustin method in MATLAB, the resulting function in the z-domain is obtained as follows:

$$\begin{gathered} T_{opt.-msbl}\left(z\right)={\displaystyle \frac{-7.979-7.979z^{-1}}{1-0.04532z^{-1}}}+{\displaystyle \frac{-0.1744-0.1744z^{-1}}{1-0.8657z^{-1}}}+{\displaystyle \frac{-0.007456-0.007456z^{-1}}{1-0.9831z^{-1}}} \\ + {\displaystyle \frac{-0.0003083-0.0003083z^{-1}}{1-0.998z^{-1}}}+{\displaystyle \frac{-1.291x{10}^{-5}-1.291x{10}^{-5}{z}^{-1}}{1-{0.999771z}^{-1}}} \\ \hspace{1em}\hspace{1em}+ 20.6626 \end{gathered}$$

(14)

Each rational part of Equation (14) can be represented as a difference equation as shown in the following example, in which the first rational component of Equation (14) is written as a difference equation:

$${\displaystyle \frac{Y\left(z\right)}{X\left(z\right)}}={\displaystyle \frac{-7.979-7.979z^{-1}}{1-0.04532z^{-1}}}$$

(15)

$$Y\left(n\right) = -7.979\ast X\left(n\right)-7.979\ast X\left(n-1\right)+0.04532\ast Y\left(n-1\right)$$

(16)

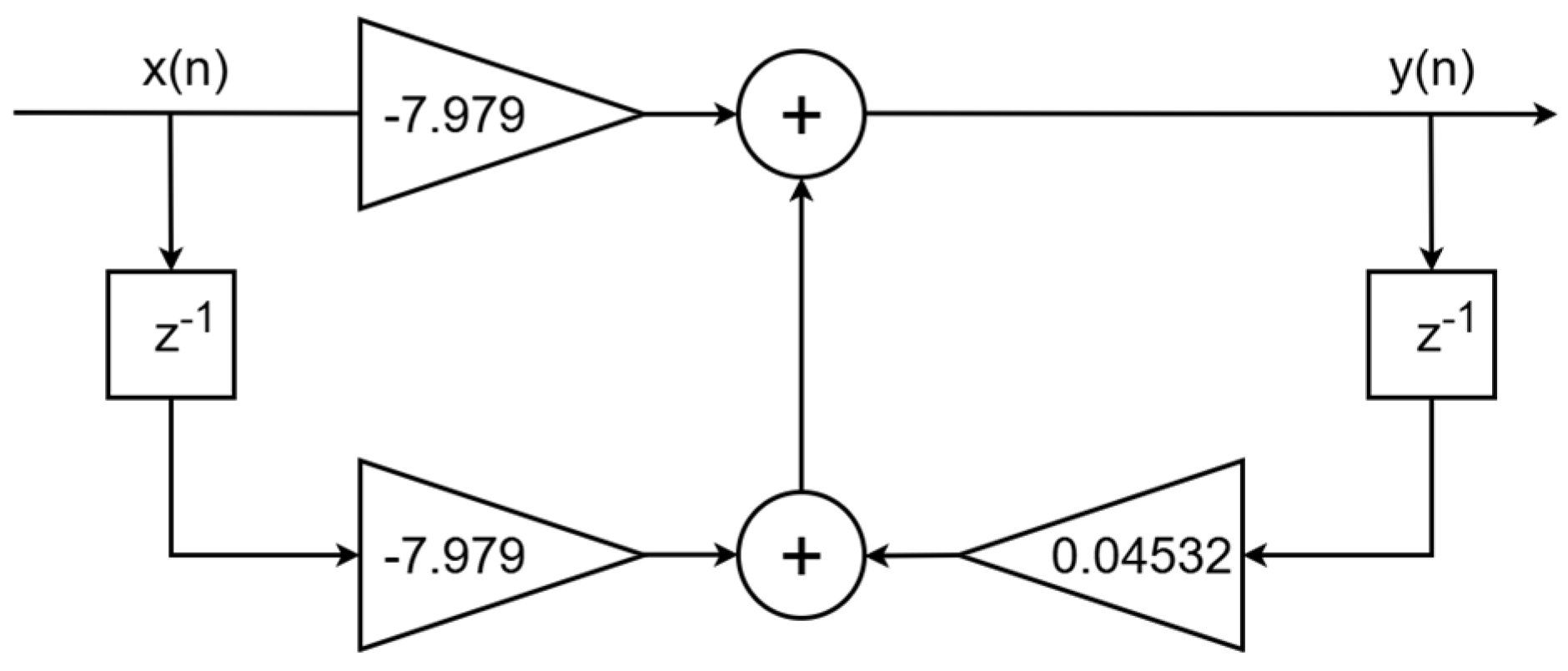
Each rational term in the transfer function relies on both present and past input values, as well as previous output values, and is therefore implemented as a sum of Infinite Impulse Response (IIR) filters. In this work, each first-order IIR filter is implemented in the Direct form I structure as depicted below. Figure 1 provides a design example for the first rational component on the right-hand side of Equation (14).

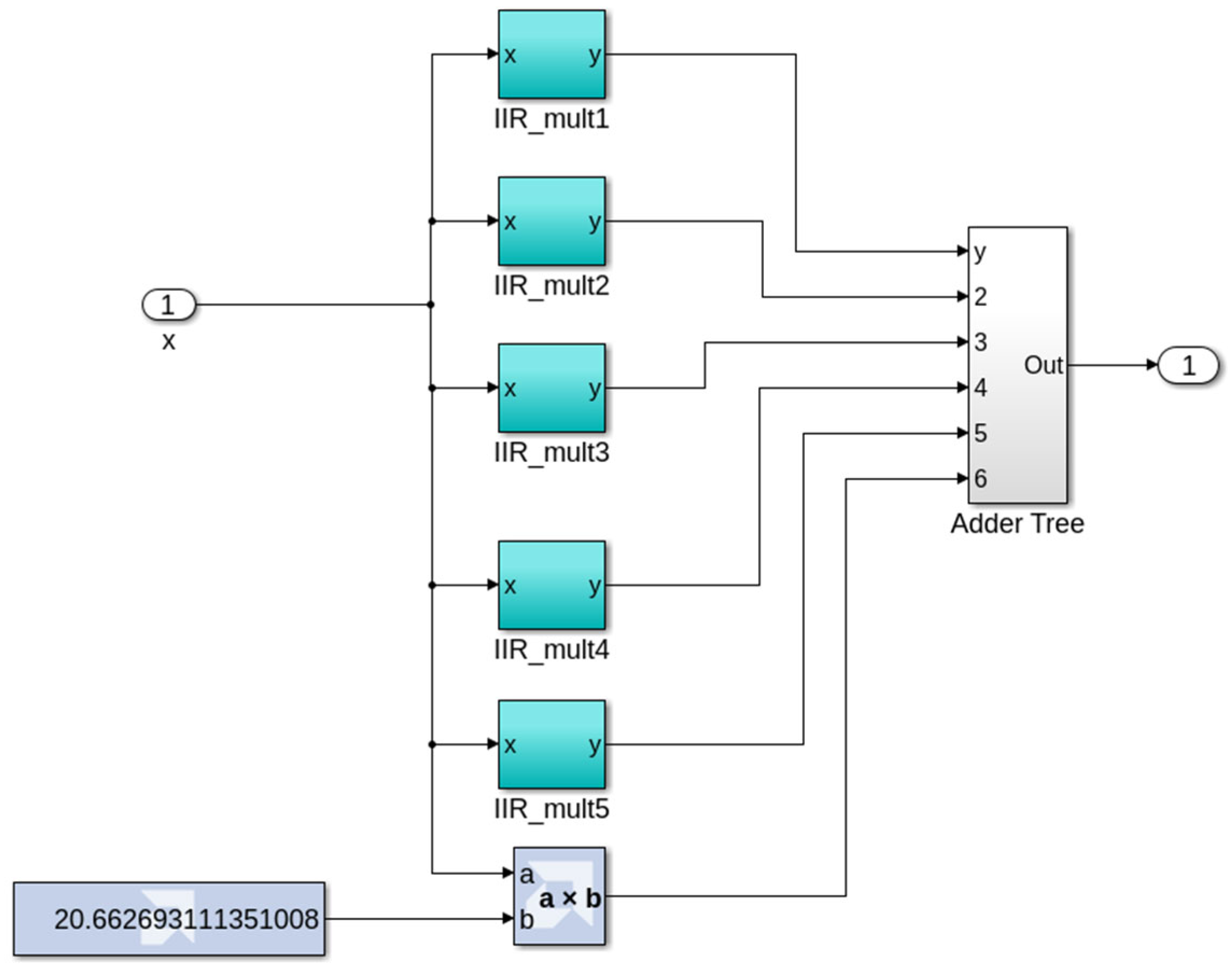
Equation (14) represents the combination of five distinct IIR filter equations along with a static gain of 20.6626. This equation is implemented in Simulink as the sum of IIR filters using the Vitis Model Composer Hub system generator tool (the official website: https://www.xilinx.com/products/design-tools/vitis/vitis-model-composer.html, accessed on 8 October 2025). The tool generates the corresponding IP core for the function, which is then utilized in the Vivado Design Suite for synthesis, Register Transfer Level (RTL) analysis, implementation, and bitstream generation for deployment on the FPGA device. The overall process is illustrated in the block diagram shown in Figure 2.

The Vitis Model Composer Hub system generator, developed by Xilinx Inc. from San Jose, CA, USA, enables the implementation of FPGA applications through a model-based design approach within MATLAB Simulink [40]. This tool operates by providing a dedicated digital signal processing (DSP) block set tailored for Xilinx devices within the Simulink environment, allowing designers to construct models according to specific design requirements.

In this work, a subsystem block is used for each rational component (IIR filter) contained in the transfer function, and these subsystems are integrated with pre-configured adder blocks. Gateway blocks are used to facilitate communication between Simulink and FPGA blocks [19,41].

3. Results and Discussion

3.1. Computational Results

The magnitude and phase responses of the fifth integer-order transfer functions obtained for the FO derivative operator s^0.5 by MSBL, Oustaloup, and Matsuda approximation methods and the proposed method are compared with the analytical frequency response of s^0.5 in Figure 3. The curves obtained by the proposed method are referred to as “Optimized MSBL” in all figures. As seen in Figure 3, the frequency response of the optimized transfer function based on the MSBL approximation method closely matches that of the original MSBL approximation method. For quantitative analysis, RMSE and MAPE values for the frequency response were computed at 10³ logarithmically distributed points within the frequency range of ω ∈ [0.01, 100] rad/s. RMSE and MAPE values were calculated for the magnitude and phase responses shown in Figure 3, and the results are summarized in

Table 1. Error comparisons for magnitude, phase, and step responses based on different frequency-based approximation methods for derivative operator s^0.5, ω ∈ [0.01, 100] rad/s.

FO Methods	RMSE			MAPE (%)
	Frequency Response		Time Response	Frequency Response		Time Response
	Magnitude	Phase	Step	Magnitude	Phase	Step
MSBL	0.1426	1.5070	0.0101	2.42	2.57	9.51
Opt. MSBL	0.1012	0.8057	0.0060	1.49	1.57	4.23
Oustaloup	0.1218	2.6933	0.0104	3.50	5.27	7.34
Matsuda	0.0942	1.6376	0.0078	1.73	2.68	2.34

. As shown in Table 1, the frequency-domain approximation performance of the proposed method is slightly superior to that of the original MSBL method and other approximation methods in general. This shows that an improvement can be achieved in the realization of the FO transfer functions when an optimization process is applied to the transfer function obtained with the FO approximation methods.

Considering that frequency-based optimization may negatively affect the time response, 100 s step responses were obtained for the transfer functions based on the specified approximation methods and the FMINCON optimization method and analyzed by comparing with the analytical response of s^0.5. The comparison of step responses is presented in Figure 4. As seen in this figure, the step response based on the optimization of the MSBL approximate transfer function follows the analytical step response slightly better than the other step responses based on the other approximation methods. For quantitative analysis, RMSE and MAPE values are calculated for the step responses shown in Figure 4, and the results are presented in Table 1. As seen in Table 1, RMSE and MAPE values denote that frequency-based optimization does not negatively affect the time response and even causes a slight improvement in the time response.

Also, to check the validity of the proposed method, the method was tested at different frequency ranges. The frequency responses of the transfer functions obtained for the fifth-order MSBL approximation method and the proposed method were comparatively illustrated for the derivative operator s^0.5 in the frequency ranges of [0.1–10] rad/s, [0.01–100] rad/s, and [0.001–1000] rad/s in Figure 5, and the error values obtained for this figure are shown in

Table 2. Error comparison of the frequency responses of the transfer functions obtained for the 5th order MSBL approach and the proposed method for the derivative operator s^0.5 in the frequency ranges of [0.1–10] rad/s, [0.01–100] rad/s, and [0.001–1000] rad/s.

Frequency Range (rad/s)	FO Methods	RMSE		MAPE (%)
		Magnitude	Phase	Magnitude	Phase
[0.1–10]	MSBL	0.0020	0.1296	0.10	0.22
	Opt. MSBL	0.0015	0.0654	0.09	0.12
[0.01–100]	MSBL	0.1426	1.5070	2.42	2.57
	Opt. MSBL	0.1012	0.8057	1.49	1.57
[0.001–1000]	MSBL	1.1261	4.3136	9.46	8.13
	Opt. MSBL	0.7443	3.0711	5.21	6.00

. As seen in Figure 5 and Table 2, the proposed method has exhibited better results compared to the conventional MSBL method, even in different frequency ranges.

Additionally, the performance of the method was checked for a different approximation order (third order). The frequency responses of the transfer functions obtained for the third-order MSBL approximation method and the proposed method were comparatively illustrated for the derivative operator s^0.5 in the frequency ranges of [0.01–100] rad/s in Figure 6, and the error values obtained for this figure are shown in

Table 3. Error comparison of the frequency responses of the transfer functions obtained according to the 3rd order MSBL approximation and the proposed method for the derivative operator s^0.5 in the frequency range of 0.01–100 rad/s.

FO Methods (3rd Order)	RMSE		MAPE (%)
	Magnitude	Phase	Magnitude	Phase
MSBL	0.5483	7.6514	15.78	14.50
Opt. MSBL	0.3716	4.7587	7.88	9.13

. As seen in Figure 6 and Table 3, the proposed method has exhibited better results compared to the conventional MSBL method for the third-order approximation, too. So, one can conclude that the proposed method shows high performance for different frequency ranges and different orders of the approximation.

To evaluate the performance of this optimization method for different systems, it is applied to an FOPID controller transfer function which is taken as

$$C\left(s\right) = 5+{\displaystyle \frac{1}{s^{0.8}}}+2s^{0.5}$$

(17)

By applying the optimization method to MSBL-based approximate transfer function, the approximate FO transfer function for C (s) can be expressed as

$$\begin{gathered} F_c\left(s\right)\cong {\displaystyle \frac{55.12s^{10}+5642s^9+1.712\cdot {10}^5{s}^8+1.666\cdot {10}^6{s}^7+5.977\cdot {10}^6{s}^6+\dots }{1.19s^{10}+280.5s^9+1.246\cdot {10}^4{s}^8+1.703\cdot {10}^5{s}^7+7.296\cdot {10}^5{s}^6+\dots }} \\ {\displaystyle \frac{\dots +7.987\cdot {10}^6{s}^5+4.171\cdot {10}^6{s}^4+8.827\cdot {10}^5{s}^3+7.802\cdot {10}^4{s}^2+2466s+25.18}{\dots +1.087\cdot {10}^6{s}^5+5.256\cdot {10}^5{s}^4+8.822\cdot {10}^4{s}^3+4507s^2+68.09s+0.1178}} \end{gathered}$$

(18)

The frequency response of F_c (s) is illustrated in Figure 7. As illustrated in this figure, optimizing the transfer function coefficients does not result in any significant deterioration in either the magnitude or phase response; in fact, an enhancement in the phase response can be observed. The frequency response error was evaluated at 10³ logarithmically spaced points within the frequency range ω ∈ [0.01, 100] rad/s, with the results summarized in

Table 4. The error values for magnitude, phase, and step responses based on different frequency-based approximation methods for FOPID controller, ω ∈ [0.01, 100] rad/s.

FO Methods	RMSE			MAPE (%)
	Frequency Response		Time Response	Frequency Response		Time Response
	Magnitude	Phase	Step	Magnitude	Phase	Step
MSBL	0.3770	1.0743	0.9279	1.28	4.31	2.12
Opt. MSBL	0.3117	0.4546	0.2909	0.83	3.19	0.59
Oustaloup	0.3354	1.8939	0.6540	1.83	8.08	1.41
Matsuda	0.2645	1.1130	0.0692	1.00	3.58	0.17

. The RMSE and MAPE error values presented in the table demonstrate that the optimization method has effectively improved the frequency response of the FOPID controller.

Figure 8 presents a 100 s analytical step response of F_c (s) in comparison with the step responses obtained by the proposed method and the other FO approximation methods. The step response based on the optimized transfer function demonstrates satisfactory performance over a 100 s step response. Notably, the difference between the step response based on the MSBL approximate transfer function and that of the optimized MSBL function clearly shows that the applied optimization method also results in an improvement in the time response. The RMSE and MAPE values for the time response, provided in Table 4, further confirm that the FMINCON optimization algorithm has effectively enhanced the time response for the MSBL approximation.

Although the FMINCON optimization targeted the frequency-domain magnitude and phase errors, it preserved the dominant pole–zero structure associated with the system’s transient behavior. Consequently, the time response was not degraded and, in some cases, was slightly improved due to better alignment of damping and phase margin. Time-domain degradation could only occur if the optimization were overly biased toward high-frequency accuracy or if the poles were shifted too close to the imaginary axis—conditions that were prevented in the present formulation.

As another example, the optimization method is applied to optimize a transfer function obtained by MSBL approximation method for an FO low pass filter that is expressed as

$$H\left(s\right) = {\displaystyle \frac{2}{0.5\cdot s^{1.1}+3}}$$

(19)

By using the proposed method, approximate integer-order transfer function for FO filter is obtained as

$$F_{lp}\left(s\right)\cong {\displaystyle \frac{2.335s^5+233.1s^4+2211s^3+2458s^2+321.8s+4.181}{1.045s^6+83.95s^5+964.2s^4+3869s^3+3746s^2+483.3s+6.271}}$$

(20)

In Figure 9, the frequency response based on the optimized transfer function given in Equation (20) was compared with the analytical frequency response and the frequency responses based on the MSBL, Oustaloup, and Matsuda approximate transfer functions for the FO low pass filter. As shown, the responses produced by the various approximation methods are closely aligned. While the optimized MSBL method demonstrates moderate performance relative to the other methods for the fractional-order filter under consideration, the RMSE and MAPE values in

Table 5. The error comparisons of magnitude and phase responses based on different frequency-based approximation methods for FO low pass filter, ω ∈ [0.01, 100] rad/s.

FO Methods	RMSE		MAPE (%)
	Magnitude	Phase	Magnitude	Phase
MSBL	0.0008	0.3121	0.23	2.56
Opt. MSBL	0.0008	0.1438	0.29	1.42
Oustaloup	0.0019	0.4774	0.49	1.02
Matsuda	0.0009	0.3399	0.26	0.49

indicate that the optimized MSBL method yields lower error values compared to the original MSBL method, especially for the phase response.

3.2. Digital Realization Results

To realize the derivative operator s^0.5 in FPGA simulation, the optimized continuous-time approximate transfer function of s^0.5 was first expressed in the form of sum of low pass filters by fractional expansion method, and then this expression was converted to a discrete-time approximate transfer function in the form of sum of IIR filters by Tustin method as shown in Equation (11). Each rational part of Equation (11), which represents an IIR filter, is designed using Vitis Model Composer Hub system generator in the base of the explanations mentioned in Section 2.3. The continuous-time transfer functions obtained by Oustaloup, Matsuda, MSBL approximation methods, and the proposed method are converted to the discrete-time transfer functions. Then, all the discrete-time transfer functions are implemented in parallel with each other as shown in Figure 10. The input and output signals, which are colored yellow for each discrete-time transfer function, are displayed and compared with each other in a time scope.

Each discrete-time transfer function, which is composed of the sum of first-order IIR filters, which are colored with turquoise blue blocks and a gain block, was realized as the sum of subsystems, referred to as IIR_multx. The IIR_multx subsystems were integrated using the adder tree block from the Xilinx DSP library to produce the output of the function considered (see in Figure 11).

Within the subsystems, the Direct form I implementation of each IIR filter is realized using multipliers, two registers, a data type conversion block, and an adder tree. In Figure 12, the first rational component of Equation (14) is realized. The data type for constants is set to a 32-bit double-precision floating point. This choice is motivated by the high precision and wide dynamic range offered by floating-point representation, which allows for the accurate representation of very large and very small numbers, as well as fractions, with a reduced risk of overflow or underflow. Furthermore, floating-point precision simplifies the design and debugging process for many signal processing, control, and mathematical algorithms.

Then, different waveforms were applied to the input of the system to check the accuracy, consistency, and practicality for FPGA implementation. Initially, a chirp signal within the frequency range of [0.001, 1000] Hz was applied to the inputs to obtain the frequency response. For each FO approximation method, the resulting magnitude and phase response were plotted as shown in Figure 13. The RMSE and MAPE values were calculated within the frequency range of ω ∈ [1, 100] rad/s. These error values presented in

Table 6. The error comparisons of magnitude and phase responses for s^0.5 based on different frequency-based approximation methods for FPGA outputs, ω∈ [1, 100] rad/s.

FO Methods	RMSE		MAPE (%)
	Magnitude	Phase	Magnitude	Phase
MSBL	0.1983	1.5065	4.08	2.60
Opt. MSBL	0.0152	0.7778	3.08	1.45
Oustaloup	0.0177	2.5586	3.53	4.88
Matsuda	0.0460	1.6908	3.62	2.67

demonstrate that the optimization algorithm has effectively improved the frequency response of the MSBL approximation method. As seen in the table, this optimization-based method gives relatively better results compared to those based on the non-optimized discrete-time transfer functions obtained by the other FO approximation methods. The realization results indicate that the transfer function based on the optimization of the transfer function obtained by MSBL approximation method offers notable improvements in both magnitude and phase accuracy, especially at high frequencies.

To examine the practicality of the proposed method, the optimized transfer function, Equation (14), obtained for s^0.5 derivative operator was implemented on a Nexys 4 DDR Artix-7 FPGA (XC7A100T) by using Verilog HDL and basic digital design techniques. Xilinx Vivado Design Suite was utilized to generate the bitstream file for device programming. A sine input voltage of 0.1 V and 10 Hz was employed to evaluate the frequency response for comparison purposes. For testing, the input voltage was stored in a Look-Up Table (LUT) within the FPGA. The Pmod DA4 digital-to-analog converters were used to convert the FPGA’s digital outputs into analog signals, which were then visualized on an oscilloscope, as shown in Figure 14. A digital oscilloscope (FNIRSI-1013D) with two integrated analog input channels was employed to display the data waveforms [42].

In Figure 15, the yellow signal shows the sinusoidal input voltage of 0.1 V and 10 Hz stored in the LUT. When this signal is applied as input to the pre-configured FPGA, the output signal shown in blue is obtained. When the experimentally obtained gain and phase shift at the specified frequency are examined, it is seen that the obtained values are in great agreement with the gain and phase shift corresponding to the same frequency in the magnitude and phase response based on the simulation, shown in Figure 13.

The experiment was repeated ten times to assess repeatability and stability. The standard deviation of the measured magnitude and phase values across trials was below approximately 2% and 2°, respectively. The dominant uncertainty sources were attributed to the 12-bit DAC quantization and sampling jitter inherent to the FPGA clock. Furthermore, the implemented transfer function was tested under varying environmental conditions. Specifically, FPGA clock variations within ±0.2% and ambient temperature changes between 20 °C and 30 °C were introduced. No measurable degradation was observed in the output response, indicating that the realized system maintained its stability and accuracy under these conditions. Hardware resource utilization for the proposed optimized MSBL method (Equation (14)) was shown for the FO derivative operator s^0.5 in Figure 16.

4. Conclusions

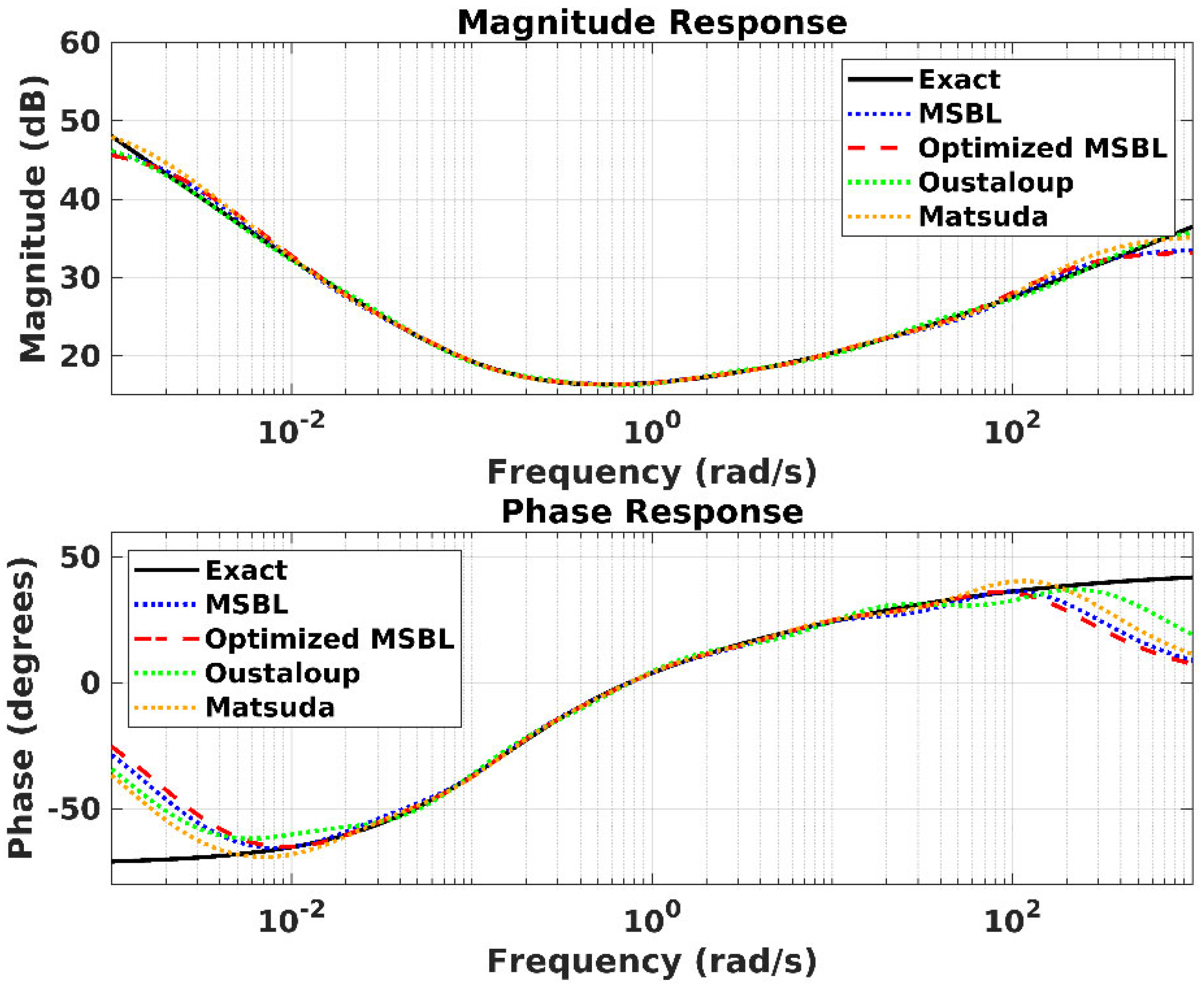
In practical applications of FO systems, because the FO operator cannot be implemented directly, frequency-domain approximation methods are often used to represent the FO transfer functions with integer-order approximate ones. For a more accurate implementation, it is crucial that the frequency responses based on the integer-order transfer functions obtained by these methods greatly agree with the analytically obtained responses. To enhance reliability and minimize errors, FMINCON optimization algorithm is applied to the cost function that considers the difference between analytically obtained frequency response and the frequency response of the integer-order transfer function obtained by the MSBL approximation method. The frequency–time responses of the optimized approximate transfer function were comparatively analyzed by considering the analytically obtained frequency–time responses and the frequency–time responses based on the MSBL, Oustaloup, and Matsuda approximation methods. Also, quantitative metrics such as RMSE and MAPE were employed to evaluate the approximation performance of the methods considered in both frequency and time domains. As a result of the optimization, a new transfer function, whose coefficients have been slightly modified, is obtained. This method was applied to an FO operator, an FOPID controller, and an FO low pass filter to check whether the predicted improvement in the realization performance was achieved. Application results have revealed that the proposed method generally resulted in expected improvements in the frequency response. Such improvements in the frequency response are particularly valuable for achieving optimal control performance in FO control systems. Additionally, the time responses for the FO operator and the FOPID controller were investigated, and it was observed that the proposed method did not have a salient negative effect on the time response but rather provided a small improvement in the time response in general.

Furthermore, to show the practicality and make a comparative analysis, the fifth-order approximate transfer functions based on the MSBL, Oustaloup, Matsuda approximation methods, and the proposed method, were digitally implemented for the derivative operator s^0.5 on an FPGA using the Vitis Model Composer Hub system generator block within the MATLAB Simulink environment. The results of the FPGA implementation confirmed the effectiveness of the proposed method by exhibiting good agreement with the analytical frequency response in the defined frequency range. Following the realization in simulation environment, the optimized transfer function was experimentally implemented on a Nexys 4 DDR Artix-7 FPGA (XC7A100T). It was observed that the FPGA implementation and simulation results were in good agreement with each other when the gain and phase shift are considered at the operating frequency. The agreement confirms that FPGA provides high accuracy and reliability in replicating the dynamic behavior in the specified frequency range.

These findings demonstrate that applying an optimization method immediately after applying any integer-order approximation method to an FO system and then proceeding with the implementation will increase the accuracy and reliability of the implementation. The proposed FMINCON-based optimization is not specific to the MSBL method and can be generalized for other methods. It can also be directly applied to other FO approximation methods, such as Carlson, CFE, Oustaloup, etc., to improve their frequency responses. At this point, it is crucial to carefully select the optimization method to be applied.