Evaluation of the Interactions of Multiple Inverter-Based Resources Using 2DOF Elastic Energy Equivalent System
Abstract
1. Introduction
- (1)
- The 2DOF-EEES is proposed to describe the interactions in the power systems integrated with multiple IBRs in real time.
- (2)
- The 2DOF-EEES can decouple the interactions of the IBRs to the grid and IBR to the IBR. This is achieved by calculating the work performed in the direction of the common branch and in its vertical direction for the 2DOF-EEES, which is defined as the common-mode energy and differential-mode energy.
- (3)
- The existence of the differential-mode energy will affect the common-mode energy through the equivalent elastic structure in the 2DOF-EEES, thus affecting the interaction between the wind farm and the network.
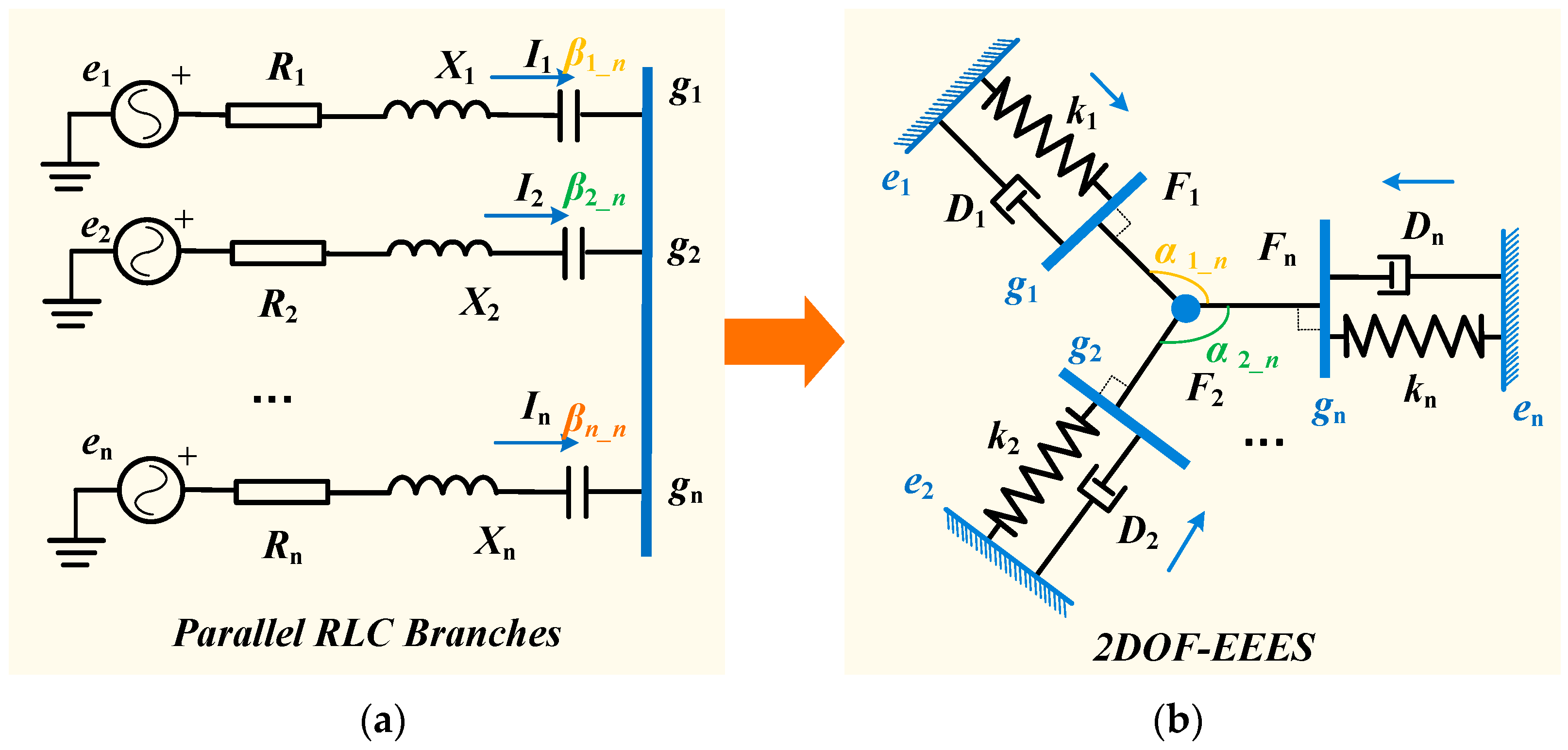
2. Proposed 2DOF Elastic Energy Equivalent System
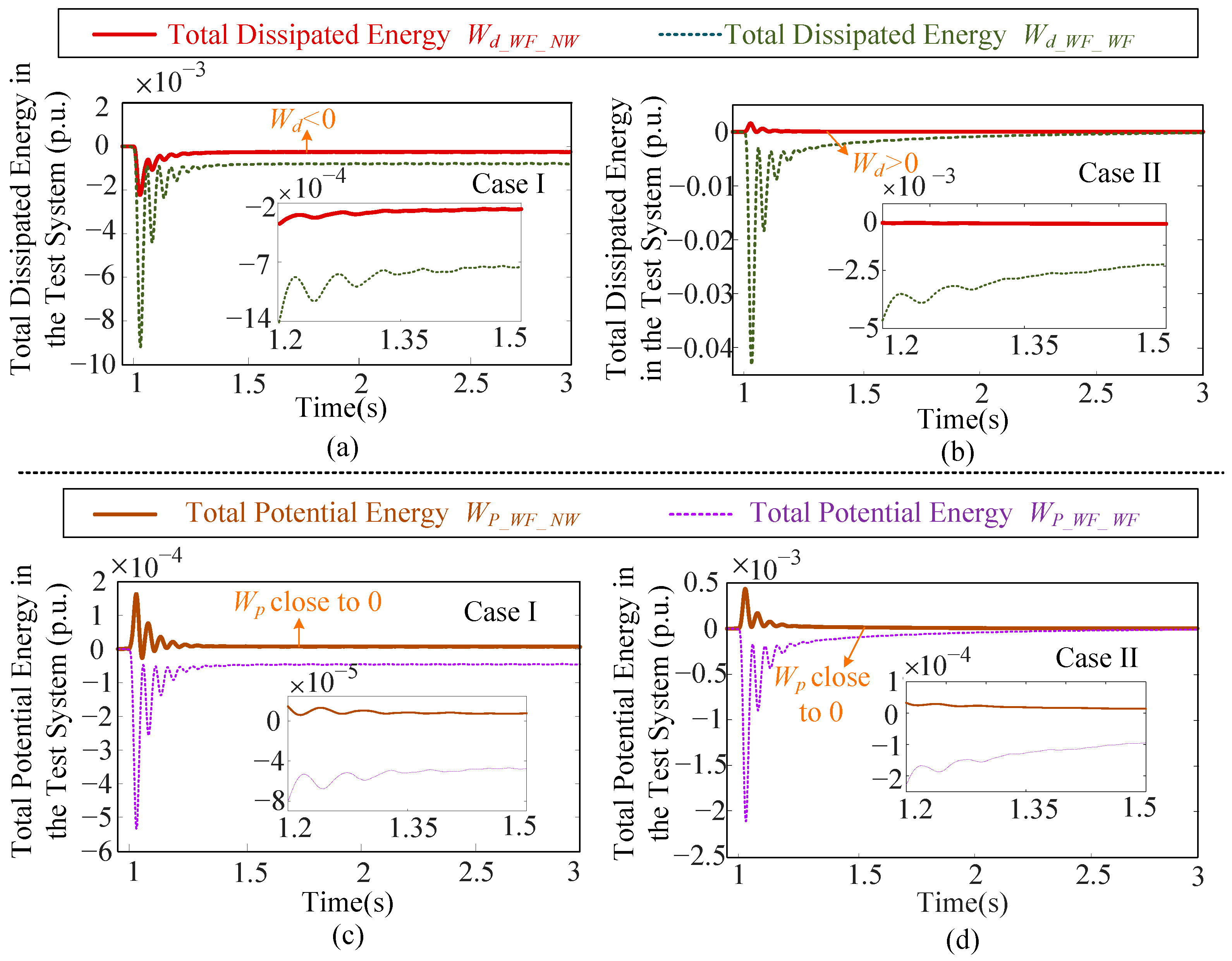
- (1)
- The dissipated work of the 2DOF-EEES is negative.
- (2)
- The work related to the potential energy of the 2DOF-EEES is close to zero. In the next section, the proposed 2DOF-EEES is applied to analyze the SSCI.
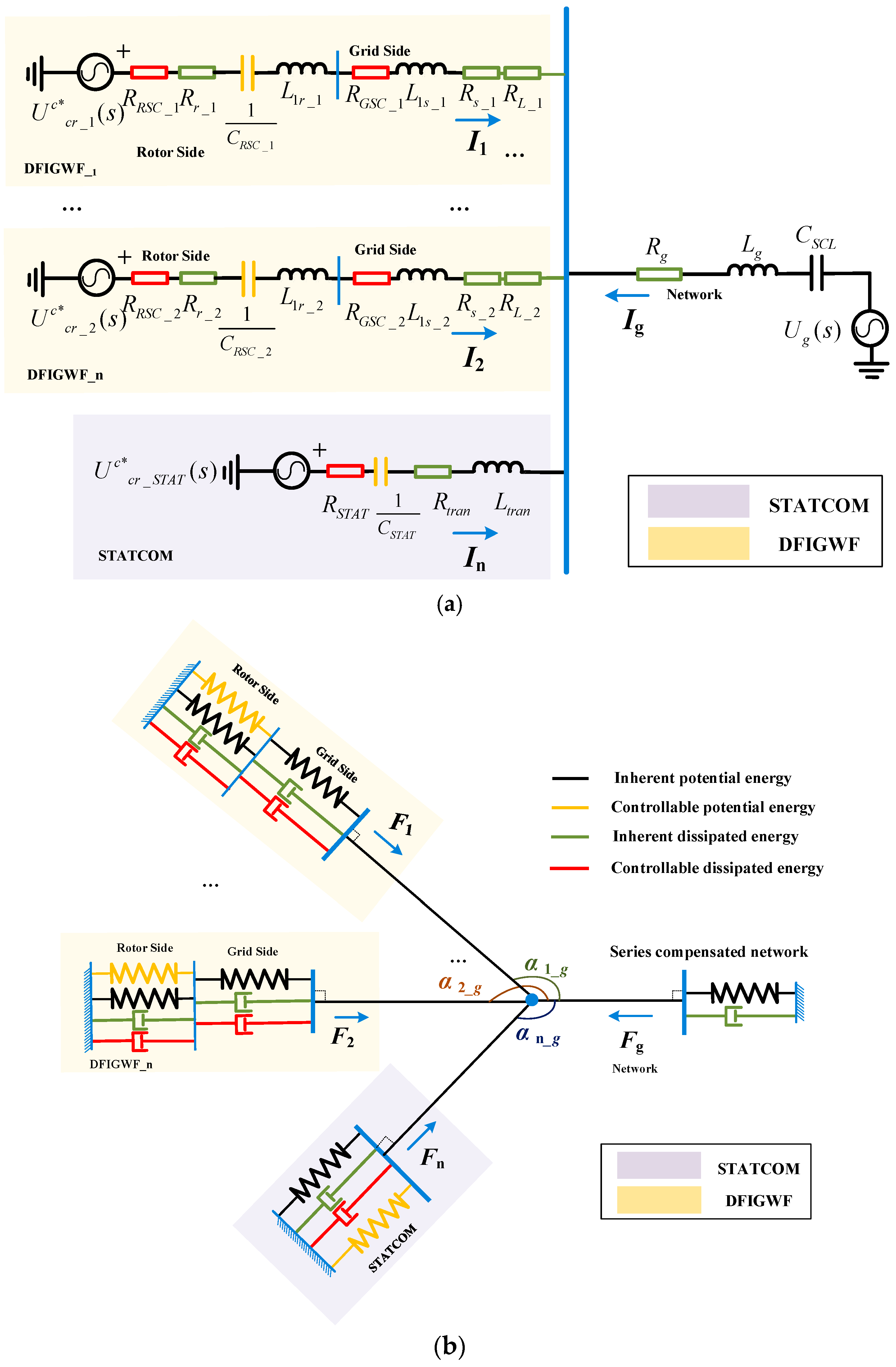
3. The 2DOF-EEES of the DFIG-Based Wind Farms
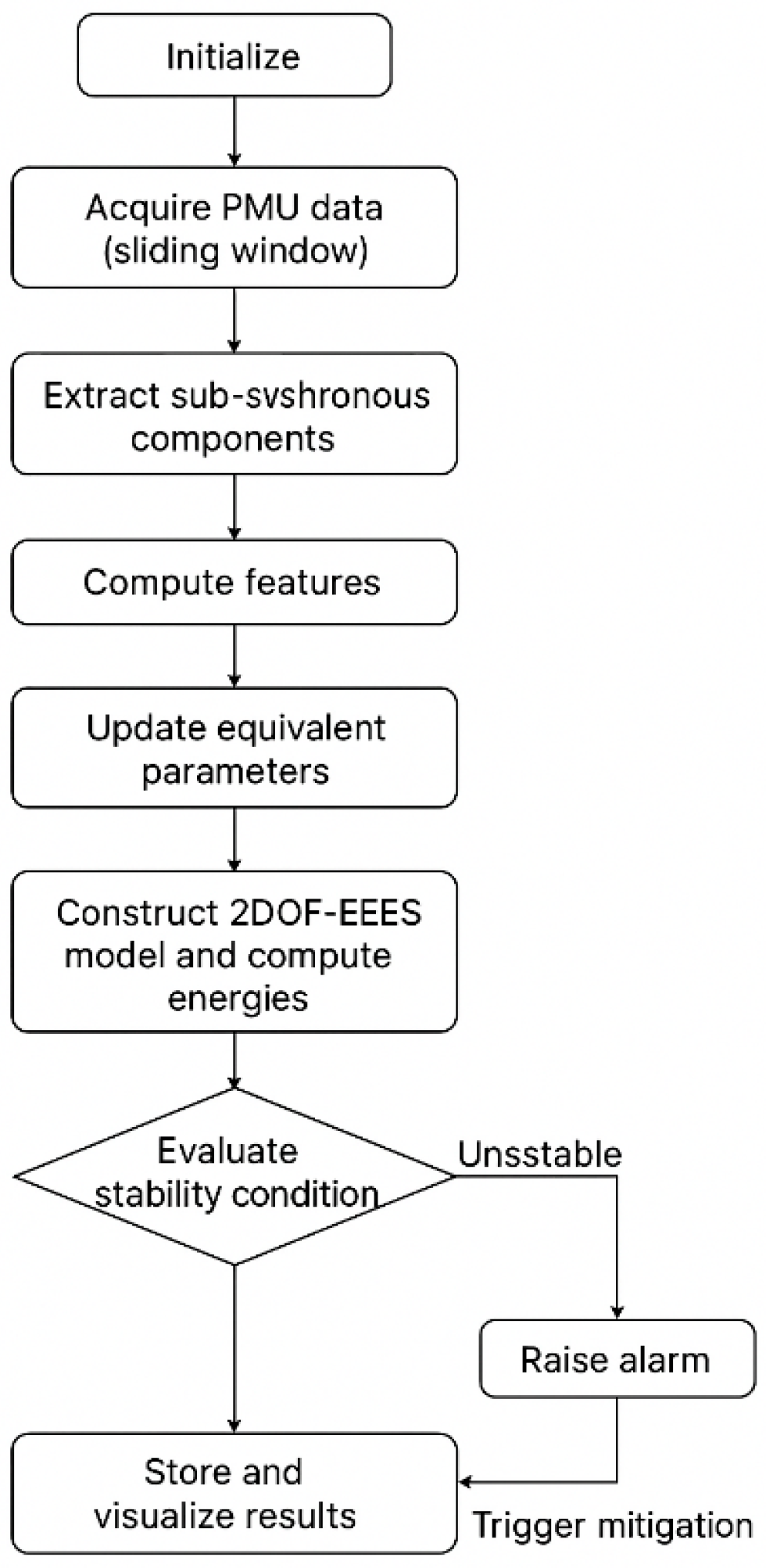
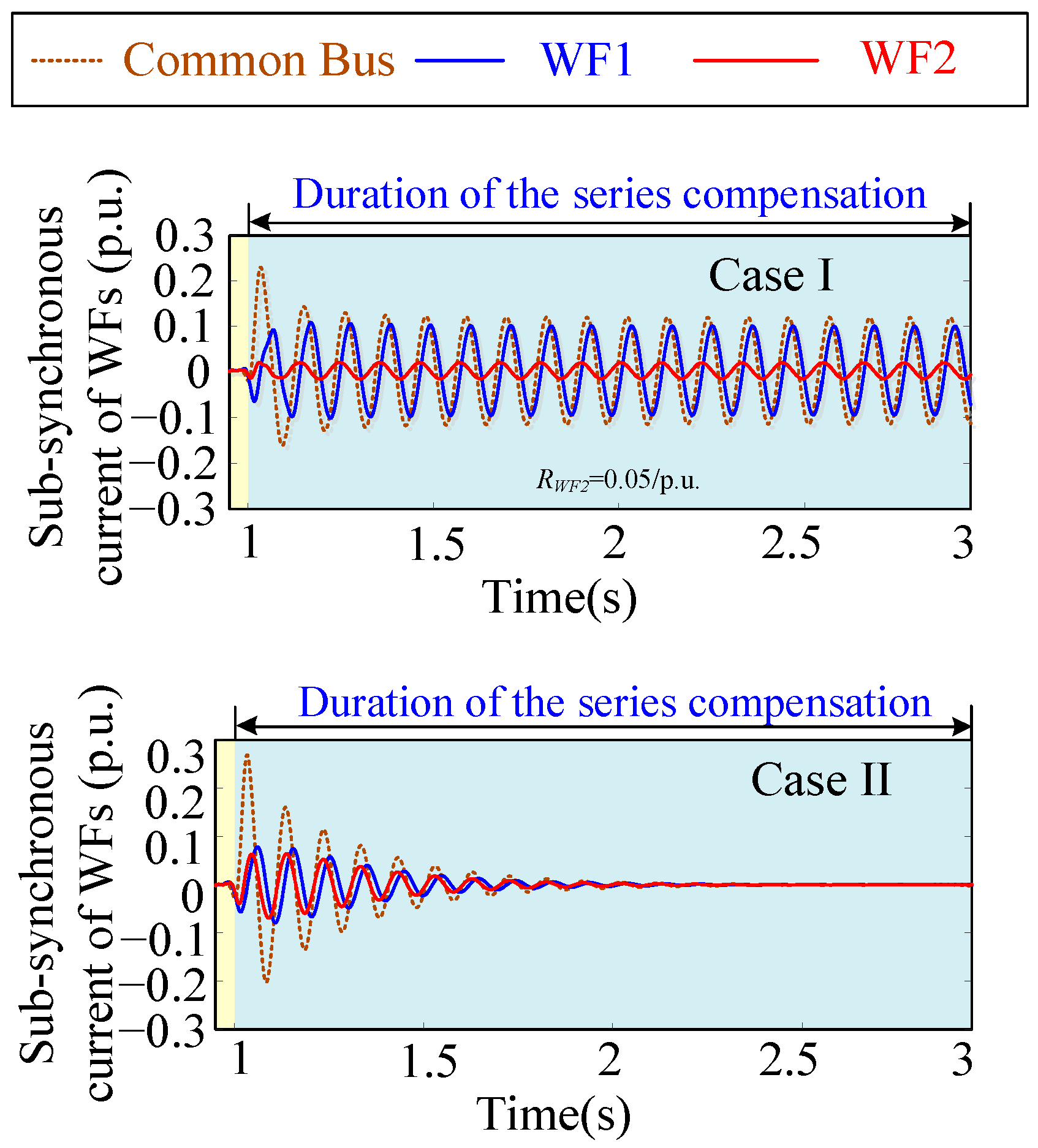
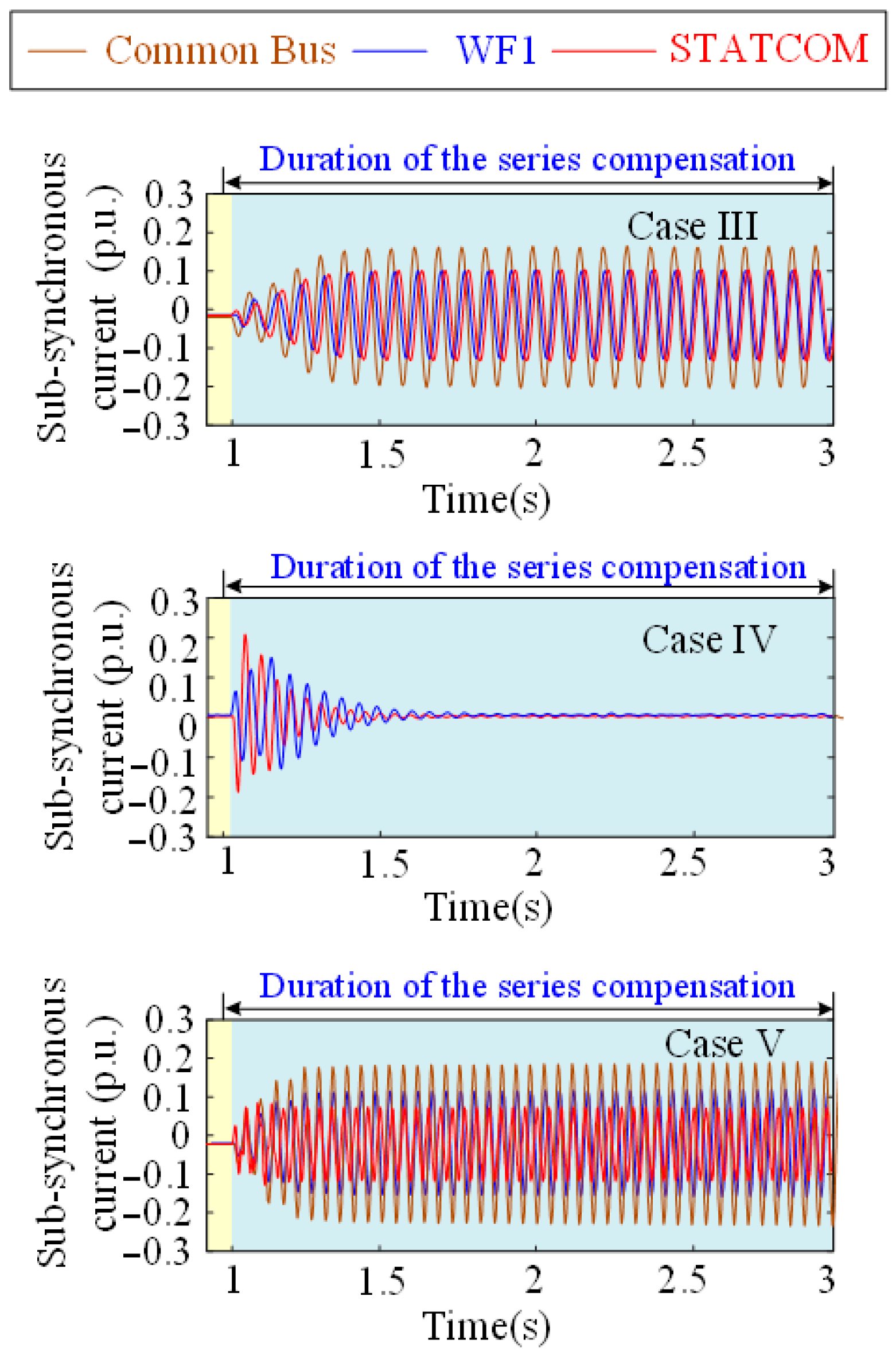
4. Case Study and Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variables | Definition |
|---|---|
| βn_n | The current phase angle of the common branch, βn_n = 0. |
| βi_n | The current phase angle deviation between the common branch and ith RLC branch. |
| αi_n | The angle deviation for the ith spring–damper branch. |
| Wh, Wv | The work performed in the direction of the common branch and in its vertical direction. |
| Wh_d, Wv_d | The dissipated energy of the 2DOF-EEES in the horizontal direction and vertical direction. |
| Wh_p, Wv_p | The potential energy of the 2DOF-EEES in the horizontal direction and vertical direction. |
| Fi, li | The force and deformation of the ith branch. |
| θeg | The voltage phase deviation of the RLC branch |
| Ri, Xi | The resistance and reactance of the ith series RLC branch. |
| Di, ki | The damping and stiffness coefficients of the ith equivalent spring–damper branch. |
| ωm | The angular frequency of mechanical system. |
| ωe | The angular frequency of series RLC circuit. |
| I0, I | The initial and real-time RMS value of the branch current. |
| DDFIGWF_i, kDFIGWF_i | The damping and stiffness coefficients of ith DFIG-based wind farm. |
| DSTATCOM, kSTATCOM | The damping and stiffness coefficients of the STATCOM. |
| Wd_WF_NW, Wp_WF_NW | The common-mode dissipated energy and potential energy between the wind farms and the network. |
| Wd_WF, Wp_WF | The differential-mode dissipated energy and potential energy among the IBRs. |
| Ii | The output current of ith DFIG-based wind farm. |
| Rr_i, Rs_i, RL_i | The resistances of the rotor winding, stator winding, and transmission line of the ith DFIG-based wind farm. |
| L1r_i, L1s_i, LL_i | The inductances of the rotor winding, stator winding, and transmission line of the ith DFIG-based wind farm. |
| Lm | The magnetizing inductance. |
| Es | The amplitude of stator voltage. |
| RwRSC_i, RwGSC_i | The equivalent resistances of the RSC and GSC of the ith DFIG-based wind farm. |
| CwRSC_i, CwGSC_i | The equivalent capacitor of the RSC and GSC controller of the ith DFIG-based wind farm. |
| RSTAT, LSTAT | The equivalent resistance and inductance of the STATCOM. |
| kp1, ki1 | The proportional and integral gains of the outer loop in RSC controller. |
| kp2, ki2 | The proportional and integral gains of the inner loop in RSC controller. |
| kp3, ki3 | The proportional and integral gains of the Udc regulator in GSC controller. |
| kp4, ki4 | The proportional and integral gains of the current regulator. |
References
- Salehi, F.; Matsuo, I.B.M.; Brahman, A.; Tabrizi, M.A.; Lee, W.-J. Sub-Synchronous Control Interaction Detection: A Real-Time Application. IEEE Trans. Power Deliv. 2020, 35, 106–116. [Google Scholar] [CrossRef]
- Wu, X.; Xu, S.; Feng, S.; Fan, L.; Gu, W. Time-varying Sub-synchronous Oscillation Mitigation Strategy for DFIG Wind Farms Based on Improved Adaptive Notch Filter. Proc. CSEE 2024, 44, 1836–18498. [Google Scholar]
- Shair, J.; Xie, X.; Wang, L.; Liu, W.; He, J.; Liu, H. Overview of emerging subsynchronous oscillations in practical wind power systems. Renew. Sust. Energ. Rev. 2019, 99, 159–168. [Google Scholar] [CrossRef]
- Virulkar, V.; Gotmare, G. Sub-synchronous resonance in series compensated wind farm: A review. Renew. Sustain. Energy Rev. 2016, 55, 1010–1029. [Google Scholar] [CrossRef]
- Bin, Z.; Feng, X.; Miao, Z.; Kong, X.; Li, P.; Shao, B. Frequency Characteristic Analysis of the VSC-HVDC DC Oscillating Power under AC Sub-Synchronous Disturbances. Electronics 2024, 13, 3445. [Google Scholar] [CrossRef]
- Chao, W.; Deng, C.; Huang, J.; Dai, L.; Min, Y.; Cheng, Y.; Wang, Y.; Liao, J. A Sub-Synchronous Oscillation Suppression Strategy Based on Active Disturbance Rejection Control for Renewable Energy Integration System via MMC-HVDC. Electronics 2023, 12, 2885. [Google Scholar] [CrossRef]
- Shair, J.; Xie, X.; Liu, W.; Li, X.; Li, Z. Modeling and stability analysis methods for investigating sub-synchronous control interaction in large-scale wind power systems. Renew. Sustain. Energy Rev. 2021, 135, 110420. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Gao, X.; Liu, H.; Li, Y. Stability analysis of SSR in multiple wind farms connected to series-compensated systems using impedance network model. IEEE Trans. Power Syst. 2018, 33, 3118–3128. [Google Scholar] [CrossRef]
- Miao, Z. Impedance-model-based SSR analysis for Type 3 wind generator and series-compensated network. IEEE Trans. Energy Convers. 2012, 27, 984–991. [Google Scholar] [CrossRef]
- Shao, B.; Zhao, S.; Gao, B.; Yang, Y.; Blaabjerg, F. Adequacy of the Single-Generator Equivalent Model for Stability Analysis in Wind Farms with VSC-HVDC Systems. IEEE Trans. Energy Convers. 2021, 36, 907–918. [Google Scholar] [CrossRef]
- Li, H.; Shair, J.; Zhang, J.; Xie, X. Investigation of sub-synchronous oscillation in a DFIG-based wind power plant connected to MTDC grid. IEEE Trans. Power Syst. 2023, 38, 3222–3231. [Google Scholar]
- Bostani, Y.; Jalilzadeh, S.; Mobayen, S.; Skruch, P.; Fekih, A.; Din, S. Damping sub-synchronous resonance in DFIG wind farms: An innovative controller utilizing wide-area measurement systems. Energy Rep. 2023, 10, 333–343. [Google Scholar] [CrossRef]
- Han, J.; Liu, C. Distributed Damping Evaluation for Series-Compensated DFIG-Based Wind Farms During the SSCI. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023. [Google Scholar]
- Du, W.; Chen, X.; Wang, H. DFIG oscillation modes causing strong dynamic interactions to degrade the damping of power system low-frequency electromechanical oscillations. Electr. Power Compon. Syst. 2019, 47, 288–300. [Google Scholar] [CrossRef]
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.; Bak, C.L. Bus participation factor analysis for harmonic instability in power electronics-based power systems. IEEE Trans. Power Electron. 2018, 33, 10341–10351. [Google Scholar] [CrossRef]
- Wu, M.; Xie, L.; Cheng, L.; Sun, R. A Study on the impact of wind farm spatial distribution on power system sub-synchronous oscillations. IEEE Trans. Power Syst. 2016, 31, 2154–2162. [Google Scholar] [CrossRef]
- Fan, L.; Zhu, C.; Miao, Z.; Hu, M. Modal analysis of a DFIG-based wind farm interfaced with a series compensated network. IEEE Trans. Energy Convers. 2011, 26, 1010–1020. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, H.; Ye, J.; Wang, J.; Liu, Q.; Li, S. Eigen-Sensitivity-Based Sliding Mode Control for LFO Damping in DFIG-Integrated Power Systems. Energies 2023, 16, 4256. [Google Scholar] [CrossRef]
- Zha, S.; Liao, M.; Huang, Z.; Yang, Z.; Sun, J. Dynamic aggregation modeling of grid-connected inverters using Hamilton’s-action based coherent equivalence. IEEE Trans. Ind. Electron. 2019, 66, 6437–6448. [Google Scholar] [CrossRef]
- Liao, S.; Chen, Y.; Huang, M.; Fu, X.; Zha, X.; Wang, L.; Luo, A.; Guerrero, J.M. Clustering-Based Modeling and Interaction Analysis of Multiple Differently Parameterized Grid-Side Inverters in PMSG Wind Turbines. IEEE Trans. Energy Conver. 2021, 36, 3031–3043. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, G.; Wang, X.; Wang, H.; Wang, L. Sub-Synchronous Oscillation Suppression Strategy Based on Impedance Modeling by Attaching Virtual Resistance Controllers for Doubly-Fed Induction Generator. Electronics 2022, 11, 2272. [Google Scholar] [CrossRef]
- Sun, D.-Y.; Qian, Z.-J.; Shen, W.-Q.; Zhou, K.; Jin, N.-Z.; Chen, Q.-G. Mechanism Analysis of Multiple Disturbance Factors and Study of Suppression Strategies of DFIG Grid-Side Converters Caused by Sub-Synchronous Oscillation. Electronics 2023, 12, 2293. [Google Scholar] [CrossRef]
- Ma, J.; Wang, L.; Cheng, P. An active damping control strategy for grid-tied Type-4 wind turbine generator based on energy feedback. IEEE Trans. Power Electron. 2022, 37, 5003–5020. [Google Scholar] [CrossRef]
- Ma, J.; Shen, Y.; Phadke, A.G. Stability assessment of DFIG susynchronous oscillation based on energy dissipation intensity analysis. IEEE Trans. Power Electron. 2020, 35, 8074–8087. [Google Scholar] [CrossRef]
- Liu, C.; Han, J. Evaluation of the Sub-Synchronous Control Interaction Based on the Elastic Energy Equivalent System. IEEE Trans. Power Syst. 2023, 38, 3897–3910. [Google Scholar] [CrossRef]
- Han, J.; Liu, C. Performance evaluation of the SSCI damping controller based on the elastic energy equivalent system. Appl. Energy 2023, 331, 120270. [Google Scholar] [CrossRef]



| Impedance Models | 2DOF-EEES |
|---|---|
| R | ωmD |
| X/ωe | k |
| I | l |
| U | F |
| β | α |
| Variables | Definition | Value |
|---|---|---|
| PW1 | The capacity of the wind farm 1. | 46 MW |
| PW2 | The capacity of the wind farm 2. | 154 MW |
| Un | The rated voltage of wind farm. | 0.69 kV |
| fn | The synchronous frequency. | 50 Hz |
| Udc | The rated value of DC voltage between RSC and GSC. | 1.15 kV |
| Cdc | The value of DC capacitor between RSC and GSC. | 10 mF |
| kp1, ki1 | The proportional and integral gains of the outer loop in RSC controller. | 0.5, 10 |
| kp2, ki2 | The proportional and integral gains of the inner loop in RSC controller. | 0.6, 8 |
| kp3, ki3 | The proportional and integral gains of the Udc regulator in GSC controller. | 8, 400 |
| kp4, ki4 | The proportional and integral gains of the current regulator. | 0.83, 5 |
| Rs | The stator resistance. | 0.023 p.u. |
| Rr | The rotor resistance. | 0.016 p.u. |
| L1s | The inductances of the rotor winding. | 0.18 p.u. |
| L1r | The inductances of the stator winding. | 0.16 p.u. |
| Lm | The magnetizing inductance. | 2.9 p.u. |
| Es | The amplitude of stator voltage. | 1.0 p.u. |
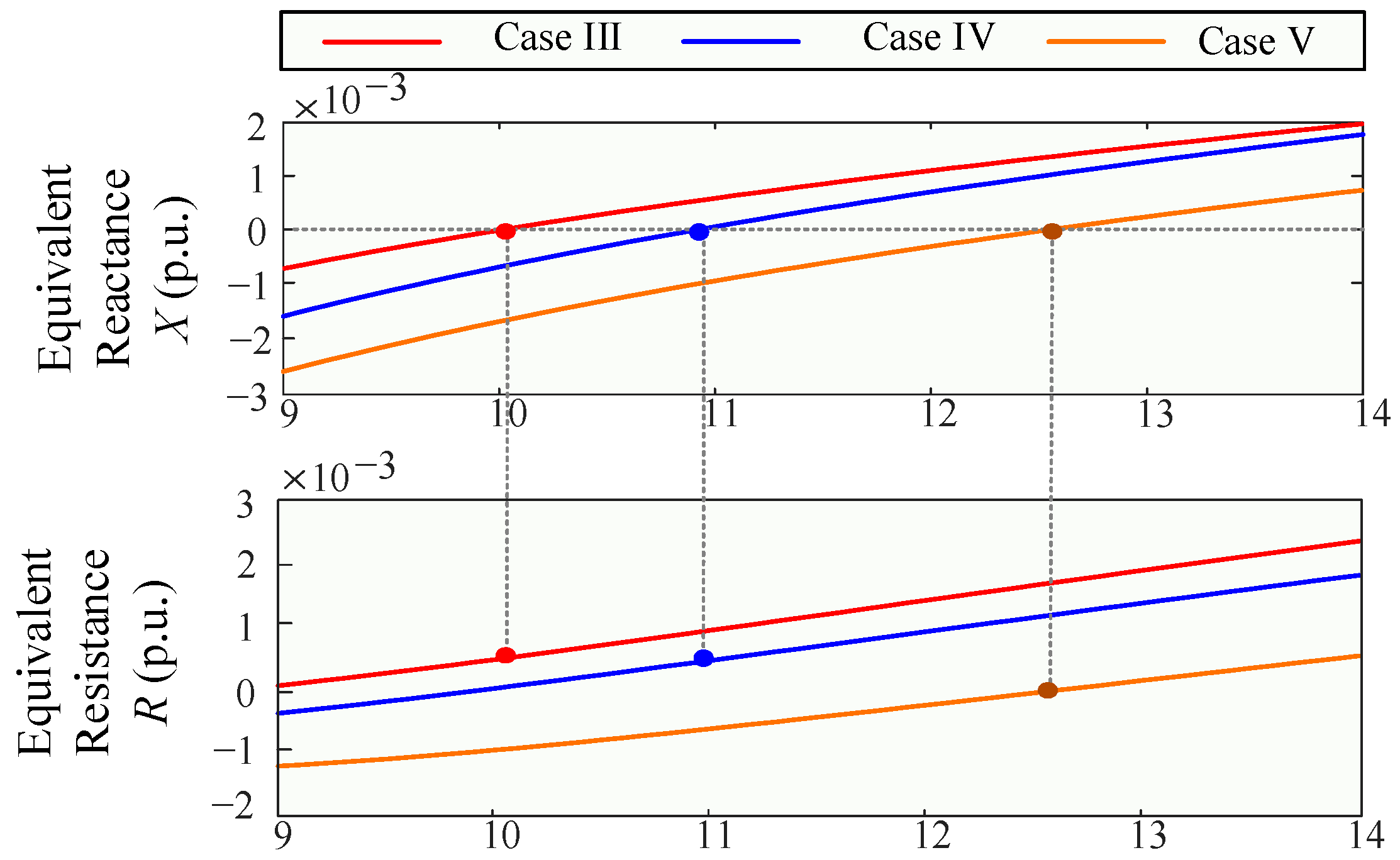
| Resonant Frequency | Equivalent Impedances | Phase Angle | |
|---|---|---|---|
| Case I | 10.3 Hz | −0.0093 p.u. | 182.5 |
| Case II | 9.5 Hz | −0.0087 p.u. | 181.6 |
| Energy Classification | Parameters | Variation Range |
|---|---|---|
| Common-mode dissipated energy | Wind speed Vw | −0.002–0.001 |
| Inner current control parameter of STATCOM kp4 | −0.0015–−0.0005 | |
| Common-mode potential energy | Wind speed Vw | 0.000005–0.00004 |
| Inner current control parameter of STATCOM kp4 | 0.00001–0.00002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Zheng, X.; Yu, Y.; Shang, L.; Bai, J.; Zheng, Y.; Wang, Y.; Ding, H.; Su, Z.; Dong, X. Evaluation of the Interactions of Multiple Inverter-Based Resources Using 2DOF Elastic Energy Equivalent System. Electronics 2025, 14, 4479. https://doi.org/10.3390/electronics14224479
Han J, Zheng X, Yu Y, Shang L, Bai J, Zheng Y, Wang Y, Ding H, Su Z, Dong X. Evaluation of the Interactions of Multiple Inverter-Based Resources Using 2DOF Elastic Energy Equivalent System. Electronics. 2025; 14(22):4479. https://doi.org/10.3390/electronics14224479
Chicago/Turabian StyleHan, Jiangbei, Xulin Zheng, Yilan Yu, Lei Shang, Jingjing Bai, Yang Zheng, Yuanyuan Wang, Hao Ding, Zhixiong Su, and Xuzhu Dong. 2025. "Evaluation of the Interactions of Multiple Inverter-Based Resources Using 2DOF Elastic Energy Equivalent System" Electronics 14, no. 22: 4479. https://doi.org/10.3390/electronics14224479
APA StyleHan, J., Zheng, X., Yu, Y., Shang, L., Bai, J., Zheng, Y., Wang, Y., Ding, H., Su, Z., & Dong, X. (2025). Evaluation of the Interactions of Multiple Inverter-Based Resources Using 2DOF Elastic Energy Equivalent System. Electronics, 14(22), 4479. https://doi.org/10.3390/electronics14224479






