Research on the Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate in a Moving Platform Distributed Coherent Synthesis System
Abstract
1. Introduction
- Theoretical Innovation: This research develops a generative error modeling framework grounded in stochastic process theory, moving beyond conventional white noise assumptions. By reversing the operation of the Adaptive Robust Kalman Filter (ARKF), it transforms the filter from a state estimator into a high-fidelity error trajectory generator that effectively captures temporal error inertia.
- Methodological Innovation: A hybrid adaptive compensation strategy incorporating a multi-index fusion adaptive factor is designed to ensure stable and efficient synthesis. This approach formulates the compensation task as an adaptive control problem, employing a mode-switching control law based on multiple fused innovation indicators. Theoretical analysis confirms this strategy guarantees global stability and mitigates the risk of divergence common in standard predictive filters under high dynamic conditions.
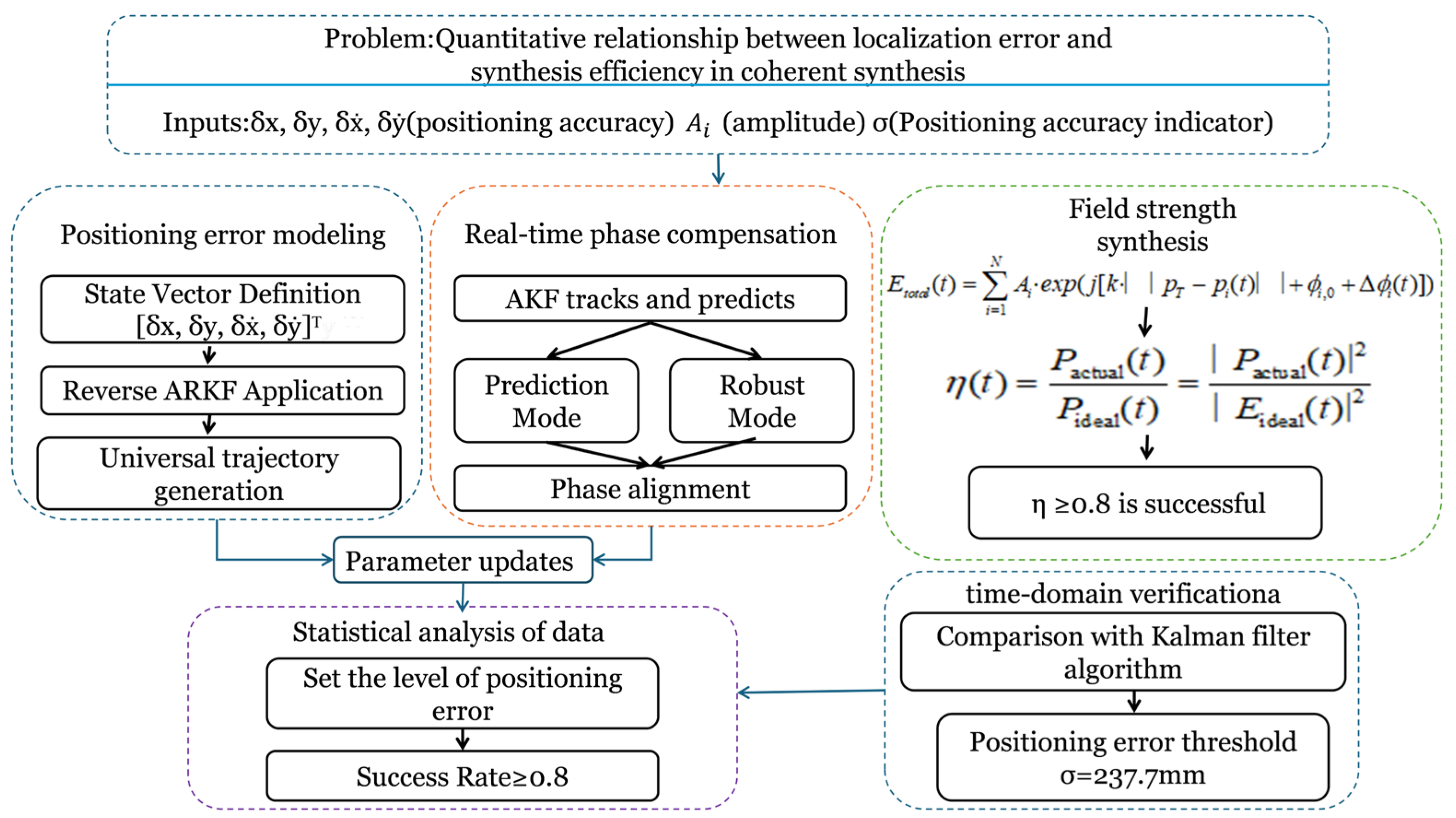
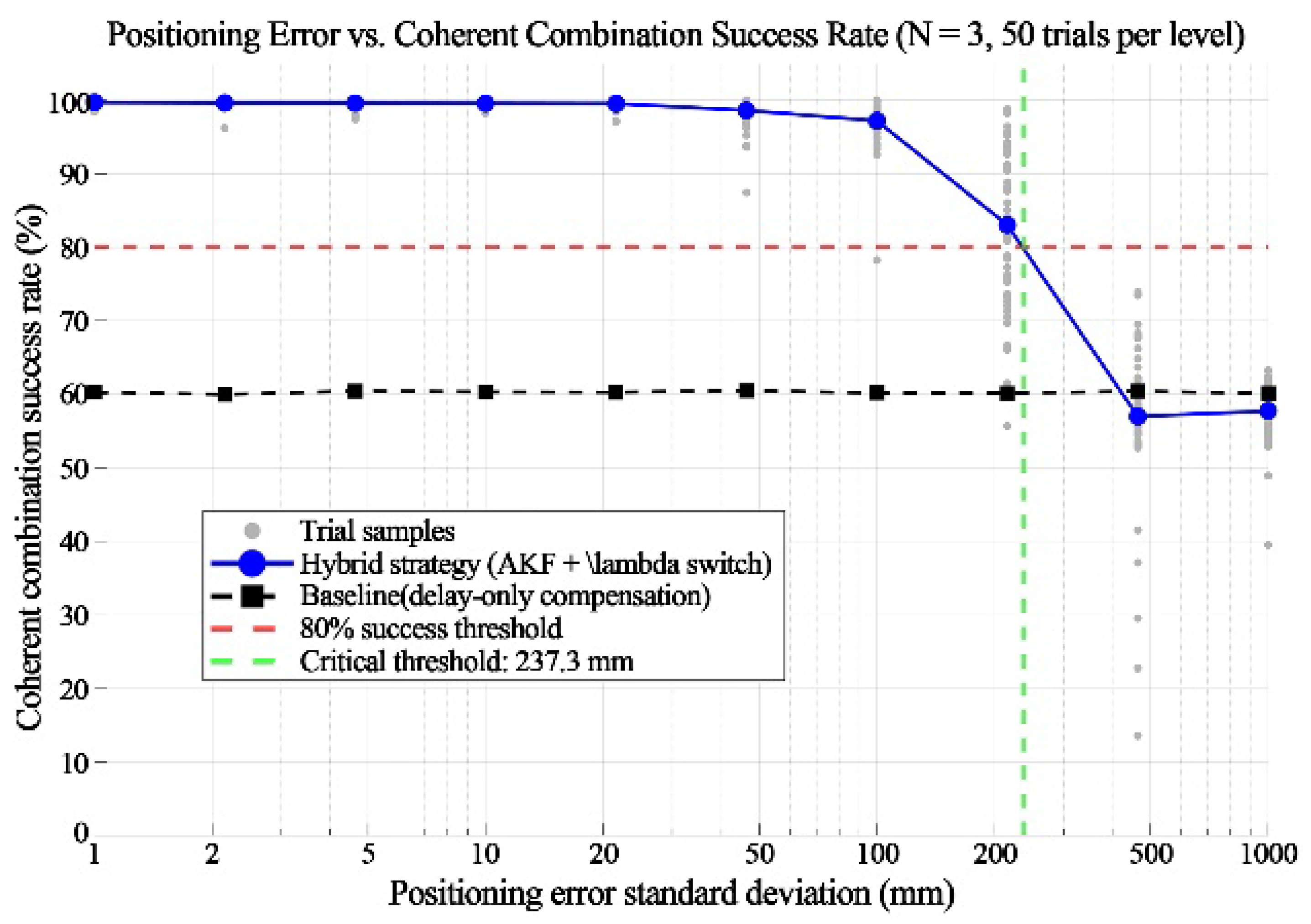
- Paradigm Innovation: A quantitative design paradigm mapping localization errors to synthesis performance is established for the first time, providing clear design criteria for system engineers. Specifically, through Monte Carlo simulations based on our framework, the quantitative relationship “positioning error standard deviation σ versus coherent synthesis success rate” is systematically charted for the first time, yielding critical performance thresholds (e.g., σ = 237.7 mm). This directly translates abstract error statistics into concrete, actionable specifications for navigation system accuracy design. The research block diagram of this paper is presented below.
2. Proposed Methodology and Simulation Framework
2.1. Universal Positioning Error Modeling
2.2. Real-Time Phase Compensation Strategy
2.3. Field Strength Synthesis and Performance Evaluation Standards
2.4. Simulation Setup
2.5. Experimental Setup and Evaluation Metrics
2.5.1. Input Data and Parameters
2.5.2. Output Results and Performance Metrics
3. Results and Discussion
3.1. Positioning Error Modeling Results and Discussion
3.1.1. Validation of ARKF Error Trajectory Characteristics
- (1)
- Temporal Continuity: Errors evolve smoothly, avoiding abrupt changes;
- (2)
- Error Inertia: Exhibiting systematic error characteristics similar to gyro drift, more realistically reflecting the physical properties of navigation systems [20].
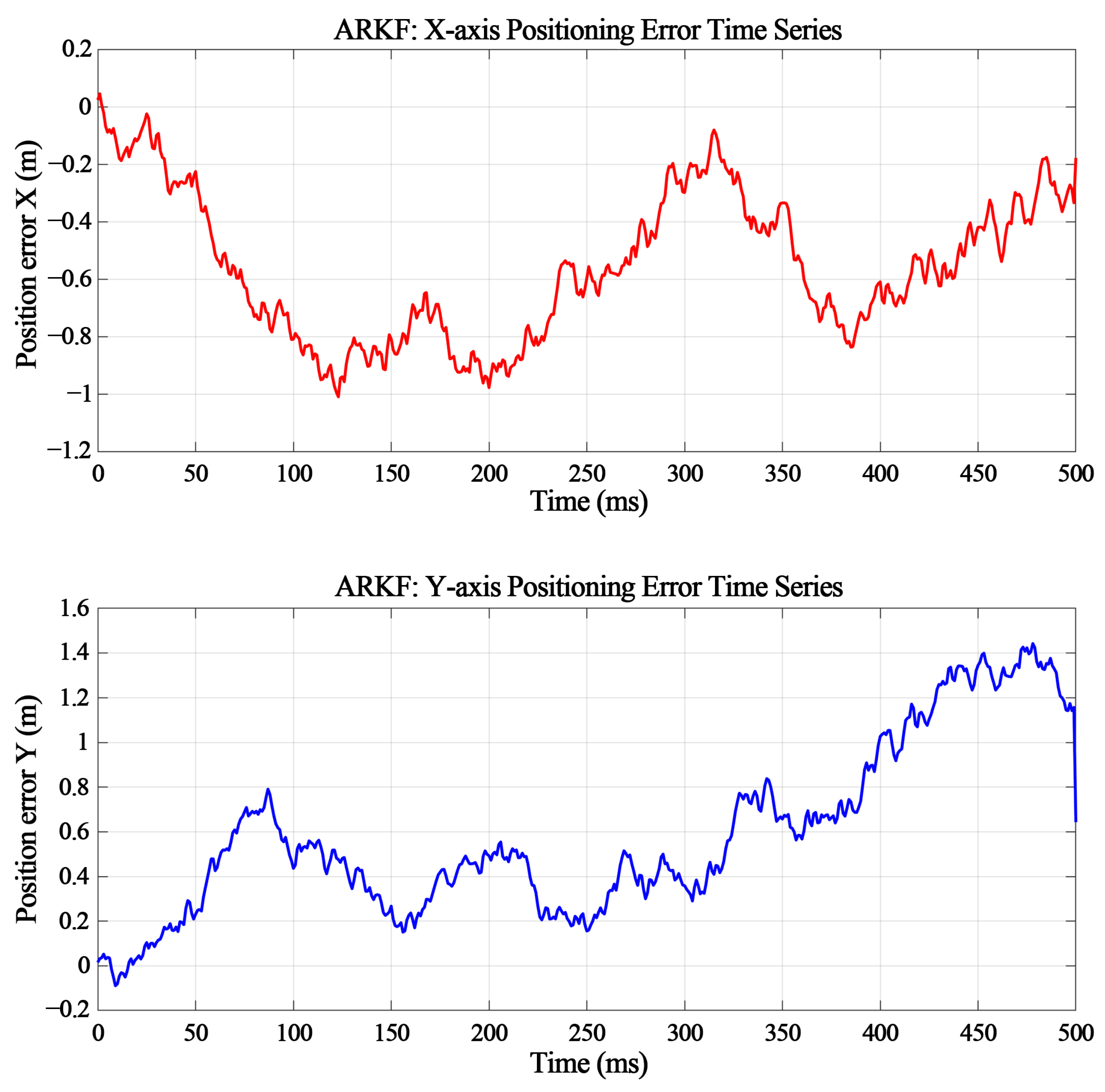
3.1.2. Comparative Analysis with Existing Error Modeling Methods
3.1.3. Model Parameter Sensitivity Analysis
3.2. Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate
3.2.1. Quantitative Analysis of Positioning Error Impact
3.2.2. Comparative Analysis with Existing Compensation Methods
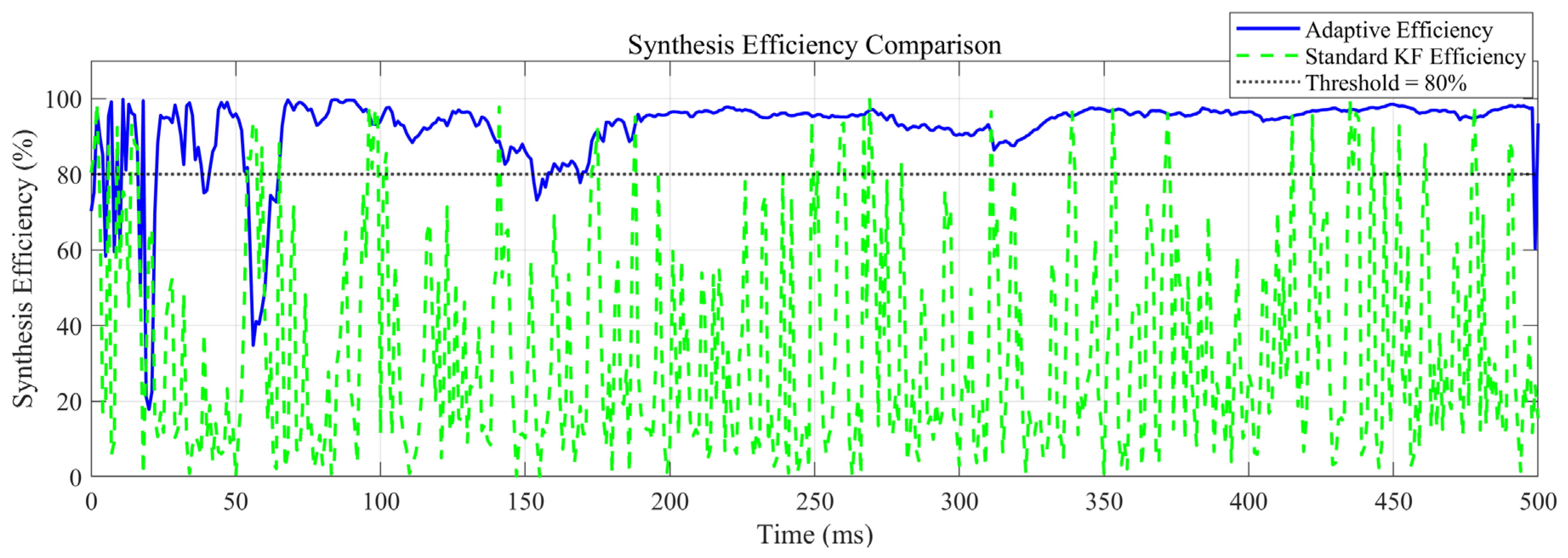
3.2.3. Comparative Analysis with Kalman Filtering Method
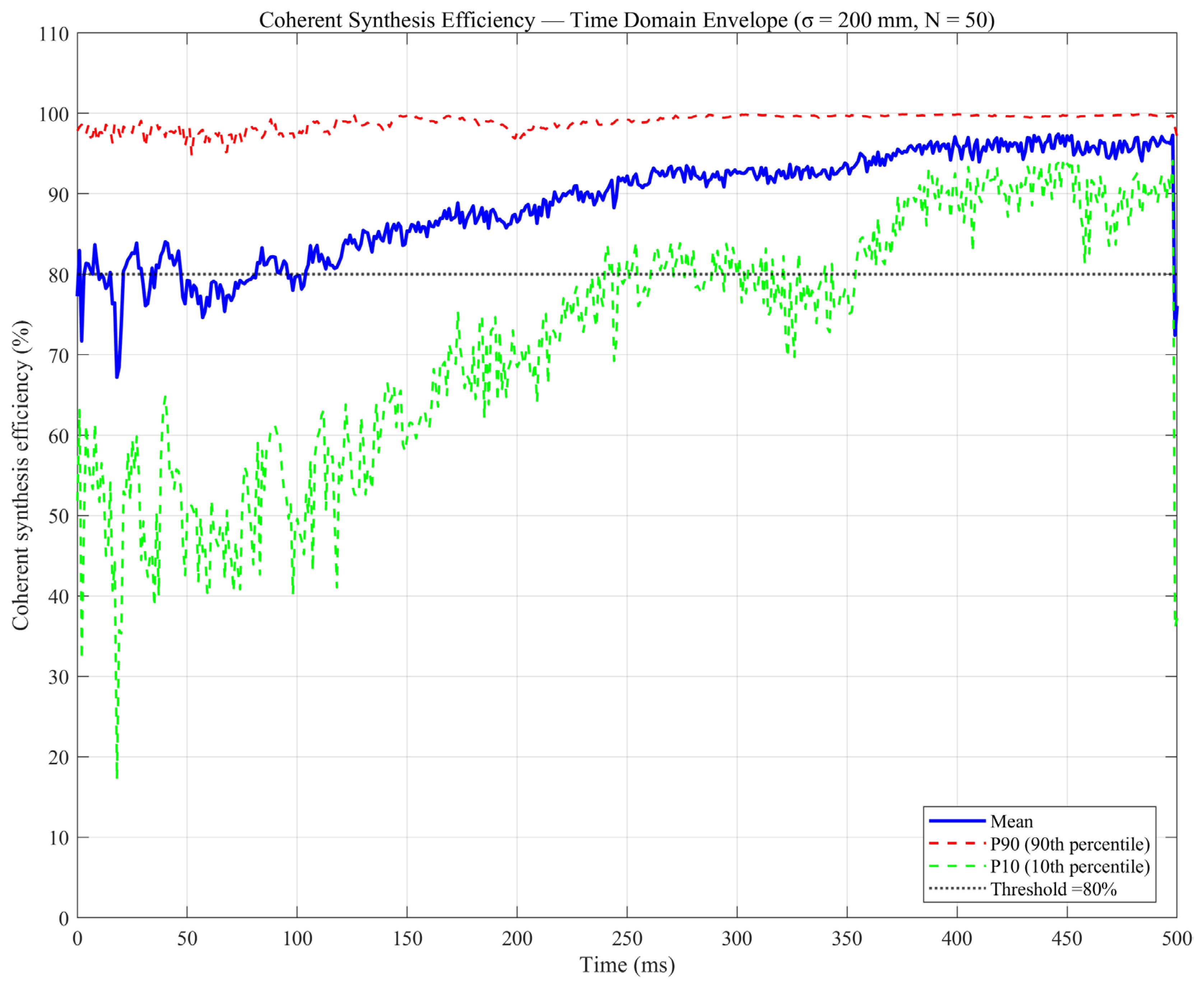
3.3. Time-Domain Validation
- (1)
- Theoretical Innovation: The ARKF error modeling, as a supporting module, enables us to establish, for the first time in the context of distributed coherent synthesis, a reliable quantitative relationship between the statistical characteristics of positioning errors and the coherent success rate, avoiding the evaluation bias caused by traditional white noise models.
- (2)
- Methodological Innovation: A hybrid adaptive compensation strategy is designed to intelligently switch between predictive and robust modes, thereby maximizing compensation performance while maintaining system stability.
- (3)
- Engineering Value: By establishing, for the first time, a quantitative relationship between positioning error and coherent synthesis performance, this work provides concrete guidance for designing and optimizing distributed coherent synthesis systems.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coutts, S.; Cuomo, K.; McHarg, J.; Robey, F.; Weikle, D. Distributed Coherent Aperture Measurements for Next Generation BMD Radar. In Proceedings of the Fourth IEEE Workshop on Sensor Array & Multichannel Processing, Waltham, MA, USA, 12–14 July 2006; IEEE: New York, NY, USA, 2008; pp. 391–393. [Google Scholar]
- Liu, X.; Zhou, D.; Gao, H.; Liu, Z.; Lu, Y. A Receive-Coherent Detector of Moving Target for Airborne Distributed Coherent Aperture Radar in Heterogeneous Clutter. Signal Process. 2023, 213, 109214. [Google Scholar] [CrossRef]
- Cheng, L.; Fu, Z. An Adaptive Kalman Filter Loosely Coupled Indoor Fusion Positioning System Based on Inertial Navigation System and Ultra-Wide Band. Measurement 2025, 244, 116412. [Google Scholar] [CrossRef]
- Wang, X.; Lu, H.; Zhang, J.; Zeng, Y. Double-Side Delay Alignment Modulation for Multi-User Millimeter Wave and Terahertz Communications. Digit. Commun. Netw. 2025, in press. [Google Scholar] [CrossRef]
- Tan, L.; Pan, J.; Jiang, Q.; Liu, F. Application of Time-Reversal in Electromagnetic Power Synthesis under Distributed Motion Platform. Heliyon 2022, 8, e11822. [Google Scholar] [CrossRef]
- Russell, R.S.; Anderson, B.E.; Denison, M.H. Using Time Reversal with Long Duration Broadband Noise Signals to Achieve High Amplitude and a Desired Spectrum at a Target Location. Appl. Acoust. 2025, 236, 110744. [Google Scholar] [CrossRef]
- Yin, Z.; Yang, J.; Ma, Y.; Wang, S.; Chai, D.; Cui, H. A Robust Adaptive Extended Kalman Filter Based on an Improved Measurement Noise Covariance Matrix for the Monitoring and Isolation of Abnormal Disturbances in GNSS/INS Vehicle Navigation. Remote Sens. 2023, 15, 4125. [Google Scholar] [CrossRef]
- Yin, S.; Li, P.; Gu, X.; Yang, X.; Yu, L. Adaptive Kalman Filter with LSTM Network Assistance for Abnormal Measurements. Meas. Sci. Technol. 2024, 35, 075113. [Google Scholar] [CrossRef]
- Zhang, L.; Lou, Y.; Song, W.; Zhang, W.; Peng, Z. Performance Enhancement of PPP/SINS Tightly Coupled Navigation Based on Improved Robust Maximum Correntropy Kalman Filtering. Adv. Space Res. 2024, 74, 2078–2091. [Google Scholar] [CrossRef]
- Liu, J.; Liu, T.; Ji, Y.; Sun, M.; Lyu, M.; Xu, B.; Lu, Z.; Xu, G. A Robust Nonlinear Filter Strategy Based on Maximum Correntropy Criterion for Multi-GNSS and Dual-Frequency RTK. Remote Sens. 2022, 14, 4578. [Google Scholar] [CrossRef]
- Lou, T.-S.; Chen, N.-H.; Chen, Z.-W.; Wang, X.-L. Robust Partially Strong Tracking Extended Consider Kalman Filtering for INS/GNSS Integrated Navigation. IEEE Access 2019, 7, 151230–151238. [Google Scholar] [CrossRef]
- Liu, F.; Wang, Z.; Dai, Y.; Liu, X.; Sun, R. A robust adaptive filtering algorithm based on predicted residuals in integrated navigation. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 1301–1310. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd Edition [Book Review]. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Shin, E.H. Estimation Tech-Niques for Low-Cost Inertial Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly Coupled Integration of Multi-GNSS PPP and MEMS Inertial Measurement Unit Data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-Cost, High-Precision, Single-Frequency GPS–BDS RTK Positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, Y.; Wang, X.; Ma, H.; Xu, X.; Liu, Z. Coherent beam combination of three two-tone fiber amplifiers using stochastic parallel gradient descent algorithm. Opt. Lett. 2009, 34, 2939–2941. [Google Scholar] [CrossRef]
- He, Z.; Ma, Y.; Tafazolli, R. Posterior Cramer-Rao Bound for Inertial Sensors Enhanced Mobile Positioning under the Random Walk Motion Model. IEEE Wirel. Commun. Lett. 2012, 1, 629–632. [Google Scholar] [CrossRef][Green Version]
- Li, S.; Zhang, M.; Ji, Y.; Zhang, Z.; Cao, R.; Chen, B.; Li, H.; Yin, Y. Agricultural Machinery GNSS/IMU-Integrated Navigation Based on Fuzzy Adaptive Finite Impulse Response Kalman Filtering Algorithm. Comput. Electron. Agric. 2021, 191, 106524. [Google Scholar] [CrossRef]
- Zou, X.; Li, Z.; Tang, W.; Wang, Y.; Li, Y.; Zhang, S.; Zhang, Y. A Real-Time Accuracy Prediction Model on Time-Relative Positioning Method Considering the Correlation of Position Increment Errors. GPS Solut. 2024, 28, 15. [Google Scholar] [CrossRef]
- Crespillo, O.G.; Joerger, M.; Langel, S. Overbounding GNSS/INS Integration with Uncertain GNSS Gauss-Markov Error Parameters. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; IEEE: New York, NY, USA, 2020; pp. 481–489. [Google Scholar]
- Anderson, B.; Moore, J. Optimal Filtering; Prentice Hall: New Jersey, NJ, USA, 1979. [Google Scholar]
- Hui, F.; Qin, F. The Design of Global Navigation Satellite System/Inertial Navigation System Ultra-Tight Integration for High Dynamic Applications. In Proceedings of the 2016 Eighth International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Macau, China, 11–12 March 2016; IEEE: New York, NY, USA, 2016; pp. 739–742. [Google Scholar]
- Liu, N.; Hu, K.; Hu, B.; Li, H.; Shen, K.; Qi, W.; Fan, J.; Su, Z. Research on the Navigation Method of High Speed Differential Rotation Guided Ammunition with Ballistic Assistance Prediction under GNSS Denial. Def. Technol. 2025, 49, 275–289. [Google Scholar] [CrossRef]
- Bulbul, S.; Bilgen, B.; Inal, C. The Performance Assessment of Precise Point Positioning (PPP) under Various Observation Conditions. Measurement 2021, 171, 108780. [Google Scholar] [CrossRef]
- Wang, E.; Yu, T.; Sun, X.; Qu, P.; Chen, T.; Hong, X.; Xu, S.; Liu, Z. A GNSS PPP Integrity Monitoring Algorithm Based on ARKF and MHSS. Adv. Space Res. 2025, 75, 7397–7406. [Google Scholar] [CrossRef]
- Ren, X.; Yang, H.; Xu, G.; Yao, K.; Zhang, Y.; Zhang, X. Global Real-Time PPP Using Galileo HAS Compared with WHU RTS. Adv. Space Res. 2025, 76, 3291–3304. [Google Scholar] [CrossRef]
- Wei, M.; Liu, L.; Li, S.; Wang, D.; Li, W. Gauss-AUKF Based UWB/IMU Fusion Localization Approach. Ad Hoc Netw. 2025, 175, 103855. [Google Scholar] [CrossRef]
- Tao, Z.; Li, Z.; Wang, G.; Chen, Z.; Chen, W.; Zhao, Z. An Improved Student’s t Model-Based Variational Robust Filter for GNSS/INS Tightly Coupled Integration. Adv. Space Res. 2025, 76, 3220–3238. [Google Scholar] [CrossRef]
| Navigation System Level | Typical Applications/Accuracy | Process Noise Q (State-Dependent) | Measurement Noise R | Reason for Selection |
|---|---|---|---|---|
| Consumer-grade GNSS | Smartphone, low-cost receiver. Accuracy: meter-level (1–5 m) | The value is relatively large, indicating high uncertainty in the model, diag([1.0, 1.0, 0.1, 0.1]) | The value is relatively large, indicating a high level of observation noise. For example: 25.0 m2 | As a classic textbook in the field of navigation, this book clearly states that the error of consumer-grade GNSS in non-ideal environments (urban canyons) can reach several meters or even tens of meters. R = 25 m2 (Std = 5 m) is a typical representative of this accuracy range [13]. |
| Vehicle-mounted/drone-level (GNSS/INS loose integration) | Medium-precision navigation. Precision: sub-meter level (0.1–1 m) | The value is medium, diag([0.1, 0.1, 0.025, 0.025]) | The value is medium. For example: 0.25 m2 | This doctoral dissertation provides a detailed analysis of the performance of low-cost IMU and GNSS loose integration, pointing out that its horizontal positioning accuracy is typically within the range of 0.5–2 m. Our parameter R = 0.25 m2 (Std = 0.5 m) falls at the high-performance end of this range [14] |
| Tactical-level INS (tightly integrated) | High-precision platform, unmanned system. Precision: centimeter-level (1–10 cm) | The value is relatively small, indicating a low drift rate of the inertial sensor. diag([0.01, 0.01, 0.001, 0.001]) | The value is relatively small. For example: 0.01 m2 | The study demonstrates that the tight integration of technology can achieve positioning accuracy ranging from centimeter level to decimeter level. Setting R to 0.01 m2 (Std = 0.1 m) aligns with the conservative accuracy estimation of such systems under dynamic conditions [15] |
| High-precision surveying and mapping grade (PPP/RTK) | Precision surveying and mapping, scientific research. Accuracy: millimeter-to-centimeter level (<1 cm—several cm) | The value is very small, indicating a high degree of precision in the model. diag([0.001, 0.001, 0.0001, 0.0001]) | The value is very small. For example: 0.0001 m2 | The paper demonstrates that low-cost single-frequency RTK can achieve centimeter-level (even 1–2 cm) real-time positioning accuracy. The parameter R = 0.0001 m2 (Std = 0.01 m) is precisely designed to simulate such high-precision application scenarios [16] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Chen, L.; Li, L.; Yang, M. Research on the Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate in a Moving Platform Distributed Coherent Synthesis System. Electronics 2025, 14, 4408. https://doi.org/10.3390/electronics14224408
Li P, Chen L, Li L, Yang M. Research on the Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate in a Moving Platform Distributed Coherent Synthesis System. Electronics. 2025; 14(22):4408. https://doi.org/10.3390/electronics14224408
Chicago/Turabian StyleLi, Peiheng, Liang Chen, Long Li, and Meng Yang. 2025. "Research on the Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate in a Moving Platform Distributed Coherent Synthesis System" Electronics 14, no. 22: 4408. https://doi.org/10.3390/electronics14224408
APA StyleLi, P., Chen, L., Li, L., & Yang, M. (2025). Research on the Quantitative Relationship Between Positioning Error and Coherent Synthesis Success Rate in a Moving Platform Distributed Coherent Synthesis System. Electronics, 14(22), 4408. https://doi.org/10.3390/electronics14224408








