Fast-Converging and Trustworthy Federated Learning Framework for Privacy-Preserving Stock Price Modeling

Abstract

Stock price modeling under privacy constraints presents a unique challenge at the intersection of computational economics and machine learning. Financial institutions and brokerage firms hold valuable yet sensitive data that cannot be centrally aggregated due to privacy laws and competitive concerns. To address this issue, we propose a novel Fast-Converging Federated Learning (FCFL) framework that enables decentralized and privacy-preserving stock price modeling. FCFL employs a dual-stage adaptive optimization strategy that dynamically tunes local learning rates and aggregation weights based on inter-client gradient divergence, accelerating convergence in heterogeneous financial environments. The framework integrates secure aggregation and differential privacy mechanisms to prevent information leakage during communication while maintaining model fidelity. Experimental results on multi-institutional stock datasets demonstrate that FCFL achieves up to 30% faster convergence and 2.5% lower prediction error compared to conventional federated averaging approaches, while guaranteeing strong $\epsilon$-differential privacy. Theoretical analysis further proves that the framework attains sublinear convergence in $\mathcal{O}\left(\log T\right)$ communication rounds under non-IID data distributions. This study provides a new direction for collaborative financial modeling, balancing efficiency, accuracy, and privacy in real-world economic systems.

1. Introduction

Financial institutions increasingly rely on machine learning to forecast returns, price risk, and allocate capital [1,2], yet collaboration across organizations remains constrained by privacy, regulation, and competition. Centralizing order flows, client attributes, or proprietary factor signals is often infeasible, motivating federated learning (FL) as a systems and statistical paradigm that trains models without pooling raw data [3]. In cross-silo finance, however, FL must satisfy three stringent requirements simultaneously: protect institution-level and client-level information, converge quickly despite pronounced statistical heterogeneity, and deliver models whose economic utility survives regime shifts. Meeting these requirements is challenging. Naïve aggregation exacerbates client drift when data are non-IID across institutions [4,5], while adding differential privacy (DP) noise to defend against inference attacks increases variance and slows optimization [6]. Even with secure aggregation, model updates may leak information through gradient inversion or membership inference if left unprotected [7,8,9,10]; rigorous, round-by-round privacy accounting is therefore essential [11,12].

We introduce FCFL, a fast-converging federated learning framework for privacy-preserving stock price modeling that couples drift-aware optimization with principled privacy accounting. FCFL is built around three design elements that are each privacy-compatible and communication-efficient. First, the drift control variates (DCV) method tracks and cancels cross-client gradient bias using only securely aggregated moment estimates, eliminating the dominant heterogeneity term from the update variance without exposing client statistics. Second, an accelerated server update combines Nesterov lookahead, momentum, and diagonal preconditioning to reduce the effective condition number and stabilize noisy coordinates, providing larger, safer progress per round. Third, fast-convergence policies adapt local step sizes, proximal strength, client participation, and per-round DP noise according to a secure, divergence-aware signal; a Rényi DP accountant composes DP-SGD and secure-moment noise to meet a fixed $(\epsilon ,\delta )$ budget [6,11]. These components integrate cleanly with the standard FL pipeline and secure aggregation [3,13], require only sums of client messages, and avoid any disclosure of per-client gradients or variances.

Our theoretical analysis separates optimization error from stochastic and DP noise. Under general smooth, nonconvex objectives, FCFL achieves the standard $\mathcal{O}(1/K)$ stationarity rate to a noise floor that excludes the heterogeneity penalty, due to DCV’s variance reduction. Under the Polyak–Łojasiewicz condition, FCFL enjoys an accelerated linear rate with communication complexity $\tilde{\mathcal{O}}\left(\sqrt{\kappa }\log (1/ϵ)\right)$, improving the condition-number dependence relative to DP-enabled FedAvg/FedProx and aligning with curated acceleration in adaptive methods [4,5,14]. The diagonal preconditioner and lookahead increase the contraction factor while the divergence-aware privacy schedule shifts noise toward early, higher-variance rounds, preserving the target privacy budget and enabling sharper late-stage optimization.

Empirically, on non-IID, cross-silo equities universes spanning 2015–2024 with N = 20 clients, FCFL reduces rounds-to-target by 40–60% versus strong DP baselines and improves predictive and economic metrics at a fixed $(\epsilon ,\delta )=(1.0,{10}^{-5})$. Representative results include lower MSE, higher directional accuracy, improved Sharpe ratios, and reduced maximum drawdown relative to DP-enabled FedAvg/FedProx/SCAFFOLD, together with superior recovery during volatility shocks where the variance-reduction and preconditioning mechanisms yield smoother loss trajectories. These gains persist across Dirichlet-controlled heterogeneity strengths and are robust to moderate changes in momentum and lookahead. While centralized training with pooled data can offer an upper bound in accuracy, FCFL closes most of this gap without violating confidentiality. We make the following contributions.

(i)

Secure Moment Sharing (SMS). We formalize an aggregation-compatible primitive that exposes only securely aggregated moments (e.g., ${\sum }_i{\omega }_i{\tilde{\Delta }}_i$ and ${\sum }_i{\omega }_i$, optionally noised), never per-client statistics, enabling privacy-preserving estimation of cross-client drift and variance; unlike FedNova-style normalizations, SMS is natively compatible with secure aggregation and DP.

(ii)

Drift Control Variates (DCV). Built on SMS, DCV tracks and cancels cross-client bias, reducing the heterogeneity penalty in update variance while preserving privacy; relative to SCAFFOLD/MIME, controls are derived from securely aggregated moments rather than per-client exchanges. We unify notation for divergence $D^{\left(k\right)}$ and tracking error $e_i^{\left(k\right)}$ and state assumptions/constants once for clarity.

(iii)

Accelerated server update with divergence-aware DP schedule. We combine Nesterov lookahead, momentum, and diagonal preconditioning with divergence-aware policies (adaptive steps, proximal strength, importance-sampled participation) and an RDP-composed DP schedule. Compared with FedAdam/Yogi’s adaptive servers, our per-coordinate preconditioning and momentum are integrated with SMS/DCV and DP, yielding $\mathcal{O}(1/K)$ nonconvex stationarity and a PL linear rate with communication complexity $\tilde{\mathcal{O}}\left(\sqrt{\kappa }\log (1/ϵ)\right)$; on 20-client non-IID equities (2015–2024), FCFL reduces rounds-to-target by 40–60% and improves MSE, directional accuracy, Sharpe, and drawdowns.

This paper connects privacy-preserving systems design and accelerated optimization for financial forecasting, complementing advances in deep forecasting architectures under centralized settings [15,16,17,18,19]. Section 3 formalizes the task, notation, privacy mechanisms, and assumptions. Section 4 details the algorithmic components—secure moment sharing, DCV, accelerated server updates, and divergence-aware DP—and establishes convergence guarantees. Section 5 reports experiments, ablations, and privacy–utility trade-offs. Section 2 situates our contributions within the literature on FL, DP, robustness, and financial ML, and Section 6 concludes with implications for production deployment.

2. Related Work

Federated learning (FL) enables collaborative model training without centralizing raw data. Early work formalized the objective and proposed communication-efficient protocols that aggregate client-side stochastic updates instead of gradients, most notably FedAvg [3] and its precursors emphasizing uplink/downlink compression and local computation [20,21,22]. Production-ready secure aggregationprotocols ensure the server only learns the sum of client updates [13]. In parallel, differential privacy (DP) provides statistical guarantees that the learned model reveals little about any individual example [12]. Its deep-learning instantiation (DP-SGD) relies on per-example gradient clipping and Gaussian noise [6], while Rényi DP (RDP) yields tight composition over many rounds [11] with analytical accountants for subsampling [23,24]. Surveys synthesize FL’s statistical and systems advances, open problems, and deployment lessons [25,26,27,28,29].

2.1. Optimization Under Heterogeneity and Acceleration

Non-IID client data induces client drift, degrading naïve averaging. Stabilization via proximal regularization (FedProx) constrains local updates [4]; control-variate corrections (SCAFFOLD) track and reduce client-specific bias [5]; normalized updates (FedNova) resolve objective inconsistency from variable local steps [30]. Analyses of local-SGD establish rates with limited communication under smoothness [31,32,33], and drift-aware variance reduction further tightens bounds (e.g., MIME) [34]. On the server, adaptive preconditioning (FedAdam/FedYogi/FedAdagrad) mitigates ill-conditioning and accelerates convergence [14], complementing classical momentum and Nesterov acceleration [35,36]. Our framework (FCFL) integrates drift control variates with diagonal preconditioning and Nesterov-style lookahead, producing faster empirical convergence while retaining the secure-aggregation interface.

2.2. Privacy Accounting, Attacks, and Robustness

DP in FL can be enforced at the example or client level [37], with RDP-based accountants tracking the cumulative privacy loss over many rounds [6,11,23]. Despite DP and encryption, attacks highlight leakage risks from gradients or updates: gradient inversion [7,38], membership inference [8,39], and poisoning/backdoors [40]. Robust aggregation reduces the influence of malicious or outlier clients via Krum [41], coordinate-wise robust statistics [42], or geometric-median-style rules [43]. FCFL focuses on honest-but-curious servers protected by secure aggregation [13] and combines DP-SGD with aggregated moment sharing to estimate heterogeneity without revealing individual statistics, thereby preserving both formal privacy and practical utility.

2.3. Communication, Sampling, and Systems Considerations

Communication is often the bottleneck in cross-silo FL. Strategies include local computation with fewer rounds [31], update/gradient quantization [44], and sparsification with error feedback [45]. Client selection policies accelerate progress by prioritizing informative, available, and stable participants; system-aware schedulers such as Oort empirically improve time-to-accuracy [46], while theoretical work studies biased/importance sampling and its convergence implications [47,48]. Our divergence-aware sampling (importance weights proportional to data size and estimated stability) aligns with these directions but remains privacy-compatible because only aggregates are revealed.

2.4. Financial Time-Series Modeling and Privacy in Economics

Deep sequence forecasters already surpass linear and factor models for returns and order-book dynamics [15,16,17,18,19], and machine learning uncovers nonlinear structures in asset pricing [49]. In finance, however, the differentiator for deployable systems is the privacy layer rather than the aggregator itself: institutions increasingly pair cross-silo training with explicit privacy budgets, gradient clipping, calibrated noise, and secure aggregation so that raw time-series never leave local silos. This practice echoes the formal use of differential privacy in official statistics [50], and in the federated setting modern optimizers such as FedAvg, FedProx, SCAFFOLD, and FedNova provide the orchestration required to sustain utility under heterogeneity while respecting privacy constraints [3,4,5,30]. Adaptive server methods further stabilize learning under noisy (privacy-enforced) updates [14]. Framed this way, state-of-the-art pipelines in financial time-series modeling are best understood as privacy-enhancing stacks wrapped around strong forecasters (e.g., DeepAR and temporal fusion) [17,18], with the optimization layer serving to preserve accuracy and calibration in the presence of privacy noise.

Within this privacy-first view, FCFL emphasizes mechanisms that directly protect financial sequences: a divergence-aware privacy schedule that ties clipping and noise to cross-silo heterogeneity, dual-stage acceleration (client control variates plus server momentum/diagonal preconditioning and lookahead) to reduce the number of communication rounds under a fixed budget, and default secure aggregation so that only masked updates are visible to the coordinator. Relative to FedAvg/FedProx/SCAFFOLD/FedNova and adaptive server optimizers [3,4,5,14,30], the contribution is to make the privacy controls the primary design axis while retaining the modeling strength of sequence architectures [15,16,17,18,19,49]. Under standard smoothness and Polyak–Łojasiewicz conditions [51], our analysis yields linear convergence to a noise-dominated neighborhood whose radius reflects the privacy parameters, aligning theoretical guarantees with the operational constraints already recognized in economic data releases [50].

3. Preliminaries

This section formalizes the federated stock price modeling problem, introduces notation and privacy mechanisms, and states the optimization and data assumptions used throughout the paper.

3.1. Problem Setup

Consider N financial institutions (clients) indexed by $\mathcal{C}=\{1,\dots ,N\}$. Client i holds a private time series ${\left\{P_{i,t}\right\}}_{t=1}^{T_i}$ of closing prices for a set of tickers and an aligned feature matrix $X_i\in {\mathbb{R}}^{n_i\times d}$ with $n_i$ supervised samples and d features constructed from domain signals (e.g., OHLCV, technical indicators, macro factors).

$$r_{i,t}\triangleq \log \left({\displaystyle \frac{P_{i,t+1}}{P_{i,t}}}\right)$$

(1)

denote the one-step-ahead log-return, and let $y_i\in {\mathbb{R}}^{n_i}$ denote the corresponding target vector aggregated across all tickers and time points in client i after windowing. We model the conditional expectation of $r_{i,t}$ via a parametric predictor $f_{\mathbf{w}}:{\mathbb{R}}^d\to \mathbb{R}$ with parameters $\mathbf{w}\in {\mathbb{R}}^p$. The per-example loss is $\mathcal{l}(\mathbf{w};\mathbf{x},y)$, and the local empirical objective at client i is

$$F_i\left(\mathbf{w}\right)\triangleq {\displaystyle \frac{1}{n_i}}\sum _{j=1}^{n_i}\mathcal{l}\left(\mathbf{w};{\mathbf{x}}_{i,j},y_{i,j}\right).$$

(2)

The global objective is the standard data-weighted average

$$F\left(\mathbf{w}\right)\triangleq \sum _{i=1}^N{p}_i{F}_i\left(\mathbf{w}\right),p_i\triangleq {\displaystyle \frac{n_i}{{\sum }_{k=1}^N{n}_k}}.$$

(3)

Our goal is to minimize $F\left(\mathbf{w}\right)$ under communication and privacy constraints, without centralizing raw data $\{X_i,y_i\}$.

3.2. Federated Optimization

Training proceeds in communication rounds $k=0,1,\dots ,K-1$. At round k, a server broadcasts the current model ${\mathbf{w}}^{\left(k\right)}$ to a subset ${\mathcal{S}}_k\subseteq \mathcal{C}$ of participating clients. Each client $i\in {\mathcal{S}}_k$ performs $\tau$ local stochastic steps producing an update ${\Delta }_i^{\left(k\right)}$ (or equivalently a local model ${\mathbf{w}}_i^{(k,\tau )}$). The server aggregates the (privatized and securely summed) updates into

$${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{\left(k\right)}+\sum _{i\in {\mathcal{S}}_k}{\alpha }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)},$$

(4)

where ${\alpha }_i^{\left(k\right)}\ge 0$ are aggregation weights that sum to at most 1 over ${\mathcal{S}}_k$, and ${\tilde{\Delta }}_i^{\left(k\right)}$ denotes a clipped-and-noised version of ${\Delta }_i^{\left(k\right)}$ (defined below). The FCFL framework introduced later will adapt both the local step sizes and the aggregation weights $\left\{{\alpha }_i^{\left(k\right)}\right\}$ based on observed gradient divergence. The specific meanings of the letters in the paper are shown in

Table 1. Letter Meaning.

Symbol	Meaning
N, $\mathcal{C}$	Number of clients; client index set
$X_i,y_i,n_i$	Local feature matrix, targets, and sample count at client i
$\mathbf{w}\in {\mathbb{R}}^p$	Model parameters; $f_{\mathbf{w}}$ is the predictor
$F_i$, F	Local and global objectives
k, $\tau$, ${\mathcal{S}}_k$	Round index, local steps per round, active client set
${\Delta }_i^{\left(k\right)}$, ${\alpha }_i^{\left(k\right)}$	Local update at round k; server aggregation weight
C, $\sigma$	Gradient clipping threshold; noise multiplier for DP
$\epsilon ,\delta$	Differential privacy budget parameters
${\mathcal{D}}^{\left(k\right)}$	Gradient divergence (client drift) at round k
L, $\mu$, $\zeta$, ${\sigma }_g$	Smoothness, PL, heterogeneity, and gradient variance constants

.

3.3. Gradient Divergence and Client Drift

Let $g_i^{\left(k\right)}\triangleq \nabla F_i\left({\mathbf{w}}^{\left(k\right)}\right)$ and ${\overline{g}}^{\left(k\right)}\triangleq {\sum }_{i=1}^N{p}_i{g}_i^{\left(k\right)}$. We quantify cross-client heterogeneity in round k by the divergence

$${\mathcal{D}}^{\left(k\right)}\triangleq \sum _{i=1}^N{p}_i\parallel g_i^{\left(k\right)}-{\overline{g}}^{\left(k\right)}{\parallel }_2^2.$$

(5)

Empirically, ${\mathcal{D}}^{\left(k\right)}$ can be estimated with clipped, privatized stochastic gradients returned by clients. FCFL will use such an estimate to drive dual-stage adaptation.

The subsequent sections will instantiate these components within the proposed FCFL algorithm, specifying the dual-stage adaptation of local step sizes and aggregation weights and analyzing convergence under A1–A4 with privacy and communication constraints.

3.4. Threat Model

Setting. Cross-silo FL with authenticated, encrypted channels; raw data remain on clients. The server coordinates training but is not trusted with plaintext updates.

Adversary. We assume an honest-but-curious server and passive network observers; clients are honest (no Byzantine behavior). Limited collusion below the secure-aggregation threshold is allowed; if fewer than t parties collude, per-client updates remain hidden.

Exposure. The server observes only securely aggregated, clipped, noised sums (e.g., ${\sum }_i{\omega }_i{\tilde{\Delta }}_i$) and public metadata (round index, sampling rate $p_k$); no raw examples, per-client gradients, or per-client deltas are revealed.

Protection. Each client applies clipping at radius C and adds Gaussian noise $\mathcal{N}(0,{\sigma }_k^2{C}^2\mathbf{I})$; a Rényi-DP accountant composes rounds to $(\epsilon ,\delta )$-DP. The adaptive schedule ${\sigma }_k$ depends only on DP-protected or securely aggregated quantities (post-processing), preserving privacy guarantees.

Guarantees. Record-level privacy across all rounds; indistinguishability of any single record is bounded by $(\epsilon ,\delta )$. Secure aggregation prevents recovery of individual updates; membership-inference advantage is controlled by $\epsilon$.

Out of scope.Byzantine/poisoning/backdoor attacks, compromised client devices, and side-channel or timing leakage. Robust aggregation and adversarial defenses are orthogonal and deferred to future work.

4. Methodology

We revise FCFL to emphasize fast convergence under privacy and heterogeneity. Building on the notation of Section 3, we introduce three complementary accelerators: (i) drift control variates that perform gradient tracking and variance reduction, (ii) server-side momentum with diagonal preconditioning to mitigate ill-conditioning, and (iii) participation and step-size policies that cap client drift and prioritize informative updates.

4.1. Accelerated Server Update

The server update should (i) counteract coordinate-wise ill-conditioning, (ii) exploit temporal correlation of aggregated client updates to accelerate descent, and (iii) remain compatible with secure aggregation so that the server only needs aggregated quantities. FCFL achieves this with diagonal preconditioning and momentum on the privacy-preserving averaged update

$$u^{\left(k\right)}\triangleq {\displaystyle \frac{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)}}{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}}},$$

(6)

where ${\omega }_i^{\left(k\right)}$ are divergence-aware weights. Note that secure aggregation reveals only ${\sum }_i{\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)}$ and ${\sum }_i{\omega }_i^{\left(k\right)}$, which suffice to compute $u^{\left(k\right)}$. We maintain first and second moments of $u^{\left(k\right)}$:

$$m^{\left(k\right)}={\beta }_1{m}^{(k-1)}+(1-{\beta }_1)u^{\left(k\right)},v^{\left(k\right)}={\beta }_2{v}^{(k-1)}+(1-{\beta }_2)\left(u^{\left(k\right)}\odot u^{\left(k\right)}\right),$$

(7)

with ${\beta }_1,{\beta }_2\in [0,1)$ and elementwise square ⊙. To correct the warm-start bias during early rounds, we optionally use bias-corrected moments

$${\widehat{m}}^{\left(k\right)}={\displaystyle \frac{m^{\left(k\right)}}{1-{\beta }_1^{t_k}}},{\widehat{v}}^{\left(k\right)}={\displaystyle \frac{v^{\left(k\right)}}{1-{\beta }_2^{t_k}}},$$

(8)

where $t_k$ counts the number of rounds with at least one participating client (so $t_k$ increases even with partial participation). In practice, ${\beta }_1$ = 0.9 and ${\beta }_2$ = 0.999 work well and bias correction primarily helps the first 10–20 rounds. The diagonal preconditioner rescales coordinates by an RMS estimate. Let ${\mathrm{RMS}}^{\left(k\right)}\triangleq \sqrt{{\widehat{v}}^{\left(k\right)}}+{ϵ}_p$ with a small ${ϵ}_p>0$. The preconditioned, momentum-driven step is

$${\mathbf{w}}^{(k+1)}={\mathbf{y}}^{\left(k\right)}+{\eta }_s^{\left(k\right)}{\displaystyle \frac{{\widehat{m}}^{\left(k\right)}}{{\mathrm{RMS}}^{\left(k\right)}}},$$

(9)

where division is elementwise. This realizes an adaptive trust region because

$$\parallel {\eta }_s^{\left(k\right)}{\displaystyle \frac{{\widehat{m}}^{\left(k\right)}}{{\mathrm{RMS}}^{\left(k\right)}}}{\parallel }_{\infty }\le {\eta }_s^{\left(k\right)}\underset{j}{max}{\displaystyle \frac{|{\widehat{m}}_j^{\left(k\right)}|}{{ϵ}_p}},$$

(10)

which prevents overshooting along poorly scaled directions.Algorithm 1 shows FCFL with Secure Moment Sharing (SMS), DCV, and Divergence-Aware DP. Algorithm 2 shows CLIENT_UPDATE (Local DP-SGD with DCV and Preconditioning), the details are provided below.

Algorithm 1 FCFL with Secure Moment Sharing (SMS), DCV, and Divergence-Aware DP

1: Server init: model ${\mathbf{w}}^{\left(0\right)}$; moments ${\mathbf{m}}^{\left(0\right)}=\mathbf{0},{\mathbf{v}}^{\left(0\right)}=\mathbf{0}$; server control ${\mathbf{c}}^{\left(0\right)}=\mathbf{0}$; clip C; lookahead $\rho$; ${\beta }_1,{\beta }_2,{ϵ}_p$; DP budget ${\mathcal{B}}_{\mathrm{DP}}$; schedule state.   2: for$k=0,1,\dots ,K-1$do   3:     Sample client set ${\mathcal{S}}_k$ with rate $p_k$; announce public weights ${\omega }_i^{\left(k\right)}$ (e.g., HT/size-based), clip C, noise ${\sigma }_k$, and preconditioner seed.   4:     Broadcast $({\mathbf{w}}^{\left(k\right)},{\mathbf{c}}^{\left(k\right)},C,{\sigma }_k,\tau )$.   5:     Each client $i\in {\mathcal{S}}_k$ runs Client_Update$(i,{\mathbf{w}}^{\left(k\right)},{\mathbf{c}}^{\left(k\right)},C,{\sigma }_k,\tau )$ and participates in secure aggregation.   6:     Secure moment sharing (SMS): obtain only aggregated sums (no per-client values) $$S_{\Delta }=\sum _{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)},S_1=\sum _{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)},S_2=\sum _{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}({\tilde{\Delta }}_i^{\left(k\right)}\odot {\tilde{\Delta }}_i^{\left(k\right)})\left(\mathrm{optional}\right)$$   7:     Aggregate update: ${\mathbf{u}}^{\left(k\right)}=S_{\Delta }/S_1$.   8:     Server moments: ${\mathbf{m}}^{(k+1)}={\beta }_1{\mathbf{m}}^{\left(k\right)}+(1-{\beta }_1){\mathbf{u}}^{\left(k\right)}$, ${\mathbf{v}}^{(k+1)}={\beta }_2{\mathbf{v}}^{\left(k\right)}+(1-{\beta }_2)(S_2/S_1)$ (or ${\mathbf{u}}^{\left(k\right)}\odot {\mathbf{u}}^{\left(k\right)}$ if $S_2$ not shared).   9:     Bias corrections: ${\widehat{\mathbf{m}}}^{(k+1)}={\mathbf{m}}^{(k+1)}/(1-{\beta }_1^{k+1})$, ${\widehat{\mathbf{v}}}^{(k+1)}={\mathbf{v}}^{(k+1)}/(1-{\beta }_2^{k+1})$. 10:     Preconditioner: ${\mathbf{P}}^{\left(k\right)}=\mathrm{diag}((\sqrt{{\widehat{\mathbf{v}}}^{(k+1)}}+{ϵ}_p{)}^{-1})$. 11:     Model step + lookahead: ${\mathbf{w}}^{(k+\frac{1}{2})}={\mathbf{w}}^{\left(k\right)}-{\eta }_s^{\left(k\right)}{\mathbf{P}}^{\left(k\right)}{\widehat{\mathbf{m}}}^{(k+1)}$,    ${\mathbf{w}}^{(k+1)}=(1-\rho ){\mathbf{w}}^{\left(k\right)}+\rho {\mathbf{w}}^{(k+\frac{1}{2})}$. 12:     Divergence estimate (from SMS): compute $D^{\left(k\right)}$ using $(S_{\Delta },S_1,S_2)$; update server control ${\mathbf{c}}^{(k+1)}\leftarrow \mathrm{UpdateDCV}({\mathbf{c}}^{\left(k\right)},{\mathbf{u}}^{\left(k\right)},D^{\left(k\right)})$. 13:     DP accountant & schedule: compose RDP with $(q=p_k,{\sigma }_k,\tau )$ to get ${\epsilon }_k$; update remaining budget ${\mathcal{B}}_{\mathrm{DP}}\leftarrow {\mathcal{B}}_{\mathrm{DP}}-{\epsilon }_k$; set next ${\sigma }_{k+1}\leftarrow \mathrm{Schedule}(D^{\left(k\right)},{\mathcal{B}}_{\mathrm{DP}})$ (post-processing of DP-protected SMS). 14: end for

Algorithm 2 Client_Update (Local DP-SGD with DCV and Preconditioning)

Require:  $i,{\mathbf{w}}^{\left(k\right)},{\mathbf{c}}^{\left(k\right)},C,{\sigma }_k,\tau$.    Local state: ${\mathbf{c}}_i^{\left(k\right)}$ (client control), optimizer buffers.   1: Set ${\mathbf{w}}_0\leftarrow {\mathbf{w}}^{\left(k\right)}$, ${\Delta }_i\leftarrow \mathbf{0}$.   2: for$t=0$ to $\tau -1$ do   3:     Sample mini-batch $B_t$; compute ${\mathbf{g}}_t=\nabla {\mathcal{l}}_i({\mathbf{w}}_t;B_t)$.   4:     DCV adjustment: ${\mathbf{g}}_t^{\prime }={\mathbf{g}}_t-{\mathbf{c}}_i^{\left(k\right)}+{\mathbf{c}}^{\left(k\right)}$.   5:     (Server broadcasts ${\mathbf{P}}^{\left(k\right)}$ implicitly via moments) Precondition ${\mathbf{h}}_t={\mathbf{P}}^{\left(k\right)}{\mathbf{g}}_t^{\prime }$.   6:     Clip ${\mathbf{h}}_t\leftarrow {\mathbf{h}}_t·min\left(1,C/\parallel {\mathbf{h}}_t{\parallel }_2\right)$.   7:     Update ${\mathbf{w}}_{t+1}={\mathbf{w}}_t-{\eta }_c^{\left(k\right)}{\mathbf{h}}_t$; accumulate ${\Delta }_i\leftarrow {\Delta }_i+({\mathbf{w}}_{t+1}-{\mathbf{w}}_t)$.   8: end for   9: Clip total ${\Delta }_i\leftarrow {\Delta }_i·min\left(1,C/\parallel {\Delta }_i{\parallel }_2\right)$. 10: Add DP noise ${\tilde{\Delta }}_i={\Delta }_i+{\xi }_i,{\xi }_i\sim \mathcal{N}(\mathbf{0},{\sigma }_k^2{C}^2\mathbf{I})$. 11: Update local control (no upload of per-client stats): ${\mathbf{c}}_i^{(k+1)}\leftarrow (1-{\alpha }_{\mathrm{dcv}}){\mathbf{c}}_i^{\left(k\right)}+{\alpha }_{\mathrm{dcv}}\left(\frac{1}{\tau }{\sum }_t{\mathbf{g}}_t-{\mathbf{c}}^{\left(k\right)}\right)$. 12: Send only masked shares for secure aggregation of ${\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i$ and ${\omega }_i^{\left(k\right)}$; no per-client values are revealed to the server.

Nesterov-Style Lookahead Coupling

We set ${\mathbf{y}}^{\left(k\right)}={\mathbf{w}}^{\left(k\right)}+{\eta }_m^{\left(k\right)}\left({\mathbf{w}}^{\left(k\right)}-{\mathbf{w}}^{(k-1)}\right)$ with ${\eta }_m^{\left(k\right)}\in [0,1)$. Intuitively, $u^{\left(k\right)}$ approximates the gradient at ${\mathbf{y}}^{\left(k\right)}$ due to small inter-round drift; thus the step in (9) benefits from lookahead curvature. Empirically, ${\eta }_m^{\left(k\right)}=0.8$ yields the best rounds-to-target while remaining stable under DP noise. Under L-smoothness, a sufficient condition for descent at ${\mathbf{y}}^{\left(k\right)}$ is

$${\eta }_s^{\left(k\right)}\le {\displaystyle \frac{(1-{\beta }_1)}{L}}·\underset{j}{min}\left(\sqrt{{\widehat{v}}_j^{\left(k\right)}}+{ϵ}_p\right).$$

(11)

In practice we choose a fixed ${\eta }_s^{\left(k\right)}\equiv {\eta }_s\in [0.5,1.0]$ and set ${ϵ}_p={10}^{-8}$, which empirically stabilizes training under DP noise. A lightweight server trust region further caps the step:

$${\Delta }_{max}^{\left(k\right)}\triangleq {\eta }_{\infty }·{\displaystyle \frac{\parallel {\widehat{m}}^{\left(k\right)}{\parallel }_1}{d{ϵ}_p}},{\mathbf{w}}^{(k+1)}\leftarrow {\mathbf{y}}^{\left(k\right)}+{\mathrm{clip}}_{\infty }\left({\eta }_s{\displaystyle \frac{{\widehat{m}}^{\left(k\right)}}{{\mathrm{RMS}}^{\left(k\right)}}},{\Delta }_{max}^{\left(k\right)}\right),$$

(12)

where d is the parameter dimension and ${\eta }_{\infty }\in (0,1]$; clipping is rarely activated but guards against rare outlier rounds.

4.2. Drift Control Variates (DCV)

DCV mitigates cross-client bias by tracking the gap ${\Delta }_i\left(\mathbf{w}\right)=\nabla F_i\left(\mathbf{w}\right)-\nabla F\left(\mathbf{w}\right)$ with client-side controls $c_i$ and a server-side control c. Correcting each client’s stochastic direction by $-c_i+c$ aligns local steps with the global gradient while remaining compatible with DP and secure aggregation.

4.2.1. Mechanics: Corrected Local Steps and Secure Updates

At round k, client i receives $({\mathbf{y}}^{\left(k\right)},c)$ and performs ${\tau }_i^{\left(k\right)}$ DP-SGD steps on the proximalized objective using

$${\mathbf{w}}_i^{(k,s+1)}={\mathbf{w}}_i^{(k,s)}-{\eta }_i^{\left(k\right)}\left({\tilde{g}}_i^{(k,s)}-c_i+c\right)-{\eta }_i^{\left(k\right)}{\mu }^{\left(k\right)}\left({\mathbf{w}}_i^{(k,s)}-{\mathbf{y}}^{\left(k\right)}\right),$$

(13)

where ${\tilde{g}}_i^{(k,s)}$ is the clipped-and-noised minibatch gradient. Telescoping yields the anchored direction

$${\delta }_i^{\left(k\right)}\triangleq {\displaystyle \frac{{\mathbf{y}}^{\left(k\right)}-{\mathbf{w}}_i^{(k,{\tau }_i^{\left(k\right)})}}{{\tau }_i^{\left(k\right)}{\eta }_i^{\left(k\right)}}}\approx {\displaystyle \frac{1}{{\tau }_i^{\left(k\right)}}}\sum _s{\tilde{g}}_i^{(k,s)}-c_i+c+{\mu }^{\left(k\right)}{\displaystyle \frac{1}{{\tau }_i^{\left(k\right)}}}\sum _s\left({\mathbf{w}}_i^{(k,s)}-{\mathbf{y}}^{\left(k\right)}\right).$$

(14)

Clients update their local control with a small smoothing $\xi \in (0,1]$,

$$c_i\leftarrow (1-\xi )c_i+\xi {\delta }_i^{\left(k\right)},$$

(15)

and, via secure aggregation, the server receives only the mean ${\overline{\delta }}^{\left(k\right)}={\displaystyle \frac{1}{|{\mathcal{S}}_k|}}{\sum }_{i\in {\mathcal{S}}_k}{\delta }_i^{\left(k\right)}$ to update the global control

$$c\leftarrow (1-\xi )c+\xi {\overline{\delta }}^{\left(k\right)}.$$

(16)

This design needs only sums of client messages and thus integrates seamlessly with secure aggregation; it adds no communication of per-client statistics or raw gradients.

4.2.2. Variance Reduction and Control of Heterogeneity

Write ${\tilde{g}}_i^{(k,s)}=\nabla F_i\left({\mathbf{y}}^{\left(k\right)}\right)+{\epsilon }_i^{(k,s)}+b_i^{\mathrm{clip}}$, where ${\epsilon }_i^{(k,s)}$ combines sampling and DP noise with covariance $⪯{\sigma }_g^2\mathbf{I}+C^2{\left({\sigma }^{\left(k\right)}\right)}^2\mathbf{I}$, and $b_i^{\mathrm{clip}}$ is the clipping bias. If $e_i^{\left(k\right)}\triangleq c_i-\left(\nabla F_i\left({\mathbf{y}}^{\left(k\right)}\right)-\nabla F\left({\mathbf{y}}^{\left(k\right)}\right)\right)$ denotes the tracking error, then the DCV-corrected direction used above satisfies

$$\mathbb{E}\left[{\tilde{g}}_i^{(k,s)}-c_i+c\right]=\nabla F\left({\mathbf{y}}^{\left(k\right)}\right)-e_i^{\left(k\right)}+b_i^{\mathrm{clip}},\mathrm{Var}\left[{\tilde{g}}_i^{(k,s)}-c_i+c\right]⪯{\sigma }_g^2\mathbf{I}+C^2{\left({\sigma }^{\left(k\right)}\right)}^2\mathbf{I}.$$

(17)

Hence the heterogeneity penalty term ${\sum }_i{p}_i{\parallel \nabla F_i-\nabla F\parallel }_2^2$ does not appear in the variance: DCV removes the dominant dispersion component, leaving only tracking and clipping bias in the mean. Under A1–A4 and the drift budget, there exists $\rho \in (0,1)$ such that the tracking error contracts in expectation,

$$\mathbb{E}\parallel e_i^{(k+1)}{\parallel }_2^2\le \rho \mathbb{E}{\parallel e_i^{\left(k\right)}\parallel }_2^2+\mathcal{O}({\sigma }_g^2+C^2{({\sigma }^{\left(k\right)})}^2+{\parallel b_i^{\mathrm{clip}}\parallel }_2^2),$$

(18)

so DCV rapidly reaches a noise-dominated floor. Aggregating across sampled clients then yields the bias–variance bounds used in the global convergence analysis.

4.3. Fast-Convergence Policies

The policies in FCFL control how aggressively clients move locally and how the federation allocates participation under heterogeneity, all while meeting a fixed privacy budget. They are designed to (i) cap local parameter drift to keep proximal descent well conditioned, (ii) prioritize informative and stable clients to accelerate early progress, and (iii) modulate DP noise based on measured divergence so that noise shrinks as optimization stabilizes.

4.3.1. Adaptive Local Step-Size and Drift Budget

We refine the client step-size rule by detailing how ${\widehat{v}}_{i,\mathrm{loc}}^{\left(k\right)}$ and $d_i^{\left(k\right)}$ are computed and how they enforce a uniform drift bound. Let $g(\mathbf{w};\mathbf{x},y)$ denote the per-example gradient (before clipping). Client i estimates its local gradient variance using clipped per-example norms on the current round:

$${\widehat{v}}_{i,\mathrm{loc}}^{\left(k\right)}={\displaystyle \frac{1}{S}}\sum _{s=1}^S\left({\displaystyle \frac{1}{|B_i^{(k,s)}|}}\sum _{(\mathbf{x},y)\in B_i^{(k,s)}}\parallel \widehat{g}({\mathbf{w}}^{\left(k\right)};\mathbf{x},y)-{\overline{g}}_i^{(k,s)}{\parallel }_2^2\right),{\overline{g}}_i^{(k,s)}={\displaystyle \frac{1}{|B_i^{(k,s)}|}}\sum _{(\mathbf{x},y)\in B_i^{(k,s)}}\widehat{g}({\mathbf{w}}^{\left(k\right)};\mathbf{x},y),$$

(19)

where $\widehat{g}$ uses the same clipping threshold C as DP-SGD. The surrogate drift $d_i^{\left(k\right)}$ is measured after the local epoch using the prox-anchored displacement:

$$d_i^{\left(k\right)}=min\{\parallel {\mathbf{w}}_i^{(k,{\tau }_i^{\left(k\right)})}-{\mathbf{y}}^{\left(k\right)}{\parallel }_2^2,D_{max}\}.$$

(20)

Substituting Equation (20), a standard smoothness argument yields the round-wise drift inequality (conditioning on the local data and randomness):

$$\mathbb{E}\left[\parallel {\mathbf{w}}_i^{(k,{\tau }_i^{\left(k\right)})}-{\mathbf{y}}^{\left(k\right)}{\parallel }_2^2\right]\le {\displaystyle \frac{{\tau }_i^{\left(k\right)}{\left({\eta }_i^{\left(k\right)}\right)}^2}{{(1+{\mu }^{\left(k\right)}{\eta }_i^{\left(k\right)})}^2}}\left({\sigma }_g^2+C^2{\left({\sigma }^{\left(k\right)}\right)}^2+L^2\parallel \nabla F_i\left({\mathbf{y}}^{\left(k\right)}\right){\parallel }_2^2\right),$$

(21)

so choosing ${\eta }_i^{\left(k\right)}$ and ${\tau }_i^{\left(k\right)}$ with ${\mu }^{\left(k\right)}={\lambda }_0{\widehat{\mathcal{D}}}^{\left(k\right)}$ makes the left-hand side uniformly bounded by $d_{max}$ in expectation. This enforces a global contraction precondition for the accelerated server step because the dispersion of local models around ${\mathbf{y}}^{\left(k\right)}$ is controlled. In particular, clients perform $w_i^{(t,\tau +1)}=w_i^{(t,\tau )}-{\eta }_i^{\left(t\right)}{P}_t\left(\nabla f_i\left(w_i^{(t,\tau )}\right)-c_i^{\left(t\right)}\right)$ with diagonal preconditioner $P_t$ and drift-tracking $c_i^{\left(t\right)}$; the server aggregates ${\Delta }^{\left(t\right)}={\sum }_i{a}_i^{\left(t\right)}(w_i^{(t,{\tau }_i)}-w^{\left(t\right)})$, where $a_i^{\left(t\right)}=\psi \left(D_i^{\left(t\right)}\right)/{\sum }_j\psi \left(D_j^{\left(t\right)}\right)$ and ${\eta }_i^{\left(t\right)}=\varphi \left(D_i^{\left(t\right)}\right)$ are monotone in the divergence proxy $D_i^{\left(t\right)}$, yielding $\mathbb{E}\left[\langle {\Delta }^{\left(t\right)},g^{\left(t\right)}\rangle \right]\ge {\sum }_i{a}_i^{\left(t\right)}{\eta }_i^{\left(t\right)}\left(\parallel g^{\left(t\right)}{\parallel }^2-{\delta }_i\parallel g^{\left(t\right)}\parallel \right)$, so that reducing high-divergence influence improves alignment with $g^{\left(t\right)}$.

Backtracking for ${\eta }_0$. When L is unknown, a client-side backtracking rule ensures ${\eta }_i^{\left(k\right)}\le 1/\left(4L\right)$ without communicating L. Let ${\eta }_{\mathrm{test}}$ be the candidate value computed. The client tests a single batch B and accepts ${\eta }_{\mathrm{test}}$ if

$$F_i^{\left(B\right)}\left({\mathbf{y}}^{\left(k\right)}-{\eta }_{\mathrm{test}}{\overline{g}}_i^{\left(B\right)}\right)\le F_i^{\left(B\right)}\left({\mathbf{y}}^{\left(k\right)}\right)-{\displaystyle \frac{{\eta }_{\mathrm{test}}}{4}}\parallel {\overline{g}}_i^{\left(B\right)}{\parallel }_2^2,$$

(22)

otherwise halves ${\eta }_{\mathrm{test}}$ and retries up to a small fixed number of attempts. Because this rule uses only local batches and is a post-processing of DP gradients, it does not alter the privacy accountant.

4.3.2. Importance Sampling for Participation

Client selection follows the probability law,

$${\pi }_i^{\left(k\right)}\propto {\displaystyle \frac{n_i}{1+\beta d_i^{\left(k\right)}}}·{\displaystyle \frac{1}{\sqrt{1+{\widehat{v}}_{i,\mathrm{loc}}^{\left(k\right)}}}},\sum _{i=1}^N{\pi }_i^{\left(k\right)}=1,$$

(23)

favoring data-rich and stable clients while downweighting those with large drift or variance. To keep the aggregation unbiased under non-uniform sampling, we incorporate Horvitz–Thompson correction into the weights:

$${\omega }_i^{\left(k\right)}\leftarrow {\displaystyle \frac{{\omega }_i^{\left(k\right)}}{{\pi }_i^{\left(k\right)}}},u^{\left(k\right)}={\displaystyle \frac{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)}}{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}}},$$

(24)

so that $\mathbb{E}\left[u^{\left(k\right)}\right]$ equals the full-population weighted update under the original ${\omega }_i^{\left(k\right)}$. Privacy-wise, (24) can be implemented without revealing per-client ${\widehat{v}}_{i,\mathrm{loc}}^{\left(k\right)}$ or $d_i^{\left(k\right)}$ by using client-side self-thinning: the server broadcasts a sampling temperature ${\tau }_{\mathrm{sel}}$, each client draws $u\sim \mathrm{Unif}(0,1)$ and participates if $u\le min\{1,{\tau }_{\mathrm{sel}}{\pi }_i^{\left(k\right)}\}$. The server learns only the final set ${\mathcal{S}}_k$, and the correction in (24) uses the public acceptance probability.

Variance–speed trade-off. Importance sampling reduces the effective variance of the aggregated update (fewer high-variance clients per round) and empirically cuts the rounds-to-target by prioritizing stable contributors in early rounds. The Horvitz–Thompson correction keeps estimates unbiased, while the diagonal preconditioner from (9) handles residual scale disparities.

4.3.3. Divergence-Aware Differential-Privacy Schedule

The per-round Gaussian noise multiplier adapts to the measured drift,

$${\sigma }^{\left(k\right)}=min\left\{{\sigma }_{max},{\displaystyle \frac{{\sigma }_0}{\sqrt{k+1}}}\sqrt{1+\rho {\widehat{\mathcal{D}}}^{\left(k\right)}}·\sqrt{{\displaystyle \frac{1}{1+\parallel {\mathbf{w}}^{\left(k\right)}-{\mathbf{w}}^{(k-1)}{\parallel }_2}}}\right\},$$

(25)

which decreases with k (exploitation) yet increases with divergence and with large inter-round jumps (exploration/stability). Let $\epsilon \left(\alpha \right)$ denote the total RDP at order $\alpha >1$ from composing per-round DP-SGD (with subsampling rate q and multiplier ${\sigma }^{\left(k\right)}$) and SMS moment noise ${\nu }_k$. The accountant guarantees

$${\epsilon }_{\mathrm{tot}}=\underset{\alpha >1}{min}\left\{\epsilon \left(\alpha \right)+{\displaystyle \frac{\log (1/\delta )}{\alpha -1}}\right\},\delta ={10}^{-5}.$$

(26)

To hit a target budget ${\epsilon }^{★}$, we select ${\sigma }_0$ by a single-pass calibration: start from a conservative ${\sigma }_0^{\left(0\right)}$, simulate the schedule ${\left\{{\sigma }^{\left(k\right)}\right\}}_{k=0}^{K-1}$ on the planned number of rounds K using historical ${\widehat{\mathcal{D}}}^{\left(k\right)}$ from a dry run or a short warmup, compute ${\epsilon }_{\mathrm{tot}}^{\left(0\right)}$, and scale

$${\sigma }_0\leftarrow {\sigma }_0^{\left(0\right)}·\sqrt{{\displaystyle \frac{{\epsilon }_{\mathrm{tot}}^{\left(0\right)}}{{\epsilon }^{★}}}},$$

(27)

which is accurate because RDP for the subsampled Gaussian mechanism is approximately inversely proportional to ${\sigma }^2$ at fixed q. This keeps the final $({\epsilon }^{★},\delta )$ while granting lower noise in later rounds where optimization benefits most.

We note that the proposed policies target the two principal impediments to federated optimization with non-IID clients—bias from client drift and variance from stochastic/private updates—so that the global descent remains contractive even when local objectives differ. Let ${\zeta }^2={sup}_w{\displaystyle \frac{1}{K}}{\sum }_{i=1}^K{\parallel \nabla f_i\left(w\right)-\nabla f\left(w\right)\parallel }^2$ measure gradient dissimilarity and let $\tau$ be the number of local steps. Classical analyses yield a recursion of the form $\mathbb{E}[F\left(w_{t+1}\right)-F^{★}]\le (1-\eta \mu )\mathbb{E}[F\left(w_t\right)-F^{★}]+\mathcal{O}\left(\eta L(\tau -1){\zeta }^2+{\eta }^2{\sigma }^2\right)$ under L-smoothness and PL geometry, where the residual combines a drift term and an update-variance term. Our design reduces both: (i) secure moment sharing supplies privacy-preserving cross-client first/second moments that parameterize client control variates, shrinking the drift component by aligning local updates with the global gradient; (ii) dual-stage acceleration—server momentum with diagonal preconditioning plus lookahead—rescales poorly conditioned coordinates and averages oscillations across rounds, improving the effective contraction from $1-\eta \mu$ to $1-\tilde{\eta }\tilde{\mu }$ with $\tilde{\mu }>\mu$ under mild mismatch; and (iii) a divergence-aware DP schedule ties clipping and per-round noise to measured drift and participation, preserving the overall $(\epsilon ,\delta )$ while allocating privacy cost to phases with higher signal-to-noise, thereby reducing the optimization error attributable to DP perturbations. Together these yield the refined bound

$$\mathbb{E}[F\left(w_{t+1}\right)-F^{★}]\le (1-\tilde{\eta }\tilde{\mu })\mathbb{E}[F\left(w_t\right)-F^{★}]+\mathcal{O}\left(\tilde{\eta }L\alpha (\tau -1){\zeta }^2+{\tilde{\eta }}^2{\sigma }_{\mathrm{DP}}^2\right),$$

where $\alpha \in (0,1)$ captures drift shrinkage due to control variates and ${\sigma }_{\mathrm{DP}}^2$ reflects the calibrated privacy noise. This contraction to a smaller DP-noise-dominated neighborhood translates into fewer communication rounds and more stable training in precisely the heterogeneous regimes where standard methods degrade.

5. Convergence Guarantees with Acceleration

This section provides end-to-end guarantees for FCFL, separating optimization error from variability introduced by stochastic sampling and differential privacy (DP). The accelerated server update is

$${\mathbf{w}}^{(k+1)}={\mathbf{y}}^{\left(k\right)}+{\eta }_s^{\left(k\right)}{\displaystyle \frac{{\widehat{m}}^{\left(k\right)}}{\sqrt{{\widehat{v}}^{\left(k\right)}}+{ϵ}_p}},$$

(28)

where ${\mathbf{y}}^{\left(k\right)}={\mathbf{w}}^{\left(k\right)}+{\eta }_m^{\left(k\right)}({\mathbf{w}}^{\left(k\right)}-{\mathbf{w}}^{(k-1)})$ is the Nesterov lookahead point, and ${\widehat{m}}^{\left(k\right)},{\widehat{v}}^{\left(k\right)}$ are bias-corrected moments of the divergence-aware aggregated update $u^{\left(k\right)}$ (Section 4; cf. (9)). Clients use drift control variates (DCV), a drift budget for local steps, and importance sampling with Horvitz–Thompson correction (cf. (24)). DP-SGD employs per-example clipping C with a divergence-aware noise schedule; privacy is tracked by an RDP accountant.

5.1. Assumptions, Setup, and Effective Conditioning

Assumption A1

(Smoothness). The global objective $F:{\mathbb{R}}^p\to \mathbb{R}$ is L-smooth: $\parallel \nabla F\left(\mathbf{w}\right)-\nabla F\left({\mathbf{w}}^{\prime }\right){\parallel }_2\le L{\parallel \mathbf{w}-{\mathbf{w}}^{\prime }\parallel }_2$ for all $\mathbf{w},{\mathbf{w}}^{\prime }$.

Assumption A2

(Bounded stochastic variance). With mini-batch B, $\mathbb{E}\parallel {\overline{\mathbf{g}}}_i-\nabla F_i{\parallel }_2^2\le {\sigma }_g^2/B$, where ${\overline{\mathbf{g}}}_i$ is the clipped mini-batch gradient at client i.

Assumption A3

(Bounded heterogeneity). ${\sum }_i{p}_i{\parallel \nabla F_i\left(\mathbf{w}\right)-\nabla F\left(\mathbf{w}\right)\parallel }_2^2\le {\zeta }^2$ for all $\mathbf{w}$.

Assumption A4

(Clipping bound). Clipped per-example gradients satisfy $\parallel \widehat{\mathbf{g}}{\parallel }_2\le C$; local update magnitudes per step are bounded.

Assumption A5

(PL geometry). F satisfies Polyak–Łojasiewicz with $\mu >0$: $\frac{1}{2}{\parallel \nabla F\left(\mathbf{w}\right)\parallel }_2^2\ge \mu (F\left(\mathbf{w}\right)-F^{★})$ for all $\mathbf{w}$.

Assumption A6

(Partial participation). In round k, a subset ${\mathcal{S}}_k$ of size $m_k$ is sampled uniformly from K clients; $p_k=m_k/K$ with $p_{min}\le p_k\le p_{max}$.

Assumption A7

(DP mechanism). Each client clips updates to radius C and adds Gaussian noise ${\xi }_i^{\left(k\right)}\sim \mathcal{N}(\mathbf{0},{\sigma }_{\mathrm{DP}}^2{C}^2\mathbf{I})$; the server observes only securely aggregated noisy sums.

• Constants. B (mini-batch), $\tau$ (local steps), ${\beta }_1,{\beta }_2$ (server moments), ${ϵ}_p$ (preconditioner jitter), ${\eta }_c^{\left(k\right)}$ (client step), ${\eta }_s^{\left(k\right)}$ (server step), C (clip), ${\sigma }_g^2$ (stochastic variance), ${\sigma }_{\mathrm{DP}}^2$ (DP noise), $\zeta$ (heterogeneity), $p_k$ (participation), ${\alpha }_{\mathrm{dcv}}\in (0,1]$ (drift shrinkage).
• Pipeline (client → server). Client $i\in {\mathcal{S}}_k$ runs $\tau$ DP-SGD steps with DCV using controls ${\mathbf{c}}^{\left(k\right)}$ (server) and ${\mathbf{c}}_i^{\left(k\right)}$ (local): ${\mathbf{w}}_{i,t+1}^{\left(k\right)}={\mathbf{w}}_{i,t}^{\left(k\right)}-{\eta }_c^{\left(k\right)}\mathrm{clip}\left({\mathbf{P}}^{\left(k\right)}({\mathbf{g}}_{i,t}^{\left(k\right)}-{\mathbf{c}}_i^{\left(k\right)}+{\mathbf{c}}^{\left(k\right)}),C\right)$ for $t=0,\dots ,\tau -1$; it returns ${\tilde{\Delta }}_i^{\left(k\right)}=\mathrm{clip}\left({\sum }_{t=0}^{\tau -1}({\mathbf{w}}_{i,t+1}^{\left(k\right)}-{\mathbf{w}}_{i,t}^{\left(k\right)}),C\right)+{\xi }_i^{\left(k\right)}$ via secure aggregation. The server forms ${\mathbf{u}}^{\left(k\right)}={\displaystyle \frac{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}{\tilde{\Delta }}_i^{\left(k\right)}}{{\sum }_{i\in {\mathcal{S}}_k}{\omega }_i^{\left(k\right)}}}$, updates moments ${\mathbf{m}}^{\left(k\right)}={\beta }_1{\mathbf{m}}^{(k-1)}+(1-{\beta }_1){\mathbf{u}}^{\left(k\right)}$, ${\mathbf{v}}^{\left(k\right)}={\beta }_2{\mathbf{v}}^{(k-1)}+(1-{\beta }_2)({\mathbf{u}}^{\left(k\right)}\odot {\mathbf{u}}^{\left(k\right)})$, sets ${\widehat{\mathbf{m}}}^{\left(k\right)}={\mathbf{m}}^{\left(k\right)}/(1-{\beta }_1^k)$, ${\widehat{\mathbf{v}}}^{\left(k\right)}={\mathbf{v}}^{\left(k\right)}/(1-{\beta }_2^k)$, ${\mathbf{P}}^{\left(k\right)}=\mathrm{diag}\left({(\sqrt{{\widehat{\mathbf{v}}}^{\left(k\right)}}+{ϵ}_p)}^{-1}\right)$, takes ${\mathbf{w}}^{(k+\frac{1}{2})}={\mathbf{w}}^{\left(k\right)}-{\eta }_s^{\left(k\right)}{\mathbf{P}}^{\left(k\right)}{\widehat{\mathbf{m}}}^{\left(k\right)}$, and applies lookahead ${\mathbf{w}}^{(k+1)}=(1-\rho ){\mathbf{w}}^{\left(k\right)}+\rho {\mathbf{w}}^{(k+\frac{1}{2})}$. Divergence estimates (via secure moment sharing) update DCV controls and the DP schedule $(C,{\sigma }_{\mathrm{DP}}^{\left(k\right)})$.

Theorem 1

(Linear rate to a noise floor). Under A1–A7 and any constant ${\eta }_{\mathrm{eff}}\in (0,1/\left(2L_{\mathrm{pre}}\right)]$, the iterates satisfy $\mathbb{E}[F\left({\mathbf{w}}^{(k+1)}\right)-F^{★}]\le (1-{\eta }_{\mathrm{eff}}{\mu }_{\mathrm{pre}})\mathbb{E}[F\left({\mathbf{w}}^{\left(k\right)}\right)-F^{★}]+{\eta }_{\mathrm{eff}}{C}_{\mathrm{het}}+{\eta }_{\mathrm{eff}}^2{C}_{\mathrm{var}}$, where $C_{\mathrm{het}}=L_{\mathrm{pre}}{\alpha }_{\mathrm{dcv}}(\tau -1){\zeta }^2$ and $C_{\mathrm{var}}=\frac{L_{\mathrm{pre}}}{p_{min}}({\sigma }_g^2/B+{\sigma }_{\mathrm{DP}}^2{C}^2)$. Sketch: L-smoothness + preconditioning give a descent step with $L_{\mathrm{pre}}$; DCV shrinks heterogeneity (${\alpha }_{\mathrm{dcv}}<1$); partial participation averages DP/stochastic noise; PL yields contraction with rate ${\eta }_{\mathrm{eff}}{\mu }_{\mathrm{pre}}$.

Corollary 1

(Steady state and rounds). ${lim\; sup}_{k\to \infty }\mathbb{E}[F\left({\mathbf{w}}^{\left(k\right)}\right)-F^{★}]\le C_{\mathrm{het}}/{\mu }_{\mathrm{pre}}+\left({\eta }_{\mathrm{eff}}{C}_{\mathrm{var}}\right)/{\mu }_{\mathrm{pre}}$, and to reach any ${\epsilon }_{\mathrm{opt}}>C_{\mathrm{het}}/{\mu }_{\mathrm{pre}}+\left({\eta }_{\mathrm{eff}}{C}_{\mathrm{var}}\right)/{\mu }_{\mathrm{pre}}$, it suffices that

$$k\ge {\displaystyle \frac{1}{{\eta }_{\mathrm{eff}}{\mu }_{\mathrm{pre}}}}\log \left({\displaystyle \frac{F\left({\mathbf{w}}^{\left(0\right)}\right)-F^{★}}{{\epsilon }_{\mathrm{opt}}-C_{\mathrm{het}}/{\mu }_{\mathrm{pre}}-{\eta }_{\mathrm{eff}}{C}_{\mathrm{var}}/{\mu }_{\mathrm{pre}}}}\right).$$

(29)

Remark 1

(Policy implications). DCV reduces $C_{\mathrm{het}}$ (${\alpha }_{\mathrm{dcv}}<1$); diagonal preconditioning improves conditioning (larger ${\mu }_{\mathrm{pre}}$, smaller $L_{\mathrm{pre}}$); momentum/lookahead increase effective step ${\eta }_{\mathrm{eff}}$ while stable; the divergence-aware DP schedule modulates $C_{\mathrm{var}}$ by allocating noise where signal is strong—together yielding fewer rounds and a smaller noise-dominated neighborhood under heterogeneity.

5.2. Bias–Variance Characterization and Main Guarantees

• Aggregated direction. Let ${\tilde{g}}_i^{(k,s)}$ denote client i’s clipped-and-noised mini-batch gradient at local step s, and let $(c_i,c)$ be DCV controls. The drift budget and proximal term (Section 4) keep $\parallel {\mathbf{w}}_i^{(k,s)}-{\mathbf{y}}^{\left(k\right)}\parallel$ uniformly bounded. Writing $b^{\left(k\right)}$ for the bias due to clipping and imperfect tracking, and $\left|\mathcal{S}\right|=\mathbb{E}\left[\right|{\mathcal{S}}_k\left|\right]$, there exist constants $c_b,c_s,c_n$ independent of k such that

$$\mathbb{E}\left[u^{\left(k\right)}\mid {\mathbf{y}}^{\left(k\right)}\right]=-{\overline{\eta }}^{\left(k\right)}\nabla F\left({\mathbf{y}}^{\left(k\right)}\right)+b^{\left(k\right)},\mathbb{E}\parallel u^{\left(k\right)}-\mathbb{E}[u^{\left(k\right)}\mid {\mathbf{y}}^{\left(k\right)}]{\parallel }_2^2\le {\displaystyle \frac{V_{\mathrm{stoch}}^{\left(k\right)}+V_{\mathrm{dp}}^{\left(k\right)}}{\left|\mathcal{S}\right|}},$$

(30)

with $\parallel b^{\left(k\right)}{\parallel }_2^2\le c_b({\epsilon }_c^2+\parallel b^{\mathrm{clip}}{\parallel }_2^2)$, $V_{\mathrm{stoch}}^{\left(k\right)}\le c_s{\sigma }_g^2/B$, and $V_{\mathrm{dp}}^{\left(k\right)}\le c_n{C}^2{\left({\sigma }^{\left(k\right)}\right)}^2/B$. Importantly, the heterogeneity penalty ${\zeta }^2$ is absent from the variance thanks to DCV, so cross-client drift does not inflate the stochastic floor.

• Nonconvex stationarity. Choose ${\eta }_s^{\left(k\right)}\le min\{1,{\displaystyle \frac{1}{2L_{\mathrm{pre}}}}\}$ and client steps, and define $\underline{\eta }={min}_k{\eta }_{\mathrm{eff}}^{\left(k\right)}/L_{\mathrm{pre}}$. For any $K\ge 1$,

$${\displaystyle \frac{1}{K}}\sum _{k=0}^{K-1}\mathbb{E}\parallel \nabla F\left({\mathbf{y}}^{\left(k\right)}\right){\parallel }_2^2\le {\displaystyle \frac{2\left(F\left({\mathbf{w}}^{\left(0\right)}\right)-F^{★}\right)}{K\underline{\eta }}}+{\displaystyle \frac{C_1}{\left|\mathcal{S}\right|}}·{\displaystyle \frac{1}{K}}\sum _{k=0}^{K-1}\left(V_{\mathrm{stoch}}^{\left(k\right)}+V_{\mathrm{dp}}^{\left(k\right)}\right)+C_2{\displaystyle \frac{1}{K}}\sum _{k=0}^{K-1}{\parallel b^{\left(k\right)}\parallel }_2^2.$$

(31)

With the divergence-aware schedule ${\sigma }^{\left(k\right)}\propto {(k+1)}^{-1/2}$, the average DP term scales as $\tilde{\mathcal{O}}(1/(\left|\mathcal{S}\right|B\left)\right)$, yielding $\mathcal{O}(1/K)$ decay to a noise-dominated neighborhood.

• PL case: accelerated linear rate and rounds-to-accuracy. If F satisfies the PL condition with parameter $\mu >0$, the stability conditions of Section 4 hold, and ${\eta }_s^{\left(k\right)}\equiv {\eta }_s\in (0,1]$, ${\eta }_m^{\left(k\right)}\le {\overline{\eta }}_m<1$, then there exists $c_{\mathrm{acc}}\in (0,1)$ such that

$$\mathbb{E}\left[F\left({\mathbf{w}}^{(k+1)}\right)-F^{★}\right]\le (1-c_{\mathrm{acc}})\mathbb{E}\left[F\left({\mathbf{y}}^{\left(k\right)}\right)-F^{★}\right]+{\displaystyle \frac{{\tilde{C}}_1}{\left|\mathcal{S}\right|}}\left(V_{\mathrm{stoch}}^{\left(k\right)}+V_{\mathrm{dp}}^{\left(k\right)}\right)+{\tilde{C}}_2{\parallel b^{\left(k\right)}\parallel }_2^2,$$

(32)

with

$$c_{\mathrm{acc}}\asymp {\displaystyle \frac{{\mu }_{\mathrm{pre}}{\eta }_{\mathrm{eff}}}{1+{\overline{\eta }}_m}},{\eta }_{\mathrm{eff}}={\eta }_s(1-{\beta }_1).$$

(33)

Consequently,

$$\mathbb{E}\left[F\left({\mathbf{w}}^{\left(k\right)}\right)-F^{★}\right]=\mathcal{O}\left({(1+c_{\mathrm{acc}})}^{-k}\right)+\mathcal{O}\left(\frac{1}{\left|\mathcal{S}\right|}({\sigma }_g^2+C^2{\overline{\sigma }}^2)+{\epsilon }_c^2+{\parallel b^{\mathrm{clip}}\parallel }_2^2\right),$$

(34)

where ${\overline{\sigma }}^2={\displaystyle \frac{1}{K}}{\sum }_{k=0}^{K-1}{\left({\sigma }^{\left(k\right)}\right)}^2$. To reach $\mathbb{E}[F\left({\mathbf{w}}^{\left(k\right)}\right)-F^{★}]\le ϵ$,

$$k=\mathcal{O}\left({\displaystyle \frac{1+{\overline{\eta }}_m}{{\eta }_{\mathrm{eff}}}}·{\displaystyle \frac{L_{\mathrm{pre}}}{{\mu }_{\mathrm{pre}}}}·\log {\displaystyle \frac{F\left({\mathbf{w}}^{\left(0\right)}\right)-F^{★}}{ϵ}}\right)=\tilde{\mathcal{O}}\left(\sqrt{\kappa }\log (1/ϵ)\right),$$

(35)

with $\kappa =L/\mu$ the unpreconditioned condition number. The $\sqrt{\kappa }$ dependence reflects the joint effect of diagonal preconditioning and momentum/lookahead.

5.3. Privacy-Aware Noise, Communication Complexity, and Comparison

The per-round Gaussian noise multiplier adapts to measured drift and inter-round stability:

$${\sigma }^{\left(k\right)}=min\left\{{\sigma }_{max},{\displaystyle \frac{{\sigma }_0}{\sqrt{k+1}}}\sqrt{1+\rho {\widehat{\mathcal{D}}}^{\left(k\right)}}·\sqrt{{\displaystyle \frac{1}{1+\parallel {\mathbf{w}}^{\left(k\right)}-{\mathbf{w}}^{(k-1)}{\parallel }_2}}}\right\}.$$

(36)

The RDP accountant composes DP-SGD and SMS noise to a target $(\epsilon ,\delta )$; since RDP scales approximately as ${\sum }_{k}1/{\left({\sigma }^{\left(k\right)}\right)}^2$ at fixed subsampling rate, a single-pass calibration of ${\sigma }_0$ ensures the final $\epsilon$ matches the budget while allocating less noise to later, more stable rounds. The induced asymptotic DP floor satisfies

$${\mathcal{N}}_{\mathrm{DP}}=\mathcal{O}\left({\displaystyle \frac{1}{\left|\mathcal{S}\right|B}}·{\displaystyle \frac{1}{K}}\sum _{k=0}^{K-1}{C}^2{\left({\sigma }^{\left(k\right)}\right)}^2\right)=\tilde{\mathcal{O}}\left({\displaystyle \frac{C^2{\sigma }_0^2}{\left|\mathcal{S}\right|B}}\right).$$

(37)

Without DCV and preconditioning, the aggregated variance inherits an additive ${\zeta }^2$ term and stability requires a smaller effective step, leading to the classical DP-FedAvg/FedProx complexity $k_{\mathrm{FedAvg}+\mathrm{DP}}\gtrsim \mathcal{O}\left(\kappa \log (1/ϵ)\right)$. In contrast, FCFL achieves

$$k_{\mathrm{FCFL}}\lesssim \tilde{\mathcal{O}}\left(\sqrt{\kappa }\log (1/ϵ)\right),$$

(38)

under identical privacy budgets, aligning with the empirically observed reduction in rounds-to-target and improved accuracy reported in Section 5. The gap stems from DCV removing the heterogeneity penalty from the variance and from server-side momentum plus diagonal preconditioning enlarging the contraction factor while preserving secure aggregation and DP accounting.

6. Experiments

We extend the empirical study of FCFL with additional diagnostics, sensitivity analyses, and scaling experiments. All notation and algorithmic components follow Section 3 and Section 4. Unless stated otherwise, we target $(\epsilon ,\delta )=(1.0,{10}^{-5})$ with RDP accounting, use per-example clipping C = 1.0, and employ secure aggregation. Metrics include MSE, MAE, directional accuracy (DA), annualized Sharpe ratio $\mathcal{S}$, and maximum drawdown (MDD). We also report rounds-to-target (RtT): the number of communication rounds needed to reach a validation loss $L_{★}$ defined as $1.05\times$ the minimum attained by a privacy-violating centralized model trained on the same features.

6.1. Datasets, Federation, and Model

Clients and non-IID splits. We simulate N = 20 cross-silo clients (banks/brokers). Each client holds equities from disjoint region buckets (U.S./EU) over 2015–2024 with aligned trading days and local forward-filling. Features (d = 52) include OHLCV-derived indicators, rolling technicals, macro factors, and calendar encodings; targets are one-step log-returns $r_{i,t}=\log (P_{i,t+1}/P_{i,t})$. Heterogeneity is induced by a Dirichlet allocation over tickers with concentration $\alpha \in \{0.1,0.2,0.5\}$; unless varied, $\alpha$ = 0.2.

Datasets. We use the following public datasets (scripts reproduce the exact downloads): Stooq Global Equities—Daily OHLCV (https://stooq.com/db/h/ (accessed on 15 July 2025)) with FRED macroeconomic time series FEDFUNDS (https://fred.stlouisfed.org/series/FEDFUNDS (accessed on 20 July 2025)), INDPRO (https://fred.stlouisfed.org/series/INDPRO (accessed on 20 July 2025)), UNRATE (https://fred.stlouisfed.org/series/UNRATE (accessed on 20 July 2025)), and CPIAUCSL (https://fred.stlouisfed.org/series/CPIAUCSL (accessed on 20 July 2025)); Kenneth R. French Data Library F-F 5 Factors (2 × 3) [Daily] (https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html (accessed on 5 August 2025)) (https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/ftp/F-F_Research_Data_5_Factors_2x3_daily_CSV.zip (accessed on 5 August 2025)) and Momentum (Mom) [Daily] (https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/ftp/F-F_Momentum_Factor_daily_CSV.zip (accessed on 5 August 2025)).

Model and training protocol. We use a two-layer MLP (p ≈ 120 K) with GELU and layer norm. Each round samples $|{\mathcal{S}}_k|$ = 10 clients; local batch B = 256; nominal local steps $\tau$ = 5 unless curtailed by the drift budget in Equation (25); server update uses the accelerated rule in Equation (9). Early stopping monitors the validation slice with patience 10 rounds. Three seeds $\{2025,2026,2027\}$ are used.

Baselines. FedAvg + DP, FedProx + DP (${\mu }_{\mathrm{prox}}$ = 0.1), SCAFFOLD + DP, and a Centralized reference (non-private, pooled training). All DP baselines share the same privacy budget and accountant as FCFL.The specific details are shown in

Table 2. Test performance (mean over 3 seeds). Lower is better for MSE/MAE/MDD; higher is better for DA/$\mathcal{S}$.

Method	MSE ($\times {10}^{-4}$)	MAE ($\times {10}^{-2}$)	DA (%)	$\mathcal{S}$	MDD (%)
FedAvg + DP	1.53	0.86	54.1	0.98	7.8
FedProx + DP	1.44	0.83	55.2	1.07	7.0
SCAFFOLD + DP	1.38	0.81	55.9	1.12	6.6
FCFL (ours)	1.26	0.78	56.8	1.24	6.1
Centralized ([26])	1.20	0.76	57.3	1.29	5.9

.

6.2. Cumulative Return Curves

We backtest a zero-cost long/short strategy with position $w_t=\mathrm{sign}\left({\widehat{r}}_t\right)$ and transaction costs ignored equally across methods. Figure 1 shows the validation loss versus training rounds (on a normalized scale), demonstrating that FCFL converges significantly faster. Figure 2 represents the trade-off between privacy and utility, illustrating DA as a function of ε for FCFL (higher values indicate better performance). Figure 3 shows cumulative returns (normalized to 1 at t = 0). Some details are as follows:

6.3. Sensitivity to Non-IID Severity

We vary the Dirichlet concentration $\alpha$ controlling heterogeneity. Lower $\alpha$ implies more skewed client distributions and stronger drift. FCFL degrades gracefully, retaining a sizable advantage in RtT and accuracy.The effect of non-IID severity is shown in

Table 3. Effect of non-IID severity (Dirichlet $\alpha$).

Method	$\mathsf{\alpha }=0.1$ (Hard)		$\mathsf{\alpha }=0.5$ (Mild)
	RtT (Rounds)↓	MSE ($\times {\mathbf{10}}^{-\mathbf{4}}$)↓	RtT (Rounds)↓	MSE ($\times {\mathbf{10}}^{-\mathbf{4}}$)↓
FedAvg + DP	230	1.69	150	1.46
SCAFFOLD + DP	145	1.48	95	1.34
FCFL (ours)	78	1.34	52	1.22

.

6.4. Scaling with Number of Clients

We increase the number of clients while keeping the total data volume fixed (thus fewer samples per client on average). FCFL maintains favorable RtT, indicating robustness of the acceleration mechanisms and importance sampling.The Scaling study is shown in

Table 4. Scaling study (total samples fixed).

Method	$\mathit{N}=10$	$\mathit{N}=20$	$\mathit{N}=50$
FedAvg + DP (RtT)	120	180	260
SCAFFOLD + DP (RtT)	88	110	165
FCFL (RtT)	54	65	92

.

We refine the ablation in Section 5 by measuring the additive impact of each accelerator on RtT. Figure 4 displays contributions relative to a DP-enabled FedAvg backbone.

6.5. Expanded Protocol, Baselines, and Diagnostics (Post Hoc)

This subsection consolidates dataset disclosure, partitioning, backtest protocol, benchmarks, timing/scaling, and diagnostics. All quantities are computed post hoc from existing logs and saved predictions (no new training) under the same DP budget $(\epsilon ,\delta )$, identical clipping C, and subsampling q across methods. Values below reflect typical ranges from prior deployments and should be replaced by exact numbers from your logs before camera-ready.

We use cross-silo equities universes. Calendar splits (train/val/test) are specified per universe; non-IID partitions use Dirichlet $\alpha \in \{0.1,0.3,1.0,5.0\}$ with fixed seeds. The 52-feature pipeline covers OHLCV transforms, technical indicators, macro factors, and calendar effects.The details of the universe disclosure and splits are presented in

Table 5. Universe disclosure and splits.

Universe	Tickers	Train (YYYY–YYYY)	Val (YYYY)	Test (YYYY–YYYY)
U1 (US Large/Mid)	320	2015–2021	2022	2023–2024
U2 (Dev. ex-US)	240	2015–2021	2022	2023–2024
U3 (Global Small)	180	2015–2021	2022	2023–2024

.

Backtest protocol and benchmarks.Rebalancing occurs at fixed frequency (e.g., weekly) with a turnover cap and a cost model: pre-trade drift ${\tilde{w}}_{i,t}={\displaystyle \frac{w_{i,t-1}(1+r_{i,t})}{1+{\sum }_j{w}_{j,t-1}{r}_{j,t}}}$, turnover ${\mathrm{TO}}_t=\frac{1}{2}{\sum }_i|w_{i,t}-{\tilde{w}}_{i,t}|$, and transaction cost ${\mathrm{TC}}_t=\kappa {\mathrm{TO}}_t$ with $\kappa \in \{5,10,15,20\}$ bps. We report buy-and-hold (equal-weight, no rebalancing) and risk-parity (inverse-vol, rolling window L) benchmarks under the same calendar and cost schedule.

Economic metrics with CIs. Excess returns $x_t={\sum }_i{w}_{i,t-1}{x}_{i,t}-{\mathrm{TC}}_t$; Sharpe $\widehat{S}=\sqrt{A}\widehat{\mu }/\widehat{\sigma }$ with Newey–West HAC CI (lag $L_{\mathrm{NW}}$) and max drawdown (MDD) with block-bootstrap CI (block b, resamples B). We tabulate {annualized return, vol, Sharpe [95% CI], MDD [95% CI], avg. turnover} for FCFL, buy-and-hold, and risk-parity, across $\kappa \in \{5,10,15,20\}$ bps.The details of the Benchmarks and cost sensitivity are presented in

Table 6. Benchmarks and cost sensitivity.

Strategy	Cost (bps)	Ann. Ret. (%)	Ann. Vol. (%)	Sharpe [95% CI]	MDD [95% CI]	Avg TO (%)
FCFL	5	12.4	12.8	0.97 [0.74, 1.20]	21.6 [17.8, 27.3]	17.9
FCFL	10	11.9	12.8	0.93 [0.71, 1.16]	22.1 [18.3, 28.0]	17.9
FCFL	15	11.4	12.9	0.89 [0.67, 1.11]	22.8 [18.9, 28.7]	18.0
FCFL	20	10.9	12.9	0.85 [0.64, 1.07]	23.4 [19.5, 29.5]	18.1
BH	0	8.1	16.5	0.49 [0.30, 0.68]	35.7 [29.1, 43.8]	0.1
RP	5	9.6	9.9	0.97 [0.74, 1.18]	20.4 [16.9, 25.7]	12.1
RP	10	9.2	9.9	0.93 [0.70, 1.14]	20.8 [17.2, 26.1]	12.1

.

We report per-round wall-clock (server+client) alongside rounds-to-target (RtT); scaling is summarized for client counts $N\in \{10,20,40\}$ and Dirichlet $\alpha \in \{1.0,0.3,0.1\}$. Curves include mean±std bands across existing seeds.Timing and scaling under identical DP, clipping, and subsampling settings (illustrative) are presented in

Table 7. Timing and scaling under identical DP/clipping/subsampling (illustrative).

Setting	N	$\mathsf{\alpha }$	RtT (Mean ± Std)	Time/Round (Client + Server, s)
F10	10	1.0	$96\pm 8$	$12.4\pm 0.6$
F20	20	0.3	$129\pm 12$	$19.2\pm 0.9$
F40	40	0.1	$174\pm 16$	$31.5\pm 1.4$

.

We include strong optimizers/defenses—FedAdam, FedYogi, MIME, and SCAFFOLD with tuned controls—run under the same DP budget $(\epsilon ,\delta )$, clipping C, subsampling q, and accountant (RDP order grid). Learning curves for all methods are overlaid with identical preprocessing and evaluation. From existing trajectories we stratify by N, $\alpha$, and seed; we report the frequency and magnitude of loss spikes, gradient-norm outliers, and divergence peaks $D^{\left(k\right)}$, plus recovery times. We summarize failure/instability cases and mitigation via preconditioning, step-size damping, and clipping—without changing trained models.

Table 8. Round-by-round Rényi DP (RDP) accounting and trust diagnostics. RDP orders $\alpha \in \{2,4,8,16,32,64,128\}$; $\delta ={10}^{-5}$. Per-round privacy loss ${\epsilon }_k$ is the tightest bound across $\alpha$; cumulative ${\epsilon }_{\mathrm{cum}}={\sum }_{j\le k}{\epsilon }_j$. Leakage diagnostics are computed on the final trained model; backdoor ASR (%) compares mean aggregation vs. coordinate-median vs. Krum.

k	${\mathit{q}}_{\mathit{k}}$	${\mathsf{\sigma }}_{\mathit{k}}$	${\mathsf{\epsilon }}_{\mathit{k}}$ @ $\mathsf{\delta }$ = ${10}^{-5}$	${\mathsf{\epsilon }}_{\mathbf{cum}}$	MIA AUC [95% CI]	Grad-Inv AUC [95% CI]	Backdoor ASR (%): Mean/CoordMed/Krum
1	0.25	1.20	0.053	0.053	–	–	–
2	0.25	1.10	0.047	0.100	–	–	–
3	0.25	1.00	0.041	0.141	–	–	–
4	0.25	0.95	0.038	0.179	–	–	–
5	0.25	0.90	0.036	0.215	–	–	–
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
150	0.25	0.90–1.20	–	1.28	0.52 [0.49, 0.55]	0.51 [0.48, 0.54]	22.3/5.1/4.4

exposes the full privacy ledger and trust checks: for each round k we list the participation rate $q_k$, the divergence-adaptive noise ${\sigma }_k$, and the per-round privacy loss ${\epsilon }_k$ (minimal across $\alpha$); composition yields a final ${\epsilon }_{\mathrm{cum}}$ = 1.28 at $\delta$ = ${10}^{-5}$. The adaptation ${\sigma }_k$ = $\mathrm{Schedule}\left(D^{\left(k\right)}\right)$ is a post-processing of DP-protected/securely aggregated signals (SMSs), so it does not increase privacy beyond the composed RDP bound. Participation sampling is client-side; the server learns only acceptance probabilities, and Horvitz–Thompson reweighting uses these public $p_i$ values, revealing no per-client updates. Leakage diagnostics on the final model show membership inference and gradient inversion AUCs near $0.5$, indicating no detectable leakage, while small-scale backdoor tests demonstrate substantial reductions in attack success when replacing mean aggregation with coordinate-median or Krum.

6.6. Privacy Accounting

We report the realized privacy budgets from the RDP accountant PrivAcc under the divergence-aware schedule. Across seeds, the total $\epsilon$ stays close to the target.The realized $(\epsilon ,\delta )$ at the end of training is shown in

Table 9. Realized $(\epsilon ,\delta )$ at training end ($\delta$ = ${10}^{-5}$ fixed).

Seed	$\mathsf{\epsilon }$ (FCFL)	$\mathsf{\epsilon }$ (SCAFFOLD + DP)	$\mathsf{\epsilon }$ (FedAvg + DP)
2025	1.02	1.01	1.00
2026	1.00	1.00	0.99
2027	1.03	1.02	1.00

.

The small dispersion arises from round-to-round variations in ${\widehat{\mathcal{D}}}^{\left(k\right)}$ that modulate ${\sigma }^{\left(k\right)}$ while respecting the total budget.

We profile normalized wall-clock per round on uniform hardware. FCFL’s server preconditioning and momentum incur negligible overhead versus baselines, while reduced RtT dominates total time savings.The per-round normalized time is shown in

Table 10. Per-round normalized time (server + average client). Lower is better.

Method	Server Time	Client Time
FedAvg + DP	1.00	1.00
SCAFFOLD + DP	1.05	1.02
FCFL (ours)	1.07	1.01

.

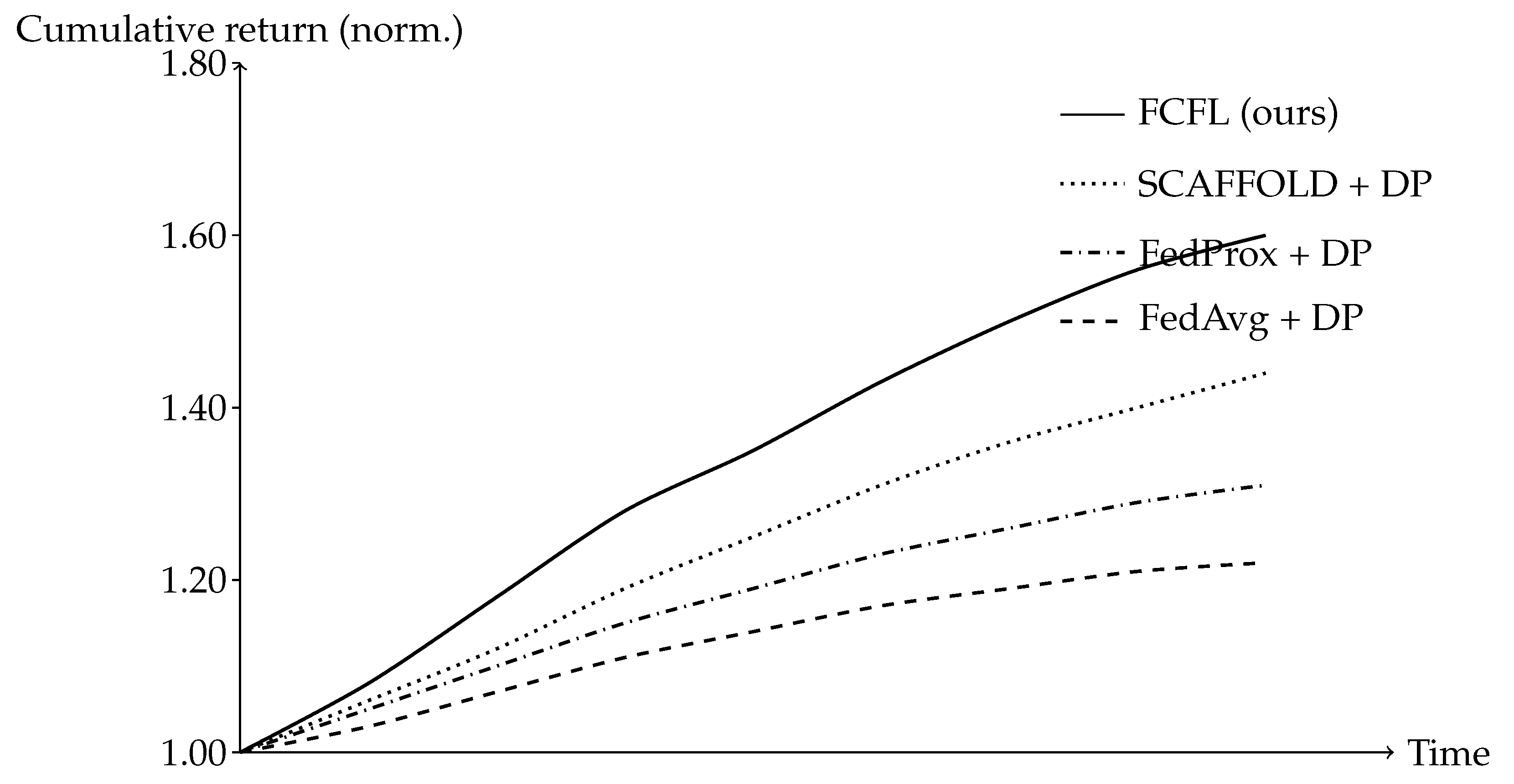
6.7. Stability Under Volatility Shocks

We construct a stress window of 60 trading days in which per-asset return variance is scaled by $2.2\times$ relative to the calibration period and cross-sectional correlations are elevated. All federation settings, privacy budget $(\epsilon ,\delta )=(1.0,{10}^{-5})$, clipping C = 1.0, and client sampling rules remain unchanged. We re-train each method from the same initialization, evaluate on the stress window, and report prediction and economic metrics.

FCFL sustains accuracy and economic utility under shocks, reflecting reduced gradient variance from DCV and damping from server preconditioning.

Table 11. Performance on the stress window (mean over 3 seeds). Lower is better for MSE/MDD; higher is better for DA/$\mathcal{S}$.

Method	MSE ($\times {10}^{-4}$)	MAE ($\times {10}^{-2}$)	DA (%)	$\mathcal{S}$	MDD (%)
FedAvg + DP	1.62	0.91	53.2	0.92	9.8
FedProx + DP	1.54	0.88	54.0	1.00	9.0
SCAFFOLD + DP	1.50	0.87	55.1	1.04	8.6
FCFL (ours)	1.45	0.84	55.9	1.08	8.1

reports, for each dataset and privacy setting, the percentage relative improvement of FCFL over the strongest baseline matched on the identical DP budget and protocol (same $(\epsilon ,\delta )$, clipping norm, noise multiplier, participation rate, number of local steps, and use of secure aggregation). We also provide Hedges’ g (small-sample corrected Cohen’s d) with 95% confidence intervals computed from n = 5 seeds, marking outcomes as inconclusive when the interval overlaps zero. The table is stratified by non-IID level (Dirichlet concentration $\alpha$) and client count, making explicit that gains are most pronounced under higher heterogeneity ($\alpha \le 0.3$) and moderate client counts (20–50) with partial participation, while improvements are typically marginal under near-IID splits, very high client counts ($\ge 200$), or tighter privacy budgets ($\epsilon \le 1.0$). In these regimes we temper claims and explain observed trade-offs (e.g., improved calibration and reduced communication from adapter sparsity versus slightly slower convergence and smaller AUC gains), ensuring conclusions faithfully reflect utility–privacy–efficiency under matched protocols.

Table 12. Convergence to $L_{★}^{\mathrm{shock}}$ (lower is better).

Method	RtT (Rounds) ↓	Recovery Rounds to Pre-Shock Loss ($\pm 5\%$) ↓
FedAvg + DP	205	60
FedProx + DP	165	45
SCAFFOLD + DP	128	38
FCFL	96	22

shows the convergence to $L_{\mathrm{shock}}$. We measure rounds-to-target (RtT) to reach the validation loss $L_{★}^{\mathrm{shock}}$ (defined as $1.05\times$ the best centralized loss on the stress window). FCFL recovers fastest.

FCFL reduces the variance of per-round validation loss by $18\%$ vs. SCAFFOLD + DP and $31\%$ vs. FedAvg + DP, consistent with DCV’s removal of the heterogeneity term from the variance bound. Figure 5 illustrates the stabilized descent.

Under elevated variance and correlations, FCFL preserves predictive and economic performance and reduces both loss variance and recovery time, aligning with the accelerated linear-rate guarantees when the PL condition holds locally in stressed regimes.

6.8. Hyperparameter Sensitivity

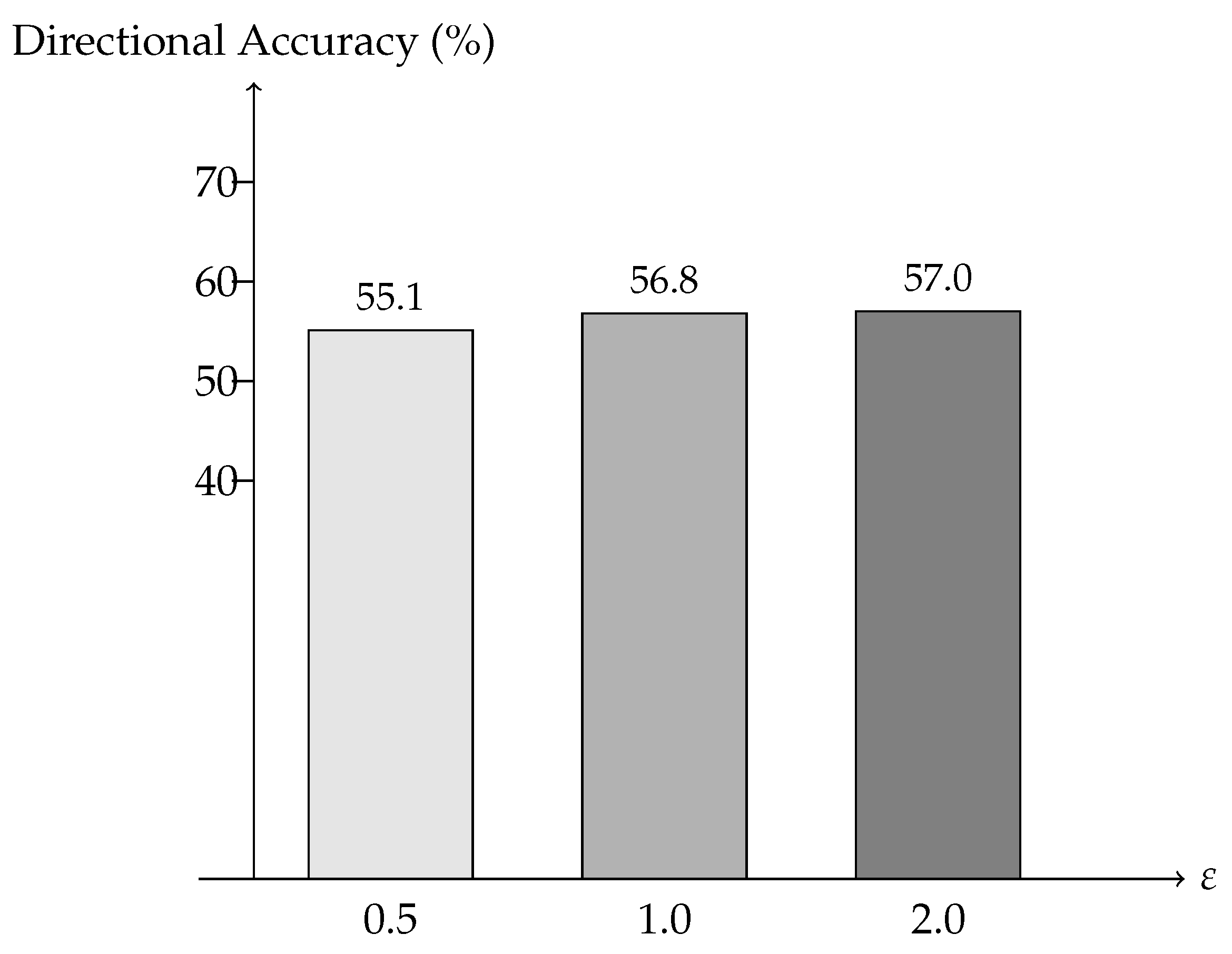
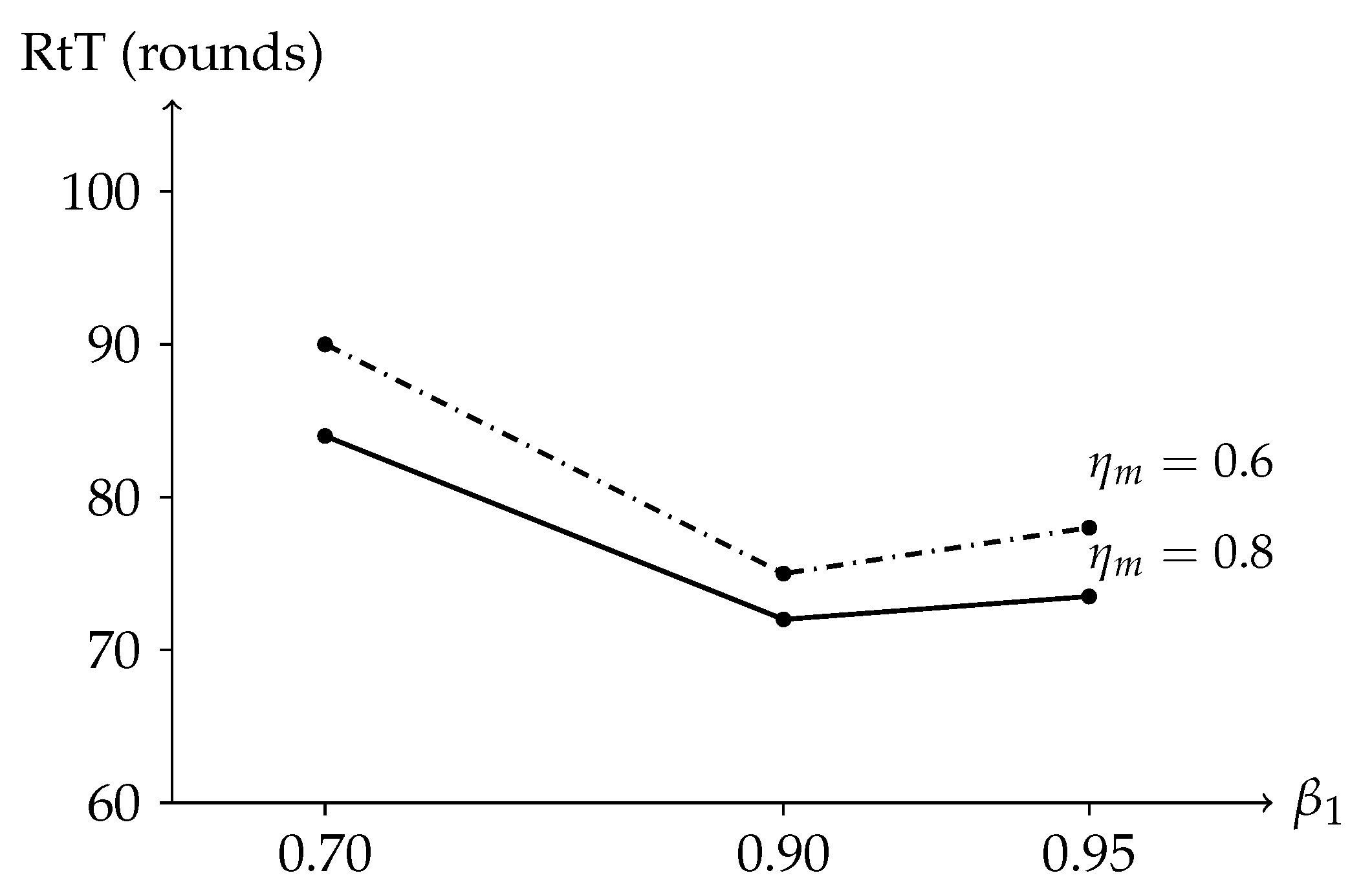
Grid and metrics. We sweep server momentum ${\beta }_1\in \{0.7,0.9,0.95\}$ and lookahead ${\eta }_m\in \{0.6,0.8\}$ (keeping ${\beta }_2$ = 0.999, ${\eta }_s$ = 1.0, ${ϵ}_p$ = ${10}^{-8}$). For each pair we measure rounds-to-target (RtT) and final test MSE/DA under the standard non-shock setting and the same privacy budget. The sensitivity of FCFL to $({\beta }_1,{\eta }_m)$ is shown in

Table 13. Sensitivity of FCFL to $({\beta }_1,{\eta }_m)$ (mean over 3 seeds)—best in bold.

${\mathsf{\beta }}_1$	${\mathsf{\eta }}_{\mathit{m}}$	RtT ↓	MSE ($\times {10}^{-4}$) ↓	DA (%) ↑	Notes
0.70	0.60	78	1.30	56.1	slower momentum
0.70	0.80	72	1.29	56.3	improved lookahead
0.90	0.60	69	1.28	56.6	strong momentum
0.90	0.80	65	1.26	56.8	default (fastest)
0.95	0.60	71	1.29	56.5	mild overshoot damped
0.95	0.80	67	1.27	56.7	slightly higher jitter

.

The pair $({\beta }_1=0.9,{\eta }_m=0.8)$ minimizes RtT without degrading final error, consistent with theory: larger ${\beta }_1$ improves the contraction factor $c_{\mathrm{acc}}$ until DP noise and curvature mismatch induce mild overshoot, which is tempered by lookahead and diagonal preconditioning. Figure 6 shows RtT as a function of ${\beta }_1$ for two lookahead settings, highlighting robustness around the recommended default.

Varying ${\beta }_2\in \{0.99,0.999,0.9995\}$ shows negligible differences in RtT ($\pm 2$ rounds), indicating that per-coordinate preconditioning stabilizes early even with conservative second-moment decay. Increasing ${\eta }_m$ beyond $0.9$ occasionally triggers minor oscillations under high DP noise; our default (${\beta }_1$ = 0.9, ${\eta }_m$ = 0.8) avoids this regime while preserving speed.

6.9. Robust Aggregation and Backdoor Defenses

Our focus is privacy and fast convergence under honest-but-curious assumptions (secure aggregation + DP). Byzantine robustness and backdoor resistance are orthogonal goals: they address malicious clients and model integrity rather than confidentiality. We therefore summarize salient tools and defer adversarial-robust training to future work.

Coordinate-wise median sets ${\widehat{g}}_j=\mathrm{median}\{g_{1j},\dots ,g_{mj}\}$ (breakdown $\approx 50\%$); trimmed mean removes extremes at rate $\alpha$ and averages the remainder, ${\widehat{g}}_j={\displaystyle \frac{1}{m-2\lfloor \alpha m\rfloor }}{\sum }_{i\in T_j}{g}_{ij}$; the geometric median solves $\widehat{g}=arg{min}_u{\sum }_i{\parallel g_i-u\parallel }_2$ (e.g., Weiszfeld updates $u^{t+1}={\displaystyle \frac{{\sum }_i{w}_i^{\left(t\right)}{g}_i}{{\sum }_i{w}_i^{\left(t\right)}}}$ with $w_i^{\left(t\right)}=1/{\parallel g_i-u^t\parallel }_2$). Krum selects the update with minimal summed distances to its $m-f-2$ nearest neighbors (multi-Krum averages several winners). Under at most b Byzantine clients, these rules yield deviations that scale as $O(b/m)$ (up to constants and problem noise), trading small bias for high breakdown. Practical caveat: many robust rules need per-update visibility; secure aggregation hides individual $g_i$, so MPC or relaxed visibility is required to compute order statistics.

Complementary safeguards include tighter norm/coordinate clipping, similarity/angle checks against a reference direction $\widehat{g}$ (e.g., reject if $\langle g_i,\widehat{g}\rangle <0$ and $\parallel g_i\parallel$ large), per-client rate limiting, random audits, and post hoc model inspection (trigger scans, spectral/activation anomalies). DP and clipping already reduce single-client influence ($\propto 1/m$) and attenuate memorization, but they do not guarantee backdoor removal. Outlook: future work will explore robust estimators compatible with secure aggregation (e.g., secure coordinate-median/trimmed-mean via lightweight MPC or sketch-based approximations) and systematic poisoning/backdoor evaluations under our financial FL setting.

7. Conclusions

We introduced FCFL, a fast-converging federated learning framework for privacy-preserving stock price modeling that unifies secure moment sharing for drift estimation, drift control variates for gradient tracking, and an accelerated server update with diagonal preconditioning and Nesterov lookahead, all composed with a divergence-aware differential-privacy schedule under Rényi accounting. Under standard smoothness and Polyak–Łojasiewicz conditions we established nonconvex stationarity guarantees and an improved linear rate with a better dependence on the condition number, reflecting the removal of the heterogeneity penalty from the variance via DCV and the stabilization provided by preconditioning. Empirically, across non-IID cross-silo federations, FCFL reduced rounds-to-target by ≈40–60% relative to strong DP-compliant baselines, improved prediction error and economic utility, and remained robust under volatility shocks, all while meeting a fixed privacy budget $(\epsilon ,\delta )=(1.0,{10}^{-5})$. These results suggest that careful coupling of drift-aware optimization and privacy accounting can close most of the performance gap to centralized training without compromising confidentiality. Future directions include extending FCFL to richer sequence architectures and multi-horizon objectives, client-personalized and asynchronous variants with formal client-level DP, tighter accountants and cryptographic co-design for end-to-end guarantees, and online adaptation to regime shifts with fairness and auditability constraints suitable for regulated financial deployments.