Bayesian FDOA-Only Localization Under Correlated Measurement Noise: A Low-Complexity Gaussian Conditional-Based Approach
Abstract
1. Introduction
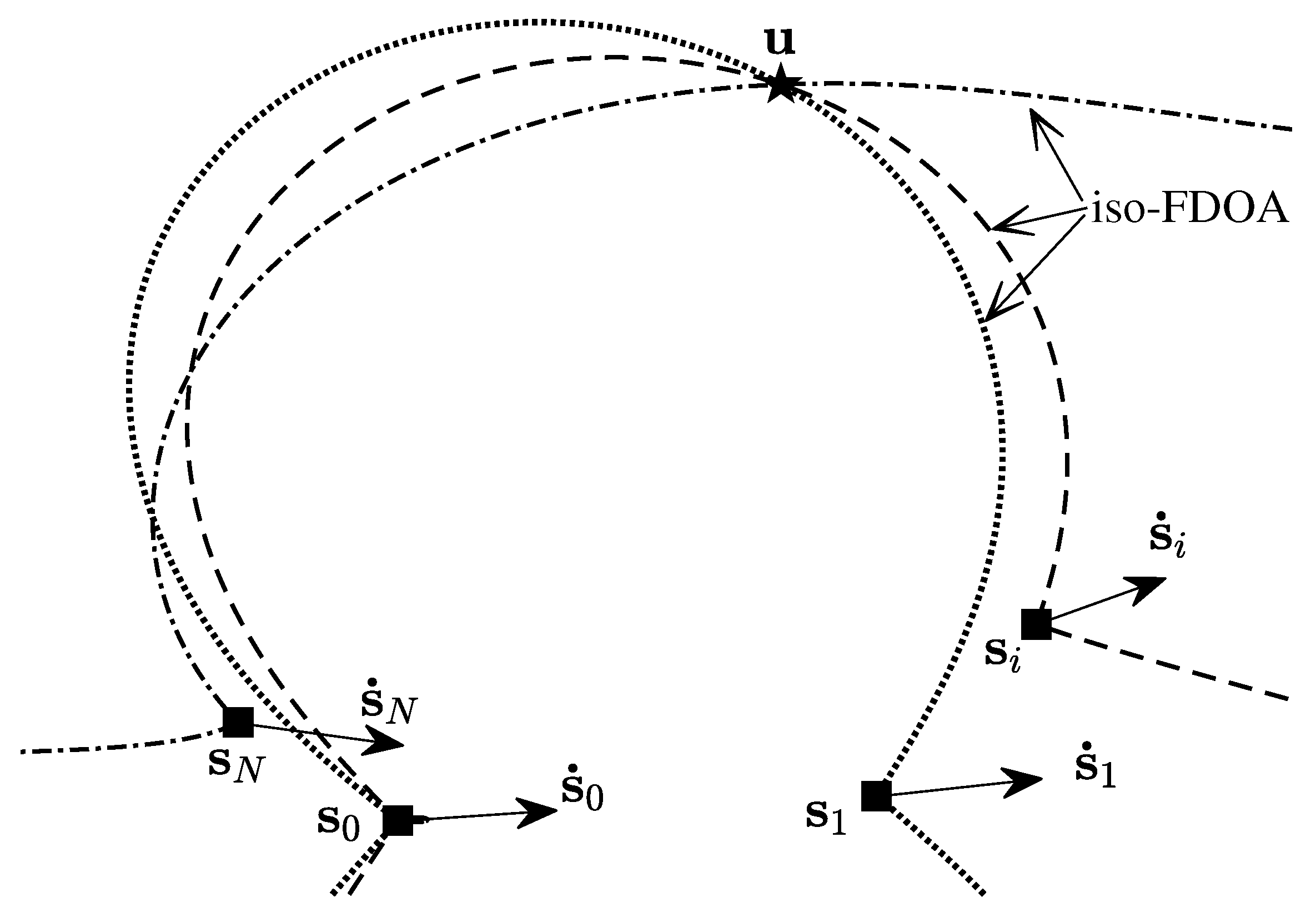
2. Problem Formulation
3. Gaussian Conditional Method
4. Computational Complexity Analysis
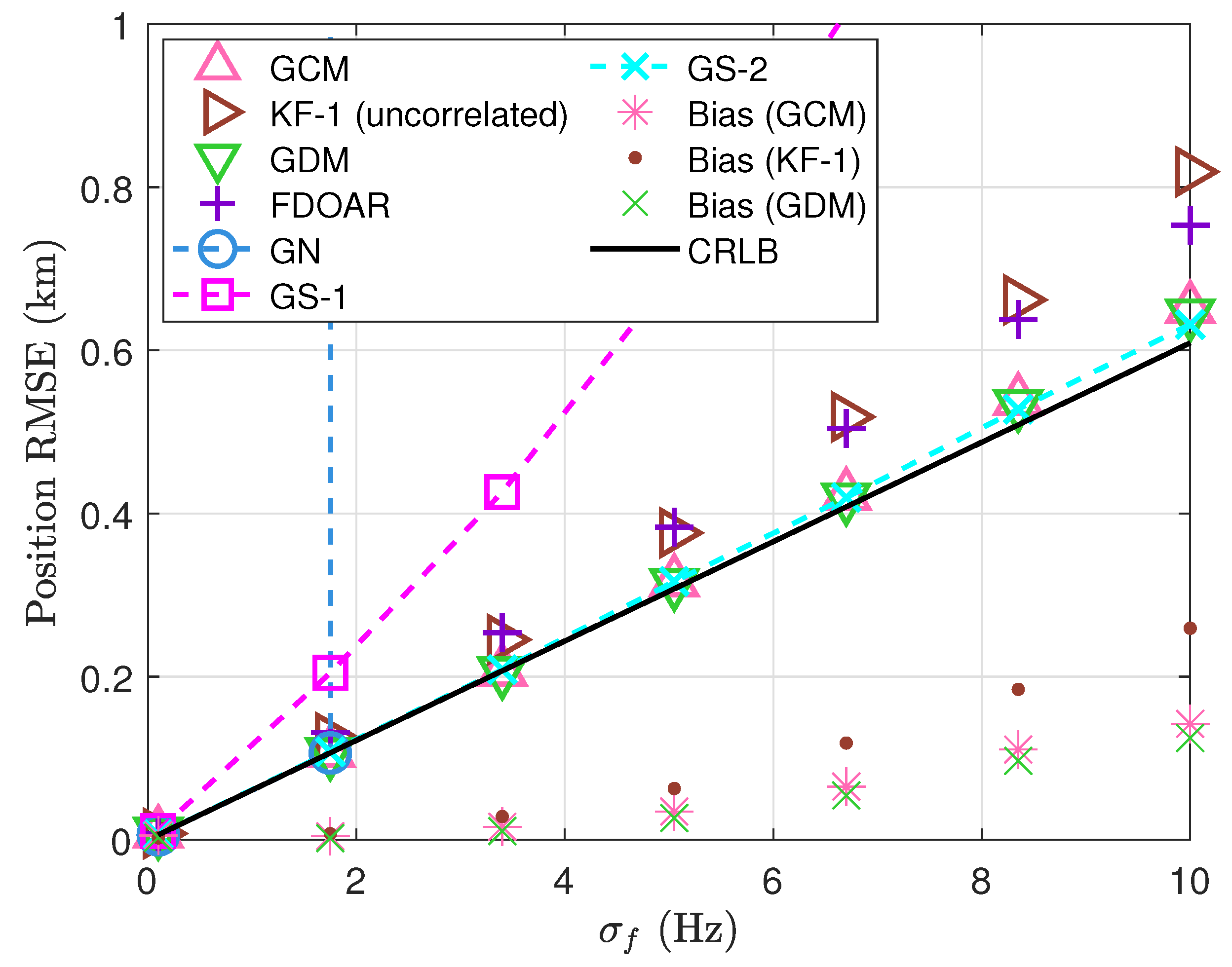
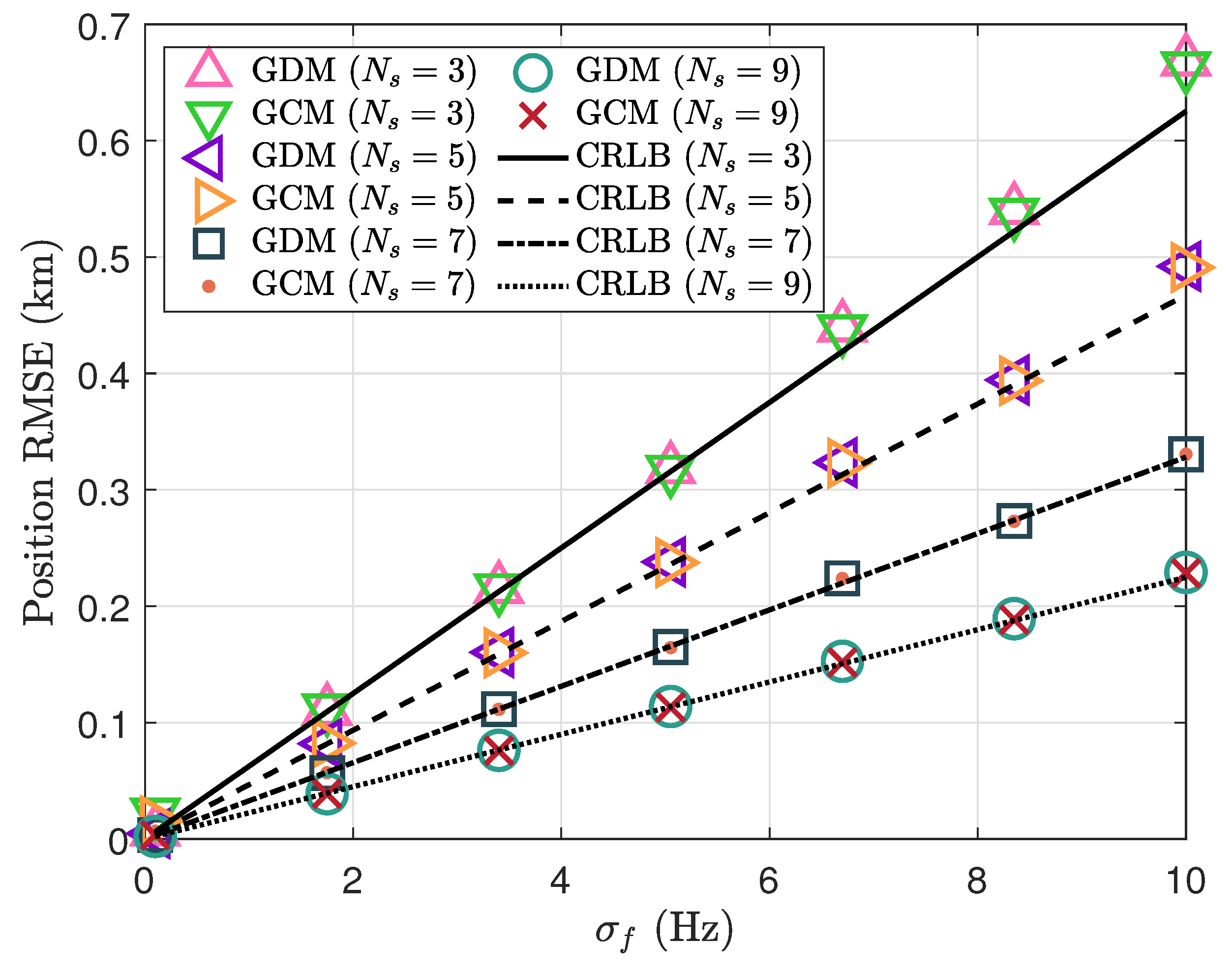
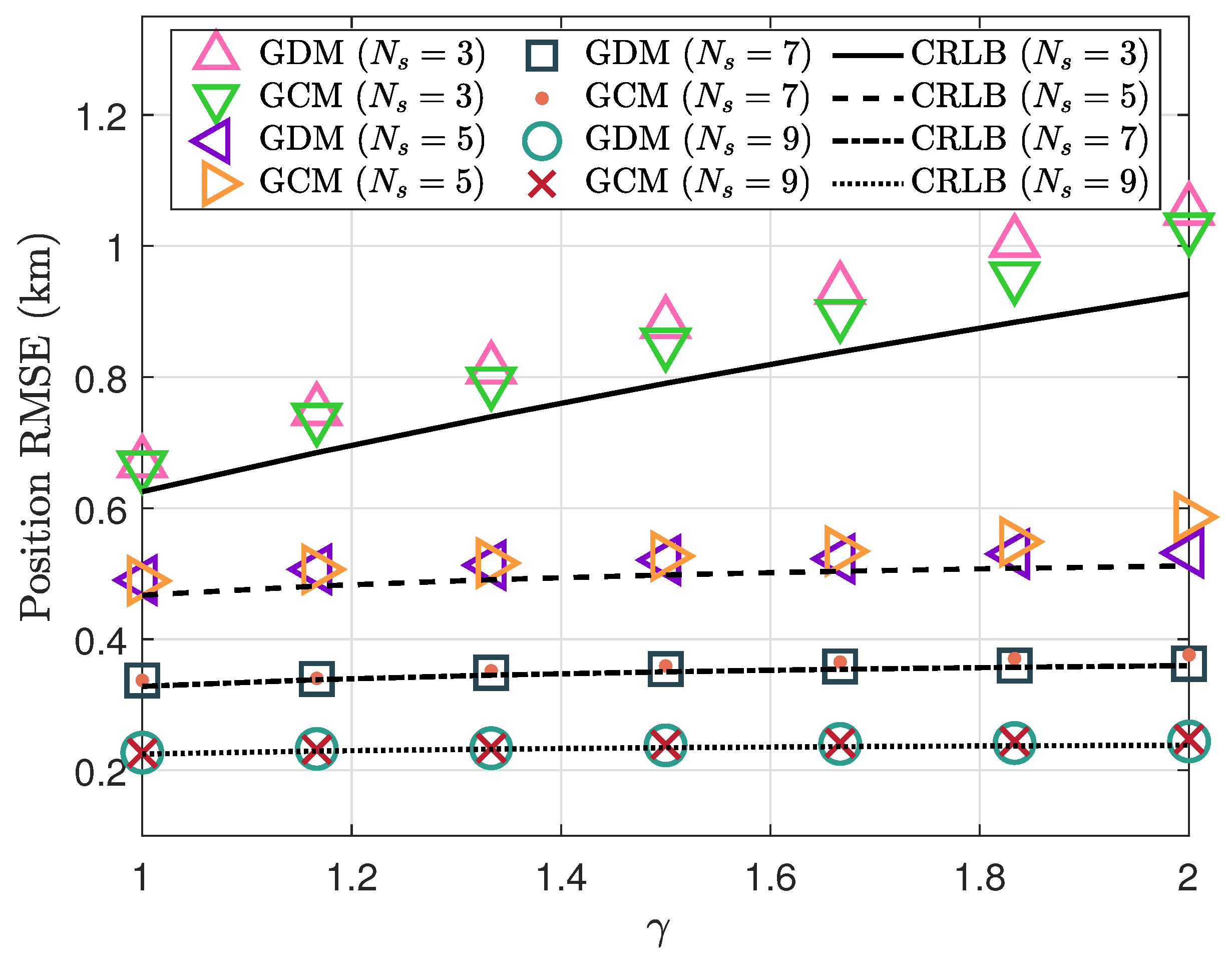
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, G.; Dong, Q.; Liao, G.; Li, S.; Xu, K.; Quan, Y. High-Precision Joint TDOA and FDOA Location System. Remote Sens. 2024, 16, 693. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y. 5G Reconfigurable Intelligent Surface TDOA Localization Algorithm. Electronics 2024, 13, 2409. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Gang, Y.; Wang, Y. TDOA-AOA Localization Algorithm for 5G Intelligent Reflecting Surfaces. Electronics 2024, 13, 4347. [Google Scholar] [CrossRef]
- Khalil, R.A.; Saeed, N.; Almutiry, M. UAVs-Assisted Passive Source Localization Using Robust TDOA Ranging for Search and Rescue. ICT Express 2023, 9, 677–682. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, S.; Huang, D. A TOA-Based Localization Algorithm with Simultaneous NLOS Mitigation and Synchronization Error Elimination. IEEE Sens. Lett. 2019, 3, 6000504. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wireless Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Arabsorkhi, M.; Zayyani, H.; Korki, M. 3-D Hybrid RSS-AOA Passive Source Localization with Unknown Path Loss Exponent. IEEE Sens. Lett. 2023, 7, 7003104. [Google Scholar] [CrossRef]
- Saeed, N. Intelligent Topology Management for TDOA-Based Localization in IoT Networks. IEEE Commun. Lett. 2025, 29, 1023–1027. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H. TDOA Localization with Unknown Signal Propagation Speed and Sensor Position Errors. IEEE Commun. Lett. 2020, 24, 1024–1027. [Google Scholar] [CrossRef]
- Zhang, S.; Zhong, W.; Du, P.; Chen, C. Experimental Demonstration of Indoor Sub-Decimeter Accuracy VLP System Using Differential PDOA. IEEE Photon. Technol. Lett. 2018, 30, 1703–1706. [Google Scholar] [CrossRef]
- Ge, F.; Shen, Y. Single-Anchor Ultra-Wideband Localization System Using Wrapped PDOA. IEEE Trans. Mobile Comput. 2022, 21, 4609–4623. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, J.; Liu, H.; Ho, K.C.; Yang, Z.; Gao, S. Optimal Sensor Placement and Velocity Configuration for TDOA-FDOA Localization and Tracking of a Moving Source. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8255–8272. [Google Scholar] [CrossRef]
- Ouyang, X.; Yao, S.; Wan, Q. Multiple Signal TDOA/FDOA Joint Estimation with Coherent Integration. Electronics 2023, 12, 2151. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, X.; Wu, L.; Yin, H. The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm Without Prior Knowledge of Radars’ Precise Locations. Electronics 2022, 11, 1577. [Google Scholar] [CrossRef]
- Lin, D.; Wang, G.; Ho, K.C. Source Localization by Frequency Measurements in Unknown Signal Propagation Speed Environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3953–3970. [Google Scholar] [CrossRef]
- Tang, B.; Sun, Y.; Heng, X.; Yang, Y.; Chen, L. Extending MPR for Locating a Moving Object Based on TDOA and FDOA. In Proceedings of the 2025 IEEE International Conference on Acoustics, Speech and and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Khalaf-Allah, M. Emitter Location Using Frequency Difference of Arrival Measurements Only. Sensors 2022, 22, 9642. [Google Scholar] [CrossRef]
- Li, J.; Guo, F.; Jiang, W. A Linear-Correction Least-Squares Approach for Geolocation Using FDOA Measurements Only. Chin. J. Aeronaut. 2012, 25, 709–714. [Google Scholar] [CrossRef]
- Vesely, J. Differential Doppler Target Position Fix Computing Methods. In Proceedings of the International Conference on Circuits Systems and Signals (CSS), Corfu, Greece, 15–17 September 2010; pp. 284–287. [Google Scholar]
- Cameron, K.J. FDOA-Based Passive Source Localization: A Geometric Perspective. Ph.D. Dissertation, Colorado State University, Fort Collins, CO, USA, 2018. [Google Scholar]
- Cameron, K.J.; Bates, D.J. Geolocation with FDOA Measurements via Polynomial Systems and RANSAC. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 676–681. [Google Scholar] [CrossRef]
- Pei, Y.; Li, X.; Yang, L.; Guo, F. A Closed-Form Solution for Source Localization Using FDOA Measurements Only. IEEE Commun. Lett. 2023, 27, 115–119. [Google Scholar] [CrossRef]
- Pei, Y.; Li, X.; Guo, F.; Zhang, M. Moving Source Localization Using Frequency Difference of Arrival Measurements Only. IEEE Trans. Veh. Technol. 2024, 74, 1052–1063. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Liu, Y.; Yang, L.; Guo, F. Bayesian FDOA Positioning with Correlated Measurement Noise. Remote Sens. 2025, 17, 1266. [Google Scholar] [CrossRef]
- Ho, K.C.; Xu, W. An Accurate Algebraic Solution for Moving Source Location Using TDOA and FDOA Measurements. IEEE Trans. Signal Process. 2004, 52, 2453–2463. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Lin, X.; Ng, M.K. A Matching Schur Complement Preconditioning Technique for Inverse Source Problems. Appl. Numer. Math. 2024, 201, 404–418. [Google Scholar] [CrossRef]
- Musicki, D.; Kaune, R.; Koch, W. Mobile Emitter Geolocation and Tracking Using TDOA and FDOA Measurements. IEEE Trans. Signal Process. 2010, 58, 1863–1874. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Guo, F.; Fan, Y.; Zhou, Y.; Zhou, C.; Li, Q. Space Electronic Reconnaissance: Localization Theories and Methods; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]

| Observer No. | Position (m) | Velocity (m/s) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
| Method | Average Time (ms) |
|---|---|
| GCM | 1.70 |
| GDM | 2.21 |
| KF-1 (uncorrelated) | 1.82 |
| FDOAR | 2.73 |
| GN | 0.17 |
| GS-1 | 0.22 |
| GS-2 | 5.01 |
| Number of Observers | KF-1 (ms) | GDM (ms) | GCM (ms) |
|---|---|---|---|
| 3 | 1.45 | 1.88 | 1.34 |
| 5 | 2.03 | 2.51 | 2.12 |
| 7 | 2.76 | 3.32 | 2.97 |
| 9 | 3.47 | 4.08 | 3.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, X.; Liu, Y.; Yang, L.; Guo, F. Bayesian FDOA-Only Localization Under Correlated Measurement Noise: A Low-Complexity Gaussian Conditional-Based Approach. Electronics 2025, 14, 4364. https://doi.org/10.3390/electronics14224364
Zhang W, Li X, Liu Y, Yang L, Guo F. Bayesian FDOA-Only Localization Under Correlated Measurement Noise: A Low-Complexity Gaussian Conditional-Based Approach. Electronics. 2025; 14(22):4364. https://doi.org/10.3390/electronics14224364
Chicago/Turabian StyleZhang, Wenjun, Xi Li, Yi Liu, Le Yang, and Fucheng Guo. 2025. "Bayesian FDOA-Only Localization Under Correlated Measurement Noise: A Low-Complexity Gaussian Conditional-Based Approach" Electronics 14, no. 22: 4364. https://doi.org/10.3390/electronics14224364
APA StyleZhang, W., Li, X., Liu, Y., Yang, L., & Guo, F. (2025). Bayesian FDOA-Only Localization Under Correlated Measurement Noise: A Low-Complexity Gaussian Conditional-Based Approach. Electronics, 14(22), 4364. https://doi.org/10.3390/electronics14224364






