Real-Time Estimation of Ionospheric Power Spectral Density for Enhanced BDS PPP/PPP-AR Performance
Abstract
1. Introduction
2. Methods
2.1. BDS Triple-Frequency UDUC PPP Model
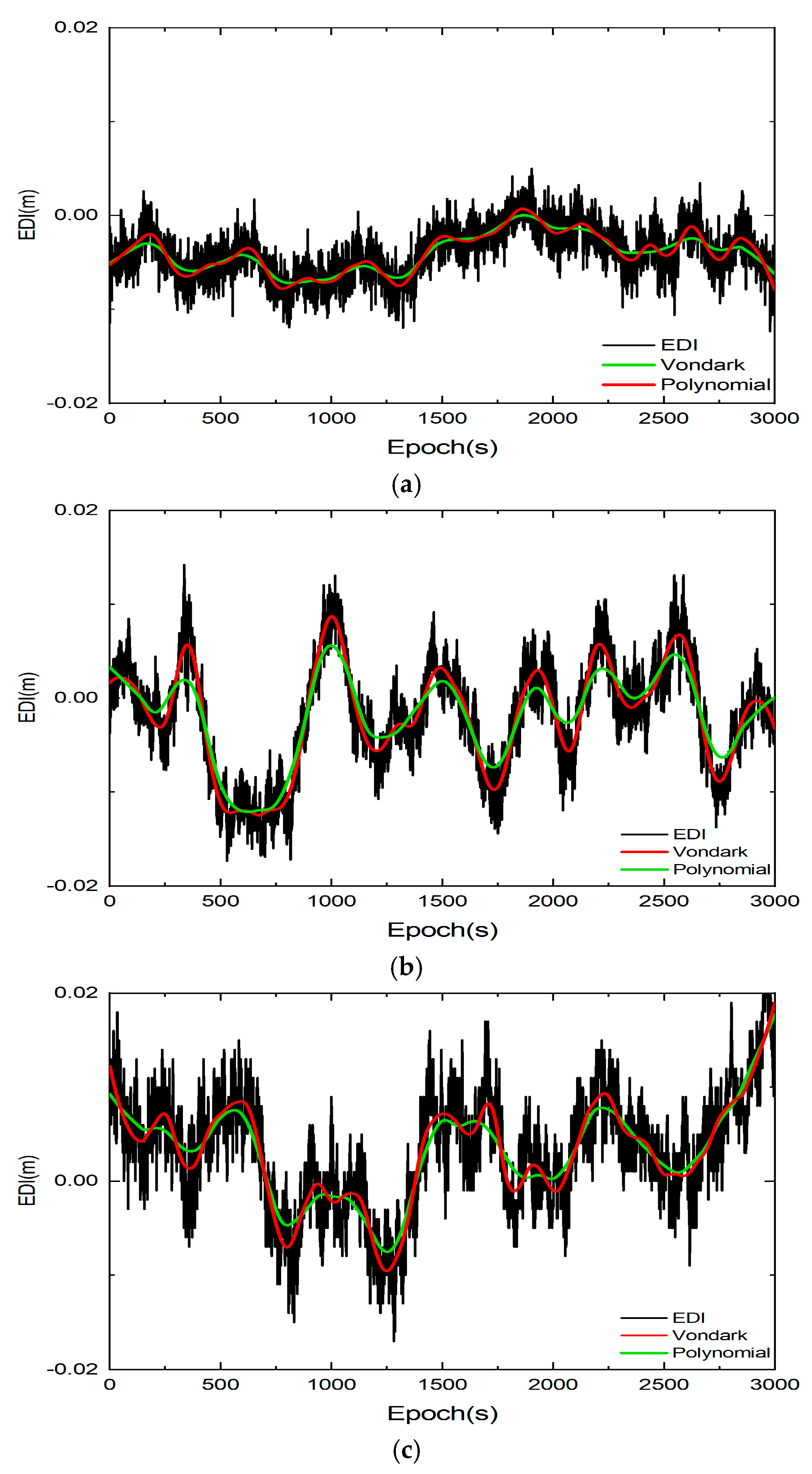
2.2. Ionospheric PSD Calculation and Smoothing Method
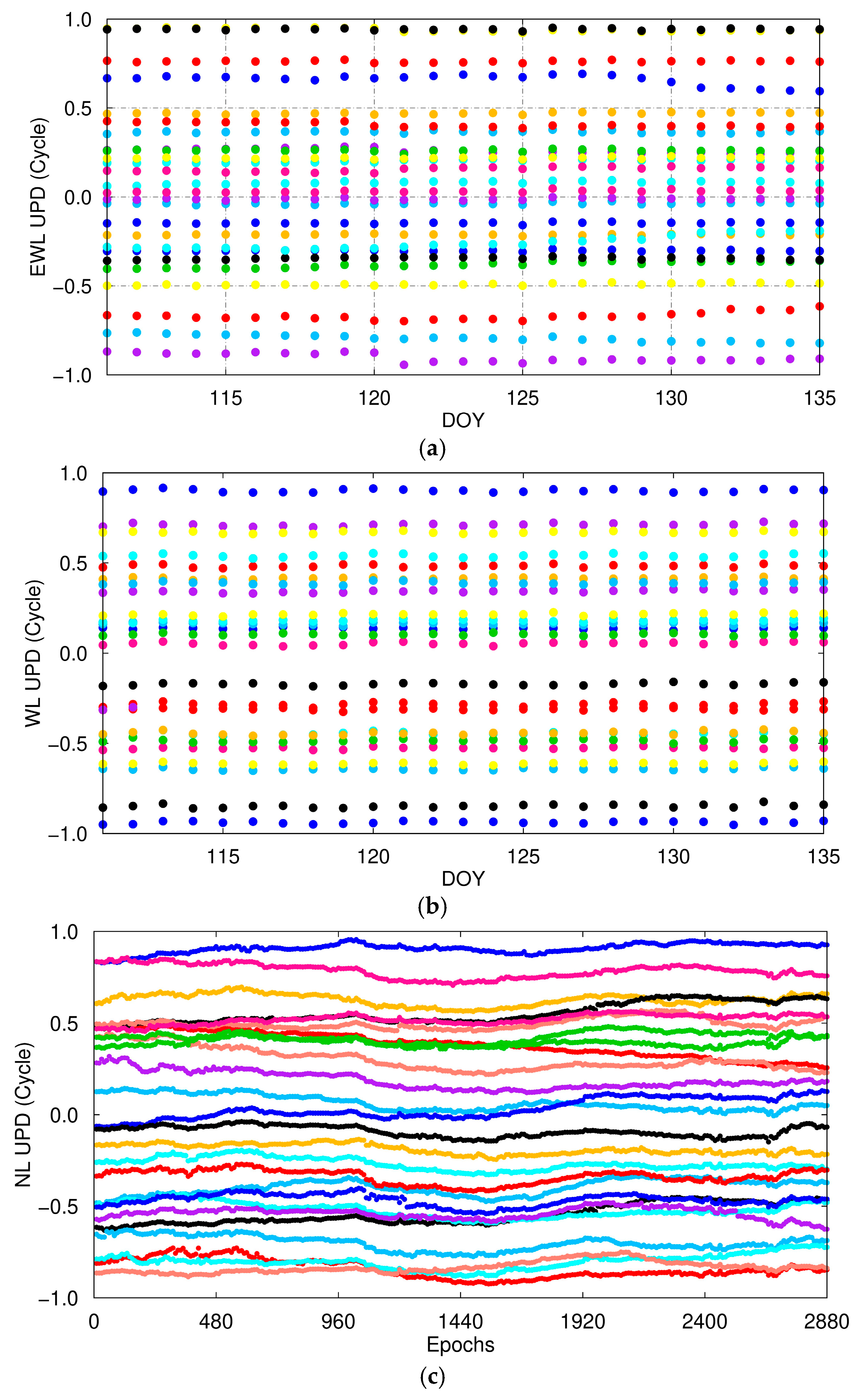
2.3. BDS Three-Frequency Undifferenced PPP-AR Method
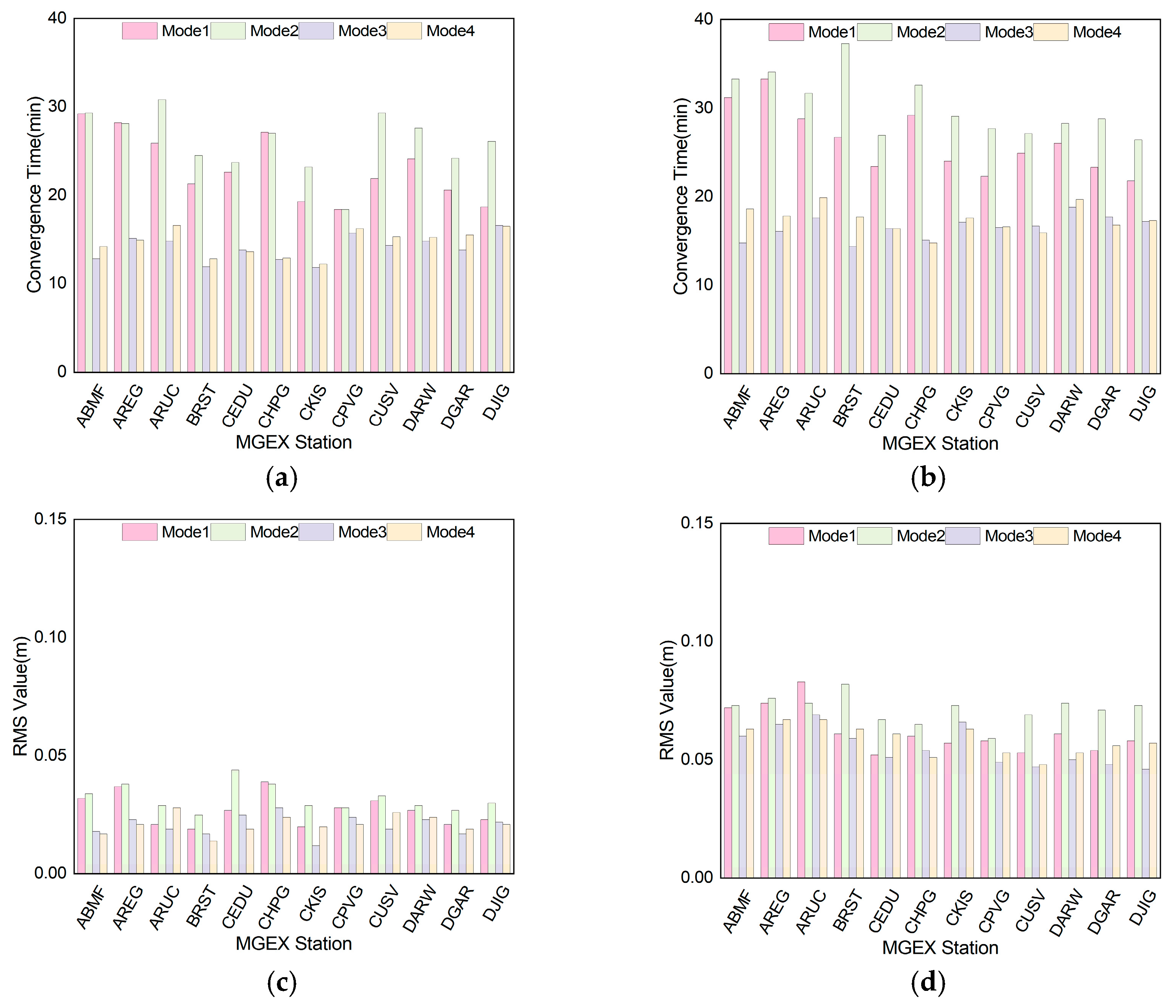
3. Results
3.1. IPSD Characteristics Analysis
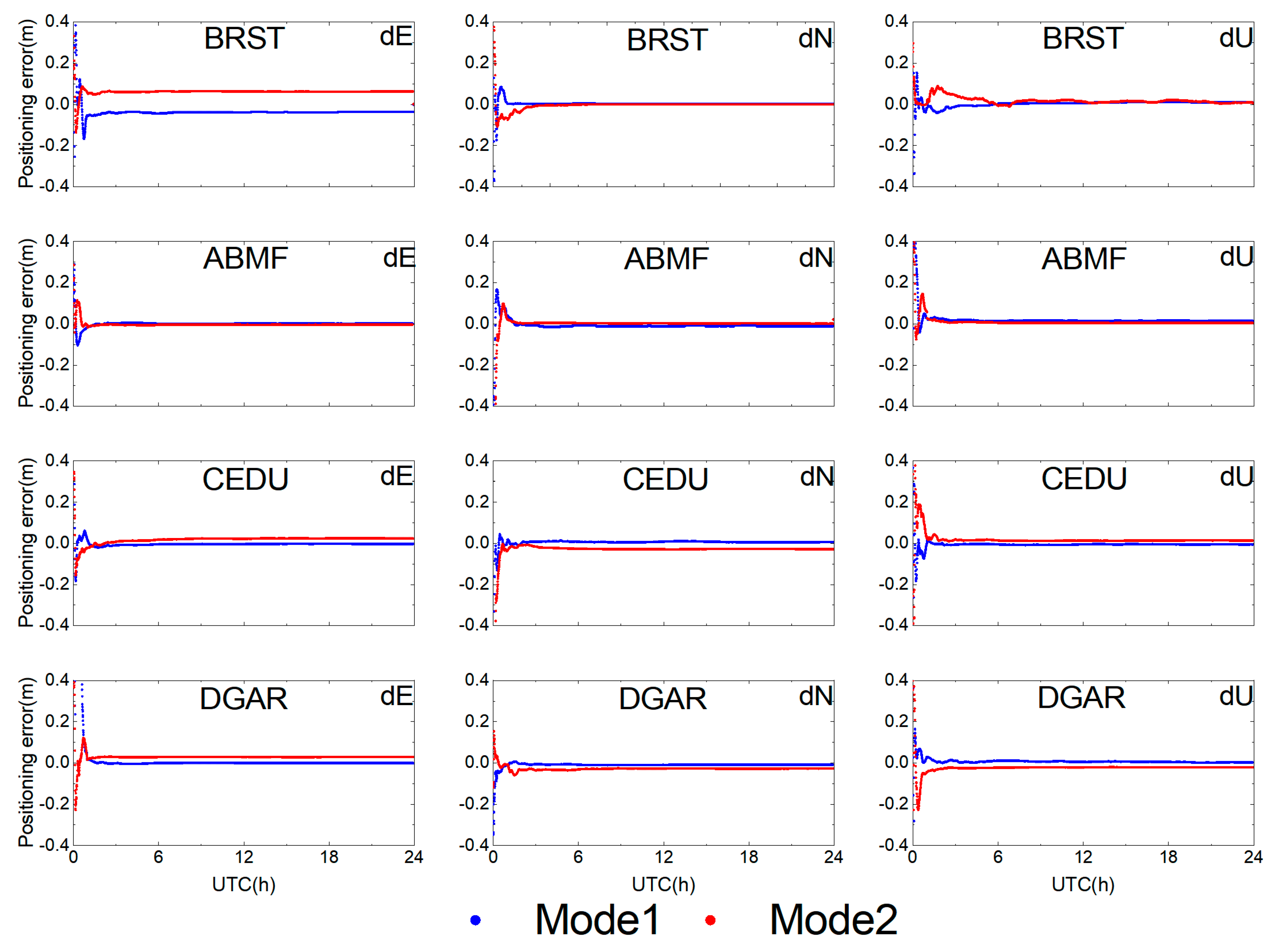
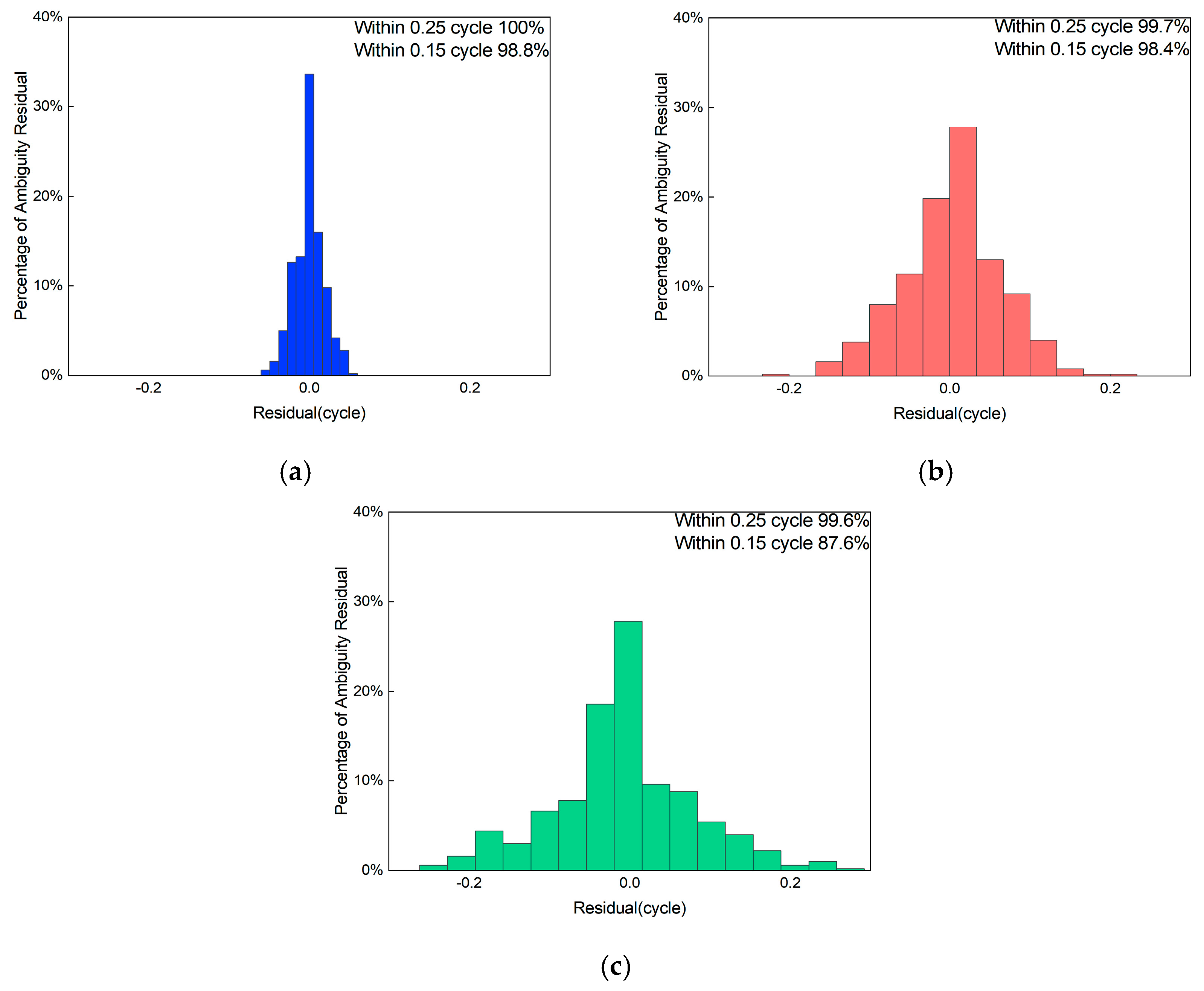
3.2. PPP/PPP-AR Positioning Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- China Satellite Navigation Office. BeiDou Navigation Satellite System Open Service Performance Standard (Version 3.0). Available online: http://www.beidou.gov.cn/xt/gfxz/202105/P020210526215541444683.pdf (accessed on 1 September 2020).
- Ma, H.; Yang, J.; Guan, X.; Wu, J.; Wu, H. Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO. Remote Sens. 2025, 17, 2351. [Google Scholar] [CrossRef]
- Liu, J.; Ye, S.; Xia, F.; Wei, P.; Fan, Y.; Song, Y. Processing and analysis of BDS-2 B1I/B3I and BDS-3 B1C/B2a joint PPP considering inter system and frequency biases. Adv. Space Res. 2025, 75, 7065–7081. [Google Scholar] [CrossRef]
- Guo, S.; Cai, H.; Meng, Y.; Geng, C.; Jia, X.; Mao, Y.; Geng, T.; Rao, Y.; Zhang, H.; Xie, X. BDS-3 RNSS Technical Characteristics and Service Performance. Acta Geod. Cartogr. Sin. 2019, 48, 810–821. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 401–412. [Google Scholar] [CrossRef]
- Gu, S.; Lou, Y.; Shi, C.; Liu, J. BeiDou Phase Bias Estimation and Its Application in Precise Point Positioning with Triple-Frequency Observable. J. Geod. 2015, 89, 979–992. [Google Scholar] [CrossRef]
- Yao, Y.; Peng, W.; Xu, C.; Shi, J.; Cheng, S.; Ouyang, C. The realization and evaluation of mixed GPS/BDS PPP ambiguity resolution. J. Geod. 2019, 93, 1283–1295. [Google Scholar] [CrossRef]
- Nacer, N.; Sunil, B. An uncombined triple-frequency user implementation of the decoupled clock model for PPP-AR. J. Geod. 2021, 95, 56. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, W.; Yao, Y.; Peng, W.; Xu, C.; Zhang, L. BDS PPP-AR positioning performance with ionospheric disturbances at low-latitudes. GPS Solut. 2025, 29, 116. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Dubey, S.; Wahi, R.; Gwal, A.K. Ionospheric Effects on GPS Positioning. Adv. Space Res. 2005, 38, 2478–2484. [Google Scholar] [CrossRef]
- Otsuka, Y.; Shinbori, A.; Sori, T.; Tsugawa, T.; Nishioka, M.; Huba, J. Plasma depletions lasting into daytime during the recovery phase of a geomagnetic storm in May 2017: Analysis and simulation of GPS total electron content observations. Earth Planet. Phys. 2021, 5, 427–434. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, N.; Xu, Y.; Tang, L.; Xu, A.; Li, L.; Gao, M. BDS Precise Point Positioning Ambiguity Resolution with High Rate Data and Its Application to Seismic Displacement and Marine Surveying. Earth Sci. Inform. 2021, 14, 2331–2346. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Guo, F.; Li, X. Model Comparison and Performance Analysis of Triple-Frequency BDS Precise Point Positioning. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 2124–2130. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, X. Partial Ambiguity Resolution Method and Results Analysis for GNSS Uncombined PPP. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 979–989. [Google Scholar] [CrossRef]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An Improved Approach to Model Ionospheric Delays for Single-Frequency Precise Point Positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Wu, G.; Chen, J.; Bai, T.; Wu, X.; Hu, J. Wide-Area Between-Satellite Single-Difference VTEC Ionospheric Model and Its Assessment for Undifferenced and Uncombined PPP. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 928–937. [Google Scholar] [CrossRef]
- Gu, S.; Dai, C.; He, C.; Fang, L.; Wang, Z. Analysis of Semi-tightly Coupled Multi-GNSS PPP-RTK/VIO for Vehicle Navigation in Urban Areas. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1852–1861. [Google Scholar] [CrossRef]
- Song, W.; He, C.; Gu, S. Performance Analysis of Ionospheric Enhanced PPP-RTK in Different Latitudes. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1832–1842. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, X.; Chen, J.; Zuo, X.; Mei, D.; Liu, W. Investigating GNSS PPP--RTK with external ionospheric constraints. Satell. Navig. 2022, 3, 11. [Google Scholar] [CrossRef]
- Li, J.; Zhu, H.; Xu, A.; Lu, Y.; Lei, X. BDS long-range RTK positioning algorithm considering the time-varying properties of ionosphere. Acta Geod. Et Cartogr. Sin. 2023, 52, 383–396. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, H.; Ge, M.; Huang, G. A real-time ionospheric model based on GNSS Precise Point Positioning. Adv. Space Res. 2013, 52, 1125–1134. [Google Scholar] [CrossRef]
- Fu, Z.; Shen, X.; Liu, Q.; Wang, N. Ionospheric Disturbances from the 2022 Hunga-Tonga Volcanic Eruption: Impacts on TEC Spatial Gradients and GNSS Positioning Accuracy Across the Japan Region. Remote Sens. 2025, 17, 3108. [Google Scholar] [CrossRef]
- Li, J.; Zhu, H.; Xu, A.; Xu, Z. Estimating ionospheric power spectral density for long-range RTK positioning using uncombined observations. GPS Solut. 2023, 27, 120. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Xu, Y.; Li, J.; Yang, N.; Shi, S. A Method for Estimating Ionospheric Power Spectral Density in BDS Undifferenced and Uncombined PPP. Geomat. Inf. Sci. Wuhan Univ. 2025, 50, 628–636. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Li, L.; Li, X.; Lv, H. An improved carrier-phase smoothing pseudorange algorithm with self-modeling of ionospheric delay variation. Acta Geod. Cartogr. Sin. 2019, 48, 1107–1118. [Google Scholar] [CrossRef]
- Zhu, H.; Li, J.; Tang, L.; Ge, M.; Xu, A. Improving the Stochastic Model of Ionospheric Delays for BDS Long-Range Real-Time Kinematic Positioning. Remote Sens. 2021, 13, 2739. [Google Scholar] [CrossRef]
- Zheng, D.; Zhong, P.; Ding, X.; Chen, W. Filtering GPS time-series using a Vondrak filter and cross-validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.; Odijk, D. Combined GPS + BDS for short to long baseline RTK positioning. Meas. Sci. Technol. 2015, 26, 045801. [Google Scholar] [CrossRef]





| Satellite PRN | Epoch Difference Interval | |||
|---|---|---|---|---|
| 1 s | 30 s | 90 s | ||
| C02 | STD | 0.0021 | 0.0030 | 0.0036 |
| Mean Value | 0.0000041 | 0.00013 | 0.00038 | |
| C10 | STD | 0.0019 | 0.0028 | 0.0044 |
| Mean Value | 0.0000016 | 0.000052 | 0.00012 | |
| C35 | STD | 0.0019 | 0.0032 | 0.0053 |
| Mean Value | 0.0000051 | 0.00016 | 0.00031 | |
| Station | Latitude(°) | Longitude(°) |
|---|---|---|
| ABMF | 16.262 | −61.528 |
| AREG | −16.465 | −71.493 |
| ARUC | 40.286 | 44.086 |
| BRST | 48.38 | −4.497 |
| CEDU | −31.867 | 133.81 |
| CHPG | −22.682 | −45.002 |
| CKIS | −21.201 | −159.801 |
| CPVG | 16.732 | −22.935 |
| CUSV | 13.736 | 100.534 |
| DARW | −12.844 | 131.133 |
| DGAR | −7.27 | 72.37 |
| DJIG | 11.526 | 42.847 |
| Project | Strategy |
|---|---|
| Sampling Interval | 30 s |
| Cutoff Elevation Angle | 10° |
| Satellite Orbit and Clock Bias | WHU Analysis Center Precise Products |
| Ionospheric Delay | Random Walk, PSD (Estimated IPSD) |
| Random Walk, PSD (Empirical Value 1.7 × 10−5 m2/s) | |
| Tropospheric Delay | Random Walk, PSD (Empirical Value 1.7 × 10−5 m2/s) |
| Receiver Clock Bias | Epoch-by-Epoch Estimation |
| Antenna Calibration | IGS20 File Correction |
| Tidal Disturbance Correction | Correcting for Solid Tide, Ocean Tide, and Polar Motion Tide Separately |
| UPD Estimation | Extra-Wide Lane: Estimate one value per day Wide Lane: Estimate one value per day Narrow Lane: Estimate one value every 30 s |
| Ambiguity Strategy | Inter-Satellite Single-Difference for Partial AR |
| Float Solution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhu, H.; Xu, Q.; Li, J.; Song, C. Real-Time Estimation of Ionospheric Power Spectral Density for Enhanced BDS PPP/PPP-AR Performance. Electronics 2025, 14, 4342. https://doi.org/10.3390/electronics14214342
Wang Y, Zhu H, Xu Q, Li J, Song C. Real-Time Estimation of Ionospheric Power Spectral Density for Enhanced BDS PPP/PPP-AR Performance. Electronics. 2025; 14(21):4342. https://doi.org/10.3390/electronics14214342
Chicago/Turabian StyleWang, Yixi, Huizhong Zhu, Qi Xu, Jun Li, and Chuanfeng Song. 2025. "Real-Time Estimation of Ionospheric Power Spectral Density for Enhanced BDS PPP/PPP-AR Performance" Electronics 14, no. 21: 4342. https://doi.org/10.3390/electronics14214342
APA StyleWang, Y., Zhu, H., Xu, Q., Li, J., & Song, C. (2025). Real-Time Estimation of Ionospheric Power Spectral Density for Enhanced BDS PPP/PPP-AR Performance. Electronics, 14(21), 4342. https://doi.org/10.3390/electronics14214342







