Abstract
In recent years, remote data management environments have been increasingly deployed across diverse infrastructures, accompanied by a rapid surge in the demand for sharing and collaborative processing of sensitive data. Consequently, ensuring data security and privacy protection remains a fundamental challenge. A representative example of such an environment is the cloud, where efficient mechanisms for secure data sharing and access control are essential. In domains such as finance, healthcare, and public administration, where large volumes of sensitive information are processed by multiple participants, traditional access-control techniques often fail to satisfy the stringent security requirements. To address these limitations, Key-Aggregate Proxy Re-Encryption (KA-PRE) has emerged as a promising cryptographic primitive that simultaneously provides efficient key management and flexible authorization. However, existing KA-PRE constructions still suffer from several inherent security weaknesses, including aggregate-key leakage, ciphertext insertion and regeneration attacks, metadata exposure, and the lack of participant anonymity within the data-management framework. To overcome these limitations, this study systematically analyzes potential attack models in the KA-PRE setting and introduces a novel KA-PRE scheme designed to mitigate the identified vulnerabilities. Furthermore, through theoretical comparison with existing approaches and an evaluation of computational efficiency, the proposed scheme is shown to enhance security while maintaining practical performance and scalability.
1. Introduction
Recently, remote data management has emerged as a fundamental requirement across diverse services and application domains. In such environments, a Sender securely stores its data in the cloud, while an authorized Receiver can access and utilize the data when necessary [1,2,3,4]. However, cloud servers are generally regarded as semi-trusted entities, typically modeled under the honest-but-curious adversarial assumption. In this setting, servers faithfully execute prescribed operations yet may attempt to infer or extract sensitive information from user data [5,6,7,8,9,10]. Consequently, ensuring data security and privacy within these semi-secure and ambiguous environments remains a major research challenge, prompting the development of various cryptographic mechanisms for fine-grained access control [11,12].
Among the representative techniques, the Key-Aggregate Cryptosystem (KAC) achieves efficient key management by enabling a compact aggregate key to represent decryption rights for multiple ciphertext classes, while Proxy Re-Encryption (PRE) enables secure and flexible data sharing by allowing ciphertexts to be transformed from one user’s key domain to another without revealing the plaintext [13,14,15]. The Key-Aggregate Proxy Re-Encryption (KA-PRE) paradigm combines the advantages of both approaches: a Sender can delegate decryption capabilities for multiple data classes through a single aggregate key, thereby supporting scalable and efficient data sharing in remote data-management systems. In recent years, Key-Aggregate Proxy Re-Encryption (KA-PRE) and related proxy-based cryptographic paradigms have been extensively studied across various application domains, including medical Internet of Things (IoT), decentralized cloud environments, and intelligent transportation systems [16]. Moreover, these schemes have evolved into diverse forms, such as CCA-secure and lattice-based PRE constructions, reflecting continuous advancements in both theoretical and practical aspects of proxy re-encryption [17,18].
Despite these benefits, existing KA-PRE schemes exhibit several security limitations. Specifically, they are vulnerable to (i) the derivation of new aggregate keys by algebraically combining previously issued ones, (ii) ciphertext-based attack patterns such as insertion and replay attacks, (iii) leakage of metadata pertaining to data-class identifiers, and (iv) the absence of anonymity guarantees for participating entities. For example, during the re-encryption process, metadata associated with particular data classes can inadvertently leak through the parameters transmitted to the Proxy Server. Likewise, an adversary may craft or replay ciphertexts to subvert data-integrity guarantees. Moreover, conventional public-key-based frameworks expose the identities of Senders and Receivers, thereby failing to ensure anonymity during data-sharing operations.
To overcome these vulnerabilities and mitigate threats arising during interactions with the Proxy Server, this paper proposes an enhanced and security-reinforced KA-PRE model. The primary contributions of this study are summarized as follows:
- Security Analysis: We identify and formally characterize the security weaknesses inherent in existing KA-PRE schemes and provide detailed attack models for each vulnerability.
- Based on these analyses, we define a comprehensive set of security requirements that must be satisfied in a robust KA-PRE environment.
- Proposed Construction: We design and present an improved KA-PRE scheme that addresses the shortcomings of prior works and offers enhanced protection against the identified attack vectors.
The remainder of this paper is organized as follows. Section 2 reviews related work and derives the security requirements. Section 3 describes the system model and presents the proposed KA-PRE protocol in detail. Section 4 provides a comprehensive security analysis and discusses the satisfaction of the identified requirements. Section 5 concludes the paper and outlines directions for future research.
2. Background
In this section, we define the security requirements derived from existing research trends and the corresponding attack models identified in the KA-PRE setting.
2.1. Key-Aggregate Proxy Re-Encryption
Key-Aggregate Proxy Re-Encryption (KA-PRE) is a cryptographic construction that integrates the principles of Key-Aggregate Cryptosystems (KACs) and Proxy Re-Encryption (PRE). In KA-PRE, a Sender aggregates decryption privileges for multiple data classes into a single compact aggregate key, while a Proxy Server performs a re-encryption operation that enables only the designated Receiver to obtain the corresponding decryption rights. The Key-Aggregate Cryptosystem (KAC) was originally proposed to achieve efficient access control and scalable key management in data-sharing environments such as cloud-based storage systems [11,14,15,19,20]. KAC allows a Sender to generate a constant-size aggregate key that grants the Receiver decryption capability over multiple ciphertext classes. This significantly reduces the overhead associated with key distribution and management while ensuring that all data remain encrypted throughout their lifecycle. The Proxy Re-Encryption (PRE) primitive, first introduced by Blaze, Bleumer, and Strauss in 1998 [21], represents a specialized form of public-key cryptography. PRE enables a Sender to securely delegate decryption rights to a designated Receiver through an untrusted Proxy Server, without revealing the Sender’s private key [22,23,24,25,26,27]. By combining the advantages of both KAC and PRE, KA-PRE offers an efficient and flexible framework for fine-grained data access control. Recently, KA-PRE and related proxy-based encryption paradigms have continued to evolve across various domains such as medical IoT, decentralized cloud, and intelligent transportation systems [16,17,18]. However, existing KA-PRE constructions still suffer from a range of security vulnerabilities and remain exposed to various attack models. The detailed descriptions and analyses of these attack models are presented in Section 2.2.
2.2. Attack Model for KA-PRE
In this Subsection, we provide a detailed analysis of the attack models.
- Attack Model . (Aggregate Key Leakage)Description. If the aggregate key generated by the Sender (see Algorithm 1) is exposed while stored on an untrusted device, an adversary who collects multiple aggregate keys may combine them algebraically to derive a new aggregate key. The adversary’s goal is to construct an aggregate key for a set of data classes that was never issued by the Sender, thereby obtaining unauthorized access to those classes. Such key-derivation attacks critically violate confidentiality and key-management assumptions [28,29].
- Attack Model . (Ciphertext Injection)Description. As illustrated in Algorithm 2, an adversary may modify selected components of a tuple-formatted ciphertext so that the integrity-verification step fails [30,31]. The objective of this manipulation is to prevent a legitimate Receiver from completing decryption, thereby directly compromising data availability and potentially inducing a Denial-of-Service (DoS) condition.
- Attack Model . (Ciphertext Regeneration)Description. Because ciphertexts are produced using identical parameter sets and a fixed format, and because the system relies solely on integrity checks, an adversary can craft malicious ciphertexts that preserve the original structural format while embedding altered parameters [32,33]. As illustrated in Algorithm 3, the adversary’s goal is to produce a ciphertext that appears structurally legitimate but contains attacker-chosen parameters; once injected into the system, such ciphertexts can bypass simple integrity verification. By doing so, an adversary may insert unauthorized messages, corrupt protocol state, or otherwise disrupt normal data flows.
- Attack Model . (Metadata Leakage)Description. During the re-encryption process, metadata associated with the ciphertext is transmitted to the Proxy Server. Because the Proxy Server is only semi-trusted, an adversary that controls or compromises the Proxy (or observes its inputs/outputs) may infer which data class a given ciphertext belongs to. As illustrated in Algorithm 4, this enables the adversary to harvest metadata independently of any granted data-access privileges, thereby mounting a metadata-leakage attack [34,35]. Such leakage can significantly weaken privacy guarantees: even without decrypting content, an adversary can perform profiling, traffic analysis, or linkability attacks that expose sensitive relationships between data owners, data classes, and access patterns.
| Algorithm 1: Aggregate Key Leakage Attack () |
|
| Algorithm 2: Ciphertext Injection () |
|
| Algorithm 3: Ciphertext Regeneration Attack () |
|
| Algorithm 4: Metadata Leakage () |
|
- 5.
- Attack Model. Unlinkability and Anonymity ViolationDescription. If the identities of the Sender and Receiver are associated with metadata without appropriate anonymization (see Algorithm 5), an adversary can infer relationships among participants or reconstruct a Sender’s behavioral patterns. In particular, repeated requests for the same data class or the accumulation of aggregate-key usage records enable an adversary to learn associations between specific participants and data classes over time, thereby violating unlinkability and anonymity guarantees [36,37]. Such linkability enables profiling and deanonymization attacks that can expose collaboration patterns, sensitive interests, or operational behaviors even when the underlying plaintext remains encrypted.
| Algorithm 5: Unlinkability and Anonymity Violation Attack () |
|
2.3. Related Work
In this Subsection, we analyze the security vulnerabilities of existing KA-PRE schemes with respect to the attack models – described in Section 2.2.
Kajita & Ohtake propose KA-IB-PRE, a scheme aimed at enabling secure data sharing within personal data storage environments. In this construction, the Sender generates an identity-based key and issues decryption privileges for multiple data classes through an aggregate key, while the Proxy Server executes the re-encryption to ensure that the Receiver can only access the intended data. Furthermore, the ExKeyReGen step prevents data class metadata from being directly exposed to the Proxy Server. However, when analyzing the scheme of Kajita & Ohtake with respect to attack model , all ciphertexts are generated in an identical format and rely on the same parameter set . Consequently, even if an adversary selects a new random value and regenerates a forged ciphertext with the same structure, the integrity verification step is unable to distinguish between them. Moreover, under attack model , the identity values of the Sender and Receiver in the identity-based structure are directly embedded in the metadata and re-encryption parameters. As a result, an adversary can track the activities of a specific user by observing repeated identity tags across multiple sessions.
Chen et al. present a scheme that integrates PRE with KAC, enabling the Sender to generate aggregate keys while permitting the proxy to re-encrypt only a specified subset of ciphertexts. This design alleviates the excessive key storage overhead associated with conventional PRE schemes and ensures that an adversary cannot directly infer the underlying plaintext [38]. This construction mitigates the excessive key storage overhead inherent in conventional PRE schemes and ensures that an adversary cannot directly infer the underlying plaintext. However, under Attack Model , the scheme of Chen et al. generates all ciphertexts using an identical format and a common random parameter r. Consequently, even if an adversary regenerates a forged ciphertext with the same structure, the verification procedure merely confirms , rendering the Receiver unable to distinguish between genuine and forged ciphertexts. Furthermore, under Attack Model , if an alternative aggregate key , corresponding to the same data class is compromised, the adversary can derive a new aggregate key through operation . Finally, when analyzing Attack Model , both the data class S and index values are explicitly reflected in the plaintext-dependent ciphertext components , enabling the Proxy Server to directly observe this information. Moreover, since participant identifiers are not anonymized, the scheme fails to preserve anonymity.
Pareek & Purushothama provide flexibility by enabling the Sender to re-encrypt an aggregate key with either a different aggregate key or a different data class, and further supports multiple functionalities through two transformation steps [39]. However, under Attack Model , the ciphertext structure is generated using an identical format and the same random parameter r thereby allowing an adversary to regenerate a forged ciphertext with the same structure. Moreover, under Attack Model , if an adversary obtains an alternative aggregate key corresponding to the same data class, the adversary can derive a new aggregate key through operation . Finally, under Attack Model , the data class S is directly transmitted to the Proxy Server during the re-encryption process, resulting in the explicit leakage of metadata S. In addition, the lack of anonymization of participant identifiers results in a failure to preserve anonymity.
Therefore, existing schemes commonly exhibit security weaknesses corresponding to attack models . Furthermore, the schemes proposed by Pareek & Purushothama and by Chen et al. are particularly susceptible to and .
2.4. Security Theorems
In this Subsection, we analyze the limitations of existing studies and the corresponding attack models discussed in Section 2.2 and Section 2.3 and subsequently present five security requirements derived from this analysis.
- Aggregate Key Confidentiality Preservation: The aggregate key generated by the Sender must be unique and must not be exposed to external entities. To ensure this property, the aggregate key should be generated differently for each Receiver and for each set of aggregated data classes, and it must be infeasible to derive a valid aggregate key for a new data class by performing computations on aggregate keys corresponding to different data classes.
- Resistance Against Ciphertext-Based Attack: This attack is divided into two types as follows.
- (a)
- Resistance Against Ciphertext Injection Attack: If an adversary alters the ciphertext structure within the Proxy Server or tampers with the contents of its components, such modifications must be verifiable through the scheme’s integrity mechanisms.
- (b)
- Robustness Against Ciphertext Regeneration Attack: If an adversary generates a ciphertext with the same structure using newly chosen parameter values or attempts to retransmit a stolen ciphertext, must prevent such ciphertexts from being accepted as legitimate messages.
- Metadata Confidentiality and Leakage Prevention: The Proxy Server is assumed to operate in a semi-trusted capacity. As it cannot be regarded as fully trusted, metadata pertaining to the data classes specified by the re-encryption key must remain concealed during the transmission of the re-encryption key to the Proxy Server.
- Anonymity for Data Management: Since sensitive data originating from the Sender is transmitted and received, the anonymity of participants must be preserved. Moreover, while ensuring anonymity throughout the data management process, the legitimacy of the Sender must remain verifiable in scenarios that require identity validation, such as ciphertext regeneration or replay attacks.
2.5. Security Definitions
Definition 1 (IND-CCA Security for KA-PRE).
Let Π be a KA-PRE scheme. An adversary interacts with and . In the challenge phase, submits . The challenger samples and returns (or obtained by applying under valid inputs). Oracle access continues with standard IND-CCA exclusions on decrypting and any trivially derived ciphertexts. We say Π is IND-CCA secure if is negligible in λ.
Definition 2 (Aggregate-Key Unforgeability (AK-UF)).
No PPT adversary given oracle access to derive for adaptively chosen can produce a new verifiable for a nontrivial except with negligible probability.
Definition 3 (Re-Encryption-Key Unforgeability/Legitimacy (REK-UF)).
No PPT adversary can forge a valid that passes the scheme’s legitimacy verification while violating the binding to , except with negligible probability.
Definition 4 (Anonymity and Unlinkability (Anon/UL)).
Given a challenge instance where one of two candidate identities (or sessions) underlies the ciphertext (or re-encrypted ciphertext), no PPT adversary can distinguish or link the underlying sender/receiver/session beyond negligible advantage.
Definition 5 (Class-Hiding (IND-CH)).
Given two class sets of equal size, an adversary cannot distinguish which set was used to derive the target ciphertext or re-encrypted ciphertext beyond negligible advantage.
Table 1 presents the mapping between attack models (A1–A5) and the corresponding formal security notions. We provide formal games and reductions for these notions in Appendix B.

Table 1.
Mapping between attack models (A1–A5) and formal security notions.
2.6. Adversarial Oracles and Corruption Model
We consider a PPT adversary with oracle access:
- ;
- ;
- ;
- ;
- ;
- , .
This is subject to standard exclusions in the challenge games below. We allow collusion between the proxy and receivers unless stated otherwise.
The complete challenger/oracle simulations used in our reductions are detailed in Appendix B.
3. Proposed Scheme
In this section, we propose a Secure and Efficient KA-PRE Scheme that fulfills the security requirements described in Section 2.
3.1. System Scenario
The proposed scheme is designed based on the scenario illustrated in Figure 1. The system model comprises four entities: the Sender, Proxy Server, Receiver, and Trusted Third Party. The roles of these entities are defined as follows.
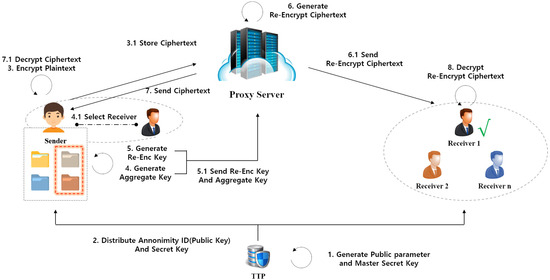
Figure 1.
Proposed scheme overview.
- Sender: As the data owner, the Sender shares data by encrypting the data class it belongs to together with its anonymous identifier, and then stores it on the Proxy Server. The Sender subsequently generates the cryptographic keys (e.g., re-encryption keys and aggregate keys) required for delegated distribution of the data.
- Receiver: The Receiver obtains re-encrypted ciphertexts from the Proxy Server and performs the decryption process to recover the original data.
- Proxy Server: The Proxy Server stores the Sender’s initial ciphertexts and, upon request, produces re-encrypted ciphertexts. It then delivers the generated re-encrypted ciphertexts to the designated Receiver.
- Trusted Third Party (TTP): The TTP generates public system parameters and issues private keys and pseudonymous identifiers to participants (i.e., Sender and Receiver). Furthermore, when identity verification is required in specific situations, the TTP may also serve as a verifier.
The detailed operational procedure of the Secure and Efficient KA-PRE scheme is constructed as an eight-phase process, based on the five assumptions outlined in Section 3.2.
Phase 1.
Setup Phase: The TTP generates the public parameters and the master secret key.
Phase 2.
KeyGen Phase: The TTP issues pseudonymous identifiers (serving as public keys) and private keys to the participants.
Phase 3.
Encrypt Phase: The Sender uses its pseudonymous identifier (as the public key) to generate the initial ciphertext.
Phase 4.
Aggregate KeyGen Phase: The Sender generates an aggregate key and the corresponding verification value for a designated set of data classes.
Phase 5.
Re-KeyGen Phase: The Sender creates a re-encryption key to delegate decryption capability to the Receiver.
Phase 6.
Re-Encrypt Phase: The Proxy Server generates a re-encrypted ciphertext enabling the Receiver to perform decryption.
Phase 7.
Decrypt1 Phase: The Sender decrypts the initial ciphertext.
Phase 8.
DecryptR Phase: The Receiver decrypts the re-encrypted ciphertext using its private key and aggregate key.
3.2. Assumptions
The assumptions underlying the Secure and Efficient KA-PRE scheme are as follows:
- The proposed scheme operates in an environment supporting bilinear pairings.
- The TTP is a fully trusted authority for all participants. However, in practical deployments, even a semi-honest or curious TTP could potentially observe verification queries, such as , and infer session-level linkability or user behavior patterns through timing or frequency analysis. Although the proposed scheme performs local verification in the re-encryption and decryption phases to minimize online dependency, residual privacy risks may still arise if the TTP logs verification events. To mitigate such risks, future work may incorporate local verification tokens, blind signatures, or zero-knowledge proofs to eliminate the need for online TTP involvement in every operation while preserving the same security goals against and .
- The Proxy Server correctly follows the prescribed protocol but may attempt to infer additional information about participants’ data from the information it obtains (i.e., it is semi-honest).
- Session-specific aggregate keys or re-encryption keys may be exposed; however, the master secret key of the TTP, as well as the secret keys of the Sender and Receiver, remain uncompromised.
3.3. System Parameters
In this Subsection, we present the overall system parameters of the proposed scheme, as summarized in Table 2.

Table 2.
System parameters for the proposed scheme.
3.4. Proposed Scheme
In this Subsection, we describe the detailed operational flow of the proposed scheme. The scheme is composed of eight phases, and the operations performed in each phase are as follows. The proposed KA-PRE scheme ensures correctness, and the corresponding proof is provided in Appendix A. Formal security proofs are presented in Appendix B.
3.4.1. Setup Phase
In the Setup phase, the TTP executes the setup procedure prior to system operation, allowing each participant to subsequently utilize the Proxy Server. In this stage, the TTP generates the master secret key, which is known only to itself, along with the public parameters which are published to all users.
- (: This phase is executed by the TTP. Given the security parameter and the maximum number of data classes n, the TTP performs the following steps:Step 1. Define two cyclic groups of prime order p.Step 2. Define a bilinear map .Step 3. Select a generator .Step 4. Choose a master secret key , and for each , compute .Step 5. Define a set of cryptographic hash functions and .Step 6. Output the system public parameters .
3.4.2. KeyGen Phase
The key generation phase consists of three sub-phases: Masking ID Generation, Secret Key Generation, and Verification Value Generation.
These operations are executed by the TTP. The TTP receives the identity of each participant (Sender, Receiver) and uses a random value to generate a masked identity . Using the generated together with the master secret key and hash function , the TTP computes the secret key . Finally, a verification value is derived for validation of . The resulting values are then transmitted to the participants over an encrypted channel.
- Masking ID Generation (, : This phase is executed by the TTP. The TTP receives the identity from each participant (Sender, Receiver). Given the inputs , the master secret key and a random value , the TTP performs the following operation:Concatenate with the random value generated by the TTP, and apply the hash function to derive the masked identity
- Secret Key Generation (, : This phase is executed by the TTP. The TTP receives the identity of each participant (Sender, Receiver) together with the corresponding masked identity , the master secret key , and the hash function . Given these inputs, the TTP performs the following operation:The TTP hashes using , and then exponentiates the result with the master secret key to compute the participant’s secret key .
- Verification value Generation (): This phase is executed by the TTP. The TTP takes as input the masked identity , the real identity , the random value , and the timestamp indicating the expiration time, and performs the following operation:The TTP computes a hash of using the hash function . It then derives the verification value , which is used to confirm that has been legitimately generated by the TTP.
3.4.3. Encrypt Phase
The encryption phase is executed by the Sender. The Sender first selects a message to be encrypted, and then chooses a random value R. The Sender computes the hash value t using the hash function . The generated parameters are subsequently used to construct the initial ciphertext C, which consists of the tuple . Finally, the resulting initial ciphertext is stored on the Proxy Server.
- Encryption (): This phase is executed by the Sender. The Sender first selects the message to be encrypted and chooses a random value R. Using and , the Sender computes by applying the hash function . With the computed values and the inputs , the Sender proceeds as follows:Step 1. The Sender determines the message and selects a random value R. Then, the Sender computes .Step 2. Using the random values , the verification value generated by the TTP, the public parameters , the message , the participant’s masked identity , the Sender generates the components of the initial ciphertext .Step 3. The resulting ciphertext C is then stored on the Proxy Server.
3.4.4. Aggregate KeyGen Phase
The aggregate key generation phase is executed by the Sender. The Sender generates random values and , which are then used to compute the value r for the key generation process. Using the computed r value, the public parameters , and the data class , the Sender generates the aggregate key and subsequently computes the verification value .
- Aggregate Key Generation (, , , v) → (, ): This phase is executed by the Sender. The Sender first selects the data class for which re-encryption will be performed. Next, using the session-specific random values and , the Sender computes the value r and generates the aggregate key . Finally, after generating a random value v, the Sender computes the verification value using and as input, in order to validate the correctness of the aggregate key.Step 1. Select random values and .Step 2. The Sender compute the value r to be used in the aggregate key generation process by taking , , and the hash function as input.Step 3. The Sender computes the aggregate key using the derived value r, the system parameters , and the data class .Step 4. The Sender computes the verification value for the aggregate key. The validation value is used when aggregate key validation is required.
3.4.5. Re-KeyGen Phase
The re-encryption key generation phase is executed by the Sender, who computes the re-encryption key . Subsequently, the Sender transmits the re-encryption key together with the aggregate key and the verification value (generated in Section 3.4.4) to the Proxy Server.
- Re-Encryption Key Generation : This phase is executed by the Sender. The Sender computes the re-encryption key .Step 1. the Sender select a random value to be used for re-encryption key generation.Step 2. Using the parameters , , and r generated during the Aggregate KeyGen Phase, together with the Sender’s identity , the Receiver’s identity , the random value s, and the public parameters , the Sender generates the components of the re-encryption key .Step 3. The generated re-encryption key , together with the aggregate key and the verification value (produced in Section 3.4.4), is then transmitted to the Proxy Server.
3.4.6. Re-Encrypt Phase
The re-encryption phase is executed by the Proxy Server, which transforms the initial ciphertext C into the re-encrypted ciphertext such that the Receiver can decrypt it using its private key. The re-encrypted ciphertext , together with the aggregate key , is then transmitted to the Receiver.
- Re-Encryption : The Proxy Server performs verification before transforming the initial ciphertext C into the re-encrypted ciphertext .Step 1. The Proxy Server verifies whether the ciphertext originates from a valid identity issued by the TTP. To this end, the Proxy Server directly performs the verification using which was generated during the KeyGen Phase, along with the components and of the initial ciphertext C. The verification is performed locally by the Proxy Server.Step 2. Once the validity of the identity is confirmed, an integrity verification of the ciphertext is conducted. This verification procedure uses the values of , the Receiver’s public key, and the system parameters . A total of three verification checks are performed, and if any of them fails, the re-encrypted ciphertext is not generated.Step 3. If all verification steps succeed, the Proxy Server computes the re-encrypted ciphertext using the aggregate key , the initial ciphertext C, the re-encryption key , and the system parameters .Step 4. The generated re-encrypted ciphertext is then transmitted to the Receiver.
3.4.7. Decrypt1 Phase
The decryption of the initial ciphertext is performed exclusively by the Sender, who decrypts the initial ciphertext C using its private key.
- Decryption : This phase is executed by the Sender. The Sender selects the initial ciphertext C to be decrypted. Next, using and , the Sender verifies whether C has been tampered with. If the verification is successful, the Sender proceeds with the following steps using , its private key , the selected initial ciphertext C, and the public key .Step 1. Before decrypting the initial ciphertext C, the Sender verifies the integrity of the data using the components of the ciphertext. This step is identical to the verification steps described in (10)–(12).Step 2. If the integrity verification is successful, the Sender computes the random value R used during encryption. The message is then derived by performing an XOR operation with the ciphertext component . Finally, the decryption of the initial ciphertext C is completed.
3.4.8. DecryptR Phase
The re-decryption phase is executed by the Receiver, who obtains the re-encrypted ciphertext and the aggregate key from the Proxy Server. The Receiver then decrypts using its private key.
- Re-Decryption : This phase is executed by the Receiver. Before performing the decryption of the re-encrypted ciphertext, the Receiver conducts a verification process. This process first confirms that the ciphertext originates from a valid identity issued by the TTP, and subsequently performs integrity verification of the re-encrypted ciphertext and aggregate key. If all verifications succeed, the Receiver proceeds with the following steps using , its identity , its private key , the aggregate key , and the requested data class .Step 1. The Receiver verifies whether the re-encrypted ciphertext originates from a valid identity issued by the TTP. To this end, the Receiver directly performs the verification using which was generated during the KeyGen Phase, together with the components and of the re-encrypted ciphertext . The verification is performed locally by the Receiver.Step 2. Once the transmission is confirmed to originate from a valid identity, the Receiver performs integrity verification of the aggregate key. The Receiver generates the received value and compares it to verify whether the aggregate key has been tampered with.Step 3. Finally, the Receiver performs integrity verification of the re-encrypted ciphertext. This verification procedure uses the values of , the Receiver’s identity , and the system parameters . Two verification checks are performed in total, and if any of them fails, the decryption process is aborted.Step 4. If all verification steps succeed, the Receiver computes the parameter required for decryption. Using the generated and , the value is derived. Then, and are used to compute , while and are used to compute r. Finally, the derived r together with is used to recover the plaintext message .
The detailed scenario encompassing all phases of the proposed scheme is illustrated in Figure 2.
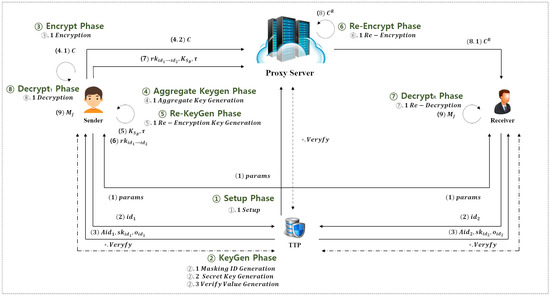
Figure 2.
Detailed operation process of the proposed scheme.
4. Analysis of the Proposed Scheme
In this section, we analyze the security of the proposed scheme with respect to the requirements presented in Section 2 and provide a comparative analysis of the computational costs compared with existing schemes.
4.1. Analysis of Security Requirements
- Aggregate Key Confidentiality Preservation: The proposed scheme enforces aggregate key confidentiality by employing fresh, independent randomness in each aggregate-key generation. Consequently, even if an adversary obtains aggregate keys corresponding to multiple data classes, it is computationally infeasible—under the underlying cryptographic hardness assumptions—to derive a valid aggregate key for a distinct data class by performing algebraic operations on the collected keys.Here, r is , where and .Therefore, the aggregate key produced in each generation is different even if it is shares the same class.If an adversary collects two aggregate keys for that share the same data class , and attempts to generate a new , it cannot be correctly generated as follows.The adversary, possessing two aggregate keys that share the same data class , performs the following operation.Here, are constructed as follows.Here, and are different values created in different sessions, so step (23) is not possible.
- Resistance Against Ciphertext-Based Attack: Resistance Against Ciphertext-Based Attack is divided into two types:
- (a)
- Resistance Against Ciphertext Injection Attack: Before decrypting ciphertexts and re-encrypted ciphertexts, the Receiver verifies the integrity of the data using the values contained in the ciphertext and the public parameters, as in (10)–(12). The proof proceeds as follows.Using (26), the integrity of and is verified. Thereafter, via (27), the integrity of and is checked. Finally, using (28), the integrity of is verified. If the integrity checks succeed, then the ciphertext components can be confirmed as untampered.
- (b)
- Robustness Against Ciphertext Regeneration Attack: Since ciphertexts share an identical structure, if an adversary freshly generates a message and the randomness used to form the ciphertext structure, i.e., with , then the adversary may construct a new ciphertext that can pass the integrity verification steps (26)–(28). The proposed scheme, however, performs a check—specifically, step (8) of Section 3.4.6—that verifies whether the Sender is an entity issued a valid identity by the TTP prior to performing the integrity verification. The proof proceeds as follows.Here, is , and it includes the Sender’s pseudonymous ID , the real ID , the verification secret randomly generated by the TTP, and the timestamp indicating the expiration time.Therefore, even if an adversary constructs a new ciphertext, they cannot compute for Furthermore, since in step (30) can only be generated by the TTP, even if an adversary freshly generates all randomness to form a ciphertext, verification of the value which contains the TTP’s secret parameters will be infeasible, thus maintaining security.
Even if a malicious Proxy colludes with a Receiver and both possess the re-encryption key , the private key , and the re-encrypted ciphertext , they cannot reconstruct the Sender’s secret key or any valid aggregate key because the re-encryption key binds both pseudonymous identifiers and session-specific randomness .Specifically, is computed using and unique to each session, and the pairing checks in Equations (10)–(12) enforce binding to the TTP-issued identity . Thus, even joint knowledge does not allow key inversion or unauthorized re-encryption, ensuring resilience against collusion. - Metadata Confidentiality and Leakage Prevention: The Proxy Server generates the re-encrypted ciphertext with the following inputs, as in Section 3.4.6: . Here, denotes publicly released parameters; denotes the re-encryption key generated by the Sender and transmitted to the Proxy Server; C denotes the initial ciphertext stored by the Proxy Server; denotes the pseudonymous identity; denotes the aggregate key for the data class; and denotes the verification value for the aggregate key. All inputs received by the Proxy Server are either public or already possessed by the Proxy Server. Therefore, no metadata pertaining to the Sender’s data is included.
- Anonymity for Data Management: Participants in the proposed scheme, except for the Proxy Server and the TTP, must have their anonymity preserved. To guarantee anonymity, participants transmit their real identity to the TTP and obtain a pseudonymous identity . The pseudonym is generated as follows.The TTP generates using the real identity and the verification secret . By the security of the hash function, the real identity is securely concealed. In this manner, while guaranteeing participants’ anonymity, when it is necessary to identify anonymity in cases such as regeneration or replay attacks, a mechanism to verify the Sender’s legitimacy must be provided. To this end, the ID verification value is generated. is generated as follows.Upon an ID verification request, the TTP computes and executes the check in (31). If (31) is satisfied, the TTP can verify the legitimacy of the Sender.To formally define the achieved anonymity, we consider an indistinguishability game between a challenger and a probabilistic polynomial-time adversary as follows. adaptively issues pseudonym queries and submits two distinct identities to . The challenger randomly selects , computes using freshly generated randomness , and returns it to . The scheme preserves anonymity if cannot distinguish whether the returned pseudonym corresponds to or with non-negligible advantage.Similarly, unlinkability is defined such that, given two pseudonyms and generated in different sessions, no polynomial-time adversary can determine whether they correspond to the same entity under independent random values and . Since each pseudonym is refreshed per session with independent randomness, long-term behavioral correlation across multiple sessions remains computationally infeasible.
4.2. Comparison of Schemes
In this Subsection, we analyze whether the attack models presented in Section 2.2 (see Table 3) can be prevented by the conventional KA-ABE and by the proposed scheme, and we compare the proposed scheme with the conventional KP-ABE scheme as summarized in Table 4 and Table 5. (Table 5 excludes operations, such as hashing, that have little impact on the overall computational cost.)

Table 3.
Comparison of Proposed Scheme with Related Works.

Table 4.
Comparison of computation output sizes of related works.

Table 5.
Comparison of computation costs of related works.
- Aggregate Key Confidentiality Preservation: Pareek & Purushothama and Chen et al. generate aggregate keys as follows.Here, is a component of the master secret key that, once generated, does not change. If multiple aggregate keys are generated using such a , then all aggregate keys are derived from the pre-generated master secret key; consequently, if aggregate keys are collected or leaked to adversaries, the adversary can also generate aggregate keys for other data classes.The proposed scheme prevents aggregate-key exposure by generating the aggregate key in the Aggregate KeyGen Phase based on a one-time random value that is used only once per session. In addition, the verification value is used to bind the key to the corresponding session. This eliminates correlations among aggregate-key values across sessions, thereby preventing an adversary from deriving or estimating keys.
- Resistance Against Ciphertext-Based Attack: Resistance Against Ciphertext-Based Attack is divided into the following two categories.
- (a)
- Resistance Against Ciphertext Injection Attack: To mitigate ciphertext injection attacks, all compared schemes perform ciphertext integrity verification prior to decryption.By performing integrity verification on the ciphertext components , ciphertext-injection attacks are prevented.
- (b)
- Robustness Against Ciphertext Regeneration Attack: Existing schemes employ a uniform ciphertext structure; consequently, an adversary can freshly generate a message and the randomness used to form the ciphertext structure, i.e., with , to construct a new ciphertext that the adversary stores on the Proxy Server or, after exfiltration, retransmits to the Receiver. In such cases, the Receiver is unable to determine that the message was generated by an adversary. To prevent ciphertext-regeneration attacks, this work requires the TTP to generate an ID-verification value during the KeyGen Phase that certifies legitimate ID issuers. The value is generated after the Sender submits the real identity to the TTP; only a legitimate Sender transmits and obtains a pseudonymous identity and secret key while is produced. Because is generated using the random value chosen by the TTP, can be generated only by the TTP. Furthermore, by embedding an expiration timestamp , the validity period of is defined so that reuse of after expiration can be detected. By requesting verification of from the TTP prior to protocol execution, one can prove based on the verification outcome—that the ciphertext was generated by a legitimate Sender. In this way, it is possible to demonstrate that the Sender is authorized by the TTP.
- Metadata Confidentiality and Leakage Prevention: The schemes of Pareek & Purushothama and of Chen et al. directly transmit the data-class metadata value to the Proxy Server during the transmission of the re-encryption key in the Re-Encrypt Phase. When the data-class value is revealed in this manner, the Proxy Server can infer the class membership of specific data and, by analyzing Sender-specific access patterns, perform preparatory actions for targeted attacks.To prevent this, the proposed scheme transmits the aggregate key to the Proxy Server instead of the original data-class value . The aggregate key is computed as , and therefore does not permit identification of . Hence, the original data-class value remains unknown to the Proxy Server.
- Anonymity for Data Management: Kajita & Ohtake employ standard ID-based PRE. Pareek & Purushothama and Chen et al. employ standard public-key-based PRE. If plain IDs with no additional measures are used, as in Kajita & Ohtake, participants’ identities may be directly exposed. Pareek & Purushothama and Chen et al. encrypt using the Sender’s public key and a data-class identifier. In this case, one can directly trace which Sender a particular class belongs to via the public key. This issue, combined with the metadata-exposure problem described above, allows the inference of metadata for data sent to specific targets and may serve as the starting point for secondary attacks.To prevent this, the proposed scheme issues pseudonymous IDs to participants based on their real IDs via the TTP. The pseudonymous ID is generated by the TTP as . The value is a random value generated by the TTP for ID issuance, and only the TTP knows the holder of the real ID. However, guaranteeing anonymity in this manner can be abused; to address this, the proposed scheme generates a pseudonym verification value . The value includes the random nonce generated by the TTP and a timestamp specifying the expiration time.
The proposed scheme exhibits no significant difference from existing schemes in terms of the sizes of generated values and computational costs. However, the addition of the verification-value generation and verification steps introduces two hash evaluations and one exponentiation; this, nonetheless, does not materially affect the overall computational overhead. As illustrated in Figure 3, the execution times were derived from a benchmark simulation reflecting realistic hardware conditions, where each primitive operation (, , ) was assigned latency values measured from practical server and client environments. Each algorithmic phase (KeyGen, Encryption, Aggregate KeyGen, Re-KeyGen, Re-Encryption, and Decryption) was executed 30 times with ±5% stochastic jitter to emulate runtime variability. The parameters were configured as (the size of the aggregate set at decryption) and (the number of generators used in key aggregation). The results confirm that the proposed scheme achieves nearly identical performance to Chen et al. across all phases, indicating that the added verification procedures introduce only negligible additional computational cost.
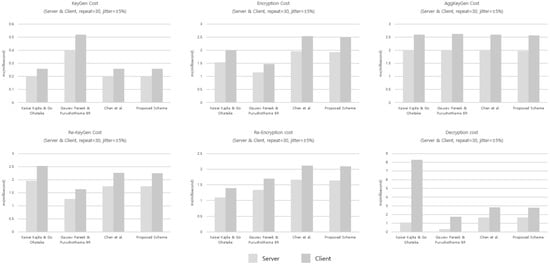
Figure 3.
Execution time comparison of the four KA-PRE schemes for each algorithmic phase (KeyGen, Encryption, Aggregate KeyGen, Re-KeyGen, Re-Encryption, Decryption) under the server and client hardware profiles [38,39].
5. Conclusions
This paper analyzed security weaknesses in Key-Aggregate Proxy Re-Encryption (KA-PRE) architectures employed in remote data-management environments and proposed an improved model to mitigate these weaknesses. Although conventional KA-PRE schemes were originally introduced to enable secure data sharing by providing efficient key management and flexible privilege delegation, our analysis demonstrates that they remain susceptible to multiple attack models, including the Aggregate Key Leakage Attack , Ciphertext Injection Attack , Ciphertext Regeneration Attack and , and the Unlinkability and Anonymity Violation Attack .
In response to these findings, we specified five core security requirements and proposed a novel KA-PRE construction that meets these requirements. The proposed scheme mitigates the identified vulnerabilities by integrating pseudonymous ID-based authentication, introducing additional verification procedures, and minimizing the parameters transmitted to the Proxy Server.
Through the experimental evaluation presented in Section 4, we confirmed that the proposed scheme significantly reduces computational and communication overhead compared to conventional KA-PRE approaches, while maintaining strong confidentiality and integrity guarantees.
The benchmark results, as illustrated in Figure 3, demonstrate the practicality of our construction under a real server–client environment, verifying that the additional verification steps do not impose excessive performance costs.
We contend that the proposed construction is applicable across diverse domains that demand secure data sharing and fine-grained access control—such as cloud platforms and Personal Data Stores (PDSs). In particular, the scheme is relevant to settings handling highly sensitive information (e.g., financial services, healthcare, and public-sector data), where strong confidentiality and privacy guarantees are essential.
Nevertheless, this work has several limitations. First, although the security properties of the proposed scheme are supported by formal analysis and proofs, empirical evaluation of performance and system overhead in realistic distributed deployments is still lacking. Second, further study is required to address collusion among multiple Receivers and to improve scalability in group settings. Third, the scheme’s resilience against a broader spectrum of cryptographic attack scenarios remains to be explored.
For future work, we plan to, first, conduct experimental evaluations of the scheme in real cloud and PDS environments to quantify performance and operational overhead, second, design scalable extensions that accommodate multi-user and group contexts—including mechanisms to mitigate collusion—and, third, integrate complementary cryptographic primitives to achieve strong anonymity together with conditional traceability. These directions will aim to enhance both the practicality and the security guarantees of the proposed KA-PRE construction.
Author Contributions
Conceptualization, D.S. and D.G.L.; methodology, J.S. and D.G.L.; validation, J.S., D.G.L. and W.K.; formal analysis, J.S.; investigation, J.S. and D.G.L.; resources, D.S. and S.-H.K.; data curation, J.S. and D.G.L.; writing—original draft preparation, J.S.; writing—review and editing, S.-H.K. and W.K.; visualization, J.S.; supervision, D.S.; project administration, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by BK21 FOUR (Fostering Outstanding Universities for Research) (No.:5199990914048), Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (RS-2025-25453740, Development of a large-scale mixed device control and management platform for edge AI server systems) and the Technology Innovation Program (RS-2024-00443436) funded By the Ministry of Trade, Industry & Energy (MOTIE, Korea).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
We prove the Proposed Scheme based on bilinear pairing properties. From the Encryption Phase, we obtain (Appendix A.1). By Aggregate KeyGen Phase, we obtain (Appendix A.2). By Re-KeyGen Phase, we obtain (Appendix A.3). By Re-Enc Phase, we obtain (Appendix A.4). By Decrypt1 Phase, we obtain (Appendix A.5). By DecryptR Phase, we obtain (Appendix A.6).
Appendix A.1. Encryption Phase
Step A1.1. The parameters required for generating the initial ciphertext are as follows:
Step A1.2. The initial ciphertext is generated as follows:
Appendix A.2. Aggregate KeyGen Phase
Step A2.1. The parameters required for generating the aggregate key are as follows:
Step A2.2. The aggregate key is generated as follows:
Step A2.3. The verification value is generated as follows:
Appendix A.3. Re-KeyGen Phase
Step A3.1. The parameters required for generating the re-encryption key are as follows:
Step A3.2. The re-Encryption key is generated as follows:
Appendix A.4. Re-Enc Phase
Step A4.1. The identity verification procedure is as follows:
Step A4.2. The ciphertext integrity verification phase consists of three steps (A15)–(A17), as follows:
Step A4.3. The Re-Encryption Ciphertext is generated as follows:
Appendix A.5. Decrypt 1 Phase
Step A5.1. The integrity verification in this phase is identical to Step A4.2 (A15)–(A17):
Step A5.2. The decryption phase for the initial ciphertext is structured as follows:
Appendix A.6. Decrypt R Phase
Step A6.1. The pre-decryption verification phase for the re-encrypted ciphertext is structured as follows:
Step A6.2. The step for computing the value before the final message decryption is as follows:
Step A6.3. The step for computing the value a using the value obtained from (A24) is as follows:
Step A6.4. The step for computing using the value of a obtained from (A25) is as follows:
Step A6.5. The process for computing the value R using the parameters obtained from (A24)–(A26) is as follows:
Step A6.6. The final message decryption process is as follows:
Appendix B
We prove game-based Security Proofs. The following subsections present game-based proofs for confidentiality (IND-CCA), aggregate-key unforgeability (AK-UF), re-encryption unforgeability (REK-UF), class hiding, and anonymity/unlinkability properties of the scheme.
Appendix B.1. Formal Security Model for the Proposed KA-PRE Scheme
Syntax. The proposed Key-Aggregate Proxy Re-Encryption (KA-PRE) scheme is defined over bilinear groups of prime order p with generator (see Table 2). Each algorithm is defined as follows:
- : Executed by the TTP to generate public parameters and master secret .
- : Generates a pseudonymous identity , a secret key , and a credential .
- : Outputs the initial ciphertext as defined in Equation (A5).
- : Produces the re-encryption key for delegation.
- : The Proxy transforms C into a re-encrypted ciphertext .
- : The Receiver decrypts to recover the message M.
Adversarial Model. An adversary interacts with oracles , , , , and that expose session-level aggregate or re-encryption keys but never the master secret or long-term . The Proxy Server is semi-honest but may collude with a Receiver, as described in Section 3.2.
Appendix B.2. Security Definitions Corresponding to A1–A5
- A1—Aggregate-Key Leakage Resistance. For all PPT (Probabilistic Polynomial-Time) adversaries having oracle access as above, the advantage of producing a valid for a new class set is negligible (Aggregate-Key).
- A2—Ciphertext-Based Attack Resistance. The scheme provides Ciphertext Integrity if no PPT adversary can generate a ciphertext that passes the pairing verifications in Equations (10)–(12) without knowledge of a legitimate key.
- A3—Re-Encryption Forgery Resistance. Given , no PPT adversary can output that satisfiesor Equations (A18)–(A19) without a valid or .
- A4—Metadata Hiding. Let choose two class sets of equal size. The scheme is considered secure if cannot distinguish the challenge ciphertext re-encrypted under with non-negligible advantage.
- A5—Anonymity and Unlinkability. Given two pseudonyms with equal privileges, no PPT adversary can distinguish whether the challenge ciphertext was created under or .
Appendix B.3. Theorems and Security Justification
Theorem A1 (Confidentiality).
Under the hardness of the q-BDHI assumption in and the random-oracle model for , the proposed KA-PRE scheme achieves IND-CCA security.
Proof (Sketch).
The challenger embeds the q-BDHI instance into the public parameters and simulates oracles by programming the random oracles and . If the adversary can distinguish the challenge ciphertext, the simulator can solve the q-BDHI problem with non-negligible probability. □
Theorem A2 (Transform and Aggregate-Key Unforgeability).
Assuming the soundness of the pairing verification and the EUF-CMA security of the verification token , the proposed scheme satisfies both REKUF and AKUF.
Theorem A3 (Anonymity and Unlinkability).
If each session uses a fresh random value and defines , then under the random-oracle assumption on , the scheme achieves computational anonymity and unlinkability.
References
- Sookhak, M.; Gani, A.; Talebian, H.; Akhunzada, A.; Khan, S.U.; Buyya, R.; Zomaya, A.Y. Remote Data Auditing in Cloud Computing Environments: A Survey, Taxonomy, and Open Issues. ACM Comput. Surv. 2015, 47, 1–34. [Google Scholar] [CrossRef]
- Sai, A.M.V.V.; Wang, C.; Cai, Z.; Li, Y. Navigating the digital twin network landscape: A survey on architecture, applications, privacy and security. High-Confid. Comput. 2024, 4, 100269. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, Z.; Hu, H.; Li, Y.; Li, W. zkCrowd: A hybrid blockchain-based crowdsourcing platform. IEEE Trans. Ind. Inform. 2019, 16, 4196–4205. [Google Scholar] [CrossRef]
- Zheng, X.; Cai, Z. Privacy-preserved data sharing towards multiple parties in industrial IoTs. IEEE J. Sel. Areas Commun. 2020, 38, 968–979. [Google Scholar] [CrossRef]
- Ali, M.; Malik, S.U.R.; Khan, S. DaSCE: Data Security for Cloud Environment with Semi-Trusted Third Party. IEEE Trans. Cloud Comput. 2015, 5, 642–655. [Google Scholar] [CrossRef]
- Xue, K.; Hong, P. A Dynamic Secure Group Sharing Framework in Public Cloud Computing. IEEE Trans. Cloud Comput. 2014, 2, 459–470. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, Z.; Li, Y.; Zhang, H.; Chen, Y.; Zhao, Z.; Zheng, J. A Survey of Data Security Sharing. Symmetry 2025, 17, 1259. [Google Scholar] [CrossRef]
- Bag, S.; Ghosh Ray, I.; Feng, H. A new leakage resilient symmetric searchable encryption scheme for phrase search. In Proceedings of the 19th International Conference on Security and Cryptography SECRYPT, Lisbon, Portugal, 11–13 December 2022; SciTePress: Setúbal, Portugal, 2022; Volume 1, pp. 366–373. [Google Scholar] [CrossRef]
- Domingo-Ferrer, J.; Farràs, O.; Ribes-González, J.; Sánchez, D. Privacy-preserving cloud computing on sensitive data: A survey of methods, products and challenges. Comput. Commun. 2019, 140–141, 38–60. [Google Scholar] [CrossRef]
- He, Z.; Cai, Z. Trading aggregate statistics over private internet of things data. IEEE Trans. Comput. 2023, 73, 394–407. [Google Scholar] [CrossRef]
- Chu, C.K.; Chow, S.S.; Tzeng, W.G.; Zhou, J.; Deng, R.H. Key-aggregate cryptosystem for scalable data sharing in cloud storage. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 468–477. [Google Scholar] [CrossRef]
- Matsuo, T. Proxy re-encryption systems for identity-based encryption. In Proceedings of the International Conference on Pairing-Based Cryptography, Tokyo, Japan, 2–4 July 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 247–267. [Google Scholar]
- Chen, W.H.; Fan, C.I.; Tseng, Y.F. Efficient key-aggregate proxy re-encryption for secure data sharing in clouds. In Proceedings of the 2018 IEEE Conference on Dependable and Secure Computing (DSC), Kaohsiung, Taiwan, 10–13 December 2018; IEEE: New York, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Patranabis, S.; Shrivastava, Y.; Mukhopadhyay, D. Provably Secure Key-Aggregate Cryptosystems with Broadcast Aggregate Keys for Online Data Sharing on the Cloud. IEEE Trans. Comput. 2017, 66, 891–904. [Google Scholar] [CrossRef]
- Liu, J.; Qin, J.; Wang, W.; Mei, L.; Wang, H. Key-aggregate based access control encryption for flexible cloud data sharing. Comput. Stand. Interfaces 2024, 88, 103800. [Google Scholar] [CrossRef]
- Pei, H.; Yang, P.; Li, W.; Du, M.; Hu, Z. Proxy re-encryption for secure data sharing with blockchain in internet of medical things. Comput. Netw. 2024, 245, 110373. [Google Scholar] [CrossRef]
- Singh, A.; Rathee, G.; Kerrache, C.A.; Ghanem, M.C. A Relay-Chain-Powered Ciphertext-Policy Attribute-Based Encryption in Intelligent Transportation Systems. arXiv 2025, arXiv:2508.16189. [Google Scholar]
- Günsay, E.; Yayla, O. Decentralized anonymous IoT data sharing with key-private proxy re-encryption. Int. J. Inf. Secur. Sci. 2024, 13, 23–39. [Google Scholar] [CrossRef]
- Jadhav, R.; Nargundi, S. Review on key-aggregate cryptosystem for scalable data sharing in cloud storage. Int. J. Res. Eng. Technol. 2014, 3, 376–379. [Google Scholar] [CrossRef]
- Pareek, G.; Maiti, S. Efficient dynamic key-aggregate cryptosystem for secure and flexible data sharing. Concurr. Comput. Pract. Exp. 2023, 35, e7553. [Google Scholar] [CrossRef]
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Espoo, Finland, 31 May–4 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 127–144. [Google Scholar]
- Chu, C.K.; Tzeng, W.G. Identity-based proxy re-encryption without random oracles. In Proceedings of the International Conference on Information Security, Valparaíso, Chile, 9–12 October 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 189–202. [Google Scholar]
- Green, M.; Ateniese, G. Identity-based proxy re-encryption. In Proceedings of the International Conference on Applied Cryptography and Network Security, Zhuhai, China, 5–8 June 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 288–306. [Google Scholar]
- Yang, N.; Tian, Y.; Zhou, Z.; Zhang, Q. A provably secure collusion-resistant identity-based proxy re-encryption scheme based on NTRU. J. Inf. Secur. Appl. 2023, 78, 103604. [Google Scholar] [CrossRef]
- Dutta, P.; Susilo, W.; Duong, D.H.; Roy, P.S. Collusion-resistant identity-based proxy re-encryption: Lattice-based constructions in standard model. Theor. Comput. Sci. 2021, 871, 16–29. [Google Scholar] [CrossRef]
- Ge, C.; Liu, Z.; Xia, J.; Fang, L. Revocable identity-based broadcast proxy re-encryption for data sharing in clouds. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1214–1226. [Google Scholar] [CrossRef]
- Rawal, B.S.; M, P.; Manogaran, G.; Hamdi, M. Multi-tier stack of block chain with proxy re-encryption method scheme on the internet of things platform. ACM Trans. Internet Technol. (TOIT) 2021, 22, 1–20. [Google Scholar] [CrossRef]
- Andola, N.; Verma, K.; Venkatesan, S.; Verma, S. Proactive threshold-proxy re-encryption scheme for secure data sharing on cloud. J. Supercomput. 2023, 79, 14117–14145. [Google Scholar]
- You, W.; Lei, L.; Chen, B.; Liu, L. What if keys are leaked? towards practical and secure re-encryption in deduplication-based cloud storage. Information 2021, 12, 142. [Google Scholar] [CrossRef]
- Fábrega, A.; Pérez, C.O.; Namavari, A.; Nassi, B.; Agarwal, R.; Ristenpart, T. Injection attacks against end-to-end encrypted applications. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; IEEE: New York, NY, USA, 2024; pp. 2648–2665. [Google Scholar]
- Fábrega, A.; Namavari, A.; Agarwal, R.; Nassi, B.; Ristenpart, T. Exploiting leakage in password managers via injection attacks. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 4337–4354. [Google Scholar]
- Grubbs, P.; Ristenpart, T.; Shmatikov, V. Why your encrypted database is not secure. In Proceedings of the 16th Workshop on Hot Topics in Operating Systems, Whistler, BC, Canada, 7–10 May 2017; pp. 162–168. [Google Scholar]
- Weng, J.; Deng, R.H.; Ding, X.; Chu, C.K.; Lai, J. Conditional proxy re-encryption secure against chosen-ciphertext attack. In Proceedings of the 4th International Symposium on Information, Computer, and Communications Security, Sydney, Australia, 10–12 March 2009; pp. 322–332. [Google Scholar]
- Eskandarian, S.; Corrigan-Gibbs, H.; Zaharia, M.; Boneh, D. Express: Lowering the cost of metadata-hiding communication with cryptographic privacy. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Virtual, 11–13 August 2021; pp. 1775–1792. [Google Scholar]
- Zhan, D.; Hai, R. Will Sharing Metadata Leak Privacy? In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering Workshops (ICDEW), Utrecht, The Netherlands, 13–16 May 2024; IEEE: New York, NU, USA, 2024; pp. 317–323. [Google Scholar]
- Pfitzmann, A.; Hansen, M. A Terminology for Talking About Privacy by Data Minimization: Anonymity, Unlinkability, Undetectability, Unobservability, Pseudonymity, and Identity Management. 2010. Available online: https://dud.inf.tu-dresden.de/literatur/Anon_Terminology_v0.34.pdf (accessed on 10 September 2025).
- Heurix, J.; Zimmermann, P.; Neubauer, T.; Fenz, S. A taxonomy for privacy enhancing technologies. Comput. Secur. 2015, 53, 1–17. [Google Scholar] [CrossRef]
- Chen, W.H.; Fan, C.I.; Tseng, Y.F. CCA-Secure Key-Aggregate Proxy Re-Encryption for Secure Cloud Storage. arXiv 2024, arXiv:2410.08120. [Google Scholar]
- Pareek, G.; Purushothama, B. KAPRE: Key-aggregate proxy re-encryption for secure and flexible data sharing in cloud storage. J. Inf. Secur. Appl. 2021, 63, 103009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).