Abstract
In this paper, we investigate the Adaptive Service Migration (ASM) problem in dynamic satellite edge computing networks, focusing on Low Earth Orbit satellites with time-varying inter-satellite links. We formulate the ASM problem as a constrained optimization problem, aiming to minimize overall service cost, which includes both interruption cost and processing cost. To address this problem, we propose ASM-DRL, a deep reinforcement learning approach based on the soft Actor-Critic framework. ASM-DRL introduces an adaptive entropy adjustment mechanism to dynamically balance exploration and exploitation, and adopts a dual-Critic architecture with soft target updates to enhance training stability and reduce Q-value overestimation. Extensive simulations show that ASM-DRL significantly outperforms baseline approaches in reducing service cost.
1. Introduction
The sixth generation mobile communication system (6G) aims to build an integrated space–air–ground network with global coverage by deep integrating satellite communication and terrestrial mobile communication technologies, thereby enabling seamless connectivity services worldwide [1]. However, traditional terrestrial networks are limited by geographical restrictions and natural disasters, resulting in significant coverage gaps in polar regions, oceans, and remote areas, which fails to meet the ubiquitous connectivity requirements of the 6G era. In contrast, the satellite network can offer wide area coverage, making it a key solution to overcome the limitations of terrestrial network coverage [2]. Compared to Medium Earth Orbit (MEO) and Geosynchronous Earth Orbit (GEO) satellites, Low Earth Orbit (LEO) satellites have drawn increasing attention due to their low altitude, short transmission delay, and low path loss [3,4].
With the rapid development of Mobile Edge Computing (MEC) [5], a new paradigm, Satellite Edge Computing (SEC) [6,7], has been emerged. By deploying MEC servers on LEO satellites, SEC extends edge computing to the space domain, which pushes computing resources closer to users across wide geographic areas and improving service availability. Nevertheless, SEC faces several practical challenges due to its highly dynamic nature. For example, since LEO satellites move rapidly (typically around 7.8 km/s relative to ground users), multi-hop relays are often required to maintain service continuity. Thus, this may lead to an increase in transmission delay. Moreover, the rapid movement of LEO satellites causes frequent changes in inter-satellite links (ISLs), as connections continuously alternate between active and inactive states. Apparently, such time-varying connectivity results in fluctuating link quality, thereby degrading the performance of multi-hop communications. As a result, this potentially increases transmission latency or even cause service interruptions. Therefore, service migration is essential for maintaining continuous services for users under dynamic satellite networks. It allows the redeployment of service instances on LEO satellites with more stable connections and reduces the impact of frequent link disruptions. Without timely migration, users would rely on longer or unstable transmission paths, which can result in higher latency or even communication failures. However, frequent topological variations, dynamic user access, and heterogeneous resources pose significant challenges for efficient service migration in SEC networks. Consequently, designing efficient migration strategies that can ensure service continuity and low-latency performance is still a critical and open research problem.
To address these challenges, optimization-based or heuristic approaches [8,9,10] are proposed, yet they struggle to adapt to the highly dynamic nature of SEC. Recently, reinforcement learning approaches such as Deep Q-Network (DQN) [11,12] and Proximal Policy Optimization (PPO) [3] have been used to improve adaptability. However, these approaches still face difficulties in balancing exploration and exploitation effectively. To address this limitation, the Soft Actor-Critic (SAC) [13] leverages entropy regularization to achieve a better balance between exploration and exploitation. However, its fixed entropy coefficient limits adaptability to time-varying network conditions, leading to unstable convergence in highly dynamic scenarios.
Therefore, we propose ASM-DRL, an enhanced SAC-based deep reinforcement learning framework designed for dynamic SEC environments with time-varying ISLs. Specifically, ASM-DRL introduces an ISL volatility coefficient to characterize the dynamics of satellite topology and leverages dual-Critic networks with soft Q-learning to ensure stable policy learning. Moreover, an adaptive entropy adjustment mechanism is designed to regulate policy stochasticity during training. Our main contributions are summarized as follows:
- We formulate the adaptive service migration (ASM) problem as a constrained optimization problem that taking ISL variability into account. The objective is to minimize the average user service cost by jointly considering service interruption and service processing costs.
- We propose ASM-DRL, an enhanced SAC-based migration framework that integrates entropy-regularized soft Q-learning. To improve stability and convergence, we adopt a dual-Critic architecture with target networks to mitigate value overestimation. Furthermore, we design an adaptive entropy adjustment mechanism to automatically balance exploration and exploitation, allowing ASM-DRL to adapt to dynamic network conditions and make optimized migration decisions.
- We conduct extensive simulation experiments to evaluate ASM-DRL. The results demonstrate that ASM-DRL significantly outperforms baseline methods in reducing service latency and overall service cost.
The organization of the rest of this paper is as follows. Section 2 reviews related studies. Section 3 introduces the system model and problem formulation. Section 4 presents the ASM-DRL approach. Section 5 evaluates ASM-DRL experimentally. Section 6 presents a discussion of ASM-DRL. Finally, Section 7 concludes this paper and points out future work.
2. Related Work
In this section, we review existing work on service migration, focusing on the challenges and methodologies.
2.1. Service Migration Problem
With the rapid growth of edge computing, the service migration problem has received increasing attention in recent years for maintaining high-quality and low-latency services. Many studies model the service migration problem as an optimization problem that considers constraints such as service latency, migration cost, and limited computing or bandwidth resources. To name a few, in terrestrial edge computing, ref. [14] formulated a time-aware Markov decision process model under constraints of user mobility, path loss effects, and edge server coverage. They then proposed a dynamic decision-making framework to decide when and where to migrate services, aiming to minimize the long-term system network costs. Ref. [5] considered the mobility of both service providers and users and proposed a DRL-based digital twin migration strategy under computational and storage resource constraints to optimize migration cost, synchronization delay, and service request delay. Ref. [15] considered user mobility and service diversity, and combined trajectory prediction (via recurrent neural networks) with DRL to optimize migration decisions. They aimed to minimize overall system delay. Ref. [16] proposed a mobility-aware dynamic strategy for vehicular MEC, optimizing the trade-off between migration cost and user-perceived latency.
However, these studies typically assume edge servers are usually deployed at fixed locations such as base stations or access points. Therefore, the service migration is primarily driven by user mobility and resource heterogeneity. In contrast, LEO satellites move at high speeds and form a time-varying network topology caused by frequent disconnections and reconnections of ISLs. These time-varying topologies critically affect service delay and stability, making the problem fundamentally different from terrestrial networks. As a result, the ISL variability in SEC introduces significant uncertainty in service migration. Although some studies [17,18] have addressed these issues by modeling service continuity under mobility constraints, many still overlook the impact of frequent inter-satellite link disconnections and reconnections, thereby affecting the service performance. To name a few, ref. [17] formulated the service migration problem as a nonlinear integer program and employed an artificial electric field algorithm to jointly optimize task offloading and service migration with the objective of maximizing user utility while ensuring uninterrupted connectivity. Additionally, by considering inter-satellite collaboration with dynamic resource awareness, ref. [18] developed a distributed dueling double deep Q-learning approach to jointly optimize task offloading and service migration under satellite mobility and load imbalance, with the aim of minimizing service delay.
Motivated by these observations, we propose an ISL-aware service migration framework that incorporates the dynamics of inter-satellite connectivity into the migration decision process to achieve more adaptive service delivery in SEC networks.
2.2. Service Migration Methodologies
To tackle the service migration problem, various methodologies have been developed, such as heuristic algorithms and reinforcement learning-based approaches.
Among heuristic methods, ref. [9] proposed an online migration strategy combining Lyapunov optimization and Particle Swarm Optimization. By decomposing long-term optimization into real-time subproblems, they efficiently balanced energy consumption and service delay. Ref. [8] designed a multi-objective optimization framework using heuristic search to identify weak Pareto optimal solutions, which dynamically adjust migration paths and resource allocation to jointly optimize latency and load balancing.
Recently, deep reinforcement learning (DRL) has emerged as a promising solution for service migration in edge computing. For example, ref. [19] formulated the resource allocation problem in edge computing networks as a service function chain embedding problem and proposed an algorithm based on reinforcement learning. Ref. [12] proposed a multi-agent DRL approach for the joint service migration and mobility optimization problem in vehicular edge computing. In the SEC scenarios, ref. [6] developed a DRL-based dual-cloud offloading framework integrating GEO/ground clouds with LEO edges to minimize latency and energy consumption. Ref. [7] addressed a cost-constrained online service deployment problem in mega-LEO satellite networks by considering time-varying on-board resources and limited visible time. To solve the problem, they proposed a convolutional PPO-based online approach. while ref. [10] proposed a heuristic minimized dynamic service function chain migration algorithm that triggers migration only when new requests are rejected.
Despite recent progress achieved by traditional optimization and DRL-based approaches, service migration in SEC remains challenging due to diverse user demands, limited resources, and highly dynamic topologies. Ref. [20] considered the problem of dynamic service migration in terrestrial edge environments and proposed a multi-agent PPO-based approach to reduce redundant migration overhead. Ref. [21] investigated online task offloading in industrial IoT networks and developed a prioritized experience-based double dueling DQN approach to improve learning stability and convergence efficiency. Considering the resource constraints and mobility of LEO satellites, ref. [22] proposed a bandwidth-aware service migration framework for satellite edge computing, aiming to minimize long-term delay while meeting task deadlines. By jointly optimizing service migration and power control, ref. [23] proposed a DRL-based approach for space-centric task offloading in energy-harvesting LEO satellite networks, aiming to minimize end-to-end task offloading latency. More recently, ref. [24] proposed a DRL-based resource management scheme for task inference in LEO-based satellite-ground collaborative networks, which jointly optimizes task offloading, computing, and communication resource allocation to minimize overall system cost.
Although these studies have made important advances, most of them assume static or pre-defined link stability metrics and thus cannot fully capture real-time topological volatility in the time-varying SEC environment, as summarized in Table 1. While reinforcement learning has been widely employed for optimization, these approaches were not originally designed for the ASM problem under highly time-varying satellite conditions considered in our work. Even when adapted, they may encounter limitations in effectively migrating decisions when the network topology changes rapidly, potentially leading to infeasible or inefficient solutions. To address these issues, our ASM-DRL introduces an ISL Volatility Coefficient that quantifies connectivity dynamics by jointly modeling temporal stability and neighbor diversity. Furthermore, it integrates adaptive entropy adjustment and a dual-critic architecture into the SAC framework to form a volatility-aware adaptive learning framework. As a result, it can enhance the stability and adaptability under dynamic LEO topologies.

Table 1.
Comparison between our work and the most relevant works.
3. System Model and Problem Statement
In this section, we consider an SEC network with N heterogeneous LEO satellites, each equipped with an edge server for processing user requests. Let denote the set of LEO satellites, where each satellite has a computing capacity and storage capacity . We assume that he time horizon is divided into equal-length time slots indexed by , with each slot of duration . To capture the dynamic nature of the time-varying network topology, we employ a snapshot-based method to sample the satellite network topology at the beginning of each time slot. When time slot is sufficiently small, the network topology is assumed to be quasi-static within each slot. Thus, the dynamic topology is modeled as a discrete-time graph sequence , where V is the set of LEO satellites and is the set of ISLs at time slot t. If there exists a direct inter-satellite link between LEO satellites i and j at time slot t, then . To characterize the dynamics of computational load, a computation queue is maintained at each LEO satellite n for time slot t, where the queue length indicates the processing workload of satellite n.
At time slot t, we consider a set of U users denoted by . Each user generates a service request characterized by the tuple , where is the input data size (kb), is the required computational workload (CPU cycles), and is the required storage resource (MB). Each user u is associated with an LEO satellite within its communication range. This satellite is referred to as user u’s access satellite, denoted by . However, the user’s service request may be executed by a different LEO satellite. We refer to this satellite as user u’s service satellite, denoted by . For each user u, if , the service data must be forwarded from its access satellite to the service satellite via multi-hop transmissions over the ISLs. The performance of such transmissions is highly affected by the dynamic satellite topology and time-varying link availability.
Let denote the binary migration decision vector for user u at time slot t, where indicates that user u’s service is migrated to and executed by LEO satellite n, and otherwise. To ensure that each user is served by at most one LEO satellite at any time, we have , .
3.1. Node and Link Volatility Model
In SEC networks, the high-speed orbital movement of LEO satellites results in frequent changes in the ISLs. These variations lead to a highly dynamic network topology and consequently affect service migration performance, especially when multi-hop ISL paths are involved. We define two types of volatility, including (1) Satellite Connectivity Volatility, reflecting the stability of a LEO satellite’s ISL neighbors over time, and (2) ISL Volatility, describing the stability of an individual ISL.
(1) Satellite Connectivity Volatility. Define as a binary indicator of ISL connectivity between LEO satellites i and j at time slot t. if a direct ISL exists, i.e., , and otherwise. Let denote the connection indicator function, which indicates whether a connection between LEO satellites i and j exists within a time window T:
For each LEO satellite , we introduce the concept of satellite connectivity volatility coefficient , which reflects the ability of LEO satellite i to maintain stable ISL connectivity with its neighbors over a given time horizon , expressed as follows:
where the item denotes the total number of time slots during which LEO satellite i maintains active ISLs with its neighbors. The item denotes the number of LEO satellites that have been connected to i at least once during T. A smaller indicates that LEO satellite i maintains a relatively stable set of neighbors. Conversely, a larger indicates frequent ISL switching and higher topological volatility, which may increase the risk of service interruption during migration. Therefore, LEO satellites with lower volatility coefficients are preferred for hosting services due to their more stable connectivity.
To illustrate the calculation of the satellite connectivity volatility coefficient, we consider an example with 14 LEO satellites. The edge connectivity states over four consecutive time slots are shown in Figure 1. LEO satellites 1 and 2 are selected as representative cases to analyze their connection dynamics. As shown in Figure 1a, LEO satellite 1 exhibits high link diversity. It connects to LEO satellites {2, 3, 4, 5}, {2, 3, 4, 6}, {2, 3, 4, 7}, and {2, 3, 4, 8} in time slots 1 through 4, respectively. The set of LEO satellites connected to LEO Satellite 1 is therefore . The ISL volatility coefficient of LEO Satellite 1 is calculated as follows: . In contrast, LEO satellite 2 maintains a consistent neighbor set across all time slots. As shown in Figure 1b, it connects to Satellites {1, 9, 10, 11} in all four time slots. Thus, its connected neighbor set is , and ISLs volatility coefficient is . Since , LEO satellite 2 exhibits more stable connectivity, implying fewer changes in ISL connections and a lower risk of service disruption during topology updates.
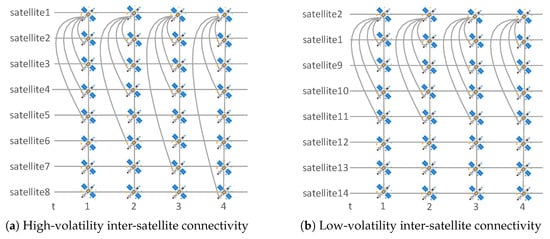
Figure 1.
Illustration of ISL volatility in LEO satellite connectivity, where (a) the high-volatility case shows frequently changing neighbor sets, while (b) the low-volatility case maintains a consistent neighbor set, illustrating the contrast between dynamic and stable ISL connectivity.
(2) ISL Volatility. A highly volatile ISL is more likely to disconnect or require rerouting during migration, increasing the risk of service interruption. To quantify the migration risk over each ISL in the migration path, we define the ISL volatility coefficient on a link as the average connectivity volatility coefficient of its two adjacent LEO satellites i and j, expressed by . This metric captures the overall stability of the ISL based on the dynamic behavior of its endpoints. A lower indicates that both LEO satellites i and j are relatively stable in their connections, implying a more stable and reliable ISL. Conversely, a higher reflects increased topological uncertainty.
3.2. Migration Interruption Cost Model
To reduce service disruption during migration, we adopt a real-time migration strategy with proactive transmission, where the necessary data and execution state of the service instance are pre-transmitted from the source LEO satellite to the target LEO satellite before the actual migration occurs [25,26]. However, even with this mechanism, migration still incurs service interruption due to transmission latency and network instability. In this section, we jointly consider two key factors: service interruption delay and ISL volatility, to model the interruption cost incurred during service migration.
When a service instance is migrated between adjacent LEO satellites i and j, the interruption delay is defined as follows:
where denotes the size of the service instance and is the available transmission rate between adjacent LEO satellites i and j (The transmission rate may vary depending on ISL bandwidth, coding schemes, and concurrent traffic.). As Equation (3) shows, the delay increases with the length of the migration path, which is proportional to the number of ISLs involved [27].
By combining service interruption delay and link volatility (given in Section 3.1), we define the interruption cost for migrating a service instance from satellite to satellite n at time slot t as follows:
where denotes the ISL path from LEO satellites to n at time slot t, which can be obtained by using Dijkstra’s algorithm [27].
Suppose that user u’s service instance is hosted on LEO satellite at time slot , i.e., , and migrated to LEO satellite n at time slot t, i.e., , the overall migration interruption cost is as follows:
3.3. Service Processing Cost Model
The service processing cost is modeled as the sum of three components: communication delay, queuing delay, and computing delay.
(1) Communication Delay. The communication delay for user u to access its service satellite at time slot t, is denoted as . This delay includes both satellite-to-ground and inter-satellite communication, depending on whether the service is executed locally or migrated to another satellite. The details are as follows:
- If , the service is executed locally on user u’s access satellite . In this case, includes only the satellite-to-ground delay, which consists of the propagation and transmission delay over the satellite-ground link.
- If , the service is migrated to a different satellite (i.e., the service satellite of user u). Consequently, user u’s request is first uploaded to the access satellite and then forwarded over a multi-hop ISL path to the target service satellite . Therefore, additionally incorporates the inter-satellite communication delay, which includes both propagation and transmission delays along the multi-hop ISL path from to .
Then, the communication delay is expressed as follows:
where c is the speed of light. To simplify the representation, both satellite-ground and inter-satellite communication processes are unified into a single formulation. Specifically, denotes the propagation distance between nodes a and b, which determines the corresponding propagation delay . For instance, when and , refers to the distance between user u and its access satellite , i.e., the propagation distance over the satellite-ground link. Similarly, is the transmission rate on link , which may represent either a satellite-ground link or an ISL. This rate can be calculated by the following:
where is the bandwidth, is the transmit power, is the noise power, and represents the link loss between nodes a and b.
(2) Queuing Delay. The queuing delay represents the waiting time experienced by a service request before being processed at its service satellite. For user u, the queuing delay at service satellite n at time slot t is denoted as and is given by the following:
where is the current queue length at LEO satellite n, and denotes its computing capability. Equation (8) is derived under the assumption of a first-come-first-served (FCFS) queuing model with homogeneous task demands. This can be further extended to accommodate other scheduling policies or resource-sharing mechanisms.
(3) Computing Delay. The computing delay represents the actual execution time for processing user u’s request on the service satellite. For user u, we denote the computing delay at LEO satellite at time slot t as :
For user u served by LEO satellite n at time slot t, the total service processing cost is defined as the sum of communication, queuing, and computation delays:
where only the selected service satellite (i.e., ) contributes to the total processing cost for user u at time slot t.
3.4. Problem Statement
To jointly consider the service interruption cost and the service processing cost , we adopt a linear weighting approach to integrate them into a unified service cost for user u served by LEO satellite n at time t, which is defined as follows:
where is a weighting coefficient that balances the importance between service interruption and service processing. Both and are normalized using the min–max method.
Based on Equation (11), our objective is to minimize the average service cost across all users and time slots. Accordingly, the service migration problem can be formulated as follows:
where Constraint (12b) defines the binary decision for service migration. Constraint (12c) ensures that each user’s service is migrated to exactly one satellite in each time slot. Constraint (12d) imposes the storage capacity constraint on each satellite, ensuring that the total size of all hosted service instances does not exceed its available capacity.
It is noted that Problem P is a nonlinear integer programming problem, which is computationally intractable in general. Although exact methods such as branch-and-bound and dynamic programming can be applied, they suffer from exponential worst-case complexity, even for a single user. To address this challenge efficiently, we adopt a DRL-based approach named ASM-DRL, to make adaptive service migration decisions.
4. Approach Design for ASM-DRL
4.1. Reformulated Problem
We formalize the service migration Problem P as a Markov Decision Process (MDP) defined by a tuple: , where is the state space, is the action space, and is the reward function. The details are as follows:
(1) State Space . The system state captures the dynamic status of the SEC network in each time slot t. It includes information about the satellite network topology, access satellites of users, computational workloads of LEO satellites, and historical service migration decisions. Specifically, as mentioned above, we denote as the satellite network topology, where V is the time-varying set of LEO satellites and is the set of ISLs. Access satellite information is denoted as , where indicates the access satellite for user u. Given the task queue length of LEO satellite n, we denote as the computational workload information. Finally, previous migration decisions are defined as , where denotes the service migration decision for user u’s required service in the previous time slot. Accordingly, the system state is defined as follows:
(2) Action Space . Based on the observed state , the system selects an appropriate action to determine which user’s service to migrate in each time slot t. Let denote the action taken at time slot t, which determines the service migration decisions for all users. As mentioned above, we denote as migrated information for user u’s service. Thus, the action at time slot t can be expressed as follows:
It is noted that, since each user can choose from candidate LEO satellites and there are users, the total number of possible actions at each time slot is , which grows exponentially with the number of users.
(3) Reward Function . Reinforcement learning typically aims to maximize a reward function to guide the agent toward optimal decision-making. To minimize user service costs in the SEC system, we define the reward as the negative of the total end-to-end service costs incurred in time slot t, i.e., .
Moreover, Constraints (12b) and (12c) are treated as hard constraints and strictly enforced during action selection. In contrast, Constraint (12d), which limits the storage capacity of each LEO satellite, is considered a soft constraint and incorporated into the reward function as a penalty term. To penalize violations of the satellite storage constraint, therefore, we introduce an additional term that reflects the extent to which the aggregate storage demand exceeds the satellite’s available capacity. Let denote the reward function at time slot , given by the following:
where and are positive coefficients that control the weight of the service cost and the storage penalty, respectively. This reward design encourages the agent to reduce total service cost while avoiding overload on any satellite.
Given the MDP model above, we define the policy for problem P as a mapping from to action , i.e., . It determines the action to be taken in each state . Furthermore, in MDP, each feasible policy must satisfy all constraints. Thus, problem P can be reformulated as finding the optimal feasible policy that maximizes the long-term discounted cumulative rewards while satisfying all constraints, denoted as follows:
where, for any action , Constraints (12b)–(12d) must be met. is the discount factor and used to balance immediate and future rewards. When , the system prioritizes immediate rewards in the current time slot. In contrast, when , it emphasizes long-term rewards.
4.2. ASM-DRL Overview
In the SEC network, the heterogeneity of satellite resources and the volatility of ISLs result in a high-dimensional and time-varying environment. This substantially increases the complexity of solving Problem P. Moreover, such characteristics make it challenging for traditional DRL algorithms to achieve stable and efficient training in SEC environments. For example, DQN and PPO often struggle to balance sample efficiency with convergence stability in such complex and dynamic settings. To address these challenges, we propose ASM-DRL, an enhanced SAC-based migration framework to solve Problem P. Because, by introducing the entropy regularization, SAC can maintain an adaptive balance between exploration and exploitation, thereby enabling efficient learning in high-dimensional state spaces. In addition, it utilizes an experience replay buffer to reuse interaction data collected by the central controller. This improves sample efficiency during training and reduces the need for new samples at every iteration.
Figure 2 illustrates the architecture of ASM-DRL, which includes one Actor network, two Critic networks (i.e., Evaluation Networks 1 and 2), two target Critic networks, and an experience replay buffer. Specifically, as follows:
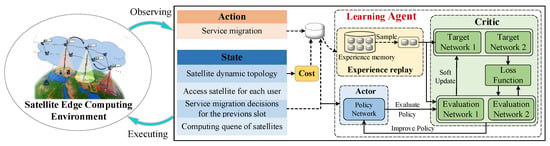
Figure 2.
The framework of ASM-DRL. The SAC-based agent observes system states, evaluates migration actions via a dual-Critic network, and adjusts entropy adaptively to stabilize training.
(1) Actor Network (). This network is referred as to the policy network that maps the observed system state to a stochastic migration action . Its parameter is optimized to maximize expected cumulative reward while maintaining policy entropy through the entropy regularization term.
(2) Critic Networks (). The two Q-networks independently estimate the state–action value function. Each outputs a soft Q-value representing the expected cumulative future reward when taking action in state under the current policy. To mitigate Q-value overestimation during policy optimization, we compute the target Q-value using .
(3) Target Critic Networks (). These are delayed replicas of the main critic networks that provide stable target values for policy evaluation. Their parameters are updated via Polyak averaging, as presented in Formula (20) in Section 4.3. This slow update mechanism effectively suppresses high-frequency oscillations in value estimates, substantially improving training stability and convergence.
(4) Experience Replay Buffer . It is used to store historical experience tuples . During training, random mini-batches are sampled from this buffer to reduce correlation between samples, thereby enhancing training stability and generalization.
The synergistic interaction between these components enables effective policy optimization in dynamic SEC environments. The actor network refines migration decisions using value estimates from the critics, while the target networks provide consistent learning signals. Concurrently, the experience replay buffer ensures efficient utilization of collected transition data, making this framework particularly suitable for resource-constrained SEC scenarios.
4.3. Network Training
To promote sustained exploration during training, we introduce an entropy term into the objective function. The policy entropy is defined as which quantifies the uncertainty in action selection under policy at state . Higher entropy indicates more randomness in the policy’s decisions, encouraging broader exploration and helping prevent premature convergence to suboptimal deterministic strategies. According to the soft Bellman formulation, the soft Q-function for policy is defined as follows:
where is the future time step relative to the current time slot t, used to index the trajectory along which rewards and entropy terms are accumulated. is the discount factor that balances immediate and future rewards, and is the entropy regularization coefficient that controls the trade-off between exploitation and exploration. A higher promotes more randomness in policy outputs, leading to wider exploration. This soft Q-function thus incorporates both the cumulative expected reward and the entropy bonus, enabling the agent to maintain a stochastic and exploratory policy throughout the learning process.
The parameters of the two Critic networks are updated by minimizing the loss function :
where is the target soft Q value, computed using the target Critic networks:
where is an action sampled from the current policy.
To stabilize the training of Critic networks, we use a soft target update strategy for the target network parameters (), which is updated via Polyak averaging:
where is the soft update coefficient controlling the rate of target network updates.
The Actor network parameter is updated by minimizing the loss function :
where is sampled from the current policy, i.e., . This objective encourages the policy to select actions that yield higher expected Q-values while preserving a certain degree of randomness. In other words, it promotes policies that both maximize expected return and maintain stochasticity, effectively balancing exploitation and exploration.
Moreover, the entropy regularization coefficient is automatically adjusted to control the desired policy entropy. The loss function for updating is defined as follows:
where is the target entropy, typically a negative constant that controls the minimum randomness. To minimize this loss, we compute its gradient with respect to , i.e., . Then, the coefficient is updated via gradient descent:
where is the learning rate. Intuitively, when the actual policy entropy is lower than the target , increases to encourage exploration. Otherwise, it decreases to favor exploitation. This adaptive mechanism maintains a balance between exploration and exploitation during training.
Similar to the entropy coefficient , the parameters and are updated using stochastic gradient descent. Let and denote the learning rates for the Critic and Actor networks, respectively. Specifically, the Critic parameters are updated by minimizing the loss function using learning rate , while the Actor parameters are updated by minimizing the loss using learning rate .
The pseudocode of ASM-DRL is provided in Algorithm 1. It is noted that the training of ASM-DRL is conducted centrally at the controller. All parameters are trained using mini-batches of experience tuples sampled from the replay buffer . Meanwhile, expectations are approximated empirically based on these sampled mini-batches. Once training converges, the optimal policy is deployed at the central controller. At each time slot t, the controller observes the current system state and outputs the corresponding migration decision .
| Algorithm 1: ASM-DRL |
 |
5. Experimental Evaluation
5.1. Emulation Setup
In the simulation experiments, we evaluate the performance of ASM-DRL by varying the number of users served by each LEO satellite from 5 to 25. User requests for input data per unit time are assumed to follow a uniform distribution [28] within the range [1000, 2000] kb. The Actor, Critic, and Target Critic networks are all designed with two hidden layers of 256 neurons each, using ReLU as the activation function. Each experiment is independently repeated 50 times, and the mean results are reported. The detailed parameter settings are summarized in Table 2, following [29,30].

Table 2.
Detailed parameter settings.
For performance evaluation, three metrics are considered, i.e., average service interruption delay, average service processing delay, and user average service cost. To provide a comprehensive comparison, ASM-DRL is evaluated against four benchmark approach as follows:
- SAC: It is the SAC-based service migration approach derived from [13]. Unlike our ASM-DRL, it does not take inter-satellite link volatility into account.
- DQN: It is derived from [12]. It integrates Q-learning with deep neural networks, and employs experience replay and a target network to stabilize training.
- GSM: It is a greedy algorithm and iteratively determines migration decisions.
- RAN: It is a baseline approach and randomly chooses migration destinations.
In the simulations, user requests are generated by following a uniform distribution. To ensure a fair and consistent comparison, some parameters (e.g., bandwidth and processing capacity) are fixed, similar to previous satellite edge computing studies [28,29,30]. Please note that the proposed ASM-DRL is not constrained by these fixed assumptions, as the volatility coefficient and DRL-based decision mechanism can be retrained or fine-tuned to adapt to time-varying service demands. Moreover, future work will consider heterogeneous service patterns and dynamic system parameters to further evaluate the robustness and applicability of ASM-DRL in practical satellite networks.
5.2. Weight Coefficient and Convergence Analysis
Figure 3 shows the impact of the weight coefficient on user service cost, considering both service interruption and processing costs. As increases, interruption cost decreases while processing cost rises. A larger emphasizes minimizing interruption cost, leading to fewer migrations but longer communication delay and thus higher processing cost. Conversely, a smaller prioritizes processing cost, resulting in more migrations and higher interruption cost. In practice, can be flexibly adjusted according to application requirements. In subsequent experiments, is set to 0.5.

Figure 3.
Effect of the weight coefficient . Increasing decreases service interruptions but increases processing cost, whereas a smaller yields the opposite trend. An intermediate value of provides a good trade-off between latency and migration overhead.
Figure 4 illustrates the convergence performance of ASM-DRL over 500 learning rounds. The reward value steadily converges and becomes stable after about 300 rounds. This demonstrates that ASM-DRL adapts well to dynamic environments while maintaining learning efficiency in high-dimensional decision spaces.
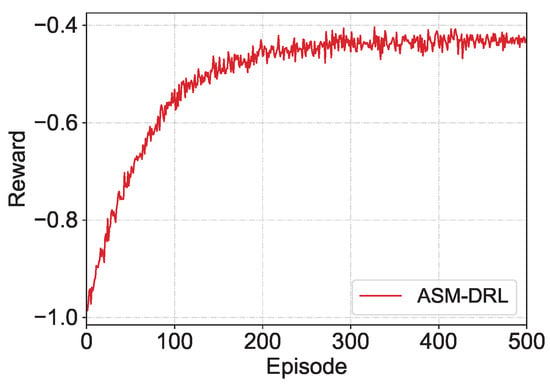
Figure 4.
Convergence performance of ASM-DRL during training, where the cumulative reward stabilizes after approximately 300 episodes.
5.3. Performance Comparison
5.3.1. Performance Under Different User Numbers
Figure 5 shows the changes in average service interruption delay (Figure 5a), average service processing delay (Figure 5b), and user average service cost (Figure 5c) as the number of users grows. All three metrics increase because more users compete for the same limited resources.
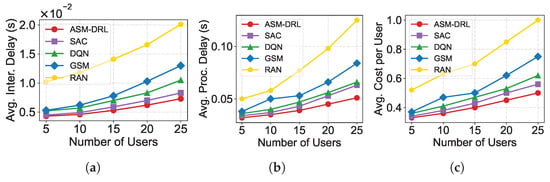
Figure 5.
Performance comparison of ASM-DRL and baseline algorithms under different user numbers: (a) average service interruption delay, (b) average processing delay, and (c) average cost per user. ASM-DRL consistently achieves lower latency and cost, demonstrating superior advantages with increasing the number of users.
Compared to SAC, DQN, GSM, and RAN, ASM-DRL achieves the best performance across all metrics. This is mainly due to ASM-DRL’s adaptive handling of dynamic link conditions. Obviously, RAN performs random service migration without optimization and achieves the weakest performance. GSM adopts a greedy approach that cannot adapt well to dynamic environments. DQN relies on a fixed -greedy strategy, which restricts adaptive exploration and often results in local optimization. Although SAC and ASM-DRL share the same framework, ASM-DRL further incorporates inter-satellite link fluctuations into its migration decisions. As a result, ASM-DRL maintains more stable connectivity and achieves superior performance across all three metrics. The overall average results across all cases are given in Table 3. This shows that ASM-DRL achieves lower service interruption delay and processing delay than SAC, DQN, GSM, and RAN by 15.25%, 22.60%, 38.70%, and 61.93%, and by 11.15%, 21.44%, 32.61%, and 51.19%, respectively. In addition, ASM-DRL reduces the average service cost per user by 6.5%, 13.3%, 24.0%, and 44.5% compared to SAC, DQN, GSM, and RAN, respectively. This further verifies the efficiency and cost-effectiveness of ASM-DRL.

Table 3.
Average performance comparison of different approaches under different number of users.
5.3.2. Performance Under Different Satellite Computing Capabilities
Figure 6 presents the average service interruption delay (Figure 6a), average service processing delay (Figure 6b), and user average service cost (Figure 6c) of each method under different satellite computing capabilities. The results show that with stronger computing power, all three metrics decline, since each satellite can process more user requests, thereby reducing interruption delay, processing delay, and overall user cost.
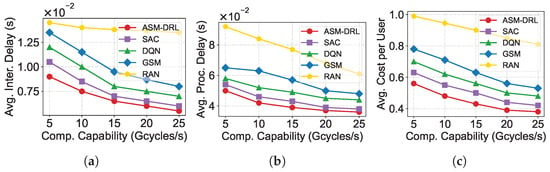
Figure 6.
Performance comparison of ASM-DRL and baseline algorithms under varying satellite computing capabilities: (a) average service interruption delay, (b) average processing delay, and (c) average cost per user. As computing capability increases, all approaches achieve better performance, while ASM-DRL consistently maintains the best overall results.
Compared with SAC, DQN, GSM, and RAN, the proposed ASM-DRL consistently achieves superior performance across all metrics. Similarly, Table 4 presents the average results under varying satellite computing capabilities. On average, ASM-DRL reduces the service interruption delay by 8.93%, 20.28%, 31.11%, and 49.22%, and decreases the service processing delay by 11.46%, 20.61%, 29.64%, and 46.53%, respectively. The reasons for these advantages are consistent with those discussed in the previous subsection and are not repeated here. Moreover, ASM-DRL achieves lower average service cost per user by 12.0%, 22.4%, 30.0%, and 50.3% compared to SAC, DQN, GSM, and RAN, respectively. These results demonstrate that ASM-DRL can achieves superior performance in dynamic SEC environments.

Table 4.
Average performance comparison of different approaches under different satellite computing capabilities.
6. Discussion
Compared with existing DRL-based approaches summarized in Table 1, ASM-DRL takes the ISL volatility into the decision-making process account and adjusts its learning policy accordingly. This design allows the learning policy to remain stable and effective even under time-varying LEO topologies, which is demonstrated in Figure 4. Each LEO satellite independently computes its ISL volatility value from recent connectivity observations, with a per-node complexity of , where denotes the set of neighboring satellites connected to LEO satellite i. Since the neighborhood size is typically small in LEO constellations, this additional computation incurs negligible overhead during learning. Furthermore, the volatility feature is represented as a single scalar in the state vector. This prevents parameter expansion in the Actor-Critic network and keeps the overall training complexity constant when the number of LEO satellites increases. Consequently, this demonstrates that ASM-DRL has good scalability and convergence stability when dealing with large-scale ASM problem in most real-world SEC environments. Additionally, as demonstrated by the experimental results reported in Section 5.3, ASM-DRL can make decisions with better performance, outperforming representative competing approaches.
Overall, ASM-DRL enhances the SAC framework with the volatility awareness, thereby enhancing adaptability in dynamic SEC environments.
7. Conclusions
In this paper, we investigated the adaptive service migration (ASM) problem in satellite edge computing by considering inter-satellite link (ISL) variability. Our objective is to minimize user service costs, including migration-induced interruptions and processing delays. To this end, we proposed ASM-DRL, a volatility-aware deep reinforcement learning framework based on the Soft Actor-Critic algorithm. By introducing an ISL volatility coefficient and adaptive entropy adjustment, ASM-DRL achieves stable and efficient migration decisions in time-varying LEO satellite networks. Experimental results demonstrate that ASM-DRL effectively reduces latency and service cost compared with existing approaches.
However, ASM-DRL assumes that each LEO satellite can accurately obtain local link state information, which may not always hold in practice due to sensing or communication delays. It mainly focuses on service migration, without jointly optimizing service placement/caching, task offloading, resource allocation, or energy management. Moreover, the current evaluation is simulation-based, and real-system validation remains to be conducted. In the future, we will extend ASM-DRL to integrated service management by enhancing the robustness of the framework against satellite failures and other dynamic uncertainties. We will also plan to explore lightweight distributed training for large-scale satellite networks.
Author Contributions
Conceptualization, L.Z. and J.Z.; methodology, L.G.; Writing—original draft, S.N. and W.Q.; writing—review and editing, L.Z. and K.L.; software, L.G.; supervision, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Province under Grant No. BK20230351, and the National Natural Science Foundation of China under Grants No. 62402233, No. 62472232, and No. U24A20248.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, X.; Cioni, S.; Charbit, G.; Chuberre, N.; Hellsten, S.; Boutillon, J.F. On the Path to 6G: Embracing the Next Wave of Low Earth Orbit Satellite Access. IEEE Commun. Mag. 2021, 59, 36–42. [Google Scholar] [CrossRef]
- Tang, L.; Wang, S.; Zhou, M.; Ding, Y.; Wang, C.; Wang, S.; Sun, Z.; Wu, J. Research on recognition algorithm for gesture page turning based on wireless sensing. Intell. Converg. Netw. 2023, 4, 15–27. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, Y.; Zhao, L.; Cai, H.; Xiao, F. Adaptive Task Offloading with Spatiotemporal Load Awareness in Satellite Edge Computing. IEEE Trans. Netw. Sci. Eng. 2024, 11, 5311–5322. [Google Scholar] [CrossRef]
- Ferre, R.M.; Lohan, E.S.; Kuusniemi, H.; Praks, J.; Kaasalainen, S.; Pinell, C.; Elsanhoury, M. Is LEO-Based Positioning with Mega-Constellations the Answer for Future Equal Access Localization? IEEE Commun. Mag. 2022, 60, 40–46. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Liang, W. Deep Reinforcement Learning for Mobility-Aware Digital Twin Migrations in Edge Computing. IEEE Trans. Serv. Comput. 2025, 18, 704–717. [Google Scholar] [CrossRef]
- Zhou, J.; Liang, J.; Zhao, L.; Wan, S.; Cai, H.; Xiao, F. Latency-Energy Efficient Task Offloading in the Satellite Network-Assisted Edge Computing via Deep Reinforcement Learning. IEEE Trans. Mob. Comput. 2025, 24, 2644–2659. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Liu, C.; Li, X.; Ji, H.; Leung, V.C.M. Online Service Deployment on Mega-LEO Satellite Constellations for End-to-End Delay Optimization. IEEE Trans. Netw. Sci. Eng. 2024, 11, 1214–1226. [Google Scholar] [CrossRef]
- Xu, J.; Ma, X.; Zhou, A.; Duan, Q.; Wang, S. Path Selection for Seamless Service Migration in Vehicular Edge Computing. IEEE Internet Things J. 2020, 7, 9040–9049. [Google Scholar] [CrossRef]
- Zhou, X.; Ge, S.; Qiu, T.; Li, K.; Atiquzzaman, M. Energy-Efficient Service Migration for Multi-User Heterogeneous Dense Cellular Networks. IEEE Trans. Mob. Comput. 2023, 22, 890–905. [Google Scholar] [CrossRef]
- Yuhui, G.; Niwei, W.; Xi, C.; Xiaofan, X.; Changsheng, Z.; Junyi, Y.; Zhenyu, X.; Xianbin, C. Service Function Chain Migration in LEO Satellite Networks. China Commun. 2024, 21, 247–259. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, W.; Wu, Q.; Fan, P.; Fan, Q.; Wang, J.; Letaief, K.B. Distributed Deep Reinforcement Learning-Based Gradient Quantization for Federated Learning Enabled Vehicle Edge Computing. IEEE Internet Things J. 2025, 12, 4899–4913. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, J.; Zhou, H.; Lin, T.; Luo, G.; Shen, X. A Joint Service Migration and Mobility Optimization Approach for Vehicular Edge Computing. IEEE Trans. Veh. Technol. 2020, 69, 9041–9052. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1861–1870. [Google Scholar]
- Shamsadini, A.; Entezari-Maleki, R. Time-aware MDP-based Service Migration in 5G Mobile Edge Computing. In Proceedings of the 2022 27th International Computer Conference, Computer Society of Iran (CSICC), Tehran, Iran, 23–24 February 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Tran, T.P.; Yoo, M. Mobility-aware Service Migration in MEC System. In Proceedings of the 2024 International Conference on Information Networking (ICOIN), Ho Chi Minh City, Vietnam, 17–19 January 2024; pp. 653–656. [Google Scholar] [CrossRef]
- Khamari, S.; Rachedi, A.; Ahmed, T.; Mosbah, M. Adaptive Deep Reinforcement Learning Approach for Service Migration in MEC-Enabled Vehicular Networks. In Proceedings of the 2023 IEEE Symposium on Computers and Communications (ISCC), Gammarth, Tunisia, 9–12 July 2023; pp. 1075–1079. [Google Scholar] [CrossRef]
- Wang, X.; Ju, X.; Xie, R.; Tang, Q.; Chen, T.; Huang, T. Service Continuity Guarantee for Coordinated Optimization of Offloading and Migration in LEO Satellite Computing Power Networks. In Proceedings of the 2024 10th International Conference on Computer and Communications (ICCC), Chengdu, China, 12–15 December 2024; pp. 1857–1862. [Google Scholar] [CrossRef]
- Wu, H.; Yang, X.; Bu, Z. Task Offloading With Service Migration for Satellite Edge Computing: A Deep Reinforcement Learning Approach. IEEE Access 2024, 12, 25844–25856. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, X.; Zhang, L.; Wang, J. Reinforcement-Learning-Assisted Service Function Chain Embedding Algorithm in Edge Computing Networks. Electronics 2024, 13, 3007. [Google Scholar] [CrossRef]
- Chen, S.; Rui, L.; Gao, Z.; Yang, Y.; Qiu, X.; Guo, S. Service migration with edge collaboration: Multi-agent deep reinforcement learning approach combined with user preference adaptation. Future Gener. Comput. Syst. 2025, 165, 107612. [Google Scholar] [CrossRef]
- Chi, J.; Zhou, X.; Xiao, F.; Lim, Y.; Qiu, T. Task Offloading via Prioritized Experience-Based Double Dueling DQN in Edge-Assisted IIoT. IEEE Trans. Mob. Comput. 2024, 23, 14575–14591. [Google Scholar] [CrossRef]
- Deng, P.; Gong, X.; Que, X. A bandwidth-aware service migration method in LEO satellite edge computing network. Comput. Commun. 2023, 200, 104–112. [Google Scholar] [CrossRef]
- Chen, J.H.; Kuo, W.C.; Liao, W. SpaceEdge: Optimizing Service Latency and Sustainability for Space-Centric Task Offloading in LEO Satellite Networks. IEEE Trans. Wirel. Commun. 2024, 23, 15435–15446. [Google Scholar] [CrossRef]
- Fan, W.; Meng, Q.; Wang, G.; Bian, H.; Liu, Y.; Liu, Y. Satellite Edge Intelligence: DRL-Based Resource Management for Task Inference in LEO-Based Satellite-Ground Collaborative Networks. IEEE Trans. Mob. Comput. 2025, 24, 10710–10728. [Google Scholar] [CrossRef]
- Ma, L.; Yi, S.; Carter, N.; Li, Q. Efficient Live Migration of Edge Services Leveraging Container Layered Storage. IEEE Trans. Mob. Comput. 2019, 18, 2020–2033. [Google Scholar] [CrossRef]
- Abdullaziz, O.I.; Wang, L.C.; Chundrigar, S.B.; Huang, K.L. Enabling Mobile Service Continuity Across Orchestrated Edge Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 1774–1787. [Google Scholar] [CrossRef]
- Wang, S.; Urgaonkar, R.; Zafer, M.; He, T.; Chan, K.; Leung, K.K. Dynamic Service Migration in Mobile Edge Computing Based on Markov Decision Process. IEEE/ACM Trans. Netw. 2019, 27, 1272–1288. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, Q.; Zhao, L.; Dai, H.; Xiao, F. Mobility-Aware Computation Offloading in Satellite Edge Computing Networks. IEEE Trans. Mob. Comput. 2024, 23, 9135–9149. [Google Scholar] [CrossRef]
- Tang, Q.; Xie, R.; Fang, Z.; Huang, T.; Chen, T.; Zhang, R.; Yu, F.R. Joint Service Deployment and Task Scheduling for Satellite Edge Computing: A Two-Timescale Hierarchical Approach. IEEE J. Sel. Areas Commun. 2024, 42, 1063–1079. [Google Scholar] [CrossRef]
- Yan, Z.; Cola, T.d.; Zhao, K.; Li, W.; Du, S.; Yang, H. Exploiting Edge Computing in Internet of Space Things Networks: Dynamic and Static Server Placement. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).