Abstract
In Industry 4.0 environments, edge intelligence plays a critical role in enabling real-time analytics and autonomous decision-making by integrating artificial intelligence (AI) with edge computing. However, deploying deep neural networks (DNNs) on resource-constrained edge devices remains challenging due to limited computational capacity and strict latency requirements. While conventional methods primarily focus on structural model compression, we propose an adaptive input-centric approach that reduces computational overhead by pruning redundant features prior to inference. A Bayesian network is employed to quantify the influence of each input feature on the model output, enabling efficient input reduction without modifying the model architecture. A bidirectional chain structure facilitates robust feature ranking, and an automated algorithm optimizes input selection to meet predefined constraints on model accuracy and size. Experimental results demonstrate that the proposed method significantly reduces memory usage and computation cost while maintaining competitive performance, making it highly suitable for real-time edge intelligence in industrial settings.
1. Introduction
Industry 4.0 represents a paradigm shift in manufacturing, characterized by intelligent and interconnected systems that enable autonomous production, predictive maintenance, and real-time decision-making. This transformation is underpinned by the convergence of cloud and edge computing, which together form a distributed cloud–edge architecture capable of handling both latency-sensitive and data-intensive workloads in industrial environments [1,2]. When integrated with artificial intelligence (AI), this architecture gives rise to edge intelligence—the ability to perform low-latency analytics and autonomous control directly on edge devices. This paradigm is increasingly applied across diverse Industry 4.0 domains, such as smart factories, precision agriculture, and intelligent healthcare, where real-time responsiveness is critical. However, deploying state-of-the-art deep neural networks (DNNs) on edge devices remains challenging due to their large parameter sizes and intensive floating-point operation requirements, which exceed the limited computational resources and memory of embedded controllers, wearables, and industrial sensors. To mitigate this gap, model compression techniques—such as pruning, quantization, and knowledge distillation—have been widely studied to reduce model complexity while preserving inference accuracy in recent years [3,4].
A common approach to addressing the deployment challenge of DNNs on resource-constrained edge devices is to compress the model by modifying its structure—for example, by removing redundant layers or reducing the number of neurons. This class of methods, often categorized under structural regularization, includes techniques such as pruning [5], quantization [6], and the design of lightweight network architectures [7]. These methods have proven effective in reducing the number of parameters and computational costs while preserving predictive performance [8]. However, they also suffer from several inherent limitations. First, pruning strategies typically depend on manually defined thresholds, making them highly sensitive to hyperparameter tuning; aggressive compression may significantly degrade model accuracy. Second, these methods often require extensive fine-tuning after compression to restore performance, which results in prolonged training times and increased computational overhead. Additionally, many traditional approaches still impose substantial demands on storage and bandwidth, and cannot automate compression based on predefined constraints. Finally, the compressed models often require exhaustive empirical testing to verify stability and generalization, thereby increasing the development workload and limiting deployment scalability.
Considering the limitations of existing structural compression methods, this paper approaches the problem from an innovative perspective. More precisely, it reduces input data and optimizes the pruning strategy based on the impact of input data on model outputs. The motivation is not to compress model weights or layers, but to reduce input dimensionality and improve computational efficiency—particularly for deployment in resource-constrained environments. An influence score serves as an indicator to assess the relevance of an input to the output of the model. The higher influence score indicates stronger relevance, while the lower score indicates weaker relevance. A Bayesian network is employed to calculate the influence score of input features on the results. By removing unnecessary input features, the model achieves greater efficiency while maintaining predictive accuracy. Then, a designated algorithm is used to compress the model automatically according to users’ expectations in accuracy and compression ratio. The major contributions of this paper are summarized as follows.
- Unlike conventional feature selection methods that rely on statistical correlations, our approach evaluates input influence on model outputs through Bayesian networks and systematically removes features with low influence.
- We proposed a novel method to realize the influence score calculation. Specifically, we analyze the correlation between model inputs and outputs using a Bayesian network, based on which, the influence scores of input features can be obtained.
- We construct a bidirectional chain structure to represent influence scores and facilitate decision-making when generating the model compression strategies. This structure significantly reduces the time complexity and thus improves compression efficiency. We propose an algorithm that automatically reduces model complexity while meeting predefined size and accuracy requirements.
- We conducted comprehensive experiments to evaluate our method against representative methods with three datasets.
The remainder of this paper is organized as follows. We overview related work in Section 2. Next, we introduce the proposed adaptive feature selection method in Section 3. Section 4 shows the experimental results on three different datasets. Finally, we conclude this paper and point out future work in Section 5.
2. Related Work
2.1. Model Compression
To realise the model compression, many methods have been proposed in recent years, focusing on modifying the network structure. Representative compressed models includes MobileNets [9], SqueezeNet [10], ShuffleNet [11], ShuffleNet v2 [12], and ESPNetv2 [13]. These models are compact, lightweight, and energy-efficient. Compared with deploying MobileNets at the edge, these networks use fewer computational resources and are more power-efficient. Extensive research has developed and refined model compression techniques, facilitating the deployment of deep learning models across diverse platforms. To name a few, Han et al. introduced a seminal compression method [14] incorporating pruning, weight sharing, quantization, and encoding to achieve significant reductions in model size.
Sparsity-inducing regularization for DNNs has been explored in [15]. These methods aim to regularize the network structure to achieve compression, though they often face challenges related to ensuring model convergence and optimizing training processes. A dynamic network surgery [16] involves iterative pruning and retraining phases, where unimportant weights in the original model are initially pruned. Then, the new model is iteratively retrained to recover any necessary weights. However, measuring the importance of weights remains a significant challenge, which requires careful retraining to restore essential parameters pruned before.
Knowledge distillation [17] includes the following: (1) teacher–student method where a small student model learns from a larger teacher model’s outputs, aiming to achieve comparable prediction accuracy with reduced complexity; (2) feature-based distillation that mimics intermediate representations; (3) self-distillation in which model learns from its own predictions. However, existing knowledge distillation methods often impose stringent constraints on model performance, occasionally leading to suboptimal results. Furthermore, advanced techniques such as low-rank factorization [18] and attention-based methods [19] have also been investigated, offering promising avenues for enhancing model efficiency without compromising performance.
Most model compression techniques are designed based on DNNs’ architectures, which typically impose strict requirements on the computational load of edge devices, memory usage, hardware configuration, and network bandwidth. In recent years, some researchers have applied statistical methods [20] to model compression. Others have combined principal component analysis with logistic regression and dimensionality reduction techniques for feature selection [7], employing different machine learning algorithms for information classification. Such methods have led to higher accuracy and reduced training time.
2.2. Feature Selection
In practice, some information in a dataset might be unnecessary or cannot contribute significantly to the model’s performance. Some elements and/or features might be irrelevant or redundant. Feature selection methods have been proposed aiming at reducing the data scale while maintaining model accuracy. By decreasing the number of data features, these methods reduce the input features of the model, further compressing it. Feature selection techniques are classified into three categories: filter methods, wrapper methods, and embedded methods [21].
Filter methods are techniques for feature selection that evaluate and rank each feature independently based on certain criteria, without considering interactions between features. They are widely used in input feature reduction because they are generally fast, simple to implement, and work well as a preliminary step to reduce dimensionality. However, they may miss feature interactions and cannot account for redundancy between features, and thus often have lower accurate than the wrapper and embedded methods [22].
Wrapper methods represent a more sophisticated method than filter methods for feature selection. They evaluate subsets of features by using the machine learning algorithm that will ultimately be deployed as part of the assessment process. The limitations of wrapper methods include the following: (1) computationally expensive, especially for large feature sets; (2) risk of overfitting to the training data; (3) low efficiency for complex models or large datasets. However, wrapper methods usually provide more accurate results than filter methods. The subset generation in wrapper methods is based on various search strategies, which can be divided into three categories [23] including exhaustive, sequential, and random selection strategies. In exhaustive methods, the number of evaluated features increases exponentially with the size of the feature set. Although this method provides accurate results, its high computational cost makes it impractical for actual application. Examples of exhaustive search strategies include exhaustive search and branch-and-bound methods [24]. Sequential algorithms add or remove features in a specific order. Once a feature is included or removed in a selected subset, it cannot be further modified, which may lead to local optima. Random algorithms introduce randomness to explore the search space, thus avoiding the problem of getting trapped in local optima.
Embedded methods combine aspects of both filter and wrapper methods. They integrate feature selection directly into the model training process, making them particularly elegant for feature selection. Unlike filter methods which select features independently or wrapper methods which use the model as a black box, embedded methods incorporate feature selection as part of the learning algorithm itself [25]. Limitations of such methods includes the following: (1) performance may rely highly on algorithms that provide feature importance or support regularization; (2) may be model-specific and not transferable; (3) are usually sensitive to hyperparameter tuning.
2.3. Bayesian Networks
Bayesian networks can effectively depict and analyze uncertainty and handle the state space explosion problem [26,27]. A Bayesian network connects variables with causal relationships or conditional independencies using directed arrows. If a unidirectional arrow connects two nodes, one node is considered the “cause” and the other the “effect,” and they generate a conditional probability value. In a Bayesian network, nodes represent random variables, which can be either discrete or continuous and reflect different states or events in the system. Directed edges denote the conditional dependencies between random variables, while edges point from parent nodes to child nodes, indicating that the state of a child node depends on the state of its parent node. Each node has a conditional probability table that describes the probability distribution of the node given the different states of its parent nodes.
With their graphical representation and probabilistic reasoning capabilities, Bayesian networks have been applied in various fields of data analysis, including risk analysis [28], security engineering [29], fault diagnosis [30,31], consumer services, and healthcare sectors [32]. They have facilitated the identification of causal relationships in complex problems, demonstrating Bayesian networks’s superiority in uncovering hidden connections and identifying early issues through analytical results.
2.4. Edge Computing
The widespread adoption of the Internet of Things (IoT) and the success of cloud services have facilitated the emergence of a new computing paradigm known as edge computing. Edge computing requires data processing at the network edge and is capable of addressing issues such as response time, battery life limitations, transmission cost, as well as data security and privacy concerns.
As an increasing volume of data is generated at the network edge, processing data locally becomes more efficient and convenient. Previous works, such as micro data centers [33], cloudlets [34], and fog computing [35], have been introduced to the community, highlighting that cloud computing is not always effective for data processing, particularly when data is generated at the network edge. Ref. [36] proposed a framework that addresses the challenges in managing computational resources across multiple UAVs in edge environments. This work emphasizes task prioritization and efficient resource distribution, contributing to the growing body of research on edge computing systems.
Although offloading all computing tasks to the cloud has proven to be an effective method for data processing, given the cloud’s superior computational capabilities compared to edge devices, network congestion and related issues can hinder overall performance, especially when fast data processing is required. With the growing volume of data generated at the edge, transmission speed is increasingly becoming a critical bottleneck [37,38].
DNNs, as a major technology in machine learning, have become a focal point of research. However, due to their high computational demands and energy consumption, it is challenging to run DNNs on resource-constrained mobile devices. Offloading DNNs computation to the cloud can suffer from unpredictable cloud-side performance, primarily due to uncontrollable wide-area network (WAN) latency. To address these challenges, researchers have proposed a collaborative on-demand DNNs inference framework based on device–edge cooperation [39]. This approach first partitions DNNs computation between devices and the edge by adjusting the DNNs layers, leveraging adjacent hybrid computational resources for real-time inference. Moreover, by enabling early exits at appropriate intermediate DNNs layers, the framework further reduces computation delay. Prototype implementation and extensive evaluation based on Raspberry Pi devices have demonstrated the effectiveness of Edgent in achieving on-demand, low-latency edge intelligence.
Other studies have similarly focused on optimizing the computational efficiency of edge devices by employing advanced methods like model compression, feature pruning, and network optimization [9,14,40]. However, most of these methods have not fully explored the relationship between input data compression and model efficiency in resource-constrained environments. Our work adds to this conversation by focusing on input feature pruning and its implications for edge intelligence, where reducing computational overhead is crucial.
3. Adaptive Feature Selection for Input Compression
This paper presents an adaptive feature selection method that reduces the input feature space by pruning irrelevant or redundant attributes, thereby improving the model’s generalization ability and computational efficiency. Although reducing input dimensionality may lead to a more compact model, the primary objective is performance enhancement rather than model compression alone. First, a Bayesian network is employed to determine the influence scores of input features on the model outputs. Then, a new chain structure is used to store the influence scores and reduce the time complexity incurred by feature reduction. Finally, an algorithm is proposed to adaptively and automatically compress the model based on predefined size and accuracy thresholds. Our feature selection approach is grounded in the principles of Bayesian networks, which model the conditional dependencies between input features and the output. By quantifying each feature’s influence on the output label, we can rank features based on their relevance and selectively prune those with low impact. This enables efficient dimensionality reduction, reduces noise, mitigates overfitting, and ultimately improves the model’s generalization ability and training efficiency.
In essence, our method aligns with the concept of marginalization in Bayesian inference, where weakly related features are eliminated to optimize model efficiency. Moreover, the proposed input feature pruning operates entirely at the data preprocessing stage, without modifying model architectures or requiring retraining. This lightweight, model-agnostic design is particularly well-suited for deployment on resource-constrained edge devices, and complements traditional model compression techniques by further reducing the computational burden during inference.
3.1. Influence Model and Algorithm Based on Bayesian Network
The Bayesian network is a probabilistic graphical model that represents the relationships between complex data using mathematical formulas, achieving high accuracy in result prediction with a lightweight structure and minimal resource consumption. Different from previous studies, our method does not rely on conventional structure learning or dependency modeling. Instead, we adopt the Bayesian inference formulation to estimate the class-conditional influence of each feature. This formulation enables lightweight and interpretable influence computation without the need to construct a global graphical model. The resulting influence scores are then used to guide a novel chain-based feature pruning algorithm that supports adaptive input pruning under accuracy and resource constraints.
Before influence computation, we apply preprocessing to normalize feature formats. Continuous features are discretized into a finite number of bins using an equal-width partitioning scheme, with the number of bins determined by the Freedman–Diaconis rule to balance detail and statistical stability. Categorical features are converted into numerical form via label encoding, preserving their semantic categories. Missing values, when present, are either removed (if rare) or imputed using statistically reasonable estimates, depending on the proportion of missing entries. These preprocessing steps are guided by the following assumptions: (1) features are treated as conditionally independent when computing influence scores; (2) discretization approximates the continuous feature distributions without introducing significant bias; (3) label encoding preserves categorical distinctions; (4) missing value handling does not substantially distort the estimated probabilities. This ensures that both discrete and continuous attributes are consistently represented for Bayesian probability estimation.
Let us assume that there are a total number of n features with l possible categories for each feature and m possible outcomes for data predictions, the probability of the w-th feature (where ), having a value of i (where ) and resulting in an outcome with index j (where ), is calculated by Equation (1):
where denotes the probability of feature w with a value of i, is the probability that the output value is j.
These probability values reflect the influence of an input data i with a feature of w on the output result j. These probabilities, computed under the conditional independence assumption, quantify the influence of a feature value on the prediction outcome. The corresponding algorithm is shown in Algorithm 1. The definitions are as follows: m is the number of output classes, n is the number of input features, and l is the number of possible categories per feature.
The influence score computation is grounded in the Naïve Bayes formulation, which assumes that input features are conditionally independent given the output label. This assumption reduces the computational complexity of probability estimation from exponential to linear in the number of features, making the approach suitable for resource-constrained edge environments. Continuous variables are discretized into bins using an equal-width partitioning scheme, where the bin width is determined by the Freedman–Diaconis rule to balance resolution and statistical robustness. Categorical attributes are label-encoded to preserve semantic meaning in probability calculations. While these assumptions enhance computational efficiency and reduce memory usage, they may limit the model’s ability to capture higher-order dependencies or irregular feature distributions. Relaxing the independence assumption and adopting adaptive discretization strategies constitute important directions for future work.
| Algorithm 1: Calculation of probabilities for input and output. |
| Input: Data in the training set, m, n, l |
| Output: Set of probability values reflecting the relationship between inputs and outputs |
 |
In Algorithm 1, the vector stores the probabilities of inputs that lead to the same output value j. Vector stores the influence of all inputs with the same feature w on those outputs. In fact, the vector U is a combination of and .
Discussion: In cases where data is missing, features with missing values are directly deleted to ensure the accuracy of the analysis results. However, in practical edge computing scenarios, missing values are not simply removed. Instead, reasonable predictions for the missing data are calculated. When the number of missing values is small, it does not significantly affect the results.
Since Bayesian networks are probabilistic graphical models that do not explicitly quantify feature influence, and because the number of model outputs may vary, this paper defines the influence of an input feature as a vector of probabilities reflecting its impact on each output dimension. In particular, the input influence vector measures the extent to which the w-th input feature affects the model’s predictions, as formalized in Equation (2). This formulation is advantageous because it directly evaluates feature impact on prediction probabilities, providing a conceptually straightforward and computationally efficient metric.
Consider a trained model with m output dimensions and n input features indexed from 1 to n. The influence of the w-th input feature on the predictive output is represented by the feature influence vector:
where each element quantifies the marginal contribution of feature w to the prediction of the j-th output dimension. Formally, is computed as the average absolute deviation of the predicted conditional probabilities from their mean , expressed as
where
Here, l denotes the number of distinct values that the input feature w takes, indexed by , and indexes the output dimensions. The term corresponds to the predicted probability of the model outputting class or value j conditioned on the i-th value of input feature w, obtained via Bayesian network inference as detailed in Equation (1). For continuous features, discretization into bins is performed to define these distinct values l, ensuring the method is applicable to both discrete and continuous input features.
Intuitively, measures the sensitivity of the output prediction probability j to changes in input feature w. A higher average absolute deviation indicates a stronger influence of that feature on the corresponding output dimension. This approach balances interpretability and computational efficiency, offering an advantage over computationally intensive global importance metrics such as Shapley values or purely statistical measures like mutual information.
Example 1.
Suppose a model has output classes, and an input feature w takes distinct values. The predicted conditional probabilities obtained via Bayesian inference for output j and input value i are
For output dimension , calculate the mean , and then compute
Similarly, for output , , and
Thus, the influence vector for input feature w is
This indicates a moderate influence of feature w on both output classes.
The computation procedure is summarized in Algorithm 2. Note that is a vector of length m, representing the influence of the w-th input feature on each output dimension, and the full influence set contains such vectors for all input features.
| Algorithm 2: Influence of input feature on output feature |
| Input: Predicted probability sets generated by Algorithm 1 for all input feature values and output dimensions |
| Output: Influence vectors for all input features |
 |
3.2. Influence-Based Input Feature Ranking
Based on the influences calculated by Algorithm 2, we rationally rank the input features and apply the pruning strategy according to the ranking when optimize DNN models. The feature ranking is based on influence scores computed for each feature. These scores reflect the strength of the relationship between each feature and the output label. While the influence scores can be sorted in descending order, it is important to note that multiple features may have similar scores. To address this, we adopt a bidirectional chain structure, which allows for more efficient adjustment of pruning thresholds. The chain structure helps to manage features with similar influence scores by allowing for more precise and dynamic pruning decisions. The ranking structure is illustrated in Figure 1.
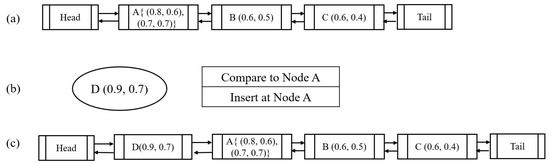
Figure 1.
Bidirectional chain structure for feature influence ranking: (a) initial chain with three nodes; (b) insertion of a new node (0.9, 0.7); (c) updated chain after insertion.
As shown in Figure 1, the new structure is a bidirectional chain. Each node in the chain represents a feature from the input dataset, and the edges encode the influence relationships between features based on their calculated influence scores. The chain allows traversal in both forward and backward directions, enabling dynamic insertion, deletion, and reordering of features during the optimization process. The structure supports efficient updates and helps identify high- or low-influence features for adaptive selection. Initially, it contains two empty nodes, i.e., a head node and a tail node, for convenient querying. When a new influence score is inserted into the chain, if the chain is empty (in addition to the head and tail nodes), a new node is created and inserted between the head and tail nodes. If the list is not empty, the comparison is conducted starting from the head node and a suitable position can be found to store the input data feature and the corresponding influence score. Taking Figure 1 as an example, the current chain has three nodes with influence scores, shown in Figure 1a. Given a new node with a score (0.9, 0.7), shown in Figure 1b, the algorithm compares new node with Node A. As the new node’s average influence score is 0.8, which is greater than the first node in the current chain, it will be inserted to the chain right after the head node, i.e., the new node becomes the first data node in the updated chain, as shown in Figure 1c. The structure enables efficient feature pruning by iteratively evaluating and removing features with minimal impact on model performance. The algorithm begins by considering the most influential feature and proceeds through the chain in both directions, quantifying the incremental contribution of each feature to the model’s overall accuracy. This process selectively eliminates irrelevant or redundant features, resulting in a more compact model that enhances both training efficiency and generalization.
Unlike traditional ranking structures such as heaps or trees, which typically allow access and updates from a single direction or require costly rebalancing during dynamic changes, our bidirectional chain enables efficient incremental updates and traversal from both ends. This dual-directional capability facilitates flexible feature pruning and re-addition during optimization without the need to reconstruct the entire ranking structure. Consequently, the bidirectional chain balances fine-grained compression control with computational efficiency. Furthermore, it naturally aligns with the sequential ordering of feature influence scores, simplifying bookkeeping during iterative model size reduction and accuracy evaluation. These advantages make the bidirectional chain particularly suitable for handling large-scale or high-dimensional datasets, where dynamic and precise pruning decisions are critical to maintaining model performance.
The chain is constructed according to the vector K output by Algorithm 2. Features and their influence scores are compared and inserted individually. The insertion mainly involves two scenarios, either creating a new node or inserting data into an existing node. In this paper, we use the head-insertion method to compare data in the nodes sequentially to extract the optimal position. For instance, if the data is greater than every item in the nodes, the pointer is moved forward. If the data is smaller than all items in the current node, since the data is necessarily larger than the previous node’s data, a new node is created in front of the current pointer node, and the data is inserted. In the third case, the data are inserted into the current node pointed by the pointer, if the values in the node are the same as the new data to be inserted. The bidirectional design allows the pointer to move backward and/or forward smoothly. By constructing the chain in this way, the time complexity for inserting data is minimized, and the input features can be sorted in ascending order of influence. The algorithm for constructing the chain is described in Algorithm 3 as follows.
Randomly pruning features without considering their influences is expensive, as excessive retraining of the model is needed, which can lead to significant computational overheads. In this paper, with the dedicated chain structure, the influence scores of features within the same node are the same. By sequentially deleting each feature stored in the chain nodes from the original model (until the threshold conditions are met), the number of retraining iterations after feature removal can be reduced. In cases of insufficient accuracy after the compression, it is easy to restore the removed features based on information stored in the chain.
| Algorithm 3: Ranking influence score. |
| Input: Model influence K |
| Output: Sorted chain of the influence of each input feature |
 |
3.3. Adaptive Input Reduction
In traditional model compression methods [41], it is necessary to determine the number of parameters to be removed and iteratively retrain the model with retained parameters, thereby ensuring the precision of the compressed model. This process imposes significant workloads on developers, as the time spent on retraining often outweighs the time spent on the compression algorithm itself. To reduce retraining time and streamline feature selection, this paper leverages influence scores stored in the bidirectional chain to guide input pruning. A developer/user can preset the thresholds for expected model size and performance, say, accuracy used in this paper. Then, the algorithm automatically determines the reduced input features and iteratively trains the updated model, until the user’s requirements are fulfilled.
We should point out that this paper focuses on reducing input data features. Thus, the current size of the model is estimated using Equation (5) to determine whether it meets the preset threshold. Accordingly, the reduction rate is the number of features removed from the input data over the total number of features in the original input.
where i denotes the number of input neurons, h denotes the number of hidden neurons, o denotes the number of output neurons, b denotes the number of bias parameters.
Features are deleted in bulk based on chain nodes. The model is then retrained, and its accuracy is calculated. If the accuracy meets the user-defined threshold, feature deletion continues until the model size cannot be further reduced. If the accuracy of the modified model meets the user’s requirements, the operation is considered successful. If the accuracy does not meet the threshold, feature refill operations are performed. While this process is closely related to feature selection, the key difference is that the primary goal is to optimize the model for efficient deployment, rather than solely improving accuracy.
The algorithm is specified in Algorithm 4. The final output of the algorithm is categorized into two cases. (a) If the algorithm successfully reduces the model size and meets both the size and accuracy requirements, the updated model and its accuracy are output. (b) If the algorithm fails to meet both requirements, the output will be the accuracy of the last model that satisfied the size threshold, prompting the developer to adjust the feature reduction strategy. This process not only reduces the computational load but also helps maintain the model’s predictive power, making it ideal for edge deployment scenarios.
| Algorithm 4: Automatic Model Optimization. |
| Input: Influence chain K; Training data; Expected model size threshold ; Expected accuracy threshold ; Initial model size ; |
| Output: Optimized model and the corresponding accuracy |
 |
Discussion: In practice, the preset compression expectation might be infeasible. For example, if the correlation between model inputs and outputs is high or if the compression rate is too aggressive, the accuracy of the compressed model can deteriorate significantly. Therefore, in situations where model compression fails, this paper will output the highest accuracy achieved that meets the compression rate, allowing users to adjust parameters more effectively.
3.4. Algorithm Complexity Analysis
The proposed adaptive compression algorithm consists of two major stages: influence score computation and feature organization.
Influence Score Computation: For each input feature, the influence on the output is estimated using a Bayesian Network. Assuming m is the number of output classes, n is the number of input features, and l is the number of possible categories per feature after discretization, the computational complexity of this step is
Feature Organization via Bidirectional Chain: After scoring, features are inserted into a bidirectional chain structure for efficient ranking and adaptive pruning. Each insertion operation requires at most time, leading to an overall complexity of for organizing all features.
Automatic Model Optimization: After sorting, features are pruned according to the expected accuracy and expected size. The complexity of this step is .
Space Complexity: The algorithm requires storing the influence scores and the bidirectional chain structure. Thus, the space complexity is , ensuring memory efficiency suitable for edge deployment.
Overall, the proposed method maintains a reasonable time and space complexity, making it well-suited for real-time edge intelligence applications.
4. Experimental Evaluation
4.1. Experiment Settings
Metrics: To validate the performance of the proposed method, we employ the following metrics that are widely used in model evaluation [42,43]. We employ the precision and recall metrics to evaluate the model’s performance. Given that accuracy, precision, and recall are inversely related, the F1-score is used as an additional metric to provide a balanced measure of precision and recall. Considering that edge devices in practical scenarios have limited resources, we also measure the memory usage, training time, and infrencing time to investigate the effectiveness and efficiency of those optimized models.
Datasets and Model Training: We employ three datasets for experiments, including the Census-Income dataset (https://doi.org/10.24432/C5GP7S), Election dataset (https://doi.org/10.24432/C5NS5M), and the Mushroom dataset (https://doi.org/10.24432/C5959T). Table 1 provides a brief overview of the datasets used in this study, including their size and application domain. For consistency, we adopt the five-fold evaluation in which 80% of data are used for training and 20% of data are used for testing. We use a classic DNN-based classification model [44] as the original model. The neural network used in our experiments follows a typical CNN architecture, consisting of several 3 × 3 convolutional layers with ReLU activations, where the number of filters increases progressively. After flattening the output of the convolutional layers, fully connected layers are applied for classification. ReLU is used as the activation function for both the convolutional and fully connected layers to introduce non-linearity. The key hyperparameters are as follows: a learning rate of 0.001 with a decay scheduler, a batch size of 32, and 50 epochs with early stopping based on validation accuracy. This model takes textual information as input and predicts the corresponding class. Initially, it is trained for 400 iterations to achieve the best performance, which is taken as the benchmark to evaluate the performance of compressed models. Without special circumstances, we set the compression rate as 60%. This compression rate is applied consistently across all methods to enable a fair comparison. Compressed models are retrained for 100 iterations to ensure convergence.

Table 1.
Overview of datasets used in this study.
Comparison Approaches: For ease of reference, we call our method proposed in this paper as influence-based method hereafter to highlight its features and strategies in input feature compression. We compare our method against three representative model compression methods, as described below. The three state-of-the-art methods represent the current advance in model compression based on structure compression, wrapper-based feature selection, and embedded-based feature selection, respectively. We also include PCA, ICA, and SVD in the evaluation. All the algorithms are implemented in Python.
- Structural Method [4]: This method focuses on compression efficiency by employing a computationally efficient pipeline for model pruning. It leverages the inherent layer-level complexities of CNNs. Specifically, layers are selected for pruning based on their contribution to reducing model complexity, particularly by evaluating their impact on floating-point operations (FLOPs). This approach ensures that the pruning process efficiently reduces the model size while maintaining performance.
- Wrapper Method [45]: This method adopts a differentiable neural input razor named i-Razor to jointly optimize the dimension search and feature selection. It learns the relative importance of different embedding regions of each feature via a differentiable model. Then, it uses a flexible pruning algorithm to filter unuseful features and derivate dimensions in the meantime.
- Embedded Method [46]: This is an end-to-end feature selection method tackling data sparsity problem. By adding sparse parameters to features and designing loss functions composed of cross-entropy loss and sparse regularization, the proposed method pays more attention to features with good prediction performance.
- Principal Component Analysis (PCA) [47]: This is a classical linear dimensionality reduction technique that addresses feature redundancy. By transforming the original correlated features into a new set of orthogonal components, PCA captures the directions of maximum variance in the data. The proposed method retains only the top principal components, thereby reducing noise and improving computational efficiency while preserving the most informative aspects of the original dataset.
- Independent Component Analysis (ICA) [48]: This is an unsupervised feature extraction technique designed to separate statistically independent components from multivariate data. By maximizing the non-Gaussianity of projections, ICA is effective in revealing underlying latent features. The method focuses on extracting independent signals, making it suitable for tasks involving source separation and informative feature identification.
- Singular Value Decomposition (SVD) [49]: This is a matrix factorization-based technique widely used for dimensionality reduction and latent semantic analysis. By decomposing the data matrix into orthogonal matrices and singular values, SVD identifies the most significant patterns in the data. Retaining only the top singular components reduces dimensionality while preserving essential structure and minimizing information loss.
Platform: We emulated an edge device with Raspberry Pi Computing Module 5, equipped with Broadcom BCM2712, Quad-core Cortex-A76 (ARM v8) 64-bit SoC @ 2.4GHz processor, 8G memory, and 32G storage.
4.2. Impact of Model Optimization Methods on Prediction Performance
Now we study the impact of our feature selection method on the prediction performance of model. To be precise, we train the original model, referred to as original model hereafter, and then apply our feature selection method to generate a optimized model, referred as influence-based method for short. According to the experiment settings discussed before, we adopt the five-fold verification strategy to separate each dataset into five pieces. We use four pieces, i.e., 80%, as the training set and the remaining one piece (20%) as the test set. All three datasets are used for evaluation and four metrics, including accuracy, precision, recall, and F1-score, are measured. As previously stated, the influence-based method removes around 60% of redundant features. For the other representative model compression methods, we compressed the original model by each method and generated the corresponding new models, namely structural method, wrapper method, and embedded method, respectively. All baseline methods were implemented carefully by following the original papers’ methodologies or using publicly available code when accessible. Hyperparameters for these baselines were tuned to the best of our ability via cross-validation within commonly recommended ranges to achieve competitive performance.
Table 2, Table 3 and Table 4 report mean ± standard deviation performance results along with p-values calculated via paired t-tests across the cross-validation folds. Table 2 compares model performance on the Census-Income dataset. We observe that the Influence-based Method yields slightly better or equivalent performance compared to the Original Model. Additionally, it achieves significantly higher scores in Accuracy, Precision, and F1 compared to other compression methods. In contrast, models compressed by Structural, Wrapper, or Embedded Methods generally show performance degradation. This observation aligns with the expectation that substantial compression often reduces performance with conventional methods, as discussed in Section 1.

Table 2.
Performance of optimized models on Census-Income dataset (mean ± std; p-values vs. Original Model).

Table 3.
Performance of optimized models on Election dataset (mean ± std; p-values vs. Original Model).

Table 4.
Performance of optimized models on Mushroom dataset (mean ± std; p-values vs. Original Model).
The same phenomena can be observed with both the Election dataset and the Mushroom dataset, as shown in Table 3 and Table 4, respectively. Interestingly, the Mushroom dataset is relatively easy for both models to give a correct classification result. Therefore, the original model achieves an almost perfect performance, e.g., 0.999 in Precision, Recall, and F1-score. There is no room to further improve the performance. However, the influence-based method proposed in this paper achieves the same performance.
The results demonstrate that the proposed input compression method preserves predictive accuracy at the stated compression rate. By definition, the p-value measures the probability of observing a difference at least as extreme as the one measured, assuming the null hypothesis of equal performance holds. A smaller p-value indicates stronger evidence against the null hypothesis. Although the number of folds is limited (five-fold cross-validation), the paired t-tests show p-values < 0.05 across all datasets, indicating statistically significant differences between the Original Model and the Influence-based Method. Importantly, the differences are very small, demonstrating that the method effectively retains predictive performance even after substantial feature reduction.
In particular, the Influence-based Method attains mean ± std scores comparable to the Original Model—e.g., Accuracy 0.853 ± 0.002 vs. 0.853 ± 0.002 on Census-Income—while reducing input features by approximately 60% (from 14 to 6 in Census-Income, from 25 to 10 in Election, and from 21 to 8 in Mushroom). This translates into lower computation time, memory usage, and data acquisition costs, which is beneficial for deployment on resource-constrained edge devices.
While the Mushroom dataset exhibits near-perfect performance due to its binary classification nature, the Influence-based Method maintains performance very close to the Original Model even on more complex datasets such as Census-Income and Election. The slightly lower performance on these more complex datasets can be attributed to factors such as higher feature dimensionality, complex feature interactions, and potential class imbalance, which naturally make learning more challenging. The small but statistically significant differences (p < 0.05) reflect natural variability rather than meaningful degradation, highlighting the method’s robustness. Addressing challenges such as complex feature interactions and potential class imbalance may further improve performance and is an important direction for future work.
Overall, the experimental results highlight that the proposed method consistently outperforms PCA, ICA, and SVD across evaluation metrics with statistically significant differences, while maintaining predictive performance nearly identical to the Original Model. This confirms both the robustness and practical applicability of the Influence-based Method for real-world scenarios requiring efficient model deployment, demonstrating that even a limited number of experimental repetitions can provide meaningful and statistically valid evidence of its effectiveness.
4.3. Model Optimization Effectiveness and Efficiency
In this section, we evaluate the impact of the bidirectional chain structure on model optimization in terms of compression time and pruning quality. For each dataset, we construct the bidirectional chain representation and apply the same compression rate as in other methods. To further validate the claimed efficiency advantage, we compare the bidirectional chain with an Influence-score Sorting strategy, where features are sorted once according to their influence scores and pruned in that order.
Unlike the one-shot sorting approach, the bidirectional chain dynamically updates the feature order after each pruning step, allowing early termination when the desired pruning performance is achieved. Table 5 reports the average compression time and number of iterations over five runs for the Census-Income, Election, and Mushroom datasets. Results show that the bidirectional chain consistently reduces both compression time and iterations by approximately 8–16% compared to influence-score sorting, indicating its advantage in scenarios requiring frequent feature reordering without sacrificing pruning quality.

Table 5.
Efficiency comparison between Influence-score Sorting and Bidirectional Chain (mean ± std over 5 runs). Percentage improvement of Bidirectional Chain over Influence-score Sorting is shown in parentheses.
Following this, we evaluate the effectiveness and efficiency of the proposed input influence-based method. For each dataset, we divide it into five small datasets, and for each small dataset, we adopt a five-fold evaluation, i.e., 80% of data are randomly selected for model training and the rest for testing. Using the same DNN architecture, a 5-fold cross-validation is conducted, where each fold is trained on a distinct subset of the training data and validated on the corresponding held-out set, denoted as Fold 1 through Fold 5. Following the procedure in previous evaluations, each fold is trained for 400 interaction steps. For instance, in the Census-Income dataset, the full dataset is partitioned into five folds; in each run, four folds (80%) are used for training and the remaining fold (20%) for testing. This process is applied independently to the Census-Income, Election, and Mushroom datasets. With the same compression rate, different compression methods are applied to the resulting models, and each compressed model is retrained for 100 iterations to ensure convergence.
The effectiveness is measured by the memory usage, the lower the better. In addition, the compression efficiency is measured by the training time taken by model retraining. For the proposed influence-based method, the time consumption also includes the time taken for calculating the influence values. We compare our input influence-based method against the structural compression method. To ensure fairness and consistency across all experiments, we conducted all tests on the same hardware and software environments, using standard libraries and frameworks for implementation. We minimized the influence of external factors, such as hardware differences, on the results. Additionally, efforts were made to follow best coding practices and utilize commonly used tools consistently across implementations to reduce variability caused by coding proficiency or tool familiarity. Nevertheless, some minor differences due to implementation details may remain.
The results on the Census-Income dataset are reported in Table 6 and Figure 2. Figure 2 (left) presents the training time of the optimized models, in which the y-axis is the time consumption with a unit of second (s). Figure 2 (right) depicts the memory usage, in which the y-axis is the amount of occupied memory with a unit of megabyte (MB). It is easy to see that the proposed input influence-based optimization method outperforms the conventional structural compression method in all cases. In particular, it takes less time to train the model and inference, and also involves less memory. For example, the average training time for folds optimized using the input influence-based method is 45.74 s, with an average memory usage of 163.2 MB. In contrast, the compressed models from each fold using the model structure compression method have an average training time of 54.84 s and an average memory usage of 173.4 MB. Therefore, the input influence-based method achieves shorter training time and lower memory usage than the model structure compression method, as it reduces both the number of model parameters and the data volume required for training and testing.

Table 6.
Time consumption and memory usage on the Census-Income dataset.
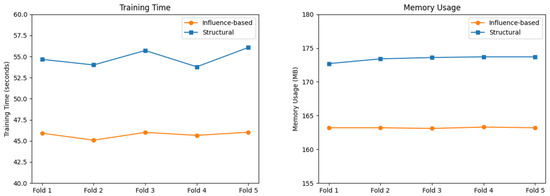
Figure 2.
Time consumption and memory usage on the Census-Income dataset.
The higher efficiency and better effectiveness allow DNNs models to be better compressed. This increases the applicability of the original models and builds up a cornerstone for them onto resource-constraint smart devices and edge devices.
Similar phenomena can be found with the Election dataset and Mushroom dataset. The results on the Election dataset are shown in Table 7 and Figure 3. In addition, the results on the Mushroom dataset are shown in Table 8 and Figure 4.

Table 7.
Time consumption and memory usage on the Election dataset.
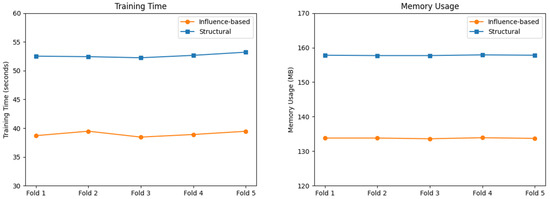
Figure 3.
Time consumption and memory usage on the Election dataset.

Table 8.
Time consumption and memory usage on the Mushroom dataset.
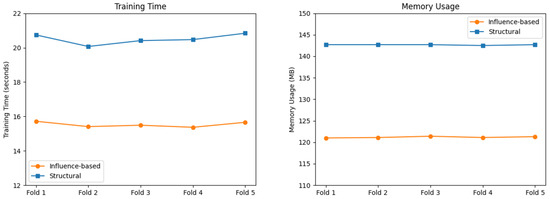
Figure 4.
Time consumption and memory usage on the Mushroom dataset.
According to Table 7 and Figure 3, the averaged training time for models optimized by the input influence-based method is 38.99 s, while for models compressed by the model structure compression method is 52.61 s. The average memory usage during runtime for the input influence-based method is 133.8 MB, compared to 157.8 MB for the model structure compression method. Therefore, the proposed method outperforms the structural model compression method again in training and memory usage.
With Table 8 and Figure 4, it is easy to see that the models optimized using the input influence-based method have less training and lower memory usage compared to those models compressed via structural compression method. The results for Folds 1–5 within each dataset are closely aligned, indicating that the proposed method maintains stable performance across different random data splits. The small variations observed reflect the consistency of the compression algorithm, rather than insensitivity to changes in the input.
4.4. Comparison with Feature Selection Models
In this section, we compare the effectiveness between the proposed input influence-based method and traditional feature selection-based methods, including the wrapper method and embedded method. For each method, we compare its training time and inferencing time. We also report the influence values of each feature calculated by different methods. Please note that we sort those features in descending order according to their influence values.
The results on the Census-Income dataset are shown in Table 9.

Table 9.
Time consumption and feature ranking on the Census-Income dataset.
The time consumption of the influence-based method is lower than that of the other two methods, and the optimized model achieves the best prediction performance on all three datasets. Notably, on the Census-Income dataset, the influence-based method achieves a 33% reduction in inference time compared to the wrapper method (38 ms vs. 57 ms), and a 12% improvement compared to the embedded method (38 ms vs. 43 ms). We can see from Table 9 that different feature selection methods usually priorities different attributes/features. For example, both the embedded method and the influence-based method assign the highest influence value to feature 10. In contrast, the wrapper method takes feature 13 as the most important feature.
For the Election dataset, the time consumption and ordered features are shown in Table 10. It is easy to see that the influence-based method again spends the least time and the inference time reductions reach up to 35%. The influence-based method takes a slightly longer time than the embedding method. The wrapper method has a significantly longer runtime compared to the other methods.

Table 10.
Time consumption and feature ranking on the Election dataset.
For the Mushroom dataset, the time consumption of the three methods is shown in Table 11. Without surprise, our influence-based method takes a shorter time than the other two methods.

Table 11.
Time consumption and feature ranking on the Mushroom dataset.
The time consumption of the three methods is impacted by the number of features and the size of the datasets. For example, when dealing with smaller datasets, the runtime of the influence-based method is slightly longer than the other two methods. However, as the number of features and dataset size increase, the wrapper method’s runtime becomes significantly longer, highlighting its computational bottleneck.
These inference time results clearly illustrate the lightweight nature of the proposed method, which stems from its early-stage feature pruning strategy that eliminates redundant inputs prior to model training and inference. This preprocessing approach avoids the computational burden typically associated with wrapper methods (which involve repeated model evaluations) and embedded methods (which rely on internal regularization terms and iterative optimization). More importantly, the method’s ability to reduce both training and inference costs without compromising accuracy makes it especially suitable for edge computing environments, where computational resources are limited and service latency is critical. Edge devices such as IoT sensors, mobile wearables, and industrial controllers benefit significantly from this input-centric compression, resulting in smaller memory footprints, lower power consumption, and faster decision-making cycles.
Based on these experimental results, the proposed method can effectively reduce input features and thus model parameters. As a result, it reduces the required training data scale, improves training speed, and lowers memory usage of the compressed model. Compared to embedded and wrapper methods, the proposed method achieves a balance between runtime and accuracy, providing efficient model reduction with minimal time cost. However, in the datasets used—especially Census-Income and Mushroom—there are many categorical and redundant variables with limited or no positive contributions to prediction performance. Through the experimental results, we see our influence-based method can identify and remove such noisy, low-influence features, resulting in better performance compared with other state-of-the-art methods.
In addition to these performance improvements, the feature rankings produced by our method offer practical insights into the relative importance of each input feature, which can be valuable for feature engineering and understanding the underlying data. However, the effectiveness and interpretation of these rankings depend on specific dataset characteristics. Moreover, differences in dataset characteristics—such as feature dimensionality, class imbalance, and correlations among features—can significantly affect the performance and stability of feature selection methods. A deeper investigation into how these factors influence our method’s effectiveness is essential for adapting it to diverse real-world scenarios. We consider this an important direction for future work to enhance the robustness and applicability of the proposed approach.
4.5. Case Study: Feature Subsets Selected on Census-Income Dataset
To clarify differences between feature selection methods, we present a case study on the Census-Income dataset with 14 features. The top 40% most important features are retained. Table 12 shows that different methods select distinct features due to their unique selection strategies.

Table 12.
Top 6 selected features by different methods on the Census-Income dataset.
Table 12 presents the top six features selected by the proposed influence-based method alongside those identified by baseline approaches for the Census-Income dataset, with feature indices provided in parentheses for clarity. While no additional quantitative evaluation of individual feature importance was performed, the differences in selected features provide valuable qualitative insights into the distinct selection criteria of each method. Our Bayesian-driven influence scoring prioritizes economically significant and semantically interpretable attributes—such as capital-gain, capital-loss, and education-num—which are directly relevant to income prediction and serve as robust indicators of an individual’s earning potential and financial status.
Several features chosen by alternative methods are notably absent from our selection. For example, fnlwgt (final weight), selected by the wrapper method, mainly serves population-level statistical adjustment and lacks direct predictive relevance at the individual level, potentially introducing noise. Similarly, features like age and sex, selected by embedded methods, often exhibit weak or dataset-specific correlations with income and may have nonlinear or context-dependent effects. Such characteristics reduce their importance within the class-conditional influence framework, which emphasizes discriminative power over general correlation. This contrast underscores the advantage of our influence-driven selection strategy: rather than relying on broadly correlated or demographically descriptive features, it focuses on those with strong, class-specific discriminative capacity. Consequently, the influence-based method yields a more compact and relevant feature subset, enhancing model performance and efficiency by excluding variables that increase dimensionality without meaningful classification contribution.
5. Conclusions and Future Work
In this paper, we proposed a feature reduction method aimed at optimizing model performance by eliminating less influential input features. Specifically, our approach quantifies the influence of each feature on the model output using a Bayesian network formulation. A bidirectional chain structure was introduced to store and rank these influence scores efficiently. Leveraging this structure, we developed an adaptive algorithm that automatically prunes input features under predefined constraints on model size and predictive accuracy. Experimental results demonstrate that our method can achieve up to 60% dimensionality reduction with minimal performance degradation. This input-centric optimization emphasizes runtime memory efficiency, making it particularly well-suited for edge devices with constrained computational resources where input overhead is a critical bottleneck. One limitation of our current study is that the observed training time might be influenced by implementation-level factors. For instance, differences in coding proficiency, optimization technique usage, and familiarity with development tools could potentially confound the results. As such, partial observed performance gains might stem from the implementer’s skills. This poses threats to the internal validity of the experimental evaluation reported in Section 4.
This paper focuses on introducing a general-purpose, input-centric compression method applicable across different model architectures and tasks. The specific performance in real-world industrial scenarios will depend on the choice of downstream model and task requirements. As future work, we plan to integrate and validate the proposed method in representative Industry 4.0 applications, such as visual defect detection on manufacturing lines and energy consumption prediction at the edge, to further demonstrate its feasibility and benefits in practical deployments.
While the method demonstrates strong performance across multiple structured and multivariate datasets, we acknowledge several limitations. First, the algorithm may be sensitive to highly correlated features, which can affect the optimality of the selected feature subset. This study evaluates each feature’s influence independently, without explicitly modeling correlations among input features. Consequently, multicollinearity may cause redundant features to be retained or informative ones pruned. Future work could address this by incorporating correlation-based penalties, mutual information analysis, or correlation-aware regularization to improve feature selection robustness. To demonstrate broader applicability, the method should also be tested on regression tasks, evaluating metrics to verify that pruning preserves predictive accuracy and generalizes across different problem types. Second, the accuracy and reduction thresholds require empirical tuning, potentially limiting generalizability. Third, the method has so far been validated primarily on tabular datasets. We plan to evaluate the influence-based selection method across more datasets, including regression problems, high-dimensional text, time series, and sensor data, to further examine its applicability and limitations. In particular, we aim to better understand how the method performs under varying levels of feature redundancy and noise. However, its applicability to other data modalities—such as image, sequential, or high-dimensional continuous data—remains an open question. For such domains, additional preprocessing steps, including feature discretization or deep feature extraction, may be required to support reliable and interpretable influence estimation.
For future work, we plan to broaden the experimental scope to include more complex data types (e.g., images, time series, and sensor data such as ECG, EMG, and human activity recognition), which are particularly relevant in edge intelligence scenarios. We also intend to apply the method to more complex neural network architectures, like RNNs and transformer-based models. Moreover, we will explore its generalizability across a wider range of machine learning algorithms and problem types to assess the robustness and transferability of the proposed method across different learning paradigms. To enhance algorithm efficiency, we aim to reduce retraining overhead and memory usage. A theoretical analysis of convergence and optimality is also planned. Finally, to strengthen evaluation, we will incorporate more recent and diverse baselines—such as input-based pruning methods and AutoML tools—and include statistical analyses (e.g., standard deviations, confidence intervals) to assess the significance of observed improvements. This will help clarify whether performance gains are consistent and robust. We will also continue to study trade-offs between feature reduction and model accuracy, contributing to a more nuanced understanding of practical deployment in real-world scenarios.
Author Contributions
Conceptualization, J.G. and B.Z.; methodology, software, H.Z.; validation, H.Z., X.W., and B.Z.; formal analysis, H.Z.; investigation, resources, data curation, writing—original draft preparation, H.Z. and X.W.; writing—review and editing, J.G. and B.Z.; visualization, H.Z. and X.W.; supervision, J.G. and B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, L.; Xiao, F.; Li, B.; Zhou, J.; Xu, X.; Yang, Y. Availability-Aware Revenue-Effective Application Deployment in Multi-Access Edge Computing. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 1268–1280. [Google Scholar] [CrossRef]
- Li, B.; He, Q.; Chen, F.; Lyu, L.; Bouguettaya, A.; Yang, Y. EdgeDis: Enabling fast, economical, and reliable data dissemination for mobile edge computing. IEEE Trans. Serv. Comput. 2023, 17, 1504–1518. [Google Scholar] [CrossRef]
- Choudhary, T.; Mishra, V.; Goswami, A.; Sarangapani, J. A comprehensive survey on model compression and acceleration. Artif. Intell. Rev. 2020, 53, 5113–5155. [Google Scholar] [CrossRef]
- Zawish, M.; Davy, S.; Abraham, L. Complexity-driven model compression for resource-constrained deep learning on edge. IEEE Trans. Artif. Intell. 2024, 5, 3886–3901. [Google Scholar] [CrossRef]
- Guo, J.; Ouyang, W.; Xu, D. Multi-dimensional pruning: A unified framework for model compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1508–1517. [Google Scholar]
- Gong, C.; Chen, Y.; Lu, Y.; Li, T.; Hao, C.; Chen, D. VecQ: Minimal loss DNN model compression with vectorized weight quantization. IEEE Trans. Comput. 2020, 70, 696–710. [Google Scholar] [CrossRef]
- Dantas, P.V.; Sabino da Silva, W., Jr.; Cordeiro, L.C.; Carvalho, C.B. A comprehensive review of model compression techniques in machine learning. Appl. Intell. 2024, 54, 11804–11844. [Google Scholar] [CrossRef]
- Gupta, M.; Agrawal, P. Compression of deep learning models for text: A survey. ACM Trans. Knowl. Discov. Data (TKDD) 2022, 16, 1–55. [Google Scholar] [CrossRef]
- Howard, A.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Sankaranarayanan, R.; Senthilkumar, M. Optimized twin spatio-temporal convolutional neural network with squeezenet transfer learning model for cancer miRNA biomarker classification. Appl. Soft Comput. 2024, 167, 112270. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Mehta, S.; Rastegari, M.; Shapiro, L.; Hajishirzi, H. Espnetv2: A light-weight, power efficient, and general purpose convolutional neural network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 9190–9200. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning structured sparsity in deep neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 2082–2090. [Google Scholar]
- Guo, Y.; Yao, A.; Chen, Y. Dynamic network surgery for efficient dnns. Adv. Neural Inf. Process. Syst. 2016, 29, 1387–1395. [Google Scholar]
- Ba, J.; Caruana, R. Do deep nets really need to be deep? Adv. Neural Inf. Process. Syst. 2014, 27, 2654–2662. [Google Scholar]
- Saha, R.; Srivastava, V.; Pilanci, M. Matrix compression via randomized low rank and low precision factorization. Adv. Neural Inf. Process. Syst. 2023, 36, 18828–18872. [Google Scholar]
- Lu, W.; Jiang, Y.; Jing, P.; Chu, J.; Fan, F. A novel channel pruning approach based on local attention and global ranking for cnn model compression. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; IEEE: New York, NY, USA, 2023; pp. 1433–1438. [Google Scholar]
- Bhalgaonkar, S.; Munot, M.; Anuse, A. Model compression of deep neural network architectures for visual pattern recognition: Current status and future directions. Comput. Electr. Eng. 2024, 116, 109180. [Google Scholar] [CrossRef]
- Zhang, W.; Biswas, G.; Zhao, Q.; Zhao, H.; Feng, W. Knowledge distilling based model compression and feature learning in fault diagnosis. Appl. Soft Comput. 2020, 88, 105958. [Google Scholar] [CrossRef]
- Marco, V.S.; Taylor, B.; Wang, Z.; Elkhatib, Y. Optimizing deep learning inference on embedded systems through adaptive model selection. ACM Trans. Embed. Comput. Syst. (TECS) 2020, 19, 1–28. [Google Scholar] [CrossRef]
- Wang, J.; Bai, H.; Wu, J.; Cheng, J. Bayesian automatic model compression. IEEE J. Sel. Top. Signal Process. 2020, 14, 727–736. [Google Scholar] [CrossRef]
- Kuzmin, A.; Nagel, M.; Van Baalen, M.; Behboodi, A.; Blankevoort, T. Pruning vs. quantization: Which is better? Adv. Neural Inf. Process. Syst. 2023, 36, 62414–62427. [Google Scholar]
- Logeswari, G.; Roselind, J.D.; Tamilarasi, K.; Nivethitha, V. A Comprehensive Approach to Intrusion Detection in IoT Environments Using Hybrid Feature Selection and Multi-Stage Classification Techniques. IEEE Access 2025, 13, 24970–24987. [Google Scholar] [CrossRef]
- Del Ser, J.; Martinez-Seras, A.; Bilbao, M.N.; Lobo, J.L.; Laña, I.; Herrera, F. Balancing Performance, Efficiency and Robustness in Open-World Machine Learning via Evolutionary Multi-objective Model Compression. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–8. [Google Scholar]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
- Li, H.; Ren, X.; Yang, Z. Data-driven Bayesian network for risk analysis of global maritime accidents. Reliab. Eng. Syst. Saf. 2023, 230, 108938. [Google Scholar] [CrossRef]
- Shi, W.; Mena, C. Supply chain resilience assessment with financial considerations: A Bayesian network-based method. IEEE Trans. Eng. Manag. 2021, 70, 2241–2256. [Google Scholar] [CrossRef]
- Guo, D.; Yang, W.; Tao, F.; Song, B.; Liu, H.; Sun, L.; Wang, J. Multiple elastic networks with time delays for early fault detection and prognostics. IEEE Access 2020, 8, 129387–129396. [Google Scholar] [CrossRef]
- Yan, H.; Wang, F.; He, D.; Wang, Q. An operational adjustment framework for a complex industrial process based on hybrid Bayesian network. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1699–1710. [Google Scholar] [CrossRef]
- Hunte, J.L.; Neil, M.; Fenton, N.E. A hybrid Bayesian network for medical device risk assessment and management. Reliab. Eng. Syst. Saf. 2024, 241, 109630. [Google Scholar] [CrossRef]
- Greenberg, A.; Hamilton, J.; Maltz, D.; Patel, P. The Cost of a Cloud: Research Problems in Data Center Networks. Comput. Commun. Rev. 2009, 39, 68–73. [Google Scholar] [CrossRef]
- Satyanarayanan, M.; Bahl, P.; Caceres, R.; Davies, N. The Case for VM-Based Cloudlets in Mobile Computing. IEEE Pervasive Comput. 2009, 8, 14–23. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R. Fog Computing and its Role in the Internet of Things. In Proceedings of the MCC Workshop on Mobile Cloud Computing, Helsinki, Finland, 17 August 2012; pp. 13–16. [Google Scholar] [CrossRef]
- Hao, H.; Xu, C.; Zhang, W.; Yang, S.; Muntean, G.M. Joint Task Offloading, Resource Allocation, and Trajectory Design for Multi-UAV Cooperative Edge Computing With Task Priority. IEEE Trans. Mob. Comput. 2024, 23, 8649–8663. [Google Scholar] [CrossRef]
- Li, B.; He, Q.; Chen, F.; Jin, H.; Xiang, Y.; Yang, Y. Auditing Cache Data Integrity in the Edge Computing Environment. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1210–1223. [Google Scholar] [CrossRef]
- Cui, G.; He, Q.; Li, B.; Xia, X.; Chen, F.; Jin, H.; Xiang, Y.; Yang, Y. Efficient Verification of Edge Data Integrity in Edge Computing Environment. IEEE Trans. Serv. Comput. 2022, 15, 3233–3244. [Google Scholar] [CrossRef]
- Li, E.; Zhou, Z.; Chen, X. Edge intelligence: On-demand deep learning model co-inference with device-edge synergy. In Proceedings of the 2018 Workshop on Mobile Edge Communications, Budapest, Hungary, 20 August 2018; pp. 31–36. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient inference. arXiv 2016, arXiv:1611.06440. [Google Scholar]
- Hou, Z.; Qin, M.; Sun, F.; Ma, X.; Yuan, K.; Xu, Y.; Chen, Y.K.; Jin, R.; Xie, Y.; Kung, S.Y. Chex: Channel exploration for CNN model compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12287–12298. [Google Scholar]
- He, Q.; Li, B.; Chen, F.; Grundy, J.; Xia, X.; Yang, Y. Diversified third-party library prediction for mobile app development. IEEE Trans. Softw. Eng. 2020, 48, 150–165. [Google Scholar] [CrossRef]
- Li, B.; He, Q.; Chen, F.; Xia, X.; Li, L.; Grundy, J.; Yang, Y. Embedding app-library graph for neural third party library recommendation. In Proceedings of the 29th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Athens, Greece, 23–28 August 2021; pp. 466–477. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, B.; He, H.; Sheng, D.; Wang, K.; Xiao, L.; Cao, H. I-Razor: A differentiable neural input razor for feature selection and dimension search in dnn-based recommender systems. IEEE Trans. Knowl. Data Eng. 2023, 36, 4736–4749. [Google Scholar] [CrossRef]
- Tao, M.; Fu, X.; Lin, Y.; Wang, Y.; Yao, Z.; Shi, S.; Gui, G. Resource-constrained specific emitter identification using end-to-end sparse feature selection. In Proceedings of the GLOBECOM 2023-2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; IEEE: New York, NY, USA, 2023; pp. 6067–6072. [Google Scholar]
- Shlens, J. A tutorial on principal component analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, J.; He, K.; Sun, J. Accelerating very deep convolutional networks for classification and detection. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1943–1955. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).