An Efficient Ciphertext-Policy Decryptable Attribute-Based Keyword Search Scheme with Dynamic Attribute Support
Abstract
1. Introduction
1.1. Our Contributions
- We introduce a commit-to-point mechanism that supports dynamic and efficient attribute set expansion without reinitialising public parameters.
- We design a CP-DABKS scheme using Type-3 pairings to improve computation efficiency and reduce ciphertext size compared to Type-1 pairing-based designs.
- We implement the proposed CP-DABKS scheme and evaluate it on the Enron email dataset, demonstrating its practical feasibility and performance benefits in real-world scenarios.
1.2. Organisation of the Paper
2. Related Work
3. Preliminaries
3.1. Bilinear Pairings
- Bilinearity: For all and valid group elements, the map is linear in each argument, i.e., .
- Non-degeneracy:
- -
- Type-1: For generators , in .
- -
- Type-3: For generators , , in .
This ensures the pairing does not map all input pairs to the identity element. - Efficient Computability: The function can be evaluated efficiently for any inputs from the appropriate groups.
3.2. Access Structure
3.3. Linear Secret Sharing Scheme
3.4. Pedersen Commitment Scheme
- : The parameters are published.
- : To commit to a value , the committer selects a random and computesThe output C serves as the commitment, which conceals both m and r.
- : To reveal the commitment, the committer discloses , and the verifier accepts ifholds.
3.5. Discrete Logarithm (DLOG) Assumption
3.6. Computational Bilinear Diffie–Hellman (CBDH) Assumption
3.7. Decisional Bilinear Diffie–Hellman (DBDH) Assumption
3.8. Division Decisional Diffie–Hellman (DDDH) Assumption
3.9. Decisional q-Parallel Bilinear Diffie–Hellman Exponent (q-BDHE) Assumption
4. CP-DABKS Scheme Definition and Security Definition
4.1. CP-DABKS Scheme Definition
- Setup: Executed by the KGC, this algorithm initialises the system on input of the security parameter and the initial attribute universe U. It outputs the public configuration parameters and the master secret key .
- Key Generation: Each entity generates its own cryptographic keys according to its role. The sender derives a pair from ; the cloud server produces using the same parameters; and for each receiver with attribute set , the KGC issues an attribute secret key and an individual key pair based on and .
- Encryption: Given a message m, a keyword w, and an access policy , the sender uses to produce the ciphertext , which embeds both the encrypted message and keyword components consistent with the specified policy.
- Trapdoor Generation: A receiver possessing an attribute key computes a search token for keyword w using , enabling the cloud server to perform keyword testing without revealing w.
- Testing: The cloud server, on input , the token , and ciphertext , verifies whether the receiver’s attribute set satisfies the policy and whether the keyword matches. If successful, it returns a partially decrypted ciphertext ; otherwise it outputs ⊥.
- Decryption: The receiver applies its private key to to recover the plaintext message m.
4.2. Security Definition
4.2.1. CP-ABE-CPA Security
- Initialisation: The adversary commits to a challenge access structure .
- Setup: The challenger executes the Setup algorithm and provides the public system parameters to .
- Query Phase 1: adaptively issues secret key queries for sets of attributes S. The challenger responds only if S does not satisfy .
- Challenge: The adversary provides two equal-length messages, and . The challenger randomly selects , encrypts with respect to , and returns the ciphertext to the adversary .
- Query Phase 2: This phase is a repetition of Phase 1, under the same constraint.
- Guess: The adversary outputs its guess for .
4.2.2. IND-CPA Security
- Setup: The challenger initialises the system, generating all common parameters and key pairs. The adversary, acting as the cloud server, submits its public key to the challenger.
- Query Phase 1: The adversary adaptively requests the encryption of any messages of its choice and receives the corresponding ciphertexts from the challenger.
- Challenge: The adversary selects two distinct messages and of identical length. The challenger samples a random bit encrypts , and outputs the corresponding challenge ciphertext.
- Query Phase 2: The adversary may issue further encryption queries, as in Phase 1, but is forbidden from querying the challenge messages or .
- Guess: The adversary outputs its guess for .
4.2.3. IND-KGA Security
- Setup: The challenger initialises the system parameters. The adversarial cloud server generates its key pair and provides the public component to the challenger.
- Query Phase 1: The adversary may request trapdoors for arbitrary keywords w and obtain ciphertexts for chosen terms. The challenger answers all such queries faithfully.
- Challenge: The adversary selects two keywords and , after which the challenger samples a random bit and issues the ciphertext associated with .
- Query Phase 2: The adversary can continue to make trapdoor and ciphertext queries for any keyword, with the sole restriction that it cannot query or .
- Guess: The adversary outputs its guess for .
4.2.4. IND-CKA Security
- Setup and Query Phase 1: Identical to the setup and first query phase defined in the IND-KGA game.
- Challenge: The adversary chooses two challenge keywords, and . The challenger then samples a random bit and returns the ciphertext corresponding to the keyword .
- Query Phase 2: The adversary may again issue queries as in Phase 1, with the exception that it cannot request trapdoors or ciphertexts for the challenge keywords or .
- Guess: The adversary outputs its guess for .
5. CP-DABKS Scheme with Dynamic Attribute Universe
5.1. Commit-to-Point
5.2. The Proposed CP-DABKS Construction in Type-3 Pairings
- Setup: The KGC initialises the scheme by taking the security parameter and the initial attribute universe U as inputs, then performing the following setup procedure:
- Choose cyclic groups , , and , each of prime order p.
- Define generators and .
- Establish a bilinear pairing .
- Sample random elements and .
- For each attribute i in the universe U, select a random exponent .
- Define two cryptographic hash functions: and for a suitable key length k.
- The common parameters are published as:
- The Master Secret Key is set to .
- KeyGenS : A data sender generates its key pair by picking a random and setting the public key and the private key .
- KeyGenCS : The cloud server selects a random , defining its public key as and its private key as .
- KeyGenR : Given a receiver whose attribute set is , the KGC performs the following:
- Choose two random values .
- Compute the primary decryption component .
- Compute .
- For every attribute , generate an attribute-specific key .
- The receiver’s attribute-based secret key is .
- The receiver independently produces a personal key pair, where the public key is and the secret key is .
- Encrypt : To encrypt a message m with a keyword w under an LSSS access policy , where M is an matrix, the sender executes:
- Policy Encryption:
- -
- Choose a random vector to share the secret s.
- -
- For each row i of M (), select a random .
- -
- Compute the policy ciphertext components:In this construction, , where denotes the i-th row of the access matrix M. Let .
- Message Encryption:
- -
- Pick a random .
- -
- Compute the message ciphertext:Let .
- Keyword Encryption:
- -
- Select a random .
- -
- Compute the keyword ciphertext:
Let . - The resulting ciphertext is subsequently transmitted to the cloud server for storage.
- Trapdoor : The receiver computes a search trapdoor corresponding to the keyword as follows:where is a secure public key encryption algorithm. The generated trapdoor is transmitted to the cloud server, while the secret key remains encrypted using the server’s public key .
- Test : Upon receiving a trapdoor, the cloud server:
- Decrypts using its private key to recover the receiver’s .
- It verifies whether the attributes embedded in fulfil the access policy . If not, it aborts and outputs ⊥.
- Let be the set of indices for which the attributes are held by the receiver, and let denote a collection of reconstruction coefficients satisfying .
- Computes:
- Then, it verifies if the keyword matches by checking:If the equation holds, the server identifies the message ciphertext and computes a partial ciphertext which it returns to the receiver. Otherwise, it outputs ⊥.
- Decrypt : The receiver finalises the decryption using its private key :This step recovers the original plaintext message.
5.3. Correctness
6. Security Analysis
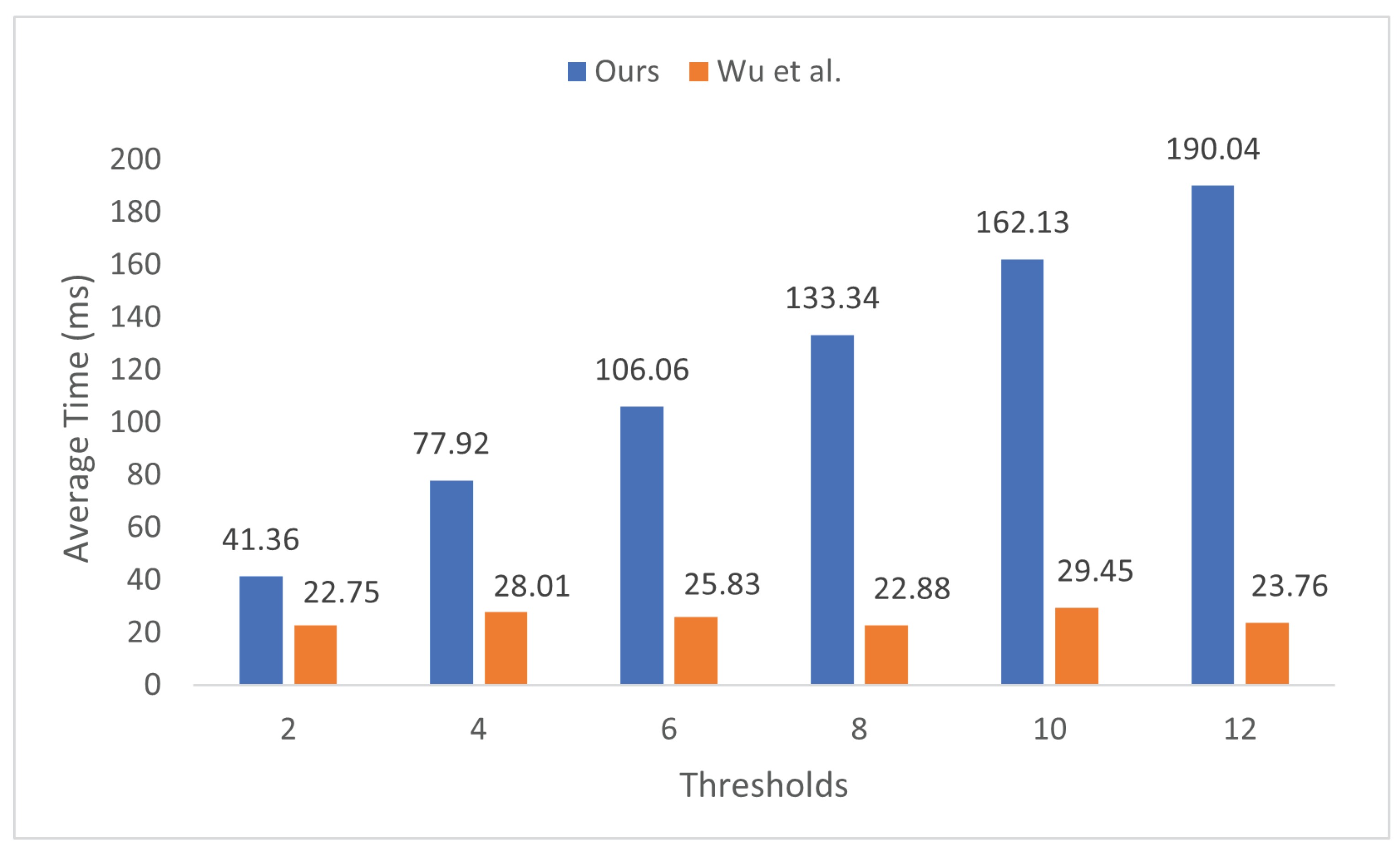
7. Performance Analysis
7.1. Trade-Offs in Applicable Scenarios
7.2. Limitations and Reproducibility Considerations
8. Future Work
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Byun, J.W.; Rhee, H.S.; Park, H.A.; Lee, D.H. Off-line keyword guessing attacks on recent keyword search schemes over encrypted data. In Workshop on Secure Data Management; Springer: Berlin/Heidelberg, Germnay, 2006; pp. 75–83. [Google Scholar]
- Yau, W.C.; Heng, S.H.; Goi, B.M. Off-line keyword guessing attacks on recent public key encryption with keyword search schemes. In International Conference on Autonomic and Trusted Computing; Springer: Berlin/Heidelberg, Germnay, 2008; pp. 100–105. [Google Scholar]
- Yang, K.; Jia, X.; Ren, K. Attribute-based fine-grained access control with efficient revocation in cloud storage systems. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 8–10 May 2013; pp. 523–528. [Google Scholar]
- Sun, W.; Yu, S.; Lou, W.; Hou, Y.T.; Li, H. Protecting your right: Verifiable attribute-based keyword search with fine-grained owner-enforced search authorization in the cloud. IEEE Trans. Parallel Distrib. Syst. 2014, 27, 1187–1198. [Google Scholar] [CrossRef]
- Guo, L.; Li, Z.; Yau, W.C.; Tan, S.Y. A decryptable attribute-based keyword search scheme on eHealth cloud in Internet of Things platforms. IEEE Access 2020, 8, 26107–26118. [Google Scholar] [CrossRef]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (SP’07), Berkeley, CA, USA, 20–23 May 2007; pp. 321–334. [Google Scholar]
- Galbraith, S.D.; Paterson, K.G.; Smart, N.P. Pairings for cryptographers. Discret. Appl. Math. 2008, 156, 3113–3121. [Google Scholar] [CrossRef]
- Hwang, Y.H.; Lee, P.J. Public key encryption with conjunctive keyword search and its extension to a multi-user system. In International Conference on Pairing-Based Cryptography; Springer: Berlin/Heidelberg, Germnay, 2007; pp. 2–22. [Google Scholar]
- Wang, C.; Li, W.; Li, Y.; Xu, X. A ciphertext-policy attribute-based encryption scheme supporting keyword search function. In Proceedings of the Cyberspace Safety and Security: 5th International Symposium, CSS 2013, Zhangjiajie, China, 13–15 November 2013; Proceedings 5. Springer: Berlin/Heidelberg, Germnay, 2013; pp. 377–386. [Google Scholar]
- Miao, Y.; Ma, J.; Liu, X.; Wei, F.; Liu, Z.; Wang, X.A. m2-ABKS: Attribute-based multi-keyword search over encrypted personal health records in multi-owner setting. J. Med. Syst. 2016, 40, 246. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Ma, J.; Liu, X.; Li, X.; Jiang, Q.; Zhang, J. Attribute-based keyword search over hierarchical data in cloud computing. IEEE Trans. Serv. Comput. 2017, 13, 985–998. [Google Scholar] [CrossRef]
- He, H.; Zhang, J.; Li, P.; Jin, Y.; Zhang, T. A lightweight secure conjunctive keyword search scheme in hybrid cloud. Future Gener. Comput. Syst. 2019, 93, 727–736. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, J.; Xiong, Y.; Ou, L.; Li, F.; Liao, S.; Li, K. CP-ABSE: A ciphertext-policy attribute-based searchable encryption scheme. IEEE Access 2019, 7, 5682–5694. [Google Scholar] [CrossRef]
- Cao, M.; Wang, L.; Qin, Z.; Lou, C. A Lightweight Fine-Grained Search Scheme over Encrypted Data in Cloud-Assisted Wireless Body Area Networks. Wirel. Commun. Mob. Comput. 2019, 2019, 9340808. [Google Scholar] [CrossRef]
- Cui, J.; Zhou, H.; Xu, Y.; Zhong, H. OOABKS: Online/offline attribute-based encryption for keyword search in mobile cloud. Inf. Sci. 2019, 489, 63–77. [Google Scholar] [CrossRef]
- Miao, Y.; Liu, X.; Choo, K.K.R.; Deng, R.H.; Li, J.; Li, H.; Ma, J. Privacy-preserving attribute-based keyword search in shared multi-owner setting. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1080–1094. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, H.; Nie, X.; Zhang, Y.; Wu, P. On the security of privacy-preserving attribute-based keyword search in shared multi-owner setting. IEEE Trans. Dependable Secur. Comput. 2019, 18, 2518–2519. [Google Scholar] [CrossRef]
- Pan, X.; Li, F. Public-key authenticated encryption with keyword search achieving both multi-ciphertext and multi-trapdoor indistinguishability. J. Syst. Archit. 2021, 115, 102075. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Lu, L. Privacy-Preserving Attribute-Based Keyword Search with Traceability and Revocation for Cloud-Assisted IoT. Secur. Commun. Netw. 2021, 2021, 9929663. [Google Scholar] [CrossRef]
- Yan, L.; Wang, G.; Yin, T.; Liu, P.; Feng, H.; Zhang, W.; Hu, H.; Pan, F. Attribute-based searchable encryption: A survey. Electronics 2024, 13, 1621. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Y.; Luo, Y.; Dong, S.; Li, T. VR-PEKS: A verifiable and resistant to keyword guess attack public key encryption with keyword search scheme. Appl. Sci. 2023, 13, 4166. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Ma, S.; Xiao, M.; Huang, Q. Revocable and verifiable weighted attribute-based encryption with collaborative access for electronic health record in cloud. Cybersecurity 2024, 7, 18. [Google Scholar] [CrossRef]
- Khan, S.; Khan, S.; Waheed, A.; Mehmood, G.; Zareei, M.; Alanazi, F. An optimized dynamic attribute-based searchable encryption scheme. PLoS ONE 2024, 19, e0268803. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Chen, L.; Tian, Y.; Manulis, M.; Liu, S. FEASE: Fast and Expressive Asymmetric Searchable Encryption. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 2545–2562. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Ben, L. On The Implementation On Pairing-Based Cryptosystems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2007. [Google Scholar]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Advances in Cryptology–EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Proceedings 24. Springer: Berlin/Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar]
- Lewko, A.; Okamoto, T.; Sahai, A.; Takashima, K.; Waters, B. Fully secure functional encryption: Attribute-based encryption and (hierarchical) inner product encryption. In Proceedings of the Advances in Cryptology–EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Proceedings 29. Springer: Berlin/Heidelberg, Germany, 2010; pp. 62–91. [Google Scholar]
- Pedersen, T.P. Non-interactive and information-theoretic secure verifiable secret sharing. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1991; pp. 129–140. [Google Scholar]
- Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996; Volume 17. [Google Scholar]
- Krawczyk, H.; Rabin, T. Chameleon hashing and signatures. Cryptol. Eprint Arch. 1998. Available online: https://eprint.iacr.org/1998/010 (accessed on 28 August 2025).
- Abe, M.; Hoshino, F.; Ohkubo, M. Design in type-i, run in type-iii: Fast and scalable bilinear-type conversion using integer programming. In Proceedings of the Advances in Cryptology–CRYPTO 2016: 36th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Proceedings, Part III 36. Springer: Berlin/Heidelberg, Germany, 2016; pp. 387–415. [Google Scholar]
- Wu, Y.; Li, X.; Liu, Z. Attribute-based keyword searchable encryption scheme for multi-authority in cloud storage. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 933–939. [Google Scholar]
- Klimt, B.; Yang, Y. The Enron corpus: A new dataset for email classification research. In Proceedings of the 15th European Conference on Machine Learning (ECML 2004), Pisa, Italy, 20–24 September 2004; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Oard, D.; Webber, W.; Kirsch, D.A.; Golitsynskiy, S. Avocado Research Email Collection; LDC2015T03; Web Download; Linguistic Data Consortium: Philadelphia, PA, USA, 2015. [Google Scholar] [CrossRef]
- Amazon Web Services, Inc. AWS SDK for Java. 2023. Available online: https://aws.amazon.com/sdk-for-java/ (accessed on 12 October 2023).
| Word | Frequency |
|---|---|
| Forwarded | 362 |
| I | 314 |
| Hey | 138 |
| Please | 109 |
| Can | 94 |
| Andy | 80 |
| You | 74 |
| Hello | 66 |
| How | 58 |
| Thanks | 58 |
| Just | 54 |
| Are | 50 |
| Dave | 50 |
| What | 48 |
| Jeff | 48 |
| Scheme | Sender/ Cloud Server Key Pair | Receiver Key Pair | Ciphertext | Trapdoor | |
|---|---|---|---|---|---|
| Guo et al. (2020) [5] | |||||
| 9222 + 1537 bits | 4611 bits | 5379 + 1537 bits | 12,296 + 3074l bits | 6148 bits | |
| Wu et al. (2022) [33] | |||||
| 6916 + 1537 bits | 4611 bits | 5379 + 3074 bits | 6148 + 1537l bits | 3074 bits | |
| The Proposed Scheme | |||||
| 9886 bits | 1019 bits | 2547 + 764 bits | 11,842 + 764l bits | 5348 bits |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, K.-M.; Heng, S.-H.; Tan, S.-Y.; Tan, S.-C. An Efficient Ciphertext-Policy Decryptable Attribute-Based Keyword Search Scheme with Dynamic Attribute Support. Electronics 2025, 14, 4325. https://doi.org/10.3390/electronics14214325
Chan K-M, Heng S-H, Tan S-Y, Tan S-C. An Efficient Ciphertext-Policy Decryptable Attribute-Based Keyword Search Scheme with Dynamic Attribute Support. Electronics. 2025; 14(21):4325. https://doi.org/10.3390/electronics14214325
Chicago/Turabian StyleChan, Koon-Ming, Swee-Huay Heng, Syh-Yuan Tan, and Shing-Chiang Tan. 2025. "An Efficient Ciphertext-Policy Decryptable Attribute-Based Keyword Search Scheme with Dynamic Attribute Support" Electronics 14, no. 21: 4325. https://doi.org/10.3390/electronics14214325
APA StyleChan, K.-M., Heng, S.-H., Tan, S.-Y., & Tan, S.-C. (2025). An Efficient Ciphertext-Policy Decryptable Attribute-Based Keyword Search Scheme with Dynamic Attribute Support. Electronics, 14(21), 4325. https://doi.org/10.3390/electronics14214325





