Design of an IoT Mimetic Antenna for Direction Finding
Abstract
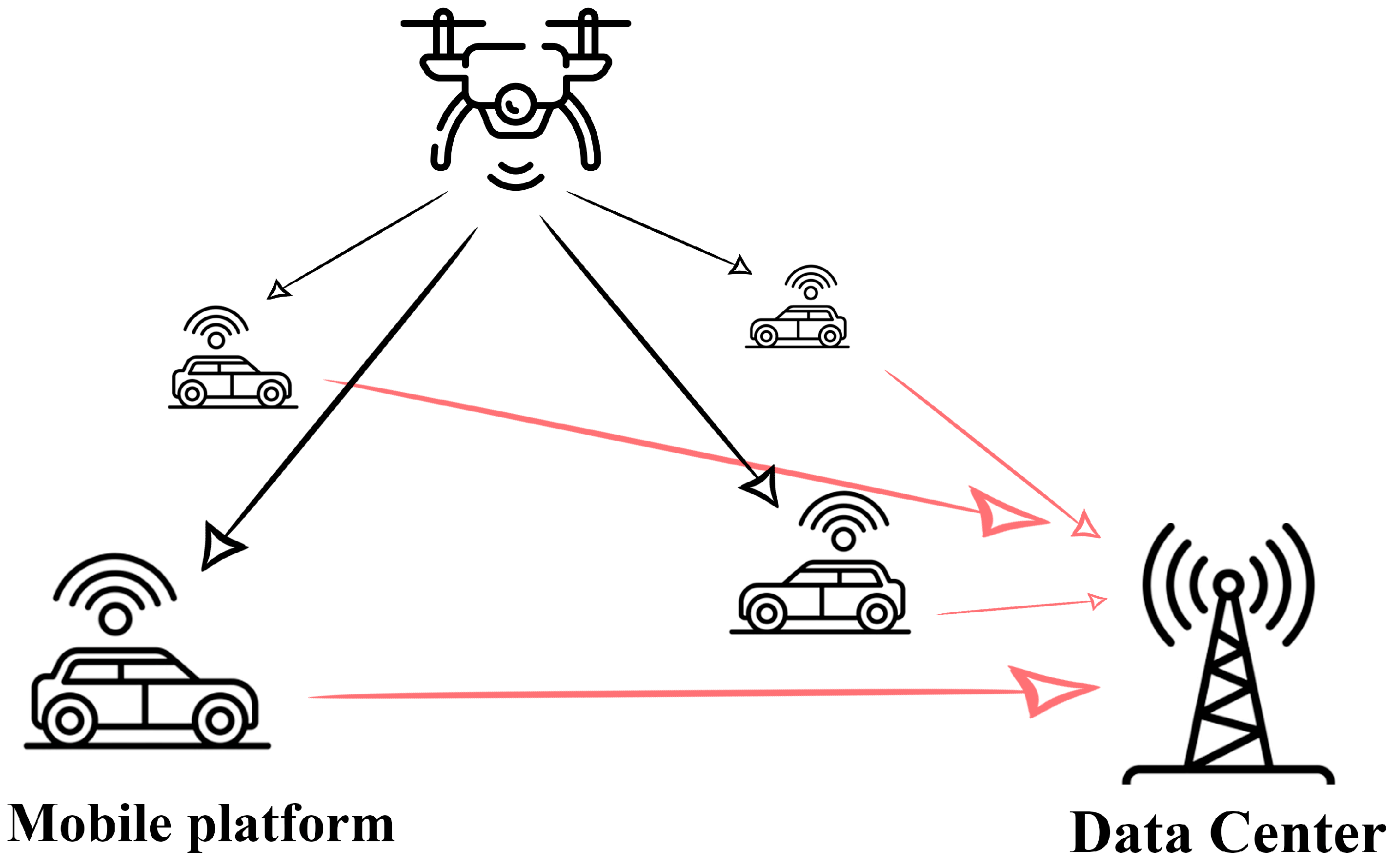
1. Introduction
2. Design Constraints and Methodology
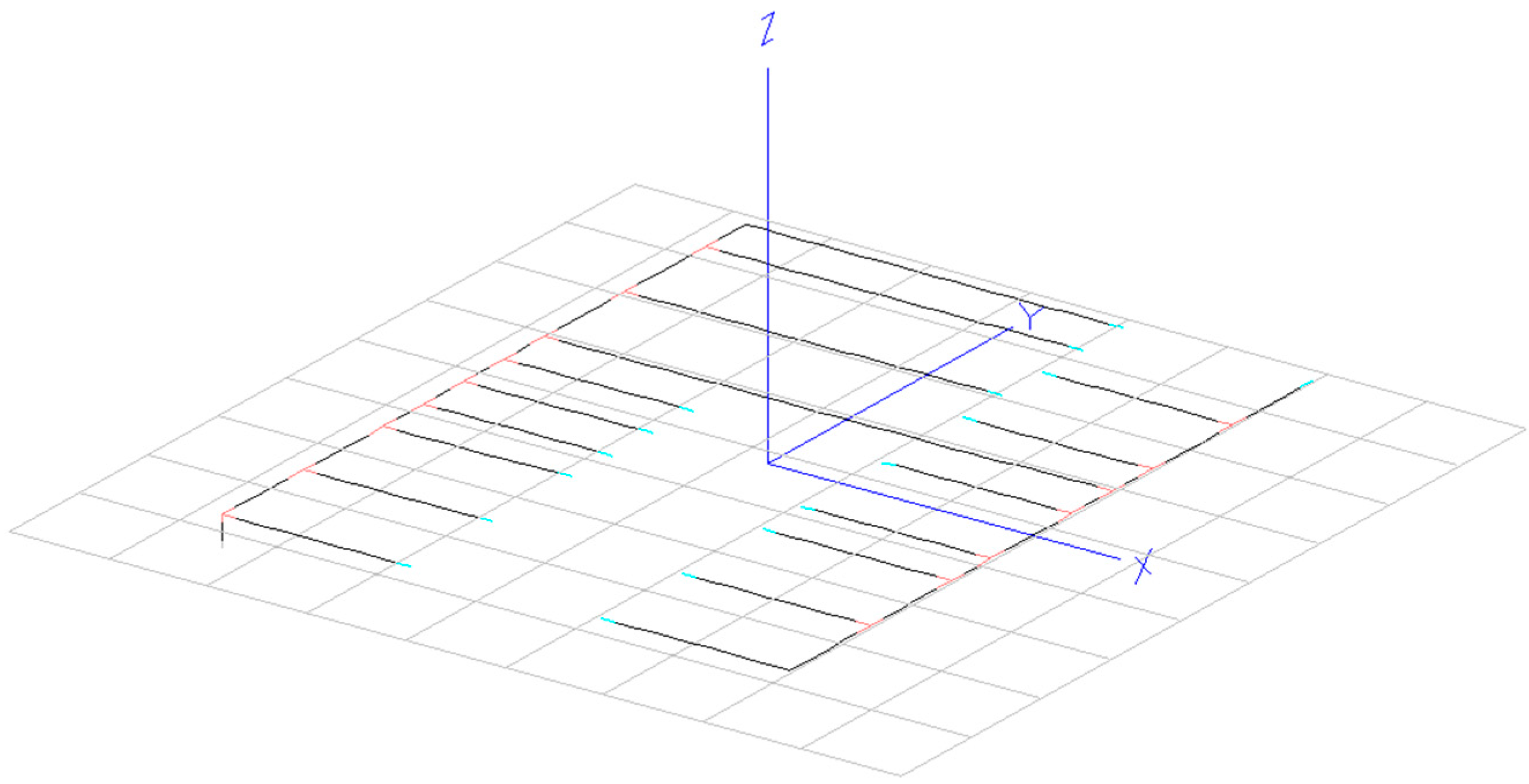
3. Antenna Design and Optimization
- (i)
- The feed segment was lengthened from 5 cm to 6.25 cm to shift the resonance closer to 2.4 GHz;
- (ii)
- Segment 1 of bar #1 was extended from 33 cm to 38 cm to provide resonance at 433 MHz.
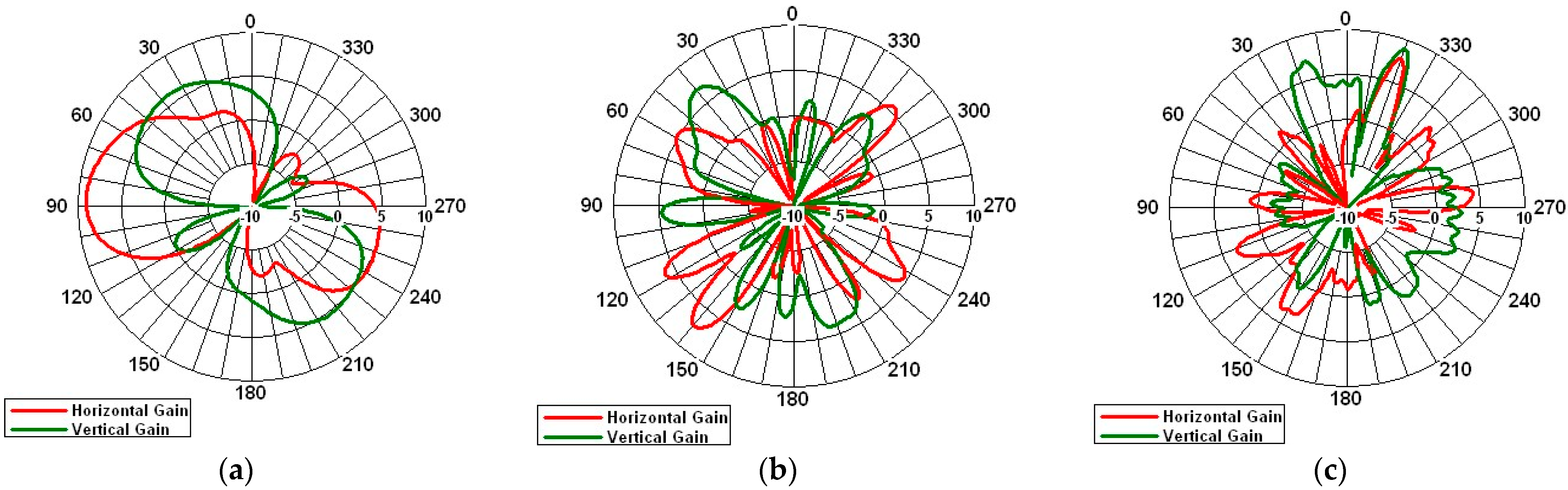
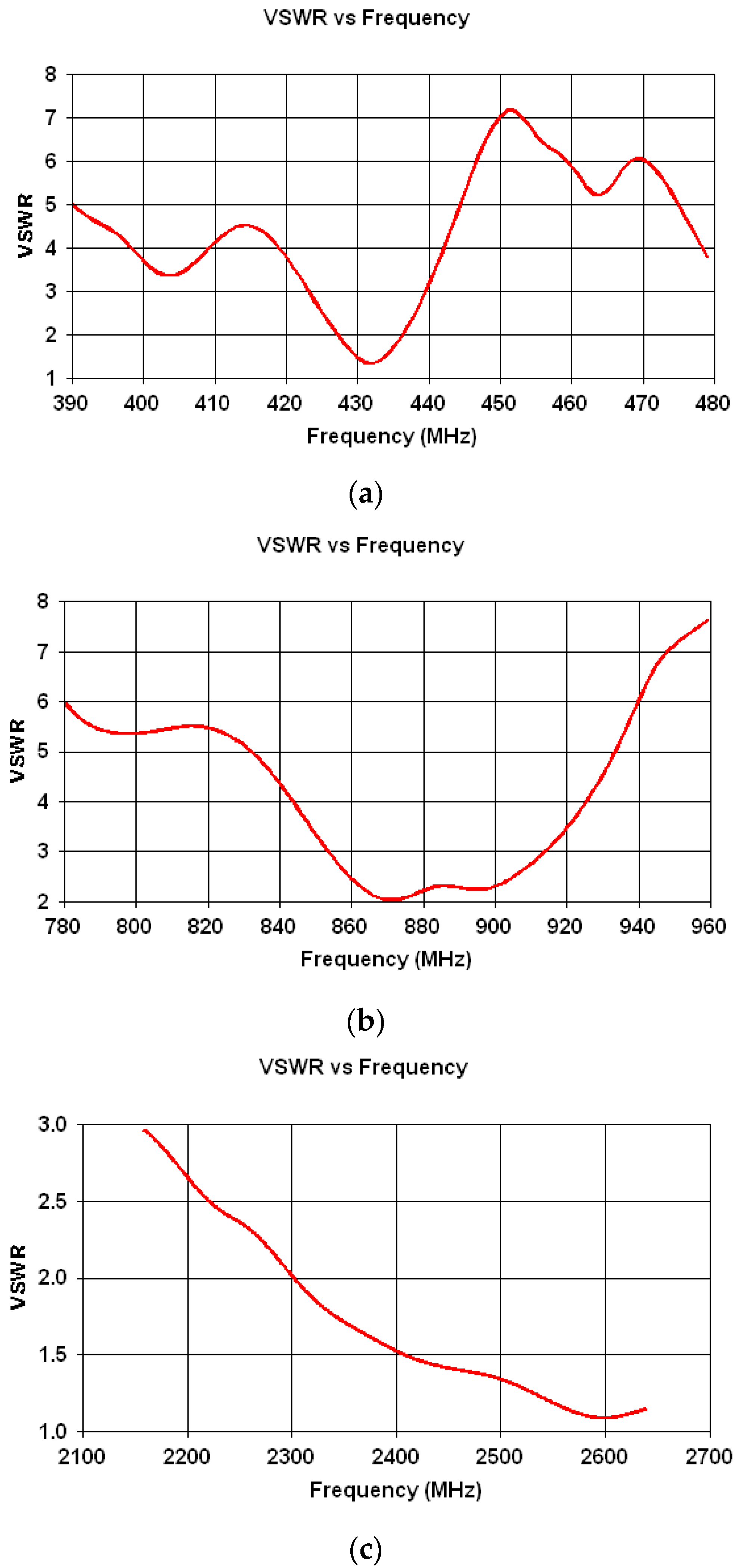
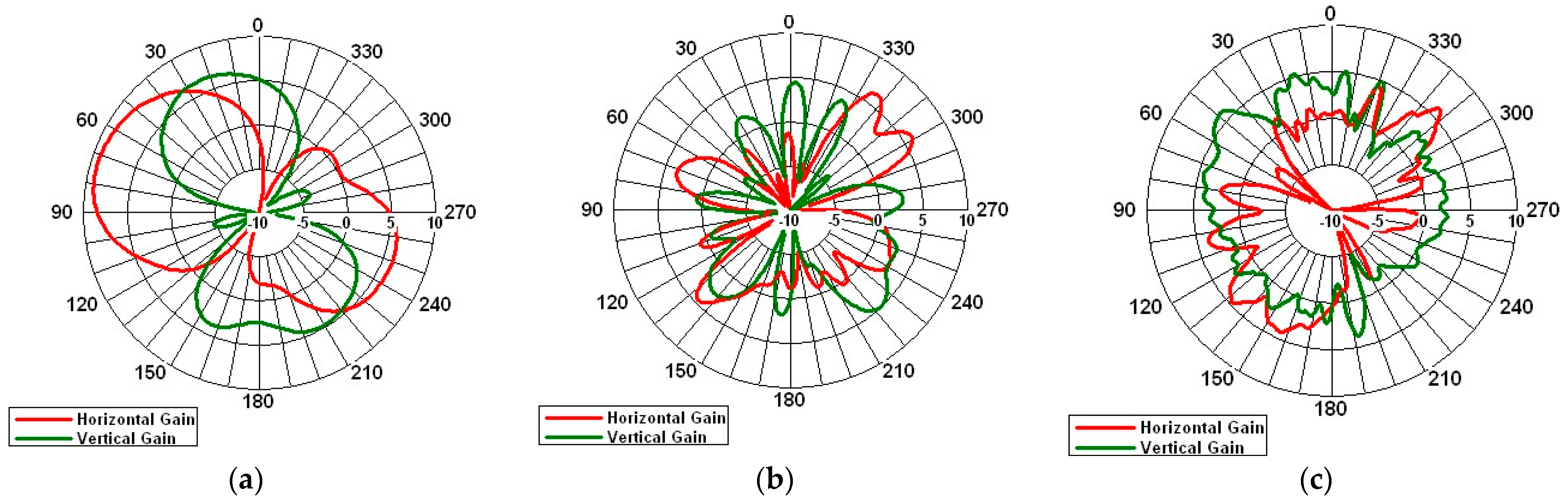
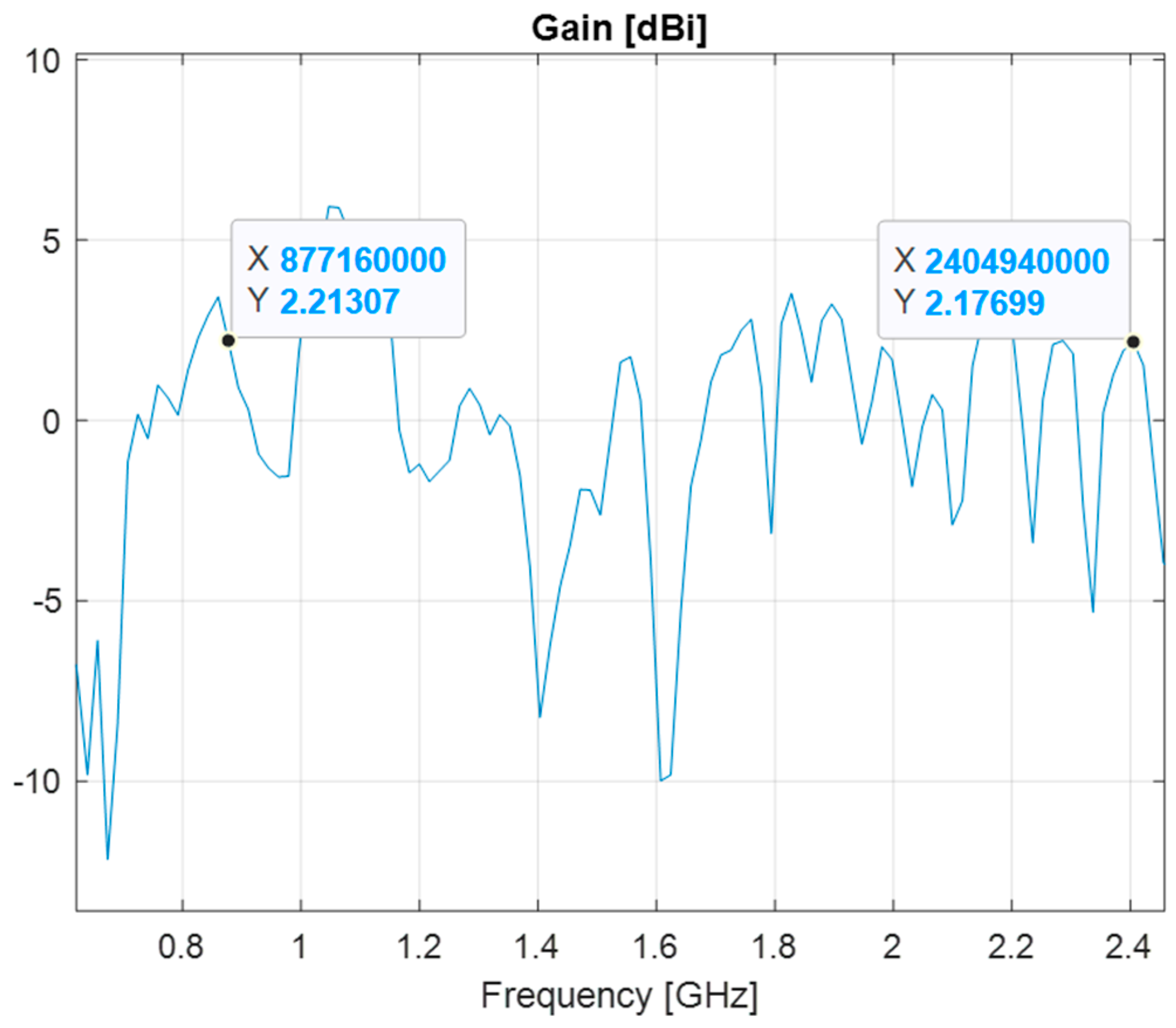
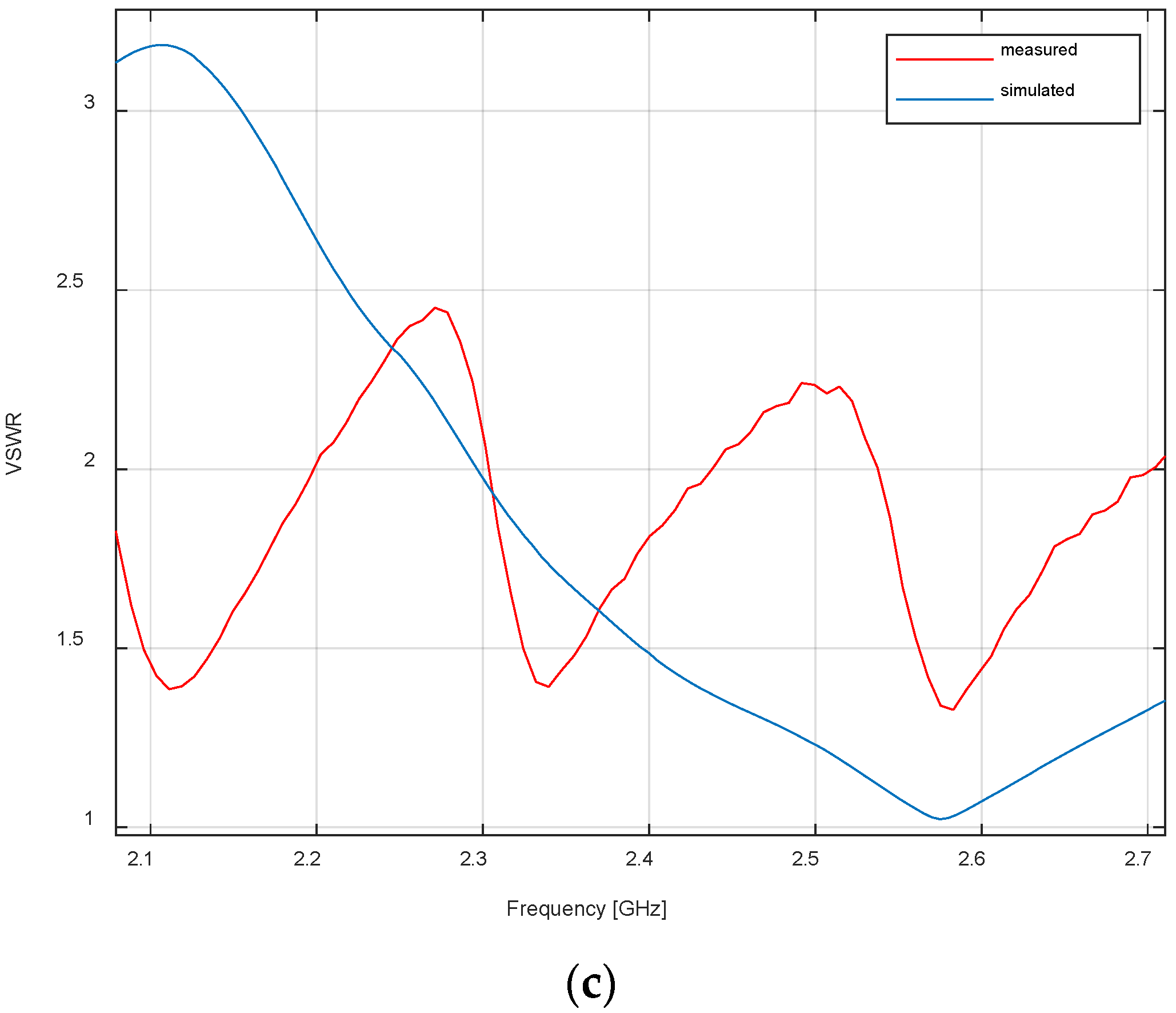
4. Experimental Results
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| UHF | Ultra-High Frequency |
| SVM | Support Vector Machine |
| MoM | Method of Moments |
| VSWR | Voltage Standing Wave Ratio |
References
- Khan, J.; Kiani, G. Parametric study of microstrip patch antenna on LCP substrate for 70 GHz applications. In Proceedings of the 2015 IEEE 4th Asia-Pacific Conference on Antennas and Propagation (APCAP), Bali, Indonesia, 30 June–3 July 2015; pp. 554–555. [Google Scholar] [CrossRef]
- Shariar, F.; Hossain, M.F. Design and Analysis of a Triple Band Microstrip Patch Antenna for Wireless Applications. In Proceedings of the 2023 6th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 7–9 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Constantin, A.; Ifrim, G.; Tamas, R.D. Innovative Dual-Band Antenna for Reliable LoRa IoT Connectivity. In Proceedings of the 2024 Advanced Topics on Measurement and Simulation (ATOMS), Constanta, Romania, 28–30 August 2024; pp. 81–84. [Google Scholar] [CrossRef]
- Heiman, C.-A.; Constantin, A.; Pastorcici, M.; Tamas, R.D. Wideband Circularly Polarized FSS-Horn Antennas. In Proceedings of the 2023 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Venice, Italy, 9–13 October 2023; pp. 35–37. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Li, N.; Xie, K. Optimization of Broadband Patch Antenna Based on Mind Evolutionary Algorithm. In Proceedings of the 2009 International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; pp. 361–364. [Google Scholar] [CrossRef]
- Bucuci, S.; Constantin, A.; Paun, M.; Pastorcici, M.N.; Tamas, R.D.; Danisor, A.; Constantinescu, R. A Compact Monopole Antenna for Underwater Acoustic Monitoring Beacons. Sensors 2022, 22, 8392. [Google Scholar] [CrossRef] [PubMed]
- Yusuf, A.N.A.; Purnamasari, P.D.; Zulkifli, F.Y. A Comparative Analysis of Machine Learning Algorithms for Predicting the Dimensions of Rectangular Microstrip Antennas. In Proceedings of the 2023 IEEE International Symposium on Antennas and Propagation (ISAP), Kuala Lumpur, Malaysia, 30 October–2 November 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Gampala, G.; Reddy, C.J. Fast and Intelligent Antenna Design Optimization using Machine Learning. In Proceedings of the 2020 International Applied Computational Electromagnetics Society Symposium (ACES), Monterey, CA, USA, 27–31 July 2020; pp. 1–2. [Google Scholar] [CrossRef]
- Misilmani, H.M.E.; Naous, T. Machine Learning in Antenna Design: An Overview on Machine Learning Concept and Algorithms. In Proceedings of the 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; pp. 600–607. [Google Scholar] [CrossRef]
- Ahmad, T.; Li, X.J.; Ashfaq, M.; Savva, M.; Ioannou, I.; Vassiliou, V. Location-enabled IoT (LE-IoT): Indoor Localization for IoT Environments using Machine Learning. In Proceedings of the 2024 20th International Conference on Distributed Computing in Smart Systems and the Internet of Things (DCOSS-IoT), Abu Dhabi, United Arab Emirates, 29 April–1 May 2024. [Google Scholar] [CrossRef]
- Jahagirdar, S.; Ghatak, A.; Kumar, A.A. WiFi based Indoor Positioning System using Machine Learning and Multi-Node Triangulation Algorithms. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chiper, F.-L.; Martian, A.; Vladeanu, C.; Marghescu, I.; Craciunescu, R.; Fratu, O. Drone Detection and Defense Systems: Survey and a Software-Defined Radio-Based Solution. Sensors 2022, 22, 1453. [Google Scholar] [CrossRef] [PubMed]
- Famili, A.; Stavrou, A.; Wang, H.; Park, J.-M.; Gerdes, R. Securing Your Airspace: Detection of Drones Trespassing Protected Areas. Sensors 2024, 24, 2028. [Google Scholar] [CrossRef] [PubMed]
- Łukasiewicz, J.; Kobaszyńska-Twardowska, A. Proposed method for building an anti-drone system for the protection of facilities important for state security. Secur. Def. Q. 2022, 39, 88–107. [Google Scholar] [CrossRef]
- Hua, Y.; Huang, L.; Lu, Y. A Compact 3-Port Multiband Antenna for V2X Communication. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 639–640. [Google Scholar] [CrossRef]
- Mousavi, P. Multiband Multipolarization Integrated Monopole Slots Antenna for Vehicular Telematics Applications. IEEE Trans. Antennas Propag. 2011, 59, 3123–3127. [Google Scholar] [CrossRef]
- Mohamed-Hicho, N.M.; Antonino-Daviu, E.; Cabedo-Fabrés, M.; Ferrando-Bataller, M. A Novel Low-Profile High-Gain UHF Antenna Using High-Impedance Surfaces. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1014–1017. [Google Scholar] [CrossRef]
- Wu, W.; Guan, B. A low-profile broadband UHF base station antenna based on lumped-element matching network. In Proceedings of the 2016 11th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Guilin, China, 18–21 October 2016; pp. 9–12. [Google Scholar] [CrossRef]
- Keum, K.-S.; Park, Y.-M.; Choi, J.-H. A Low-Profile Wideband Monocone Antenna Using Bent Shorting Strips. Appl. Sci. 2019, 9, 1896. [Google Scholar] [CrossRef]
- Alieldin, A.; Huang, Y.; Stanley, M.; Joseph, S.; Jia, T.; Elhouni, F. A Camouflage Antenna Array Integrated with a Street Lamp for 5G Picocell Base Stations. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–4. Available online: https://ieeexplore.ieee.org/document/8739400 (accessed on 12 March 2025).
- Sanz-Izquierdo, B.; Huang, F.; Batchelor, J.C. Small size wearable button antenna. In Proceedings of the 2006 First European Conference on Antennas and Propagation, Nice, France, 6–10 November 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Alieldin, A.; El-Akhdar, A.M.; Eldamak, A.R.; Abounemra, A.M.E.; Darwish, M. A Camouflage Fire Sprinkler Antenna for Indoor Sub-6 GHz 5G and WiFi Applications. In Proceedings of the 2025 International Telecommunications Conference (ITC-Egypt), Cairo, Egypt, 28–31 July 2025; pp. 1–4. [Google Scholar] [CrossRef]
- Кн-Будинжиниринг, M. Camouflage Antenna Catalog. Available online: https://www.academia.edu/37674623/_Camouflage_Antenna_Catalog (accessed on 22 October 2025).
- Shih, T.-Y.; Behdad, N. Design of vehicle-mounted, compact VHF antennas using characteristic mode theory. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1765–1768. [Google Scholar] [CrossRef]
- Yeung, S.H.; Wang, C.-F. Characteristic mode theory for practical HF antenna design. In Proceedings of the 12th European Conference on Antennas and Propagation (EuCAP 2018), London, UK, 9–13 April 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Heiman, A.; Tamas, R.D. Transforming Linear to Circular Polarization on Horn Antennas by Using Multiple-Layer Frequency Selective Surfaces. Sensors 2022, 22, 7838. [Google Scholar] [CrossRef]
- Bazgir, M.; Sheikhi, A.; Dowlatshahi, M. Resonance frequency prediction of dielectric antennas for liquid sensing via support vector regression. Sci. Rep. 2024, 14, 31410. [Google Scholar] [CrossRef] [PubMed]
- Singh, O.; Bharamagoudra, M.; Gupta, H.; Dwivedi, A.; Ranjan, P.; Sharma, A. Microstrip line fed dielectric resonator antenna optimization using machine learning algorithms. Sādhanā 2022, 47, 226. [Google Scholar] [CrossRef]
- Heiman, A.; Tamas, R.D. Neural Network-Based Predictive Design of FSS Structures for Satellite Antenna Performance Enhancement. In Proceedings of the IEEE International Conference on Antenna Measurements and Applications (CAMA)-Special Sessions: SPS16 New Technologies and Methodologies for Antenna Design, Antibes, France, 18–20 November 2025. [Google Scholar]
- Constantin, A.; Tamas, R.D. A Multi-Band AI-Miniaturized Patch Antenna for Environmental Monitoring. In Proceedings of the IEEE International Conference on Antenna Measurements and Applications (CAMA)-Special Sessions: SPS16 New Technologies and Methodologies for Antenna Design, Antibes, France, 18–20 November 2025. [Google Scholar]
- Ranjan, P.; Gupta, H.; Sharma, A.; Yadav, S.; Potrebićc, M. Investigation and Optimization of Dielectric Resonator MIMO Antenna Using Machine Learning Approach; Springer Nature: Singapore, 2022; pp. 645–655. [Google Scholar] [CrossRef]
- Huang, C.-H.; Ali, A.; Hsu, C.-C.; Tsao, H.-H. Enhanced Antenna Design Through Hyper Parameter Optimization of Diverse Machine Learning Models Using Bayesian Optimization. Res. Sq. Prepr. 2024. [Google Scholar] [CrossRef]
- Khan, T.; Roy, C. Prediction of slot-position and slot-size of a microstrip antenna using support vector regression. Int. J. RF Microw. Comput.-Aided Eng. 2018, 29, e21623. [Google Scholar] [CrossRef]

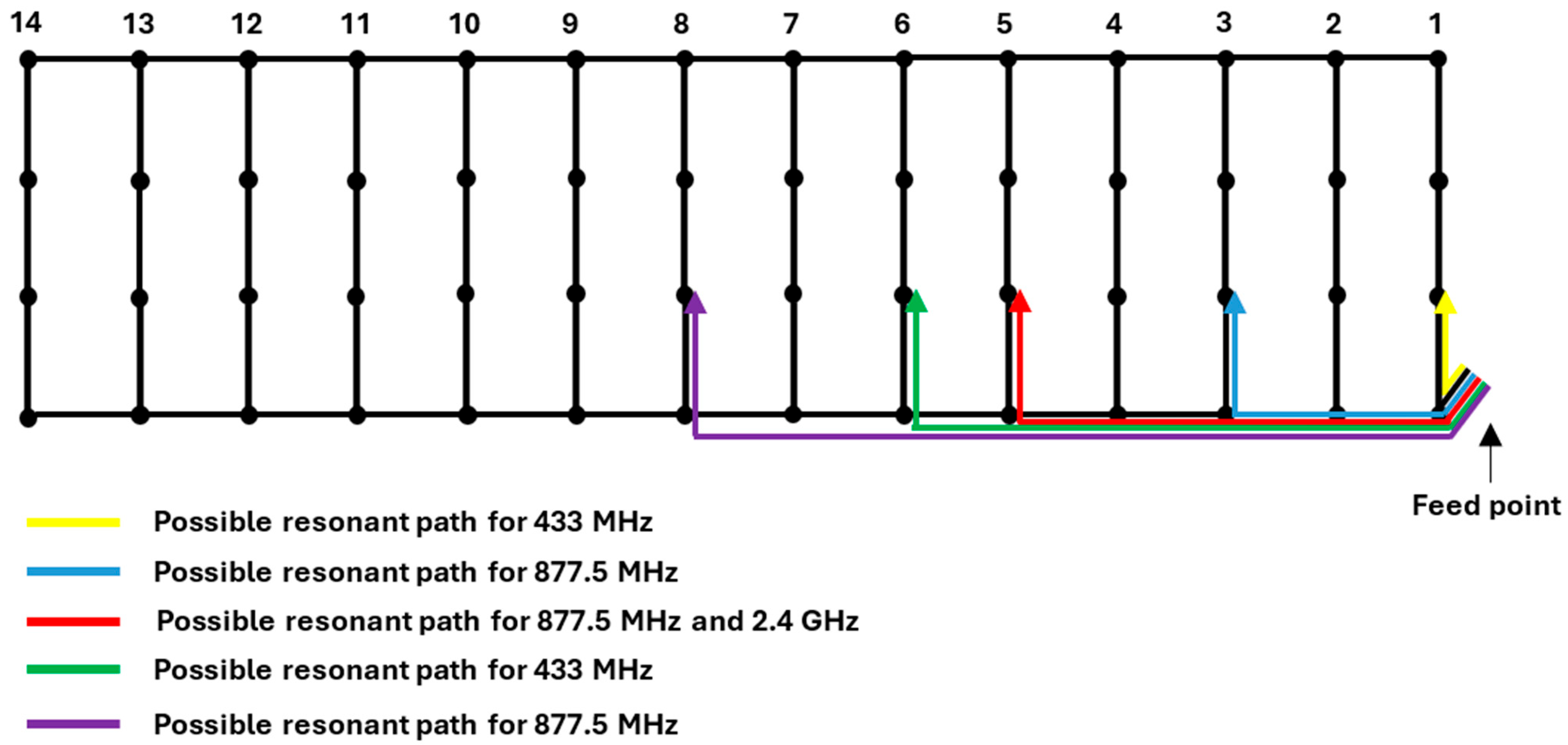






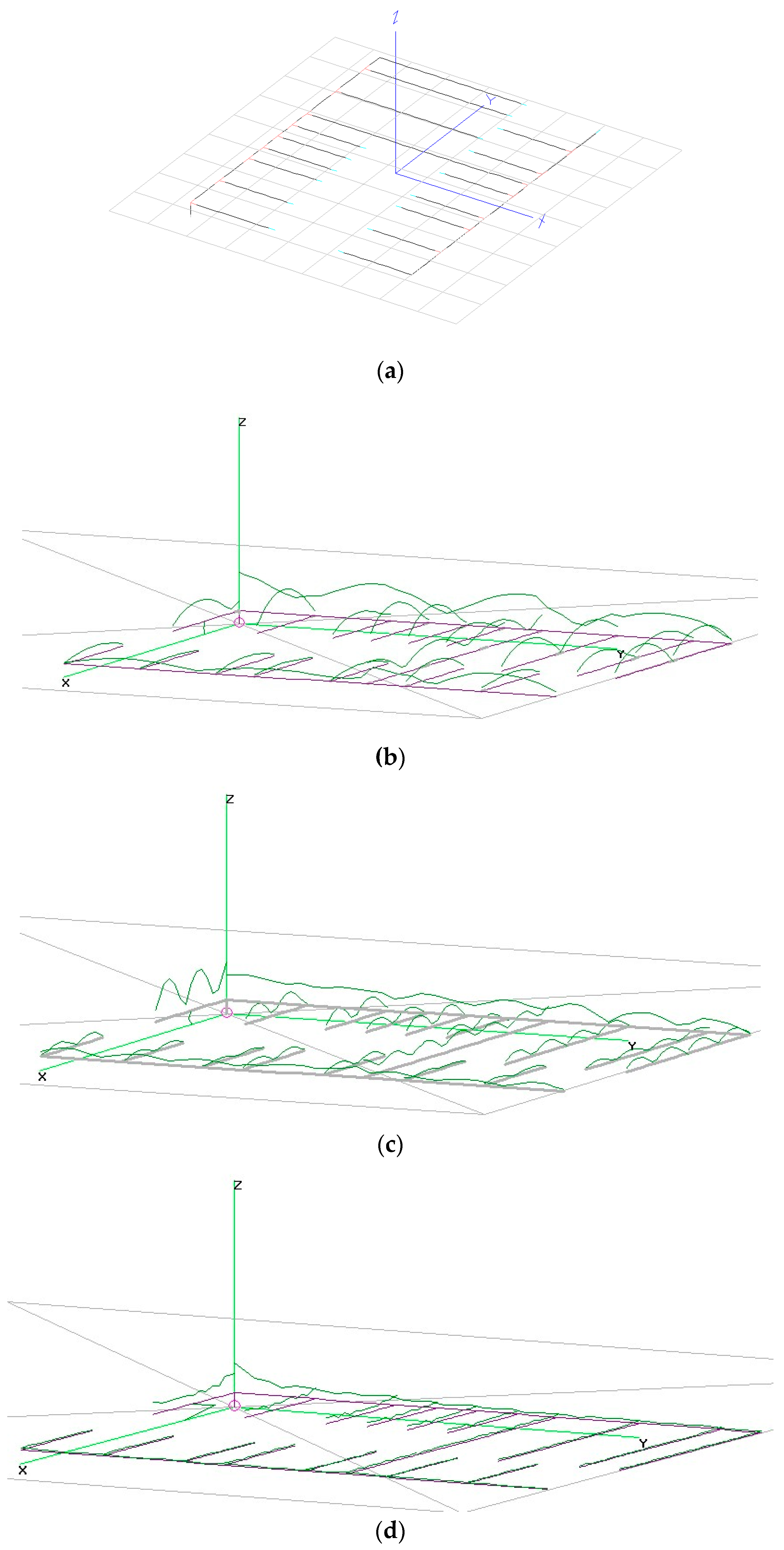




| Resonant Path | Closest Resonance (Odd Multiple of λ/4) | |
|---|---|---|
| Color (Ref. Figure 3) | Length [m] | |
| Yellow | 0.383 | approx. 1.75 λ at 433 MHz |
| Blue | 0.583 | approx. 1.75 λ at 877.5 MHz |
| Red | 0.783 | approx. 2.25 λ at 877.5 MHz approx. 6.25 λ at 2.4 GHz |
| Green | 0.883 | approx. 1.25 λ at 433 MHz |
| Purple | 1.083 | approx. 3.25 λ at 877.5 MHz |
| Code Word for the Resonant Bars # (1, 3, 5, 6, and 8) | Code Word for the Bars # (2, 4, 7, and 9–14) |
|---|---|
| 4 or 5 | 0, 1 or 3 to 7 |
| Frequency Band [MHz] | Resonant Frequency—Simulation [MHz] | VSWR— Simulation | Gain— Simulation [dBi] |
|---|---|---|---|
| 433 | 438 | 1.5 | 5 |
| 877.5 | 937 | 1.75 | 5.65 |
| 2400 | 2640 | 2.79 | 6.9 |
| Resonant Frequency [MHz] | VSWR | Gain [dBi] |
|---|---|---|
| 433 | 1.38 | 5.95 |
| 877.5 | 2.07 | 5.1 |
| 2400 | 1.52 | 6.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamas, R.D. Design of an IoT Mimetic Antenna for Direction Finding. Electronics 2025, 14, 4292. https://doi.org/10.3390/electronics14214292
Tamas RD. Design of an IoT Mimetic Antenna for Direction Finding. Electronics. 2025; 14(21):4292. https://doi.org/10.3390/electronics14214292
Chicago/Turabian StyleTamas, Razvan D. 2025. "Design of an IoT Mimetic Antenna for Direction Finding" Electronics 14, no. 21: 4292. https://doi.org/10.3390/electronics14214292
APA StyleTamas, R. D. (2025). Design of an IoT Mimetic Antenna for Direction Finding. Electronics, 14(21), 4292. https://doi.org/10.3390/electronics14214292






