Full Process Dynamics and HIL Simulation of Precise Airdrop System
Abstract
1. Introduction
2. Introduction of Precision Aerial Delivery Systems
2.1. System Composition
2.2. Brief Introduction of Airdrop
- (1)
- Deceleration parachute working stage
- (2)
- Parafoil working stage
- (3)
- Cluster parachute working stage
- Opening of the parachutes at all levels;
- Parachute inflation;
- System dynamics modeling and analysis of the object–parafoil assembly.
3. Dynamic Modeling of the Whole Process of PADS
3.1. Dynamic Model for the Opening and Inflation Stages
3.1.1. Multi-Body Dynamics Model of Opening Process
- (1)
- Under the action of the binding force, each segment of the line is pulled out of the pack in sequence;
- (2)
- Inflation commences only after the lines and the canopy are completely detached from the pack;
- (3)
- The canopy is pulled out of the pack in sequential succession;
- (4)
- The connecting sling between the deceleration parachute and the parachute pack is treated as a nonlinear damping spring.
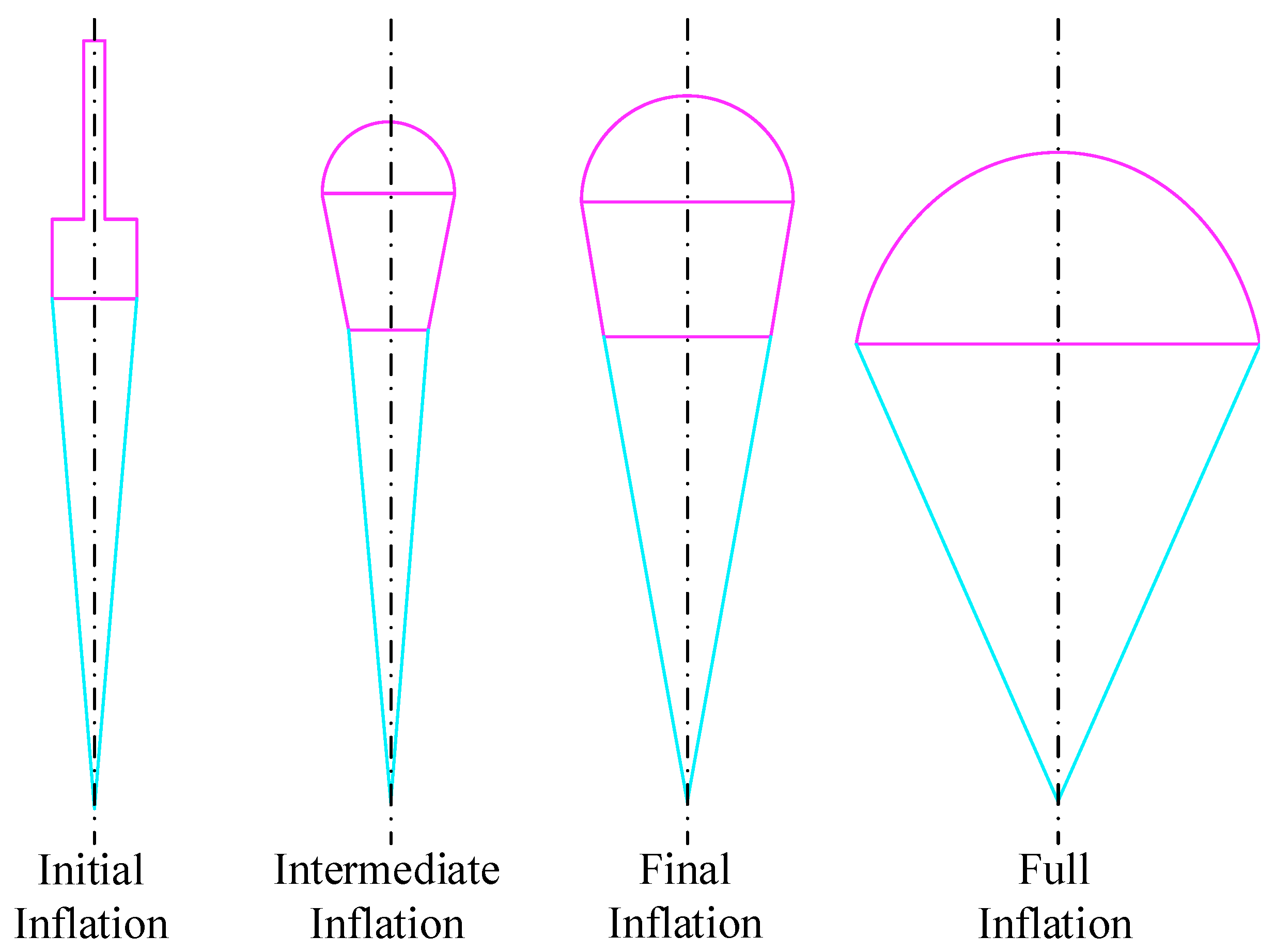
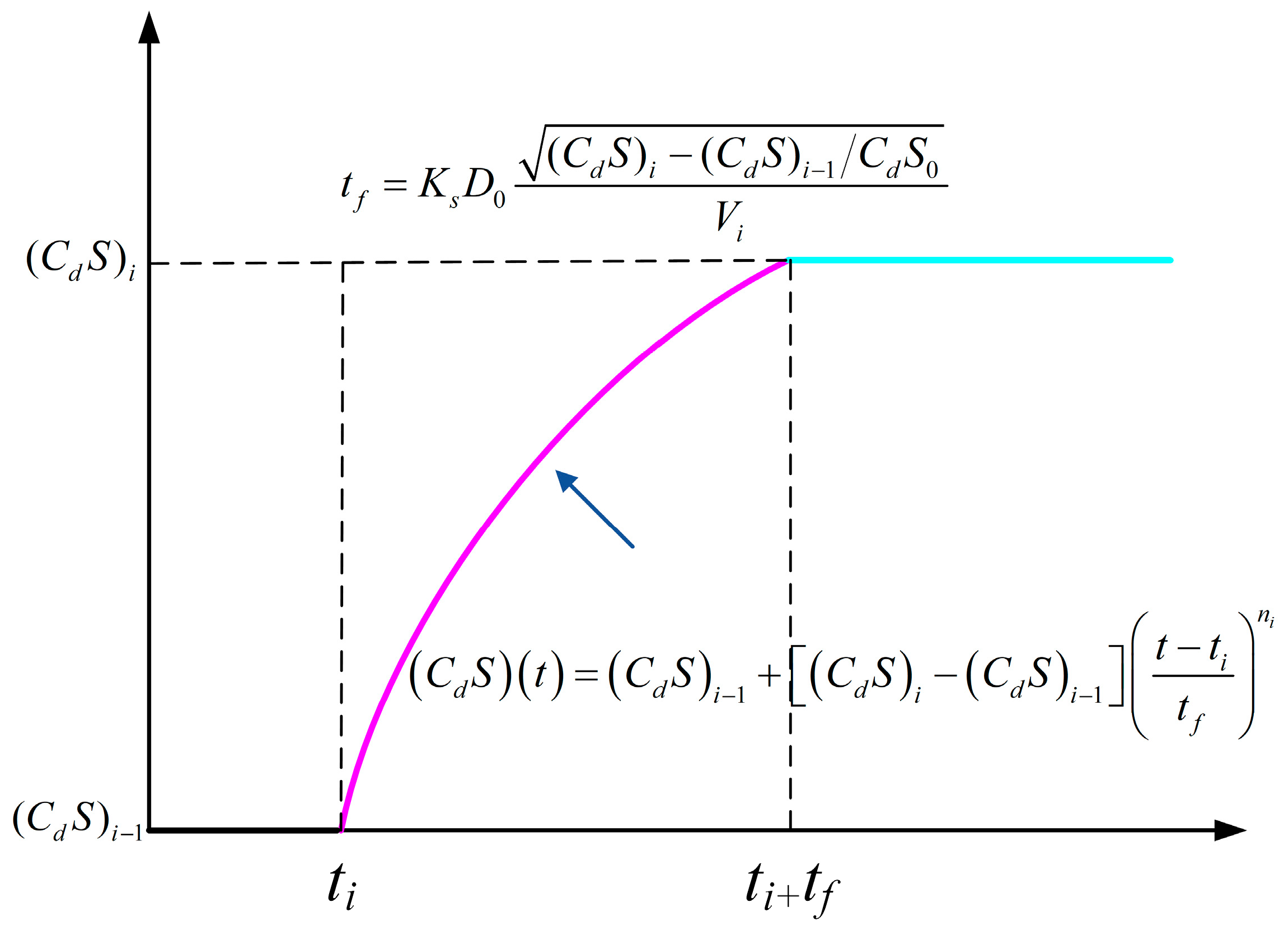
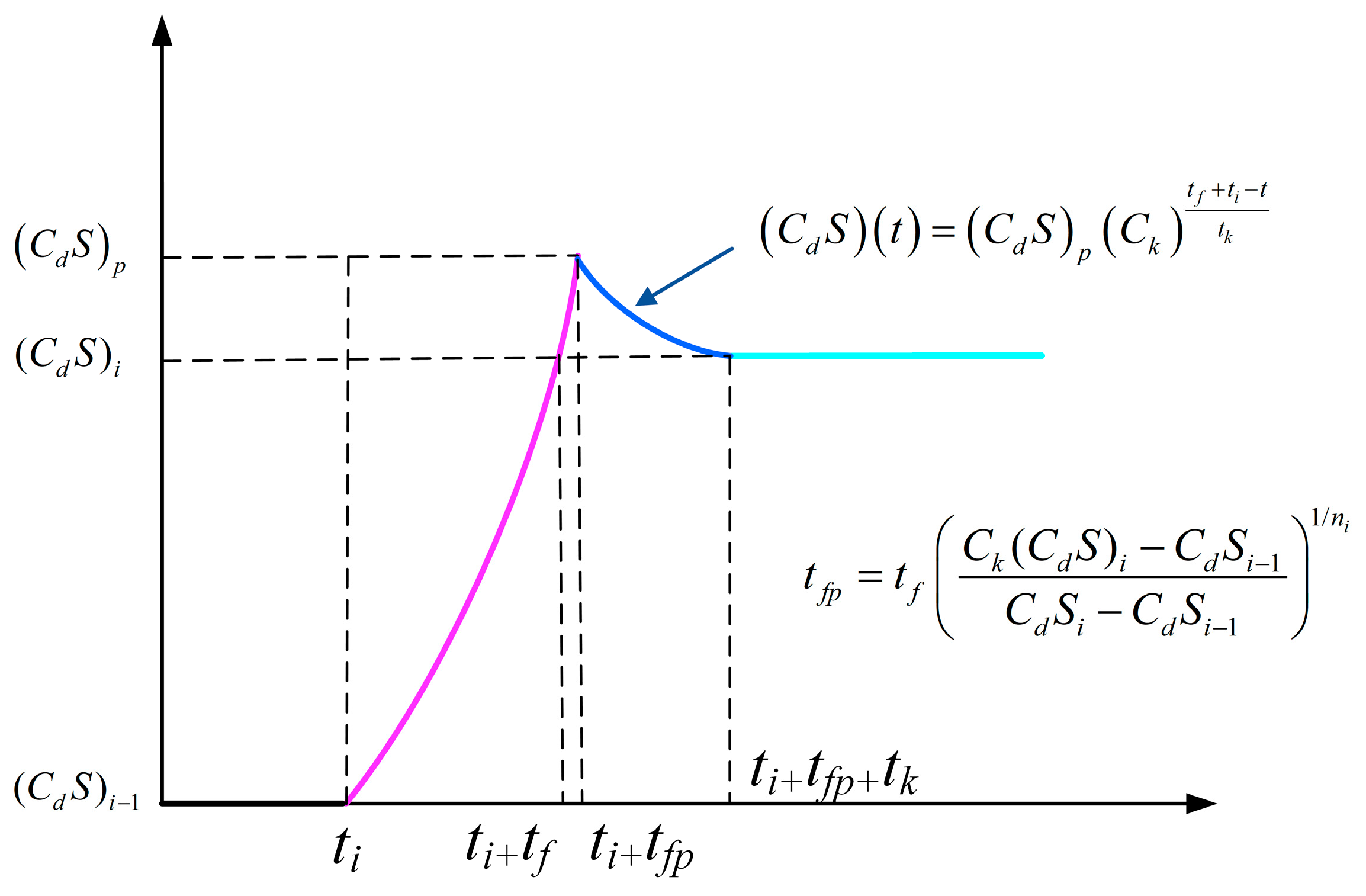
3.1.2. Dynamics Model of Parachute Inflation Process
- (1)
- Finite mass inflation model
- (2)
- Infinite mass inflation model
3.2. The 9-DoF Dynamic Model Framework
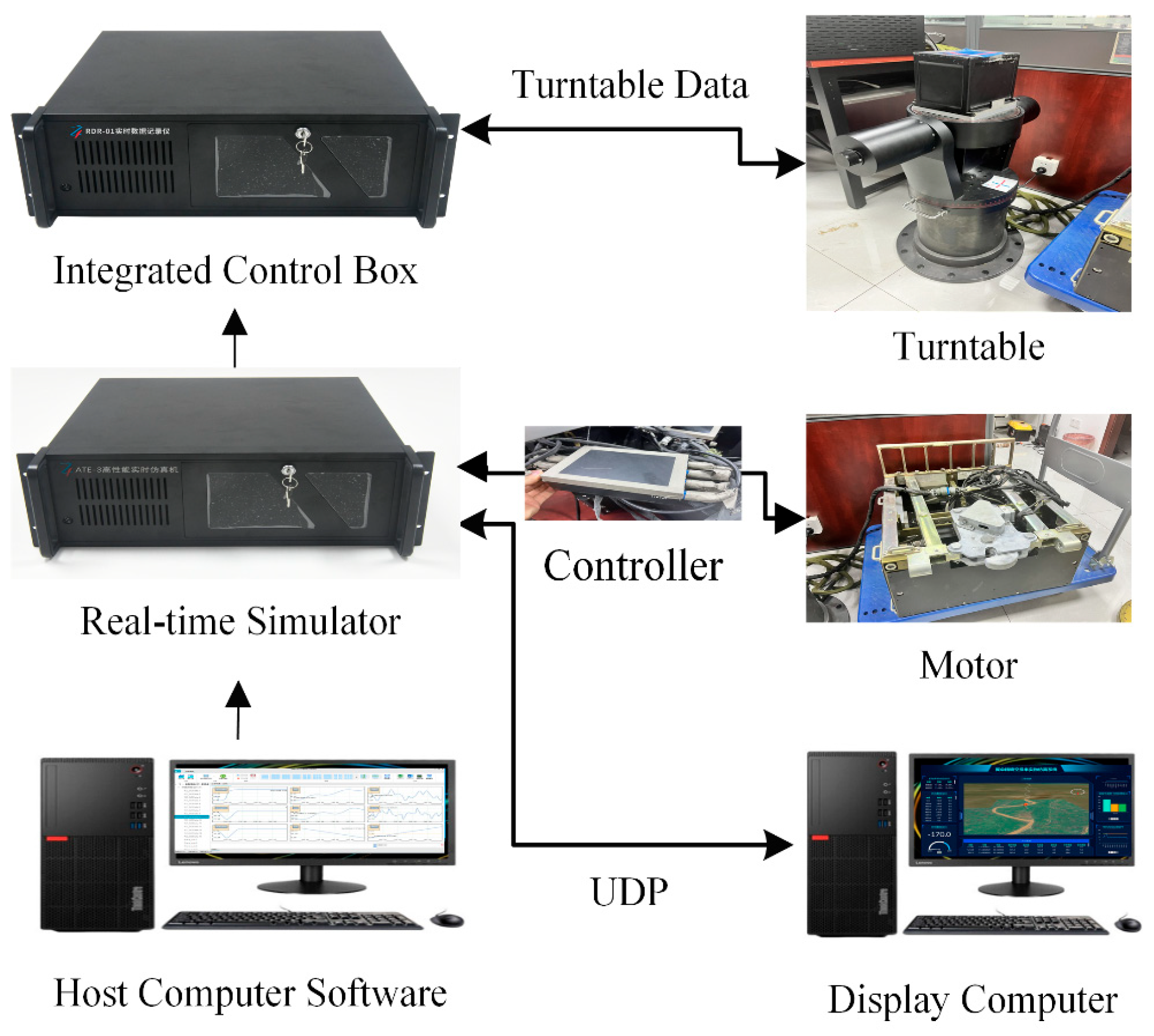
4. HIL Simulation Platform
4.1. HIL Simulation Platform Overview
4.2. HIL Simulation Platform Architecture
4.3. Operation Process of HIL Simulation Platform
4.3.1. System Preparation Phase (Airdrop Preparation Phase)
- (1)
- Integrated control box, simulation test computer, and display equipment power-up.
- (2)
- The communication and navigation control system (upper and lower chassis) and motorized three-axis rotary table (including inertial guidance module) are powered up.
- (3)
- The parafoil master control machine completes the initial parameter injection (target point, excitation point, hovering point, navigation mode, control mode, hovering radius, gliding ratio, etc.).
- (4)
- Start the ground monitoring software and read in the initial wind field data from the wind field environment toolkit.
- (5)
- Start the 3D view display software and read the geographic environment model from the Geographic Environment Modeling Toolkit.
- (6)
- Start the simulation task management software and set up the simulation task. Define the parameters of the parafoil system, select the aerodynamic data of the parafoil, the wind field environment data (initial wind field and real-time wind field), and the dynamics model.
- (7)
- The integrated control box downloads the parachute dynamics model, simulation initial parameters, and wind field data from the simulation task management software.
4.3.2. Real-Time Simulation Phase (Controlled Flight Phase)
- (1)
- The integrated control box collects the maneuvering line offset from the drive control box by means of parallel leads.
- (2)
- The integrated control box solves the wing and parachute dynamics model in real time, and uses the results to drive the load simulator, the guard-guide equivalent, the three-axis motorized rotary table, and the three-dimensional view display software, respectively.
- (3)
- The 3D view display software reads the flight state of the wing and parachute system from the dynamics simulation software and displays it online in real time.
- (4)
- The load simulator sends the simulated load control quantity to the load actuator to apply the simulated load to the maneuvering line.
- (5)
- The inertial guidance module rotates with the three-axis motorized rotary table and sends out the inertial guidance attitude data, which is corrected and supplemented (position, velocity, and heading data) and then transmitted to the guidance equivalent.
- (6)
- The guard-guidance-equivalent device integrates and processes the inertial guidance data, simulated guard guidance position, and altitude data, and sends them to the parafoil general control machine.
- (7)
- The master controller monitors the ground monitoring software for new control commands. If it monitors the valid ground instruction, it runs the control algorithm according to the ground instruction, calculates the control quantity, and sends it to the motor drive control box; if there is no valid ground instruction, it runs the pre-loaded control algorithm, calculates the control quantity, and sends it to the motor drive control box.
- (8)
- The motor controller issues commands to the parachute line manipulation actuator, which controls the motor to drive the winch to rotate and pull the manipulation line.
- (9)
- The potentiometer coaxial to the capstan follows the same angle of rotation and provides real-time feedback to the motor drive control box.
- (10)
- Repeat step (8) and continue with the new control action cycle until the system lands.
4.3.3. System Post-Processing Phase (Data Playback Phase)
5. Simulation
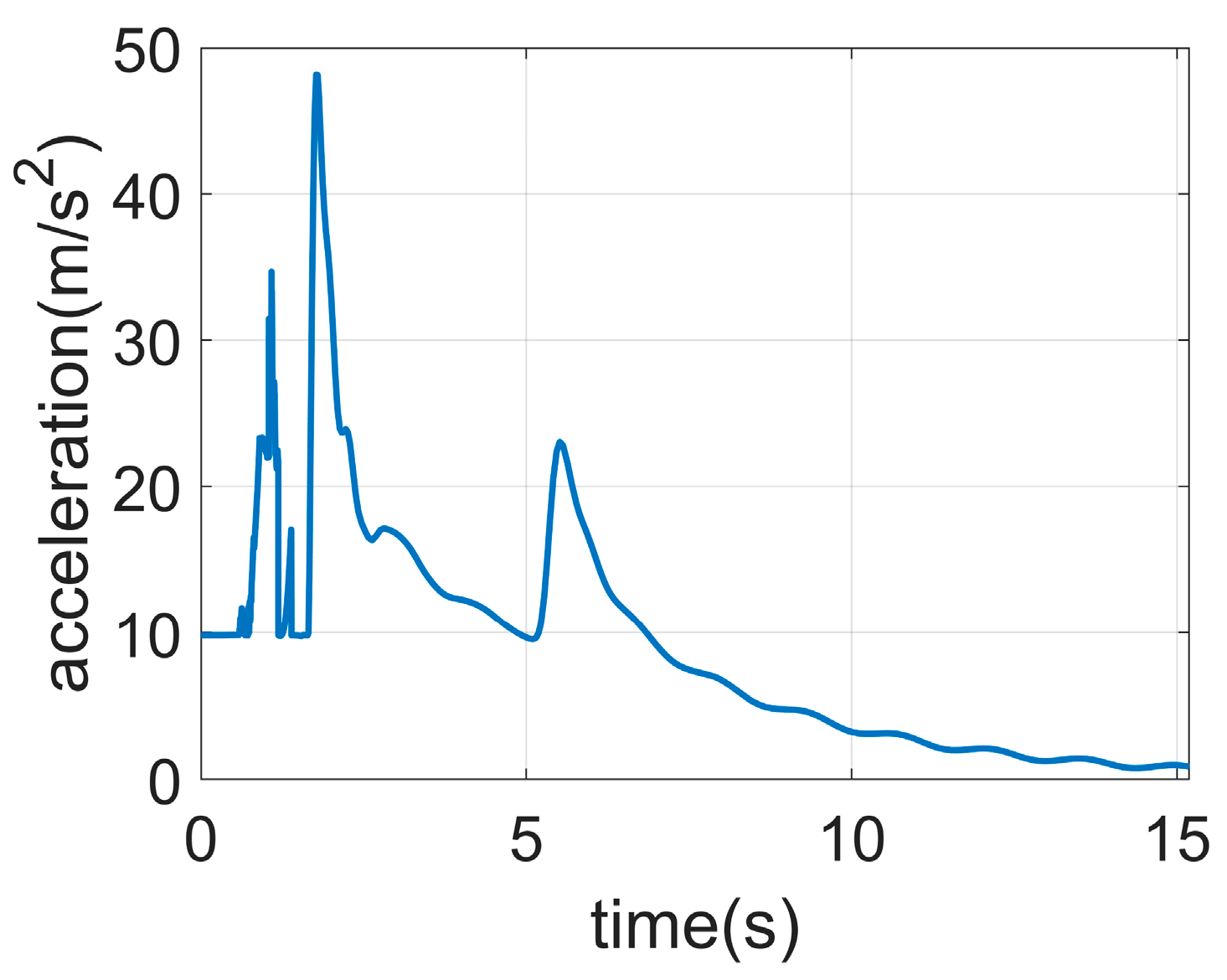
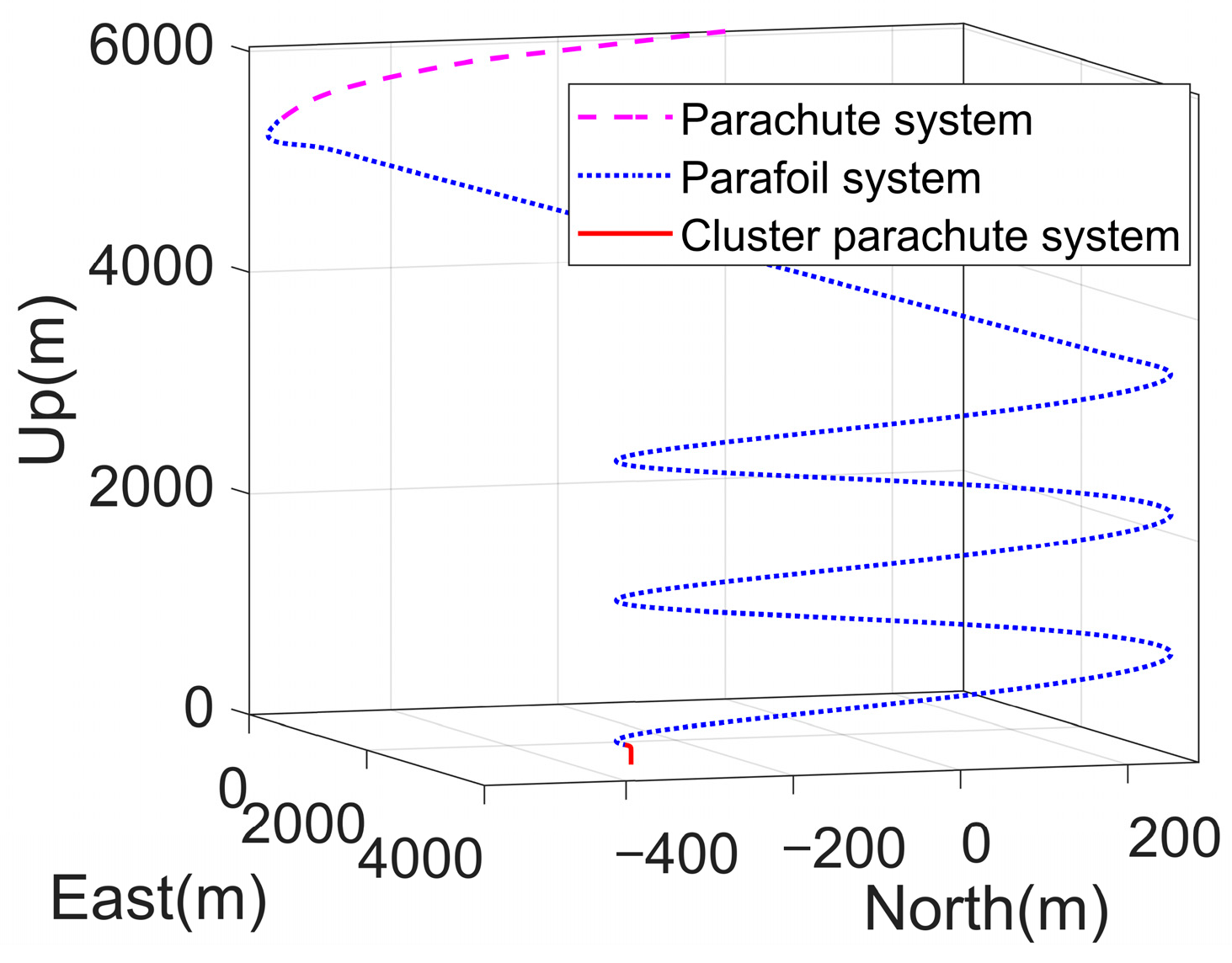
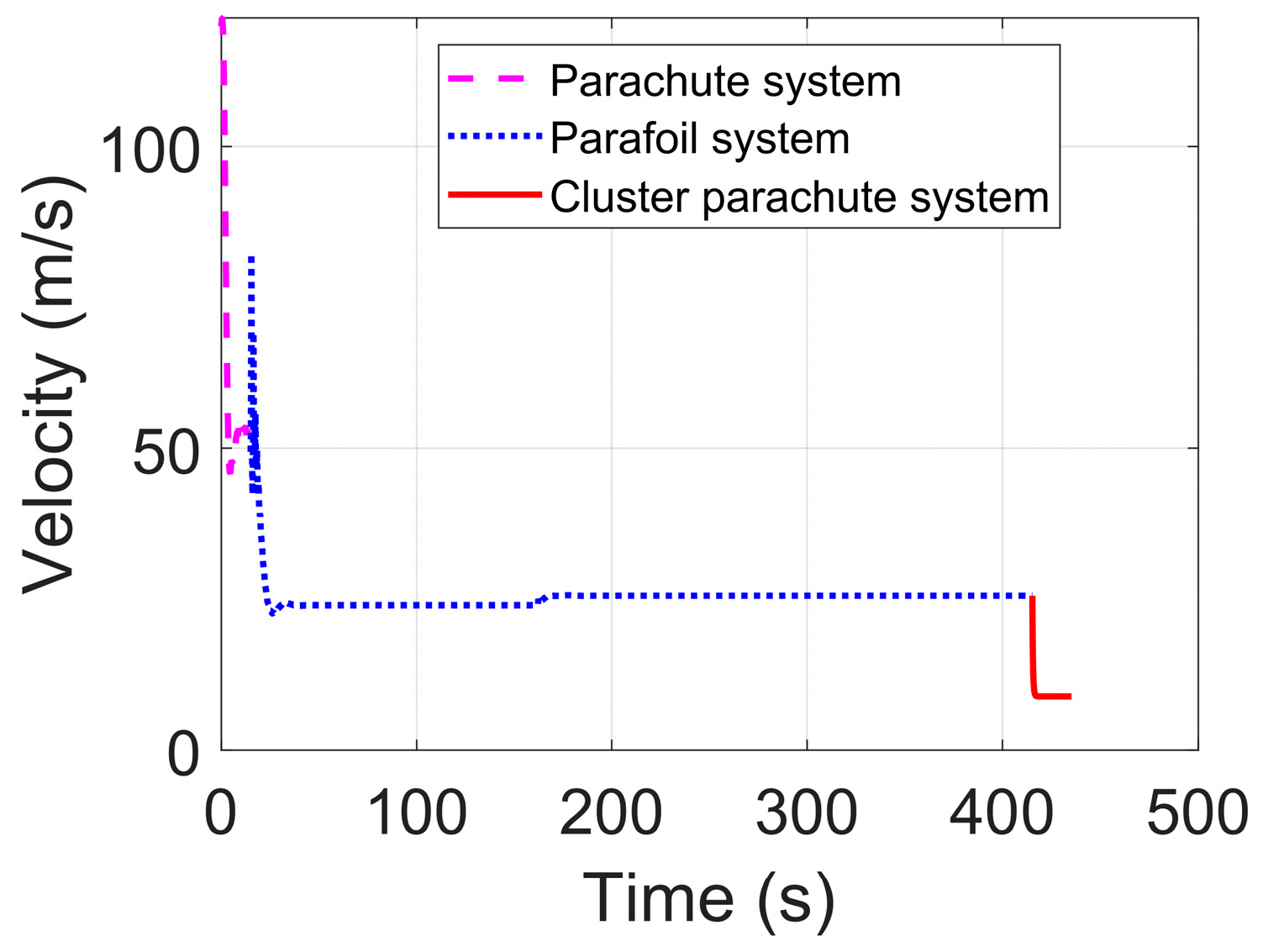
5.1. Full Process Dynamics Simulation
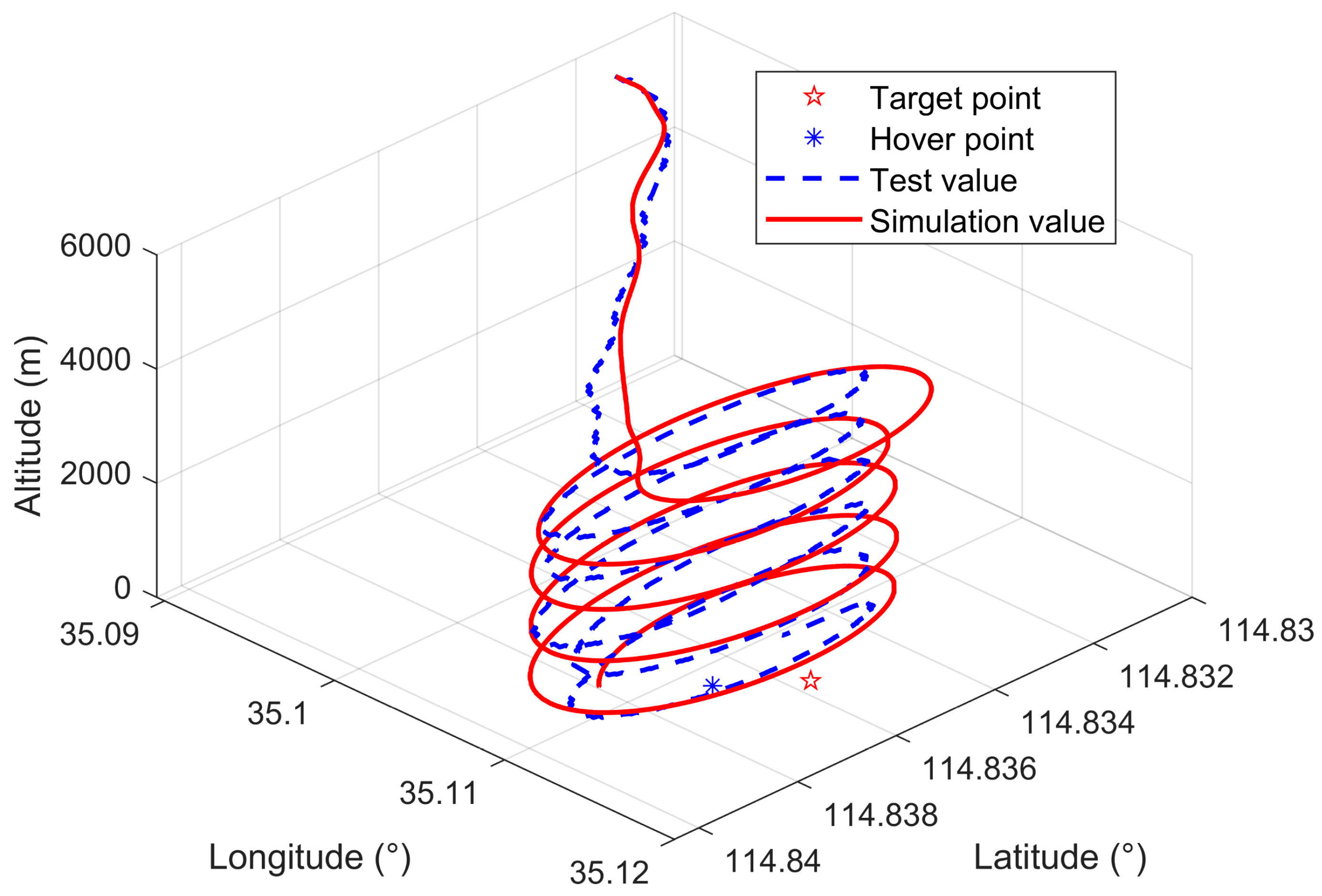
5.2. HIL Principle Prototype Verification
- Initial State Setting: Customization of initial conditions and system parameters, including initial position, paraglider parameters, target point settings, etc.
- Real-Time Simulation Efficiency: Continuous monitoring of UUT parameters (Figure 13). The control quantity of simulation data is generated at a frequency of 4 Hz. The simulated motion delay of the simulator is less than 1 ms, and it can generate dynamic model results per millisecond.
- Result Display: Three-dimensional visualization of wind fields, initial parameters, pitch–plane deviations, and real-time flight data.
6. Conclusions
- (1)
- Development and validation of a physics-based deceleration parachute model that accurately captures line-stretch and inflation dynamics; by integrating a 9-DoF dynamic framework, a full-process dynamic model for the three stages of deceleration of the parachutes, parafoils, and cluster parachutes was established.
- (2)
- Establishment of a hardware–software-integrated HIL simulation platform for end-to-end airdrop process emulation, which supports multi-scenario testing, flight performance evaluation under variable conditions, and serves as a physics-based virtual proving ground for system optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, H.; Sun, Q.; Sun, H.; Chen, Z.; Zeng, X.; Soulat, D. Aerodynamic Prediction for Flight Dynamics Simulation of Parafoil System and Airdrop Test Validation. Nonlinear Dyn. 2023, 111, 11065–11085. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, J.; Sun, Q.; Sun, H.; Chen, Z.; Sun, M.; Xie, G. Sideslip Angle Estimation Based Active Disturbance Rejection 3D Trajectory Tracking Control for Powered Parafoil System and Hardware-in-the-Loop Simulation Verification. Aerosp. Sci. Technol. 2023, 141, 108497. [Google Scholar] [CrossRef]
- Toni, R. Theory on the Dynamics of Bag Strip for a Parachute Deployment Aidedby a Pilot Chute. In Proceedings of the 2nd Aerodynamic Deceleration Systems Conference, El Centro, CA, USA, 23 September 1968. [Google Scholar]
- McVey, D.F.; Wolf, D.F. Analysis of Deployment and Inflation of Large Ribbon Parachutes. J. Aircr. 1974, 11, 96–103. [Google Scholar] [CrossRef]
- Wolf, D. A Simplified Dynamic Model of Parachute Inflation. J. Aircr. 1974, 11, 28–33. [Google Scholar] [CrossRef]
- French, K. A First-Order Theory for the Effects of Line Ties on Parachute Deployment. In Proceedings of the 6th Aerodynamic Decelerator and Balloon Technology Conference, Houston, TX, USA, 5 March 1979. [Google Scholar]
- Purvis, J. Prediction of Parachute Line Sail during Lines-First Deployment. J. Aircr. 1983, 20, 940–945. [Google Scholar] [CrossRef]
- Purvis, J. Prediction of Line Sail during Lines-First Deployment. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10 January 1983. [Google Scholar]
- Purvis, J. Numerical Prediction of Deployment, Initial Fill, and Inflation of Parachute Canopies. In Proceedings of the 8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, USA, 2 April 1984. [Google Scholar]
- Wang, H.; Qin, Z.; Song, X.; Tao, W. Analysis of the Phenomenon of Bull Whipping in the Deployment Process of Large Parachute. J. Natl. Univ. Def. Technol. 2025, 5, 34–38. [Google Scholar]
- Din, D.; Cheng, W. Validation of Large Parachute’s Dynamic Continuous Models for Linesail and Bullwhip. Spacecr. Recovery Remote Sens. 2010, 31, 22–26. [Google Scholar]
- White, F.M.; Wolf, D.F. A Theory of Three-Dimensional Parachute Dynamic Stability. J. Aircr. 1968, 5, 86–92. [Google Scholar] [CrossRef]
- Wolf, D.F.; Spahr, H.R. Parachute Cluster Dynamic Analysis. J. Aircr. 1977, 14, 321–322. [Google Scholar] [CrossRef]
- Wolf, D. Dynamic Stability of a Nonrigid Parachute and Payload System. J. Aircr. 1971, 8, 603–609. [Google Scholar] [CrossRef]
- Cockrell, D.; Haidar, N. Influence of the Canopy-Payload Coupling on the Dynamic Stability Inpitch of a Parachute System. In Proceedings of the Aerospace Design Conference, Irvine, CA, USA, 16 February 1993. [Google Scholar]
- Graham, W.R.; Moss, B.R. Comment on “A Theory of Three-Dimensional Parachute Dynamic Stability”. J. Aircr. 2017, 54, 853. [Google Scholar] [CrossRef]
- Tang, Q.; Wang, Y.; Zhang, Q.; Zhang, X.; YANG, T. Application of Dynamics and Kinematics of Parachute-Bomb System in Target Identification for a Target Sensitive Projectile | Request PDF. Acta Armamentarii 2007, 28, 796–799. [Google Scholar]
- Ginn, J.M.; Clark, I.G.; Braun, R.D. Parachute Dynamic Stability and the Effects of Apparent Inertia. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Atlanta, GA, USA, 16 June 2014. [Google Scholar]
- Ray, E. A Symmetric Time-Varying Cluster Rate of Descent Model. In Proceedings of the 23rd AIAA Aerodynamic Decelerator Systems Technology Conference, Daytona Beach, FL, USA, 30 March 2015. [Google Scholar]
- Machin, R.; Ray, E. Pendulum Motion in Main Parachute Clusters. In Proceedings of the 23rd AIAA Aerodynamic Decelerator Systems Technology Conference, Daytona Beach, FL, USA, 30 March 2015. [Google Scholar]
- Ray, E.; Janssen, S.A. Orion Main Parachute Asymmetry Testing Revisited. In Proceedings of the 26th AIAA Aerodynamic Decelerator Systems Technology Conference, Toulouse, France, 16 May 2022. [Google Scholar]
- Edwards, T.; Loya, A.; Stickley, I.; Yechout, T. Stability Characterization of the Orion Parachute System during Final Re-Entry Phase. In Proceedings of the 2024 Regional Student Conferences, Region V-Mid-West, St. Louis, MI, USA, 5–6 April 2024. [Google Scholar]
- Pei, J. Nonlinear Analysis of a Two-Parachute System Undergoing Pendulum Motion. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17 June 2019. [Google Scholar]
- Zhang, G.; Zou, W.; Zhang, Q.; Feng, Z.; Zhang, M.; Yang, T. Stability Analysis of the Parachute System with a Data-Driven Approach. J. Guid. Control Dyn. 2023, 46, 127–140. [Google Scholar] [CrossRef]
- Huang, X.; Xu, C.; Guo, M.; Li, M.; Hu, J.; Wang, X.; Zhao, Y.; Liu, W. Tianwen-1 Entry, Descent, and Landing Guidance, Navigation, and Control System Design and Validation. J. Spacecr. Rocket. 2023, 60, 1983–2002. [Google Scholar] [CrossRef]
- Goodrick, T. Comparison of Simulation and Experimental Data for a Gliding Parachute in Dynamic Flight. In Proceedings of the 7th Aerodynamic Decelerator and Balloon Technology Conference, San Diego, CA, USA, 21 October 1981. [Google Scholar]
- Slegers, N.; Costello, M. Aspects of Control for a Parafoil and Payload System. J. Guid. Control Dyn. 2003, 26, 898–905. [Google Scholar] [CrossRef]
- Toglia, C.; Vendittelli, M. Modeling and Motion Analysis of Autonomous Paragliders. Department of Computer and System Sciences Antonio Ruberti Technical Reports, 2, 2010. Available online: https://rosa.uniroma1.it/rosa00/index.php/dis_technical_reports/article/view/8850 (accessed on 3 March 2010).
- Vishniak, A. Simulation of the Payload-Parachute-Wing System Flight Dynamics. In Proceedings of the Aerospace Design Conference, Irvine, CA, USA, 16 February 1993. [Google Scholar]
- Yang, H.; He, W. Modeling and Simulation of 15-DOF Parafoil Dynmics. Spacecr. Recovery Remote Sens. 2018, 39, 45–52. [Google Scholar]
- Zhang, Q.; Gao, F.; Guo, R.; Feng, Z.; Ge, J. Multibody Dynamics Modeling of Powered Parafoil System Using Equations with Quasi-Coordinates. Acta Armamentarii 2019, 40, 1935–1942. [Google Scholar]
- Cui, Z.; Zou, W.; Feng, Z.; Zhang, Q.; Yang, T. Sparse Identification of Parafoil Dynamics Model for Path Planning. Aeronaut. J. 2025, 1–21. [Google Scholar] [CrossRef]
- Chang, H. GSWorld: Closed-Loop Photo-Realistic Simulation Suite for Robotic Manipulation. Master’s Thesis, University of California, Los Angeles, CA, USA, 2025. [Google Scholar]
- Deng, J.; Gong, M.; Du, Z.; Zhou, Z.; Chen, H.; Xiao, W.; Guan, C. Design and Implementation of Immersive Interactive Simulation System for Ship Engine Room. Chin. J. Ship Res. 2023, 18, 31–39. [Google Scholar] [CrossRef]
- Han, P.; Wang, Z.; Nan, G.; Xie, Y.; Li, J.; Zhang, Z. Small Disturbance Modeling and Stability Analysis of Doubly-Fed Wind Power System Considering Synchronization Mechanism. Electr. Power Autom. Equip. 2023, 43, 47–54. [Google Scholar]
- Huang, S.; Lu, Y.; Zhu, Q.; Li, K.; Shi, J. Cooperative Circumnavigating of Unknown Target by Multi-UAV Using Only Distance Measurements. Acta Aeronaut. Astronaut. Sin. 2024, 45, 341–361. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Zhou, X.; Peng, Y.; Sheng, H.; Alsaadi, F.E. Time-Dependent Vehicle Routing Problem with Time Windows of City Logistics with a Congestion Avoidance Approach. Knowl. Based Syst. 2020, 188, 104813. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Y.; Hou, M.; Luo, J.; Xie, X. Solving Emden–Fowler Equations Using Improved Extreme Learning Machine Algorithm Based on Block Legendre Basis Neural Network. Neural Process. Lett. 2023, 55, 7135–7154. [Google Scholar] [CrossRef]
- Chen, X.; Xu, G.; Xu, X.; Jiang, H.; Tian, Z.; Ma, T. Multicenter Hierarchical Federated Learning with Fault-Tolerance Mechanisms for Resilient Edge Computing Networks. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 47–61. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Y.; Liu, W.; Yang, Q.; Mao, X.; Li, F. Trust Based Task Offloading Scheme in UAV-Enhanced Edge Computing Network. Peer-Peer Netw. Appl. 2021, 14, 3268–3290. [Google Scholar] [CrossRef]
- Dong, L.; Liu, Z.; Jiang, F.; Wang, K. Joint Optimization of Deployment and Trajectory in UAV and IRS-Assisted IoT Data Collection System. IEEE Internet Things J. 2022, 9, 21583–21593. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X. Truthful Resource Trading for Dependent Task Offloading in Heterogeneous Edge Computing. Future Gener. Comput. Syst. 2022, 133, 228–239. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, Y.; Wang, K.; Dong, L.; Yang, K. MARS: A DRL-Based Multi-Task Resource Scheduling Framework for UAV with IRS-Assisted Mobile Edge Computing System. IEEE Trans. Cloud Comput. 2023, 11, 3700–3712. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Yan, K.; Li, W.; Wang, K.I.-K.; Ma, J.; Jin, Q. Edge-Enabled Two-Stage Scheduling Based on Deep Reinforcement Learning for Internet of Everything. IEEE Internet Things J. 2023, 10, 3295–3304. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, K.; Dong, L.; Pan, C.; Yang, K. Stacked Autoencoder-Based Deep Reinforcement Learning for Online Resource Scheduling in Large-Scale MEC Networks. IEEE Internet Things J. 2020, 7, 9278–9290. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, X.; Cui, X.; Shi, J.; Liang, W.; Yan, Z.; Yang, L.T.; Shimizu, S.; Wang, K.I.-K. Digital Twin Enhanced Federated Reinforcement Learning with Lightweight Knowledge Distillation in Mobile Networks. IEEE J. Sel. Areas Commun. 2023, 41, 3191–3211. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, D.; Chen, X.; Xu, X.; Xu, Z. Capital Equilibrium Strategy for Uncertain Multi-Model Systems. Inf. Sci. 2024, 653, 119607. [Google Scholar] [CrossRef]
- Zhou, X.; Tian, J.; Wang, Z.; Yang, C.; Huang, T.; Xu, X. Nonlinear Bilevel Programming Approach for Decentralized Supply Chain Using a Hybrid State Transition Algorithm. Knowl. Based Syst. 2022, 240, 108119. [Google Scholar] [CrossRef]
- Zou, W. Multibody Dynamics Modeling of Parachute and Payload System and Homing Method Based on Data-Driven Approach. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2024. [Google Scholar]
- Desai, P.N.; Prince, J.L.; Queen, E.M.; Schoenenberger, M.M.; Cruz, J.R.; Grover, M.R. Entry, Descent, and Landing Performance of the Mars Phoenix Lander. J. Spacecr. Rocket. 2011, 48, 798–808. [Google Scholar] [CrossRef]
- Guo, P. Research on the Opening Process of Large Parachute System. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Zou, W.; Cui, Z.; Li, G.; Feng, Z.; Wang, Z.; Gao, Q.; Zhang, Q.; Yang, T. Reentry Capsule Reachable Tube Boundary Prediction via Evolutionary Multiobjective Optimization. Int. J. Aerosp. Eng. 2024, 2024, 2311998. [Google Scholar] [CrossRef]


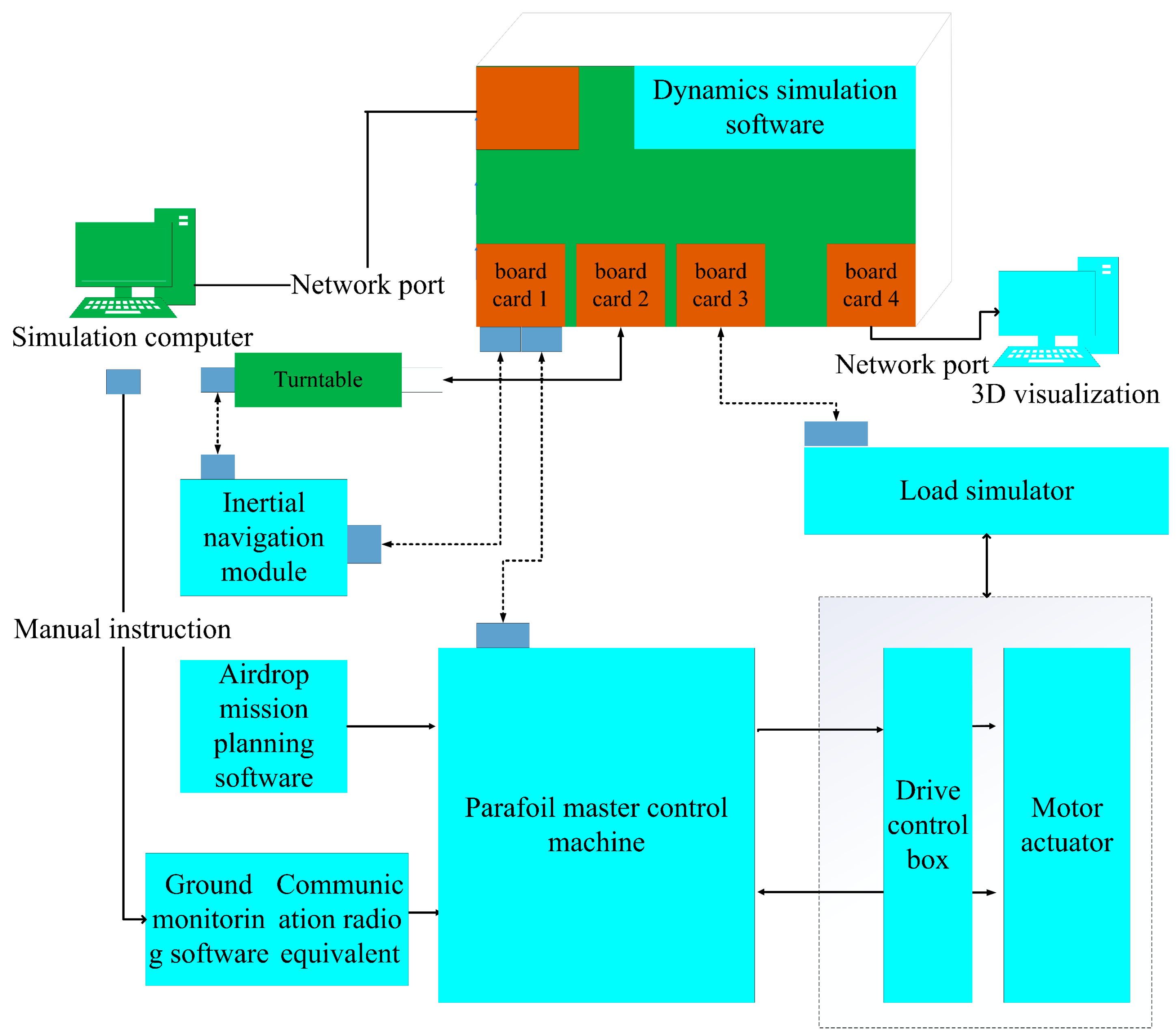


| Component | Elements | Function |
|---|---|---|
| Unit Under Test (UUT) |
| Physical hardware embedded in the simulation loop for performance validation |
| Dynamic Models |
| Real-time emulation of airdrop physics (deceleration/gliding/landing) |
| Emulators |
| Interface fidelity preservation and environmental simulation: |
GNSS Emulator:
| ||
Radio Emulator:
| ||
Load Simulator:
| ||
| Simulators |
| Execute models and render outputs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, W.; Cui, Z.; Li, J.; Zhang, Q. Full Process Dynamics and HIL Simulation of Precise Airdrop System. Electronics 2025, 14, 4285. https://doi.org/10.3390/electronics14214285
Zou W, Cui Z, Li J, Zhang Q. Full Process Dynamics and HIL Simulation of Precise Airdrop System. Electronics. 2025; 14(21):4285. https://doi.org/10.3390/electronics14214285
Chicago/Turabian StyleZou, Wen, Zhanxin Cui, Jiaoyan Li, and Qingbin Zhang. 2025. "Full Process Dynamics and HIL Simulation of Precise Airdrop System" Electronics 14, no. 21: 4285. https://doi.org/10.3390/electronics14214285
APA StyleZou, W., Cui, Z., Li, J., & Zhang, Q. (2025). Full Process Dynamics and HIL Simulation of Precise Airdrop System. Electronics, 14(21), 4285. https://doi.org/10.3390/electronics14214285






