Cryptanalysis and Improvement of a Medical Image-Encryption Algorithm Based on 2D Logistic-Gaussian Hyperchaotic Map
Abstract
1. Introduction
- (1)
- The cryptographic analysis of the color medical image-encryption scheme proposed by Lai et al. [27] is carried out, and some security defects are found. Furthermore, we propose a cryptanalysis method incorporating differential analysis, CPA, and KPA. Consequently, the LG-IES based on Shannon’s principle [28] is cracked.
- (2)
- An improved security enhancement scheme is proposed, which uses Secure Hash Algorithm 3 (SHA-3) to establish plaintext-related Rubik’s Cube rotation rules to realize edge-pixel perturbation between channels. The experimental results show that the improved diffusion structure has better chaotic performance and has passed the security analysis.
2. The Image-Encryption Scheme of Lai et al.
2.1. 2D Logistic-Gaussian Hyperchaotic Map
2.2. Description of LG-IES
2.2.1. The Secret Key
- -
- : Two different original initial value for the chaotic sequence.
- -
- : The correlation coefficients for and , respectively.
- -
- : The original control parameter.
- -
- d: A perturbation coefficient.
2.2.2. One-Round Permutation
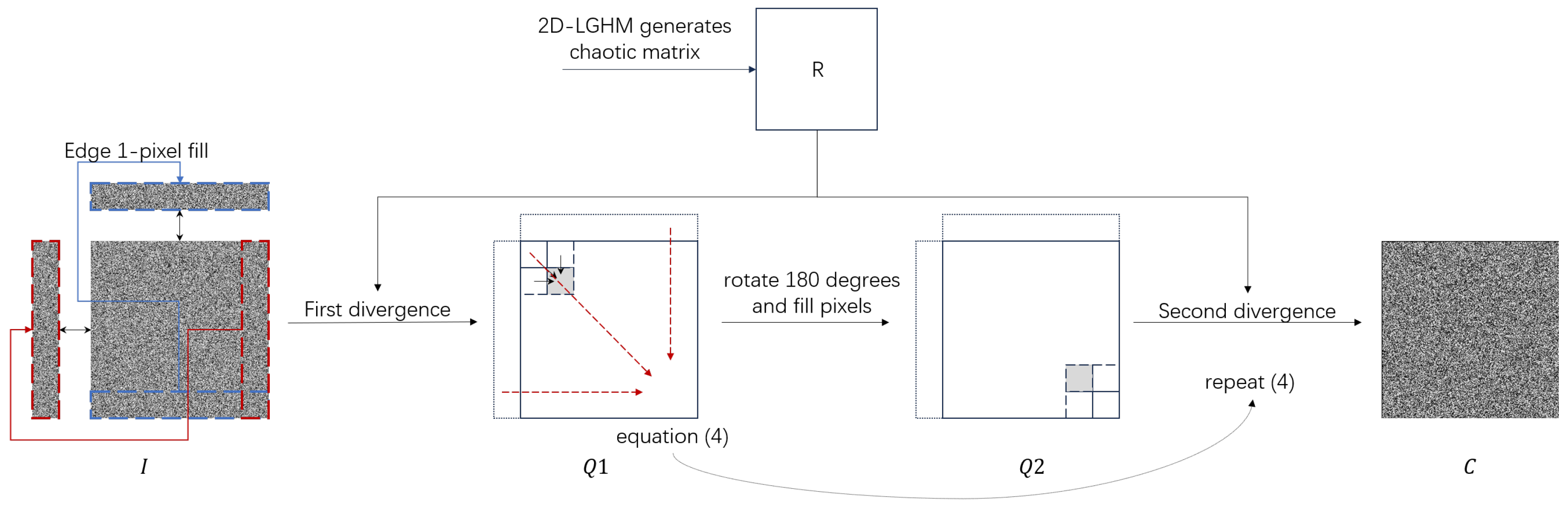
2.2.3. Two Round Diffusions
2.2.4. Encryption Algorithm of LG-IES
3. Cryptanalysis
3.1. Relevant Properties
- The first divergence:According to Equation (4) and the definition of difference image, can be written as:Here, due to the characteristics of the differential, the term is eliminated, so the difference equation for the first divergence of the first-round result does not include the chaotic matrix R.
- Rotation operation:The rotation operation does not change the difference relationship between the matrix elements. Therefore, the difference matrix retains the same difference structure as and still does not contain the terms of the chaotic matrix R.
- The second divergence:The difference equation for isSimilarly, in this differential analysis, the influence of the chaotic matrix R is eliminated. So it holds.
- If , satisfies
- Else if , satisfies
- Else if , satisfies
- If , satisfies Equation (9).
- Else if , satisfies
- Else if , satisfieswhere and .
- If , satisfies
- Else if , satisfies
- Else if , satisfies Equation (11).
3.2. Model Analysis
3.3. Chosen-Plaintext and Known-Plaintext Attacks
- (1)
- When , the key space shrinks by , reducing from to 1.
- (2)
- When , the key space shrinks by a factor of , and the security (in terms of bits) is reduced by bits.
4. Proposed SHA-3-EPFA
4.1. Encryption Scheme
| Algorithm 1: Unit Rubik’s Cube Rotation. |
| Input: cube (The Rubik’s Cube before rotation) Output: newcube (The Rubik’s Cube after rotation) for i in range : if : elif : elif : update |
4.2. Decryption Process
5. Simulation Results and Security Analysis
5.1. Simulation Results
5.2. Key Sensitivity
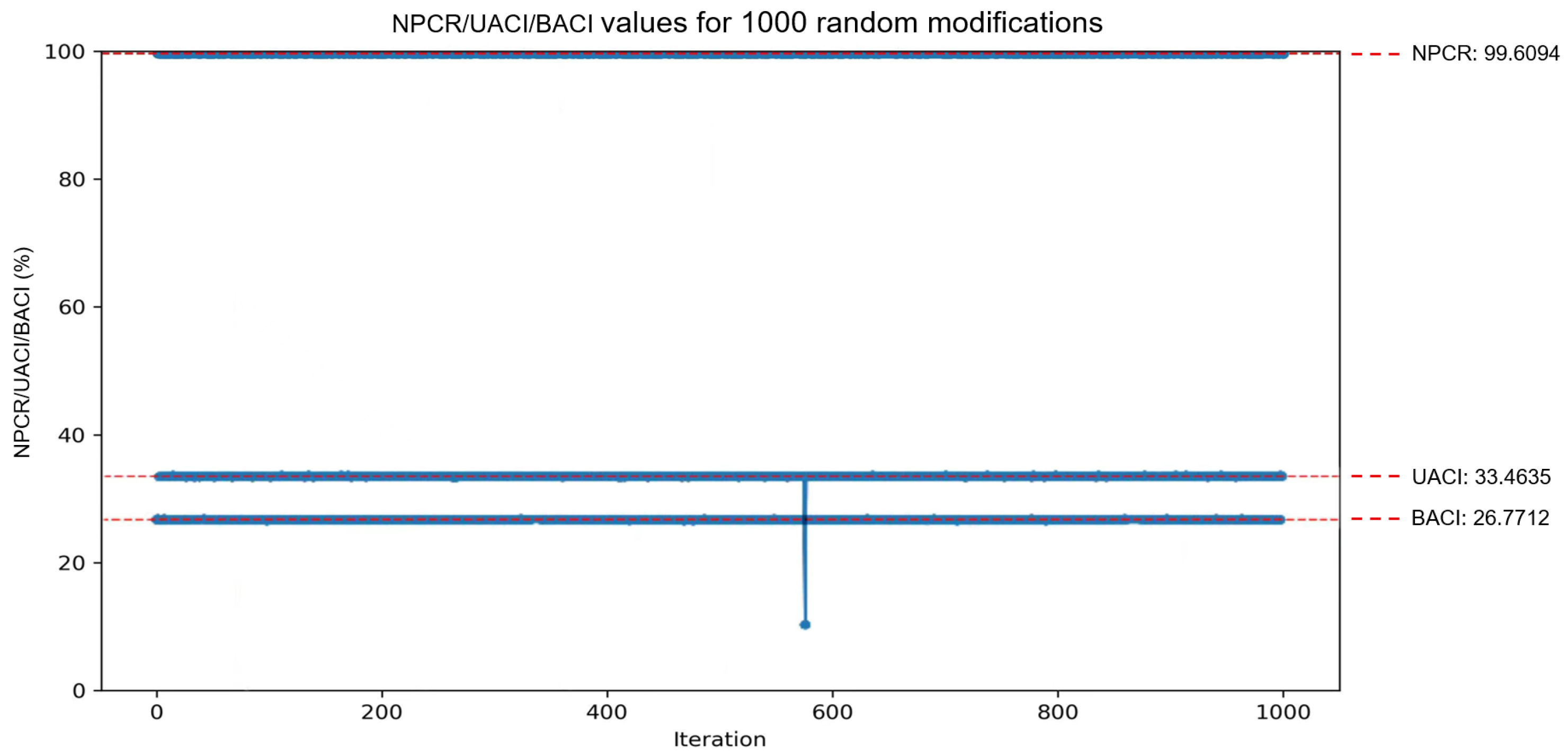
5.3. Plaintext Sensitivity Analysis
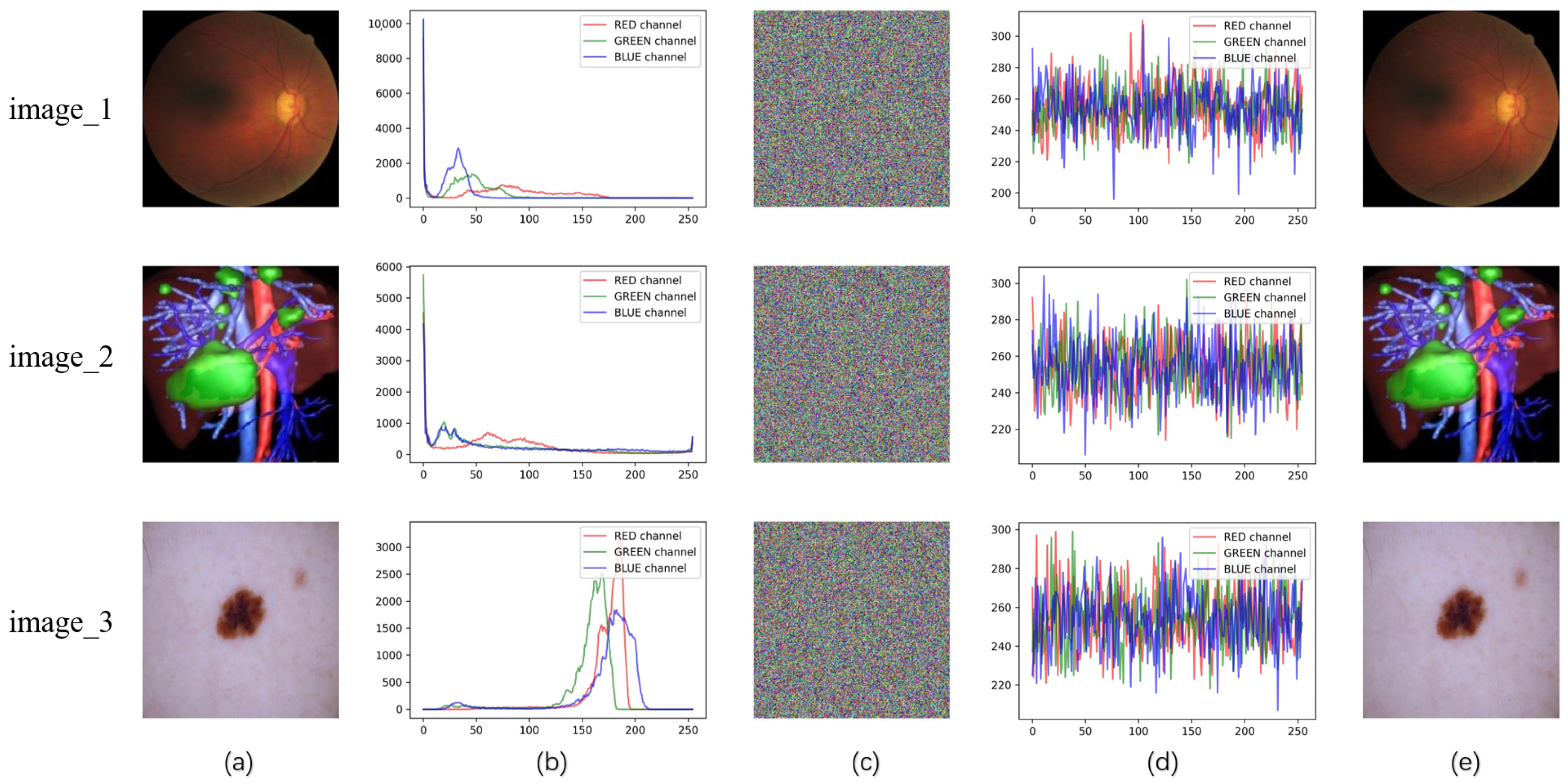
5.4. Histogram Analysis
5.5. Correlation Analysis
5.6. Entropy Analysis
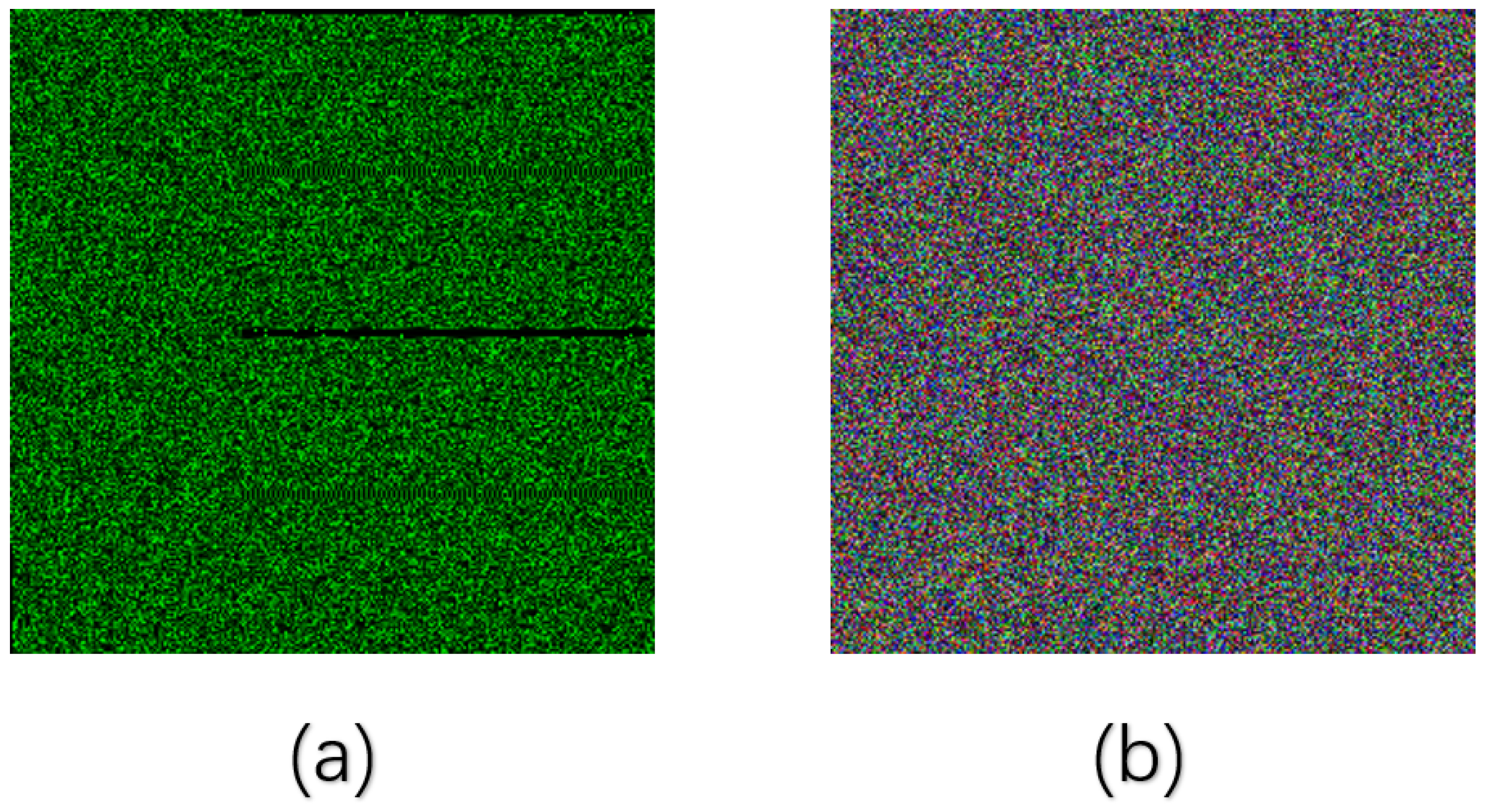
5.7. Noise and Cropping Attacks
5.8. Attacks Resistance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Specific Multi-Directional Diffusion Demonstration
Appendix B. Intermediate Ciphertext Representation of Example 2
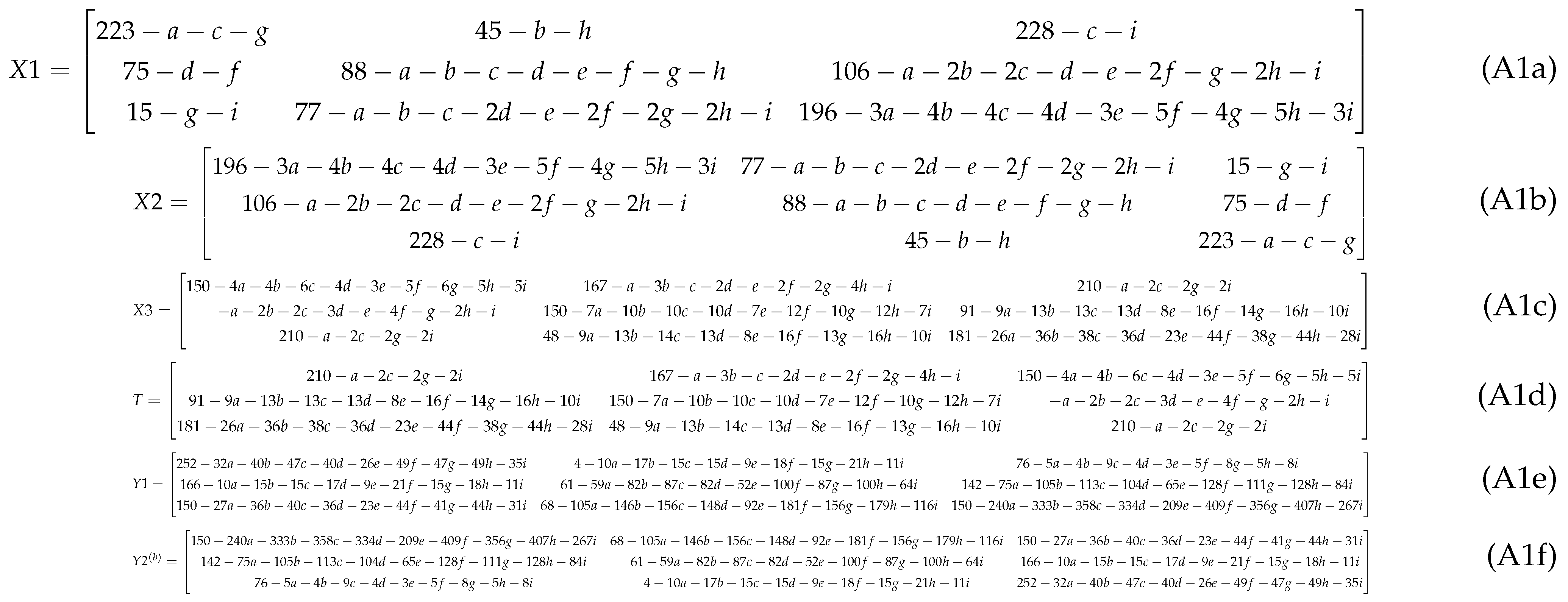
References
- Zinger, S.; Ruijters, D.; Do, L.; de With, P.H. View interpolation for medical images on autostereoscopic displays. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 128–137. [Google Scholar] [CrossRef]
- Liu, H.; Teng, L.; Zhang, Y.; Si, R.; Liu, P. Mutil-medical image encryption by a new spatiotemporal chaos model and DNA new computing for information security. Expert Syst. Appl. 2024, 235, 121090. [Google Scholar] [CrossRef]
- Kaissis, G.A.; Makowski, M.R.; Rückert, D.; Braren, R.F. Secure, privacy-preserving and federated machine learning in medical imaging. Nat. Mach. Intell. 2020, 2, 305–311. [Google Scholar] [CrossRef]
- Kaissis, G.; Ziller, A.; Passerat-Palmbach, J.; Ryffel, T.; Usynin, D.; Trask, A.; Lima, I., Jr.; Mancuso, J.; Jungmann, F.; Steinborn, M.M.; et al. End-to-end privacy preserving deep learning on multi-institutional medical imaging. Nat. Mach. Intell. 2021, 3, 473–484. [Google Scholar] [CrossRef]
- Ziller, A.; Mueller, T.T.; Stieger, S.; Feiner, L.F.; Brandt, J.; Braren, R.; Rueckert, D.; Kaissis, G. Reconciling privacy and accuracy in AI for medical imaging. Nat. Mach. Intell. 2024, 6, 764–774. [Google Scholar] [CrossRef]
- Data Encryption Standard. Data Encryption standard. Fed. Inf. Process. Stand. Publ. 1999, 112, 3. [Google Scholar]
- Paar, C.; Pelzl, J.; Paar, C.; Pelzl, J. The advanced encryption standard (AES). Understanding Cryptography: A Textbook for Students and Practitioners; Springer: Berlin/Heidelberg, Germany, 2010; pp. 87–121. [Google Scholar]
- Wang, X.; Zhao, M. An image encryption algorithm based on hyperchaotic system and DNA coding. Opt. Laser Technol. 2021, 143, 107316. [Google Scholar] [CrossRef]
- Yildirim, M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit. Chaos Solitons Fractals 2022, 155, 111631. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Jiang, D. A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3D DCT. Inf. Sci. 2021, 574, 505–527. [Google Scholar] [CrossRef]
- Wang, C.; Song, L. An image encryption scheme based on chaotic system and compressed sensing for multiple application scenarios. Inf. Sci. 2023, 642, 119166. [Google Scholar] [CrossRef]
- Brahim, A.H.; Pacha, A.A.; Said, N.H. Image encryption based on compressive sensing and chaos systems. Opt. Laser Technol. 2020, 132, 106489. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Upadhyay, D.; Gaikwad, N.; Zaman, M.; Sampalli, S. Investigating the avalanche effect of various cryptographically secure Hash functions and Hash-based applications. IEEE Access 2022, 10, 112472–112486. [Google Scholar] [CrossRef]
- Yuan, F.; Deng, Y.; Li, Y.; Chen, G. A cascading method for constructing new discrete chaotic systems with better randomness. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 053120. [Google Scholar] [CrossRef]
- Hamza, R.; Yan, Z.; Muhammad, K.; Bellavista, P.; Titouna, F. A privacy-preserving cryptosystem for IoT E-healthcare. Inf. Sci. 2020, 527, 493–510. [Google Scholar] [CrossRef]
- Mehdi, S.A.; Ali, Z.L. Image encryption algorithm based on a novel six-dimensional hyper-chaotic system. Al-Mustansiriyah J. Sci. 2020, 31, 54–63. [Google Scholar] [CrossRef]
- Liu, X.l.; Xu, K.s.; Kang, Z.c.; Xu, M.t.; Wang, M.m. New 2D inserting-log-logistic-sine chaotic map with applications in highly robust image encryption algorithm. Nonlinear Dyn. 2025, 113, 17227–17256. [Google Scholar] [CrossRef]
- Masood, F.; Boulila, W.; Alsaeedi, A.; Khan, J.S.; Ahmad, J.; Khan, M.A.; Rehman, S.U. A novel image encryption scheme based on Arnold cat map, Newton-Leipnik system and Logistic Gaussian map. Multimed. Tools Appl. 2022, 81, 30931–30959. [Google Scholar] [CrossRef]
- Chen, J.x.; Zhu, Z.l.; Fu, C.; Zhang, L.b.; Zhang, Y. An efficient image encryption scheme using lookup table-based confusion and diffusion. Nonlinear Dyn. 2015, 81, 1151–1166. [Google Scholar] [CrossRef]
- Grošek, O.; Sỳs, M. Isotopy of Latin squares in cryptography. Tatra Mt. Math. Publ. 2010, 45, 27–36. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Wang, Y.; Li, X. Cryptanalysis of a chaotic image cipher using Latin square-based confusion and diffusion. Nonlinear Dyn. 2017, 88, 1305–1316. [Google Scholar] [CrossRef]
- Li, M.; Lu, D.; Xiang, Y.; Zhang, Y.; Ren, H. Cryptanalysis and improvement in a chaotic image cipher using two-round permutation and diffusion. Nonlinear Dyn. 2019, 96, 31–47. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Q. Cryptanalysis and improvement of an image encryption algorithm based on chaotic and Latin square. Nonlinear Dyn. 2023, 111, 3831–3850. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, C.; Ye, R. Cryptanalysis and improvement of medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. 2020, 167, 107286. [Google Scholar] [CrossRef]
- Gaur, K.S.; Singh, H.; Thakran, S. Cryptanalysis of the optical cryptosystem titled “an asymmetric image encryption based on phase truncated hybrid transform”. J. Opt. 2024, 53, 605–609. [Google Scholar] [CrossRef]
- Lai, Q.; Hu, G.; Erkan, U.; Toktas, A. High-efficiency medical image encryption method based on 2D Logistic-Gaussian hyperchaotic map. Appl. Math. Comput. 2023, 442, 127738. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Kiefer, R.; Abid, M.; Steen, J.; Ardali, M.R.; Amjadian, E. A Catalog of Public Glaucoma Datasets for Machine Learning Applications: A detailed description and analysis of public glaucoma datasets available to machine learning engineers tackling glaucoma-related problems using retinal fundus images and OCT images. In Proceedings of the 2023 7th International Conference on Information System and Data Mining, Atlanta, GA, USA, 10–12 May 2023; pp. 24–31. [Google Scholar]
- Soler, L.; Hostettler, A.; Agnus, V.; Charnoz, A.; Fasquel, J.; Moreau, J.; Osswald, A.; Bouhadjar, M.; Marescaux, J. 3D Image Reconstruction for Comparison of Algorithm Database: A Patient Specific Anatomical and Medical Image Database; Technical Report; IRCAD: Strasbourg, France, 2010. [Google Scholar]
- International Skin Imaging Collaboration. ISIC Image Archive. 2024. Available online: https://www.isic-archive.com/ (accessed on 23 July 2024).
- Feng, W.; Zhang, J. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, L.; Li, T. Hyper-chaotic color image encryption based on 3D orthogonal Latin cubes and RNA diffusion. Multimed. Tools Appl. 2024, 83, 22571–22594. [Google Scholar] [CrossRef]
- Mohamed, H.G.; ElKamchouchi, D.H.; Moussa, K.H. A novel color image encryption algorithm based on hyperchaotic maps and mitochondrial DNA sequences. Entropy 2024, 22, 158. [Google Scholar] [CrossRef]
- Raghuvanshi, K.K.; Kumar, S.; Kumar, S.; Kumar, S. Image encryption algorithm based on DNA encoding and CNN. Expert Syst. Appl. 2024, 252, 124287. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Tan, R.C.; Lei, T.; Zhao, Q.M.; Gong, L.H.; Zhou, Z.H. Quantum Color Image Encryption Algorithm Based on A Hyper-Chaotic System and Quantum Fourier Transform. Int. J. Theor. Phys. 2016, 55, 5368–5384. [Google Scholar] [CrossRef]
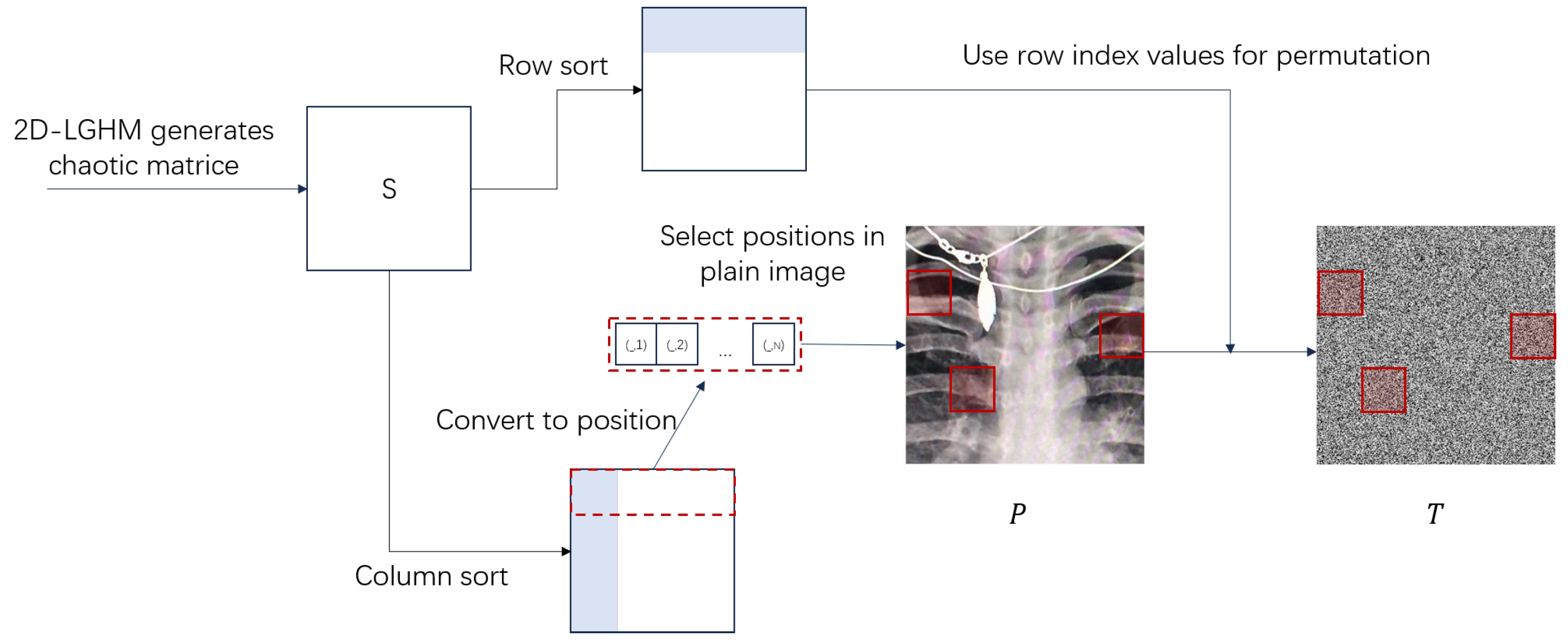
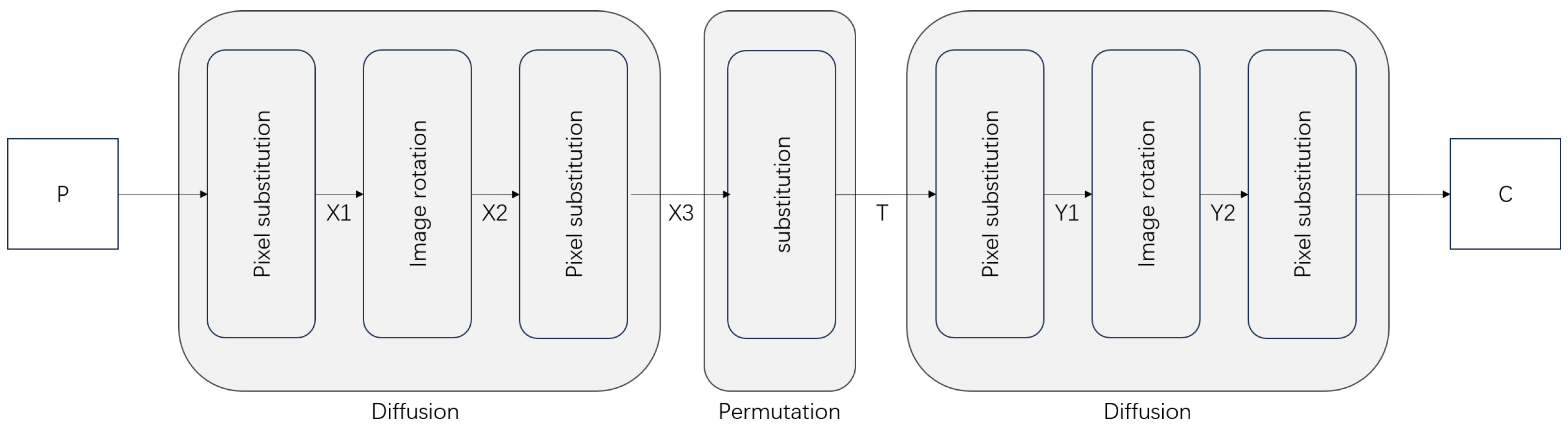




| Permuted image | |
| First diffused image | |
| Rotated image | |
| Second diffused image (Cipher image) | |
| Image Size | Rank r | Reduced Key Space | Time to Solve for R |
|---|---|---|---|
| 6 | |||
| 8 | |||
| 9 | 1 | ||
| 4000 | |||
| 4050 | |||
| 65,536 | 1 | ||
| 64,000 | |||
| 65,000 | |||
| 65,536 | 1 |
| Image Size | Scheme Type | Test Medical Image | Encryption/Decryption Time (s) | |
|---|---|---|---|---|
| Encryption Time (s) | Decryption Time (s) | |||
| 256 × 256 | LG-IES | image_1 | 0.38/0.53 | 0.42/0.53 |
| image_2 | 0.39/0.53 | 0.43/0.56 | ||
| ILG-IES | image_3 | 0.38/0.52 | 0.41/0.55 | |
| 256 × 256 × 256 | LG-IES | image_1 | 8.25/9.83 | 8.63/11.23 |
| image_2 | 8.51/8.54 | 8.87/9.87 | ||
| ILG-IES | image_3 | 8.38/8.90 | 8.72/9.02 | |
| 512 × 512 × 512 | LG-IES | image_1 | 18.72/22.13 | 19.35/23.58 |
| image_2 | 16.34/17.05 | 15.68/15.98 | ||
| ILG-IES | image_3 | 17.13/18.89 | 16.23/16.52 | |
| NPCR | UACI | BACI | ||||
|---|---|---|---|---|---|---|
| LG-IES | ILG-IES | LG-IES | ILG-IES | LG-IES | ILG-IES | |
| image_1 | 99.6740 | 99.6119 | 33.4584 | 33.5656 | 26.7960 | 26.8272 |
| image_2 | 99.5889 | 99.6358 | 33.2972 | 33.4185 | 26.7474 | 26.7764 |
| image_3 | 99.5453 | 99.6002 | 33.4222 | 33.5392 | 26.7254 | 26.8079 |
| Ref. [32] | 99.6189 | 33.4707 | - | |||
| Ref. [33] | 99.8515 | 33.5136 | - | |||
| Ref. [34] | 99.6168 | 33.4833 | - | |||
| Ref. [35] | 99.6350 | 33.3100 | - | |||
| Theoretical value | 99.6094 | 33.4635 | 26.7712 | |||
| R | G | B | ||||
|---|---|---|---|---|---|---|
| LG-IES | ILG-IES | LG-IES | ILG-IES | LG-IES | ILG-IES | |
| image_1 | 254.34 | 272.12 | 29.81 | 284.00 | 222.12 | 263,14 |
| image_2 | 274.55 | 255.32 | 274.06 | 238.30 | 251.64 | 242.45 |
| image_3 | 236.32 | 218.99 | 270.45 | 233.89 | 261.43 | 228.01 |
| Ref. [32] | 275.23 | |||||
| Ref. [33] | 258.00 | |||||
| Ref. [34] | 275.00 | |||||
| Ref. [35] | 250.33 | |||||
| Image_1 | LG-IES | ILG-IES | Ref. [32] | Ref. [33] | Ref. [37] | Ref. [35] | ||
|---|---|---|---|---|---|---|---|---|
| R | H | 0.9868 | −0.0026 | 0.0014 | 0.0044 | 0.0134 | −0.0018 | 0.0012 |
| V | 0.9747 | −0.0093 | −0.0023 | −0.0022 | −0.0122 | 0.0043 | 0.0021 | |
| D | 0.9899 | −0.0236 | 0.0018 | 0.0029 | −0.0009 | 0.0007 | 0.0015 | |
| G | H | 0.9765 | −0.0027 | 0.0016 | 0.0027 | 0.0100 | −0.0003 | −0.0014 |
| V | 0.9732 | −0.0052 | −0.0033 | −0.0033 | −0.0002 | 0.0013 | 0.0015 | |
| D | 0.9787 | 0.0169 | −0.0036 | 0.0002 | 0.0128 | 0.0017 | 0.0021 | |
| B | H | 0.9848 | −0.0053 | −0.0049 | 0.0008 | 0.0019 | −0.0023 | −0.0013 |
| V | 0.9788 | −0.0089 | −0.0018 | −0.0010 | −0.0107 | −0.0004 | 0.0003 | |
| D | 0.9821 | −0.0199 | 0.0023 | 0.0031 | −0.0098 | −0.0010 | 0.0017 |
| Image_1 | Image_2 | Image_3 | Ref. [32] | Ref. [33] | Ref. [34] | Ref. [37] | Ref. [35] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LG-IES | ILG-IES | LG-IES | ILG-IES | LG-IES | ILG-IES | ||||||
| R | 7.9973 | 7.9975 | 7.9969 | 7.9969 | 7.9971 | 7.9972 | 7.9971 | 7.9971 | 7.9970 | 7.9959 | 7.9896 |
| G | 7.9971 | 7.9973 | 7.9971 | 7.9976 | 7.9970 | 7.9973 | 7.9972 | 7.9970 | 7.9978 | 7.9951 | 7.9996 |
| B | 7.9969 | 7.9976 | 7.9980 | 7.9974 | 7.9970 | 7.9968 | 7.9972 | 7.9970 | 7.9987 | 7.9957 | 7.9996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Wang, S. Cryptanalysis and Improvement of a Medical Image-Encryption Algorithm Based on 2D Logistic-Gaussian Hyperchaotic Map. Electronics 2025, 14, 4283. https://doi.org/10.3390/electronics14214283
Wu W, Wang S. Cryptanalysis and Improvement of a Medical Image-Encryption Algorithm Based on 2D Logistic-Gaussian Hyperchaotic Map. Electronics. 2025; 14(21):4283. https://doi.org/10.3390/electronics14214283
Chicago/Turabian StyleWu, Wanqing, and Shiyu Wang. 2025. "Cryptanalysis and Improvement of a Medical Image-Encryption Algorithm Based on 2D Logistic-Gaussian Hyperchaotic Map" Electronics 14, no. 21: 4283. https://doi.org/10.3390/electronics14214283
APA StyleWu, W., & Wang, S. (2025). Cryptanalysis and Improvement of a Medical Image-Encryption Algorithm Based on 2D Logistic-Gaussian Hyperchaotic Map. Electronics, 14(21), 4283. https://doi.org/10.3390/electronics14214283






