Improving the Downstream Performance of Mixture-of-Experts Transformers via Weak Vanilla Transformers

Abstract

Recently, mixture-of-experts (MoE) Transformers have garnered increased attention for their advantages in model capacity and computational efficiency. However, studies have indicated that MoE models excel in pre-training but fail to translate those gains to downstream tasks, which diminishes their practical value. To explain this issue, we propose that the pre-training performance and transfer capability of a model jointly determine its downstream task performance. More specifically, we argue that MoE models exhibit weaker transfer capability compared to vanilla models, resulting in inferior performance on downstream tasks. To address this issue, we introduce the concept of transfer capability distillation, positing that although vanilla models have weaker performance, they are effective teachers of transfer capability. The MoE models—guided by vanilla models—can achieve both strong pre-training performance and transfer capability, ultimately enhancing their performance on downstream tasks. We developed a specific distillation method and conducted experiments using the BERT architecture. Experimental results show significant improvements in the downstream performance of MoE models, and further evidence supports the concept of transfer-capability distillation. Finally, we attempt to interpret transfer capability distillation and provide insights from the perspective of model features.

1. Introduction

Recent research has revealed that pre-trained language models demonstrate powerful general capabilities [1,2,3,4] and an exceptional ability to enhance performance through scaling [5,6]. However, scaling up these models incurs significant costs in practical applications due to rapidly increasing computational demands. As a result, there is a growing interest in mixture-of-experts (MoE) models [7,8,9,10,11]. These models process inputs using distinct experts. The number of experts determines the number of parameters while having a limited effect on the computational cost, thereby expanding model capacity with lower computational expense.

However, existing research indicates that while MoE models excel in pre-training language modeling tasks, their efficacy diminishes in downstream tasks, especially when a large number of experts are involved. Fedus et al. [12] proposed the Switch Transformer based on the MoE architecture and revealed that MoE models consistently underperform vanilla models when fine-tuned on the SuperGLUE benchmark [13], when pre-training performances are equivalent. Artetxe et al. [14] conducted more experiments, and their published results likewise show that MoE models consistently achieve weaker fine-tuning results on downstream tasks when pre-training performance is equivalent. Shen et al. [15] similarly observed that, on many downstream tasks, single-task fine-tuned MoE models underperform their dense counterparts.

We conducted a relevant validation experiment, pre-training two scales of vanilla BERT models and MoE-BERT models with 64 experts (top-1 activation), followed by fine-tuning on the GLUE benchmark [16]. Some experimental results are shown in Figure 1. We observe that, for both scales, the MoE-BERT models must reach a much higher level of pre-training performance (as measured by log-likelihood) to achieve GLUE scores comparable to those of the vanilla BERT models. This implies that the pre-training performance gains brought about by introducing multiple experts in MoE-Transformer models do not translate effectively into improvements in downstream task performance, thereby significantly diminishing the practical value of MoE-Transformer models.

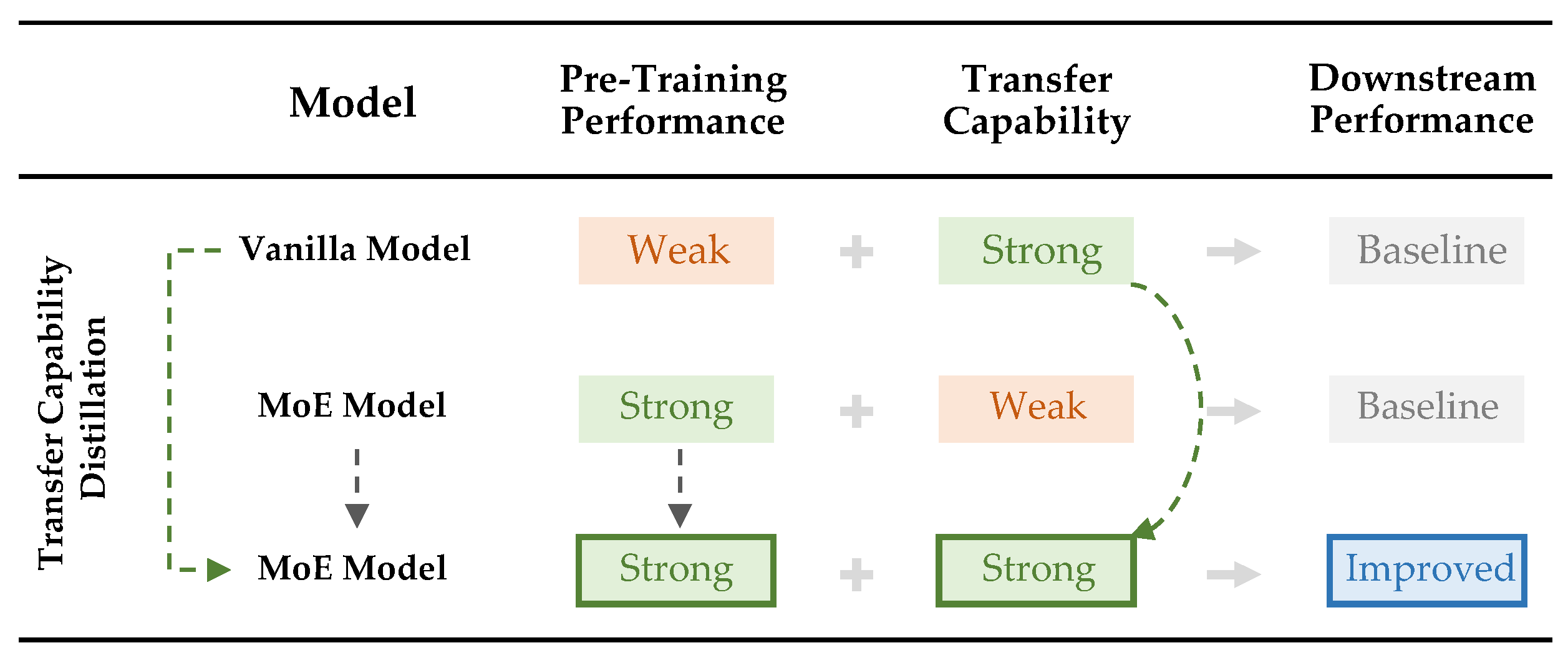
We attempt to address this issue. Initially, we need to explain the poor performance in the downstream tasks of the MoE models. We believe that the downstream performance of a model is determined by both pre-training performance and transfer capability. Pre-training performance is obtained through training, whereas transfer capability is an inherent attribute of the model. The latter is an abstract concept of capability, analogous to generalization capability in a supervised learning setting, which determines the extent to which the former can be converted into downstream performance. Vanilla models—despite their smaller capacity and weaker pre-training performance—possess strong transfer capability. In contrast, MoE models, although having larger capacity and stronger pre-training performance, exhibit only weak transfer capability. We believe that the poor performance of MoE models in downstream tasks is due to their limited transfer capability, as summarized in Figure 2.

Based on the above explanation, we propose a solution to this issue—since the transfer capability of vanilla models is strong, it may be possible to transfer this capability to MoE models through distillation. We call this idea transfer capability distillation (TCD). The underlying logic is that although the pre-training and downstream performance of vanilla models are relatively weak, their transfer capability is stronger. By using them as teachers, we can enhance the transfer capability of MoE models. Combined with the strong pre-training performance of MoE models, this approach could lead to a comprehensive improvement in MoE models, as depicted in Figure 2.

The most counterintuitive feature of this method in the pre-training domain is that a teacher model—inferior in both pre-training and downstream performance—can paradoxically distill a student model that is superior in those aspects.

Based on the above ideas, we designed a distillation scheme and conducted experiments. Some results are shown in Figure 1. The results indicate that the downstream performance of the MoE model with TCD not only improves over that of the original MoE model but also surpasses that of its teacher model. This supports the concept of transfer capability distillation, demonstrating its effectiveness in improving MoE models.

Moreover, we further discuss the differences in transfer capability from a model-feature perspective and explain why our distillation method is effective.

The contributions of our work are as follows:

• We differentiate between pre-training performance and transfer capability as distinct influencers of downstream performance, attributing the poor downstream performance of MoE models to their inferior transfer capability.
• We introduce transfer capability distillation, identifying vanilla Transformers as effective teachers and proposing a distillation scheme to enhance transfer capability.
• Through transfer capability distillation, we address the issue of weak transfer capability in MoE models, thereby enhancing downstream performance.
• We provide insights into the differences in transfer capability from a model feature perspective and offer a basic explanation of the mechanisms of transfer capability distillation.

The remainder of this paper is organized as follows. Section 2 reviews the related work relevant to this study. Section 3 details the proposed method. Section 4 describes the experimental setup and reports the results. Section 5 presents a comprehensive comparison between transfer capability distillation and general knowledge distillation. Section 6 provides an in-depth analysis to explain why transfer capability distillation works effectively. Finally, Section 8 concludes the paper.

2. Related Work

Our work is related to mixture-of-experts (MoE) models and general knowledge distillation.

The MoE model is a type of dynamic neural network that excels in expanding model capacity with low computational cost. Shazeer et al. [8] added an MoE layer to LSTM, showing for the first time that MoE architecture can be adapted to deep neural networks. Lepikhin et al. [9] enhanced machine translation performance using a Transformer model with the MoE architecture. Fedus et al. [12] introduced the well-known Switch Transformers, demonstrating the application of MoE Transformers in pre-trained language models. Artetxe et al. [14] conducted extensive experiments on MoE-Transformer models, establishing their significant efficiency advantages over dense language models. Our work builds upon the existing MoE layer design, enhancing transfer capability in a non-invasive manner.

General knowledge distillation primarily aims to reduce model size and computational cost. Hinton et al. [17] initially proposed knowledge distillation, transferring knowledge learned on a large model to a smaller model. This concept was later adapted to pre-trained language models. Sun et al. [18] compressed BERT into a shallower model through output distillation and hidden representation distillation. Sanh et al. [19] successfully halved the number of BERT layers through distillation during both pre-training and fine-tuning stages. Jiao et al. [20] designed a distillation for BERT with multi-position constraints, also covering both stages. Sun et al. [21] proposed a distillation pre-training method from large dense models to small dense models, which can retain transfer capability and offer greater versatility. Our work is different from general knowledge distillation. Although our work in transfer capability distillation extends the general techniques of general knowledge distillation, it differs significantly in its application. General knowledge distillation focuses on distilling either pre-training performance or task-specific performance for model compression, whereas transfer capability distillation distills the abstract transfer capability to enhance the performance of student models. Therefore, there is a fundamental difference between transfer capability distillation and general knowledge distillation.

3. Method

3.1. Overview

In this work, we propose a transfer capability distillation scheme. The core idea is as follows:

First, a teacher model with low capacity but strong transfer capability is pre-trained, exhibiting weaker performance in both pre-training and downstream tasks. Then, during the pre-training of the high-capacity student model, not only is the original pre-training loss optimized, but an additional transfer capability distillation loss is also applied. Finally, the student model acquires strong transfer capability on top of strong pre-training performance, achieving transfer capability distillation.

In the following sections, we will first introduce the vanilla BERT model as the teacher model and the MoE-BERT as the student model. Subsequently, we introduce the specific implementation of transfer capability distillation and conclude with an overview of the training process.

3.2. Vanilla BERT and MoE-BERT

Our work concerns two BERT architectures: vanilla BERT and MoE-BERT. Vanilla BERT has a smaller capacity and weaker pre-training performance but exhibits strong transfer capability, making it suitable as a teacher model. MoE-BERT has a larger capacity and stronger pre-training performance but weaker transfer capability, serving as the student model.

The structure of vanilla BERT, as shown on the left side of Figure 3, consists of stacked multi-head attention (MHA) and feed-forward networks (FFNs), employing a post-layer-normalization scheme for residuals and normalization. We follow the architectural design of Devlin et al. [1], retaining the original structure of the BERT model. We denote the original masked-language-modeling loss in the pre-training phase as ${\mathcal{L}}_{MLM}$.

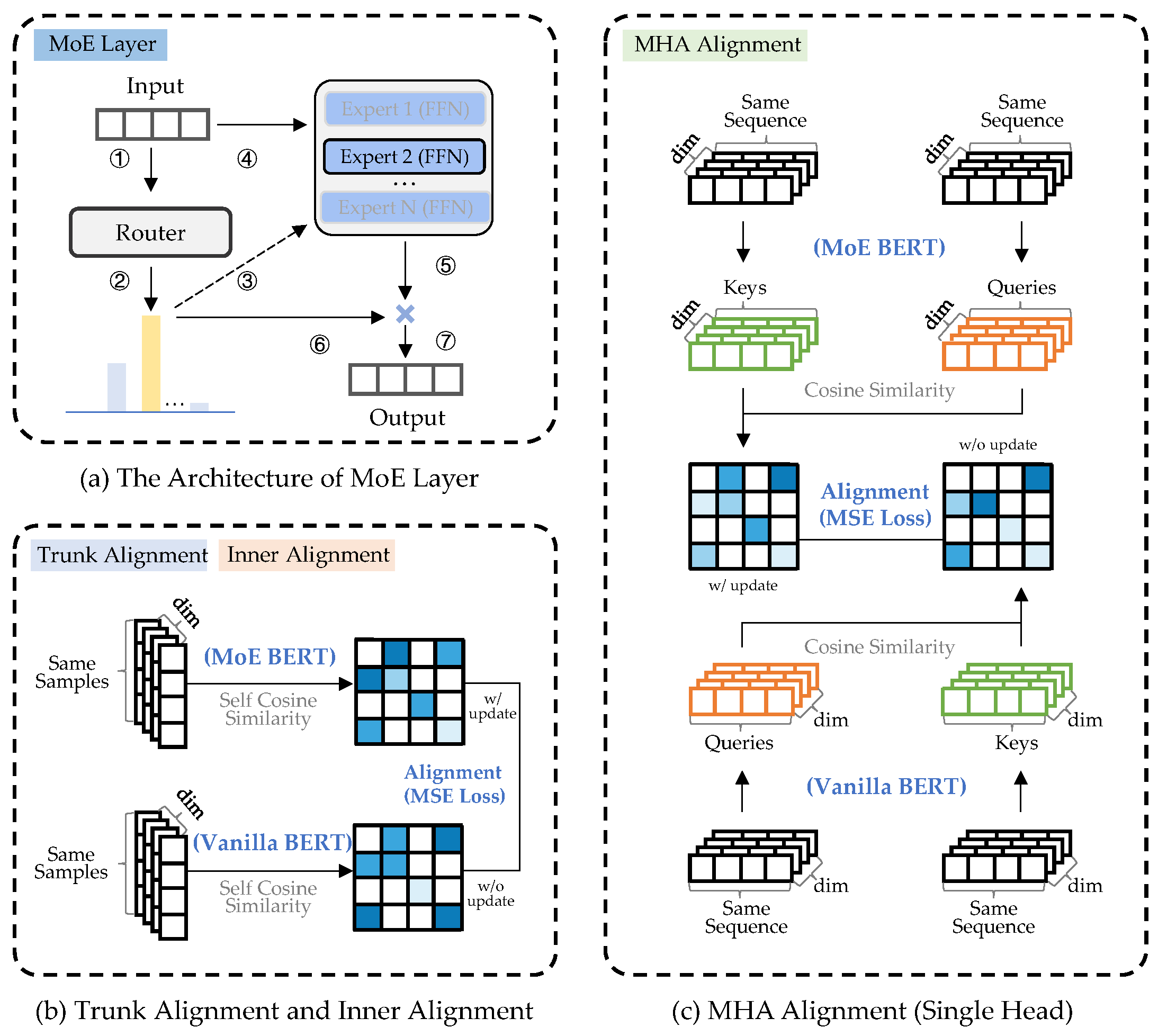
The structure of MoE-BERT, as shown on the right side of Figure 3, differs from vanilla BERT by replacing all FFN layers with MoE layers. The basic structure of an MoE layer, as illustrated in Figure 4a, does not consist of a single FFN but rather includes multiple FFNs, also known as experts. When the hidden representation of a token is fed into an MoE layer, a routing module (a linear layer with softmax activation) first predicts the probability of it being processed by each expert, and the token’s hidden representation is then processed only by the top-k experts according to these probabilities.

Assume the hidden representation is $\mathbf{x}$, and the parameters of the routing module are ${\mathbf{W}}_r$ and ${\mathbf{b}}_r$, then the process of calculating the probability of selecting each expert is as follows:

$$p\left(\mathbf{x}\right)=\mathrm{softmax}({\mathbf{W}}_r\mathbf{x}+{\mathbf{b}}_r)$$

(1)

In this work, we adhere to two key practices of the Switch Transformer [12]:

1. Only the top-1 expert, in terms of probability, processes the hidden representation. The process for determining the expert index is as follows:

$$i=\underset{k}{\mathrm{argmax}}{p}_k\left(\mathbf{x}\right)$$

(2)

2. The hidden representation of the token is first processed by the expert and then multiplied by the probability of selecting that expert to obtain the final representation. This strategy enables effective gradient-descent optimization for the routing module and has been shown to be relatively stable. No additional stabilization measures were adopted in our work. Assume the set of all experts is ${\left\{E_k\left(\mathbf{x}\right)\right\}}_{k=1}^N$, and the processing is as follows:

$$\mathbf{h}=p_i\left(\mathbf{x}\right)E_i\left(\mathbf{x}\right)$$

(3)

Additionally, for expert load balancing, we calculate the Kullback–Leibler divergence between the average probability distribution of experts selected within a batch and a uniform distribution, adding it as an additional loss term.

Assuming there are M hidden representations in a batch and that the vector of the uniform probability distribution is $\mathbf{p}$, the process is as follows:

$$\mathbf{q}={\displaystyle \frac{1}{M}}\sum _{j=1}^{M}softmax({\mathbf{W}}_r{\mathbf{x}}_j+{\mathbf{b}}_r)$$

(4)

$${\mathcal{L}}_B=KL\left(\mathbf{p}\right|\left|\mathbf{q}\right)$$

(5)

3.3. Transfer Capability Distillation

Although transfer capability distillation in this work differs in background and overall impact from general knowledge distillation, the implementation strategy is similar—it is achieved by aligning intermediate-layer representations between the student and teacher models.

Unlike existing works [18,19,20,21], we avoid the direct alignment of intermediate-layer representations; i.e., we do not use mean squared error (MSE) to make the values of individual sampled representations converge. Instead, we align the relationships between representations by making the cosine similarity of each pair of sampled representations converge.

We consider that direct alignment imposes overly strict constraints on the values of representations. Since the teacher model is a pre-trained model with weaker performance, in extreme cases, this could lead to a complete degradation of the student model’s pre-training performance to the level of the teacher model, rendering transfer capability distillation meaningless. By aligning the relationships between representations, this approach provides greater flexibility in the values of representations, potentially reducing conflicts between the pre-training and distillation objectives. In our experiments, we found that this method achieves transfer capability distillation without compromising pre-training performance.

Specifically, we select three locations in the vanilla BERT models and MoE-BERT models for relation alignment, as shown in Figure 3.

Model trunk: After layer normalization in all MHA and FFN layers, we add relational constraints to the normalized hidden representations. Specifically, multiple tokens are randomly selected from a batch, and for each token pair, the cosine similarity of their normalized hidden representations is calculated. The similarity computed by the student model is then aligned with that computed by the teacher model, as shown in Figure 4b.

Suppose that the set of tokens selected from a batch is ${\left\{x_k\right\}}_{k=1}^N$, the student model’s normalized hidden representations are ${\left\{{\mathbf{h}}_k\right\}}_{k=1}^N$, and the teacher model’s normalized hidden representations are ${\left\{{\mathbf{h}}_k^{\prime }\right\}}_{k=1}^N$; then, the process is as follows:

$$s_{ij}={\displaystyle \frac{{\mathbf{h}}_i·{\mathbf{h}}_j}{\parallel {\mathbf{h}}_i\parallel \parallel {\mathbf{h}}_j\parallel }}$$

(6)

$$s_{ij}^{\prime }={\displaystyle \frac{{\mathbf{h}}_i^{\prime }·{\mathbf{h}}_j^{\prime }}{\parallel {\mathbf{h}}_i^{\prime }\parallel \parallel {\mathbf{h}}_j^{\prime }\parallel }}$$

(7)

$${\mathcal{L}}_{Trunk}^{*}={\displaystyle \frac{1}{N^2}}\sum _{i=1}^N\sum _{j=1}^N\mathrm{MSE}(s_{ij},s_{ij}^{\prime })$$

(8)

We introduce distillation here based on some heuristic design considerations. Specifically, since models are composed of many stacked layers, old hidden representations are transformed into new hidden representations through each layer. From the perspective of distilling every layer, one natural idea is to perform distillation on both the input and output hidden representations simultaneously. When aggregated across all layers, these input and output hidden representations correspond to various positions along the model trunk.

Residual inner: Before layer normalization in all MHA and FFN layers, we add relational constraints to the hidden representations that have not undergone residual connections. This process is similar to that used in the model trunk, as shown in Figure 4b. The loss calculated is denoted as ${\mathcal{L}}_{Inner}^{*}$.

Similarly, we introduce distillation here to account for the distillation of the input and output of each layer. However, since the output actually produced by the main parameters at each layer is the hidden representation before the residual connection, we aggregate all hidden representations within the residual connections, which correspond to the various positions in the residual inner.

Multi-head attention: Considering that multi-head attention is central to the powerful performance of the Transformer architecture, and that the relationship between query and key represents important contextual information, we heuristically incorporate it into the distillation process as well.

Within all MHA layers, we calculate the cosine similarity between the query and key pairs, aligning the similarity computed by the student model with that computed by the teacher model, as shown in Figure 4c.

For a single head within an MHA layer, the student model’s query and key representations are denoted as ${\left\{{\mathbf{q}}_k\right\}}_{k=1}^M$ and ${\left\{{\mathbf{k}}_k\right\}}_{k=1}^M$, and the teacher model’s as ${\left\{{\mathbf{q}}_k^{\prime }\right\}}_{k=1}^M$ and ${\left\{{\mathbf{k}}_k^{\prime }\right\}}_{k=1}^M$, respectively. This process is as follows:

$$s_{ij}={\displaystyle \frac{{\mathbf{q}}_i·{\mathbf{k}}_j}{\parallel {\mathbf{q}}_i\parallel \parallel {\mathbf{k}}_j\parallel }}$$

(9)

$$s_{ij}^{\prime }={\displaystyle \frac{{\mathbf{q}}_i^{\prime }·{\mathbf{k}}_j^{\prime }}{\parallel {\mathbf{q}}_i^{\prime }\parallel \parallel {\mathbf{k}}_j^{\prime }\parallel }}$$

(10)

$${\mathcal{L}}_{Attention}^{\prime }={\displaystyle \frac{1}{M^2}}\sum _{i=1}^M\sum _{j=1}^M\mathrm{MSE}(s_{ij},s_{ij}^{\prime })$$

(11)

The loss for a single head is denoted as ${\mathcal{L}}_{Attention}^{\prime }$, and the average loss across multiple heads within a batch is denoted as ${\mathcal{L}}_{Attention}^{*}$.

The total losses from the three constraints are denoted as ${\mathcal{L}}_T$, ${\mathcal{L}}_I$, and ${\mathcal{L}}_A$, corresponding to the totals over all positions: ${\mathcal{L}}_{Trunk}^{*}$, ${\mathcal{L}}_{Inner}^{*}$, and ${\mathcal{L}}_{Attention}^{*}$.

3.4. Training Process

We introduce the main process of training a MoE-BERT with transfer capability distillation.

First, vanilla BERT is pre-trained to serve as the transfer capability teacher model. This model is trained using the original masked-language-modeling objective and achieves baseline performance in both pre-training and downstream tasks. The pre-training loss of this model is defined as follows:

$$\mathcal{L}={\mathcal{L}}_{MLM}$$

(12)

Next, the MoE-BERT model is pre-trained. This model not only optimizes masked language modeling loss ${\mathcal{L}}_{MLM}$ and load balancing loss ${\mathcal{L}}_B$, but also uses vanilla BERT as a transfer capability teacher model, calculating and optimizing multiple distillation losses ${\mathcal{L}}_T$, ${\mathcal{L}}_I$, and ${\mathcal{L}}_A$. The hyperparameter coefficients for the respective losses are as follows: ${\lambda }_B$, ${\lambda }_T$, ${\lambda }_I$, ${\lambda }_A$. The pre-training loss is as follows:

$$\mathcal{L}={\mathcal{L}}_{MLM}+{\lambda }_B{\mathcal{L}}_B+{{\lambda }_T\mathcal{L}}_T+{\lambda }_I{\mathcal{L}}_I+{{\lambda }_A\mathcal{L}}_A$$

(13)

Ultimately, we obtain an MoE-BERT model enhanced through transfer capability distillation, which exhibits stronger transfer capability than the original pre-trained MoE-BERT.

4. Experiments

4.1. Experimental Design

This work primarily involves experiments with three types of models, as follows: a vanilla BERT model with general pre-training, a MoE-BERT model with general pre-training, and an MoE-BERT model enhanced through transfer capability distillation. Among these, vanilla BERT acts as a transfer capability teacher and also serves as a baseline model. The general pre-trained MoE-BERT model is the subject of our improvement and is also a baseline model. The MoE-BERT model enhanced through transfer capability distillation is the model representing our method. We confirm the existence of transfer capability distillation and its effectiveness in improving the downstream task performance of MoE models by comparing the new model with two baseline models.

We pre-trained two different sizes of BERT architectures—the smaller model with 12 layers and a hidden dimension of 128, and the larger model with 12 layers and a hidden dimension of 768. We conducted experiments at both scales to ensure comprehensive validation. For both sizes, the number of experts in the MoE was set to 64, and each hidden representation was processed only by the top-1 expert. For the larger model, we utilized all distillation losses, whereas for the smaller model, we did not use the multi-head attention distillation loss (setting ${\lambda }_A$ to 0). This decision was based on experimental observations indicating that it reduced transfer capability at the smaller scale.

Our main experiments involved fine-tuning on downstream tasks using the GLUE benchmark and reporting results on the validation set. To address the potential issue of severe overfitting when fine-tuning MoE models directly, we performed both full-parameter fine-tuning and adapter-based fine-tuning [22] on all models, reporting the better result of the two for each model.

4.2. Pre-Training Procedure

All experiments were conducted in English only. This work utilized the same pre-training corpus as that of [1], namely, Wikipedia and BooksCorpus [23]. A subset of the pre-training corpus was randomly selected as a validation set to evaluate model performance during pre-training.

For the masked language modeling task, we adopted the same approach as in [1]. Specifically, 15% of the tokens in a sequence were selected for masking, with 80% of these replaced by the [MASK] token, 10% substituted with random tokens, and the remaining 10% left unchanged. Unlike the method proposed in [1], we omitted the next-sentence-prediction task and instead used longer continuous text segments as pre-training input sequences. Additionally, different masking schemes were applied to the same input sequence in different epochs.

Our smaller-scale models have a hidden dimension of 128, 12 layers, 2 attention heads, and 6.3 M parameters. Our larger-scale models have a hidden dimension of 768, 12 layers, 12 attention heads, and 110 M parameters. The maximum sequence length for all models is 128 tokens. All models use the same vocabulary as the BERT model published by Devlin et al. [1], containing 30,522 tokens. Each MoE model contains 64 experts. The smaller-scale (H = 128) MoE models have 105 M parameters, and the larger-scale (H = 768) MoE models have 3.6 B parameters. We employed the FastMoE framework proposed in [24,25] for the implementation of MoE-BERT models. In addition, we also used PyTorch 2.1.2 (https://pytorch.org/ (accessed on 17 September 2025)) and Transformers 4.38.2 (https://github.com/huggingface/transformers (accessed on 17 September 2025)) libraries.

For all MoE-BERT models, ${\lambda }_B$ was set to 1000. For MoE-BERT models undergoing transfer capability distillation, ${\lambda }_T$ and ${\lambda }_I$ were both set to 1; for larger-scale models, ${\lambda }_A$ was set to 1, while for smaller-scale models, ${\lambda }_A$ was set to 0. The relational constraints at the model trunk and residual inner required sampling tokens from each batch. We sampled 4096 tokens and divided them into 32 groups, with each group comprising 128 representations for pairwise cosine-similarity calculations.

All models were pre-trained for a maximum of 40 epochs, although this maximum was not reached in practice. Some checkpoints from specific epochs were selected for alignment and experimentation. Pre-training for all models was conducted using the Adam optimizer [26], with a learning rate of $1\times {10}^{-4}$, ${\beta }_1=0.9$, ${\beta }_2=0.999$, and an L2 weight of 0.01. The learning rate was warmed up over the first 10,000 steps, followed by linear decay. The smaller-scale models were pre-trained with a batch size of 512 on 4 × NVIDIA Tesla V100 GPUs, and the total GPU days are approximately 42 days. The larger-scale models were pre-trained with a batch size of 1024 on 4 × NVIDIA Tesla A100 GPUs, and the total GPU days are approximately 98 days.

To ensure a fair comparison, all models were pre-trained from scratch. However, due to limited computational resources, our pre-training tokens were generally fewer than those in the original BERT paper [1], which may lead to some discrepancies in the downstream task results compared to the original BERT paper.

4.3. Fine-Tuning Procedure

We conducted fine-tuning experiments on the GLUE benchmark [16]. The maximum number of training epochs for all models was set to 10, with a batch size of 32. The optimizer was Adam [26], with a warm-up ratio of 0.06, a linearly decaying learning rate, and a weight decay of 0.01. We reported the average performance of multiple runs.

For full parameter fine-tuning, the learning rates were {1 $\times {10}^{-5}$, 2 $\times {10}^{-5}$, and 5 $\times {10}^{-5}$}. For adapter fine-tuning, the learning rates were {1 $\times {10}^{-4}$, 2 $\times {10}^{-4}$, and 3 $\times {10}^{-4}$}. The adapter sizes for the small models (H = 128) were {16, 64, 128}, and for the large models (H = 768) were {16, 64, 128, 256}.

Additionally, there were some exceptions. For the MNLI, QNLI, and QQP datasets, the limited number of fine-tuning epochs for smaller models during adapter-based fine-tuning restricted performance, so we increased the maximum number of training epochs to 20. For the MNLI dataset, using a small adapter size in smaller models during adapter-based fine-tuning also restricted performance, so we conducted an additional experiment with an adapter size of 512.

4.4. Main Results

For smaller-scale models (H = 128), we enabled vanilla BERT to undergo 20 epochs of pre-training and then used it as a transfer capability teacher to distill MoE-BERT for 5 epochs. For larger-scale models (H = 768), we pre-trained vanilla BERT for 10 epochs and then used it to distill MoE-BERT for 10 epochs.

Regarding the MoE-BERT model with general pre-training, we pre-trained two models with different pre-training epochs for each scale, corresponding to two different settings—pre-training performance alignment and pre-training epoch alignment.

4.4.1. Pre-Training Performance Alignment

The first setting involves aligning the pre-training performance between a general pre-trained MoE-BERT and a MoE-BERT that has undergone transfer capability distillation. This is achieved by ensuring both models exhibit equivalent performance on the validation set of the masked language modeling task, followed by comparing their downstream task performance. This setting allows for a more intuitive assessment of the improvement in the new model’s transfer capability since its pre-training performances are identical.

For smaller-scale models (H = 128), the original MoE-BERT was pre-trained for 6 epochs. For larger-scale models (H = 768), the original MoE-BERT was pre-trained for 12 epochs. The specific results are shown in

Table 1. Experimental results under pre-training-performance alignment settings on the dev set of the GLUE benchmark. Bold numbers indicate the best results within the same group. MoE-BERT w/TCD achieves superior average performance on the GLUE benchmark.

	Model	Pre-Train Epoch	Pre-Train Pref.	CoLA (8.5 k)	MRPC (3.7 k)		SST-2 (67 k)	STS-B (7.0 k)		RTE (2.5 k)	MNLI (393 k)		QNLI (108 k)	QQP (364 k)		Avg. Score
Pre-Training Performance Alignment (H = 128)
	Vanilla BERT (Teacher)	20.0	−2.65387	33.88	83.03	88.09	86.65	83.44	83.39	63.41	76.77	77.36	85.15	88.71	84.82	77.89
	MoE-BERT	6.0	−2.32278	37.56	82.11	87.15	86.22	83.68	83.31	62.86	74.94	76.13	84.97	87.87	83.90	77.56
	MoE-BERT w/TCD	5.0	−2.33650	44.10	84.52	89.09	87.41	84.08	83.81	65.70	77.27	78.29	86.12	88.72	85.01	79.51
Pre-Training Performance Alignment (H = 768)
	Vanilla BERT (Teacher)	10.0	−1.54597	62.03	86.93	90.65	92.73	87.64	87.31	61.97	83.73	83.88	90.72	90.71	87.44	83.81
	MoE-BERT	12.0	−1.29679	64.24	86.11	90.29	93.12	87.25	86.89	61.73	83.61	83.61	90.26	90.29	87.26	83.72
	MoE-BERT w/TCD	10.0	−1.30669	65.36	88.03	91.53	93.46	88.10	87.79	64.14	84.65	84.68	91.63	90.85	87.70	84.83

.

From these results, it is clear that for both model sizes, the general pre-trained MoE-BERT and the MoE-BERT with transfer capability distillation achieved closely aligned pre-training performance. The new models demonstrated significant improvements across all downstream tasks, confirming that our method effectively enhanced the transfer capability of MoE-BERT. Notably, the MoE-BERT with transfer capability distillation outperformed its teacher model in both pre-training and downstream performance, demonstrating the effectiveness of transfer capability distillation and validating our proposition that vanilla Transformers serve as effective transfer capability teachers.

4.4.2. Pre-Training Epoch Alignment

The second setting involves aligning the actual pre-training epochs between a general pre-trained MoE-BERT and an MoE-BERT that has undergone transfer capability distillation. Since our new model requires pre-training a vanilla BERT teacher model before distillation, it effectively undergoes a greater amount of pre-training. Therefore, to validate the practical value of our method, we increased the number of pre-training epochs for the baseline MoE-BERT to match the total pre-training epochs of both the teacher and student models.

For the smaller-scale models (H = 128), we increased the number of pre-training epochs for the original MoE-BERT from 6 to 25. For the larger-scale models (H = 768), we increased them from 12 to 20. The corresponding results are presented in

Table 2. Experimental results under pre-training-epoch alignment settings on the dev set of the GLUE benchmark. Bold numbers indicate the best results within each group. MoE-BERT w/TCD achieves superior average performance on the GLUE benchmark.

	Model	Teacher Epoch	Pre-Train Epoch	Pre-Train Pref.	CoLA (8.5 k)	MRPC (3.7 k)		SST-2 (67 k)	STS-B (7.0 k)		RTE (2.5 k)	MNLI (393 k)		QNLI (108 k)	QQP (364 k)		Avg. Score
Pre-Training Epoch Alignment (H = 128)
	MoE-BERT	-	25.0	−2.08134	42.72	82.75	87.57	87.64	84.10	84.02	62.98	76.46	77.47	86.07	88.17	84.26	78.68
	MoE-BERT w/TCD	20.0	5.0	−2.33650	44.10	84.52	89.09	87.41	84.08	83.81	65.70	77.27	78.29	86.12	88.72	85.01	79.51
Pre-Training Epoch Alignment (H = 768)
	MoE-BERT	-	20.0	−1.20991	64.81	86.51	90.52	93.77	87.46	87.07	62.09	84.17	84.13	90.43	90.57	87.45	84.08
	MoE-BERT w/TCD	10.0	10.0	−1.30669	65.36	88.03	91.53	93.46	88.10	87.79	64.14	84.65	84.68	91.63	90.85	87.70	84.83

.

For both sizes, the baseline MoE-BERT, after additional pre-training epochs, outperformed our new model in terms of pre-training performance. However, our model still significantly surpassed it on most downstream tasks. This finding not only further demonstrates that our method effectively enhances the transfer capability of MoE-BERT—as it achieves stronger downstream performance despite weaker pre-training performance—but also confirms the practical value of our approach under a more equitable setting of pre-training steps.

4.5. Ablation Analysis

In our method, we select three locations for relation alignment—model trunk (T), residual inner (I), and multi-head attention (A). Here, we explore the necessity of applying constraints at these locations.

For the smaller-scale models (H = 128), we incrementally added constraints to these three locations on the baseline MoE-BERT. For the larger-scale models (H = 768), we compared the difference between adding and omitting the multi-head attention constraint. The performance comparison across all downstream tasks is based on aligned pre-training performance, which also reflects differences in transfer capability. The results are presented in

Table 3. The results of ablation analysis. T: Model trunk, I: residual inner, A: multi-head attention. Bold numbers indicate the best results within the same group. The relation alignment for these positions demonstrates the respective positive effects under different settings.

	Model	MRPC		STS-B		MNLI		QNLI
(H = 128, Pre-Training Performance ≈ −2.56)
	MoE-BERT	79.75	85.75	81.83	81.56	71.33	72.82	83.53
	MoE-BERT + T	80.33	86.05	82.53	82.21	74.77	75.72	84.61
	MoE-BERT + T, I	83.70	88.42	83.07	82.80	76.37	77.14	85.49
	MoE-BERT + T, I, A	82.87	88.02	82.96	82.74	75.45	76.25	85.40
(H = 768, Pre-Training Performance ≈ −1.42)
	MoE-BERT + T, I	86.60	90.53	86.78	86.57	83.16	83.46	90.33
	MoE-BERT + T, I, A	87.58	91.28	87.38	87.10	83.48	83.70	90.80

.

From the results in Table 3, we can see that the constraints at the model trunk and residual inner are crucial, leading to significant improvements in transfer capability. For the smaller-scale models, the constraint at the multi-head attention location had a negative impact, so we ultimately did not apply it in the smaller-scale models. However, for the larger-scale models, the constraint at the multi-head attention location produced a clear positive effect, so we retained it for the larger-scale models. The general principles underlying the effectiveness of the multi-head attention constraint are not yet fully understood, and we plan to explore this further in future work.

4.6. Trend Analysis

To more intuitively demonstrate the issue of interest and the effectiveness of our method, we present the performance trends of various models on the MRPC task across increasing pre-training epochs, as shown in Figure 5.

First, we can clearly see that, whether in smaller or larger models, the baseline MoE-BERT model consistently underperforms vanilla BERT on the MRPC task. This indicates a significant degradation in the transfer capability of MoE-BERT, an issue that is the primary focus of this work.

Then, MoE-BERT, after undergoing transfer capability distillation, consistently outperforms the baseline MoE-BERT model on the MRPC task. This suggests that our method effectively enhances the transfer capability of MoE-BERT and improves its downstream task performance.

Finally, the performance of MoE-BERT with transfer capability distillation even surpasses that of the teacher model on the MRPC task. This validates our proposed idea of transfer capability distillation and proves that vanilla Transformers are suitable transfer capability teachers.

5. Transfer Capability Distillation vs. General Knowledge Distillation

Transfer capability distillation is evidently distinct from general knowledge distillation. Although both types of work fall under model distillation, their contributions are different.

The core contribution of general knowledge distillation lies in the method. This type of work requires proposing stronger distillation methods and comparing them with previous methods to demonstrate their superiority, while the teacher model is simply a more powerful model.

The core contribution of transfer capability distillation lies in the teacher model. The focus is on demonstrating that a model with weaker performance but stronger transfer capability can also serve as an effective teacher, while the distillation method is not the primary concern. Since these two types of studies focus on different dimensions, comparing prior work that proposed new distillation methods with our work, which introduces a new teacher model, does not effectively demonstrate the contribution of our approach.

General knowledge distillation usually involves distilling from a larger-scale model with superior pre-training or downstream performance to produce a model that is relatively weaker in most aspects but more efficient; therefore, general knowledge distillation is usually used as a compression method.

In this work, both the pre-training and downstream performance of vanilla models are weaker, and even the scales of vanilla models are smaller; they merely possess stronger inherent transfer capability. We believe that small vanilla models can serve as transfer capability teachers, guiding distillation for larger MoE models with poorer transfer capability. A distinctive characteristic of this approach is the counterintuitive outcome in which a teacher model—inferior in both pre-training and downstream performance—can effectively distill a student model that is superior in those aspects. Therefore, fundamentally, transfer capability distillation is not a compression method, but an enhancement method.

6. Why Does Transfer Capability Distillation Work?

Although we propose transfer capability distillation and design a corresponding distillation scheme that enhances the transfer capability of MoE-BERT, our understanding of the underlying differences in transfer capability remains quite limited. It is also difficult to explain why transfer capability can be distilled, which clearly hinders further research.

Here, we propose an explanation—the difference in transfer capability may be related to the quality of features learned during the pre-training phase of models, and transfer capability distillation, to some extent, aligns the student model’s features with the high-quality features of the teacher model.

Our viewpoint stems from the observation that the original MoE-BERT, even without downstream-task fine-tuning and merely with frozen parameters for the masked-language-modeling task, exhibits significant differences from vanilla BERT.

Specifically, we tested the models’ masked-language-modeling capability on an additional out-of-distribution (OOD) corpus using the validation set of the Pile dataset [27], which covers a wide range of corpora with significant distribution differences from the pre-training corpus, such as mathematics, GitHub, etc. The experiments were conducted on both scale models, ensuring alignment of pre-training performance before comparison, as shown in

Table 4. Masked language modeling results on out-of-distribution corpus. AX: arXiv, DM: DM Mathematics, GH: GitHub, SE: Stack Exchange, UI: Ubuntu IRC. Bold numbers indicate the best results within the same group. MoE-BERT w/TCD still shows significant improvement over MoE-BERT in out-of-distribution masked language modeling.

	Model	AX	DM	GH	SE	UI
(H = 128, Pre-Training Performance ≈ −2.76)
	Vanilla BERT	−3.545	−2.955	−3.462	−3.530	−4.120
	MoE-BERT	−3.613	−3.026	−3.564	−3.585	−4.164
	MoE-BERT w/TCD	−3.563	−2.959	−3.499	−3.536	−4.118
(H = 768, Pre-Training Performance ≈ −1.57)
	Vanilla BERT	−2.338	−2.179	−2.420	−2.443	−3.052
	MoE-BERT	−2.393	−2.296	−2.481	−2.481	−3.121
	MoE-BERT w/TCD	−2.334	−2.219	−2.426	−2.444	−3.051

.

It is clear that the out-of-distribution masked-language-modeling capability of the original MoE-BERT is significantly lower than that of vanilla BERT, whereas the MoE-BERT model, after undergoing transfer capability distillation, shows a marked improvement in this regard. These results suggest that even though the models perform the same pre-training tasks, the quality of the learned features differs, which is likely the cause of the variation in transfer capability.

The mechanism for the distillation’s effectiveness can, thus, be understood as follows: The method likely works by imposing additional constraints on the learned features, prompting MoE-BERT to utilize higher-quality representations to complete the pre-training tasks, thereby indirectly enhancing its transfer capability. Furthermore, the quality of features may also manifest in other ways within the model, potentially including, but not limited to, the transferability or generalizability of embedding parameters, attention parameters, MoE expert parameters, routing parameters, etc. This requires more in-depth and careful analysis and discrimination, which we hope to explore further in future work.

7. Limitations

Although this work introduces the concept of transfer capability distillation and addresses the issue of weak transfer capability in MoE Transformers, there are still some limitations.

First, the scope of our empirical validation was constrained by available computational resources. Our proposed method was primarily validated on a specific MoE architecture. We did not extend our experiments to include other advanced MoE variants or systematically compare the effects of using different architectures for the teacher model. Similarly, our pre-training and evaluation were limited to standard corpora and benchmarks like GLUE, rather than broader, more diverse domains or tasks. We conducted experiments in a fine-tuning setting and did not extend to few-shot learning or other probing experiments. Second, we did not conduct a sensitivity analysis of the hyperparameters in the loss function, but instead adopted a simplified strategy to ensure practicality. Furthermore, certain configuration choices—such as whether to apply relation alignment in the multi-head attention position—were based on empirical observations rather than in-depth mechanistic analysis.

We plan to address these limitations in future work by exploring a wider range of model architectures, datasets, tasks, and settings, as well as conducting more in-depth analyses of the method’s hyperparameters and theoretical underpinnings.

8. Conclusions

This work focuses on the issue of MoE Transformers underperforming on downstream tasks compared to vanilla Transformers. We propose that a model’s pre-training performance and transfer capability are different factors influencing downstream task performance. And we believe that the root cause of the MoE model’s poor performance on downstream tasks is its inferior transfer capability. To address this issue, we introduce transfer capability distillation, utilizing vanilla models as teachers to enhance the transfer capability of MoE models. We designed a distillation scheme to address the weak transfer capability of MoE models, thereby improving downstream performance and validating the concept of transfer capability distillation. Finally, we provide insights into transfer capability distillation from the perspective of model features, offering directions for more in-depth future research.