Optimization Design of Spaceborne Microstrip Array by Strain Compensation Method Based on Multi-Physics Coupling Analysis
Abstract
1. Introduction
2. Spaceborne Microstrip Antenna Array
2.1. Antenna Element
2.2. Antenna Array
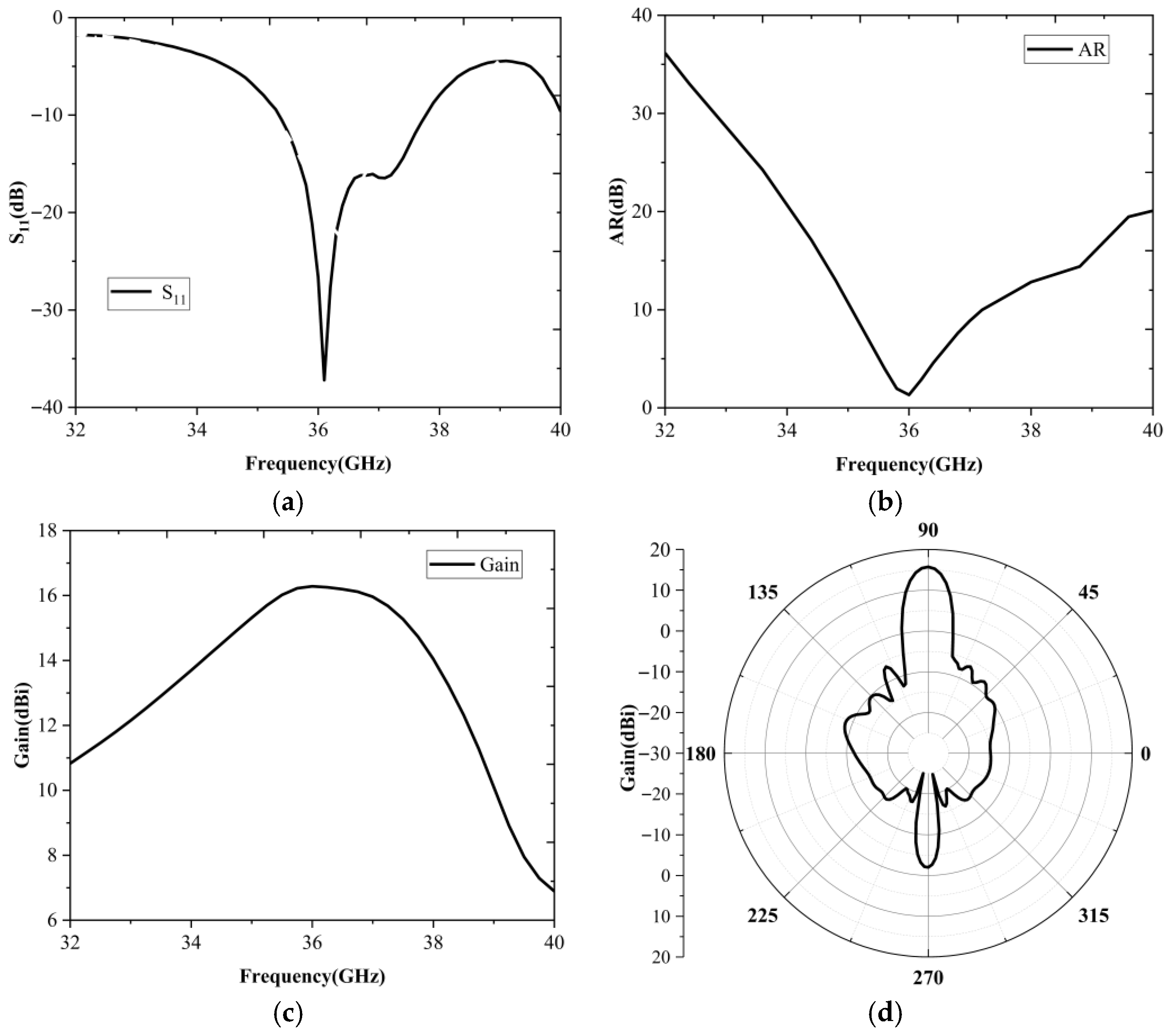
2.3. Performance Analysis of Antenna Array
3. Multi-Physics Fields Analysis of Designed Spaceborne Microstrip Antenna Array
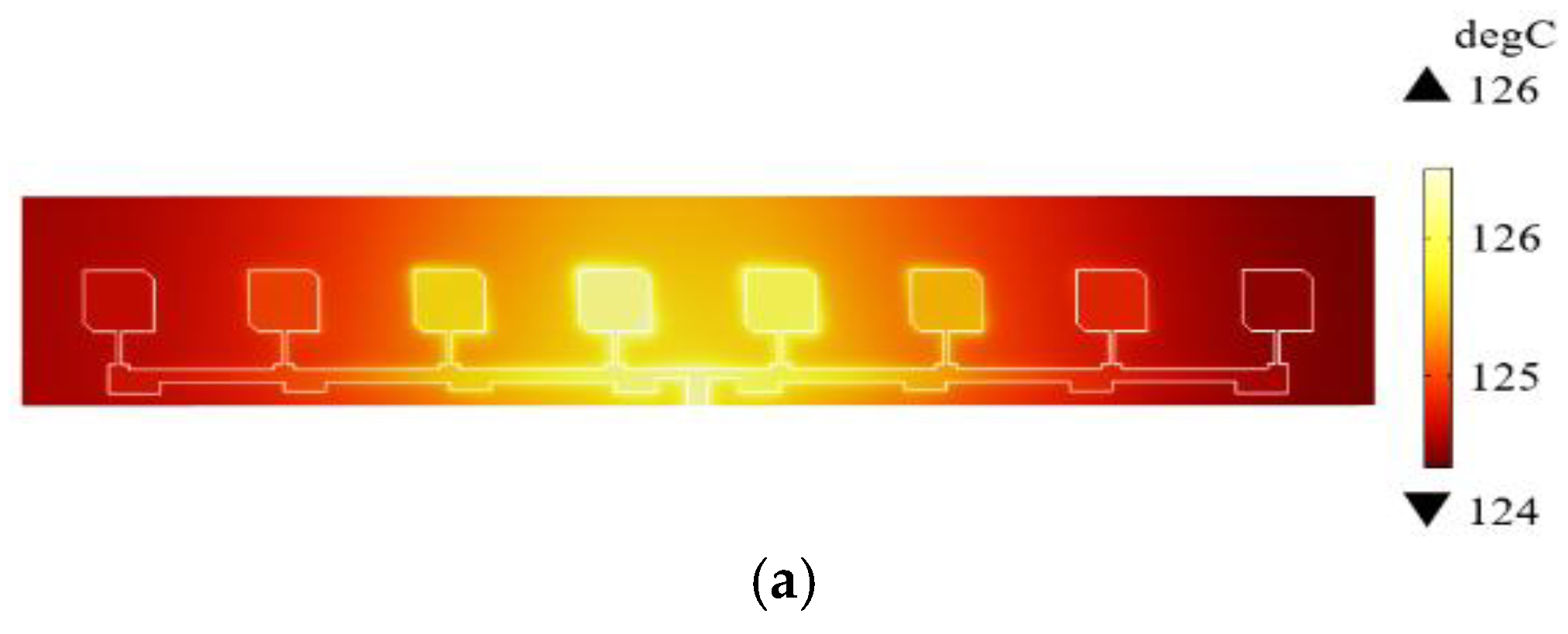
3.1. Solid Thermal Model
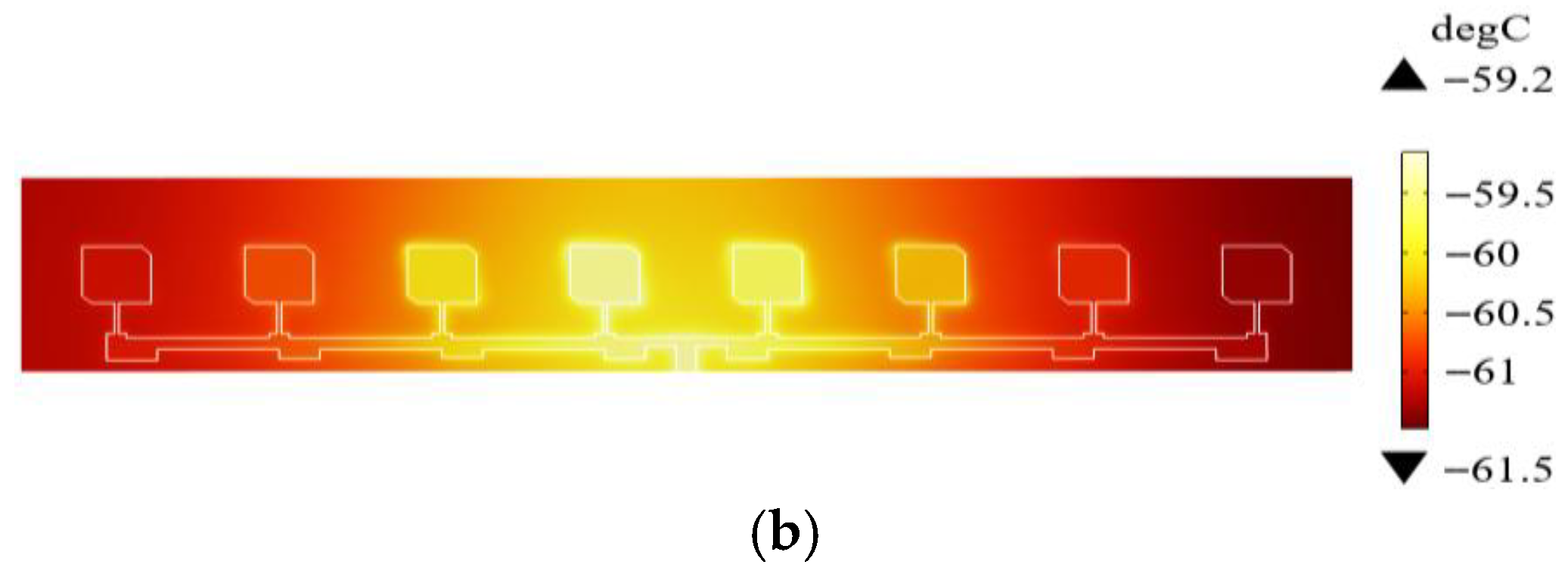
3.2. Solid Mechanical Model
3.3. Electromagnetic Field Model
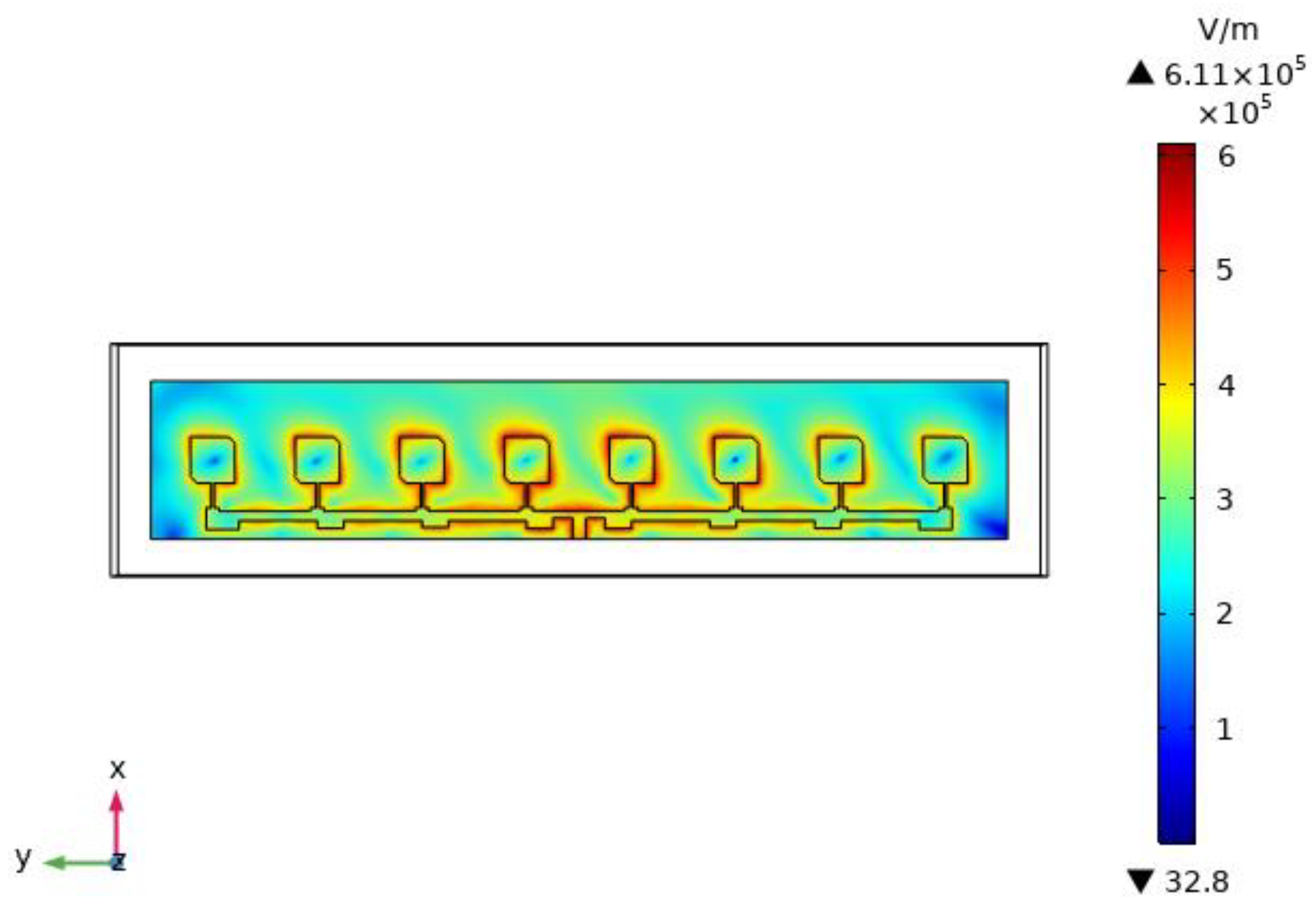
3.4. Multi-Physics Fields Analysis
4. Optimization Design by Strain Compensation Method
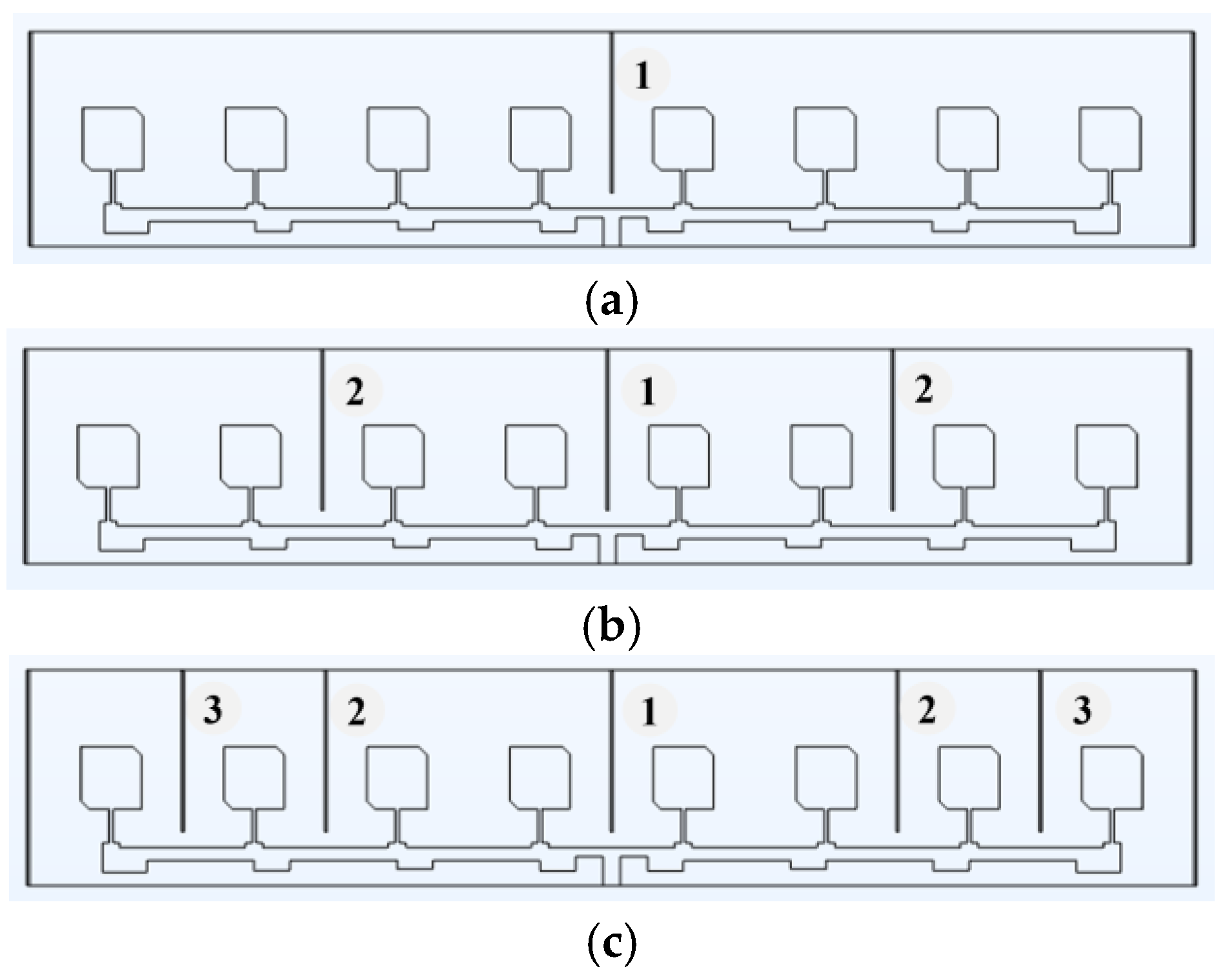
4.1. Slits Positions
4.2. Slit Sizes
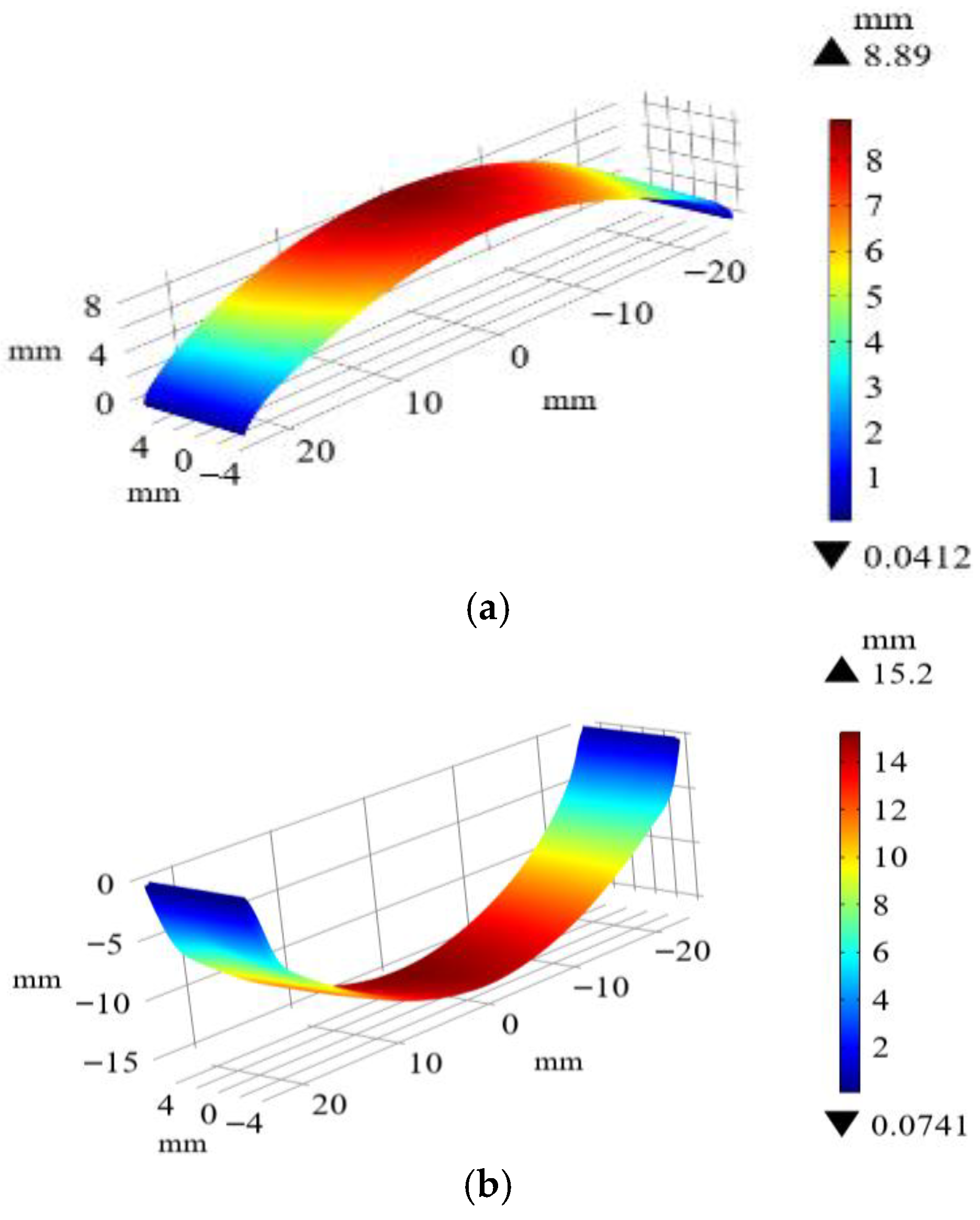
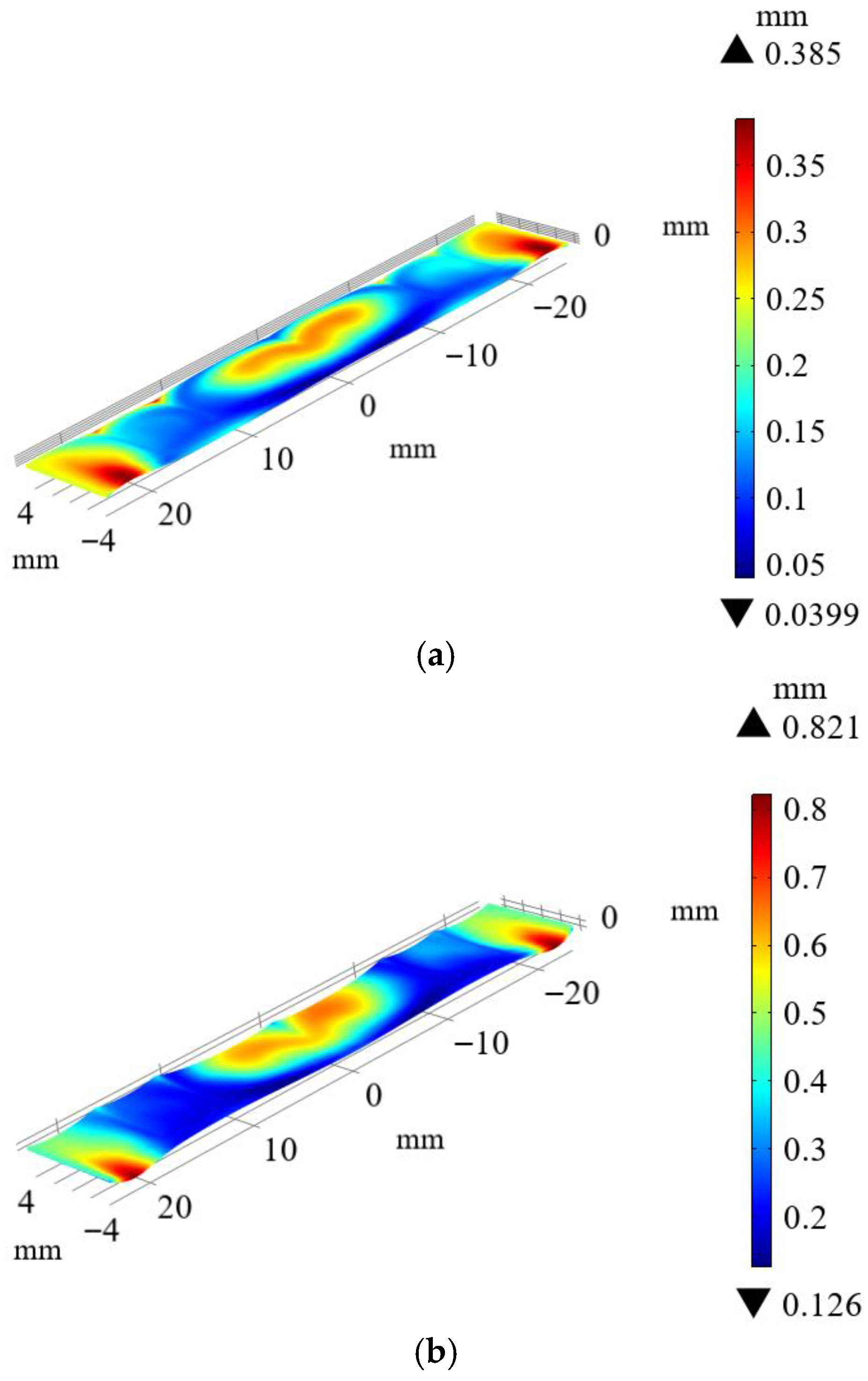
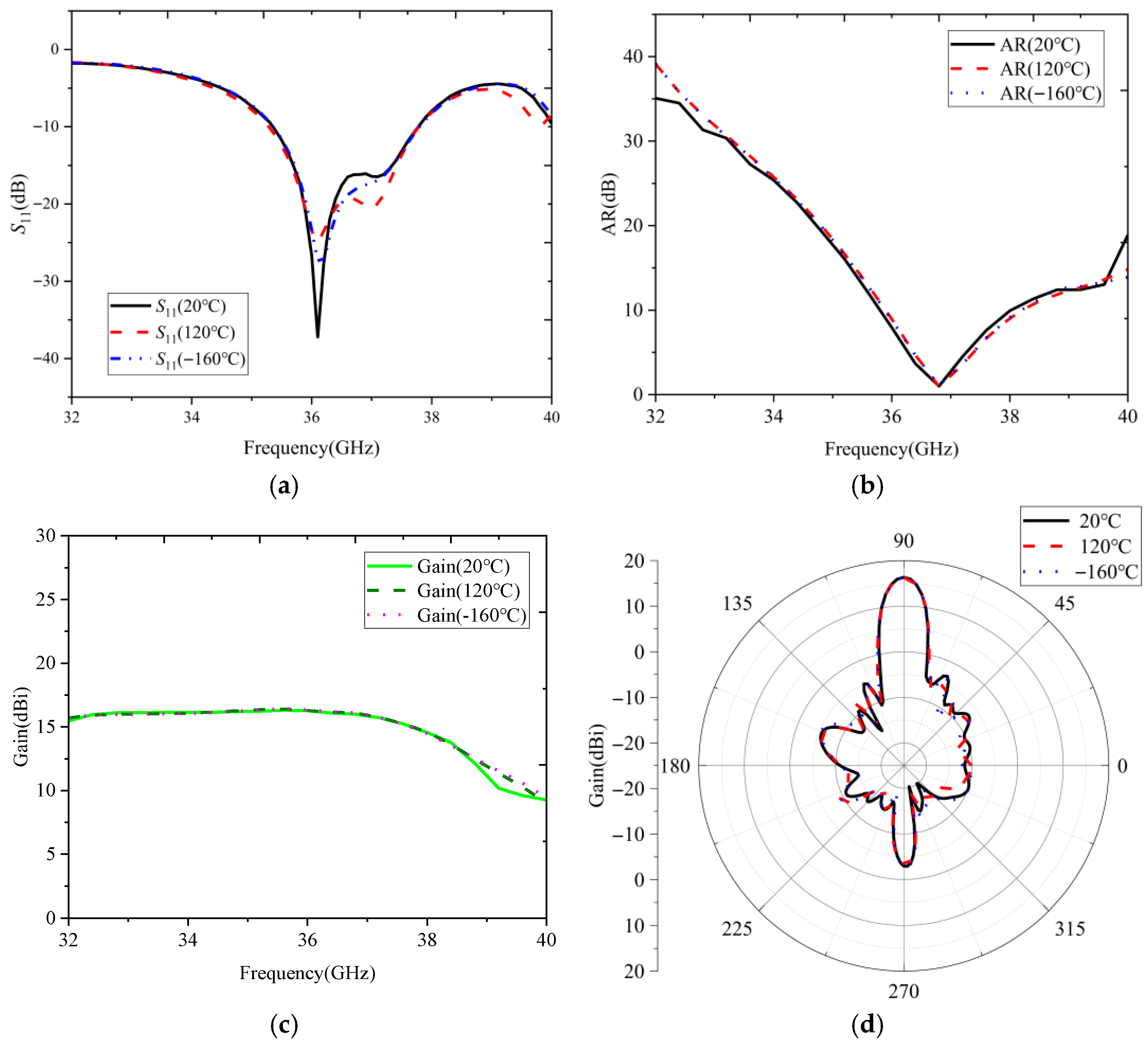
4.3. Multi-Physics Fields Analysis of Optimized Array
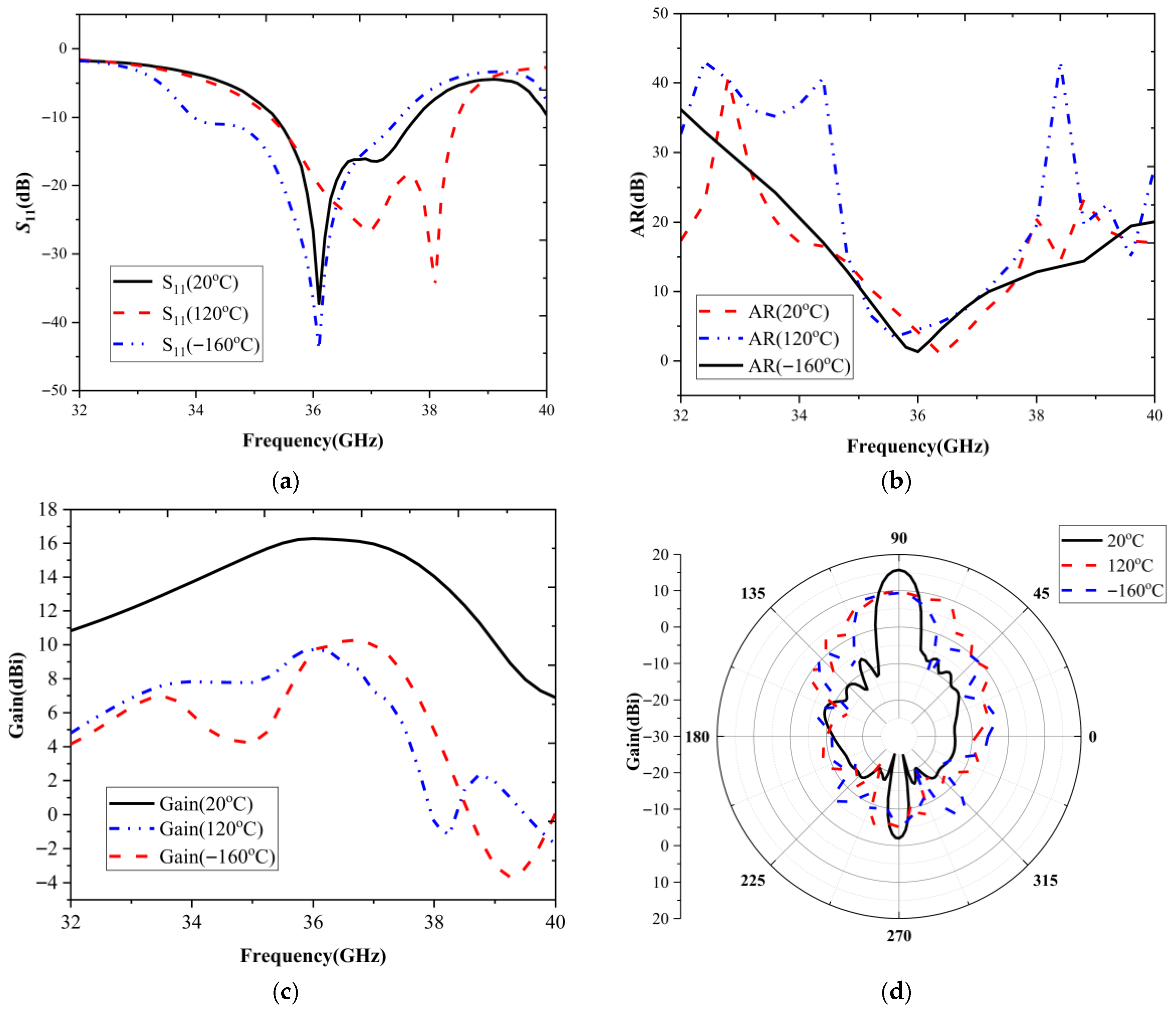
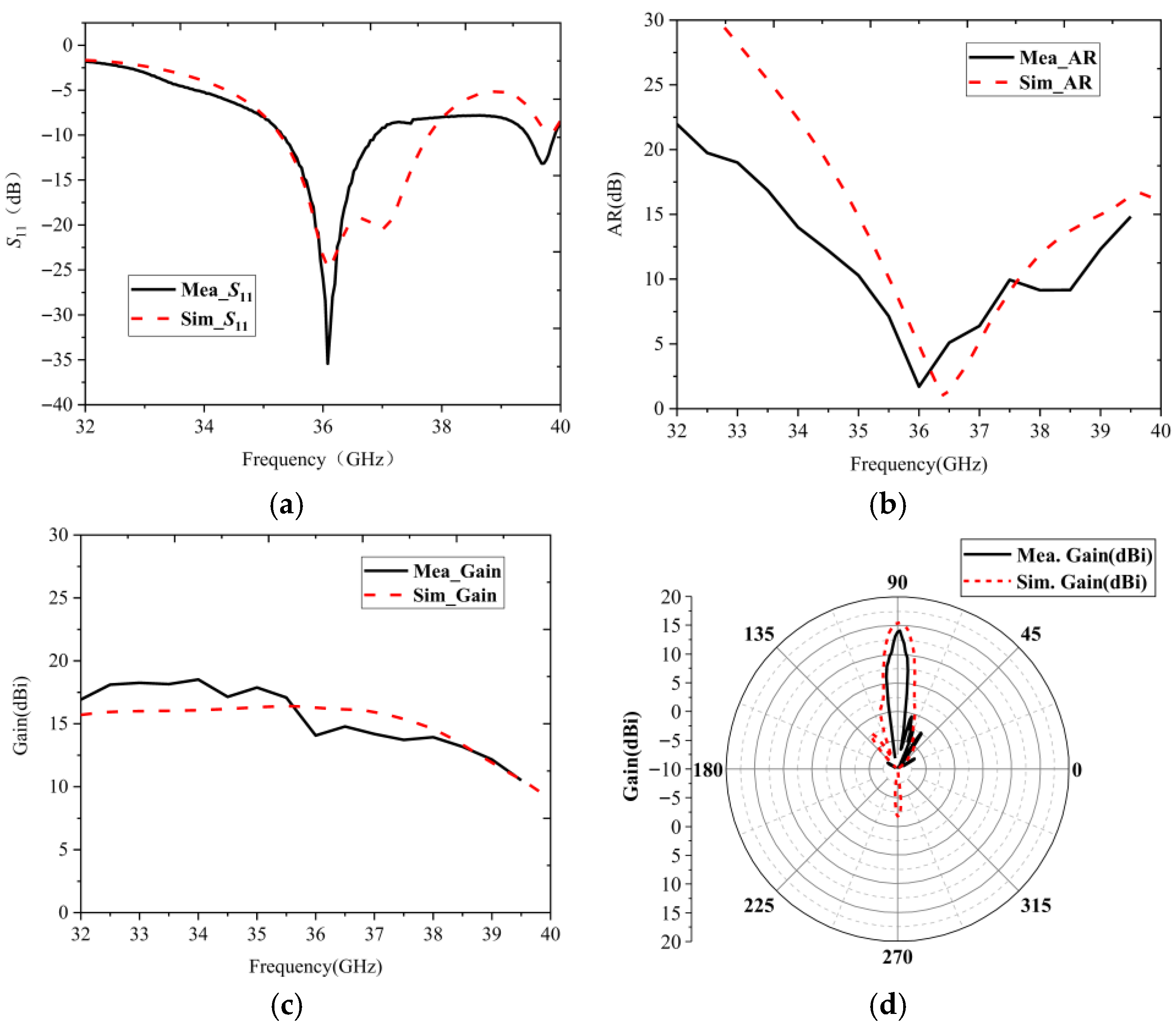
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Capovilla, G.; Cestino, E.; Reyneri, L.M.; Romeo, G. Modular multifunctional composite structure for CubeSat applications: Preliminary design and structural analysis. Aerospace 2020, 7, 17. [Google Scholar] [CrossRef]
- Saeed, N.; Elzanaty, A.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Alouini, M.S. CubeSat communications: Recent advances and future challenges. IEEE Commun. Surv. Tutor. 2020, 22, 1839–1862. [Google Scholar] [CrossRef]
- Cappelletti, C.; Robson, D. CubeSat missions and applications. In CubeSat Handbook; Elsevier: Amsterdam, The Netherlands, 2021; pp. 53–65. [Google Scholar]
- Constantine, A.B. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chahat, N. CubeSat Antenna Design; Wiley: Hoboken, NJ, USA, 2021; pp. 233–253. [Google Scholar]
- Buttazzoni, G.; Comisso, M.; Cuttin, A.; Fragiacomo, M.; Vescovo, R.; Gatti, R.V. Reconfigurable phased antenna array for extending CubeSat operations to Ka-band: Design and feasibility. Acta Astronaut. 2017, 137, 114–121. [Google Scholar] [CrossRef]
- Sundu, H.; Döner, N. Detailed thermal design and control of an observation satellite in low Earth orbit. Eur. Mech. Sci. 2020, 4, 171–178. [Google Scholar] [CrossRef]
- Tsai, J.R. Overview of satellite thermal analytical model. J. Spacecr. Rocket. 2004, 41, 120–125. [Google Scholar] [CrossRef]
- Hayashi, I.; Higuchi, R.; Yokozeki, T.; Aoki, T. Analytical study on the thermal deformation of ultralight phased array antenna. Acta Astronaut. 2021, 188, 531–544. [Google Scholar] [CrossRef]
- Wresnik, J.; Haas, R.; Boehm, J.; Schuh, H. Modeling thermal deformation of VLBI antennas with a new temperature model. J. Geod. 2007, 81, 423–431. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.; Tang, D.; Zhang, L.; Wang, Y.; Miao, E. Thermal deformation modeling for phased array antenna compensation control. Sensors 2022, 22, 2325. [Google Scholar] [CrossRef]
- Yoon, H.S.; Washington, G. An optimal method of shape control for deformable structures with an application to a mechanically reconfigurable reflector antenna. Smart Mater. Struct. 2010, 19, 105004. [Google Scholar] [CrossRef]
- Yang, G.; Tang, A.; Yuan, Z.; Yang, Z.; Li, S.; Li, Y. Surface shape stability design of mesh reflector antennas considering space thermal effects. IEEE Access 2020, 8, 89071–89083. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, Q.; Zhu, H.; Yang, W.; Meng, N. Thermal-dynamic coupling analysis of space truss antennas in actual space thermal environment. Eng. Struct. 2024, 298, 117020. [Google Scholar] [CrossRef]
- Xu, P.; Wang, Y.; Xu, X.; Wang, L.; Wang, Z.; Yu, K.; Wu, W.; Wang, M.; Leng, G.; Ge, D.; et al. Structural-electromagnetic-thermal coupling technology for active phased array antenna. Int. J. Antennas Propag. 2023, 2023, 2843443. [Google Scholar] [CrossRef]
- Feng, S.; Sun, Q.; Wu, Y.; Han, X.; Li, Z.; Angel Sotelo, M. Stochastic thermal–structural–electromagnetic coupling analysis of phased arrays with random material parameters. IEEE Trans. Antennas Propag. 2023, 71, 8030–8039. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, H.; Zhang, X. Thermal–mechanical coupling performances and parameters sensitivity analyses of a deployable Astromesh antenna under different heat radiations. Appl. Therm. Eng. 2025, 259, 124732. [Google Scholar] [CrossRef]
- Nie, R.; He, B.; Yan, S.; Ma, X. Optimization design method for mesh reflector antennas considering the truss deformation and thermal effects. Eng. Struct. 2020, 208, 110253. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, H.; Li, J. On-orbit thermal-mechanical coupling performance analysis of a deployed hoop-column antenna. Thin-Walled Struct. 2025, 214, 113312. [Google Scholar] [CrossRef]
- Dong, T.; Yuan, S.; Huang, T. Real-time shape sensing of large-scale honeycomb antennas with a displacement-gradient-based variable-size inverse finite element method. Compos. Struct. 2024, 344, 118320. [Google Scholar] [CrossRef]
- Fenf, S.; Wang, H.; Li, Z. An enhanced computational approach for multi-physics coupling analysis of active phased array antenna. Eng. Anal. Bound. Elem. 2024, 167, 105892. [Google Scholar]
- Jin, L.; Zhang, F.; Tian, D.; Wang, Q.; Cao, Q. Thermal-structural analysis of the support structure for a modular space deployable antenna. Int. J. Aerosp. Eng. 2022, 2022, 2164485. [Google Scholar] [CrossRef]
- Nösekabel, E.-H.; Ernst, T.; Haefker, W. Measurement of the thermal deformation of a highly stable antenna with pulse ESPI. Proc. SPIE 2007, 6616, 66162X. [Google Scholar]
- Yuan, S.; Sun, G.; Yu, K.; Zhou, K.; Cheng, Z.; Zhu, L. In-orbit thermal deformation monitoring for composite laminated structures of remote sensing satellites using temperature self-decoupling fiber optical system and inverse finite element method. Appl. Phys. B 2024, 130, 45. [Google Scholar] [CrossRef]
- Ma, K.; Huang, G.; Meng, J. Thermal deformation measurement of the surface shape of a satellite antenna using high-accuracy close-range photogrammetry. Sensors 2024, 24, 4722. [Google Scholar] [CrossRef] [PubMed]
- Simone, M.; Fanti, A.; Valente, G.; Montisci, G.; Ghiani, R.; Mazzarella, G. Optimized design and multiphysics analysis of a KA-band stacked antenna for CUBESAT applications. IEEE J. Multiscale Multiphys. Comput. Tech. 2021, 6, 143–157. [Google Scholar] [CrossRef]
- Wang, P.; Wang, F.; Shi, T.; Wang, B. Thermal distortion compensation of a high precision umbrella antenna. J. Phys. Conf. Ser. 2017, 916, 012051. [Google Scholar] [CrossRef]
- Wei, X.; Miao, E.; Wang, W.; Liu, H. Real-time thermal deformation compensation method for active phased array antenna panels. Precis. Eng. 2019, 60, 121–129. [Google Scholar] [CrossRef]
- Yu, H.; Wang, H.; Wang, X.; Lei, H.; Guo, X. The metamaterial with high thermal-mechanical stability and the practical application as the microwave antenna: Mechanical designs, theoretical predictions, and experimental demonstrations. Extrem. Mech. Lett. 2024, 69, 1002166. [Google Scholar] [CrossRef]
- Lu, G.Y.; Zhou, J.Y.; Cai, G.P.; Fang, G.Q.; Lv, L.L.; Peng, F.J. Studies of thermal deformation and shape control of a space planar phased array antenna. Aerosp. Sci. Technol. 2019, 93, 105311. [Google Scholar] [CrossRef]
- Jin, C.; Liu, X.; Cai, G.; Sun, J.; Zhu, D. Thermal deformation analysis and shape control of a novel large-scale two-dimensional planar phased array antenna. Astrodynamics 2025, 9, 583–604. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
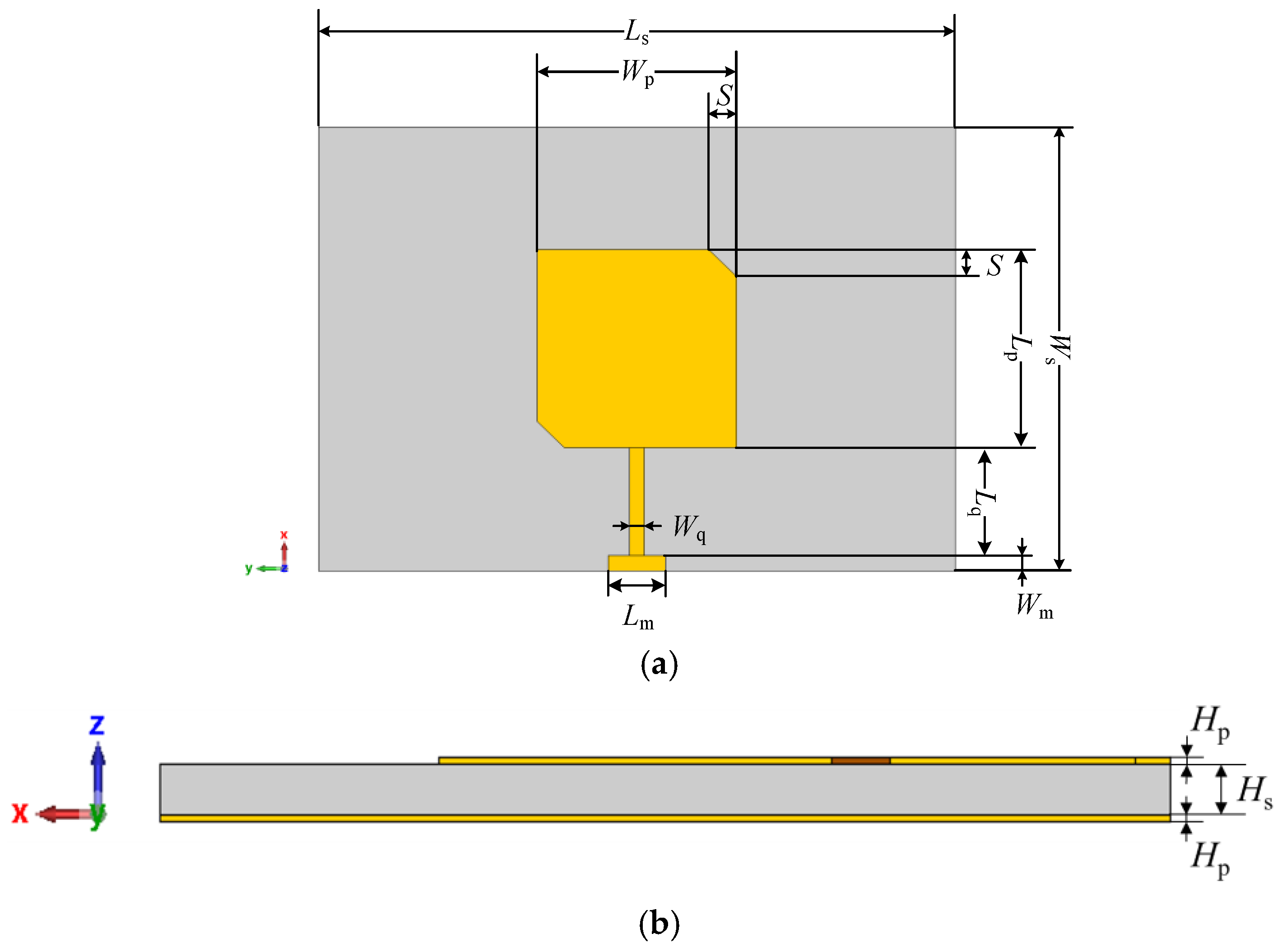
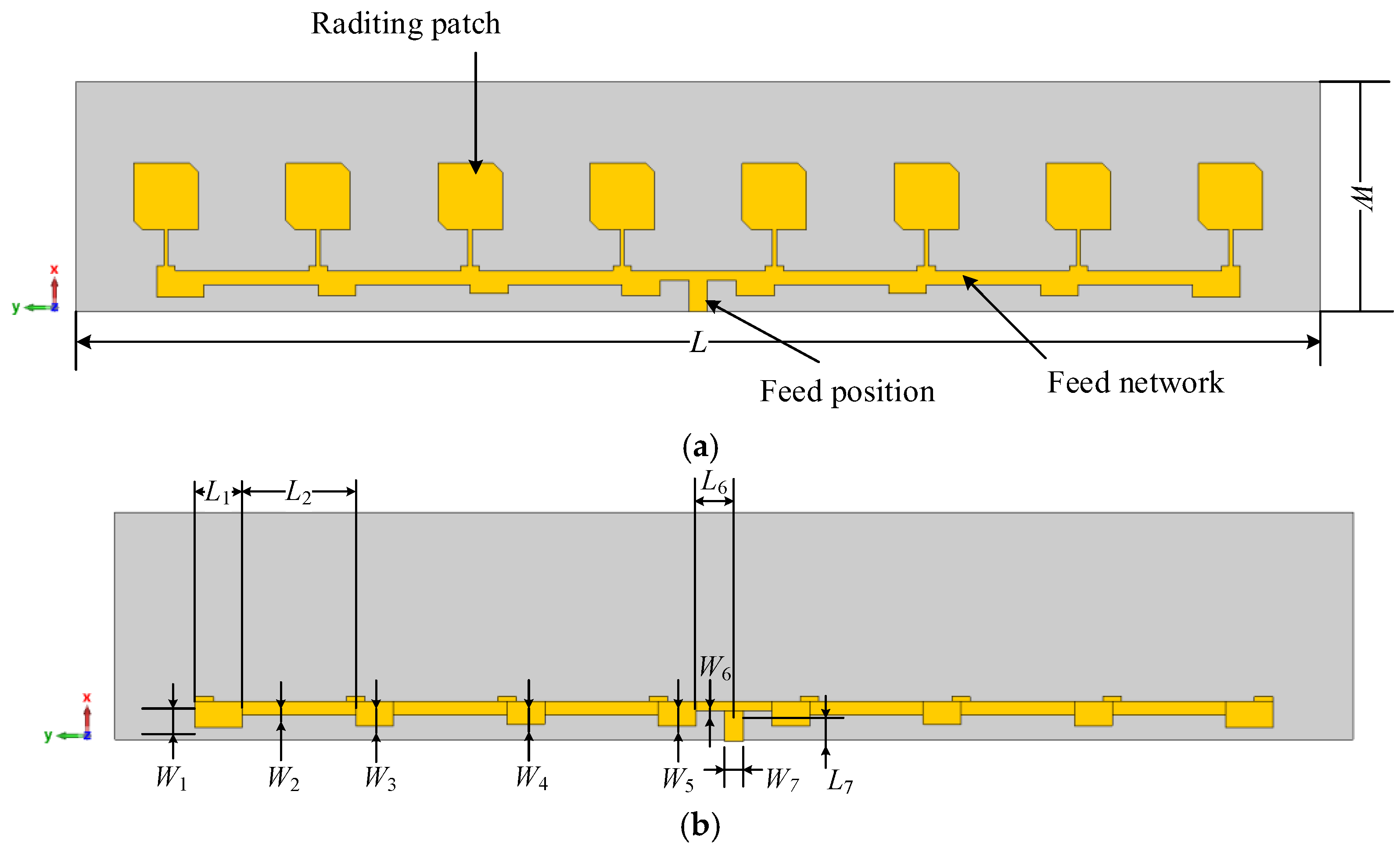








| Lp | Wp | Hp | Ls | Ws | Hs | Lq | Wq | Lm | Wm | S |
|---|---|---|---|---|---|---|---|---|---|---|
| 2.58 | 2.50 | 0.035 | 8.00 | 5.78 | 0.25 | 1.40 | 0.18 | 0.72 | 0.20 | 0.34 |
| Material | Specific Heat (J/(g⋅k) | Thermal Conductivity (W/(m⋅k) | Coefficient of Thermal Expansion (ppm/°C) |
|---|---|---|---|
| Copper | 0.39 | 400 | |
| Rogers 5880 | 0.96 | 0.2 | 31(X)/48(Y)/237(Z) |
| W1 | W2 | W3 | W4 | W5 | W6 | W7 | L1 | L2 | L6 |
|---|---|---|---|---|---|---|---|---|---|
| 1.23 | 0.53 | 0.95 | 0.89 | 0.97 | 0.37 | 7.56 | 1.84 | 4.44 | 1.48 |
| L1 (mm) | L2 (mm) | L3 (mm) |
|---|---|---|
| 4.0 | 6.7 | 7.8 |
| Deformation (mm) | High Temperature | Low Temperature | ||
|---|---|---|---|---|
| Maximum | Average | Maximum | Average | |
| Original array | 8.89 | 6.37 | 15.2 | 11.11 |
| Optimized array | 0.39 | 0.16 | 0.71 | 0.29 |
| Reduction | 95.61% | 97.49% | 95.33% | 97.39% |
| Gain (dBi) | High Temperature | Low Temperature |
|---|---|---|
| Original array | 9.82 | 9.78 |
| Optimized array | 16.22 | 16.22 |
| Increment | 65.17% | 68.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, K.; Huang, K.; Xiao, Q.; Wang, S.; Liu, H.; Wang, H. Optimization Design of Spaceborne Microstrip Array by Strain Compensation Method Based on Multi-Physics Coupling Analysis. Electronics 2025, 14, 4255. https://doi.org/10.3390/electronics14214255
Fan K, Huang K, Xiao Q, Wang S, Liu H, Wang H. Optimization Design of Spaceborne Microstrip Array by Strain Compensation Method Based on Multi-Physics Coupling Analysis. Electronics. 2025; 14(21):4255. https://doi.org/10.3390/electronics14214255
Chicago/Turabian StyleFan, Kaihang, Kui Huang, Qi Xiao, Shuting Wang, Hao Liu, and Huilin Wang. 2025. "Optimization Design of Spaceborne Microstrip Array by Strain Compensation Method Based on Multi-Physics Coupling Analysis" Electronics 14, no. 21: 4255. https://doi.org/10.3390/electronics14214255
APA StyleFan, K., Huang, K., Xiao, Q., Wang, S., Liu, H., & Wang, H. (2025). Optimization Design of Spaceborne Microstrip Array by Strain Compensation Method Based on Multi-Physics Coupling Analysis. Electronics, 14(21), 4255. https://doi.org/10.3390/electronics14214255





