Abstract
The integration of Reconfigurable Intelligent Surfaces (RISs) into wireless networks is a promising paradigm for enhancing spectral efficiency and coverage in beyond-5G systems. However, in multiuser downlink scenarios, the joint optimization of discrete RIS phase shifts and user scheduling presents a high-dimensional combinatorial challenge due to their tight coupling, which is often intractable with conventional methods. Furthermore, conventional RISs are limited by their unidirectional signal reflection, creating coverage blind spots. To address these issues, this paper first investigates a multi-user scheduling system assisted by a conventional RIS. We employed a vector projection relaxation method to transform the complex joint optimization problem, and then used an algorithm based on particle swarm optimization to jointly optimize the discrete phase shift and user scheduling. Simulation results demonstrate that this proposed algorithm significantly improves the system’s achievable data rate compared to existing benchmarks. Subsequently, to overcome the fundamental coverage limitation of conventional RISs, we extend our framework to two advanced systems: double-RIS and Simultaneously Transmitting and Reflecting RIS (STAR-RIS). For the STAR-RIS system, leveraging its energy-splitting protocol, we develop a novel joint optimization algorithm for phase shifts, amplitudes, and user scheduling based on an alternating optimization framework. This constitutes another significant contribution, as it effectively manages the added complexity of simultaneous transmission and reflection control. Simulations confirm that the STAR-RIS-assisted system, optimized by our algorithm, not only eliminates coverage blind spots but also surpasses the performance of traditional RIS, offering new perspectives for optimizing next-generation wireless communication networks.
1. Introduction
With the rapid development of information technology, wireless communication technology has become deeply integrated into daily life, especially in applications such as smartphones, the Internet of Things [1], and the sixth generation (6G) [2]. However, the sharp increase in communication demand has led to challenges in areas such as data transmission rates, network congestion, spectrum resources, and signal quality. The International Telecommunication Union predicts that global wireless communication data traffic will experience explosive growth in the next five years, with global mobile data traffic expected to exceed ten times its current volume by 2030. This places tremendous pressure on traditional wireless communication networks and urgently calls for new technologies to break through these bottlenecks. In this context, innovative technologies like ambient backscatter communications and reconfigurable intelligent surfaces are being explored to improve energy and spectral efficiency, as seen in works on joint resource management [3].
To address this challenge, Reconfigurable Intelligent Surface (RIS) technology has gradually attracted attention [4,5,6]. RIS consists of numerous adjustable artificial surface elements that can dynamically control the propagation direction, phase shift, and amplitude of electromagnetic waves, thus intelligently regulating the propagation of wireless signals. Compared to traditional communication technologies, RIS offers several advantages, such as reducing signal attenuation and multipath effects, improving communication quality, enhancing spectral efficiency, and optimizing spectrum resource utilization. It also has the benefits of low power consumption, low cost, and easy deployment. On the other hand, to cope with more complex communication scenarios, researchers have proposed STAR-RIS [7,8,9,10]. Unlike traditional RIS, STAR-RIS not only reflects signals but can also simultaneously transmit them, offering more flexible and efficient signal processing capabilities in complex environments. In dense urban environments, STAR-RIS can ensure that signals bypass obstacles and reach user locations by both reflecting and transmitting, showing advantages that traditional RIS cannot handle.
In the 6G networks, the simultaneous access of multiple users will become more common, especially in high-density scenarios, where ensuring the communication quality of each user becomes a key challenge. As technology advances, multi-user scheduling has become one of the key techniques for improving network performance. Traditional scheduling algorithms rely on base station resource allocation, but with the increase in the number of users and network density, a single resource allocation approach is insufficient to meet complex needs [11,12]. Therefore, combining RIS technology with multi-user scheduling allows for more flexible and efficient resource allocation [13,14], providing each user with an optimal signal path, reducing interference, optimizing channel quality, and enhancing overall network performance. This integration will become an important technological trend in future networks (such as 6G) and help address the more complex and dynamic communication environments.
Despite the potential, a critical challenge remains largely unaddressed: the joint optimization of discrete RIS phase shifts and user scheduling. The coupling between the high-dimensional discrete configuration of the RIS and the combinatorial nature of user scheduling results in a mixed-integer non-convex optimization problem that is computationally intractable for conventional methods. Moreover, the inherent coverage limitation of conventional RIS, which only serves one side of the surface, necessitates the investigation of more advanced architectures like double-RIS and STAR-RIS, for which efficient joint optimization algorithms are still in their infancy.
Motivated by the above challenges, this paper delves into intelligent surface-assisted multi-user scheduling systems. The main contributions of this work are summarized as follows: First, we establish a downlink multi-user communication model assisted by a conventional RIS with discrete phase shifts. To tackle the formidable joint optimization problem of phase shifts and user scheduling, we propose a novel vector projection relaxation method. This method ingeniously transforms the original problem into a more tractable form, based on which a highly efficient joint algorithm leveraging Particle Swarm Optimization (PSO) is developed. Second, to mitigate the coverage blind spots inherent in single-RIS systems, we expand our investigation to a double-RIS configuration. While this scheme enhances performance, it also increases hardware costs and path loss. Third, to fundamentally overcome the coverage limitation, we introduce a STAR-RIS-assisted system. Adopting the energy-splitting protocol, we formulate a joint optimization problem for phase shifts, amplitudes, and user scheduling. We then develop an alternating optimization (AO) based algorithm that decomposes the problem into manageable sub-problems, effectively embedding user scheduling into the iterative optimization process. Finally, extensive simulation results are provided to validate the effectiveness of our proposed algorithms. They demonstrate the following: (1) our PSO-based algorithm for conventional RIS significantly outperforms several benchmarks; (2) the STAR-RIS-assisted system, optimized by our AO algorithm, achieves superior performance compared to traditional RIS and successfully provides full-space coverage.
The remainder of this paper is organized as follows: Section 2 introduces the system model and the joint optimization problem for the RIS-assisted multiuser downlink. The proposed PSO-based algorithm is detailed in this section. Section 3 presents the double-RIS system and its results. Section 4 investigates the STAR-RIS-assisted system and the AO-based algorithm. Finally, Section 5 concludes the paper.
2. RIS-Assisted Multiuser Scheduling System
2.1. System Model
We consider a downlink communication system assisted by one RIS. As shown in Figure 1, the system consists of a single-antenna signal transmitting base station (BS), multiple single-antenna users, and an RIS with N reflective elements. Due to obstacles blocking the communication link between the BS and users, the RIS is utilized to assist communication, forming a BS-RIS-user link. Consequently, the signal received by the k-th user from the BS is expressed as follows:
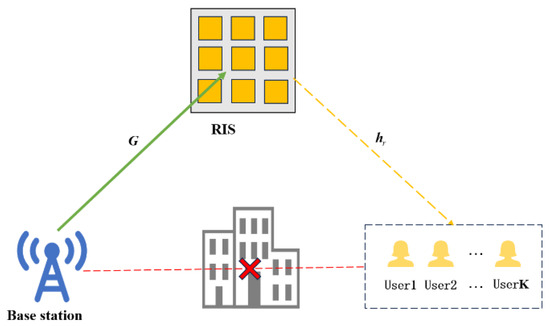
Figure 1.
RIS-assisted multi-user communication system.
Let denote the signal transmitted by the BS to the k-th user, satisfying . Let denote the channel between the BS and the reconfigurable intelligent surface (RIS), and denote the channel from the RIS to the k-th user, where the superscript H represents the Hermitian transpose. The additive white Gaussian noise is denoted by , which has zero mean and variance . The reflection matrix of the RIS is defined as , where and represent the reflection amplitude and phase shift of the n-th RIS element, respectively. Since this chapter adopts a discrete design for the RIS phase shifts, the phase shift values are selected from a discrete set denoted by .
Here, B denotes the number of quantization bits for the discrete phase shifts, which is a positive integer. It directly determines the number of discrete phase-shift values that each RIS reflecting element can take, i.e., there are 2B different discrete phase shift angles available. Assuming that perfect channel state information (CSI) is available at the transmitter and receiver, the achievable rate for user k can be expressed as:
In a multiuser communication scenario, aiming to maximize the system’s overall information transmission rate, the key to solving the problem lies in the joint optimization of the discrete phase shifts and user scheduling to obtain the optimal solution. The corresponding optimization problem can be formulated as follows:
Here, is the control function for multi-user scheduling, subject to the constraint that at most one user can be scheduled in each time slot. For any given set of phase shift angles , it can be verified that Maximum Ratio Transmission (MRT) is the optimal transmission scheme. Therefore, Equation (4) can be further simplified as follows:
Let , then Equation (5) can be expressed as follows:
Let . Therefore, Equation (6) can be written as follows:
If the above objective function is solved by brute-force search, in the worst case, 2BN possible results need to be evaluated, and the number of combinations grows exponentially with the increase of B and N, which is clearly infeasible. Therefore, it is necessary to further reformulate the objective function.
2.2. Joint Optimization Design
To address the issue of the excessively large brute-force search space in Equation (7), it is necessary to further transform the problem. Observing that the main part of the objective function to be optimized is the magnitude , the vector form can be expressed as follows:
Here, denotes the real part and denotes the imaginary part of the vector .
This paper introduces an auxiliary angle , which rotates the vector clockwise by an angle to obtain a new vector , so that it aligns with the polar axis. After the rotation, the imaginary part of the vector becomes zero, and the real part equals the magnitude of the original vector, which is the same as the scalar in the objective function. Therefore, the scalar can be represented as follows:
Let , . The above optimization problem can be further reformulated as follows:
The following section introduces the specific implementation of the algorithm. It is observed that in Equation (10), there exists a certain correlation between the auxiliary angle and the phase shift , although the mapping between them is not strictly one-to-one. If one attempts to determine the phase shift by mapping from the auxiliary angle , it would require solving for N phase shifts simultaneously, which is computationally intensive. Therefore, the optimization should focus on solving the auxiliary angle and then mapping it to the phase shift .
The position update strategy is centered around the auxiliary angle and the phase shift . First, define the search space as K-dimensional, with M particles, L iterations, and a search precision of . Before initialization, set the position boundaries of the auxiliary angle to , and the velocity boundaries to . Then, initialize the position and velocity of the auxiliary angle , map it to obtain the phase shift , and calculate the fitness. The fitness function is defined as follows:
Each particle updates its personal best fitness value and the corresponding personal best position based on the calculated fitness. Among all particles’ personal best fitness values, the global best fitness is selected, and the corresponding auxiliary angle and phase shift are considered the global best position. Take particle m as an example: its personal best fitness is , with the corresponding personal best position ; the global best fitness is , with corresponding global best position . After the above initialization is complete, the algorithm proceeds with iterations to search for the global best position . An inertia weight is set to control the search precision during the iterations. The inertia weight is updated according to the following formula:
The parameters , () are used to update the inertia weight . When updating the velocity of all auxiliary angles , it is important to note that if the new velocity exceeds the predefined velocity boundaries, it will be clipped to either the minimum or maximum allowed value, i.e., . The velocity update formula for the k-th dimension of particle m is given as:
The update formula for the position of particle m in the k-th dimension is expressed as:
The position update strategy is consistent with the velocity update strategy. When the new position is less than or greater than the predefined position boundary , the new position is set to either 0 or 2π. After obtaining the new position of the auxiliary angle , the above steps are repeated to update the global fitness. Subsequently, the individual historical best fitness values of auxiliary angle and phase shift , the individual best position , the global best fitness , and the global best position are determined. When the number of iterations reaches the maximum L, or the search accuracy is achieved, the current global best position is returned, and the iteration terminates. The system’s current rate is then calculated based on the obtained global best position . The specific algorithm process is shown in Algorithm 1.
| Algorithm 1 Multiuser Scheduling and Discrete Phase Shift Design Algorithm |
| 1: Input: |
| 2: Output: |
| 3: Initialize the auxiliary angle , and set ; |
| 4: Calculate the fitness according to the formula ; |
| 5: While: |
| 6: Update the velocity of the auxiliary angle ; |
| 7: Update the positions of the auxiliary angle and the phase shift ; |
| 8: Calculate the fitness and update the individual best fitness fpbest, the individual best position , global best fitness fgbest, and global best position ; |
| 9: |
| 10: Until: ; |
| 11: Return the current global best position . |
2.3. Joint Optimization Design Parameter Settings and Simulation Results Analysis
The channel model considered in this study takes into account both large-scale path loss and small-scale multipath fading characteristics. Specifically, the path loss exponent from the base station to the RIS is set to 2 (open area), and the path loss exponent from the RIS to the user is set to 5.5 (the suburban urban environment) [15]. For the small-scale fading model, the non-line-of-sight (NLOS) multipath propagation scenario is considered, where the channel response is dominated by multipath interference. It is assumed that the signal is transmitted through multiple independent propagation paths, with each path exhibiting a power allocation and a random phase shift caused by propagation delay differences. The resulting channel response is modeled as the sum of multipath components following a Rician fading distribution. The relevant parameters are set as: , , , and other simulation-related parameters are listed in Table 1.

Table 1.
Simulation parameter settings.
To comprehensively evaluate the performance of an RIS-assisted multi-user communication system, a series of simulation experiments was conducted to investigate the impact of key system parameters on the information transmission rate and to comparatively analyze the overall performance of different user scheduling algorithms.
The number of bits for discrete phase shifts directly affects the accuracy of phase selection and plays a crucial role in optimizing system performance. A higher number of bits allows the RIS to realize more phase shift levels with greater precision, thereby improving the quality of the reflected signal. Figure 2 illustrates the cumulative distribution of system transmission rates under different phase shift bit levels. Simulation results show that a higher number of bits leads to better system throughput, as more precise phase control facilitates coherent signal combining, which significantly enhances the overall data rate. However, increasing the number of bits also introduces higher hardware complexity, energy consumption, and implementation cost. Therefore, a trade-off between performance and cost must be considered in practical system design. High-rate and high-precision communication scenarios—such as 5G millimeter-wave and future 6G systems—benefit from higher bit resolutions, while cost-sensitive applications may opt for lower bit levels to achieve a more balanced solution.
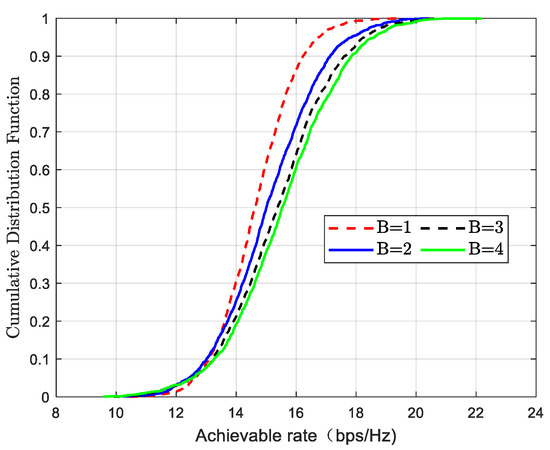
Figure 2.
Cumulative distribution of information transmission rates at different discrete phase-shifted bits.
As observed in Figure 3, in RIS-assisted wireless communication systems, the system’s information transmission rate shows a significant decreasing trend as the distance between the RIS and the end user increases. This phenomenon is primarily due to path loss effects during electromagnetic wave propagation. As the distance grows, the reflected link experiences greater spatial attenuation. Specifically, when the RIS is positioned closer to the user, the reflection path loss is relatively low, enabling the RIS to effectively enhance signal beamforming and improve the system’s transmission rate. However, as the distance increases, the reflection path loss grows exponentially, causing a sharp decline in the received signal energy. In practical deployments, it is essential to optimize the RIS position in three-dimensional space to strike a balance between coverage area and reflection efficiency. The performance of the proposed DPO algorithm is compared against three competitive benchmarks: APX [16], Manopt [17], and random phase shifts. As observed, the DPO algorithm consistently achieves a higher achievable rate. The performance gap with the Manopt method can be attributed to its inherent difficulty in directly handling discrete optimization variables, leading to performance loss during the projection step. While APX is effective, it is not specifically tailored for the joint problem of discrete phase shift and user scheduling, which is the core focus of our DPO algorithm. This result underscores the advantage of our tailored approach in solving this specific high-dimensional combinatorial problem.
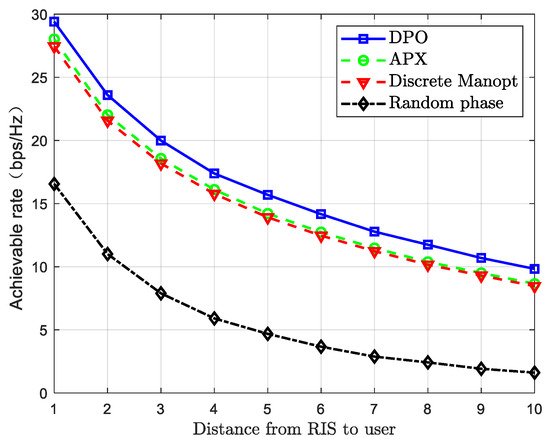
Figure 3.
Relationship between the distance from the RIS to the user and the information transmission rate.
Figure 4 presents a performance comparison of three classic user scheduling algorithms: Round-Robin (RR), Proportional Fair (PF), and MAX C/I. These algorithms represent different trade-offs between fairness and performance. The RR algorithm allocates resources to each user in a fixed order, ensuring absolute fairness, but it does not consider channel conditions, resulting in lower overall system performance. The PF algorithm seeks a balance between user throughput and channel quality, making it a compromise between fairness and efficiency. In contrast, the MAX C/I algorithm fully prioritizes system performance by always selecting the user with the best channel conditions.
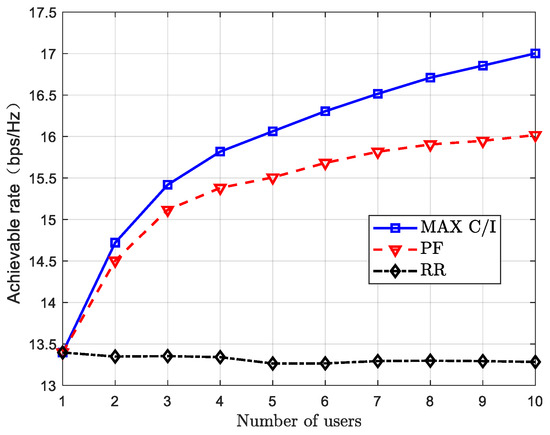
Figure 4.
Comparison of different user scheduling algorithms.
Figure 5 compares the performance of three classic resource allocation algorithms (MAX C/I, RR, and PF) in multi-user scenarios based on the Jain fairness index [18]. The Jain index measures the fairness of resource allocation. While MAX C/I maximizes system capacity, it tends to allocate resources to a few users, resulting in poor fairness. The RR algorithm allocates resources in a fixed order, offering better fairness but ignoring channel conditions, which can lead to inefficient resource utilization. The PF algorithm dynamically balances instantaneous channel quality and historical resource usage, achieving a trade-off between throughput and fairness. From a practical perspective, MAX C/I is suitable for bursty traffic scenarios that prioritize capacity, RR is better suited for static and low-power IoT systems, while PF performs well in mobile communication scenarios with rapid channel variations. In summary, the choice of resource allocation strategy should align with specific system goals and scenario characteristics to balance performance and fairness effectively.
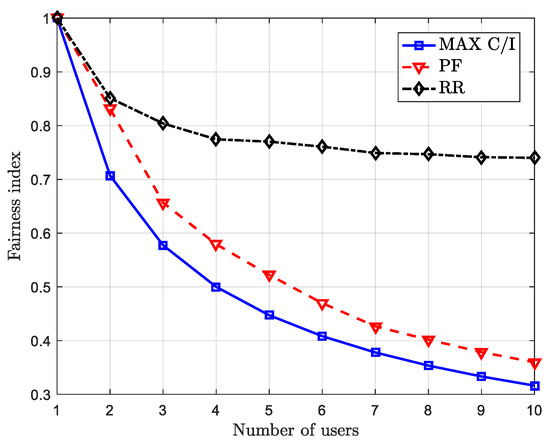
Figure 5.
Fairness index of different scheduling algorithms.
As shown in Figure 6, the convergence characteristics of the discrete phase shift algorithm based on particle swarm optimization (PSO) are validated through simulations. The results demonstrate that under different configurations of reflecting element numbers and discrete phase quantization bit levels, the algorithm can quickly converge to a stable state within a limited number of iterations. Further analysis reveals a significant positive correlation between the system’s spectral efficiency and both the number of reconfigurable intelligent surface elements and the number of quantization bits. This confirms that hardware configuration parameters have a positive regulatory effect on system performance optimization.
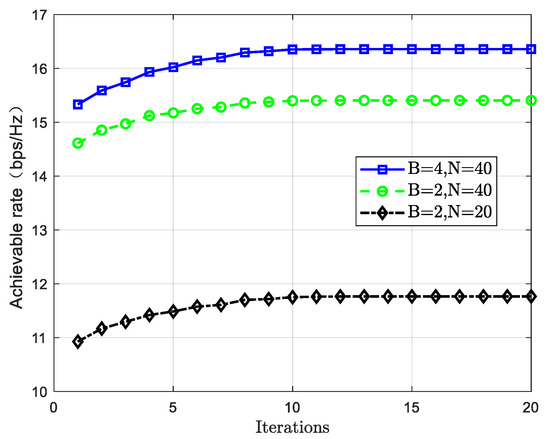
Figure 6.
Analysis of algorithm convergence.
3. Multiuser Scheduling System Assisted by Double RISs
In a single-RIS-assisted multi-user scheduling system, if the base station and users are located on opposite sides of the RIS, the RIS may not be able to effectively cover all communication paths. To overcome this limitation, a double-RIS-assisted communication system is further investigated, as illustrated in Figure 7. This system consists of one base station, two reconfigurable intelligent surfaces (RIS1 and RIS2) with N1 and N2 reflecting elements, respectively, and K users. In this setup, the BS and the users are located on opposite sides of RIS1, while both RIS1 and the users are on the same side of RIS2. Therefore, the signal transmitted from the BS firstly reaches RIS1, is reflected to RIS2, and then reflected again to the intended users. All other communication paths are assumed to be blocked. Therefore, the signal received by the user from the BS can be expressed as:
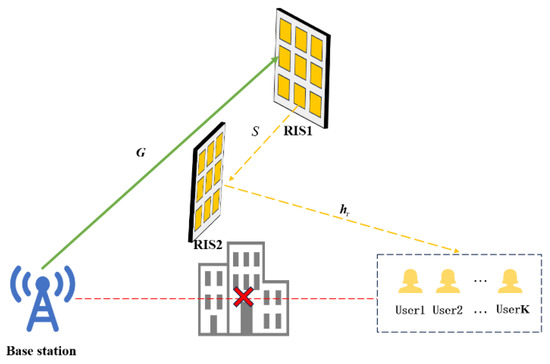
Figure 7.
Multiuser communication system assisted by double RISs.
Here, denotes the signal transmitted from the BS to the k-th user, represents the channel between the BS and RIS1, represents the channel between RIS1 and RIS2, denotes the channel from RIS2 to the k-th user, is additive white Gaussian noise with zero mean and variance . , are the reflection coefficient matrices of RIS1 and RIS2, respectively.
The optimization objective is to maximize the system’s information transmission rate, so the objective function can be expressed as
RIS1 and RIS2 adopt the DPO algorithm to optimize the phase shift parameters in order to enhance signal transmission from the base station to the users. In the double-RIS system, the number of reflecting elements on both RIS1 and RIS2 is set to N1 = N2 = 40, and the distance between RIS1 and RIS2 is 5 m, with path loss taken into account. All other system parameters remain consistent with the previous settings.
Figure 8 presents the performance comparison of the double-RIS system under different configurations. The comparison parameters include the number of reflecting elements and the number of discrete phase shift bits. As shown in the figure, with the same number of users, a larger number of reflecting elements, and higher quantization precision can significantly improve signal manipulation capability and system capacity. Moreover, as the number of users increases, the system can better utilize spatial resources through multi-user scheduling strategies, thereby improving the overall transmission rate. In summary, increasing the number of reflecting elements and the phase shift resolution is an effective way to enhance the communication performance of double-RIS systems. Compared to single-RIS systems, although performance may degrade due to path loss between the two RISs and the absence of additional reflected paths, the double-RIS architecture solves the coverage limitations of reflected signals for users.
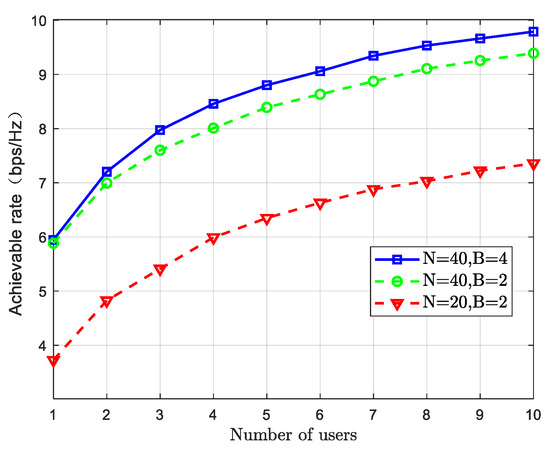
Figure 8.
Comparison of the performance of different configurations of double-RIS systems.
Figure 9 illustrates the convergence performance of the double-RIS system under different configurations. The horizontal axis represents the number of iterations, while the vertical axis shows the achievable rate, used to evaluate the system’s convergence speed and final performance under various settings of reflecting elements and discrete phase shift bit levels. As shown in the figure, all configurations exhibit good convergence behavior: the achievable rate increases with the number of iterations and gradually stabilizes. Therefore, with proper configurations, the double-RIS system can not only achieve a high achievable rate but also converge rapidly within a limited number of iterations, demonstrating strong practicality and computational efficiency.
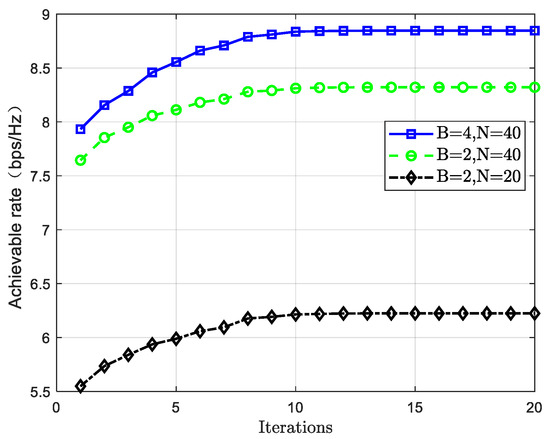
Figure 9.
Convergence analysis of double-RIS systems.
4. Multiuser Scheduling System Assisted by STAR-RIS
4.1. System Model and Problem Formulation
As shown in Figure 10, we consider a downlink communication system assisted by a STAR-RIS. The system consists of a signal transmission base station with a single antenna, users in the transmission area, users in the reflection area, and a STAR-RIS consisting of N elements. In this section, the direct links from the base station to the reflection area and transmission area are blocked, so the signals received by the users are only those that have been transmitted or reflected by the STAR-RIS. Therefore, the signals received by the user in the transmission area and the user the reflection area are denoted as follows:
where and represent the signals transmitted from the BS to users and , respectively. represents the link between the BS and the STAR-RIS, and , represent the links between the STAR-RIS and users and , respectively. are additive Gaussian white noise with zero mean and variance . and are the transmission and reflection coefficient matrices mentioned earlier. The discrete phase shift mode is still used for the phase shift design in this chapter. As a result, the achievable rates for users and are denoted as follows:
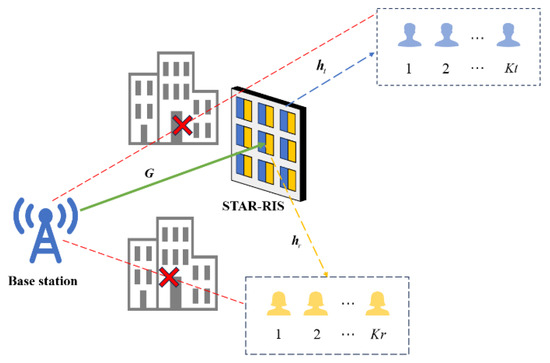
Figure 10.
STAR-RIS-assisted multi-user communication system.
Jointly optimize user scheduling and the STAR-RIS transmission and reflection coefficient matrices to maximize the system’s sum rate. The optimization problem is as follows:
It is worth noting that the adopted ES model with independent phase and amplitude control represents an idealization. In practice, the scattering parameters of a passive STAR-RIS are subject to electromagnetic coupling and reciprocity [7]. However, this model provides a valuable performance benchmark and allows us to focus on the core algorithmic challenge of joint optimization. The extension of our proposed AO framework to more physically realistic models is a promising direction for future research.
Among them, is the discrete phase shift set, and are the control functions for user scheduling. Similarly to the previous derivation, the problem can be further simplified as follows:
4.2. Phase and Amplitude Design Based on Alternating Optimization
To solve the above non-convex optimization problem, an alternating optimization algorithm is employed. The problem involves two types of coupled variables: the amplitude parameters of the transmission/reflection coefficients and the phase-shift parameters. The strong coupling between them makes direct joint optimization challenging. Therefore, the original problem is decomposed into two subproblems: first, the phase shift parameters are optimized using the DPO algorithm; then, the amplitude parameters of the transmission/reflection coefficients are solved using the Lagrange multiplier method. Specifically, the amplitude and phase shift parameters are updated in an alternating iterative manner until a convergence criterion is met or a predefined maximum number of iterations is reached, thereby gradually approaching the global optimum. User scheduling is embedded into the joint optimization of phase shifts and amplitudes by constructing a user-pair space (i.e., all combinations of transmission and reflection users). In each iteration, the optimal user pair is dynamically selected based on the current phase shift and amplitude parameters.
Based on the alternating optimization framework, before applying the DPO algorithm to optimize the transmission/reflection phase-shift parameters and user scheduling factors, it is necessary to first determine the fixed values of the amplitude parameters. Therefore, during the initialization phase of the algorithm, the amplitudes of the transmission and reflection coefficients need to be preset. In this chapter, a uniform allocation is adopted as the initial value, i.e., , which serves as a baseline starting point for the subsequent iterative process, ensuring the stable convergence of the alternating optimization algorithm.
Next, using a method similar to that in Section 3, auxiliary angles and are introduced into the objective functions of users in the transmission and reflection regions, respectively. Therefore, the above expression can be rewritten as follows:
Thus, the fitness function is obtained as follows:
When the amplitude parameters of the transmission/reflection coefficients are fixed, the two sub-terms in the objective function related to the auxiliary angles and phase shifts become decoupled. This parameter independence simplifies the phase shift optimization problem into a single-variable extremum search, allowing the direct application of the DPO algorithm to find the optimal phase shift configuration that maximizes the system’s objective function.
The Lagrange multiplier method is a classical approach to handling constrained optimization problems. Its essence lies in transforming the original constrained problem into an unconstrained optimization problem by constructing an augmented objective function. Specifically, by introducing Lagrange multipliers, the constraint conditions are combined with the objective function, and the extreme values are obtained by solving the gradient’s zero points based on the Karush–Kuhn–Tucker (KKT) conditions. Based on this principle, under the premise of fixing other optimization variables, the amplitude coupling relationship of the transmission/reflection coefficients is modeled as an equality constraint. This leads to the construction of the Lagrangian function containing this constraint, and ultimately, the optimal values of the transmission and reflection coefficients are solved through Newton’s iteration method.
When the transmission/reflection phase shift parameters are fixed, the original objective function can be simplified into a function of the amplitude parameters, as shown in Equation (25).
Among them, , , , , . Thus, the optimization objective function can be expressed as follows:
According to the constraint , , the constraint function can be constructed as follows:
For simplification, let , , , , , . Thus, the objective function and constraint function can be expressed as follows:
where
Next, by introducing Lagrange multipliers and combining the objective function with the constraint function, we can obtain the Lagrangian function as follows:
Next, we take partial derivatives of the Lagrangian function as follows:
Therefore, we can obtain the system of equations.
Due to the strong nonlinearity and complex coupling characteristics of the above system of equations, it is difficult to solve them directly. Therefore, numerical methods become an effective approach to address such problems. In this paper, the Newton-Raphson method is adopted, which approximates the solution of the system through local linearization and provides both second-order convergence speed and relatively high computational accuracy. Mathematically, this can be expressed as: the nonlinear system is uniformly represented as , where is the vector of unknown variables to be solved.
Before the first iteration, the solution vector needs to be initialized. The amplitude parameters are initialized using a uniform distribution strategy, while the Lagrange multipliers are initialized to zero. In this paper, the initial guess is set as , .
It can be computed via matrix operations. Formally, at the current iteration point , a first-order Taylor expansion is applied to locally linearize the nonlinear system .
Let , we obtain the following:
Solving for the increment , we then update the iteration point as follows:
For the global convergence control of the iterative optimization process, the algorithm sets a dual termination criterion: the optimization terminates either when the update increment between two consecutive iterations falls below a predefined threshold ε, or when the total number of iterations reaches the upper limit. This mechanism effectively balances computational accuracy and runtime. The complete iterative optimization process and its distributed implementation details are shown in Algorithm 1, including variable initialization and the coordinated update mechanism for subproblem solutions.
To efficiently solve this problem, we propose an alternating optimization (AO) algorithm, outlined in Algorithm 2. The core idea is to decouple the optimization into two tractable subproblems: (1) optimizing the discrete phase shifts and user scheduling with fixed amplitudes, which is solved by the DPO algorithm (Algorithm 1); and (2) optimizing the continuous amplitudes with fixed phases and scheduling, which is solved via the Lagrange multiplier method. The algorithm alternates between these two steps until convergence.
| Algorithm 2 Alternate optimization algorithm steps |
| 1: Initialization: Initialize the amplitude of the STAR-RIS transmission/reflection coefficients ; set the iteration index , and the convergence tolerance ; 2: Repeat: 3: Given and , solve problem using the DPO algorithm to obtain and ; 4: Given and , solve problem using the Lagrange multiplier-based method to obtain and ; 5: Update ; 6: Update r = r + 1; 7: Repeat until . |
In Algorithm 2, Step 3 corresponds to solving the phase shift and scheduling subproblem using DPO, while Step 4 solves the amplitude subproblem. This iterative process monotonically increases the objective value, ensuring convergence.
The main objective of this section is to verify, through simulation experiments, the performance improvement of the communication system assisted by STAR-RIS. For fairness, the benchmark scheme is set such that a conventional RIS uses half the number of STAR-RIS elements for signal reflection and the other half for transmission.
Figure 11 illustrates the relationship between the number of users and the achievable data rate. As shown in the figure, the data rate increases with the number of users across all RIS configurations, with a particularly significant improvement observed in the STAR-RIS system. Compared to conventional RIS systems, the STAR-RIS system can allocate resources more efficiently in multi-user environments. Not only does STAR-RIS offer broader coverage angles than traditional RIS, but it also enhances signal transmission quality and optimizes spectrum utilization by adjusting the amplitude of its transmission and reflection coefficients. This enables it to support more users and achieve higher data rates than conventional RIS systems. In addition, a comparison scenario considering hardware impairment [19] caused by discrete phase shifts—modeled as random phase errors—is included. The results indicate that such hardware impairments have a certain impact on system performance.
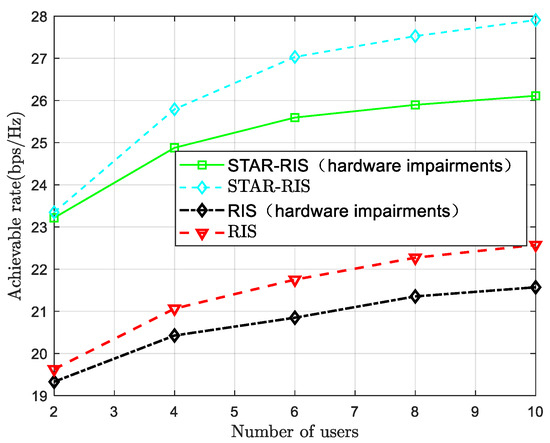
Figure 11.
The relationship between the number of users and the information transmission rate.
Figure 12 shows the relationship between the number of elements and the achievable data rate. It can be observed from the figure that as the number of elements increases, the data rate significantly improves under all configurations. A larger number of elements provides more transmission paths for the system, which is particularly beneficial in practical environments where interference and signal attenuation are prevalent. The increased number of elements allows STAR-RIS to enhance multipath propagation by adjusting both the amplitude and phase of the transmission and reflection coefficients. The performance gain of STAR-RIS over conventional RIS mainly lies in its ability to control signal amplitude. In conventional RIS, the reflective surface typically only controls the phase of the signal while the amplitude remains constant. In contrast, STAR-RIS not only adjusts the phase but also dynamically controls the amplitude. This joint control of amplitude and phase allows STAR-RIS to more precisely optimize signal transmission paths. Similarly, when hardware impairments caused by discrete phase shifts are considered, the overall system performance declines.
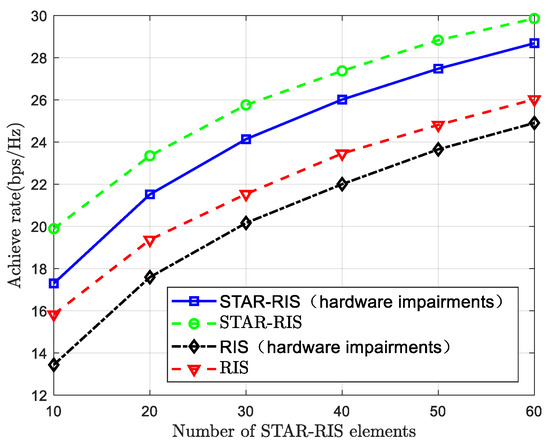
Figure 12.
Graph of the number of STAR-RIS components and the information transmission rate.
Figure 13 illustrates the impact of user location distribution on the performance of a STAR-RIS-assisted communication system. By adjusting the positions of the reflecting and transmitting users relative to the STAR-RIS, while keeping the sum of their distances constant at 10 m (i.e., , where and denote the distances from the STAR-RIS to the transmitting and reflecting users, respectively)—it is observed that an asymmetric user distribution (i.e., one user being closer to the STAR-RIS while the other is farther away) can enhance the system sum rate. This phenomenon stems from the system’s dynamic resource allocation mechanism during optimization. When a user is located closer to the STAR-RIS, the corresponding channel strength is enhanced due to lower path loss, leading the system to allocate more resources to the near-end user. However, while this asymmetric allocation strategy can improve the overall sum rate, it does so at the expense of the performance of the far-end user. When the users are symmetrically positioned (i.e., ), the sum rate reaches its minimum, as shown in the curve. This is because the channel gains for both the transmitting and reflecting users become balanced under symmetric distribution, preventing the resource allocation strategy from effectively leveraging the advantage of a stronger channel for either user.
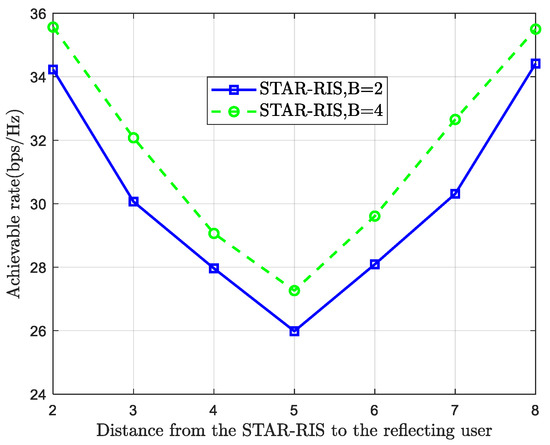
Figure 13.
Graph of user location and system rate.
5. Conclusions
With the increasing demand for communication and the growing complexity of application scenarios, this study focuses on intelligent surface-assisted multi-user scheduling systems. First, a downlink multi-user communication model based on conventional RIS is established. To address the non-convex optimization caused by discrete phase shifts and user scheduling, a vector projection relaxation method is employed, and a PSO-based joint algorithm is proposed to optimize phase shifts and scheduling. Simulation results verify the effectiveness of the proposed method in improving system performance. Subsequently, a double-RIS scheme is investigated to alleviate the coverage blind spots of single-RIS systems. Although it enhances performance, it also leads to increased hardware costs. To address this issue, STAR-RIS is introduced, adopting a power-splitting protocol to jointly control transmission and reflection. An alternating optimization algorithm for amplitude and phase is developed, embedding user scheduling into the optimization process. Simulation results show that STAR-RIS outperforms conventional RIS under the same conditions. Furthermore, the impact of the relative position distribution of users on system performance is analyzed, demonstrating the flexibility and advantages of STAR-RIS in complex multi-user scenarios.
Future work includes several promising directions. First, the fairness aspect of the scheduling algorithm will be explicitly incorporated into the optimization framework. Second, a more extensive performance comparison against a wider array of emerging user scheduling and RIS configuration algorithms will be conducted to further solidify the benchmarking. Finally, investigating the robustness of the proposed algorithms under imperfect channel state information is also of great practical interest.
Author Contributions
Methodology, X.R. and Z.D.; software, Z.D.; writing—original draft preparation, Z.D.; writing—review and editing, X.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 6G | The sixth generation |
| RIS | Reconfigurable intelligent surface |
| STAR-RIS | Simultaneously transmitting and reflecting a reconfigurable intelligent surface |
| DPO | Discrete phase optimization |
| PSO | Particle swarm optimization |
| AO | Alternating optimization |
| BS | Base station |
| CSI | Channel state information |
| MRT | Maximum ratio transmission |
| NLOS | Non-line-of-sight |
| RR | Round-robin |
| PF | Proportional fair |
| KKT | Karush–Kuhn–Tucker |
References
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G internet of things: A comprehensive survey. IEEE Internet Things J. 2021, 9, 359–383. [Google Scholar] [CrossRef]
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M.S. What should 6G be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Zheng, K.; Jia, X.; Chi, K.; Liu, X. DDPG-based Joint Time and Energy Management in Ambient Backscatter-assisted Hybrid Underlay CRNs. IEEE Trans. Commun. 2023, 1, 441–456. [Google Scholar] [CrossRef]
- ElMossallamy, M.A.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2019, 58, 106–112. [Google Scholar] [CrossRef]
- Tödtling, F.; Trippl, M.; Desch, V. New directions for RIS studies and policies in the face of grand societal challenges. Eur. Plan. Stud. 2022, 30, 2139–2156. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Schober, R. Simultaneously transmitting and reflecting (STAR) RIS aided wireless communications. IEEE Trans. Wirel. Commun. 2022, 21, 3083–3098. [Google Scholar] [CrossRef]
- Du, W.; Chu, Z.; Chen, G.; Xiao, P.; Xiao, Y.; Wu, X.; Hao, W. STAR-RIS assisted wireless powered IoT networks. IEEE Trans. Veh. Technol. 2023, 72, 10644–10658. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y.; Mu, X.; Gu, X.; Dobre, O.A. Coverage characterization of STAR-RIS networks: NOMA and OMA. IEEE Commun. Lett. 2021, 25, 3036–3040. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Liu, Y.; He, B.; Lv, L.; Chen, J. Security enhancement for coupled phase-shift STAR-RIS networks. IEEE Trans. Veh. Technol. 2023, 72, 8210–8215. [Google Scholar] [CrossRef]
- Feres, C.; Ding, Z. An unsupervised learning paradigm for user scheduling in large scale multi-antenna systems. IEEE Trans. Wirel. Commun. 2022, 22, 2932–2945. [Google Scholar] [CrossRef]
- Denis, J.; Assaad, M. Improving cell-free massive MIMO networks performance: A user scheduling approach. IEEE Trans. Wirel. Commun. 2021, 20, 7360–7374. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, T.; Yu, W. Learning based user scheduling in reconfigurable intelligent surface assisted multiuser downlink. IEEE J. Sel. Top. Signal Process. 2022, 16, 1026–1039. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J. Dynamic aerial reconfigurable intelligent surface aided multi-cell multi-user communications. IEEE Trans. Wirel. Commun. 2024, 23, 16453–16465. [Google Scholar]
- Azar, Y.; Wong, G.N.; Wang, K.; Mayzus, R.; Schulz, J.K.; Zhao, H.; Gutierrez, F.; Hwang, D.; Rappaport, T.S. 28 GHz propagation measurements for outdoor cellular communications using steerable beam antennas in New York city. In Proceedings of the International Conference on Communications, Budapest, Hungary, 9–13 June 2013; pp. 5143–5147. [Google Scholar]
- Zhang, Y.; Shen, K.; Ren, S.; Li, X.; Chen, X.; Luo, Z. Configuring intelligent reflecting surface with performance guarantees: Optimal beamforming. IEEE J. Sel. Top. Signal Process. 2022, 16, 967–979. [Google Scholar] [CrossRef]
- Bounal, N.; Mishra, B.; Absil, P.; Sepulchre, R. Manopt, a matlab toolbox for optimization on manifolds. J. Mach. Learn. Res. 2014, 15, 1455–1459. [Google Scholar]
- Adian, F.R.; Abdul, M.; Riri, F.S. A discrimination index based on Jain’s fairness index to differentiate researchers with identical H-index values. J. Data Inf. Sci. 2020, 5, 5–18. [Google Scholar]
- Xing, X.; Wang, R.; Wu, J.; Liu, E. Achievable rate analysis and phase shift optimization on intelligent reflecting surface with hardware impairments. IEEE Trans. Wirel. Commun. 2021, 20, 5514–5530. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).