Low-Power Radix-22 FFT Processor with Hardware-Optimized Fixed-Width Multipliers and Low-Voltage Memory Buffers
Abstract
1. Introduction
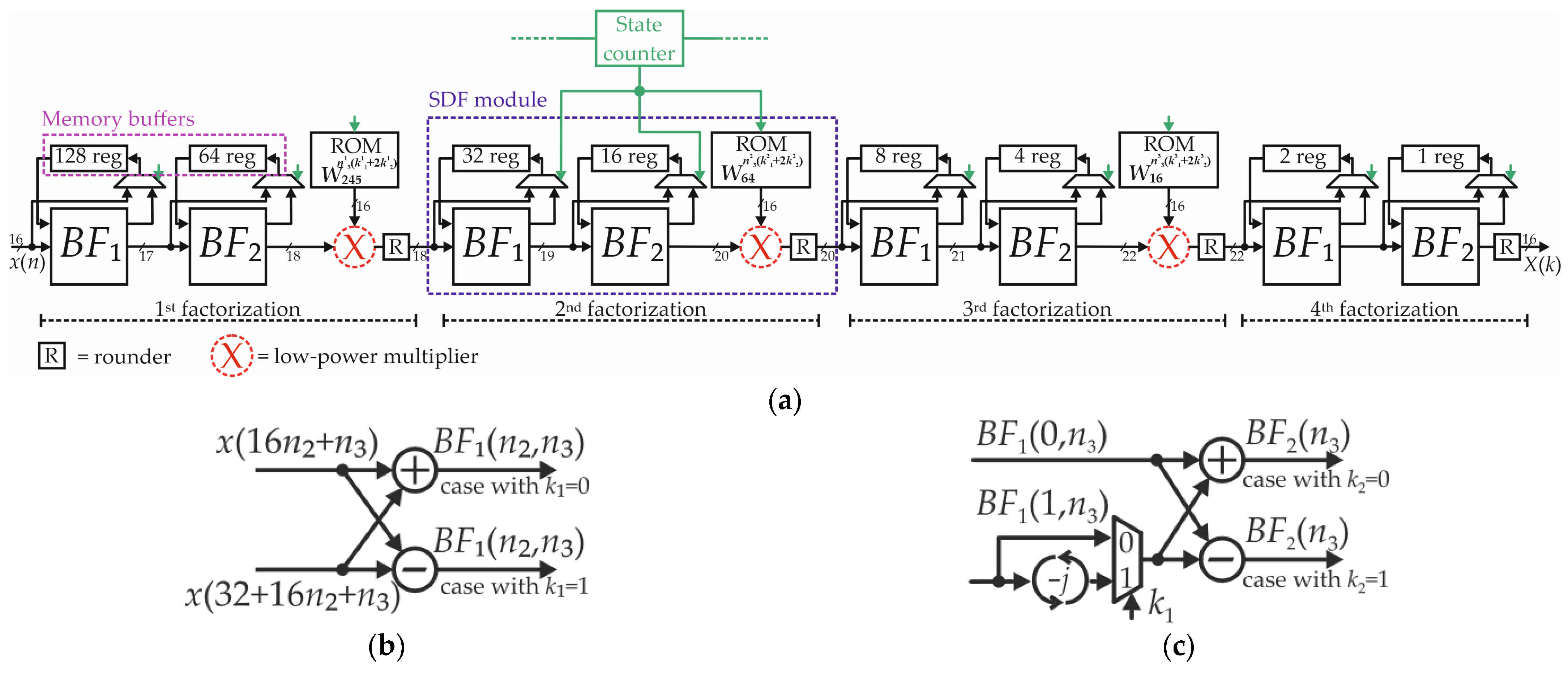
2. Radix-22 FFT Processor
3. Hardware Implementation
3.1. Multiplication with Trivial Coefficients
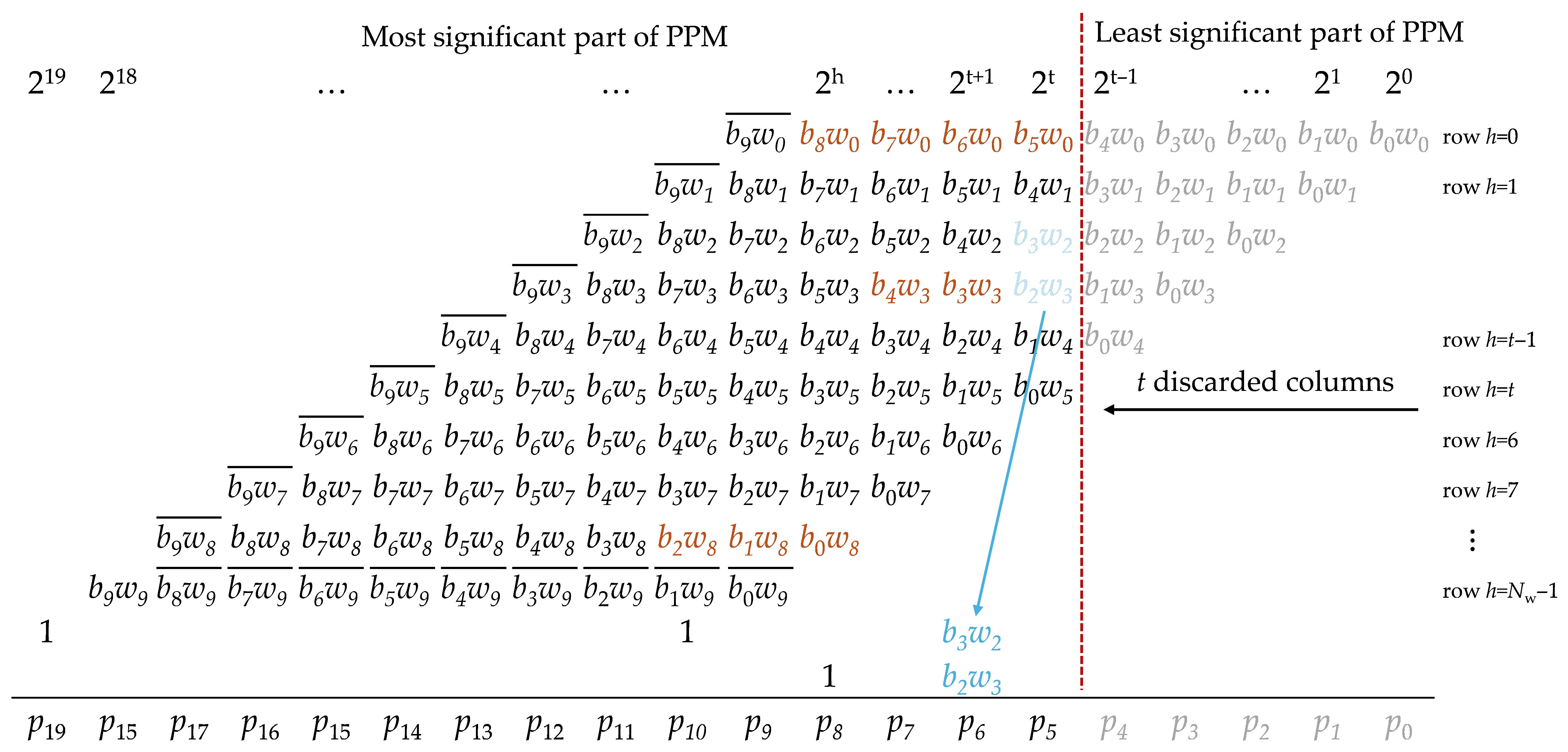
3.2. Proposed Fixed-Width Multiplier
- (i)
- rows for h < 2 and t ≤ h ≤ t + 1 have LSB of weight 2t;
- (ii)
- rows for 2 ≤ h < t have LSB of weight is 2t+1;
- (iii)
- rows for h > t + 1 the LSB weighs 2h.
3.3. Memory Buffer
4. Results
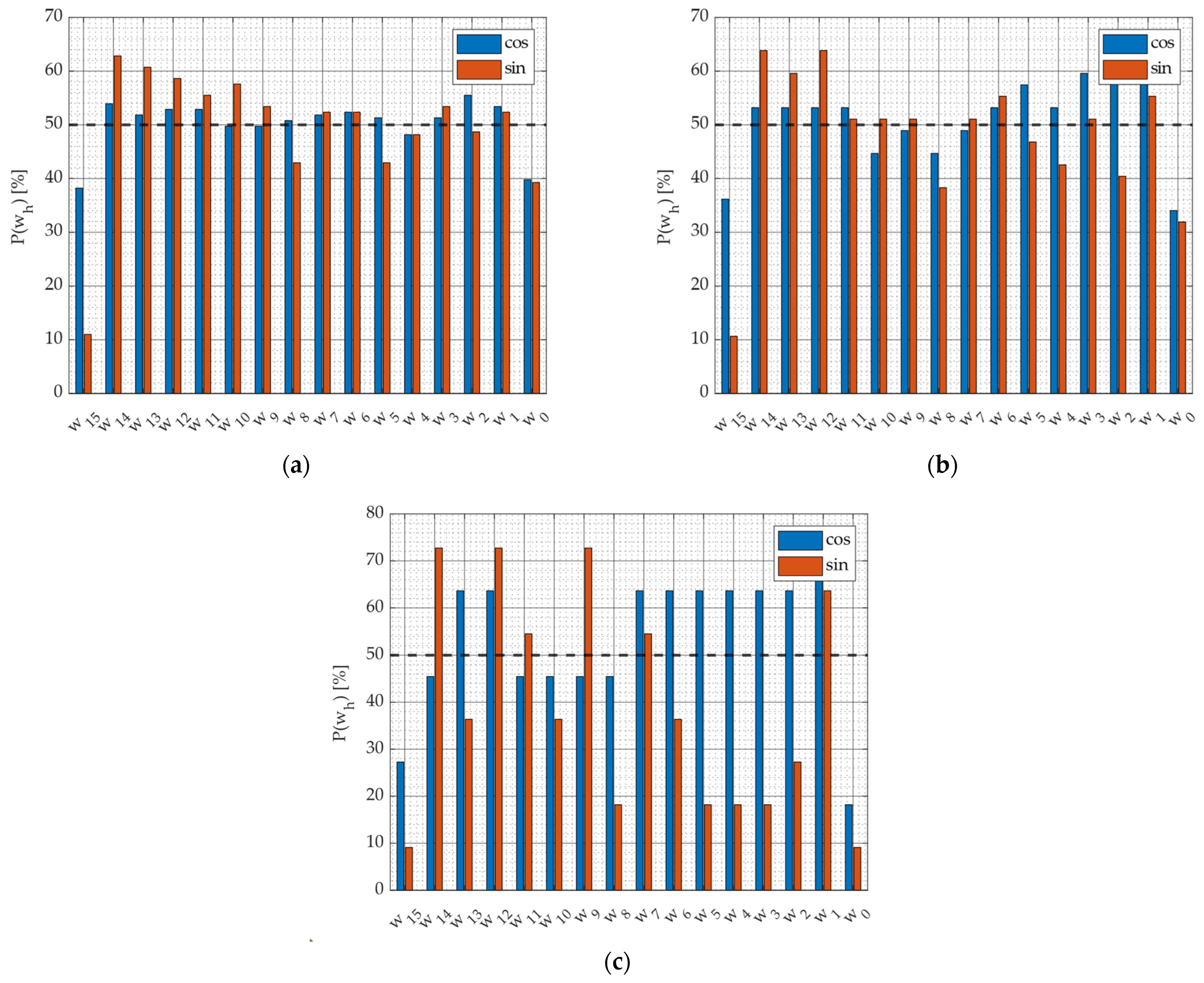
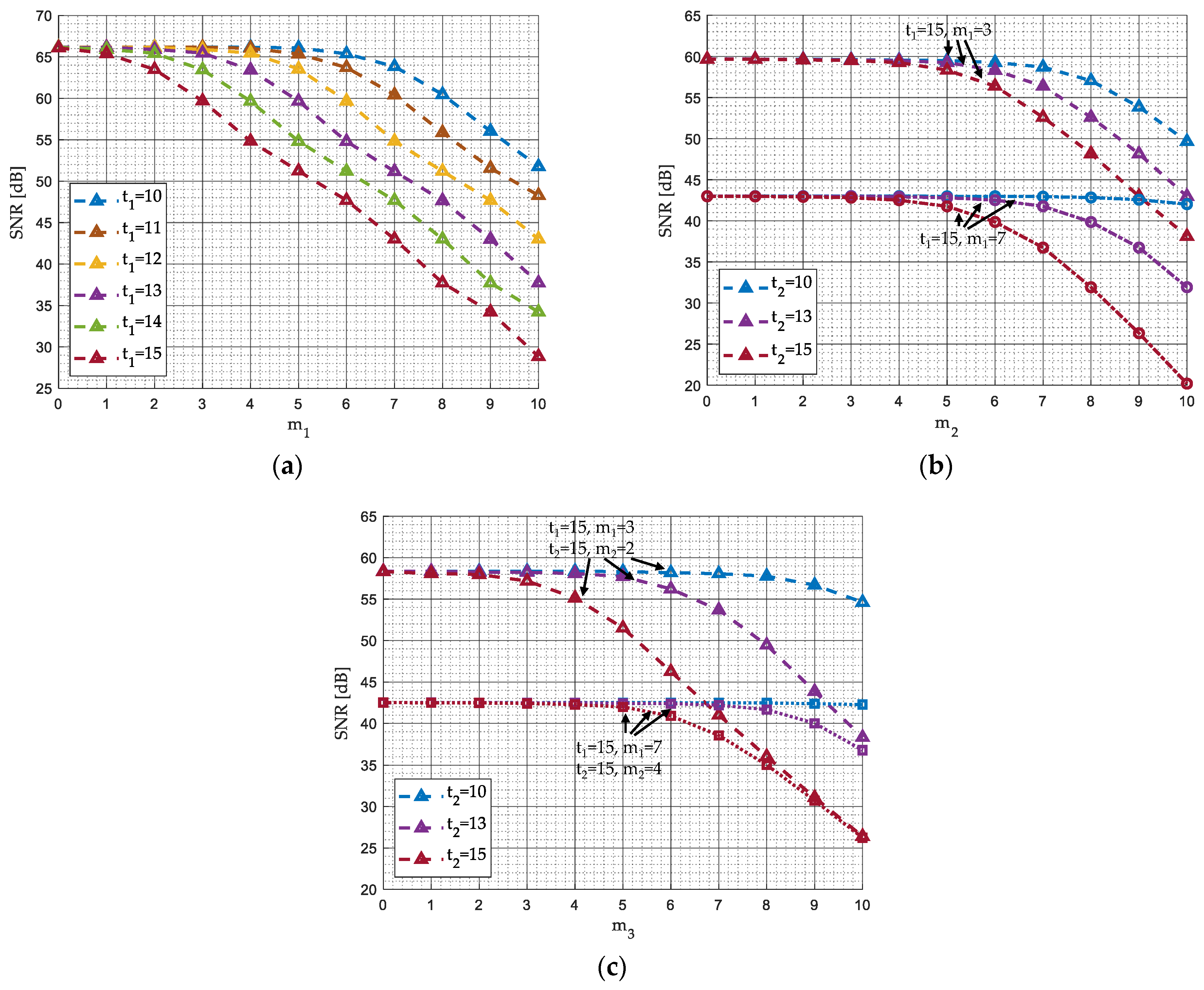
4.1. Accuracy Assessment
- A-FFT103,2,3, A-FFT106,3,4, A-FFT107,4,5, A-FFT108,8,10;
- A-FFT133,2,3 A-FFT136,3,4, A-FFT137,4,5, A-FFT138,8,10;
- A-FFT153,2,3, A-FFT156,3,4, A-FFT157,4,5 A-FFT158,8,10.
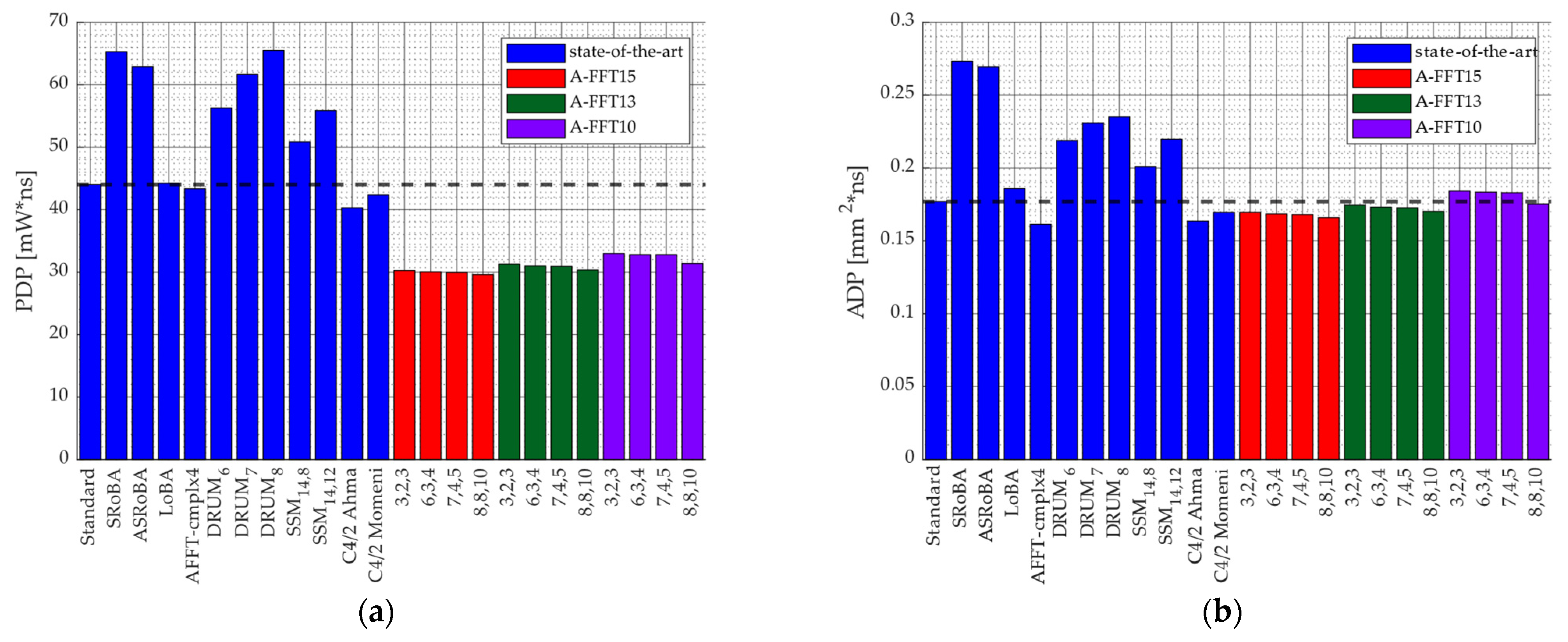
4.2. Hardware Results
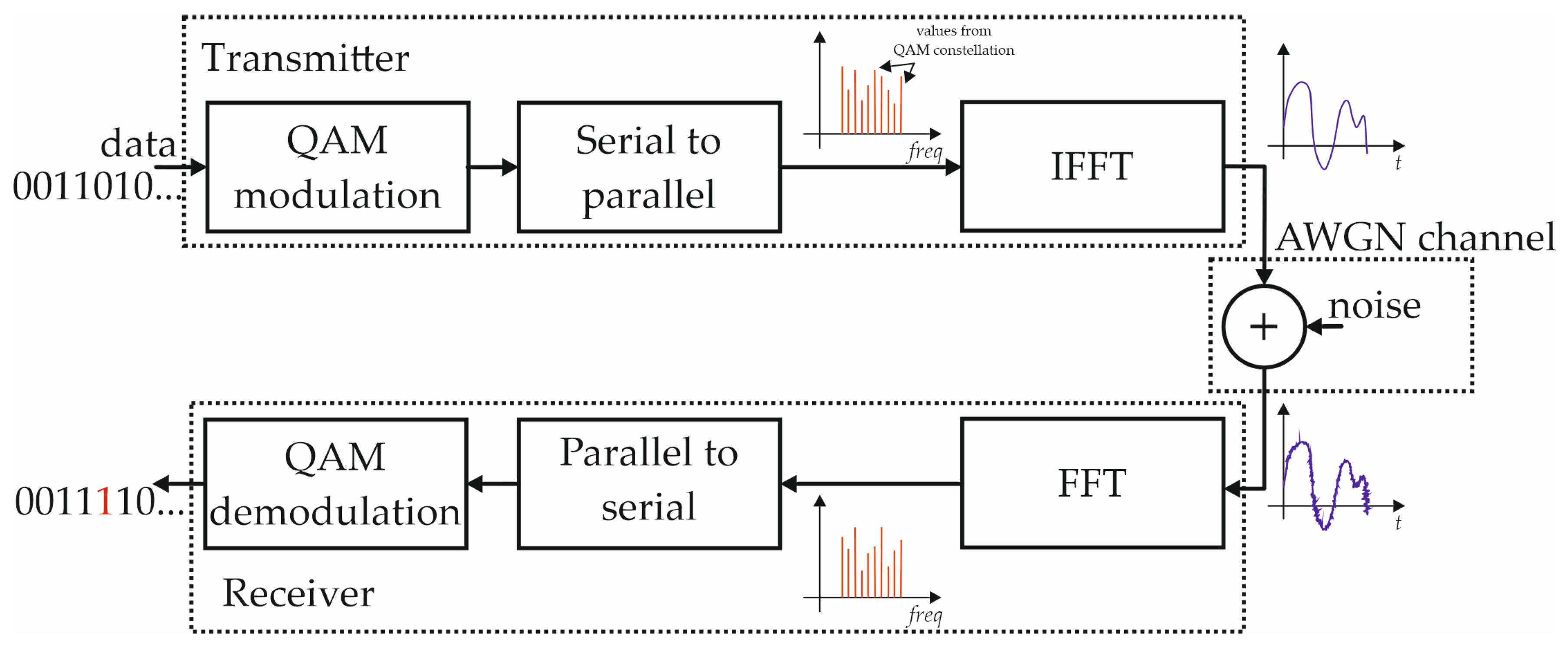
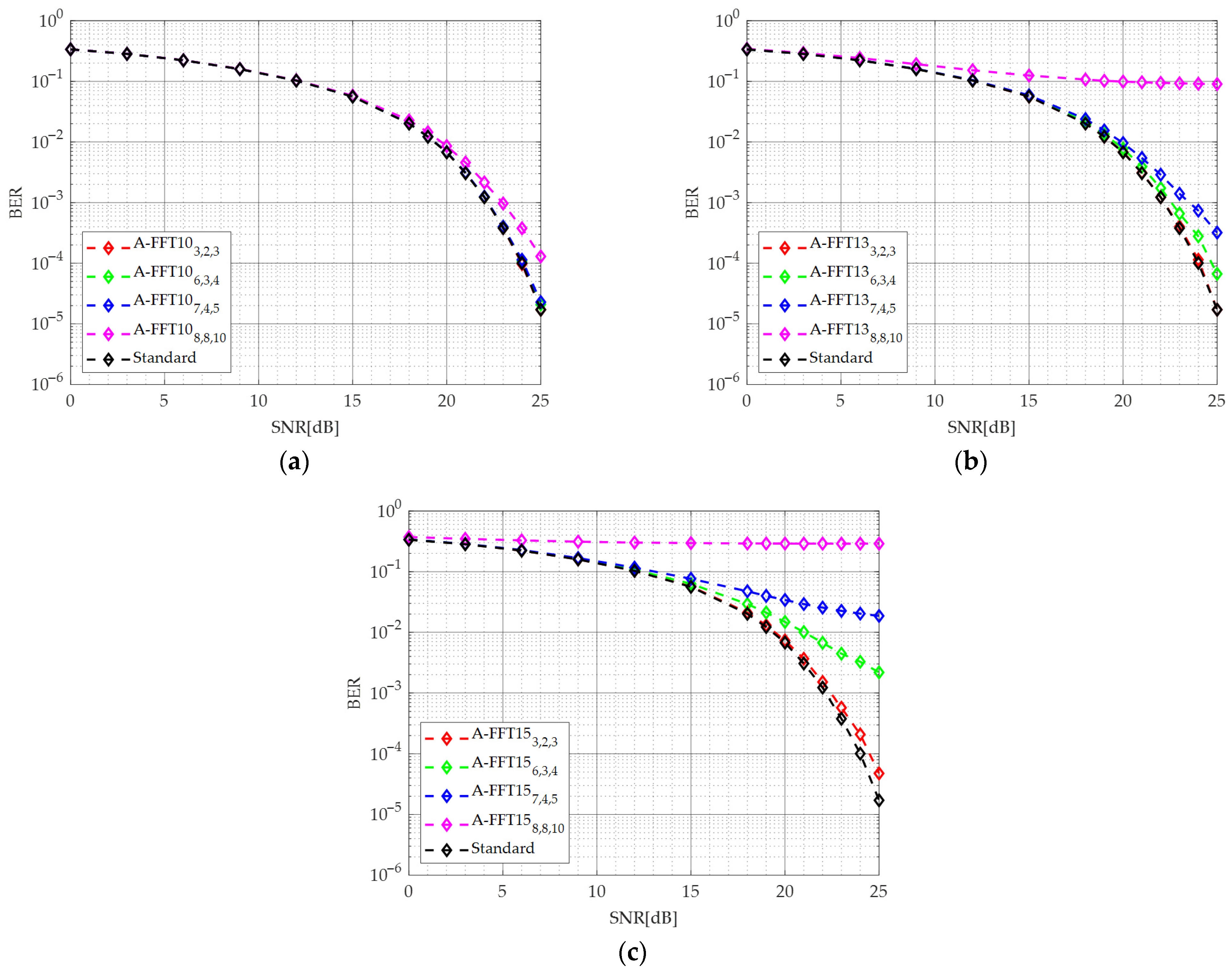
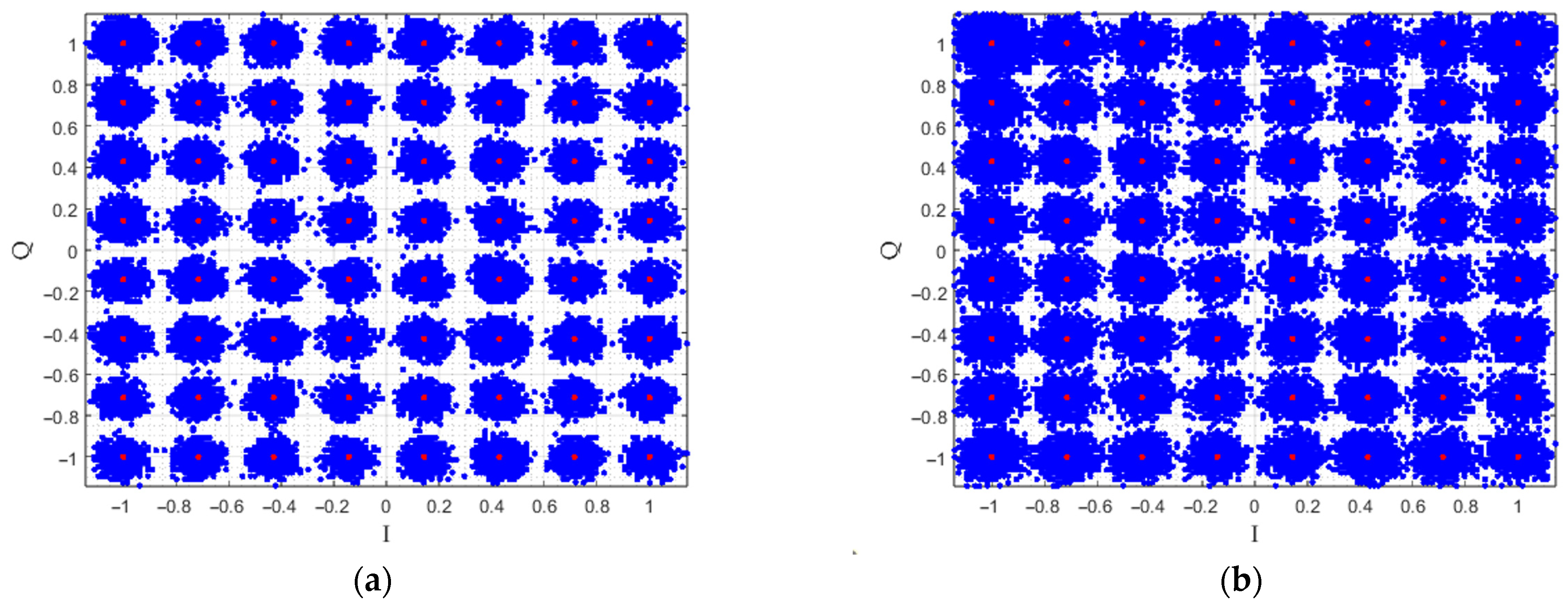
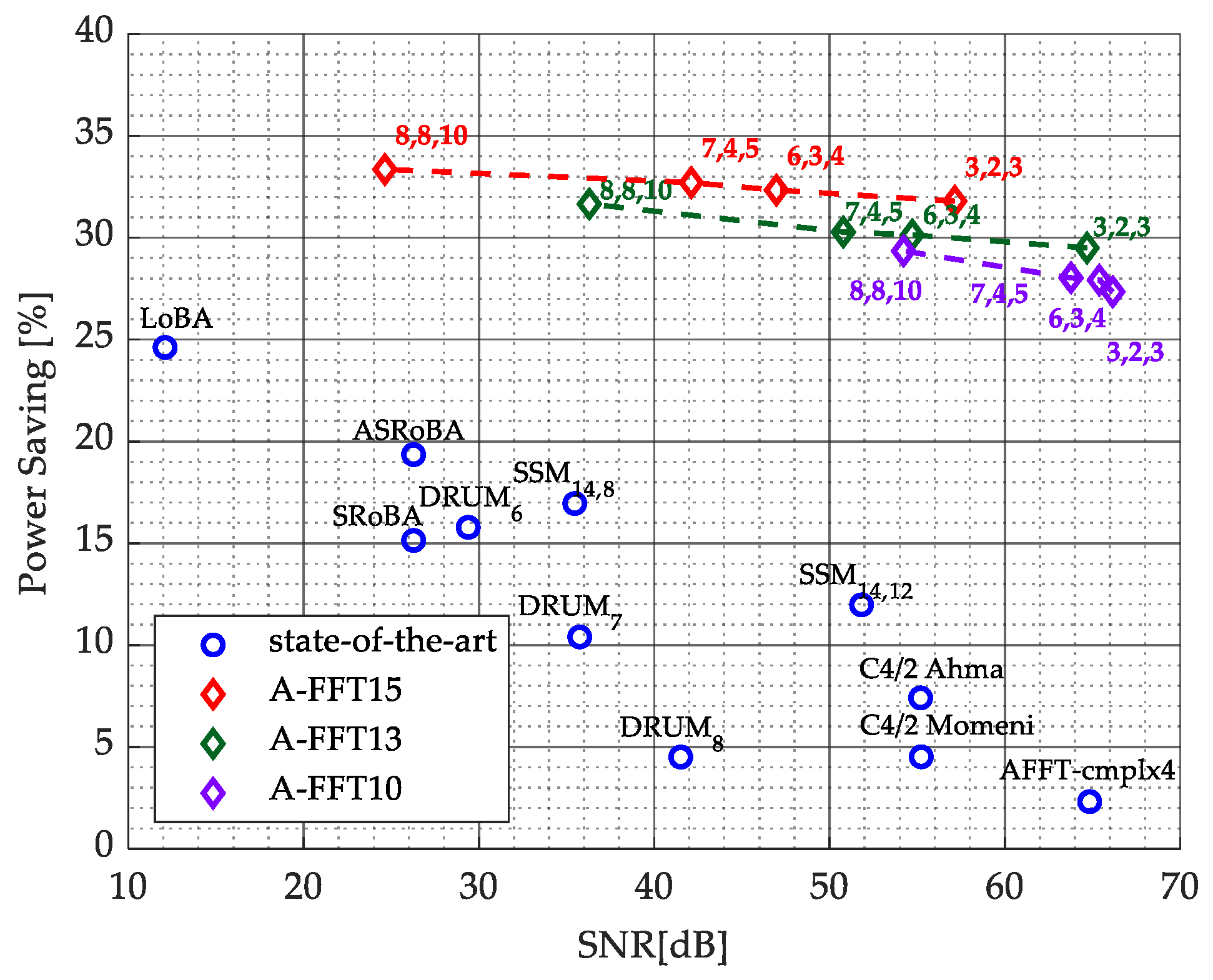
4.3. Performance in OFDM Receiver
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFT | Discrete Fourier Transform |
| FFT | Fast Fourier Transform |
| SNR | Signal-to-Noise Ratio |
| MSE | Mean Squared Error |
| BER | Bit Error Rate |
| PDP | Power-Delay-Product |
| ADP | Area-Delay-Product |
| SDF | Single-path Delay Feedback |
| SRAM | Static Random Access Memory |
Appendix A
References
- Shokry, B.; Dessouky, M.; Safar, M.; El-Kharashi, M.W. A dynamically configurable-radix pipelined FFT algorithm for real time applications. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 19–20 December 2017; pp. 402–407. [Google Scholar] [CrossRef]
- Qureshi, F.; Takala, J. New Identical Radix-2^k Fast Fourier Transform Algorithms. In Proceedings of the 2016 IEEE International Workshop on Signal Processing Systems (SiPS), Dallas, TX, USA, 26–28 October 2016; pp. 195–200. [Google Scholar] [CrossRef]
- Lee, Y.-C.; Chi, T.-S.; Yang, C.-H. A 2.17-mW Acoustic DSP Processor with CNN-FFT Accelerators for Intelligent Hearing Assistive Devices. IEEE J. Solid-State Circuits 2020, 55, 2247–2258. [Google Scholar] [CrossRef]
- Shan, W.; Yang, M.; Wang, T.; Lu, Y.; Cai, H.; Zhu, L.; Xu, J.; Wu, C.; Shi, L.; Yang, J. A 510-nW Wake-Up Keyword-Spotting Chip Using Serial-FFT-Based MFCC and Binarized Depthwise Separable CNN in 28-nm CMOS. IEEE J. Solid-State Circuits 2021, 56, 151–164. [Google Scholar] [CrossRef]
- Yue, J.; Liu, Y.; Liu, R.; Sun, W.; Yuan, Z.; Tu, Y.-N.; Chen, Y.-J.; Ren, A.; Wang, Y.; Chang, M.-F.; et al. STICKER-T: An Energy-Efficient Neural Network Processor Using Block-Circulant Algorithm and Unified Frequency-Domain Acceleration. IEEE J. Solid-State Circuits 2021, 56, 1936–1948. [Google Scholar] [CrossRef]
- Yu, C.; Yen, M.-H. Area-Efficient 128- to 2048/1536-Point Pipeline FFT Processor for LTE and Mobile WiMAX Systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 1793–1800. [Google Scholar] [CrossRef]
- Cooley, J.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Oppenheim, A.; Schafer, R. Discrete-Time Signal Processing; Prentice-Hall: Engelwood Cliffs, NJ, USA, 1989. [Google Scholar]
- Garrido, M. A Survey on Pipelined FFT Hardware Architectures. J. Signal Process. Syst. 2022, 94, 1345–1364. [Google Scholar] [CrossRef]
- He, S.; Torkelson, M. Design and implementation of a 1024-point pipeline FFT processor. In Proceedings of the IEEE 1998 Custom Integrated Circuits Conference (Cat. No.98CH36143), Santa Clara, CA, USA, 14 May 1998; pp. 131–134. [Google Scholar] [CrossRef]
- He, S.; Torkelson, M. A new approach to pipeline FFT processor. In Proceedings of the International Conference on Parallel Processing, Honolulu, HI, USA, 15–19 April 1996; pp. 766–770. [Google Scholar] [CrossRef]
- Santhosh, L.; Thomas, A. Implementation of radix 2 and radix 22 FFT algorithms on Spartan6 FPGA. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Esposito, D.; Di Meo, G.; De Caro, D.; Strollo, A.G.M.; Napoli, E. Quality-Scalable Approximate LMS Filter. In Proceedings of the 2018 25th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 849–852. [Google Scholar] [CrossRef]
- Di Meo, G.; De Caro, D.; Saggese, G.; Napoli, E.; Petra, N.; Strollo, A.G.M. A Novel Module-Sign Low-Power Implementation for the DLMS Adaptive Filter with Low Steady-State Error. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 297–308. [Google Scholar] [CrossRef]
- Ansari, M.S.; Cockburn, B.F.; Han, J. An Improved Logarithmic Multiplier for Energy-Efficient Neural Computing. IEEE Trans. Comput. 2021, 70, 614–625. [Google Scholar] [CrossRef]
- Han, J.; Orshansky, M. Approximate computing: An emerging paradigm for energy-efficient design. In Proceedings of the 2013 18th IEEE European Test Symposium (ETS), Avignon, France, 27–30 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Chippa, V.K.; Chakradhar, S.T.; Roy, K.; Raghunathan, A. Analysis and characterization of inherent application resilience for approximate computing. In Proceedings of the 2013 50th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 29 May–7 June 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Hashemi, S.; Bahar, R.I.; Reda, S. DRUM: A Dynamic Range Unbiased Multiplier for approximate applications. In Proceedings of the 2015 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Austin, TX, USA, 2–6 November 2015; pp. 418–425. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Moghaddam, H.A.; Liu, Z.; Park, T.; Kim, N.S. Energy-Efficient Approximate Multiplication for Digital Signal Processing and Classification Applications. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 1180–1184. [Google Scholar] [CrossRef]
- Di Meo, G.; Saggese, G.; Strollo, A.G.M.; De Caro, D. Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions. Electronics 2023, 12, 446. [Google Scholar] [CrossRef]
- Di Meo, G.; Saggese, G.; Strollo, A.G.M.; De Caro, D. Approximate MAC Unit Using Static Segmentation. IEEE Trans. Emerg. Top. Comput. 2024, 12, 968–979. [Google Scholar] [CrossRef]
- Momeni, A.; Han, J.; Montuschi, P.; Lombardi, F. Design and Analysis of Approximate Compressors for Multiplication. IEEE Trans. Comput. 2015, 64, 984–994. [Google Scholar] [CrossRef]
- Ahmadinejad, M.; Moaiyeri, M.H.; Sabetzadeh, F. Energy and area efficient imprecise compressors for approximate multiplication at nanoscale. AEU-Int. J. Electron. Commun. 2019, 110, 152859. [Google Scholar] [CrossRef]
- Yang, Z.; Han, J.; Lombardi, F. Approximate compressors for error-resilient multiplier design. In Proceedings of the 2015 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFTS), Amherst, MA, USA, 12–14 October 2015; pp. 183–186. [Google Scholar] [CrossRef]
- Ha, M.; Lee, S. Multipliers with Approximate 4–2 Compressors and Error Recovery Modules. IEEE Embed. Syst. Lett. 2018, 10, 6–9. [Google Scholar] [CrossRef]
- Petra, N.; De Caro, D.; Garofalo, V.; Napoli, E.; Strollo, A.G.M. Design of Fixed-Width Multipliers with Linear Compensation Function. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 947–960. [Google Scholar] [CrossRef]
- Zendegani, R.; Kamal, M.; Bahadori, M.; Afzali-Kusha, A.; Pedram, M. RoBA Multiplier: A Rounding-Based Approximate Multiplier for High-Speed yet Energy-Efficient Digital Signal Processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 393–401. [Google Scholar] [CrossRef]
- Garg, B.; Patel, S.K.; Dutt, S. LoBA: A Leading One Bit Based Imprecise Multiplier for Efficient Image Processing. J. Electron. Test. 2020, 36, 429–437. [Google Scholar] [CrossRef]
- Du, J.; Chen, K.; Yin, P.; Yan, C.; Liu, W. Design of An Approximate FFT Processor Based on Approximate Complex Multipliers. In Proceedings of the 2021 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021; pp. 308–313. [Google Scholar] [CrossRef]
- Ferreira, G.; Pereira, P.T.L.; Paim, G.; Costa, E.; Bampi, S. A Power-Efficient FFT Hardware Architecture Exploiting Approximate Adders. In Proceedings of the 2021 IEEE 12th Latin America Symposium on Circuits and System (LASCAS), Arequipa, Peru, 21–24 February 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Zhu, N.; Goh, W.L.; Zhang, W.; Yeo, K.S.; Kong, Z.H. Design of Low-Power High-Speed Truncation-Error-Tolerant Adder and Its Application in Digital Signal Processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2010, 18, 1225–1229. [Google Scholar] [CrossRef]
- Mahdiani, H.R.; Ahmadi, A.; Fakhraie, S.M.; Lucas, C. Bio-Inspired Imprecise Computational Blocks for Efficient VLSI Implementation of Soft-Computing Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 850–862. [Google Scholar] [CrossRef]
- Pereira, P.T.L.; da Costa, P.U.L.; Ferreira, G.d.C.; de Abreu, B.A.; Paim, G.; da Costa, E.A.C.; Bampi, S. Energy-Quality Scalable Design Space Exploration of Approximate FFT Hardware Architectures. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4524–4534. [Google Scholar] [CrossRef]
- Liu, W.; Liao, Q.; Qiao, F.; Xia, W.; Wang, C.; Lombardi, F. Approximate Designs for Fast Fourier Transform (FFT) with Application to Speech Recognition. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4727–4739. [Google Scholar] [CrossRef]
- Meinerzhagen, P.; Roth, C.; Burg, A. Towards generic low-power area-efficient standard cell based memory architectures. In Proceedings of the 2010 53rd IEEE International Midwest Symposium on Circuits and Systems, Seattle, WA, USA, 1–4 August 2010; pp. 129–132. [Google Scholar] [CrossRef]
- Marinberg, H.; Garzón, E.; Noy, T.; Lanuzza, M.; Teman, A. Efficient Implementation of Many-Ported Memories by Using Standard-Cell Memory Approach. IEEE Access 2023, 11, 94885–94897. [Google Scholar] [CrossRef]
- Saggese, G.; Strollo, A.G.M. A Low Power 1024-Channels Spike Detector Using Latch-Based RAM for Real-Time Brain Silicon Interfaces. Electronics 2021, 10, 3068. [Google Scholar] [CrossRef]
- Zhou, J.; Singh, K.; Huisken, J. Standard Cell based Memory Compiler for Near/Sub-threshold Operation. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
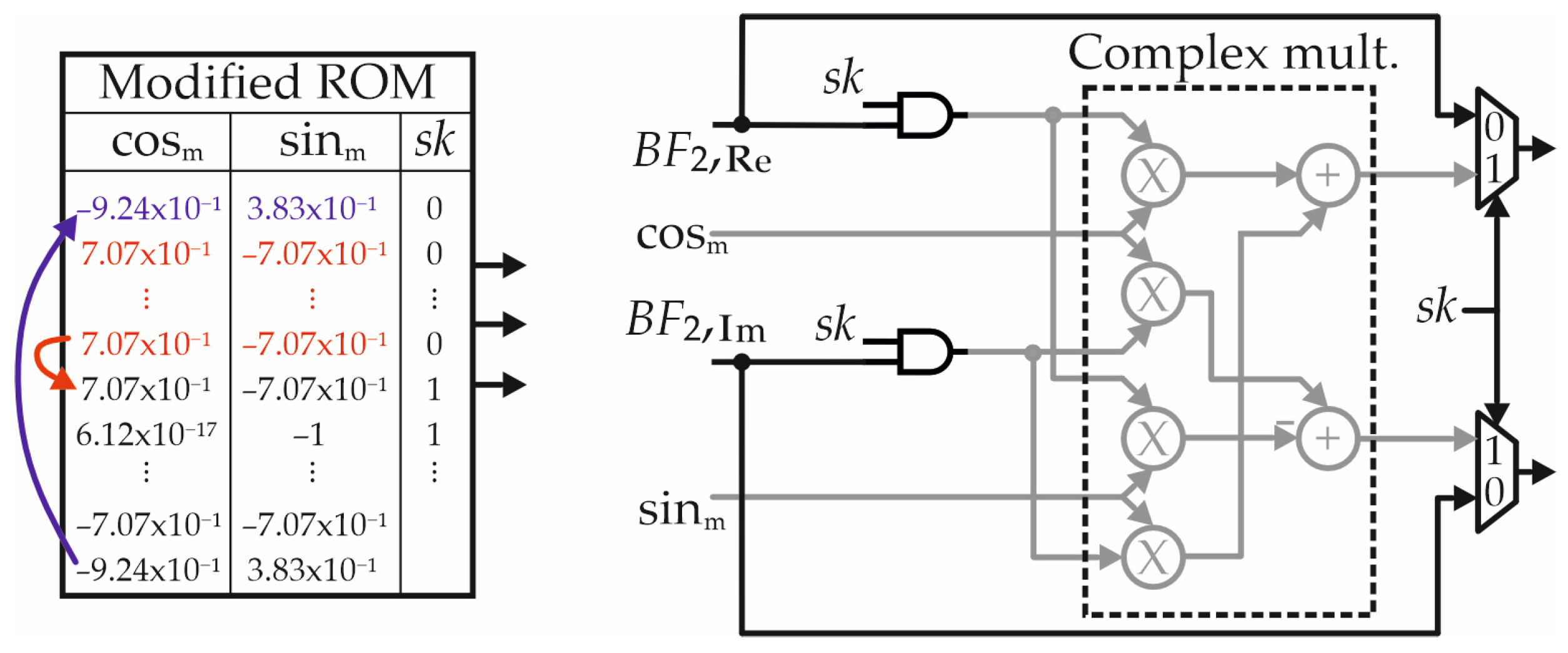

| ROM Address | sk | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 0 | 2 | 1 | 0 | 0 |
| 3 | 0 | 3 | 1 | 0 | 0 |
| 4 | 2 | 0 | 1 | 0 | 0 |
| 5 | 2 | 1 | 7.07 × 10−1 | −7.07 × 10−1 | 1 |
| 6 | 2 | 2 | 6.12 × 10−17 | −9.99 × 10−1 | 1 |
| 7 | 2 | 3 | −7.07 × 10−1 | −7.07 × 10−1 | 1 |
| 8 | 1 | 0 | 1.00 × 10−0 | 0.00 × 10−0 | 1 |
| 9 | 1 | 1 | 9.24 × 10−1 | −3.83 × 10−1 | 1 |
| 10 | 1 | 2 | 7.07 × 10−1 | −7.07 × 10−1 | 1 |
| 11 | 1 | 3 | 3.83 × 10−1 | −9.24 × 10−1 | 1 |
| 12 | 3 | 0 | 1.00 × 10−0 | 0.00 × 10−0 | 1 |
| 13 | 3 | 1 | 3.83 × 10−1 | −9.24 × 10−1 | 1 |
| 14 | 3 | 2 | −7.07 × 10−1 | −7.07 × 10−1 | 1 |
| 15 | 3 | 3 | −9.24 × 10−1 | 3.83 × 10−1 | 1 |
| Values of mh | h* < 2 and t ≤ h* < t + 1 | 2 ≤ h* < t | h* > t + 1 |
|---|---|---|---|
| h < 2 and t ≤ h < t + 1 | |||
| 2 ≤ h < t | |||
| h > t + 1 |
| FFT Implementation | SNR [dB] | MSE | Delay [ns] | Area [mm2] | Area Saving [%] | Power [mW] | Power Saving [%] |
|---|---|---|---|---|---|---|---|
| Standard | 66.2 | 4.13 × 10−5 | 5.16 | 0.0343 | - | 8.53 | - |
| SRoBA [27,33] | 26.3 | 4.03 × 10−1 | 9.02 | 0.0303 | −11.6 | 7.24 | −15.1 |
| ASRoBA [27,33] | 26.3 | 4.04 × 10−1 | 9.14 | 0.0295 | −14.1 | 6.88 | −19.4 |
| LOBA0_4 [28,33] | 12.1 | 1.05 × 10+1 | 6.88 | 0.0270 | −21.3 | 6.43 | −24.6 |
| AFFT-cmplx4 [29] | 64.8 | 5.61 × 10−5 | 5.20 | 0.0310 | −9.6 | 8.33 | −2.3 |
| DRUM6 [18,33] | 29.4 | 1.97 × 10−1 | 7.83 | 0.0279 | −18.6 | 7.18 | −15.8 |
| DRUM7 [18,33] | 35.8 | 4.56 × 10−2 | 8.07 | 0.0286 | −16.5 | 7.64 | −10.4 |
| DRUM8 [18,33] | 41.5 | 1.21 × 10−2 | 8.04 | 0.0292 | −14.7 | 8.15 | −4.5 |
| SSM14,8 [19] | 35.5 | 4.85 × 10−2 | 7.18 | 0.0280 | −18.4 | 7.08 | −17.0 |
| SSM14,12 [19] | 51.8 | 1.12 × 10−3 | 7.44 | 0.0295 | −13.9 | 7.51 | −12.0 |
| Comp4/2 Ahma [23] | 55.2 | 5.16 × 10−4 | 5.10 | 0.0321 | −6.5 | 7.90 | −7.4 |
| Comp4/2 Momeni [22] | 55.2 | 5.11 × 10−4 | 5.20 | 0.0326 | −4.9 | 8.14 | −4.5 |
| A-FFT153,2,3 | 57.1 | 3.29 × 10−4 | 5.21 | 0.0326 | −5.0 | 5.82 | −31.8 |
| A-FFT156,3,4 | 47.0 | 3.43 × 10−3 | 5.20 | 0.0324 | −5.6 | 5.77 | −32.3 |
| A-FFT157,4,5 | 42.1 | 1.05 × 10−2 | 5.21 | 0.0323 | −5.9 | 5.74 | −32.7 |
| A-FFT158,8,10 | 24.6 | 5.87 × 10−1 | 4.79 | 0.0319 | −7.1 | 5.68 | −33.4 |
| A-FFT133,2,3 | 64.7 | 5.81 × 10−5 | 5.20 | 0.0336 | −2.2 | 6.01 | −29.5 |
| A-FFT136,3,4 | 54.7 | 5.75 × 10−4 | 5.20 | 0.0333 | −2.9 | 5.96 | −30.1 |
| A-FFT137,4,5 | 50.8 | 1.42 × 10−3 | 5.20 | 0.0332 | −3.2 | 5.95 | −30.3 |
| A-FFT138,8,10 | 36.3 | 4.00 × 10−2 | 5.20 | 0.0327 | −4.6 | 5.83 | −31.7 |
| A-FFT103,2,3 | 66.2 | 4.13 × 10−5 | 5.32 | 0.0346 | +1.0 | 6.20 | −27.3 |
| A-FFT106,3,4 | 65.4 | 4.94 × 10−5 | 5.33 | 0.0344 | +0.4 | 6.15 | −27.9 |
| A-FFT107,4,5 | 63.8 | 7.16 × 10−5 | 5.34 | 0.0343 | +0.0 | 6.14 | −28.0 |
| A-FFT108,8,10 | 54.2 | 6.46 × 10−4 | 5.20 | 0.0337 | −1.8 | 6.03 | −29.4 |
| FFT Implementation | Channel SNR | ||||||
|---|---|---|---|---|---|---|---|
| 6 dB | 12 dB | 18 dB | 20 dB | 22 dB | 24 dB | 25 dB | |
| Standard | 2.22 × 10−1 | 1.03 × 10−1 | 2.01 × 10−2 | 6.75 × 10−3 | 1.22 × 10−3 | 1.01 × 10−4 | 1.71 × 10−5 |
| SRoBA [27,33] | 2.23 × 10−1 | 1.06 × 10−1 | 2.55 × 10−2 | 1.12 × 10−2 | 3.93 × 10−3 | 1.30 × 10−3 | 7.40 × 10−4 |
| ASRoBA [27,33] | 2.23 × 10−1 | 1.06 × 10−1 | 2.55 × 10−2 | 1.12 × 10−2 | 3.92 × 10−3 | 1.31 × 10−3 | 7.46 × 10−4 |
| LOBA [28,33] | 2.55 × 10−1 | 1.94 × 10−1 | 1.81 × 10−1 | 1.80 × 10−1 | 1.81 × 10−1 | 1.80 × 10−1 | 1.80 × 10−1 |
| AFFT-cmplx4 [29] | 2.22 × 10−1 | 1.03 × 10−1 | 2.02 × 10−2 | 6.72 × 10−3 | 1.24 × 10−3 | 1.01 × 10−4 | 1.71 × 10−5 |
| DRUM6 [18,33] | 2.24 × 10−1 | 1.07 × 10−1 | 2.43 × 10−2 | 9.82 × 10−3 | 2.73 × 10−3 | 5.56 × 10−4 | 2.23 × 10−4 |
| DRUM7 [18,33] | 2.23 × 10−1 | 1.05 × 10−1 | 2.14 × 10−2 | 7.50 × 10−3 | 1.58 × 10−3 | 1.73 × 10−4 | 3.81 × 10−5 |
| DRUM8 [18,33] | 2.23 × 10−1 | 1.04 × 10−1 | 2.06 × 10−2 | 6.90 × 10−3 | 1.29 × 10−3 | 1.22 × 10−4 | 2.09 × 10−5 |
| SSM14,8 [19] | 2.23 × 10−1 | 1.05 × 10−1 | 2.15 × 10−2 | 7.54 × 10−3 | 1.56 × 10−3 | 1.73 × 10−4 | 3.43 × 10−5 |
| SSM14,12 [19] | 2.22 × 10−1 | 1.03 × 10−1 | 2.02 × 10−2 | 6.87 × 10−3 | 1.27 × 10−3 | 1.10 × 10−4 | 1.71 × 10−5 |
| C4/2 Ahma [23] | 2.22 × 10−1 | 1.03 × 10−1 | 2.07 × 10−2 | 7.17 × 10−3 | 1.43 × 10−3 | 1.83 × 10−4 | 4.76 × 10−5 |
| C4/2 Momeni [22] | 2.22 × 10−1 | 1.03 × 10−1 | 2.07 × 10−2 | 7.17 × 10−3 | 1.44 × 10−3 | 1.85 × 10−4 | 4.76 × 10−5 |
| A-FFT153,2,3 | 2.23 × 10−1 | 1.04 × 10−1 | 2.11 × 10−2 | 7.31 × 10−3 | 1.51 × 10−3 | 2.09 × 10−4 | 4.76 × 10−5 |
| A-FFT156,3,4 | 2.24 × 10−1 | 1.08 × 10−1 | 2.92 × 10−2 | 1.48 × 10−2 | 6.70 × 10−3 | 3.26 × 10−3 | 2.18 × 10−3 |
| A-FFT157,4,5 | 2.28 × 10−1 | 1.17 × 10−1 | 4.74 × 10−2 | 3.41 × 10−2 | 2.55 × 10−2 | 2.03 × 10−2 | 1.86 × 10−2 |
| A-FFT158,8,10 | 3.28 × 10−1 | 3.02 × 10−1 | 2.92 × 10−1 | 2.91 × 10−1 | 2.90 × 10−1 | 2.90 × 10−1 | 2.89 × 10−1 |
| A-FFT133,2,3 | 2.22 × 10−1 | 1.03 × 10−1 | 2.03 × 10−2 | 6.80 × 10−3 | 1.23 × 10−3 | 1.14 × 10−4 | 1.71 × 10−5 |
| A-FFT136,3,4 | 2.23 × 10−1 | 1.04 × 10−1 | 2.14 × 10−2 | 7.76 × 10−3 | 1.73 × 10−3 | 2.78 × 10−4 | 6.66 × 10−5 |
| A-FFT137,4,5 | 2.23 × 10−1 | 1.05 × 10−1 | 2.38 × 10−2 | 9.61 × 10−3 | 2.89 × 10−3 | 7.37 × 10−4 | 3.20 × 10−4 |
| A-FFT138,8,10 | 2.42 × 10−1 | 1.52 × 10−1 | 1.07 × 10−1 | 9.90 × 10−2 | 9.44 × 10−2 | 9.12 × 10−2 | 9.01 × 10−2 |
| A-FFT103,2,3 | 2.22 × 10−1 | 1.03 × 10−1 | 2.01 × 10−2 | 6.76 × 10−3 | 1.22 × 10−3 | 9.71 × 10−5 | 1.71 × 10−5 |
| A-FFT106,3,4 | 2.22 × 10−1 | 1.03 × 10−1 | 2.02 × 10−2 | 6.79 × 10−3 | 1.23 × 10−3 | 1.08 × 10−4 | 2.09 × 10−5 |
| A-FFT107,4,5 | 2.23 × 10−1 | 1.03 × 10−1 | 2.02 × 10−2 | 6.82 × 10−3 | 1.25 × 10−3 | 1.14 × 10−4 | 2.28 × 10−5 |
| A-FFT108,8,10 | 2.23 × 10−1 | 1.04 × 10−1 | 2.27 × 10−2 | 8.57 × 10−3 | 2.15 × 10−3 | 3.77 × 10−4 | 1.29 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Meo, G.; Perna, C.; De Caro, D.; Strollo, A.G.M. Low-Power Radix-22 FFT Processor with Hardware-Optimized Fixed-Width Multipliers and Low-Voltage Memory Buffers. Electronics 2025, 14, 4217. https://doi.org/10.3390/electronics14214217
Di Meo G, Perna C, De Caro D, Strollo AGM. Low-Power Radix-22 FFT Processor with Hardware-Optimized Fixed-Width Multipliers and Low-Voltage Memory Buffers. Electronics. 2025; 14(21):4217. https://doi.org/10.3390/electronics14214217
Chicago/Turabian StyleDi Meo, Gennaro, Camillo Perna, Davide De Caro, and Antonio G. M. Strollo. 2025. "Low-Power Radix-22 FFT Processor with Hardware-Optimized Fixed-Width Multipliers and Low-Voltage Memory Buffers" Electronics 14, no. 21: 4217. https://doi.org/10.3390/electronics14214217
APA StyleDi Meo, G., Perna, C., De Caro, D., & Strollo, A. G. M. (2025). Low-Power Radix-22 FFT Processor with Hardware-Optimized Fixed-Width Multipliers and Low-Voltage Memory Buffers. Electronics, 14(21), 4217. https://doi.org/10.3390/electronics14214217







