Prescribed Performance Control for Robotic System with Communication Delays and Disturbances
Abstract
1. Introduction
- This paper introduces a novel PPC method to maintain the tracking performance of a robot system under state measurement delays, control input delays, and external disturbances.
- An integrated super-twisting disturbance observer was designed, which provides accurate and real-time estimates of external disturbances, thereby significantly enhancing the system’s overall robustness.
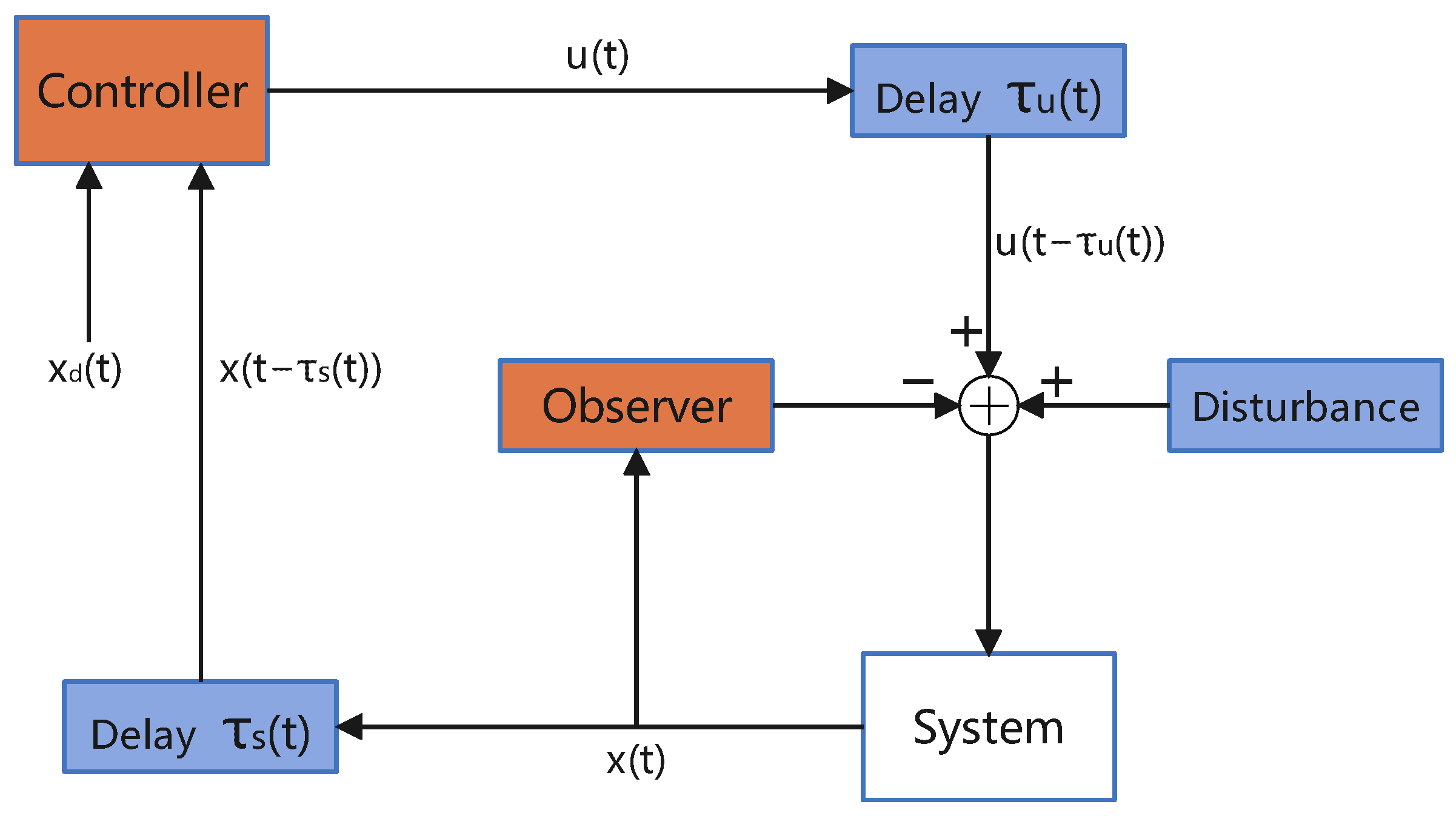
2. Materials and Methods
2.1. Dynamic Model of Robotic System
- The system output is required to track the desired trajectory in accordance with prescribed performance specifications, namely, the maximum steady-state error and the minimum convergence rate.
- A disturbance observer is designed to compensate for the external disturbances inherent in practical robotic applications.
2.2. Controller Design
2.2.1. Design of the Controller
2.2.2. Design of the Disturbance Observer
- (a)
- Finite time stability of the disturbance observer.
- (b)
- Overall stability of the closed-loop system.
3. Simulation
3.1. Simulation Conditions
- where
- and
- where , , , , and g, respectively, represent the mass, the length of each link, the moment of inertia, and the acceleration due to gravity. The system parameters are set as = 0.8 [kg], = 0.5 [kg], = 0.4 [m], = 0.2 [m], = 0.6 [kg· m2], = 0.4 [kg· m2], and g = 9.81 [m/s2].
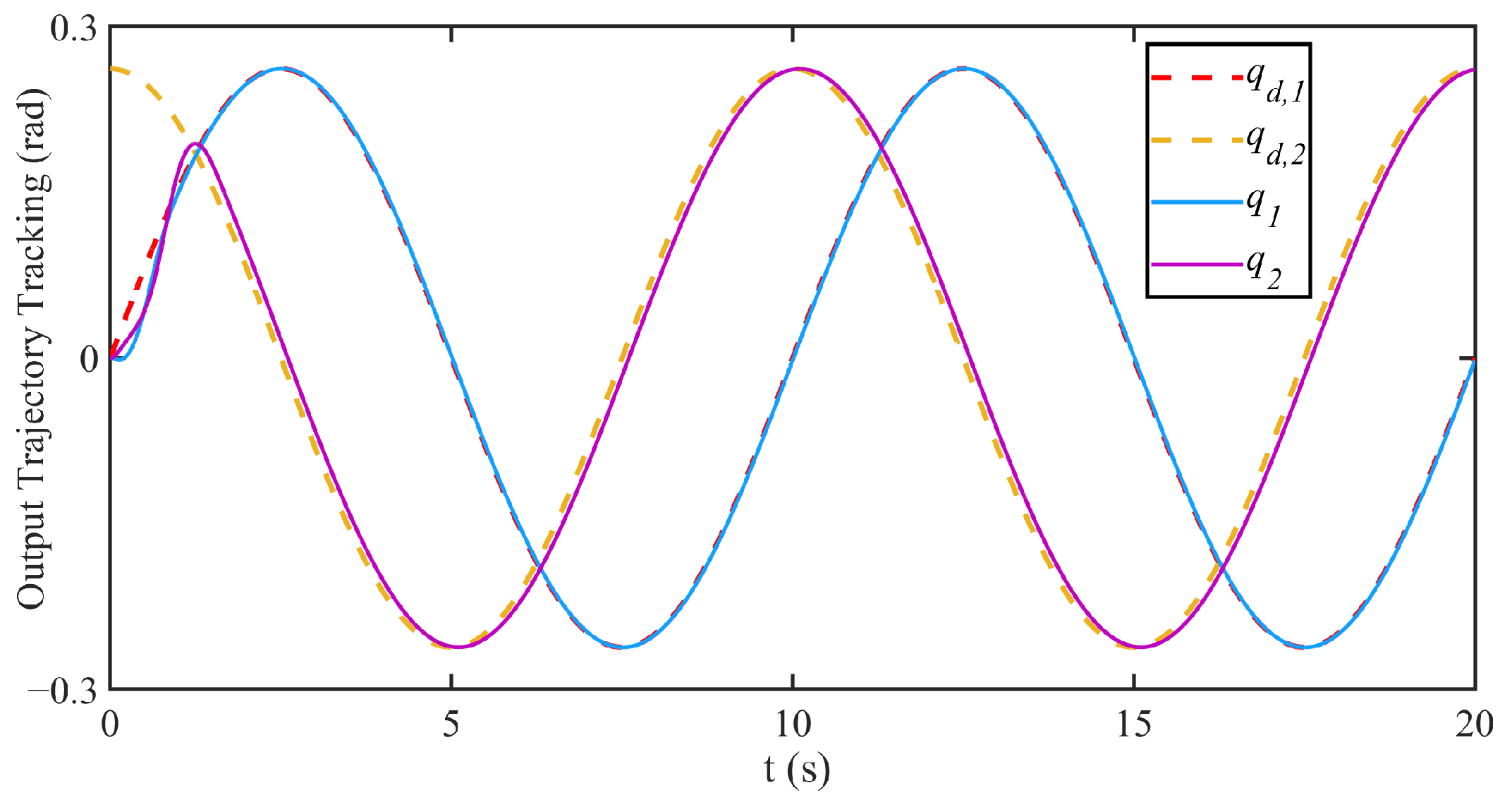
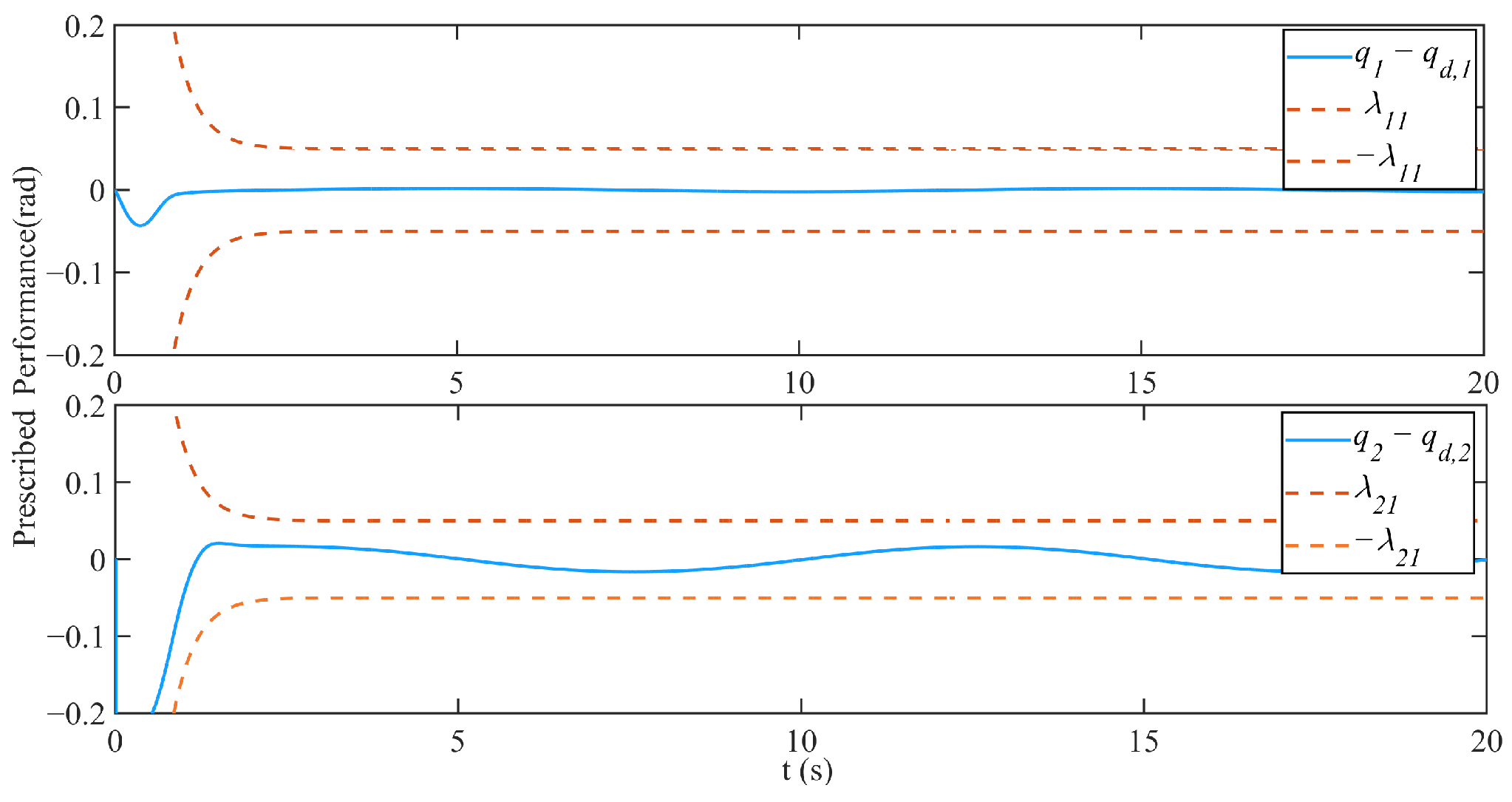
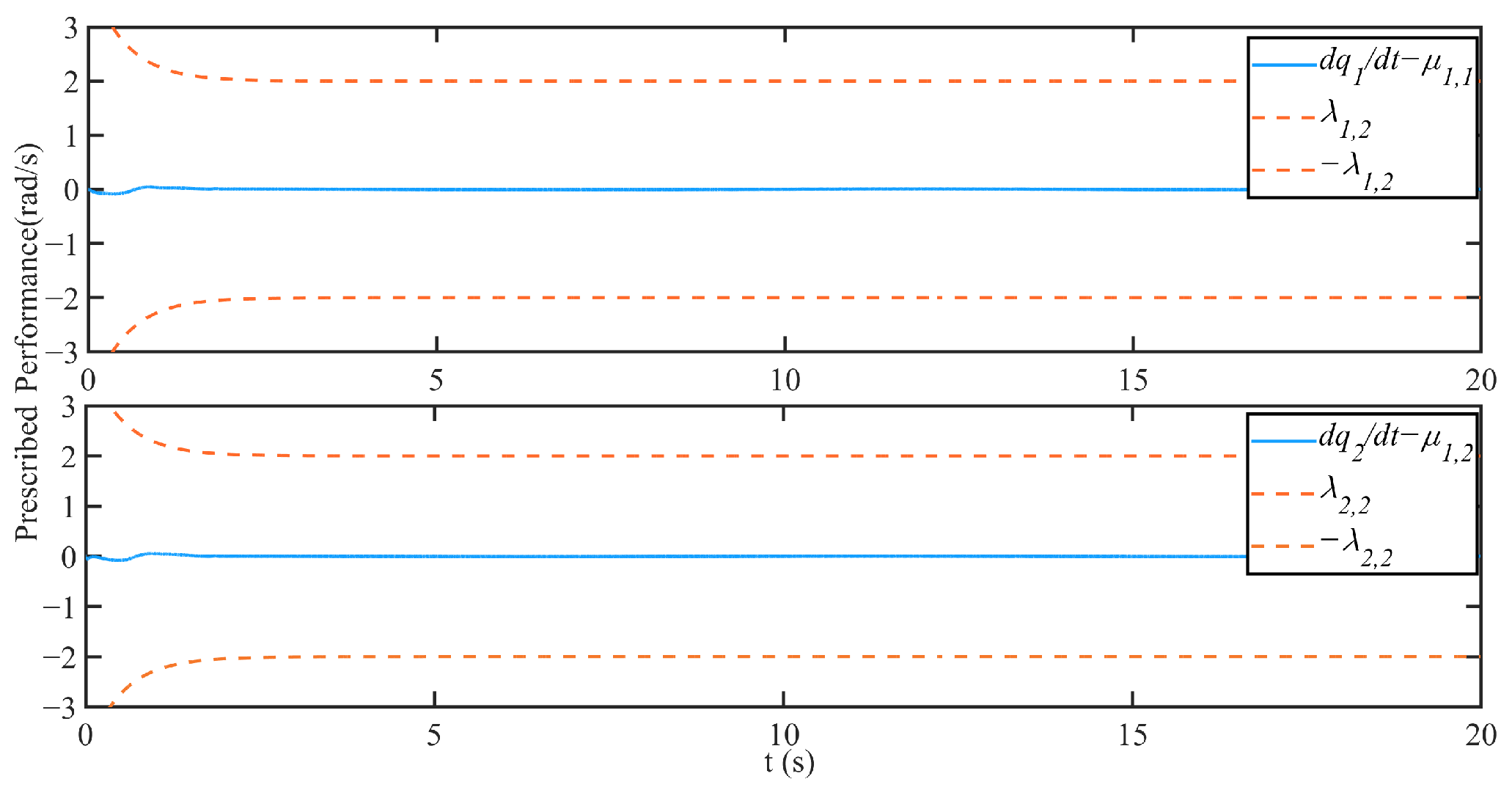
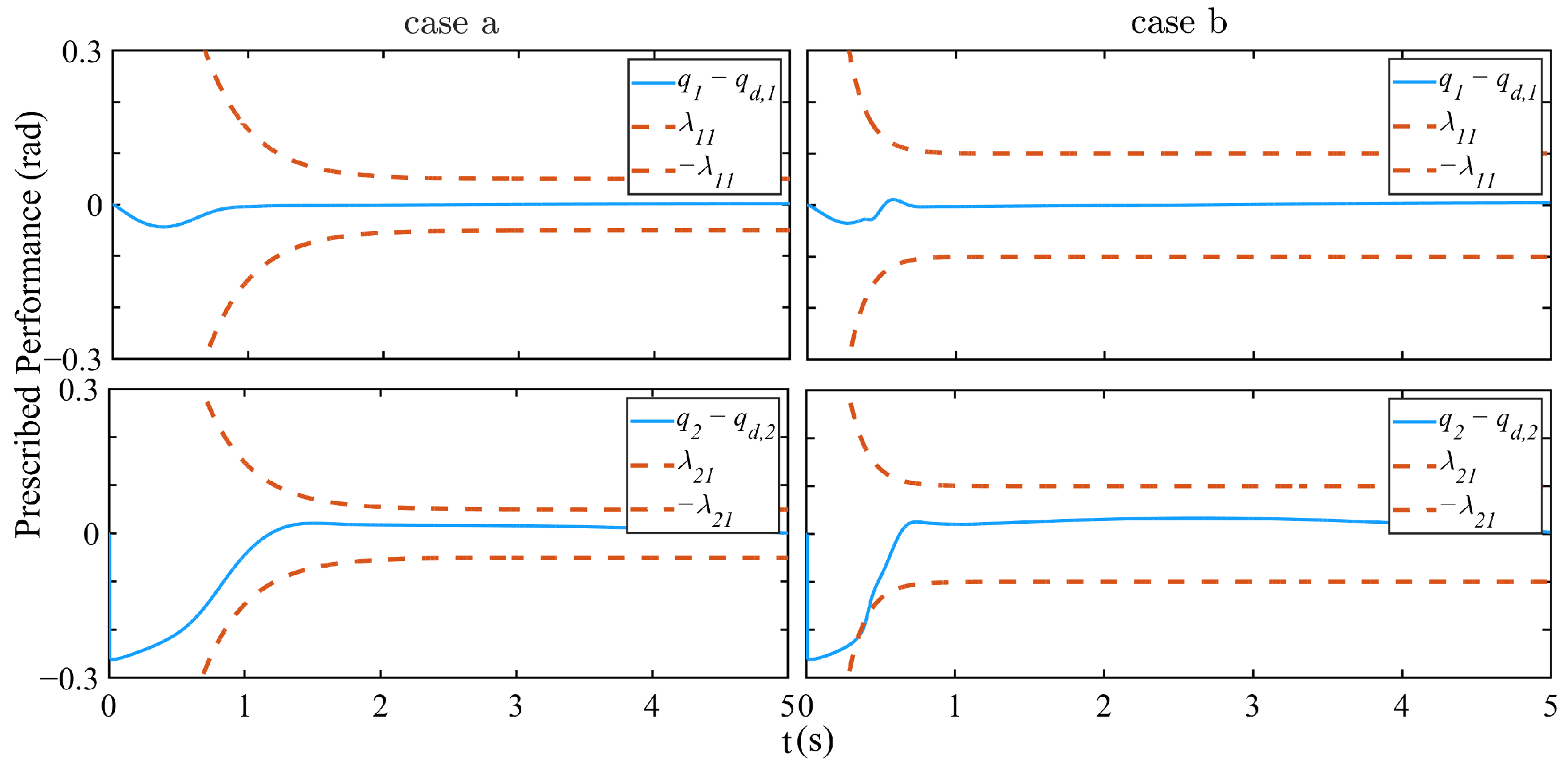
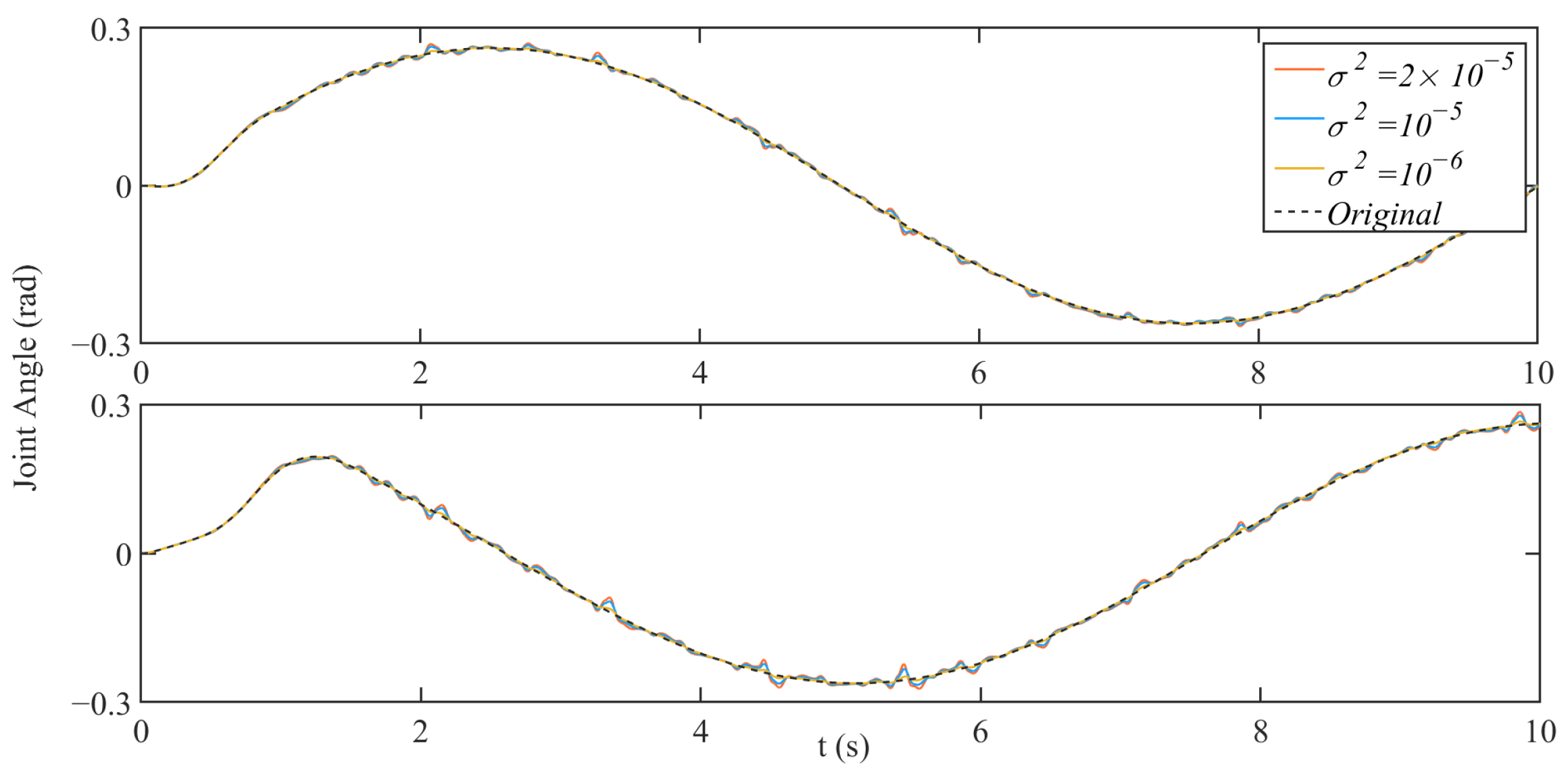
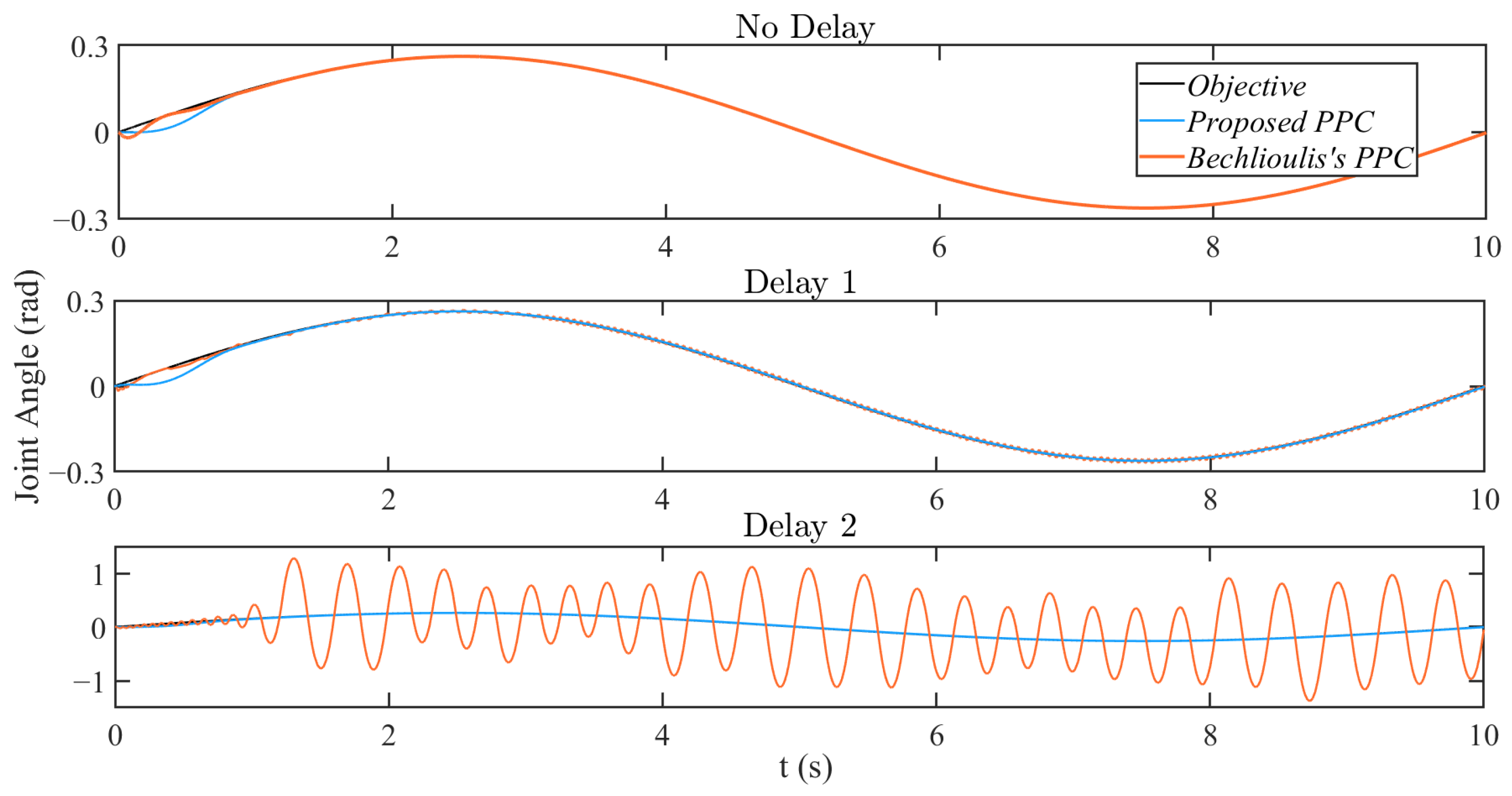
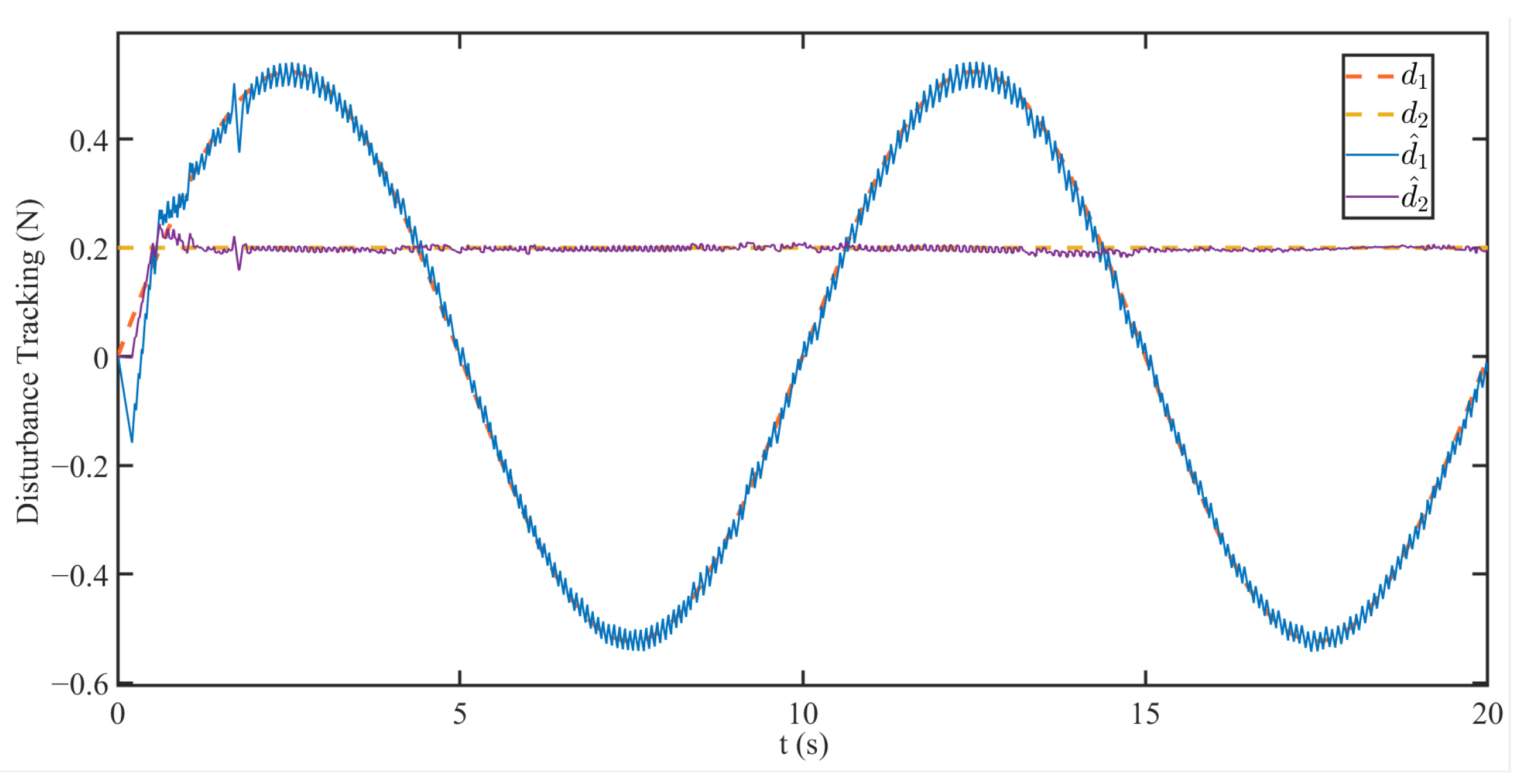
3.2. Simulation Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPC | Prescribed Performance Control |
| DOF | Degree of Freedom |
| DOB | Disturbance Observer |
| RMSE | Root Mean Square Error |
References
- Darvish, K.; Penco, L.; Ramos, J.; Cisneros, R.; Pratt, J.; Yoshida, E.; Ivaldi, S.; Pucci, D. Teleoperation of humanoid robots: A survey. IEEE Trans. Robot. 2023, 39, 1706–1727. [Google Scholar] [CrossRef]
- Bekiaris-Liberis, N.; Krstic, M. Compensation of state-dependent input delay for nonlinear systems. IEEE Trans. Autom. Control 2013, 58, 275–289. [Google Scholar] [CrossRef]
- Polyakov, A.; Efimov, D.; Perruquetti, W.; Richard, J.-P. Output stabilization of time-varying input delay systems using interval observation technique. Automatica 2013, 49, 3402–3410. [Google Scholar] [CrossRef]
- Cai, X.; Bekiaris-Liberis, N.; Krstic, M. Input-to-state stability and inverse optimality of predictor feedback for multi-input linear systems. Automatica 2019, 103, 549–557. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C.; Xie, L. Active disturbance rejection control for uncertain time-delay nonlinear systems. Automatica 2020, 112, 108692. [Google Scholar] [CrossRef]
- Zahaf, A.; Bououden, S.; Chadli, M.; Chemachema, M. Robust fault tolerant optimal predictive control of hybrid actuators with time-varying delay for industrial robot arm. Asian J. Control 2022, 24, 1–15. [Google Scholar] [CrossRef]
- Cao, L.; Pan, Y.; Liang, H.; Huang, T. Observer-based dynamic event-triggered control for multiagent systems with time-varying delay. IEEE Trans. Cybern. 2022, 53, 3376–3387. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Chen, C.P.; Liu, Z.; Wu, W. Adaptive pi event-triggered control for mimo nonlinear systems with input delay. Inf. Sci. 2024, 677, 120817. [Google Scholar] [CrossRef]
- Cai, J.; Guo, D.; Wang, W. Adaptive fault-tolerant control of uncertain systems with unknown actuator failures and input delay. Meas. Control 2025, 58, 923–934. [Google Scholar] [CrossRef]
- Xia, X.; Pan, J.; Zhang, T.; Fang, Y. Command filter based adaptive dsc of uncertain stochastic nonlinear systems with input delay and state constraints. J. Frankl. Inst. 2022, 359, 9492–9521. [Google Scholar] [CrossRef]
- Qi, X.; Xu, S.; Liu, W. Fixed-time neural adaptive control for nonlinear asymmetric constrained systems subject to time-varying input delay. IEEE Trans. Cybern. 2025, 55, 4583–4595. [Google Scholar] [CrossRef]
- Sanz, R.; Garcia, P.; Krstic, M. Observation and stabilization of ltv systems with time-varying measurement delay. Automatica 2019, 103, 573–579. [Google Scholar] [CrossRef]
- Ferdinando, M.D.; Gennaro, S.D.; Borri, A.; Pola, G.; Pepe, P. On the robustification of digital event-based stabilizers for nonlinear time-delay systems. Nonlinear Anal. Hybrid Syst. 2024, 52, 101463. [Google Scholar] [CrossRef]
- Bikas, L.N.; Rovithakis, G.A. Prescribed performance tracking of uncertain mimo nonlinear systems in the presence of delays. IEEE Trans. Autom. Control 2021, 68, 96–107. [Google Scholar] [CrossRef]
- Weston, J.; Malisoff, M. Sequential predictors under time-varying feedback and measurement delays and sampling. IEEE Trans. Autom. Control 2018, 64, 2991–2996. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Zhang, C.; Esakki, B. Desired tracking of delayed quadrotor uav under model uncertainty and wind disturbance using adaptive super-twisting terminal sliding mode control. ISA Trans. 2022, 123, 455–471. [Google Scholar] [CrossRef]
- Nozari, E.; Tallapragada, P.; Cortés, J. Event-triggered stabilization of nonlinear systems with time-varying sensing and actuation delay. Automatica 2020, 113, 108754. [Google Scholar] [CrossRef]
- Sun, X.-M.; Liu, K.-Z.; Wen, C.; Wang, W. Predictive control of nonlinear continuous networked control systems with large time-varying transmission delays and transmission protocols. Automatica 2016, 64, 76–85. [Google Scholar] [CrossRef]
- Bu, X. Prescribed performance control approaches, applications and challenges: A comprehensive survey. Asian J. Control 2023, 25, 241–261. [Google Scholar] [CrossRef]
- Bu, X.; Jiang, B.; Lei, H. Nonfragile quantitative prescribed performance control of waverider vehicles with actuator saturation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3538–3548. [Google Scholar] [CrossRef]
- Ficuciello, F.; Villani, L.; Siciliano, B. Variable impedance control of redundant manipulators for intuitive human–robot physical interaction. IEEE Trans. Robot. 2015, 31, 850–863. [Google Scholar] [CrossRef]
- Chen, W.-H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Guo, K.; Shi, P.; Wang, P.; He, C.; Zhang, H. Non-singular terminal sliding mode controller with nonlinear disturbance observer for robotic manipulator. Electronics 2023, 12, 849. [Google Scholar] [CrossRef]
- Farhat, M.; Kali, Y.; Saad, M.; Rahman, M.H.; Lopez-Herrejon, R.E. Walking position commanded nao robot using nonlinear disturbance observer-based fixed-time terminal sliding mode. ISA Trans. 2024, 146, 592–602. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yue, X.; Wen, H.; Hao, Z.; Zhu, Y. A globally exponentially stable observer for torque estimation with only position measurement. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2024, 238, 238–251. [Google Scholar] [CrossRef]
- Junplod, G.; Kornmaneesang, W.; Chen, S.-L.; Wongsa, S. Modeling of an external force estimator for an end-effector of a robot by neural networks. J. Chin. Inst. Eng. 2023, 46, 895–904. [Google Scholar] [CrossRef]
- Su, H.; Qi, W.; Li, Z.; Chen, Z.; Ferrigno, G.; Momi, E.D. Deep neural network approach in emg-based force estimation for human–robot interaction. IEEE Trans. Artif. Intell. 2021, 2, 404–412. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, Y.; Liu, Y.; Jin, J. Multirobot unknown environment exploration and obstacle avoidance based on a voronoi diagram and reinforcement learning. Expert Syst. Appl. 2025, 264, 125900. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable mimo nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Sun, T.; Cheng, L.; Wang, W.; Pan, Y. Semiglobal exponential control of euler–lagrange systems using a sliding-mode disturbance observer. Automatica 2020, 112, 108677. [Google Scholar] [CrossRef]
- Bikas, L.N.; Sidiropoulos, A.; Rovithakis, G.A.; Doulgeri, Z. Model-free control of bilateral robotic teleoperation with delays and prescribed performance guarantees. IFAC Pap. 2023, 56, 9972–9977. [Google Scholar] [CrossRef]
- Li, Z.; Zhai, J. Super-twisting sliding mode trajectory tracking adaptive control of wheeled mobile robots with disturbance observer. Int. J. Robust Nonlinear Control 2022, 32, 9869–9881. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems. Automatica 2014, 50, 1217–1226. [Google Scholar] [CrossRef]
- Chen, W.-H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, Z.; Zhang, Q.; Lin, Z.; Wang, T.; Liu, Z.; Li, D. Few-shot learning with manifold-enhanced llm for handling anomalous perception inputs in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2025. [Google Scholar] [CrossRef]

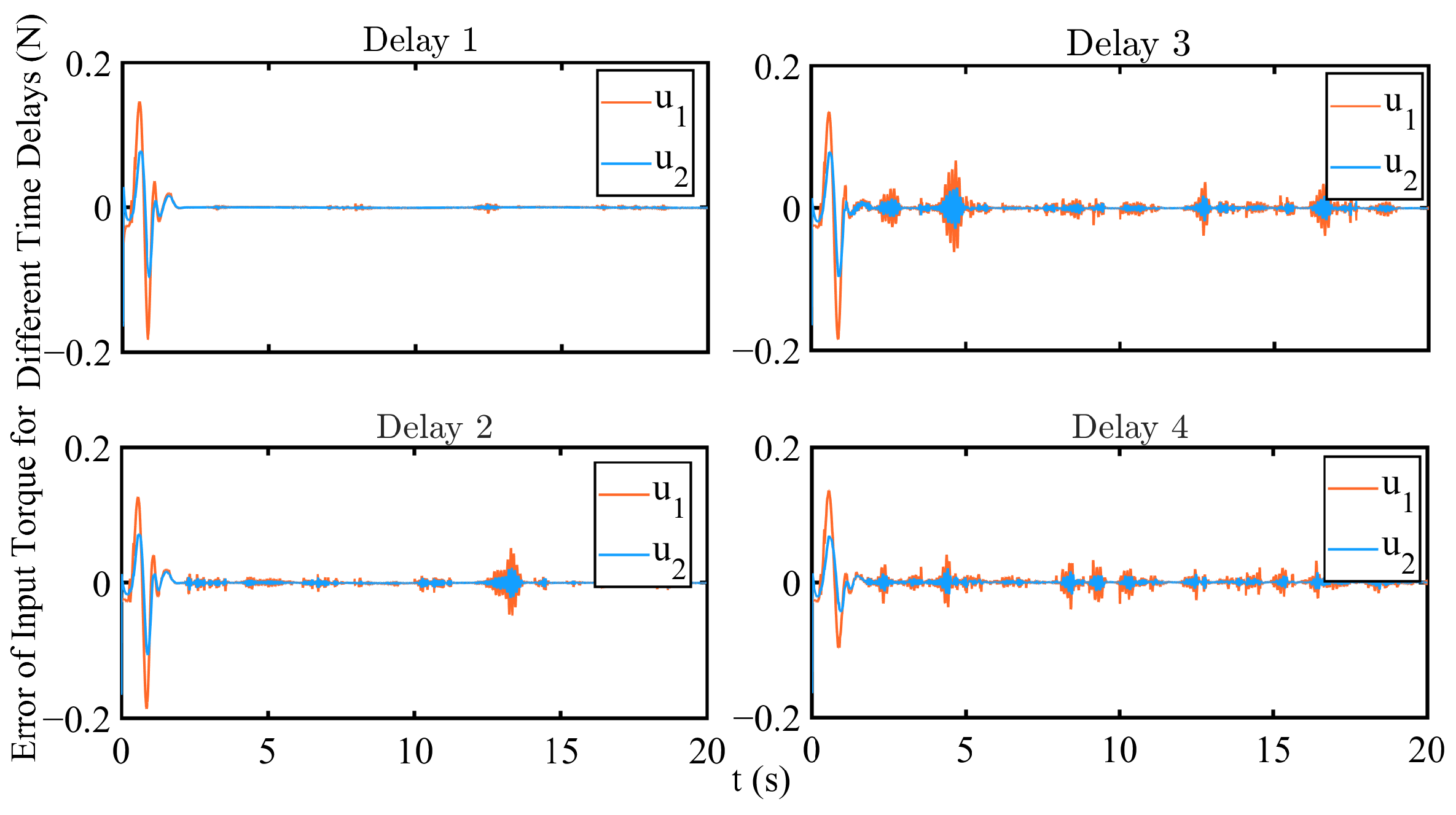


| Delay | |||
|---|---|---|---|
| Delay 1 | 0.008 | 0.008 | 0.015 |
| Delay 2 | 0.004 (1 + sin(0.5t)) | 0.006 (1 + sin(0.5t)) | 0.015 |
| Delay 3 | 0.004 (1 + sin(t)) | 0.006 (1 + sin(t)) | 0.015 |
| Delay 4 | 0.004 (1 + sin(2t)) | 0.006 (1 + sin(2t)) | 0.015 |
| Methods | RMSE of Joint 1 | RMSE of Joint 2 |
|---|---|---|
| Proposed PPC | 0.008992 | 0.071109 |
| Bechliouslis’s PPC | 0.052262 | 0.13875 |
| Proposed DOB | 0.030268 | 0.032637 |
| Chen’s DOB | 0.102193 | 0.038853 |
| Controller Gains | RMSE1 | RMSE2 | RMSE3 | RMSE4 | RMSE5 |
|---|---|---|---|---|---|
| 0.008992 | 0.010542 | 0.011263 | System instability | System instability | |
| 0.008992 | 0.010846 | 0.013394 | 0.013675 | 0.013368 | |
| 0.008992 | 0.013124 | 0.013097 | 0.012446 | 0.010172 | |
| 0.008992 | 0.012238 | 0.014691 | 0.010984 | 0.013757 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shen, S.; Li, C.; Zhang, W. Prescribed Performance Control for Robotic System with Communication Delays and Disturbances. Electronics 2025, 14, 4218. https://doi.org/10.3390/electronics14214218
Wang Y, Shen S, Li C, Zhang W. Prescribed Performance Control for Robotic System with Communication Delays and Disturbances. Electronics. 2025; 14(21):4218. https://doi.org/10.3390/electronics14214218
Chicago/Turabian StyleWang, Yao, Shaobo Shen, Chuang Li, and Wanjie Zhang. 2025. "Prescribed Performance Control for Robotic System with Communication Delays and Disturbances" Electronics 14, no. 21: 4218. https://doi.org/10.3390/electronics14214218
APA StyleWang, Y., Shen, S., Li, C., & Zhang, W. (2025). Prescribed Performance Control for Robotic System with Communication Delays and Disturbances. Electronics, 14(21), 4218. https://doi.org/10.3390/electronics14214218






