Energy-Aware Swarm Robotics in Smart Microgrids Using Quantum-Inspired Reinforcement Learning
Abstract
1. Introduction
- Present a new quantum-inspired multi-agent reinforcement learning (QI-MARL) framework for the management of swarms of autonomous robots operating in microgrids with limited energy resources.
- Facilitate adaptive energy sharing by creating a protocol that minimizes energy waste through self-organization of the robots and microgrid nodes with respect to their energy usage and requirements for carrying out their work.
- Design a scalable, five-layer system architecture for real-time robot coordination incorporating management, communication, sensing, and decision-making.
- Develop a method to dynamically assign jobs based on consideration of the location of the job, the robot’s energy level, and the microgrid’s load to better utilize swarm wisdom for efficient navigation.
- Utilize quantum-inspired probabilistic decision-making for instantaneous optimal navigation in high-dimensional state spaces instead of MARL reinforcement strategies that would significantly slow down the robot’s ability for converging toward an optimal solution.
- Investigate grounded or realistic indoor grid-based maps and analyze for sensitivity, scale, energy efficiency, task success, path optimization, and real-time feasibility.
- Link autonomous robots, smart grid management, and cyber-physical systems to real-world applications of smart buildings, industrial campuses, and distributed renewable energy systems.
2. Related Work
2.1. Energy-Aware Robot Systems
2.2. Swarm Robotics and Task Allocation
2.3. Quantum-Inspired Algorithms
2.4. Smart Microgrids, Energy Sharing, and Multi-Agent Coordination
2.5. Hybrid Approaches for Autonomous Navigation
3. Methodology
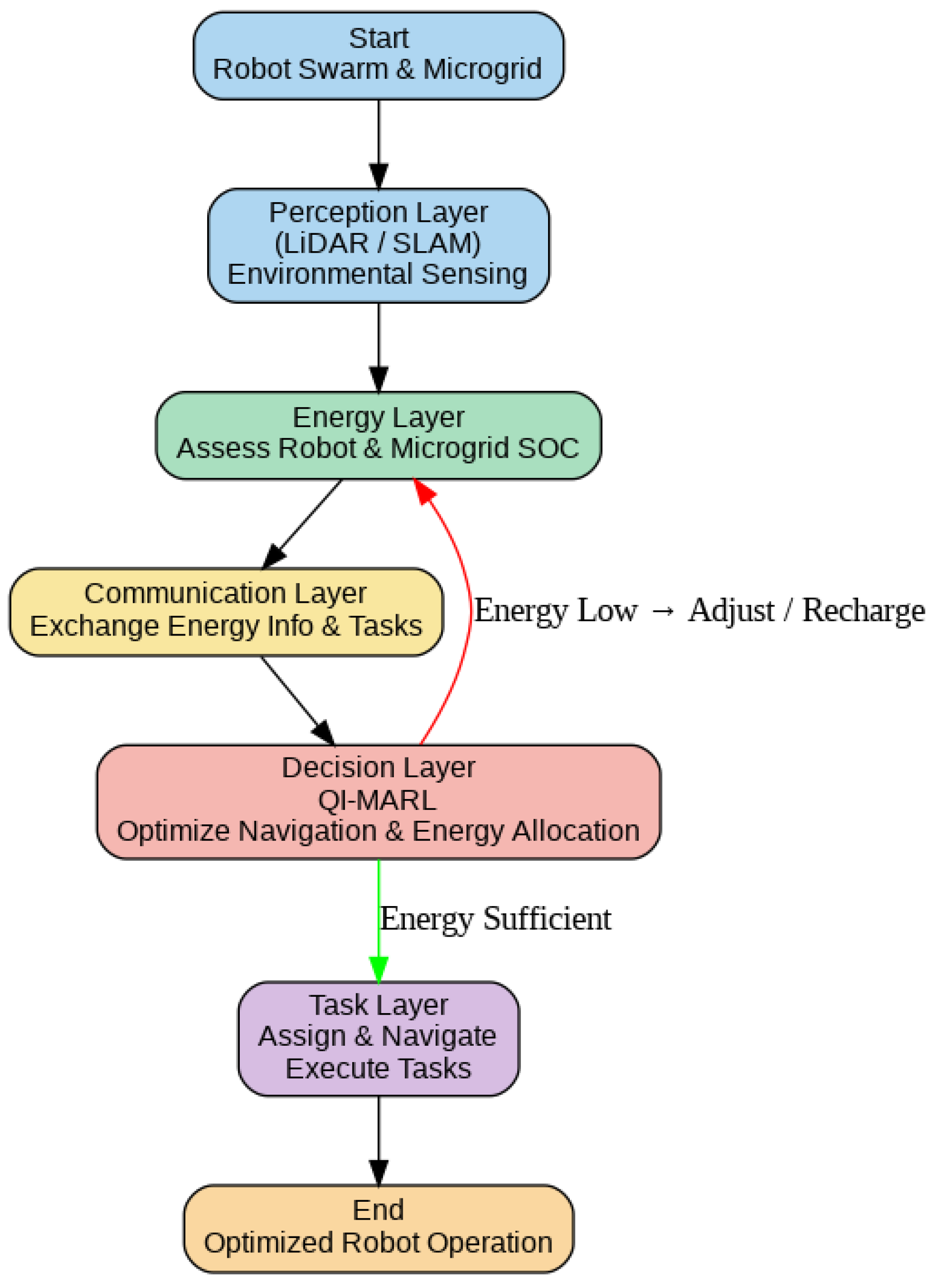
3.1. System Architecture
3.2. Flowchart of the Proposed Approach
- Dynamic task assignment based on robot energy levels and location;
- Adaptive energy scheduling supporting demand-response and time-of-use optimization;
- Prioritization of critical tasks and energy transfers to maintain microgrid stability.
3.3. Reward Function and Sensitivity Analysis
- represents the normalized energy consumption per task;
- quantifies the distribution of energy demand across nodes;
- accounts for path efficiency and collision avoidance;
- are empirically selected weights used to balance the objectives.
3.4. Learning Model
- Efficiency of energy use (less use wasted) and performance of navigation (shortest route and fewest collisions): The reduction in energy primarily refers to the energy consumption of individual robots while performing navigation and tasks. Each robot aims to minimize its own battery usage through efficient path planning and task scheduling. This individual energy efficiency also indirectly benefits the microgrid, as lower energy demand from robots reduces the load on local energy nodes, contributing to overall system efficiency.
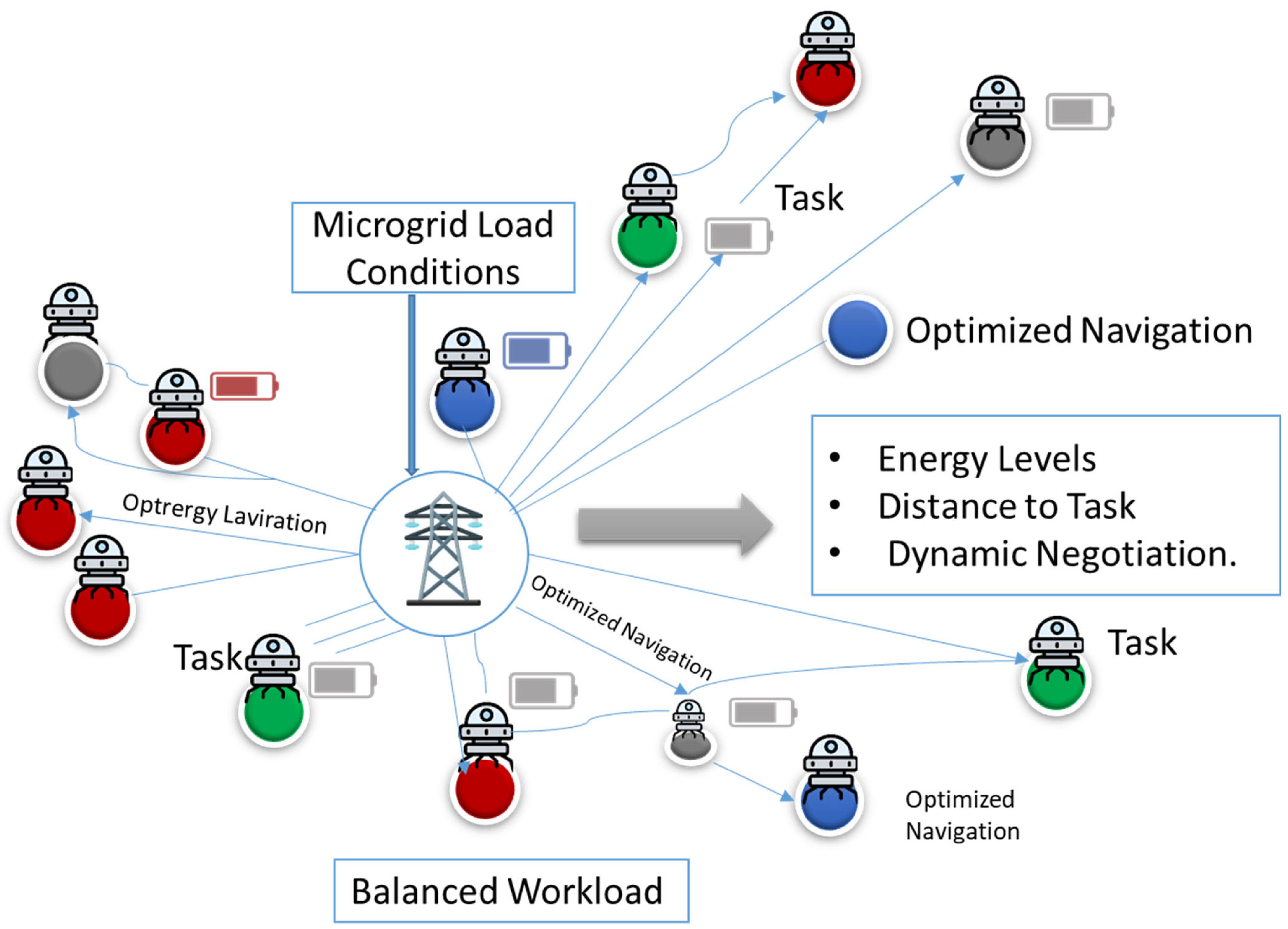
- Load balancing to prevent the overload of some microgrid nodes: Robots contribute to load balancing in the microgrid by adjusting their tasks and energy consumption according to the real-time status of nearby microgrid nodes. For example, a robot may defer non-critical tasks, reroute to less-loaded nodes, or request energy from nodes with surplus capacity. These adaptive decisions, coordinated via the QI-MARL framework and inter-agent communication, help distribute the energy demand evenly across the microgrid, preventing overloads and maintaining system stability.
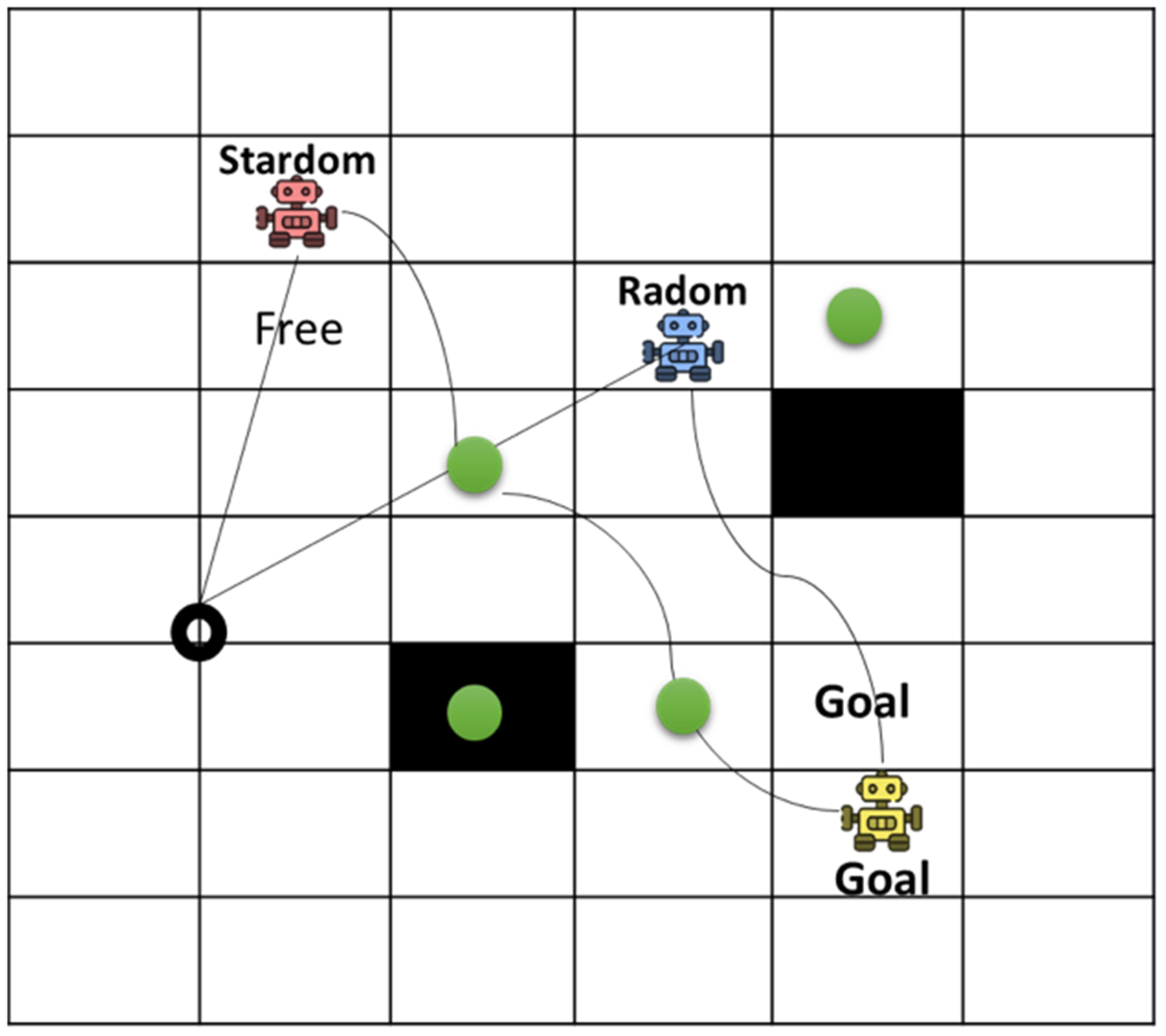
- The ability of the system to maintain service during demand variability: The QI-MARL framework is illustrated in Figure 4, where microgrid nodes and robots are treated as agents. Each agent selects an action from available options such as navigation, task execution, and energy sharing. The probability distributions, inspired by quantum mechanics, facilitate exploration and improve convergence speed. The incentive function guides agents toward optimal policies while considering load balancing, navigation capability, energy efficiency, sustainability, and reliability.
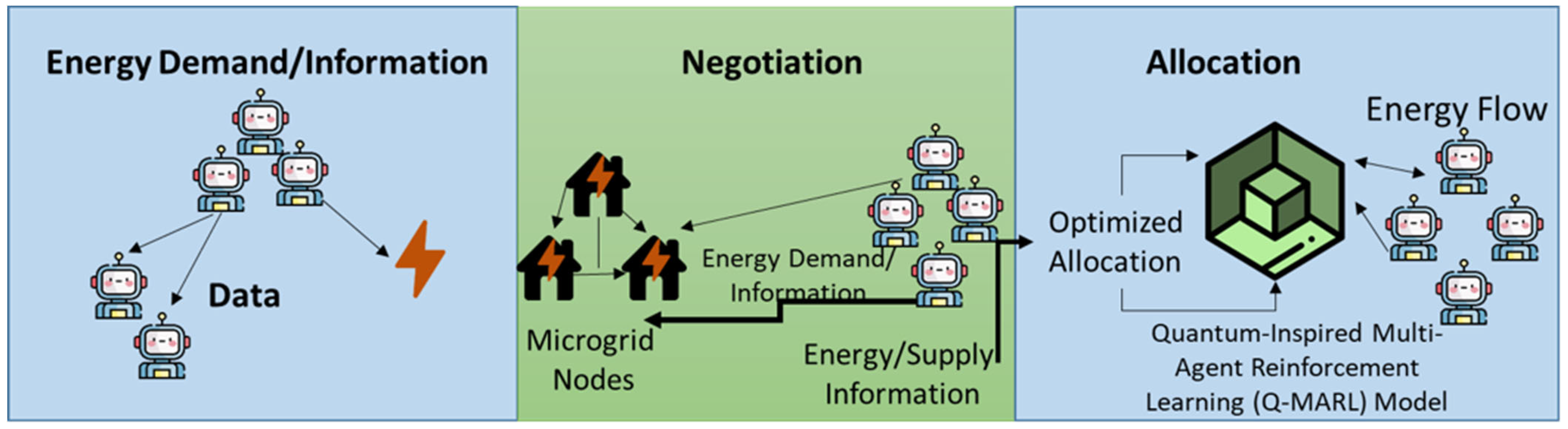
3.5. Energy Sharing Protocol
- Energy demand/information: Every robot establishes the context of energy demand.
- Negotiation: Agents exchange their offers and requests for energy through the communication layer in negotiations.
- Allocation: QI-MARL maximizes energy transfer and maintains swarm autonomy and loss.
3.6. Task Allocation Strategy
- The distance to the task location;
- The microgrid load status.
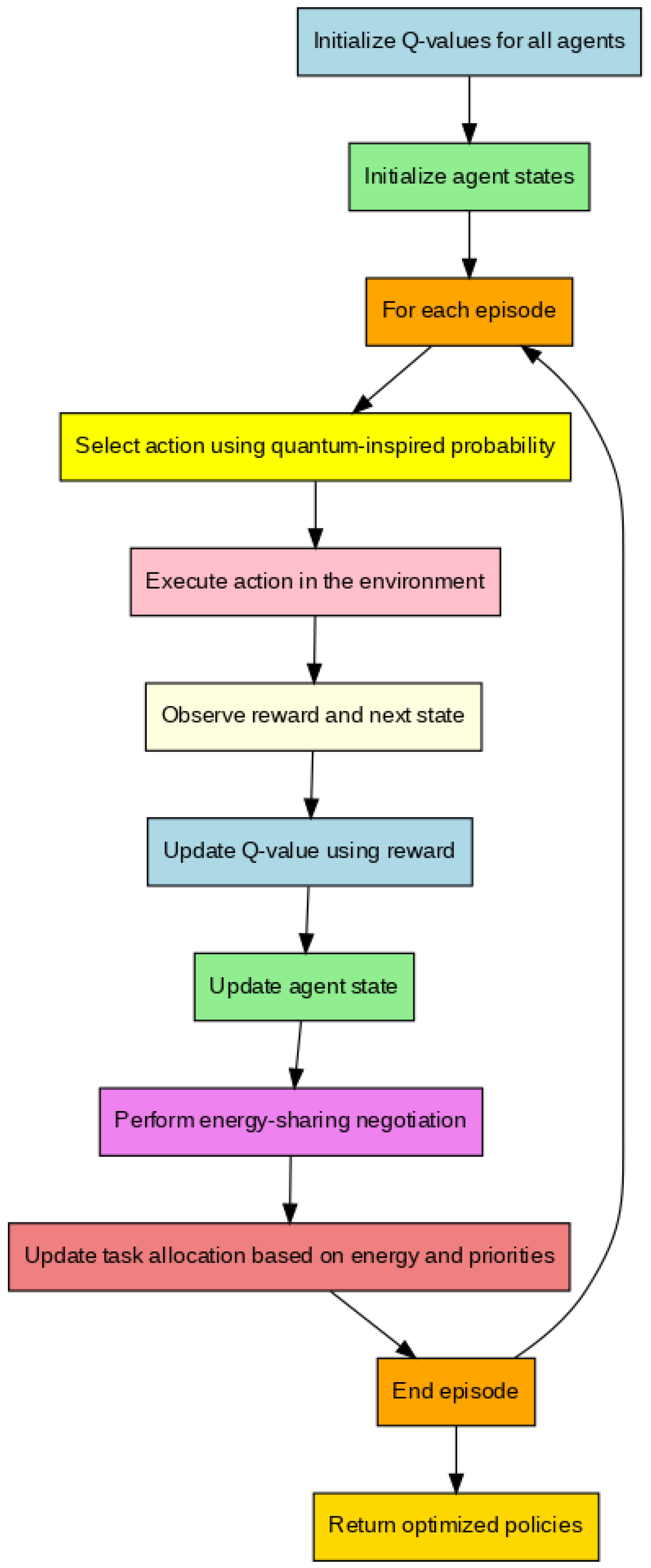
3.7. Quantum-Inspired MARL Algorithm
| Algorithm 1: QI-MARL for Energy-Aware Autonomous Robot Swarms |
| Input: S = set of states (robot positions, energy levels, microgrid conditions) A = set of actions (navigation, task execution, energy sharing) R = reward function (energy efficiency, task success, load balance) γ = discount factor α = learning rate N = number of agents (robots and microgrid nodes) Output: π = optimized policies for all agents Initialize Q-values Q(s, a) for all s ∈ S, a ∈ A For each agent i ∈ {1,…,N} do Initialize agent state s_i End for For each episode do For each agent i do Select action a_i using quantum-inspired probability distribution Execute a_i in the environment Observe reward r_i and next state s’_i Update Q-values using the Temporal Difference (TD) learning rule: Update the agent state: End for Perform energy-sharing negotiation among agents Update task allocation based on energy levels and task priorities End for Return optimized policies π for all agents |
4. Experimental Results
4.1. Dataset and Simulation Setup
4.2. Performance Evaluation Metrics
4.3. Module-Wise Evaluation of QI-MARL
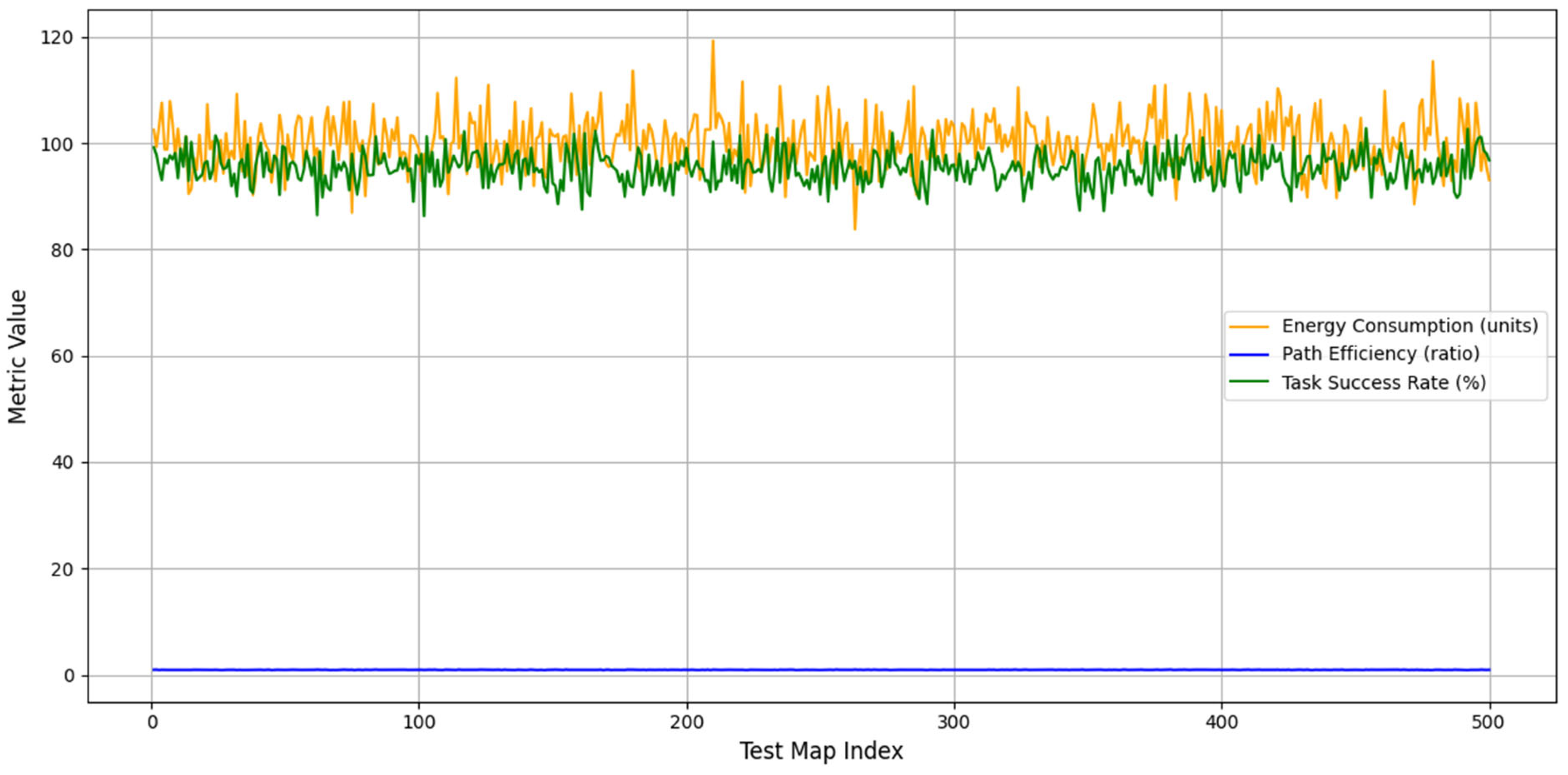
4.4. Sensitivity Analysis
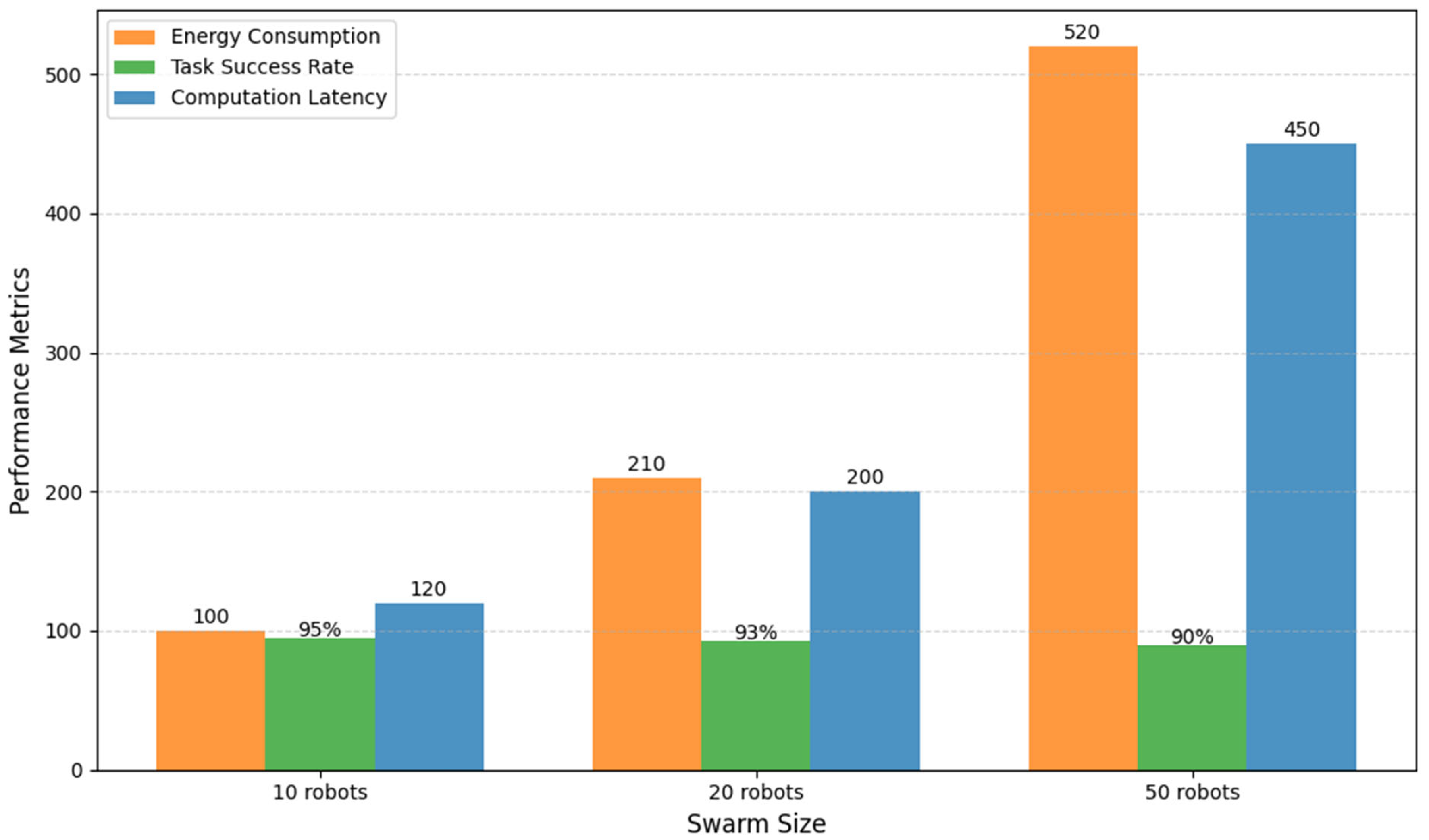
4.5. Evaluating QI-MARL Scalability
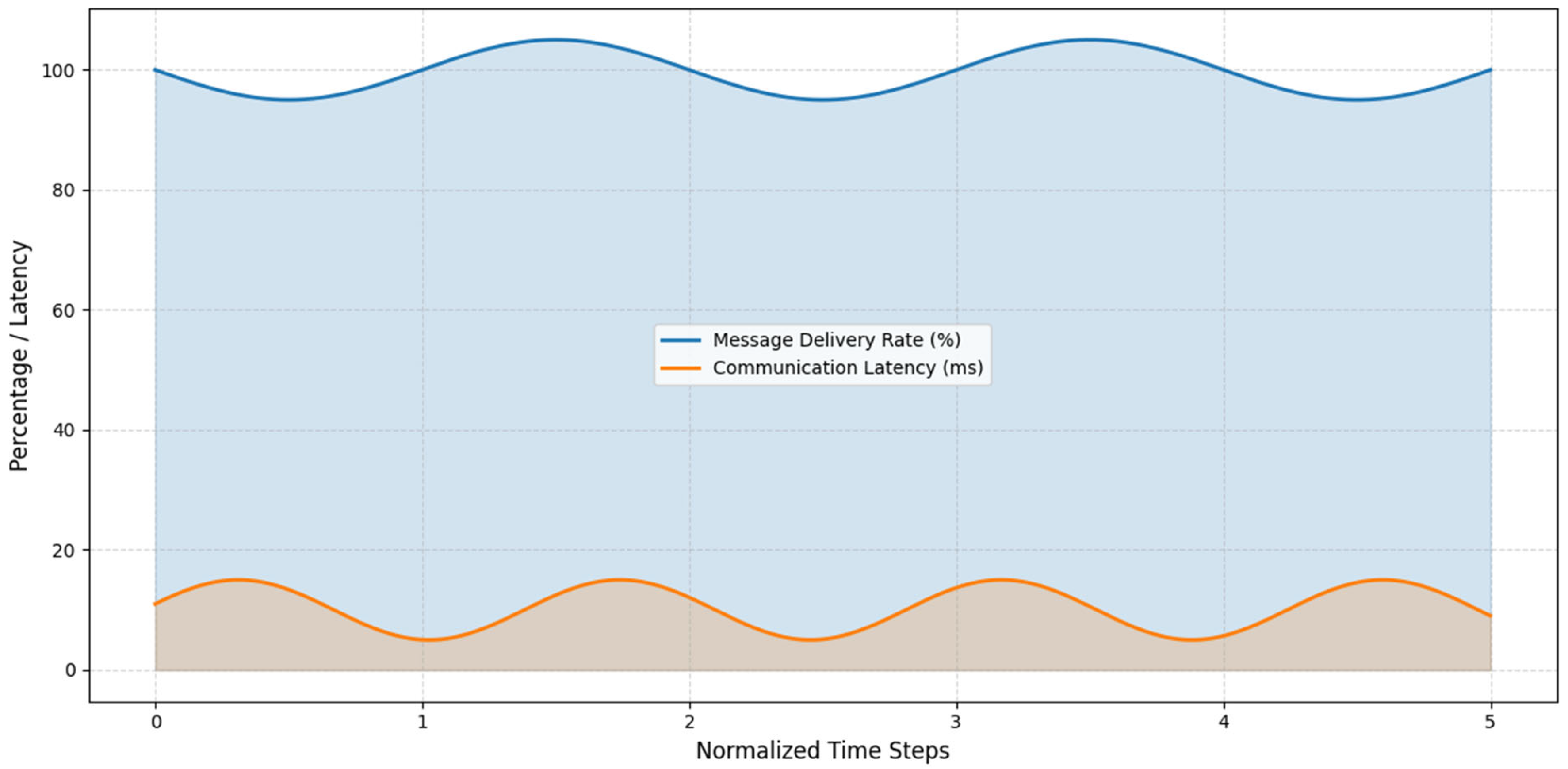
4.6. Communication Reliability and Latency Analysis
4.7. Obstacle Interaction and Navigation Efficiency
4.8. Baseline Comparisons
4.9. Convergence Analysis and Hyperparameter Ablation
4.10. Scalability and Computational Complexity Analysis
4.11. Simulation and Validation
5. Discussion and Limitations
5.1. Discussion
5.2. Limitations
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Energy Management of a Residential Microgrid under Uncertainties on Demand and Renewable Power Generation. IEEE Trans. Autom. Sci. Eng. 2021, 18, 618–637. [Google Scholar] [CrossRef]
- Shen, X.; Tang, J.; Pan, F.; Qian, B.; Zhao, Y. Quantum-inspired deep reinforcement learning for adaptive frequency control of low carbon park island microgrid considering renewable energy sources. Front. Energy Res. 2024, 12, 1366009. [Google Scholar] [CrossRef]
- Bai, Y.; Sui, Y.; Deng, X.; Wang, X. Quantum-inspired robust optimization for coordinated scheduling of PV-hydrogen microgrids under multi-dimensional uncertainties. Sci. Rep. 2025, 15, 29589. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, W.; Liu, W. Multi-agent deep reinforcement learning-based distributed optimal generation control of DC microgrids. IEEE Trans. Smart Grid 2023, 14, 3337–3351. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Fan, P.; Letaief, K.B. Federated Multiagent Actor-Critic Learning for Age Sensitive Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 1053–1067. [Google Scholar] [CrossRef]
- Tlijani, H.; Jouila, A.; Nouri, K. Optimized Sliding Mode Control Based on Cuckoo Search Algorithm: Application for 2DF Robot Manipulator. Cybern. Syst. 2023, 56, 849–865. [Google Scholar] [CrossRef]
- Wilk, P.; Wang, N.; Li, J. Multi-Agent Reinforcement Learning for Smart Community Energy Management. Energies 2024, 17, 5211. [Google Scholar] [CrossRef]
- Minghong, L.; Gaoshan, F.; Pengchao, W.; Xin, Y.; Qing, L.; Hou, T.; Shuo, Z. Behavior-aware energy management in microgrids using quantum-classical hybrid algorithms under social and demand dynamics. Sci. Rep. 2025, 15, 21326. [Google Scholar] [CrossRef]
- Liu, M.; Liao, M.; Zhang, R.; Yuan, X.; Zhu, Z.; Wu, Z. Quantum Computing as a Catalyst for Microgrid Management: Enhancing Decentralized Energy Systems Through Innovative Computational Techniques. Sustainability 2025, 17, 3662. [Google Scholar] [CrossRef]
- Fayek, H.H.; Fayek, F.H.; Rusu, E. Quantum-Inspired MoE-Based Optimal Operation of a Wave Hydrogen Microgrid for Integrated Water, Hydrogen, and Electricity Supply and Trade. J. Mar. Sci. Eng. 2025, 13, 461. [Google Scholar] [CrossRef]
- Ning, Z.; Xie, L. A survey on multi-agent reinforcement learning and its application. J. Autom. Intell. 2024, 3, 73–91. [Google Scholar] [CrossRef]
- Nie, L.; Long, B.; Yu, M.; Zhang, D.; Yang, X.; Jing, S. A Low-Carbon Economic Scheduling Strategy for Multi-Microgrids with Communication Mechanism-Enabled Multi-Agent Deep Reinforcement Learning. Electronics 2025, 14, 2251. [Google Scholar] [CrossRef]
- Guo, G.; Gong, Y. Multi-Microgrid Energy Management Strategy Based on Multi-Agent Deep Reinforcement Learning with Prioritized Experience Replay. Appl. Sci. 2023, 13, 2865. [Google Scholar] [CrossRef]
- Jouila, A.; Essounbouli, N.; Nouri, K.; Hamzaoui, A. Robust Nonsingular Fast Terminal Sliding Mode Control in Trajectory Tracking for a Rigid Robotic Arm. Aut. Control Comp. Sci. 2019, 53, 511–521. [Google Scholar] [CrossRef]
- Acharya, D.B.; Kuppan, K.; Divya, B. Agentic ai: Autonomous intelligence for complex goals–a comprehensive survey. IEEE Access 2025, 13, 18912–18936. [Google Scholar] [CrossRef]
- Wang, T.; Ma, S.; Tang, Z.; Xiang, T.; Mu, C.; Jin, Y. A multi-agent reinforcement learning method for cooperative secondary voltage control of microgrids. Energies 2023, 16, 5653. [Google Scholar] [CrossRef]
- Jung, S.-W.; An, Y.-Y.; Suh, B.; Park, Y.; Kim, J.; Kim, K.-I. Multi-Agent Deep Reinforcement Learning for Scheduling of Energy Storage System in Microgrids. Mathematics 2025, 13, 1999. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Cao, D.; Zhang, Z.; Huang, Q.; Chen, Z.; Blaabjerg, F. A multi-agent deep reinforcement learning approach enabled distributed energy management schedule for the coordinate control of multi-energy hub with gas, electricity, and freshwater. Energy Convers. Manag. 2022, 255, 115340. [Google Scholar] [CrossRef]
- Deshpande, K.; Möhl, P.; Hämmerle, A.; Weichhart, G.; Zörrer, H.; Pichler, A. Energy Management Simulation with Multi-Agent Reinforcement Learning: An Approach to Achieve Reliability and Resilience. Energies 2022, 15, 7381. [Google Scholar] [CrossRef]
- Xu, N.; Tang, Z.; Si, C.; Bian, J.; Mu, C. A Review of Smart Grid Evolution and Reinforcement Learning: Applications, Challenges and Future Directions. Energies 2025, 18, 1837. [Google Scholar] [CrossRef]
- Liu, D.; Wu, Y.; Kang, Y.; Yin, L.; Ji, X.; Cao, X.; Li, C. Multi-agent quantum-inspired deep reinforcement learning for real-time distributed generation control of 100% renewable energy systems. Eng. Appl. Artif. Intell. 2023, 119, 105787. [Google Scholar] [CrossRef]
- Ghasemi, R.; Doko, G.; Petrik, M.; Wosnik, M.; Lu, Z.; Foster, D.L.; Mo, W. Deep reinforcement learning-based optimization of an island energy-water microgrid system. Resour. Conserv. Recycl. 2025, 222, 108440. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Zhang, S.; Guo, Y.; Sun, H. Multi-Objective Robust Optimization of Integrated Energy System with Hydrogen Energy Storage. Energies 2024, 17, 1132. [Google Scholar] [CrossRef]
- Zhu, Z.; Weng, Z.; Zheng, H. Optimal Operation of a Microgrid with Hydrogen Storage Based on Deep Reinforcement Learning. Electronics 2022, 11, 196. [Google Scholar] [CrossRef]
- Jouili, K.; Jouili, M.; Mohammad, A.; Babqi, A.J.; Belhadj, W. Neural Network Energy Management-Based Nonlinear Control of a DC Micro-Grid with Integrating Renewable Energies. Energies 2024, 17, 3345. [Google Scholar] [CrossRef]
- Toure, I.; Payman, A.; Camara, M.-B.; Dakyo, B. Energy Management in a Renewable-Based Microgrid Using a Model Predictive Control Method for Electrical Energy Storage Devices. Electronics 2024, 13, 4651. [Google Scholar] [CrossRef]
- Shili, M.; Hammedi, S.; Chaoui, H.; Nouri, K. A Novel Intelligent Thermal Feedback Framework for Electric Motor Protection in Embedded Robotic Systems. Electronics 2025, 14, 3598. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Y. Integrated Demand Response in Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies 2023, 16, 4769. [Google Scholar] [CrossRef]
- Turjya, S.M.; Bandyopadhyay, A.; Kaiser, M.S.; Ray, K. QiMARL: Quantum-Inspired Multi-Agent Reinforcement Learning Strategy for Efficient Resource Energy Distribution in Nodal Power Stations. AI 2025, 6, 209. [Google Scholar] [CrossRef]
- Chen, W.; Wan, J.; Ye, F.; Wang, R.; Xu, C. QMARL: A Quantum Multi-Agent Reinforcement Learning Framework for Swarm Robots Navigation. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech, and Signal Processing Workshops (ICASSPW), Seoul, Republic of Korea, 14–19 April 2024; IEEE: New York, NY, USA, 2024; pp. 388–392. [Google Scholar]
- Shili, M.; Chaoui, H.; Nouri, K. Energy-Aware Sensor Fusion Architecture for Autonomous Channel Robot Navigation in Constrained Environments. Sensors 2025, 25, 6524. [Google Scholar] [CrossRef]
- Silva-Contreras, D.; Godoy-Calderon, S. Autonomous Agent Navigation Model Based on Artificial Potential Fields Assisted by Heuristics. Appl. Sci. 2024, 14, 3303. [Google Scholar] [CrossRef]
- Ahmed, G.; Sheltami, T. Novel Energy-Aware 3D UAV Path Planning and Collision Avoidance Using Receding Horizon and Optimization-Based Control. Drones 2024, 8, 682. [Google Scholar] [CrossRef]
- Wu, B.; Zuo, X.; Chen, G.; Ai, G.; Wan, X. Multi-agent deep reinforcement learning based real-time planning approach for responsive customized bus routes. Comput. Ind. Eng. 2024, 188, 109840. [Google Scholar] [CrossRef]
- Yuan, G.; Xiao, J.; He, J.; Jia, H.; Wang, Y.; Wang, Z. Multi-agent cooperative area coverage: A two-stage planning approach based on reinforcement learning. Inf. Sci. 2024, 678, 121025. [Google Scholar] [CrossRef]
- Lin, X.; Huang, M. An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment. Electronics 2024, 13, 3028. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Z.; Guan, X.; Shen, T.; Zhang, Z.; Duan, T.; Huang, D.; Zhao, S.; Cui, H. Agrnav: Efficient and energy-saving autonomous navigation for air-ground robots in occlusion-prone environments. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: New York, NY, USA, 2024; pp. 11133–11139. [Google Scholar]
- Wang, J.; Guan, X.; Sun, Z.; Shen, T.; Huang, D.; Liu, F.; Cui, H. Omega: Efficient occlusion-aware navigation for air-ground robots in dynamic environments via state space model. IEEE Robot. Autom. Lett. 2024, 10, 1066–1073. [Google Scholar] [CrossRef]
- Billah, M.; Zeb, K.; Uddin, W.; Imran, M.; Alatawi, K.S.; Almasoudi, F.M.; Khalid, M. Decentralized Multi-Agent Control for Optimal Energy Management of Neighborhood based Hybrid Microgrids in Real-Time Networking. Results Eng. 2025, 27, 106337. [Google Scholar] [CrossRef]
- Ghazimirsaeid, S.S.; Jonban, M.S.; Mudiyanselage, M.W.; Marzband, M.; Martinez, J.L.R.; Abusorrah, A. Multi-agent-based energy management of multiple grid-connected green buildings. J. Build. Eng. 2023, 74, 106866. [Google Scholar] [CrossRef]
- Yu, H.; Niu, S.; Shao, Z.; Jian, L. A scalable and reconfigurable hybrid AC/DC microgrid clustering architecture with decentralized control for coordinated operation. Int. J. Electr. Power Energy Syst. 2022, 135, 107476. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, H.; Yang, J.; Lin, Y. Deep reinforcement learning for path planning of autonomous mobile robots in complicated environments. Complex Intell. Syst. 2025, 11, 277. [Google Scholar] [CrossRef]
- Xing, T.; Wang, X.; Ding, K.; Ni, K.; Zhou, Q. Improved Artificial Potential Field Algorithm Assisted by Multisource Data for AUV Path Planning. Sensors 2023, 23, 6680. [Google Scholar] [CrossRef]







| Refs. | Approach | Energy Efficiency | Adaptability to Environment | Computational Complexity | Real-Time Applicability | Safety in Cluttered Spaces |
|---|---|---|---|---|---|---|
| [31,32] | Multi-agent reinforcement learning (MARL) | Moderate | High | Very High | Low | High |
| [33,34] | Energy-aware robot systems | High | Moderate | High | Moderate | Moderate |
| [35,36] | Swarm robotics and task allocation | Moderate | High | Moderate | Moderate | High |
| [37,38] | Quantum-inspired algorithms | Very High | High | Very High | Low | Moderate |
| [39,40,41] | Smart microgrids, energy sharing, and multi-agent coordination | High | Moderate | Moderate | Moderate | Moderate |
| [42,43] | Hybrid approaches for autonomous navigation | Very High | High | High | Moderate to High | High |
| This work | Quantum-inspired MARL for energy-aware autonomous robot swarms | Very High | Very High | High | Moderate to High | Very High |
| Layer | Purpose/Function | Main Components | QI-MARL Involvement |
|---|---|---|---|
| Perception layer | Gathers environmental, positional, and energy data for situational awareness. | Sensors (energy meters, GPS, LiDAR, cameras), IoT devices. | Provides input only (no direct QI-MARL processing). |
| Communication layer | Transfers information between robots and microgrid nodes to support coordination. | V2G (Vehicle-to-Grid) | Provides data flow and feedback, not active learning. |
| Decision layer | Central intelligence layer that performs task allocation, energy optimization, and navigation decisions. | QI-MARL engine, reinforcement learning models, edge processors. | Active: QI-MARL executes learning and adaptive decision-making. |
| Control layer | Executes commands from the decision layer to perform physical tasks and energy sharing. | Actuators, motion and power controllers, embedded processors. | Implements QI-MARL outputs. |
| Application layer | Oversees visualization, management, and system-level monitoring. | Dashboards, analytics tools, databases, user interfaces. | Uses results of QI-MARL for reporting and system tuning. |
| Tested Weight | Task Success Rate (%) | Path Efficiency (%) | Energy Consumption (J) | Observation |
|---|---|---|---|---|
| = 0.3) | 92 | 88 | 150 | Baseline |
| w1 +20% | 91 | 87 | 148 | Stable |
| w1 −20% | 93 | 89 | 152 | Stable |
| w2 +20% | 92 | 88 | 149 | Stable |
| w2 −20% | 91 | 87 | 151 | Stable |
| w3 +20% | 92 | 87 | 150 | Stable |
| w3 −20% | 93 | 89 | 151 | Stable |
| Attribute | Description |
|---|---|
| Dataset source | Robot Path Plan Dataset (Kaggle) |
| Number of maps used | 1000 maps for training, 500 maps for testing |
| Environment type | Grid-based layout (free cells, obstacles, energy nodes) |
| Robots simulated | 10 robots per swarm |
| Energy model | Battery capacity: 100 units; energy proportional to path length |
| Baselines | QI-MARL, classical MARL, rule-based (shortest path) |
| Simulation framework | Python 3.9.9 + OpenAI Gym + custom energy-sharing layer |
| Metric | Description |
|---|---|
| Energy consumption per task | Average battery usage per robot per navigation task (units of energy) |
| Task success rate | Proportion of robots completing tasks within energy constraints (%) |
| Path efficiency | Ratio of actual path length to the optimal shortest path (0–1, higher values indicate better efficiency) |
| Energy balance | Variance of remaining energy among robots (units2, lower is better) |
| Generalization | Performance difference between training and unseen maps (%) |
| Component Removed | Energy Consumption ↑ | Task Success ↓ | Path Efficiency ↓ |
|---|---|---|---|
| Quantum-inspired exploration | +10% | −8% | −5% |
| Energy-sharing protocol | +15% | −12% | −6% |
| Adaptive task allocation | +8% | −7% | −4% |
| Parameter | Variation Tested | Effect on Energy | Effect on Task Success |
|---|---|---|---|
| Number of robots | 5–50 | ±10% | ±12% |
| Battery capacity | 50–150 units | ±8% | ±5% |
| Communication radius | 2–10 units | ±7% | ±6% |
| Reward function weight | 0.5–1.5 scaling | ±6% | ±4% |
| Swarm Size | Energy Consumption | Task Success Rate | Latency (ms) |
|---|---|---|---|
| 10 robots | 100 units | 95% | 120 |
| 20 robots | 210 units | 93% | 200 |
| 50 robots | 520 units | 90% | 450 |
| Parameter | Variation Tested | Metric Evaluated | Description |
|---|---|---|---|
| Packet loss rate | 0–20% | Message delivery rate (%) | Fraction of messages successfully delivered |
| Communication delay | 1–50 ms | Average latency (ms) | Time taken for messages to be received |
| Communication range | 2–15 units | Task success impact (%) | Effect of range on task completion and energy sharing |
| Swarm size | 5–50 robots | Coordination reliability (%) | Impact of swarm size on communication efficiency |
| Metric | Description |
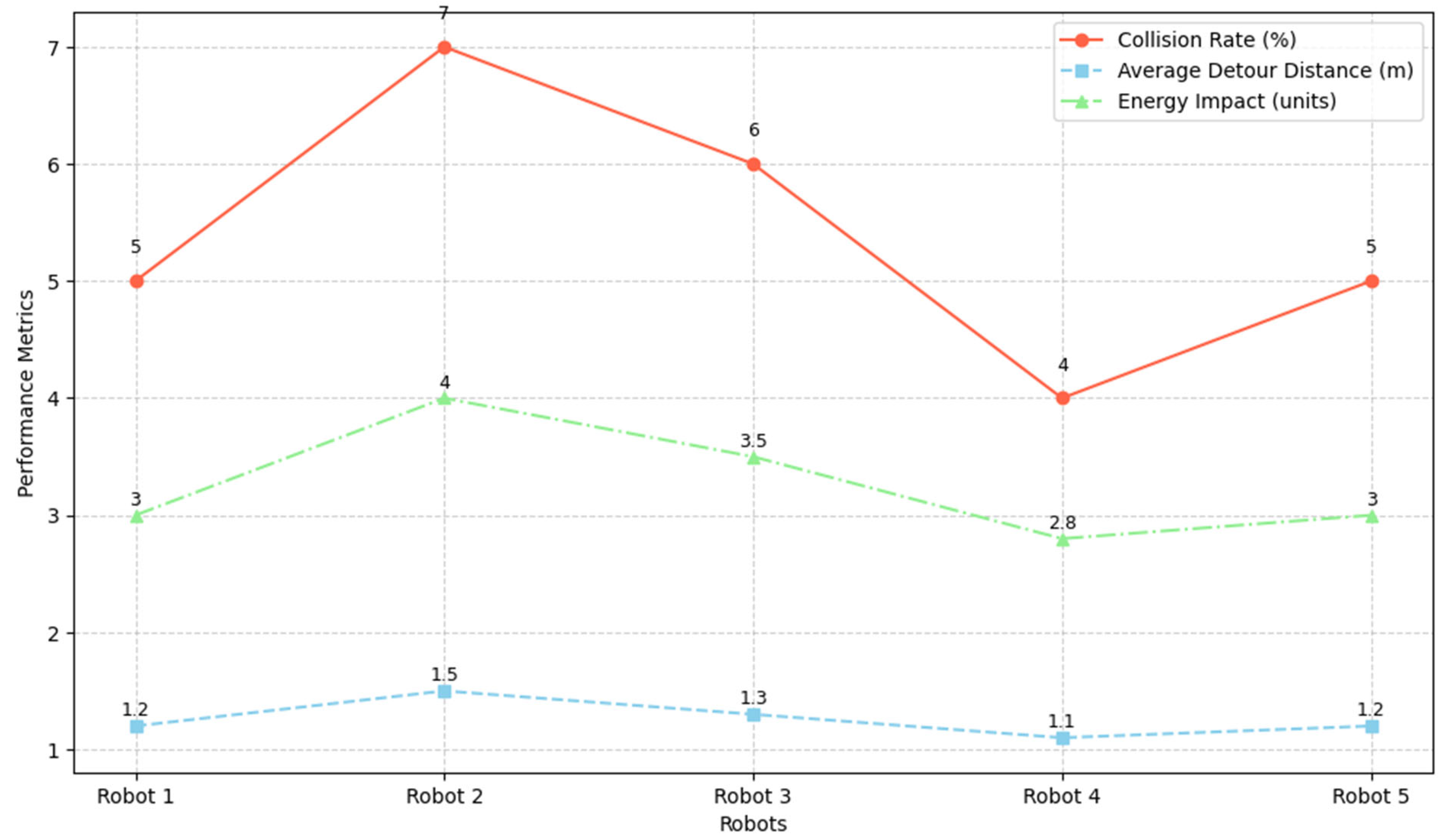
|---|---|
| Collision rate | Percentage of robot paths that intersect obstacles |
| Average detour distance | Extra path length traveled to avoid obstacles |
| Time-to-goal | Average time for robots to reach their target |
| Energy impact | Extra energy consumed due to obstacle navigation |
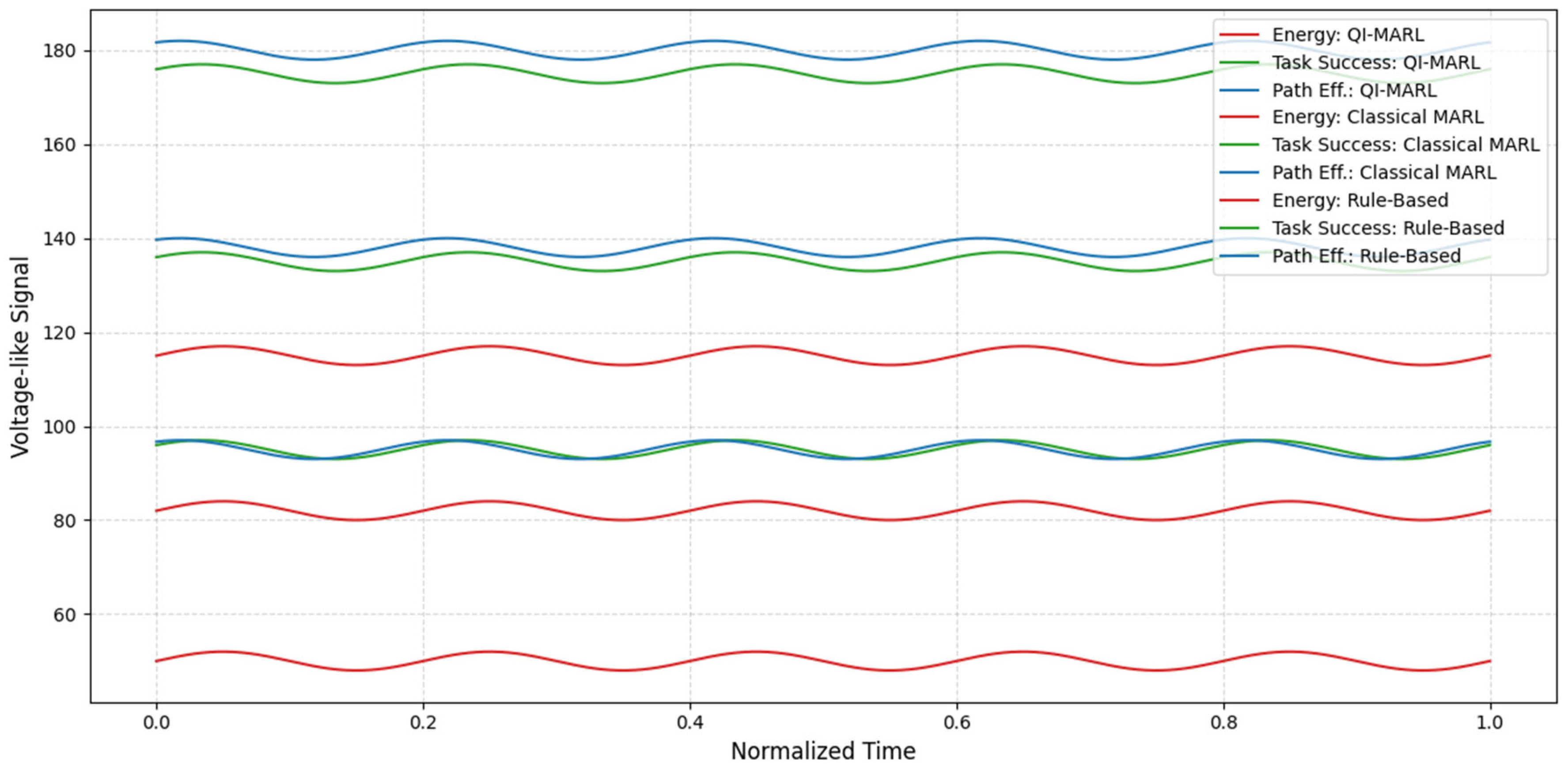
| Method | Energy Consumption | Task Success Rate | Path Efficiency |
|---|---|---|---|
| QI-MARL | 100 units | 95% | 0.95 |
| Classical MARL | 118 units | 85% | 0.88 |
| Rule-based | 135 units | 75% | 0.80 |
| Hyperparameter | Settings Tested | Energy Consumption ↑ | Task Success ↓ | Path Efficiency ↓ |
|---|---|---|---|---|
| Learning rate (α) | 0.001, 0.005, 0.01 | +5%/+3%/+2% | −4%/−2%/−1% | −3%/−2%/−1% |
| Discount factor (γ) | 0.9, 0.95, 0.99 | +4%/+2%/+1% | −3%/−2%/−1% | −2%/−1%/0% |
| Exploration probability | 0.1, 0.3, 0.5 | +6%/+3%/+2% | −5%/−3%/−2% | −4%/−2%/−1% |
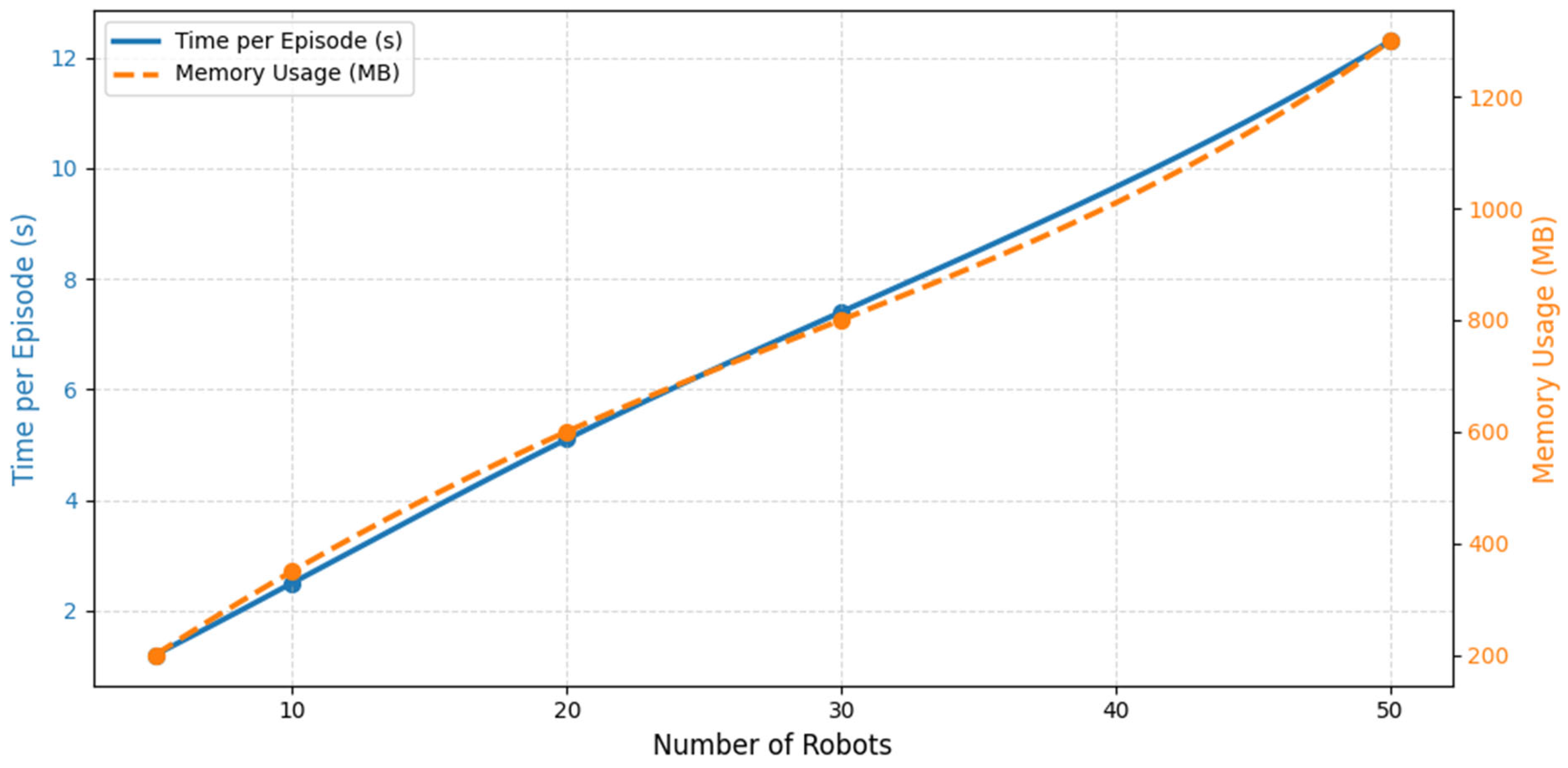
| Number of Robots | Time per Episode (s) | Memory Usage (MB) |
|---|---|---|
| 5 | 12 | 150 |
| 10 | 18 | 175 |
| 20 | 28 | 210 |
| 30 | 38 | 260 |
| 50 | 55 | 330 |
| Number of Robots | Energy Consumption ↑ | Task Success ↓ | Path Efficiency ↓ |
|---|---|---|---|
| 10 | +2% | −1% | −1% |
| 20 | +4% | −2% | −2% |
| 30 | +6% | −3% | −3% |
| 40 | +9% | −4% | −4% |
| 50 | +12% | −5% | −5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shili, M.; Hammedi, S.; Chaoui, H.; Nouri, K. Energy-Aware Swarm Robotics in Smart Microgrids Using Quantum-Inspired Reinforcement Learning. Electronics 2025, 14, 4210. https://doi.org/10.3390/electronics14214210
Shili M, Hammedi S, Chaoui H, Nouri K. Energy-Aware Swarm Robotics in Smart Microgrids Using Quantum-Inspired Reinforcement Learning. Electronics. 2025; 14(21):4210. https://doi.org/10.3390/electronics14214210
Chicago/Turabian StyleShili, Mohamed, Salah Hammedi, Hicham Chaoui, and Khaled Nouri. 2025. "Energy-Aware Swarm Robotics in Smart Microgrids Using Quantum-Inspired Reinforcement Learning" Electronics 14, no. 21: 4210. https://doi.org/10.3390/electronics14214210
APA StyleShili, M., Hammedi, S., Chaoui, H., & Nouri, K. (2025). Energy-Aware Swarm Robotics in Smart Microgrids Using Quantum-Inspired Reinforcement Learning. Electronics, 14(21), 4210. https://doi.org/10.3390/electronics14214210









