A Three-Terminal Modular-Multilevel-Converter-Based Power Electronic Transformer with Reduced Voltage Stress for Meshed DC Systems
Abstract
1. Introduction
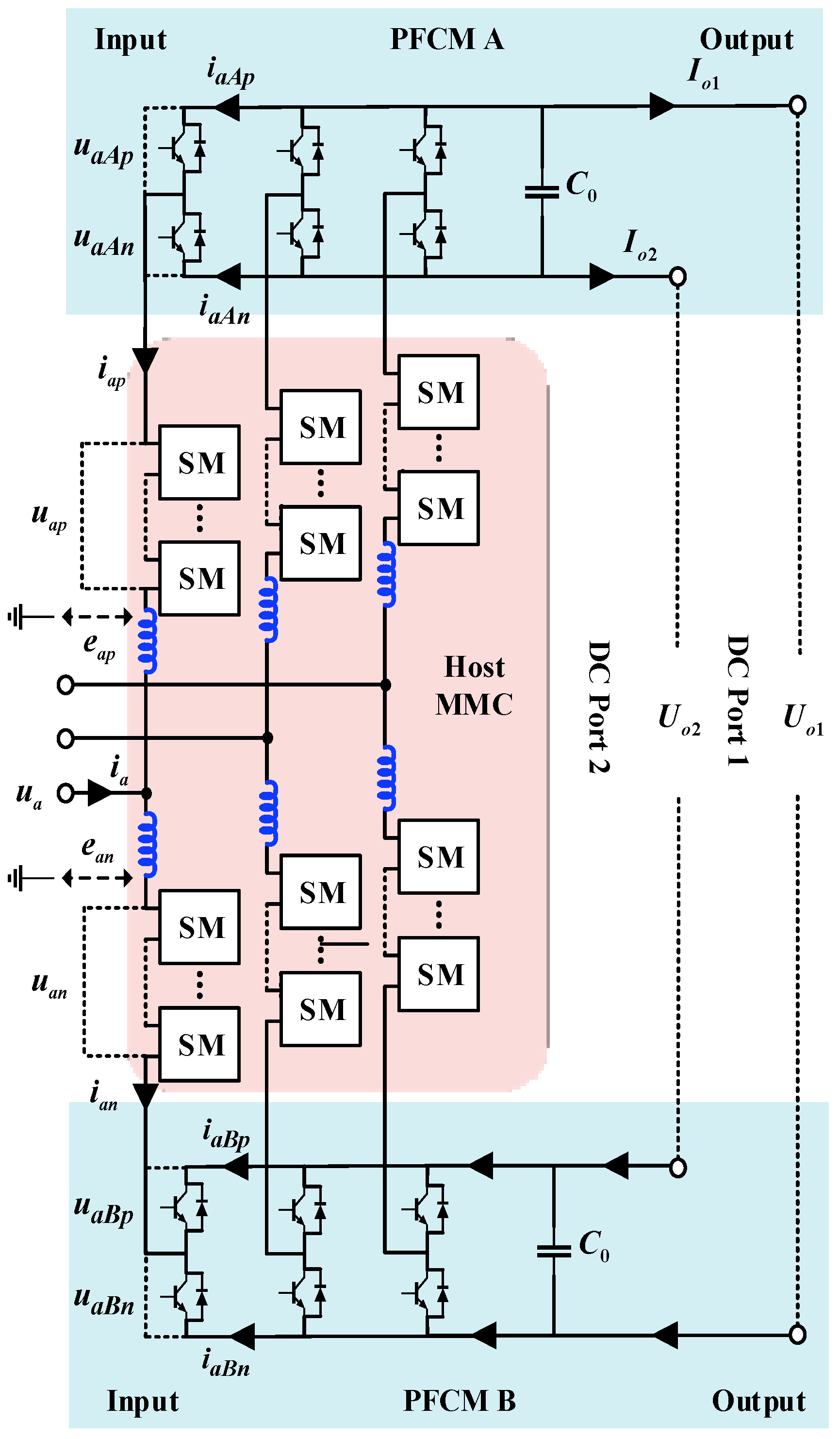
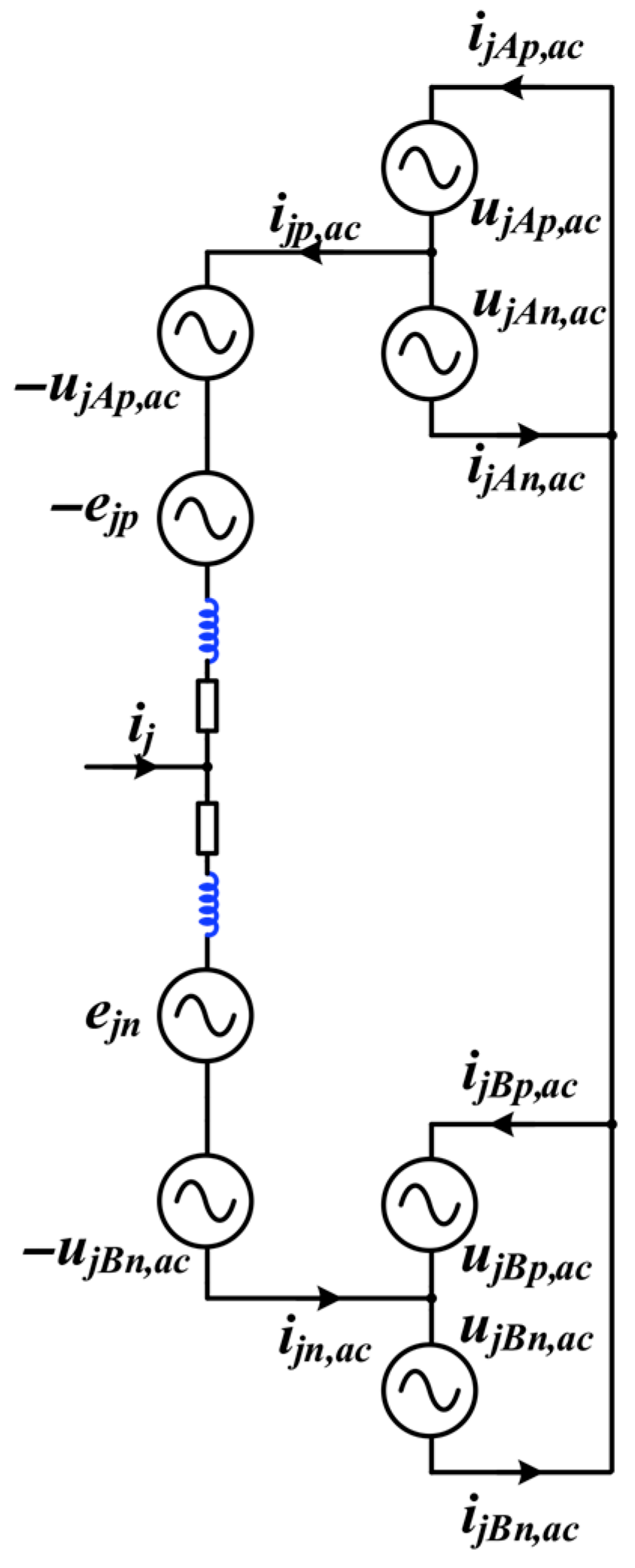
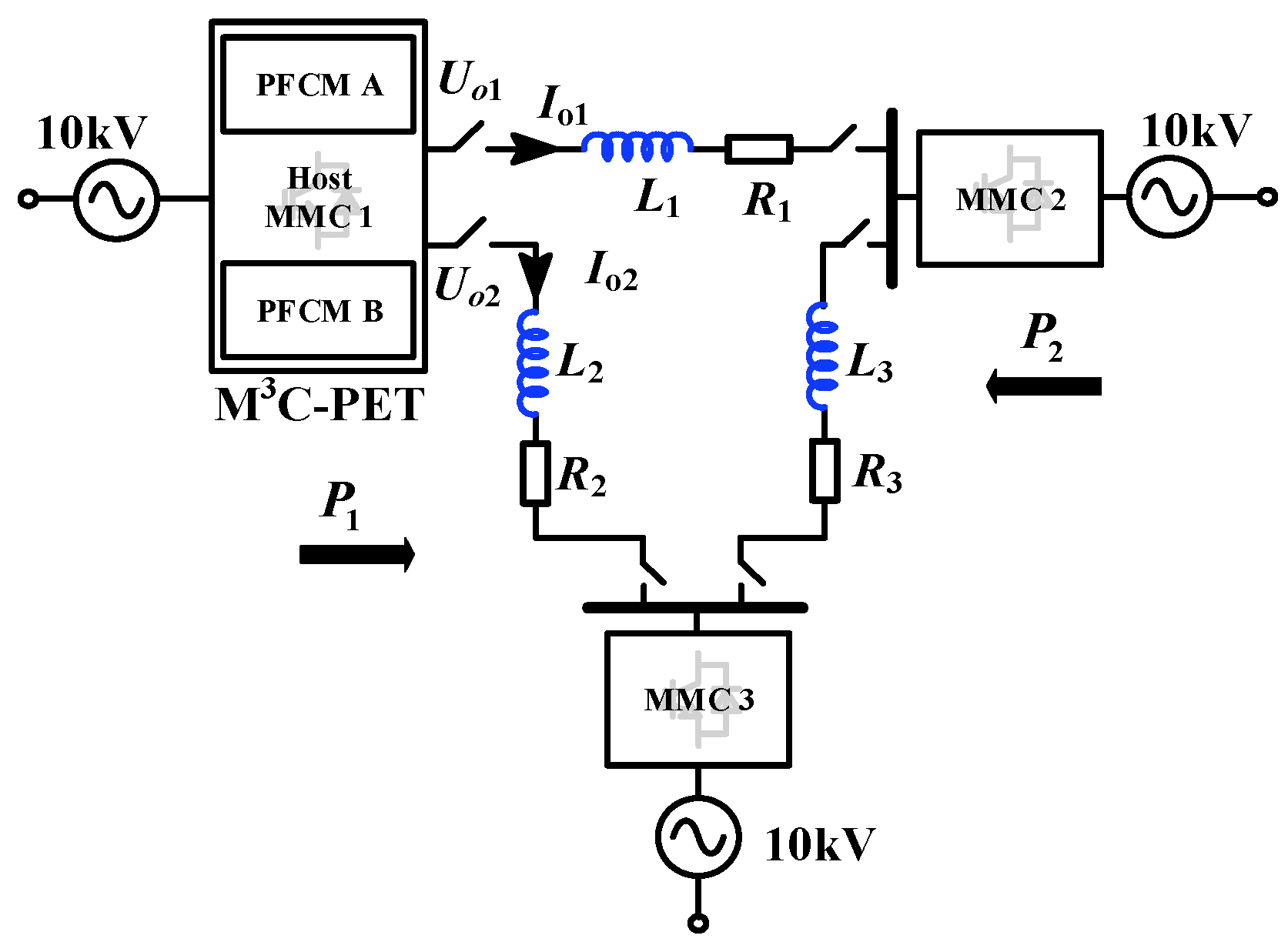
2. Topology and Operating Principle of the M3C-PET
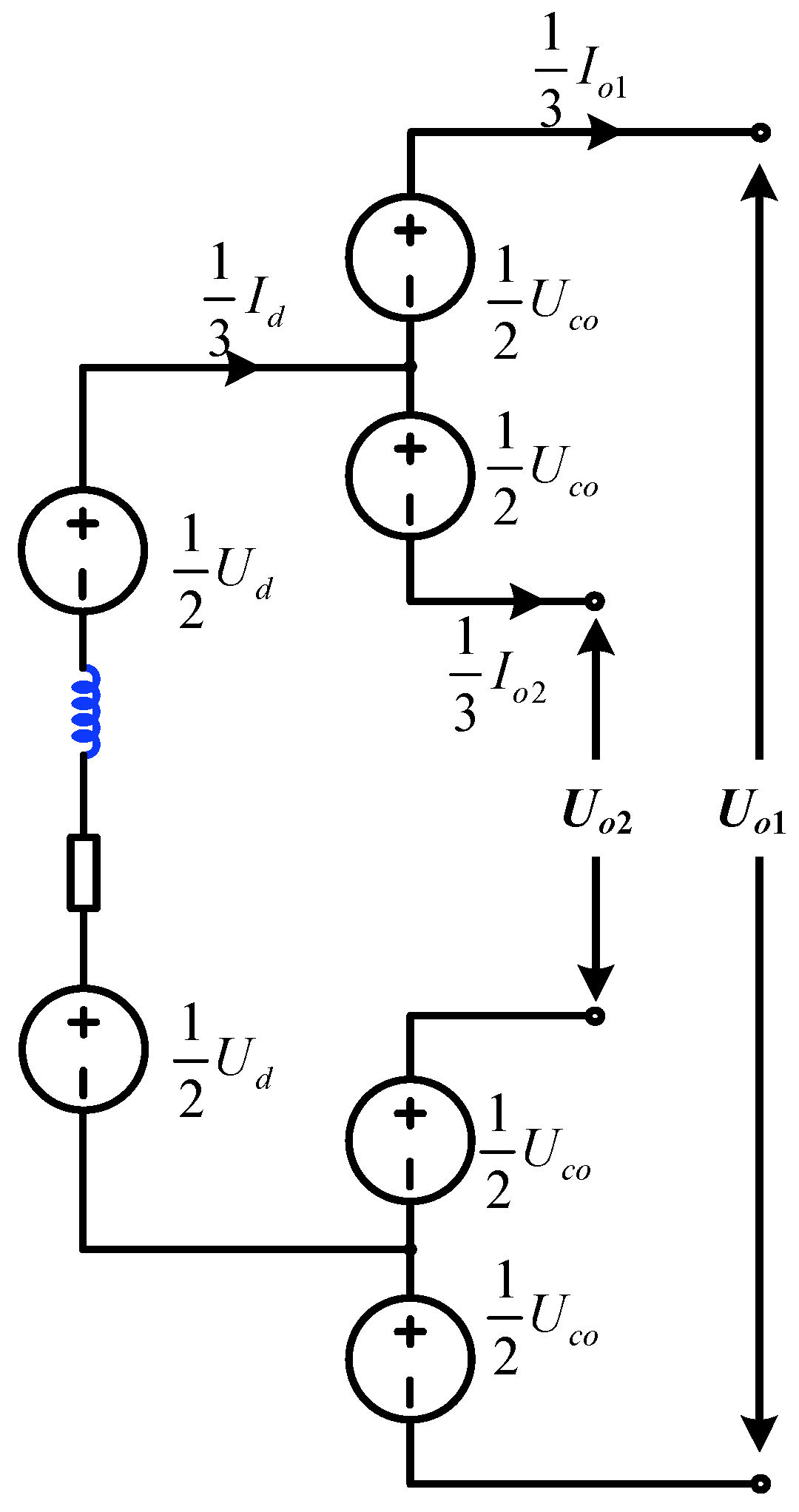
3. Parameter Design of the M3C-PET
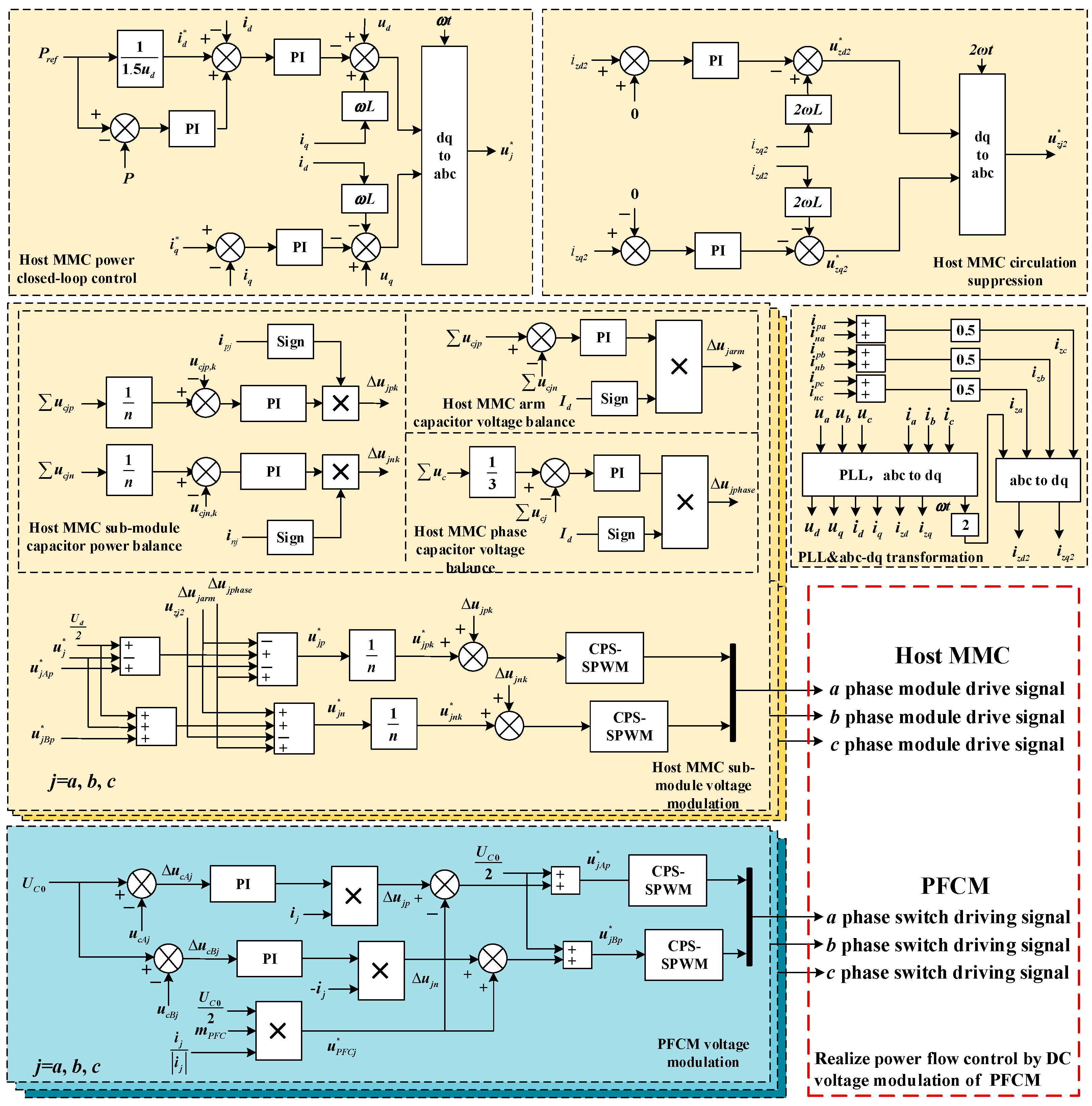
4. Coordinated Control Strategy
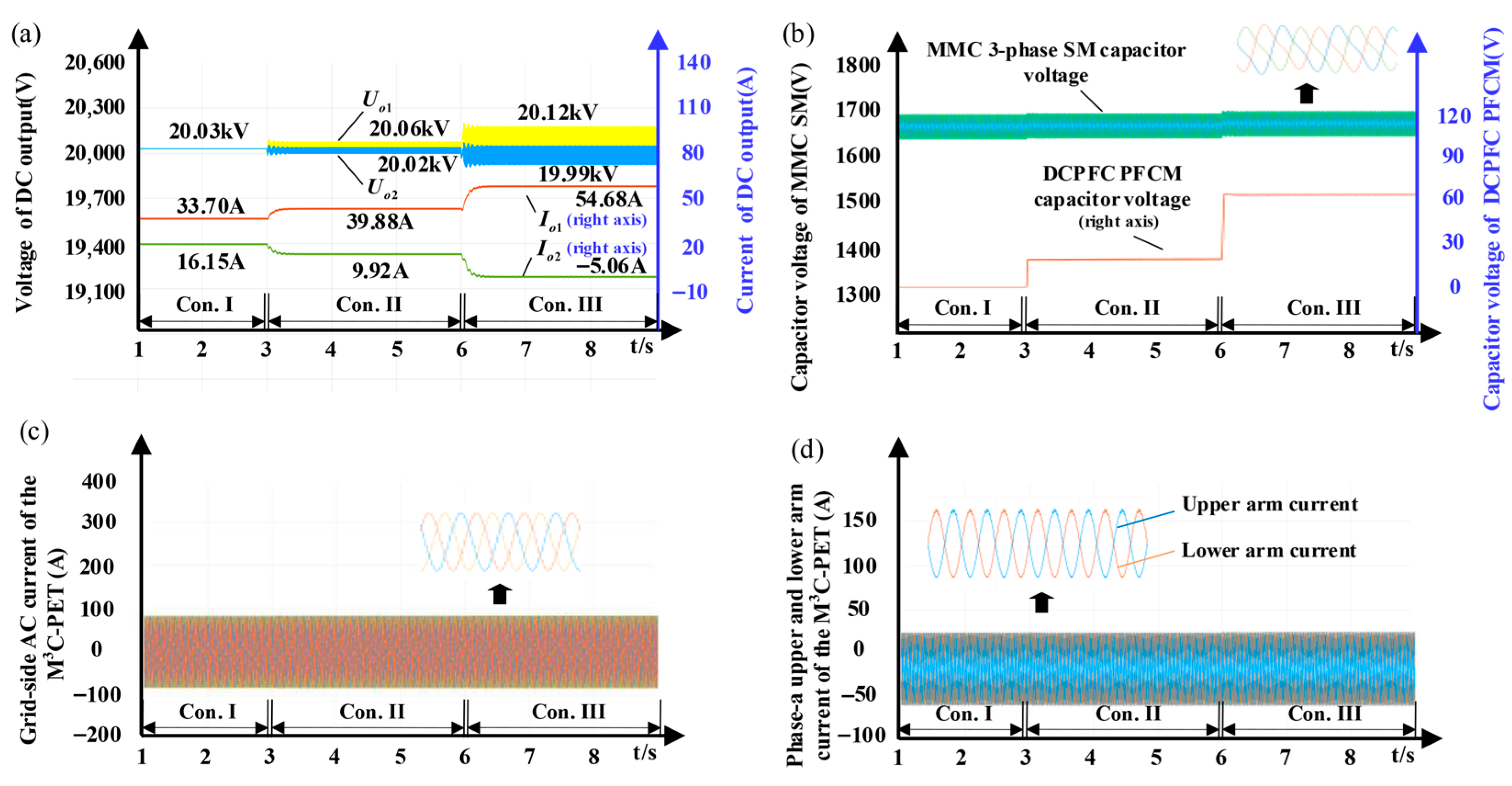
5. Simulation Verification
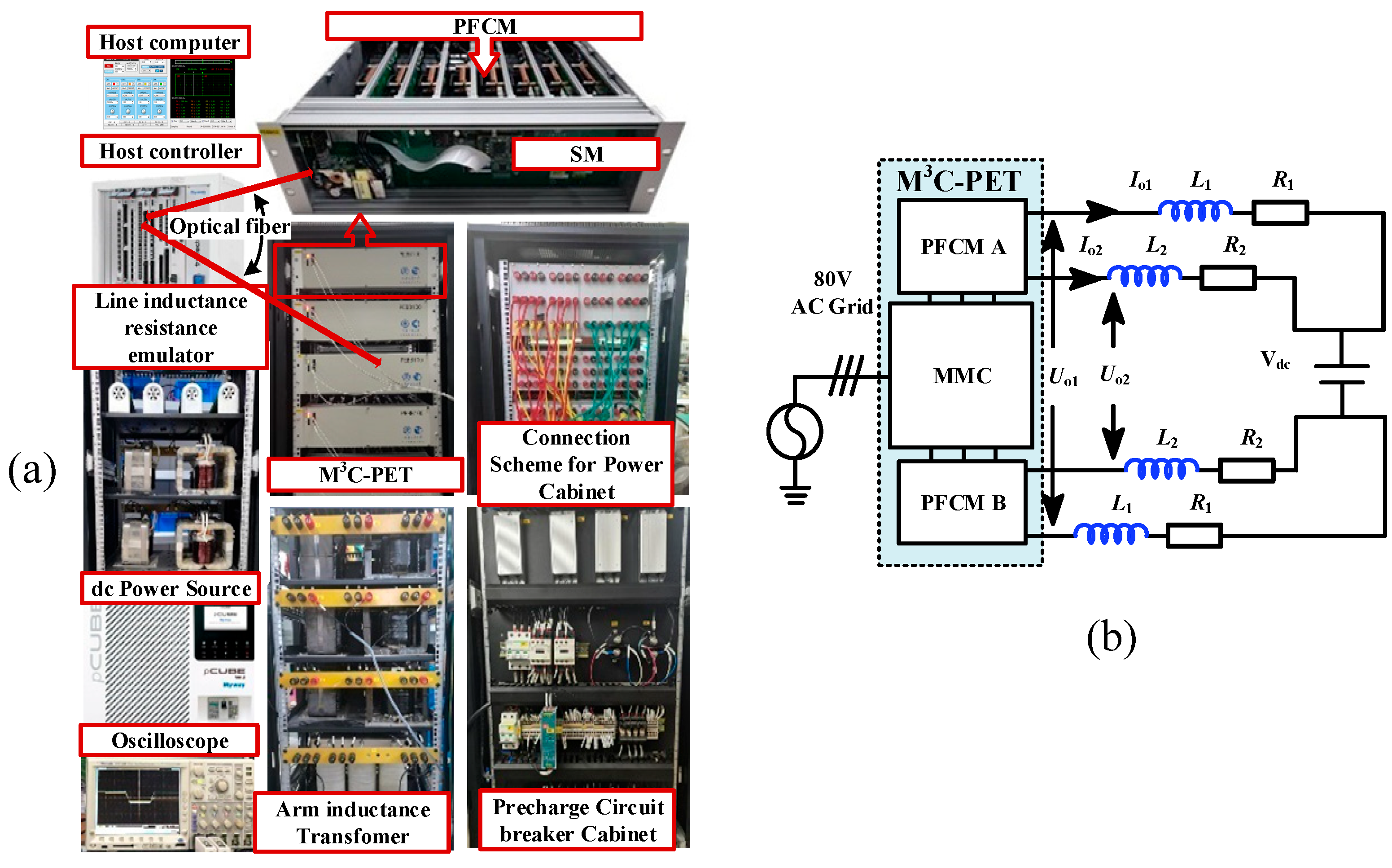
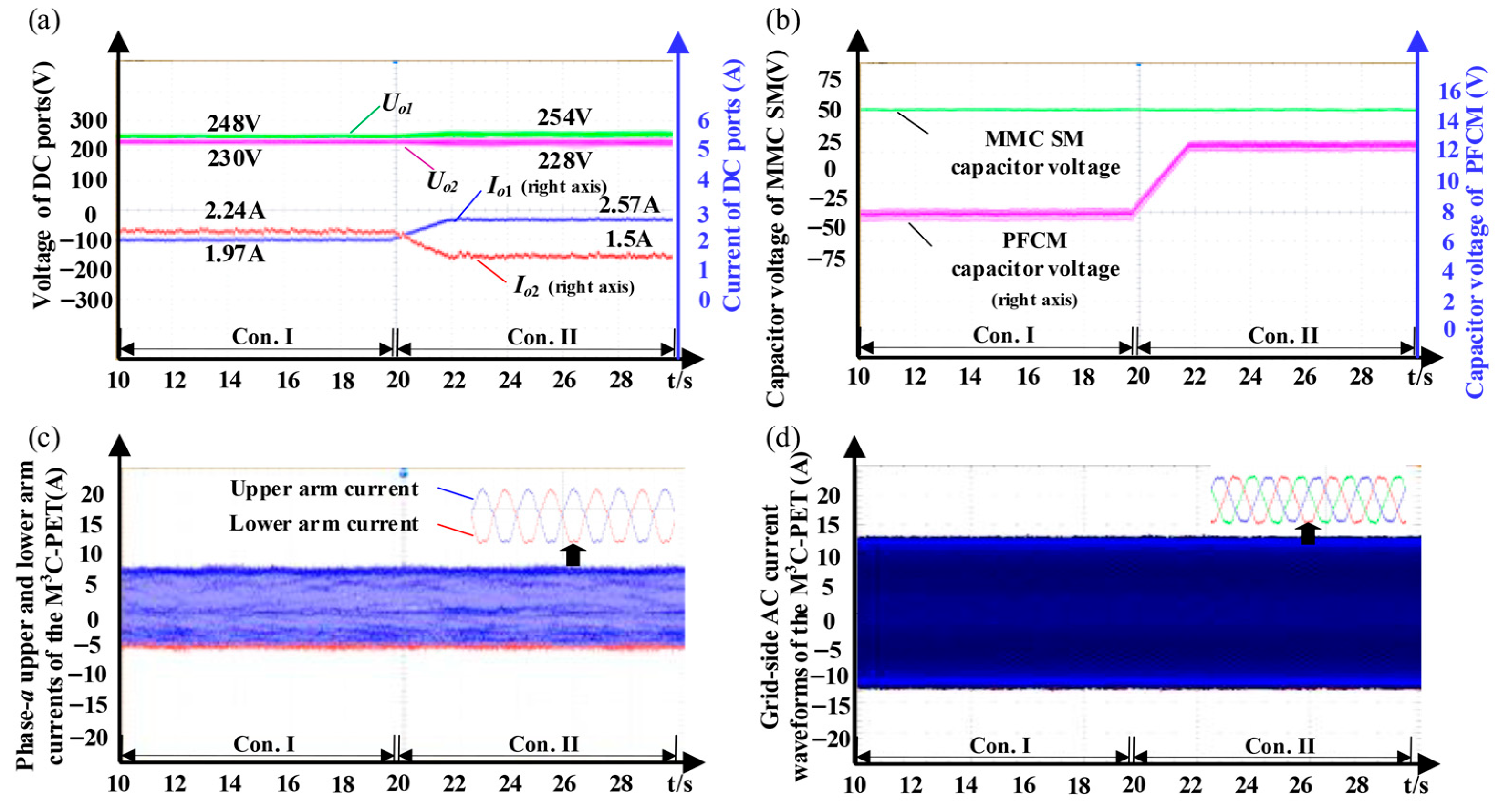
6. Experiment Verification
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Hertem, D.; Gomis-Bellmunt, O.; Liang, J. HVDC Grids: For Offshore and Supergrid of the Future; Wiley-IEEE Press: Hoboken, NJ, USA, 2016; ISBN 978-1-118-85915-5. [Google Scholar]
- Radwan, M.; Azad, S. Protection of Multi-Terminal HVDC Grids: A Comprehensive Review. Energies 2022, 15, 9552. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S.; Wang, Y.; Yang, R.; Cheng, X. An Improved AC-Link Voltage Matching Control for the Multiport Modular Multilevel DC Transformer in MVDC Applications. Energies 2024, 17, 1346. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, J.; Liu, L.; Zhang, B.; Wu, Y. A Modular Multiport DC Power Electronic Transformer Based on Triple-Active-Bridge for Multiple Distributed DC Units. IEEE Trans. Power Electron. 2024, 39, 15191–15205. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Sau-Bassols, J.; Prieto-Araujo, E.; Cheah-Mane, M. Flexible Converters for Meshed HVDC Grids: From Flexible AC Transmission Systems (FACTS) to Flexible DC Grids. IEEE Trans. Power Deliv. 2020, 35, 2–15. [Google Scholar] [CrossRef]
- Wu, W.; Wu, X.; Wang, L.; Zhao, T.; Jing, L.; Li, J. Active Damping Control of Multiport DC Power Flow Controller for MMC-MTDC With Unbalanced AC Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7395–7407. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, J.; Ye, Y.; Yang, X. Analysis of a Series-Parallel-Connected Type DC Power Flow Controller in Multiterminal Grids. IEEE Trans. Power Electron. 2022, 37, 7400–7410. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhang, J.; Zhu, M.; Huang, J. Hybrid Input-Series–Output-Series Modular DC–DC Converter Constituted by Resonant and Nonresonant Dual Active Bridge Modules. IEEE Trans. Ind. Electron. 2022, 69, 1062–1069. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Wang, Y.; Zhu, L.; Guan, Y.; Chen, S.-Z.; Zhang, G.; Yang, L. A Dual-Active-Bridge With Half-Bridge Submodules DC Solid-State Transformer for DC Distribution Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1891–1904. [Google Scholar] [CrossRef]
- Mehrabankhomartash, M.; Yin, S.; Kandula, R.P.; Divan, D.; Saeedifard, M. Analysis and Design Guidelines of the Isolated Modular Multilevel DC–DC Converter With the Impact of Magnetizing Inductance. IEEE Trans. Ind. Electron. 2023, 70, 11911–11922. [Google Scholar] [CrossRef]
- Li, B.; Wang, Y.; Jiao, Y.; Zhao, X.; Suo, Z.; Li, R.; Xu, D. Bidirectional Hybrid Isolated DC Transformer for All-DC Collection and Transmission System. IEEE Trans. Power Electron. 2025, 40, 11598–11615. [Google Scholar] [CrossRef]
- Kanaparthi, R.K.; Singh, J.P.; Ballal, M.S. A Review on Multi-Port Bidirectional Isolated and Non-Isolated DC-DC Converters for Renewable Applications. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Rouzbehi, K.; Heidary Yazdi, S.S.; Shariati Moghadam, N. Power Flow Control in Multi-Terminal HVDC Grids Using a Serial-Parallel DC Power Flow Controller. IEEE Access 2018, 6, 56934–56944. [Google Scholar] [CrossRef]
- Mu, Q.; Liang, J.; Li, Y.; Zhou, X. Power Flow Control Devices in DC Grids. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Jovcic, D.; Hajian, M.; Zhang, H.; Asplund, G. Power Flow Control in DC Transmission Grids Using Mechanical and Semiconductor Based DC/DC Devices. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; pp. 1–6. [Google Scholar]
- Zhang, S.; Li, B.; Wang, W.; Zhang, Y.; Xu, D.; Li, G.; Liang, J. A Hybrid Modular Interline Current Flow Controller for Meshed HVDC Grids. IEEE Trans. Ind. Electron. 2022, 69, 10055–10065. [Google Scholar] [CrossRef]
- Barker, C.D.; Whitehouse, R.S. A Current Flow Controller for Use in HVDC Grids. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; pp. 1–5. [Google Scholar]
- Sau-Bassols, J.; Prieto-Araujo, E.; Gomis-Bellmunt, O.; Hassan, F. Series Interline DC/DC Current Flow Controller for Meshed HVDC Grids. IEEE Trans. Power Deliv. 2018, 33, 881–891. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, M.; Li, Y.; Wang, S.; Wang, H.; Cai, X. Modular Interline DC Power Flow Controller. IEEE Trans. Power Electron. 2020, 35, 11707–11719. [Google Scholar] [CrossRef]
- Abbasipour, M.; Liang, X. Power Flow Study of MT-HVDC Grid Compensated by Multiport Interline DC Power Flow Controller. IEEE Trans. Ind. Appl. 2023, 59, 4786–4796. [Google Scholar] [CrossRef]
- Guo, H.; Chen, W.; Zhu, Y.; Zhu, M. An Expandable Interline DC Power Flow Controller. IEEE Trans. Power Electron. 2024, 39, 826–836. [Google Scholar] [CrossRef]
- Tuo, C.; Xu, Q.; Hu, J.; Guo, P.; Li, Y.; Xiao, M.; Guerrero, J.M. Decoupling and Phase Shift Control Method of Modular Interline DC Power Flow Controller. IEEE Trans. Power Deliv. 2024, 39, 661–674. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, M.; Chi, Y.; Liu, S.; Cai, X. Composite DC Power Flow Controller. IEEE Trans. Power Electron. 2020, 35, 3530–3542. [Google Scholar] [CrossRef]
- Yao, Z.; Lei, X.; Du, X. A Comprehensive Review of Condition Monitoring Technologies for Modular Multilevel Converter (MMC) HVDC Systems. Electronics 2025, 14, 3462. [Google Scholar] [CrossRef]
- Deng, F.; Liu, C.; Chen, Z. Control of MMCs. In Modular Multilevel Converters: Control, Fault Detection, and Protection; IEEE: Piscataway, NJ, USA, 2023; pp. 29–102. ISBN 978-1-119-87561-1. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| MMC rated capacity | 2 MVA | MMC switching frequency | 1 kHz |
| MMC rated AC line voltage | 10 kV | MMC SM capacitor | 1.8 mF |
| MMC rated DC voltage | 20 kV | MMC SM capacitor voltage | 1666 V |
| MMC SM number | 12 | MMC arm inductor | 0.050 p.u. |
| PFCM switching frequency | 1 kHz | PFCM capacitor | 1.8 mF |
| Line1 resistor R1 | 0.060 p.u. | Line1 inductor L1 | 0.075 p.u. |
| Line2 resistor R2 | 0.040 p.u. | Line2 inductor L2 | 0.050 p.u. |
| Line3 resistor R3 | 0.020 p.u. | Line3 inductor L3 | 0.025 p.u. |
| Condition I | Uo1/kV | Uo2/kV | Io1/A | Io2/A |
| Theoretical value | 20.03 | 20.03 | 33.36 | 16.56 |
| Simulation value | 20.03 | 20.03 | 33.70 | 16.15 |
| Condition II | Uo1/kV | Uo2/kV | Io1/A | Io2/A |
| Theoretical value | 20.06 | 20.02 | 39.88 | 9.99 |
| Simulation value | 20.06 | 20.02 | 39.88 | 9.92 |
| Condition III | Uo1/kV | Uo2/kV | Io1/A | Io2/A |
| Theoretical value | 20.12 | 19.99 | 54.68 | −5.00 |
| Simulation value | 20.12 | 19.99 | 54.68 | −5.06 |
| Condition I | Condition II | Condition III | |
|---|---|---|---|
| Theoretical value of UC0 | 0 V | 19.6 V | 64.2 V |
| Simulation value of UC0 | 0 V | 19.6 V | 64.0 V |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| MMC rated capacity | 2 kVA | MMC SM switching frequency | 1 kHz |
| MMC rated AC line voltage | 120 V | MMC SM capacitor | 1.8 mF |
| MMC rated DC voltage | 240 V | MMC SM bus voltage | 60 V |
| MMC SM number | 4 | MMC arm inductor | 2 mH |
| PFCM switching frequency | 1 kHz | PFCM capacitor | 1.8 mF |
| Line1 resistance R1 | 5 Ω | Line1 inductance L1 | 1.2 mH |
| Line2 resistance R2 | 1 Ω | Line2 inductance L2 | 1.2 mH |
| DC voltage source Vdc | 220 V |
| Condition 1 | Uo1/V | UO2/V | IO1/A | IO2/A |
| Theoretical Value | 241 | 224 | 2.08 | 2.23 |
| Experimental Value | 248 | 230 | 1.97 | 2.24 |
| Condition 2 | Uo1/V | UO2/V | IO1/A | IO2/A |
| Theoretical Value | 248 | 223 | 2.72 | 1.35 |
| Experimental Value | 254 | 228 | 2.57 | 1.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Zang, J.; Gu, H.; Zeng, G.; Wu, W.; Chen, W.; Zhai, C. A Three-Terminal Modular-Multilevel-Converter-Based Power Electronic Transformer with Reduced Voltage Stress for Meshed DC Systems. Electronics 2025, 14, 4192. https://doi.org/10.3390/electronics14214192
Cai H, Zang J, Gu H, Zeng G, Wu W, Chen W, Zhai C. A Three-Terminal Modular-Multilevel-Converter-Based Power Electronic Transformer with Reduced Voltage Stress for Meshed DC Systems. Electronics. 2025; 14(21):4192. https://doi.org/10.3390/electronics14214192
Chicago/Turabian StyleCai, Haiqing, Jiajie Zang, Haohan Gu, Guohui Zeng, Wencong Wu, Wei Chen, and Chunyang Zhai. 2025. "A Three-Terminal Modular-Multilevel-Converter-Based Power Electronic Transformer with Reduced Voltage Stress for Meshed DC Systems" Electronics 14, no. 21: 4192. https://doi.org/10.3390/electronics14214192
APA StyleCai, H., Zang, J., Gu, H., Zeng, G., Wu, W., Chen, W., & Zhai, C. (2025). A Three-Terminal Modular-Multilevel-Converter-Based Power Electronic Transformer with Reduced Voltage Stress for Meshed DC Systems. Electronics, 14(21), 4192. https://doi.org/10.3390/electronics14214192







